Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

364 CHAPTER 4

■

Logarithmic Functions and Exponential Models

(d) Use the model to estimate the light intensity at the surface.

(e) Make a scatter plot of the data, and graph the function that you found in part (a) on

your scatter plot.

Depth (ft) Light intensity (lm)

5 13.0

10 7.6

15 4.5

20 2.7

Depth (ft) Light intensity (lm)

25 1.8

30 1.1

35 0.5

40 0.3

4.5 Exponential Equations: Getting Information

from a Model

CSI Miami

■

Solving Exponential and Logarithmic Equations

■

Getting Information from Exponential Models:

Population and Investment

■

Getting Information from Exponential Models:

Newton’s Law of Cooling

■

Finding the Age of Ancient Objects: Radiocarbon Dating

IN THIS SECTION… we learn how to get information from an exponential model about

the situation being modeled. Getting this information requires us to solve exponential

equations.

The applications of algebra range over every field of human endeavor in which quan-

titative problems arise. In this section we see how algebra is used in crime scene in-

vestigations. One of the key pieces of evidence in any homicide case is the time of

death; this is often determined by comparing the temperature of the victim’s body

with normal body temperature. As a warm object cools, its temperature decreases

with time according to an exponential model. Using this model, we can find the tem-

perature of a cooling object if we know the initial temperature and the length of time

it has been cooling. When a homicide victim is discovered, we know the initial tem-

perature of the body (normal body temperature) and can measure the current body

temperature; we need to find the time when the body started to cool (the time of

death). So here is the situation:

■

The model gives us the temperature of a body if we know how long the

body has been cooling.

■

We want to find out how long the body has been cooling if we know its

current temperature.

We can get the information we want from the model; to do so, we need to solve an

equation involving exponential functions. So we start this section by learning how to

solve such equations.

Robert Voets/CBS Photo Archive via Getty Images

SECTION 4.5

■

Exponential Equations: Getting Information from a Model 365

■ Solving Exponential and Logarithmic Equations

An exponential equation is one in which the variable occurs in the exponent. For

example,

is an exponential equation. To solve this equation, we take the logarithm of each side

and then use the Laws of Logarithms to “bring down x” from the exponent as follows.

Given equation

Take the log of each side

Law 3: “Bring down the exponent”

Divide by

Calculator

The method we used to solve this equation is typical of how we solve exponential

equations in general.

x L 3.17

log 2 x =

log 9

log 2

x log 2 = log 9

log 2

= log 9

= 9

example

Solving Exponential Equations

Solve the exponential equation for the unknown x.

Solution

We first put the exponential term alone on one side of the equation.

Given equation

Divide by 5

Take the log of each side

Law 3: “Bring down the exponent”

Divide by

Calculator

Substituting into the original equation and using a calcu-

lator, we get .

■ NOW TRY EXERCISE 7 ■

2.848

L 36

x = 2.848

✓ CHECK

x L 2.848

log 2 x =

log 7.2

log 2

x log 2 = log 7.2

log 2

= log 7.2

= 7.2

= 36

example

Solving Exponential Equations

Solve the exponential equation for the unknown x.

Solution

To put the exponential term alone on one side of the equation, we divide each side

by .3

= 512

366 CHAPTER 4

■

Logarithmic Functions and Exponential Models

example

Solving Exponential Equations

Solve the exponential equation for the unknown x.

Solution 1 Algebraic

Since the exponential term is alone on one side, we begin by taking the logarithm of

each side. (We take the natural logarithm because the base in the equation is e.)

Given equation

Take ln of each side

Property of ln

Subtract 3

Multiply by

Calculator

Solution 2 Graphical

We graph the equations

in the same viewing rectangle, as in Figure 1. The solution occurs where the graphs

intersect. Zooming in on the point of intersection of the two graphs, we see that

■ NOW TRY EXERCISE 21 ■

x L 0.807

y = e

3 -2x

andy = 4

x L 0.807

x =-

1- 3 + ln 42

- 2x =-3 + ln 4

3 - 2x = ln 4

ln e

3 -2x

= ln 4

3 -2x

= 4

3 -2x

= 4

y=4

y=e

3_2x

figure 1

Given equation

Divide each side by

Rules of Exponents

Take the log of each side

Law 3: “Bring down the exponent”

Solve for x

Calculator

We substitute into each side of the original equation and

use a calculator:

✓

■ NOW TRY EXERCISE 15 ■

LHS = RHS

RHS:512

= 512

6.36

L 554,000

LHS:8

= 8

6.36

L 554,000

x = 6.36

✓ CHECK

x L 6.36

x =

log 512

logA

x log

= log 512

logA

= log 512

= 512

Rules of Exponents are

reviewed in Algebra Toolkits A.3

and A.4, pages T14 and T20.

SECTION 4.5

■

Exponential Equations: Getting Information from a Model 367

example

Solving Logarithmic Equations

Solve the following logarithmic equations for the unknown x.

(a)

(b)

(c)

Solution

(a) We first isolate the logarithm term.

Given equation

Divide by 2

Exponential form

Calculator

(b) We first combine the logarithm terms using the Laws of Logarithms.

Given equation

Laws of Logarithms

Exponential form

Divide by 5

Subtract 1

Calculator

We substitute into each side of the original equation:

✓

LHS = RHS

RHS:

1

LHS:ln1- 0.46 + 12+ ln 5 = ln 0.54 + ln 5 = ln10.54

52= ln 2.7 L 1

x =-0.46

✓ CHECK

x L-0.46

x =

- 1

x + 1 =

5 1x + 12= e

ln 51x + 1 2= 1

ln1x + 12+ ln 5 = 1

x L 31.62

x = 10

3>2

log x =

2 log x = 3

log1x + 12- log x = 2

ln1x + 12+ ln 5 = 1

2 log x = 3

We can also solve logarithmic equations, that is, equations in which a logarithm

of the unknown occurs. For example, is a logarithmic equation. To

solve for x, we write the equation in exponential form:

Given equation

Exponential form

Solve for x

The first step in solving logarithmic equations is to combine all logarithm terms in

the equation into one term (by using the Laws of Logarithms).

x = 32 - 2 = 30

x + 2 = 2

log

1x + 2 2= 5

log

1x + 2 2= 5

368 CHAPTER 4

■

Logarithmic Functions and Exponential Models

Given equation

Laws of Logarithms

Exponential form

Multiply by x

Subtract x and switch sides

Divide by 99

We substitute into each side of the original equation:

✓

■ NOW TRY EXERCISES 29, 35, AND 37 ■

The equation in the next example cannot be solved algebraically, because it is

impossible to put x alone on one side of the equation, so we can only solve the equa-

tion graphically.

LHS = RHS

RHS:2

LHS:logA

+ 1B- log

= log

100

- log

= logA

100

B= log 100 = 2

x =

✓ CHECK

x =

99x = 1

x + 1 = 100x

x + 1

= 10

log

x + 1

= 2

log1x + 12- log x = 2

example

Solving a Logarithmic Equation Graphically

Solve the equation for the unknown x.

Solution

We first move all terms to one side of the equation:

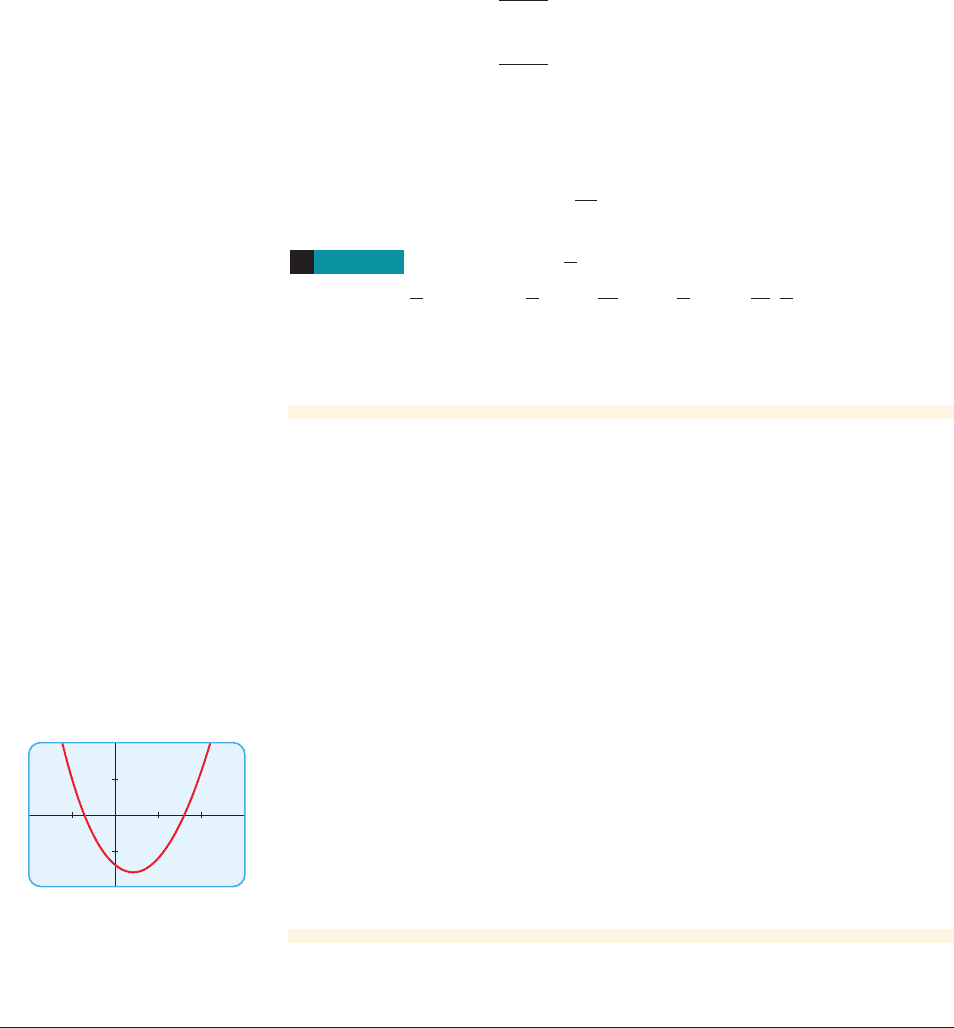
Then we graph

as in Figure 2. The solutions are the x-intercepts of the graph. Zooming in on the

x-intercepts, we see that there are two solutions: and .

■ NOW TRY EXERCISE 41 ■

x L 1.60x L-0.71

y = x

- 2 ln1x + 2 2

- 2 ln1x + 2 2= 0

= 2 ln1x + 22

figure 2

■ Getting Information from Exponential Models:

Population and Investment

We can use logarithms to determine when quantities that grow or decay exponen-

tially reach a given level. In the next two examples we solve exponential equations

involving interest on an investment and population growth.

SECTION 4.5

■

Exponential Equations: Getting Information from a Model 369

example

Investment Growth

Helen invests $10,000 in a high-yield uninsured certificate of deposit that pays 12%

interest annually, compounded every 6 months.

(a) Find a formula for the amount A of the certificate after t years.

(b) What is the amount after 3 years?

Solution

(a) We use the formula for compound interest (Section 3.1, page 265), where the

principal P is 10,000, the interest rate r is 0.12, and the number of

compounding periods n is 2:

Compound interest formula

Substitute given values

Simplify

(b) Using the formula we found in part (a) and replacing t by 3, we get

Replace t by 3

So in 3 years the certificate is worth $14,185.20.

needed to achieve this amount. We use the formula from part (a):

Formula

Replace by 25,000

Divide by 10,000

Take the log of each side

Law 3: “Bring down the exponent”

Divide by 2 log(1.06)

Calculator

It will take almost 8 years for Helen’s investment to grow to $25,000.

■ NOW TRY EXERCISE 49 ■

t L 7.863

log 2.5

2 log11.06 2

= t

log 2.5 = 2t log11.062

log 2.5 = log11.062

2.5 = 11.062

A1t 2 25,000 = 10,00011.06 2

A1t 2= 10,00011.062

= 14,185.20

A1t 2= 10,000 11.062

2132

A1t 2= 10,000 11.062

A1t 2= 10,000 a1 +

0.12

A1t 2= P a1 +

example

Doubling the Population of the World

On January 1, 2007, the population of the world was approximately 6.6 billion and

was increasing by 1.36% every year. Assume that this rate of increase continues.

(a) Find a function P that models the population after t years.

(b) What does the model predict for the population in 2015?

The rate at which a hot cup of

coffee cools is proportional to the

temperature difference between

the cup and its surroundings.

370 CHAPTER 4

■

Logarithmic Functions and Exponential Models

■ Getting Information from Exponential Models: Newton’s Law of Cooling

When a hot object, such as a cup of coffee, is left to cool, its temperature decreases

continuously at a rate proportional to the temperature difference between the object

and its surroundings. Since this difference is continually changing, the rate at which

the object cools is also continually changing. Newton’s Law of Cooling states that

the temperature T of a cooling object is modeled by

where t is the time since the object began cooling, I is the initial temperature of the ob-

ject, A is the ambient temperature (the temperature of the surroundings), and k is a con-

stant that depends on the type of object; k is called the heat transfer coefficient.

Newton’s Law of Cooling is a powerful tool in many crime scene investigations.

For example, in the infamous 1994 O.J. Simpson case two key pieces of evidence—

a cup of ice cream and a bathtub full of warm water—could have provided com-

pelling evidence for the time of death. According to court testimony, “the first offi-

T = A + 1I - A2e

-kt

Solution

(a) We use the exponential growth model (Section 3.1, page 250)

where C is the initial population and a is the growth factor. Since the popula-

tion increases by 1.36% every year, the growth factor is

. So the model we seek is

Exponential growth model

where t is the number of years after 2007.

(b) The year 2015 is eight years after 2007. Replacing t by 8 in the model we get

So the model predicts a population of about 7.35 billion in 2015.

other words, we want to find the value of t for which P(t) is 13.2 billion.

Substituting these values into the formula gives the following:

Exponential growth model

Replace P(t) by 13.2

Divide by 6.6

Take the log of each side

Law 3: “Bring down the exponent”

Divide by log 1.0136

Calculator

So it will take about 51 years for the population to double. This would happen

in the year .

■ NOW TRY EXERCISE 55 ■

2007 + 51 = 2058

t L 51.3

log 2

log 1.0136

= t

log 2 = t log 1.0136

log 2 = log11.01362

2 = 11.0136 2

13.2 = 6.611.01362

P1t 2= 6.611.01362

216.6 2= 13.2

P18 2= 6.611.01362

L 7.35

P1t 2= 6.611.01362

a = 1 + 0.0136 = 1.0136

P1t 2= Ca

SECTION 4.5

■

Exponential Equations: Getting Information from a Model 371

example

Crime Scene Investigation

Police officers arrive at a crime scene and find a tub full of warm water. A ther-

mometer shows that the water temperature is and the air temperature is .

It is known that most people fill a tub with water at .

(a) Use Newton’s Law of Cooling to model the temperature of the water in the

tub. (Measure t in minutes and use the heat transfer coefficient .)

(b) How long has the bathtub been cooling?

Solution

(a) We use Newton’s Law of Cooling, where the initial temperature I is , the

ambient temperature A is , and the heat transfer constant k is 0.018.

Newton’s Law of Cooling

Replace A by 70, I by 100, and k by 0.018

Simplify

(b) We know that the temperature of the bathtub water is , so we use the

model from part (a), replace T by 76, and solve the resulting exponential

equation for t.

Model

Replace T by 76

Subtract 70

Divide by 30

Take ln of each side

Divide by 0.018 and switch sides

Calculator

So the tub has been cooling for about 89 minutes.

■ NOW TRY EXERCISE 57 ■

t L 89.41

t =

ln 0.20

- 0.018

ln 0.20 =-0.018t

0.20 = e

-0.018t

6 = 30e

-0.018t

76 = 70 + 30e

-0.018t

T = 70 + 30e

-0.018t

76°F

T = 70 + 30e

-0.018t

T = 70 + 1100 - 702e

-0.018t

T = A + 1I - A 2e

-kt

70°F

100°F

k = 0.018

100°F

70°F76°F

cer on the scene did not test the temperature of the water in . . . [the] bathtub or pick

up the cup of melting ice cream.” In the next example we investigate how bathtub

temperature could help to determine the time when the tub was filled.

■ Finding the Age of Ancient Objects: Radiocarbon Dating

In the next example we examine how exponential equations are used to determine

the ages of ancient artifacts. Before the twentieth century archeologists had a hard

time determining the ages of the objects they found. It’s difficult to tell whether a

shard of pottery was dropped on the ground 50 years ago or 50 centuries ago. So

archeologists generally used the principle that the deeper they had to dig to find an

object, the older it probably was and that objects found at the same level, or stratum,

372 CHAPTER 4

■

Logarithmic Functions and Exponential Models

IN CONTEXT ➤

The iceman

example

Dating the Iceman

Tissue samples from the iceman indicated that his body had 57.67% of the carbon-14

that is present in a living person. Use the fact that the half-life of carbon-14 is 5730

years to estimate how long ago the iceman died.

Solution

The formula for exponential decay is

where C is the initial mass of the radioactive substance, h is its half-life, and m(t) is

the mass remaining at time t (see Example 9 in Section 3.1). We are looking for the

time t at which m(t) is 57.67% of the initial mass of carbon-14 in the iceman’s body,

that is, m(t) is 0.5767C. We now substitute the known values into the formula and

solve for t.

Radioactive decay formula

Substitute given values

Divide by C

Take the log of each side

Law 3: “Bring down the exponent”

Multiply by 5730, divide by

Calculator

So the iceman died about 4550 years ago.

■ NOW TRY EXERCISE 65 ■

t L 4550

logA

5730 log 0.5767

logA

= t

log 0.5767 =

5730

logA

log 0.5767 = logA

t>5730

0.5767 = A

t>5730

0.5767C = C˛ A

t>5730

m1t 2= C˛ A

t>h

m1t 2= C˛ A

t>h

were close in age. This was helpful in comparing the relative ages of two items, but

how could they get the actual age? And how could they compare the ages of items

found at sites 50 miles apart? The discovery that radioactive decay is exponential al-

lowed scientists to determine the age of ancient objects by comparing the amount of

radioactive carbon-14 in the object to the amount it normally would have today.

A dramatic use of radiocarbon dating occurred with the discovery of the “iceman.”

On September 19, 1991, Erika and Helmut Simon were hiking in the Alps near the

Austrian-Italian border. As they approached an ice-filled depression, they were sur-

prised to see the frozen body of a man sticking halfway out of the ice. They reported

the find to authorities, thinking that it was a recent tragic accident. But the authorities

were baffled by the find because of the frozen man’s unusual goatskin leather clothing

and the bronze ax and quiver of arrows strapped to his body. Who was this “iceman”?

Where did he come from? To answer these questions, the primary piece of information

needed was the date of the iceman’s demise. The surprising answer, which we calcu-

late in the next example, was that he lived in the Neolithic Age (Late Stone Age).

How does radiocarbon dating work? Plants absorb radioactive carbon-14 from the

atmosphere, which then makes its way into animals through the food chain. Thus, all

living creatures contain the same fixed proportion of carbon-14 to nonradioactive

carbon-12 as is in the atmosphere. After an organism dies, it stops assimilating

carbon-14, and the carbon-14 in it begins to decay exponentially. We can then deter-

mine the time elapsed since death by measuring the amount of carbon-14 left in the relic.

SECTION 4.5

■

Exponential Equations: Getting Information from a Model 373

4.5 Exercises

CONCEPTS

Fundamentals

1. Let’s solve the exponential equation .

(a) First, we isolate to get the equivalent equation

______________.

(b) Next, we take ln of each side to get the equivalent equation

______________.

2. Let’s solve the logarithmic equation .

(a) First, we combine the logarithms to get the equivalent equation

______________.

(b) Next, we write each side in exponential form to get the equivalent equation

______________.

_______.

Think About It

3. To solve the exponential equation , we first take logarithms of both sides.

What base logarithm leads to the easiest solution? Why does this base work so nicely?

4. Logarithms with any base work equally well to solve the equation . Why? First

solve the equation using common logarithms, and then solve the equation using natural

logarithms. Now use a logarithm with a different base to solve the equation. (You will need

to use the Change of Base Formula in the solution.) Do you always get the same answer?

5–18

■ Solve the exponential equation for the unknown x.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19–26

■ Solve the exponential equation (a) algebraically and (b) graphically.

19. 20.

21. 22.

23. 24.

25. 26.

27–40

■ Solve the logarithmic equation for the unknown x.

27. 28.

29. 30.

31. 32.

33. 34.

35. 36.

37. 38.

39. 40. log 2x = log 2 + log13x - 42ln 5 + ln1x - 22= ln13x 2

log

1x + 12- log

1x - 12= 2log

x - log

1x - 32= 2

log

13x - 12+ log

8 = 5log12x + 12+ log 2 = 2

4 log

13x + 52= 2log1x - 42= 3

ln 3x =-4log

8x =-2

2 log

x = 13 log x = 12

log x = 7log

x = 10

= 3

= 212

x>2

= 5

1 - x

= 6

= 342

1 - x

= 3

= 10e

= 5

13.2 2

= 35

12.6 2

= 4

x + 1

= 50

= 21

4x - 1

= 52

3x + 1

= 34

2x + 1

= 2003

1 - 4x

= 2

= 122e

12x

= 17

= 425

= 7

= 710

= 25

= 4

= 2

x + 1

log 3 + log1x - 22= log x

x =

= 50

SKILLS