Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

544 CHAPTER 6

■

Power, Polynomial, and Rational Functions

19–26

■ A rational function is given. Find all horizontal and vertical asymptotes of its

graph.

19. 20.

21. 22.

23. 24.

25. 26.

27–32

■ Use transformations of the graph of the reciprocal function to graph the

rational function, as in Example 1.

27. 28.

29. 30.

31. 32.

33–40 ■ Find the intercepts and asymptotes, and then sketch a graph of the rational

function. Use a graphing calculator to confirm your answer.

33. 34.

35. 36.

37. 38.

39. 40.

41. Focusing a Camera Lens A camera has a lens of fixed focal length F. To focus on an

object located a distance x from the lens, the film must be placed a distance y behind the

lens, where F, x, and y are related by

(See Example 2.) Suppose the camera has a wide-angle 35-mm lens .

(a) Express y as a function of x, and graph the function.

(b) What happens to the focusing distance y as the object moves farther away from the

lens?

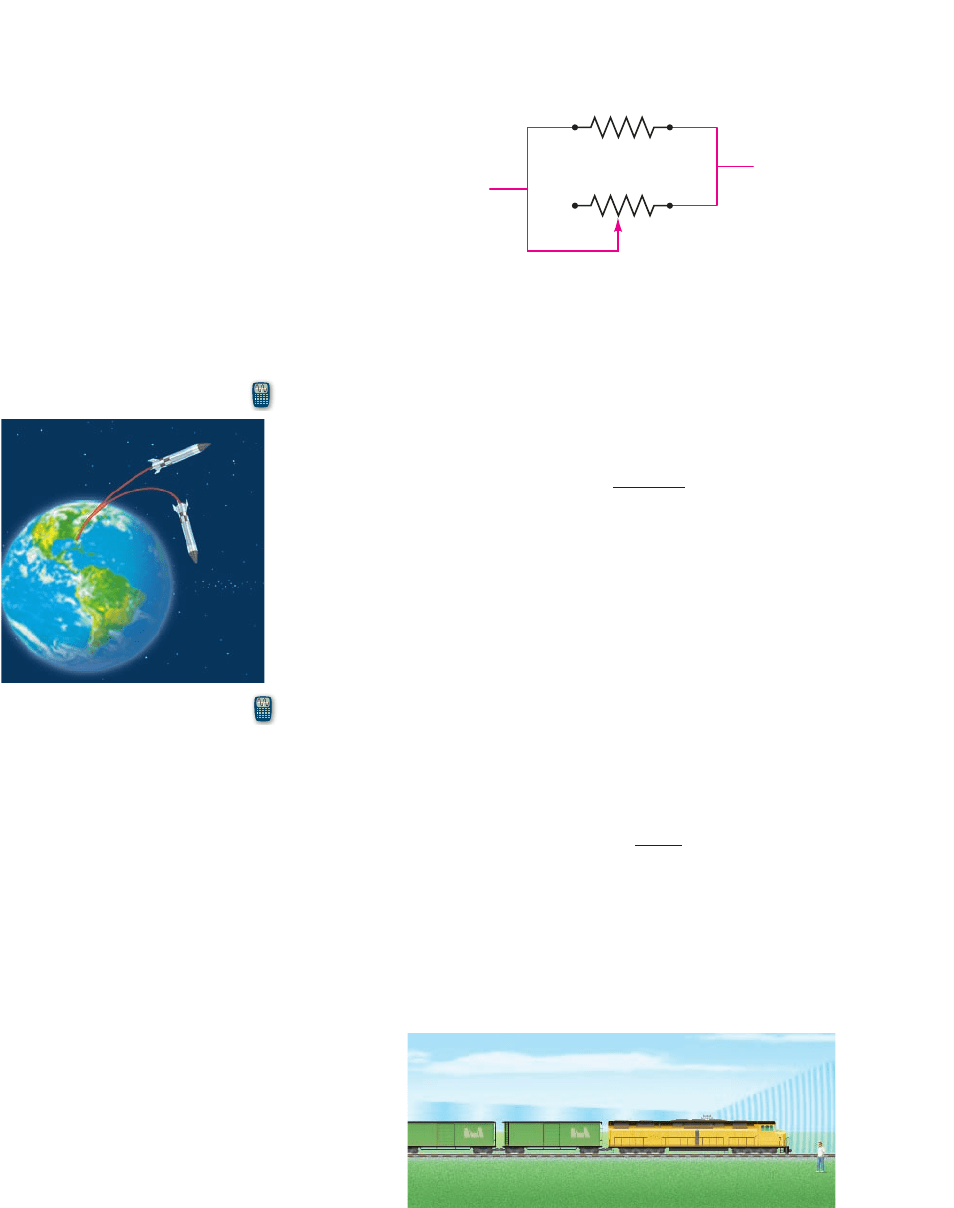
42. Resistors in Parallel When two resistors with resistances and are connected in

parallel, their combined resistance R is given by the formula

R =

+ R

1F = 352

r 1x 2=

+ 2x - 4

+ x

r 1x 2=

+ 10x - 12

+ x - 6

t1x 2=

x + 2

1x + 321x - 1 2

t1x 2=

4x - 8

1x - 421x + 1 2

s1x 2=

x - 2

1x + 12

s1x 2=

1x - 32

r 1x 2=

2x + 6

- 6x + 3

r 1x 2=

4x - 4

x + 2

s1x 2=

3x - 3

x + 2

s1x 2=

2x - 3

x - 2

r 1x 2=

- 2

x - 2

s1x 2=

x + 1

r 1x 2=

x + 4

r 1x 2=

x - 1

y = 1>x

s1x 2=

12x - 121x + 3 2

13x - 121x - 4 2

s1x 2=

15x - 121x + 1 2

13x - 121x + 2 2

s1x 2=

+ 1

+ 2x - 6

s1x 2=

+ 1

+ x - 1

r 1x 2=

2x - 4

+ x + 1

r 1x 2=

+ 2

r 1x 2=

2x - 3

- 1

r 1x 2=

x - 2

CONTEXTS

SECTION 6.6

■

Rational Functions 545

Suppose that a fixed 8-ohm resistor is connected in parallel with a variable resistor, as

shown in the figure. If the resistance of the variable resistor is denoted by x, then the

combined resistance R is a function of x.

8 ohms

(a) Find the function R.

(b) Draw a graph of the function . (Note that R and x must both be positive, so

the viewing rectangle need not contain negative values.) Give a physical

interpretation of the horizontal asymptote.

43. Flight of a Rocket Suppose a rocket is fired upward from the surface of the earth

with an initial velocity (measured in meters per second). Then the maximum height h

(in meters) reached by the rocket is given by the function

where the radius of the earth R is m and the acceleration due to gravity is

9.8 m/s

(a) If the initial velocity of the rocket is 10,400 m/s, what is the maximum height

reached by the rocket?

(b) Use a graphing calculator to draw a graph of the function . (Note that y and

must both be positive, so the viewing rectangle need not contain negative values.)

What does the vertical asymptote represent physically?

44. The Doppler Effect As a train moves toward an observer (see the figure), the pitch of

its whistle sounds higher to the observer than it would if the train were at rest, because

the crests of the sound waves are compressed closer together. This phenomenon is

called the Doppler effect. The observed pitch P is a function of the speed (measured in

m/s) of the train and is given by

where is the actual pitch of the whistle at the source, and the speed of sound in air

is 332 m/s. Suppose that a train has a whistle pitch that is 440 Hz.

(a) If the speed of the train is 30 m/s, what is the observed pitch of the train whistle?

(b) Use a graphing calculator to draw a graph of the function . What does the

vertical asymptote represent physically?

y = P1√2

P1√2= P

- √

√

y = h1√2

g6.4 * 10

h1√2=

R√

2gR - √

√

y = R1x2

546 CHAPTER 6

■

Power, Polynomial, and Rational Functions

If p is the positive rational number , then the power function is

defined by . If n is odd, then the domain of f consists of all real

numbers; but if n is even, then the domain consists of the nonnegative real numbers.

The inverse of the power function with positive integer power n is the

root function .f

-1

1x2= x

1>n

= 1x

f 1x2= x

m>n

= 1x

f 1x2= x

m>n

CHAPTER 6

REVIEW

CONCEPT CHECK

Make sure you understand each of the ideas and concepts that you learned in this chapter,

as detailed below section by section. If you need to review any of these ideas, reread the

appropriate section, paying special attention to the examples.

6.1 Working with Functions: Algebraic Operations

Functions can be added, subtracted, multiplied, or divided. For the functions f and :

■

The sum is the function defined by .

■

The difference is the function defined by .

■

The product is the function defined by .

■

The quotient is the function defined by .

The domains of , , and are the intersections of the domains of f and .

The domain of is the intersection of the domain of f and g, except that we must

remove all the points where is 0.

6.2 Power Functions: Positive Powers

A power function is a function of the form , where C and p are nonzero.

If p is a positive integer, then the shape of the graph of the power function

depends on whether p is odd or even. Graphs of for

3, 4, and 5 are shown in the figure.

p = 1, 2,f 1x2= x

f 1x2= Cx

g1x 2

f>g

gf gf - gf + g

1f>g21x2= f 1x2>g1x 2f>g

1fg21x2= f 1x2

g1x 2f g

1f - g21x 2= f 1x 2- g1x 2f - g

1f + g21x 2= f 1x 2+ g1x 2f + g

CHAPTER 6

y y y y

x x x x

y=x∞

y=x¢

y=x£

y=≈

y=x

y y y y

x x x x

y=œ

∑

∞

∑

CHAPTER 6

■

Review 547

The quantity Q is directly proportional to the quantity R if they are related by

the equation (where k is a nonzero constant called the constant of propor-

tionality). If two real-world quantities are directly proportional, then their relation-

ship can often be modeled by a power function.

6.3 Polynomial Functions: Combining Power Functions

A polynomial function is a function P of the form

where n is a nonnegative integer, are real numbers, and . The

polynomial has degree n, and is its leading term.

The end behavior of a polynomial function is a description of what happens to

its values when x becomes large in the positive and negative directions. A polyno-

mial function has the same end behavior as its leading term.

One way to graph a polynomial function is to proceed as follows:

■

Factor the polynomial into linear factors.

■

Find the zeros of the polynomial from its factors.

■

Use test points to check the sign of the values of the polynomial on each of

the intervals determined by the zeros.

■

Graph the zeros and test points, and complete the graph.

■

Use the end behavior of the polynomial as a final check on the overall shape

of the graph.

6.4 Fitting Power and Polynomial Curves to Data

Real-world data are often best modeled by a power or polynomial function. A graph-

ing calculator or computer software is the most practical way to find such a model.

To see whether a linear, power, or exponential model is most appropriate for a

given data set, we can use a scatter plot, a semi-log plot, and a log-log plot to help

us make the appropriate choice.

6.5 Power Functions: Negative Powers

Power functions in which the power p is negative occur often in the ap-

plications of mathematics. Two such functions (the ones where p is have

graphs that are typical of power functions with negative integer powers:

-1 or - 22

f 1x2= Cx

⫽ 0a

, a

P 1x2= a

+ a

n -1

+ a

x + a

Q = kR

Graph of f 1x 2=

= x

-1

Graph of f 1x 2=

= x

-2

548 CHAPTER 6

■

Power, Polynomial, and Rational Functions

The quantity Q is inversely proportional to the quantity R if they are related by

the equation (where k is a nonzero constant called the constant of propor-

tionality). Many of the laws of science are inverse proportionalities, often inverse

square laws such as the Law of Gravity.

6.6 Rational Functions

A rational function r is a quotient of two polynomials:

Most rational functions have horizontal and/or vertical asymptotes: lines that

the graph of r approaches as we move vertically or horizontally on the graph.

If P and Q are both linear functions then the graph of r can be obtained from the

graph of by shifting, stretching, and reflecting.

A rational function can be expressed in three forms: standard form, factored

form, and compound-fraction form.

To graph a rational function in which P or Q are polynomials of degree 2 or

higher, we first find the following information about the graph:

■

the x- and y-intercepts

■

the vertical asymptotes (by finding the zeros of Q)

■

the horizontal asymptotes (by determining the behavior of y as )

Then we sketch a graph that shows all this information, plot some additional points,

and complete the graph.

x Sq

f 1x2=

r 1x2=

P1x 2

Q1x 2

Q = k>R

REVIEW EXERCISES

1–4 ■ The functions f and are given.

(a) Find the functions , , fg, and and their domains.

(b) Evaluate , , , and at the indicated value, if defined.

addition.

1. ,;32. , ; 0.5

3. ,;14. ,;3

5–8

■ Sketch the graph of the given power function f. Then sketch the graph of on the

same axes by transforming the graph of f.

5. , 6. ,

7. , 8. ,

9–12

■ A statement describing a proportionality is given.

(a) Express the statement as an equation.

(b) Use the given information to find the constant of proportionality.

g1x 2= 1x + 42

1>2

- 2f 1x 2= x

1>2

g1x 2=

- 4f 1x 2= x

g1x 2=-x

+ 1f 1x2= x

g1x 2= 1x + 12

f 1x 2= x

g1x 2= x - 3f 1x 2= 1x + 1

g1x 2= 1x - 1f 1x 2= 1x

g1x 2= 2x + 1f 1x2= x

g1x 2= x - 1f 1x2= 2x

f + gg

f>gfgf - gf + g

f>gf - gf + g

CHAPTER

SKILLS

CHAPTER 6

■

Review 549

9. E is directly proportional to the square of . If , then .

10. F is directly proportional to the fourth power of x. If , then .

11. L is directly proportional to the one-third power of . If , then .

12. h is directly proportional to the cube of w. If , then .

13–14

■ Use the proportionality from the indicated exercise to solve the problem.

13. In Exercise 9 above, find E when is 4.

14. In Exercise 11 above, find when L is 3.

15–22 ■ Sketch a graph of the polynomial function. Make sure your graph shows all x- and

y-intercepts and exhibits the proper end behavior.

15. 16.

17. 18.

19. 20.

21. 22.

23–24

■ A polynomial function P is given.

(a) Graph the polynomial P in the given viewing rectangle.

(b) Find all the local maxima and minima of P.

23. ;

24. ;

25–26

■ A set of data is given.

(a) Use your graphing calculator to find the two indicated types of models for the data.

(b) Graph a scatter plot of the data together with the models.

25. Linear, cubic: 26. Linear, power:

3- 2, 24 by 3- 1, 54P 1x2= x

- 2x

+ 3

3- 3, 44 by 3- 15, 204P 1x 2= 2x

- 3x

- 12x + 10

P 1x 2= 0

P 1x 2= x

- 2x

+ 1P 1x 2= x

+ 3x

- 4

Q1x 2= x

- x

Q1x 2= x

+ 2x

- 4x - 8

P 1x 2= x

- x

- 4x + 4P 1x2=-x

+ 3x

P 1x 2=-1x - 12

1x + 22P 1x 2= x1x + 221x - 12

√

h =

w = 3

L = 36V = 8√

F = 32x = 0.5

E = 9√ = 6√

f 1x 2

1 10

2 32

3 65

4 105

5 154

6 210

7 273

f 1x 2

0 2

1 33

2 48

3 51

4 48

5 45

6 48

7 63

27–28 ■ A set of data is given.

(a) Make semi-log and log-log plots of the data.

(b) From the graphs in part (a), does an exponential or a power model seem appropriate

for the data?

plot of the data.

x y

2 15

4 44

6 80

8 124

10 173

12 229

14 288

16 352

550 CHAPTER 6

■

Power, Polynomial, and Rational Functions

27. 28.

CONNECTING

THE CONCEPTS

x y

1 3.0

10 7.8

20 20.2

30 52.5

40 136.0

29–32 ■ Sketch a graph of the given power function.

29. 30. 31. 32.

33–34

■ A statement describing a proportionality is given.

(a) Express the statement as an equation.

(b) Use the given information to find the constant of proportionality.

33. G is inversely proportional to the cube of r. If , then .

34. n is inversely proportional to the two-thirds power of t. If , then .

35–36

■ Use the proportionality from the indicated exercise to solve the problem.

35. In Exercise 33 above, find G when r is 8.

36. In Exercise 34 above, find t when n is 100.

37–40 ■ Use transformations of the graph of to graph the rational function.

37. 38.

39. 40.

41–44

■ A rational function is given.

(a) Find the x- and y-intercepts of the function.

(b) Find the horizontal and vertical asymptotes of the function.

41. 42.

43. 44.

These exercises test your understanding by combining ideas from several sections in a

single problem.

45. Linear, Exponential, and Power Functions We have studied three classes of

functions that are of particular importance in modeling real-life phenomena:

■

Linear functions:

■

Exponential functions:

■

Power functions:

(a) What type of function is each of the following?

(i) (ii) (iii) h1x2= x

g1x 2= 4xf 1x 2= 4

f 1x2= Cx

f 1x2= Ca

f 1x2= b + mx

s1x 2=

41x + 12

s1x 2=

- x - 2

r 1x 2=

- x + 4

2x + 6

r 1x 2=

2x + 2

x - 1

s1x 2=

x + 1

s1x 2=-

x - 2

r 1x 2=

x - 3

r 1x 2=

x + 2

y = 1>x

n = 40t = 0.125

G = 0.3r = 10

f 1x 2=

f 1x 2= x

-3

f 1x 2=

-2

CHAPTER 6

■

Review 551

x y

1 2

2 5

3 8

4 11

5 14

x y

1 2

2 5

3 12.5

4 31.3

5 78.1

x y

1 2

2 5

3 8.5

4 12.5

5 16.8

(b) One of the functions in part (a) actually belongs to two of the three categories.

Which one? Explain.

exponential, or power function is an appropriate model for the data. Explain how

you arrived at your answer.

table 1 table 2 table 3

(d) Find an appropriate model for each of the data sets in part (c).

46. Inverses of Functions In Section 6.2 we saw that the inverse of the power function

is the power function . In this problem we’ll investigate

the inverses of some of the other types of functions we have studied.

(a) Find the inverse of the linear function . Is the inverse a linear

function? Will this be the case for all nonconstant linear functions?

(b) Find the inverse of the exponential function . Is the inverse an

exponential function? If not, what kind of function is it?

inverse. Is it also a quotient of two linear functions? Will this be the case for all

quotients of two linear functions?

47. Revenue, Cost, and Profit Freebies, Inc. stamps company logos on pens intended

for use by employees and prospective clients. The revenue from an order of

x pens is , and the cost of producing x pens is

(both in dollars).

(a) What algebraic operation must you perform on the functions R and C to get P, the

function that gives the profit from an order on x pens? Find P(1000).

(b) What do the quotient functions and represent?

48. Range of a Projectile The range of a projectile (the horizontal distance it travels

before it hits the ground) is directly proportional to the square of its speed. Jason throws

a ball at 60 mi/h and it lands 242 ft away.

(a) Express the proportionality that relates range R to speed as an equation. What is

the constant of proportionality?

(b) What is Jason’s range if he throws the ball at 70 mi/h?

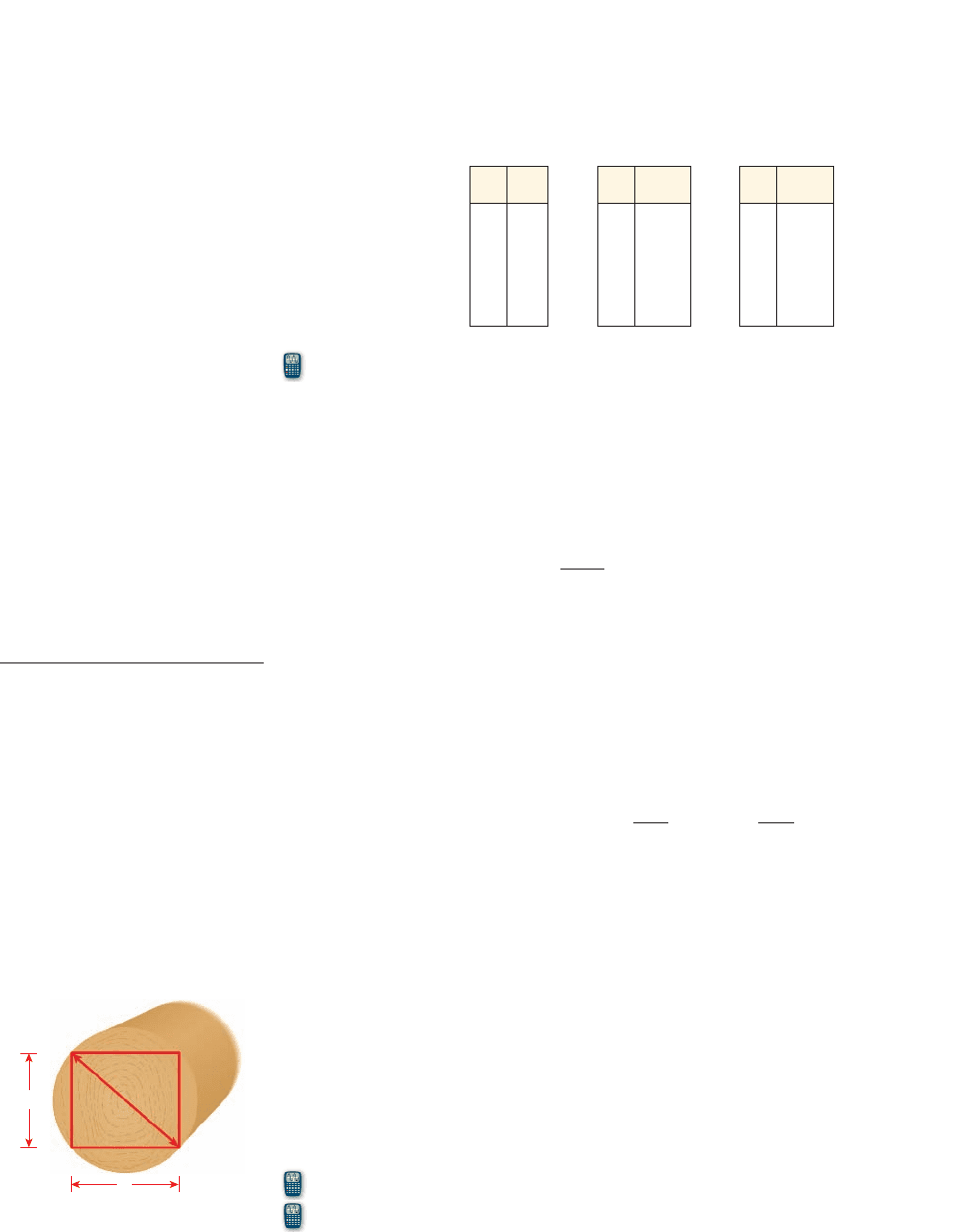
49. Strength of a Beam The strength S of a wooden beam of width x and depth y is

given by the formula . A beam is to be cut from a log of diameter 10 inches,

as shown in the figure.

(a) From Pythagoras’ Theorem we can see that . Use this fact to express

S as a polynomial function of x only.

(b) What is the domain of S (keeping in mind that the distances x and y can’t be

negative)?

(d) Find the width x that will give the beam the maximum possible strength.

+ y

= 10

S = 13.8xy

√

c1x 2=

C1x 2

r 1x 2=

R1x 2

0.00001x

C1x 2= 0.35x -

R1x 2= 0.75x - 0.00002x

f 1x 2=

2 + x

1 - x

f 1x 2= 3

f 1x 2= 3 - 5x

-1

1x 2= x

1>2

f 1x 2= x

1x 7 02

CONTEXTS

10 in.

552 CHAPTER 6

■

Power, Polynomial, and Rational Functions

50. Height of a Baseball A baseball is thrown upward, and its height in feet is measured

at 0.5-second intervals by using a strobe light. The resulting data are given in the table.

(a) Find a quadratic model that best fits the data.

(b) Draw a scatter plot of the data, and graph your model from part (a) on the scatter

plot.

ground?

(d) What is the maximum height attained by the ball?

Time (s) Height (ft)

0 4.2

0.5 26.1

1.0 40.1

1.5 46.0

2.0 43.9

2.5 33.7

3.0 15.8

51. Drug Concentration A drug is administered to a patient, and the concentration of the

drug in her bloodstream is monitored. After t hours the concentration (in mg/L) is

approximated by the rational function

(a) Does the function c have a vertical asymptote? A horizontal asymptote?

(b) From your answers in part (a), determine what happens to the concentration of the

drug in the patient’s bloodstream after a long period of time.

drug in the patient’s bloodstream and the time at which the maximum was reached.

c1t 2=

+ 1

CHAPTER 6

■

Test 553

CHAPTER

TEST

1. Let and . Find the functions , , , and and their

domains. Then find the value of each of these functions at , if the value is defined.

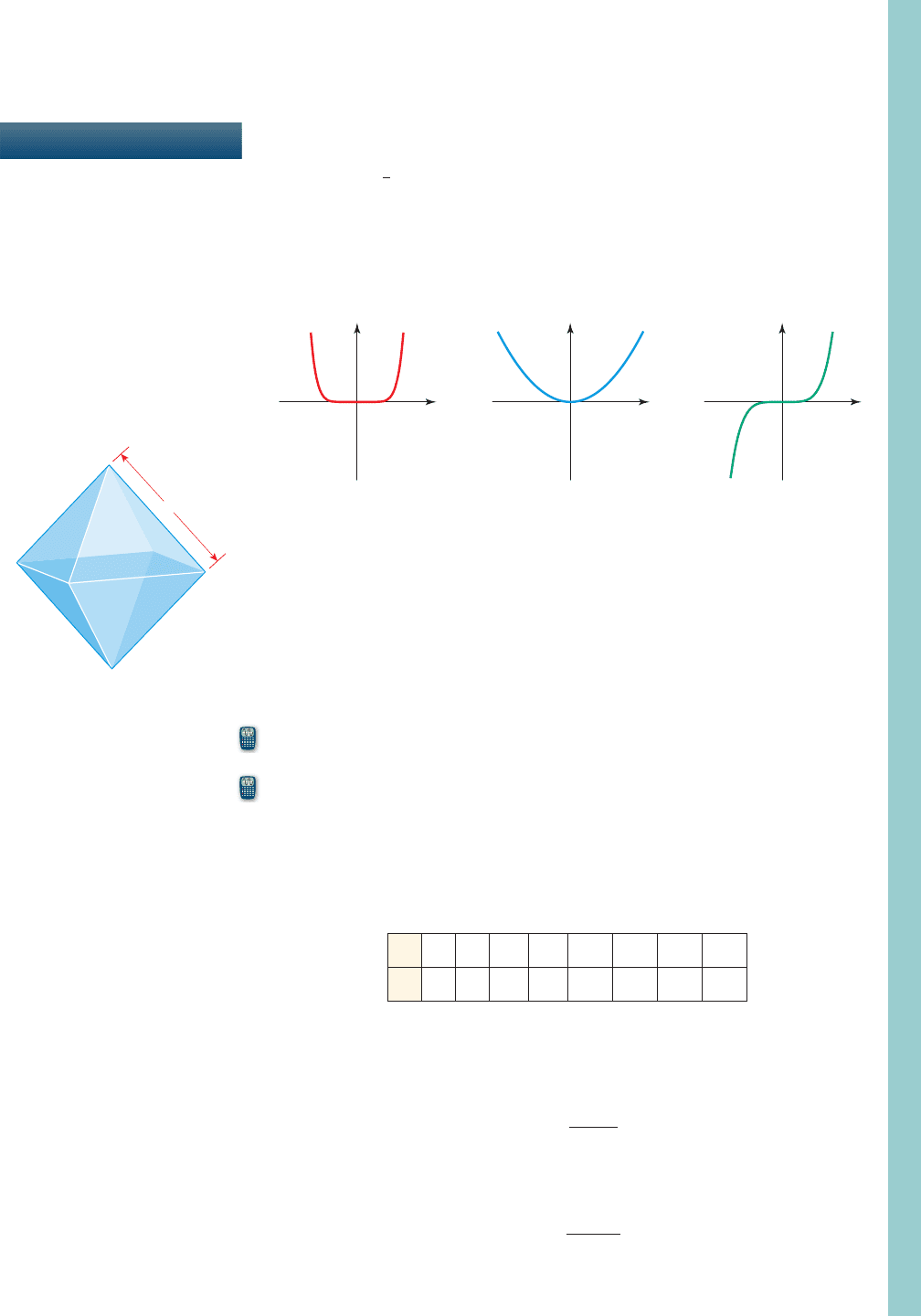
2. The graphs of , , and are shown in the figure.

(a) Match each function with its graph. Give reasons for your answers.

(b) What are the points at which all three graphs intersect?

h1x 2= x

g1x 2= x

f 1x 2= x

x = 1

f>gf gf - gf + gg1x 2= x

- 1f 1x 2= 1x

I II III

3. A regular octahedron is a solid with eight faces, all of them equilateral triangles (see the

figure). The volume of a regular octahedron is proportional to the cube of the length x

of one of its edges.

(a) Express this proportionality as an equation.

(b) A regular octahedron with edges of length 4 cm has volume . Use this

fact to find the constant of proportionality.

4. Sketch a graph of the polynomial function. Make sure your graph shows all x- and

y-intercepts and exhibits the proper end behavior.

(a) (b)

5. For the polynomial Q of Question 4(b), use a graphing calculator to find its local

maximum and minimum values and the values of x at which they occur.

6. The table gives a set of data.

(a) Make semi-log and log-log plots of the data. On the basis of your graphs, determine

whether an exponential model or a power model is more appropriate for the data.

(b) Use a graphing calculator to find an appropriate model for the data.

scatter plot. Does the function seem to fit the data well?

Q1x 2= x

- 3x

- 4P 1x 2= 1x - 12

1x + 22

30.17 cm

x 1 2 5 7 23 44 58 80

y 1 3 11 19 108 287 439 710

7. (a) Sketch a graph of the reciprocal function .

(b) By transforming the graph of the reciprocal function, sketch a graph of the rational

function

8. Find the x- and y-intercepts and the horizontal and vertical asymptotes of the following

rational function. Then sketch its graph.

r 1x 2=

x + 1

- 2x

r 1x 2=

2x - 5

x - 2

f 1x 2= 1>x