Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

(b) Use a graphing calculator to graph the surge functions for the

following values of b: 0.70, 0.60, 0.50. Sketch the graphs you obtain on

the graph in part (a).

2. (a) What is the maximum value of each of the six surge functions in Question

1? Where does the maximum value of each function occur? Use your

answers to complete the following table.

S1t 2= 2t

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

2. (a) What is the maximum value of each of the six surge functions in Question

1? Where does the maximum value of each function occur? Use your

answers to complete the following table.

Maximum

value

Maximum value

occurs at t ⴝ ?

1.0 2.8

(b) Describe how the maximum value changes as the value of a increases.

II. Experimenting with the Surge Function: Varying b

We now experiment with how changing the value of b affects the graph of a surge

function.

1. Let’s pick a particular value for a, say 2, and experiment with changing the

value of b.

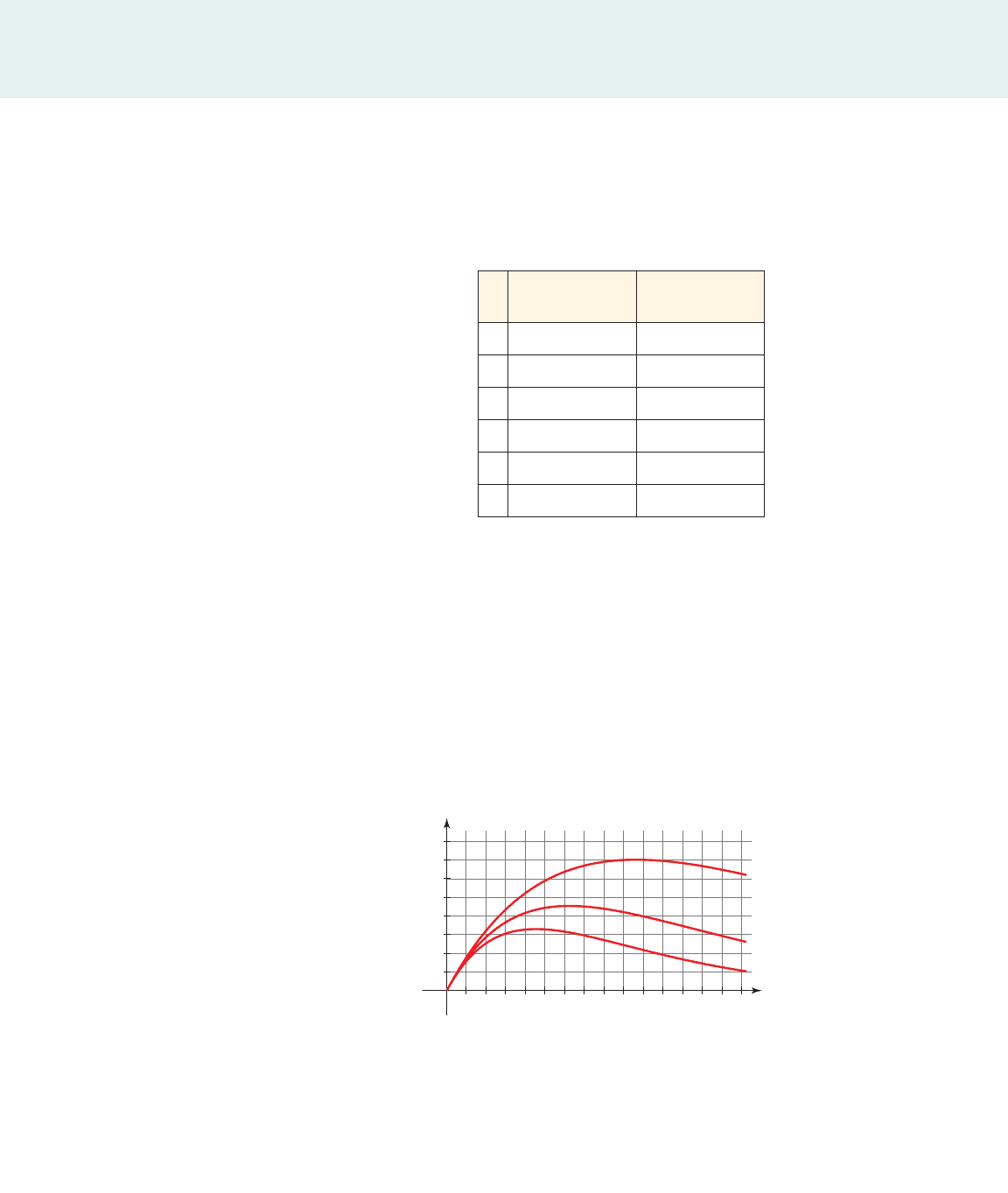
(a) Graphs of the following surge functions are shown:

Match each function with its graph.

1t 2= 2t

10.902

S

1t 2= 2t

10.85 2

S

1t 2= 2t

10.80 2

S(t)

123456789101112131415

564 CHAPTER 6

Surge functions S1t 2= at

10.7 2

(b) Describe how the maximum value changes as the value of b increases.

III. Modeling the Alcohol Data

Let’s use a surge function to model the alcohol data in the Prologue (page P2). Those

data give the blood alcohol concentration at various times following the consumption

of different amounts of alcohol. The first two columns of that table are reproduced here.

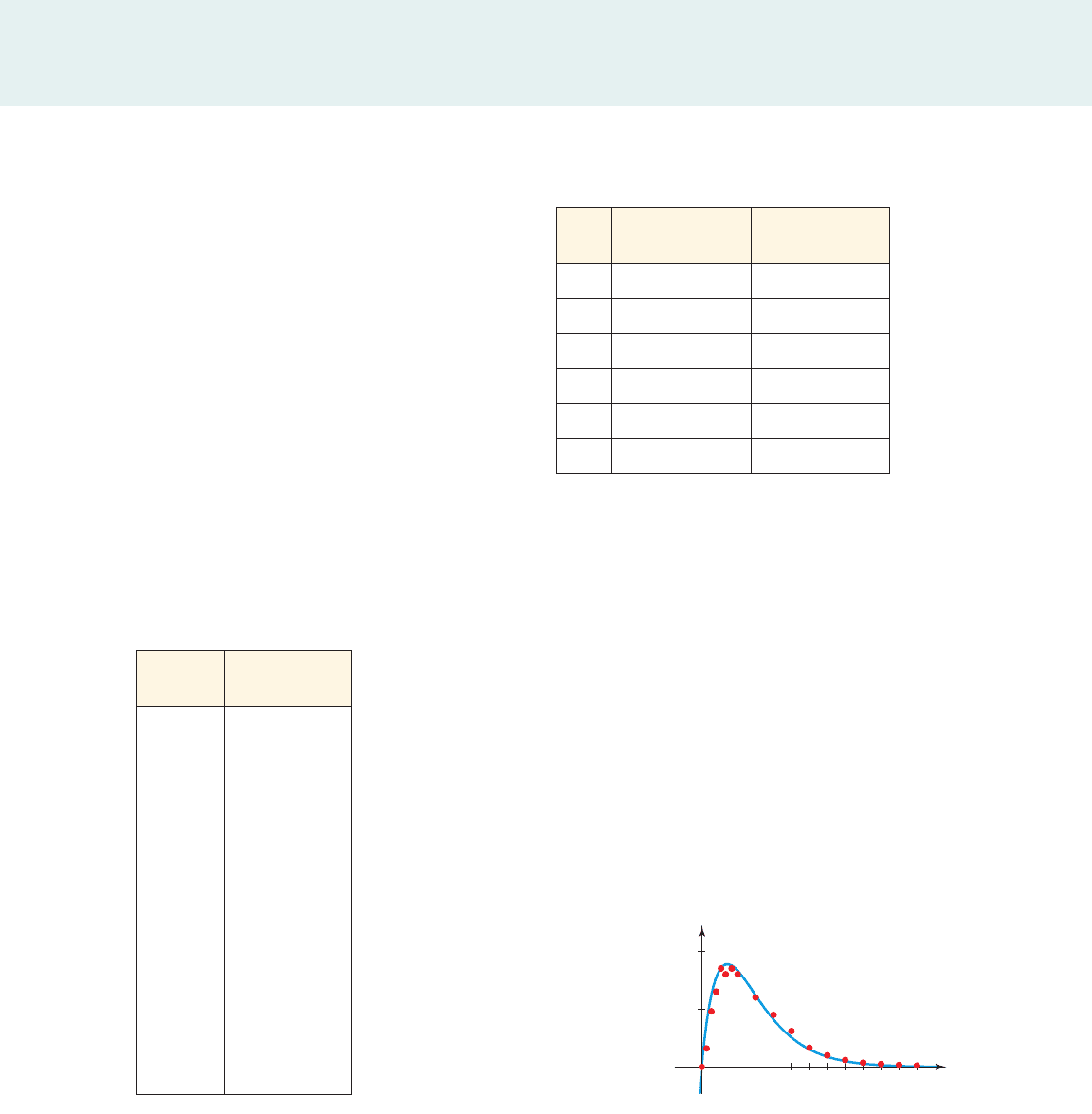
1. The data in the margin give the blood alcohol concentration in a three-hour

period following the consumption of 15 mL of ethanol.

(a) Use a graphing calculator to make a scatter plot of the data. Where does

the maximum concentration appear to occur?

(b) Try to fit a surge function to the data. Use what you learned

from Parts I and II to guess at reasonable values of a and b, and then graph

the function to see how well it fits the scatter plot. It may take several tries

to find a good fit for the data.

models the data reasonably well. How does your model compare to this?

S1t 2= at

0.2

0.1

Concentration

(mg/mL)

0.5 1.0 1.5 2.0 2.5 3.0

Time

(

)

Time (h)

Concentration

(mg/mL)

0 0

0.067 0.032

0.133 0.096

0.2 0.13

0.267 0.17

0.333 0.16

0.417 0.17

0.5 0.16

0.75 0.12

1.0 0.090

1.25 0.062

1.5 0.033

1.75 0.020

2.0 0.012

2.25 0.0074

2.5 0.0052

2.75 0.0034

3.0 0.0024

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 565

Maximum

value

Maximum value

occurs at t ⴝ ?

0.90

7.0 9.5

0.85

0.80

0.70

0.60

0.50

Surge functions S1t 2= 2t

(d) It is illegal in the United States to drive with a blood alcohol concentration

of 0.08 mg/mL or greater. (Many states have more restrictive laws for

holders of commercial drivers’ licenses.) Use the model you found to

determine how long a person must wait after drinking 15 mL of alcohol

before he or she can legally drive.

2. Use the data in the Prologue and follow the steps in Question 1 to find surge

functions that model the blood alcohol concentration following the consump-

tion of 30, 45, and 60 mL of ethanol.

3. In the table below, list the four models you obtained in Questions 1 and 2. Do

you see a pattern? If so, find a surge function that would model the blood

alcohol concentration following the consumption of 75 and 90 mL of ethanol.

Alcohol

consumption (mL)

Surge function

model

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

566 CHAPTER 6

567

Will the species survive? In the 1970s humpback whales became a focus of

controversy. Environmentalists believed that whaling threatened the whales

with imminent extinction; whalers saw their livelihood threatened by any

attempt to stop whaling. Are whales really threatened to extinction by

whaling? What level of whaling is safe to guarantee survival of the whales?

These questions motivated mathematicians to study population patterns of

whales and other species more closely. How such populations grow and

decline depends on many factors, such as the percentage of adults that

reproduce and the number of calves that reach maturity. So to model (and

forecast) the whale population, scientists must use many equations, each

having many variables. Such collections of equations, called systems of

equations, work together to describe the situation being modeled. Systems of

equations with hundreds or even thousands of variables are used extensively

by airlines to establish consistent flight schedules and by telecommunications

companies to find efficient routings for telephone calls. In this chapter, on a

smaller scale, we learn how to solve systems of equations that consist of

several equations in several variables.

7.1 Systems of Linear Equations

in Two Variables

7.2 Systems of Linear Equations

in Several Variables

7.3 Using Matrices to Solve

Systems of Linear Equations

7.4 Matrices and Categorical Data

7.5 Matrix Operations: Getting

Information from Data

7.6 Matrix Equations:

Solving Linear Systems

EXPLORATIONS

Collecting Categorical Data

2 Will the Species Survive?

Systems of Equations

and Data in Categories

Josef78/Shutterstock.com 2009

568 CHAPTER 7

■

Systems of Equations and Data in Categories

7.1 Systems of Linear Equations in Two Variables

■

Systems of Equations and Their Solutions

■

The Substitution Method

■

The Elimination Method

■

Graphical Interpretation: The Number of Solutions

■

Applications: How Much Gold Is in the Crown?

IN THIS SECTION… we learn that it is sometimes necessary to use two or more

equations to model a real-world situation. We learn how to solve such systems of linear

equations.

GET READY… by reviewing linear equations and their graphs in Sections 2.3 and 2.7.

Archimedes (287–212 B.C.) was the greatest mathematician of the ancient world. He

was born in Syracuse, a Greek colony on the island of Sicily. One of his many dis-

coveries is the law of the lever (see Exercise 33 in Section 2.6, page 209).

Archimedes famously said, “Give me a place to stand and a fulcrum for my lever,

and I can lift the earth.” Renowned as a mechanical genius for his many engineering

inventions, he designed pulleys for lifting large ships and a spiral screw for trans-

porting water to higher levels.

King Hiero of Syracuse once suspected a goldsmith of keeping part of the gold

intended for the king’s crown and replacing it with an equal weight of silver. So the

crown was the proper weight, but was it solid gold? The king asked Archimedes for

advice. Archimedes quickly realized that he needed more information to solve this

problem: He needed to know the volume of the crown. The problem contains two

variables: weight and volume. But how do we find the volume of an irregularly

shaped crown?

While in deep thought at a public bath, Archimedes discovered the solution

when he noticed that his body’s volume was the same as the volume of water it dis-

placed from the tub. Using this insight, he was able to measure the volume of the

crown. As the story is told, Archimedes ran home naked, shouting, “Eureka, eu-

reka!” (“I have found it, I have found it!”). This incident attests to Archimedes’

enormous powers of concentration—an essential element in the process of prob-

lem solving.

We solve the crown problem in Example 5. But first, we learn how to solve a

system of two equations in two variables.

Archimedes discovers the solution

to the crown problem.

■ Systems of Equations and Their Solutions

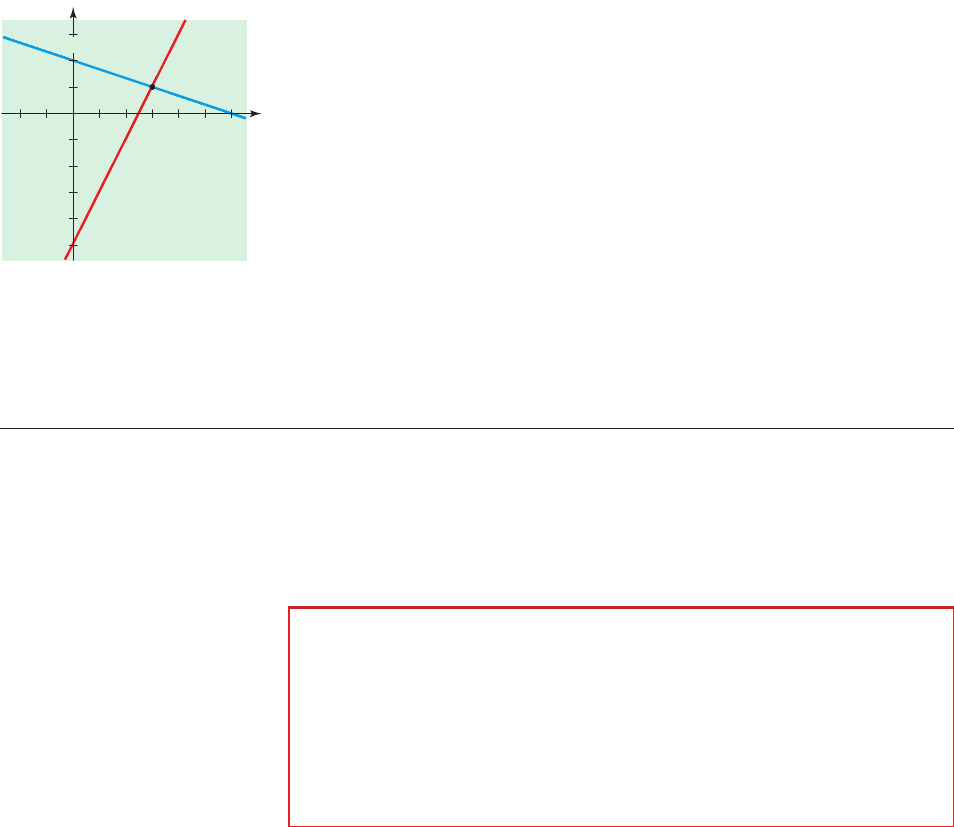
A system of equations is a set of equations in which each equation involves the

same variables. For example, here is a system of two equations in the two variables

x and y:

Equation 1

Equation 2

2x - y = 5

x + 4y = 7

SECTION 7.1

■

Systems of Linear Equations in Two Variables 569

A solution of a system is a pair of values for the variables that make each equation

true. We can check that if we choose x to be 3 and y to be 1 we get a solution of the

above system.

Equation 1 Equation 2

✓✓

We can also express this solution as the ordered pair (3, 1).

Note that the graphs of Equations 1 and 2 are lines (see Figure 1). Since the so-

lution (3, 1) satisfies each equation, the point (3, 1) lies on each line. So it is the point

of intersection of the two lines.

3 + 4112= 72132- 1 = 5

x + 4y = 72x - y = 5

■ The Substitution Method

In the substitution method we start with one equation in the system and solve

for one variable in terms of the other variable. The following box describes the

procedure.

Substitution Method

(3, 1)

2x-y=5

x+4y=7

figure 1

Lines and their graphs are studied in

Chapter 2.

1. Solve for one variable. Choose one equation, and solve for one variable

in terms of the other variable.

2. Substitute. Substitute the expression you found in Step 1 into the

other equation to get an equation in one variable, then solve for that

variable.

3. Back-substitute. Substitute the value you found in Step 2 back into the

expression found in Step 1, and solve for the remaining variable.

example

Substitution Method

Find all solutions of the system.

Equation 1

Equation 2

Solution

We solve for y in the first equation.

Equation 1

Solve for y

Now we substitute for y in the second equation and solve for x.

y = 1 - 2x

2 x + y = 1

2x + y = 1

3x + 4y = 14

570 CHAPTER 7

■

Systems of Equations and Data in Categories

Equation 2

Substitute

Expand

Simplify

Subtract 4

Solve for x

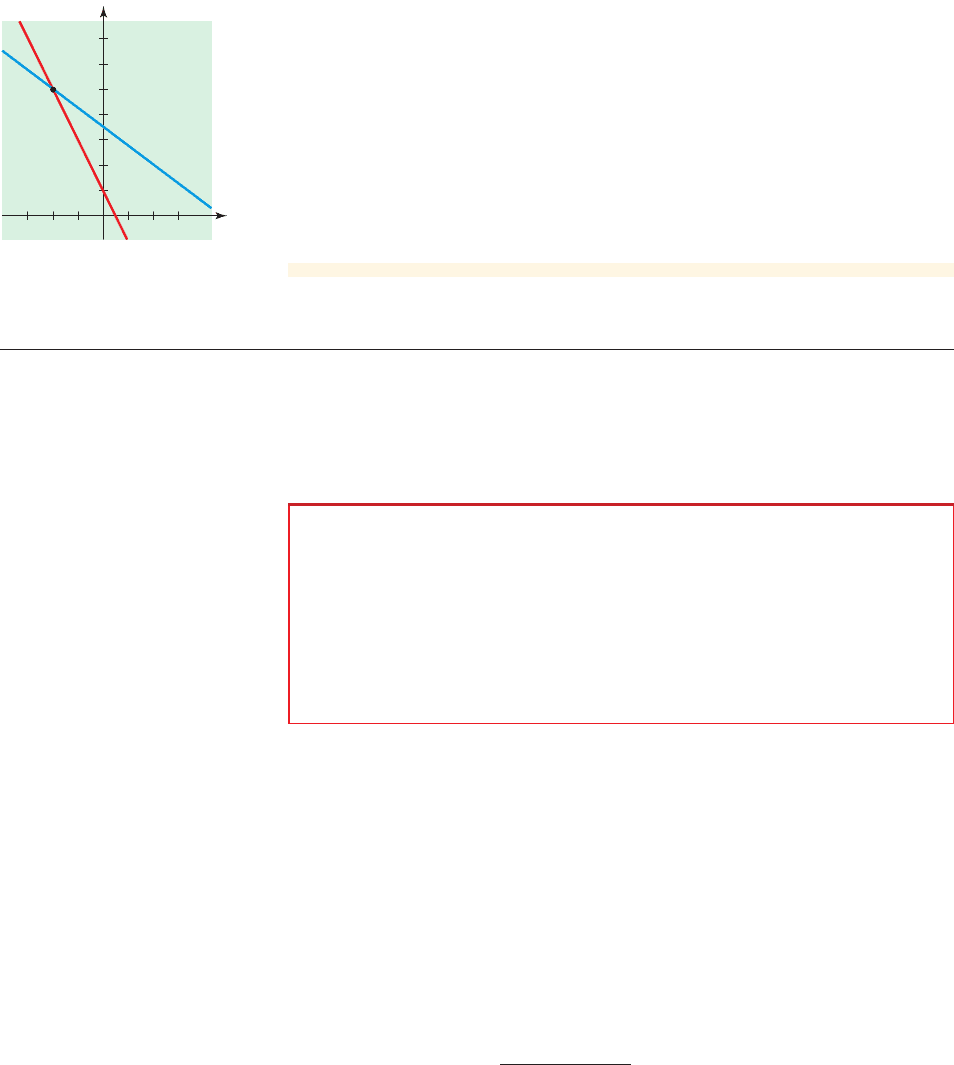
Next we back-substitute into the equation .

Back-substitute

Thus, and , so the solution is the ordered pair . Figure 2 shows

that the graphs of the two equations intersect at the point .

■ NOW TRY EXERCISE 17 ■

1- 2, 52

1- 2, 52y = 5x =-2

y = 1 - 21- 22= 5

y = 1 - 2xx =-2

x =-2

- 5x = 10

- 5x + 4 = 14

3 x + 4 - 8x = 14

y = 1 - 2x 3 x + 411 - 2x 2= 14

3 x + 4y = 14

■ The Elimination Method

To solve a system using the elimination method, we try to combine the equations

using sums or differences so as to eliminate one of the variables.

Elimination Method

example

Elimination Method

Find all solutions of the system.

Equation 1

Equation 2

Solution

Since the coefficients of the y-terms are negatives of each other, we can add the equa-

tions to eliminate y.

System

Add

Solve for x

x = 4

4 x = 16

3x + 2y = 14

x - 2y = 2

3x + 2y = 14

x - 2y = 2

(-2, 5)

2x+y=1

3x+4y=14

figure 2

1. Adjust the coefficients. Multiply one or more of the equations by

appropriate numbers so that the coefficient of one variable in one

equation is the negative of its coefficient in the other equation.

2. Add the equations. Add the two equations to eliminate one variable,

then solve for the remaining variable.

3. Back-substitute. Substitute the value that you found in Step 2 back into

one of the original equations, and solve for the remaining variable.

SECTION 7.1

■

Systems of Linear Equations in Two Variables 571

Now we back-substitute into one of the original equations and solve for y.

Let’s choose the second equation because it looks simpler.

Equation 2

Back-substitute

Subtract 4

Solve for y

The solution is (4, 1). Figure 3 shows that the graphs of the equations in the system

intersect at the point (4, 1).

■ NOW TRY EXERCISE 21 ■

y = 1

- 2y =-2

x = 4 4 - 2y = 2

x - 2y = 2

x = 4

(4, 1)

x-2y=2

3x+2y=14

figure 3

■ Graphical Interpretation: The Number of Solutions

The graph of a system of two linear equations in two variables is a pair of lines. The

solution of the system is the intersection point of the lines. Two lines may intersect

at a single point, they may be parallel, or they may coincide, as shown in Figure 4.

So there are three possible outcomes in solving such a system.

Number of Solutions of a Linear System in Two Variables

For a system of linear equations in two variables, exactly one of the following

is true.

1. The system has exactly one solution.

2. The system has no solution.

3. The system has infinitely many solutions.

A system that has no solution is said to be inconsistent. A system with infinitely

many solutions is called dependent.

y y y

0 00

One solution No solution

Lines intersect at a

single point.

Lines are parallel—

they do intersect.

Infinitely many solutions

Lines coincide.

figure 4

Examples 1 and 2 are systems with one solution. In the next two examples we

solve systems that have no solution or infinitely many solutions.

572 CHAPTER 7

■

Systems of Equations and Data in Categories

example

A Linear System with No Solution

Solve the system, and graph the lines.

Equation 1

Equation 2

Solution

We try to find a suitable combination of the two equations to eliminate the variable

y. Multiplying the first equation by 3 and the second equation by 2 gives

Add

Adding the two equations eliminates both x and y in this case, and we end up with

, which is obviously false. No matter what values we assign to x and y,we

cannot make this statement true, so the system has no solution. Figure 5 shows

that the lines in the system are parallel; hence they do not intersect. The system is

inconsistent.

■ NOW TRY EXERCISE 29 ■

0 = 29

2 * Equation 2

3 * Equation 1

24x - 6y = 15

- 24x + 6y = 14

8x - 2y = 5

- 12x + 3y = 7

8x-2y=5

_12x+3y=7

figure 5

example

A Linear System with Infinitely Many Solutions

Solve the system.

Equation 1

Equation 2

Solution

We multiply the first equation by 4 and the second by 3 to prepare for subtracting the

equations to eliminate x. The new equations are

We see that the two equations in the original system are simply different ways of

expressing the equation of one single line. The coordinates of any point on this

line give a solution of the system. Writing the equation in slope-intercept form, we

have .Soifwelett represent any real number, we can write the solu-

tion as

We can also write the solution in ordered-pair form as

where t is any real number. The system has infinitely many solutions (see Figure 6).

■ NOW TRY EXERCISE 31 ■

1t,

t - 22

y =

t - 2

x = t

y =

x - 2

3 * Equation 2

4 * Equation 1

12x - 24y = 48

3x - 6y = 12

4x - 8y = 16

(

t-2

)

t=4

t=1

figure 6

SECTION 7.1

■

Systems of Linear Equations in Two Variables 573

■ Applications: How Much Gold Is in the Crown?

We are now ready to solve the problem about the amount of gold in King Hiero’s

crown, as discussed at the beginning of this section. Recall that King Hiero suspected

that his goldsmith had replaced part of the gold intended for the king’s crown with

an equal weight of silver. Archimedes was able to determine the volume of the crown

by immersing it in water and observing the amount of water the crown displaced.

The density of gold and silver are well known. The density D of a substance is its

weight W divided by its volume . We have

The densities of gold is 19.3 g/cm

, and the density of silver is 10.5 g/cm

. In other

words a cubic centimeter of gold weighs 19.3 grams, and a cubic centimeter of sil-

ver weighs 10.5 grams.

D =

orV =

example

How Much Gold Is in the Crown?

Suppose King Hiero’s crown weighs 235 g and has a volume of . Find the

weight of the gold and the weight of the silver in the crown.

Solution

Let x and y be the weights of the gold and the silver in the crown, respectively. Since

the crown weighs 235 g, we have . The volume of gold in the crown is

/ ; similarly, the volume of silver in the crown is . Since the

volume of the crown is , we have . So we have the sys-

tem of equations

Weight Equation

Volume Equation

We solve the system by elimination. First, to eliminate fractions, we multiply the

Volume Equation by . Then we multiply the Weight Equation

by to get

Add

Solve for y

Now we substitute for y in the Volume Equation and solve for x.

Volume Equation

Substitute

Subtract 42

So the crown has 193 grams of gold and 42 grams of silver.

■ NOW TRY EXERCISE 53 ■

x = 193

y = 42 x + 42 = 235

x + y = 235

y = 42

8.8y = 369.6

202.65 * Volume Equation

- 10.5 * Weight Equation

- 10.5x - 10.5y =-2467.5

10.5x + 19.3y = 2837.1

- 10.5

119.3 2110.52= 202.65

•

x + y = 235

19.3

10.5

= 14

x>19.3 + y>10.5 = 1414 cm

y>10.5D = x>19.3V = W

x + y = 235

14 cm