Stewart J. Calculus

Подождите немного. Документ загружается.

REVIEW

CONCEPT CHECK

interpretations of curl and div ?

10. If , how do you test to determine whether is

conservative? What if is a vector ﬁeld on ?

11. (a) What is a parametric surface? What are its grid curves?

(b) Write an expression for the area of a parametric surface.

12. (a) Write the deﬁnition of the surface integral of a scalar func-

tion over a surface .

(b) How do you evaluate such an integral if is a parametric

surface given by a vector function ?

(d) If a thin sheet has the shape of a surface , and the density

at is , write expressions for the mass and

center of mass of the sheet.

13. (a) What is an oriented surface? Give an example of a non-

orientable surface.

(b) Deﬁne the surface integral (or ﬂux) of a vector ﬁeld F over

an oriented surface S with unit normal vector n.

surface given by a vector function ?

(d) What if S is given by an equation ?

14. State Stokes’ Theorem.

15. State the Divergence Theorem.

16. In what ways are the Fundamental Theorem for Line Integrals,

Green’s Theorem, Stokes’ Theorem, and the Divergence

Theorem similar?

z 苷 t共x, y兲

r共u,

v兲

␳

共x, y, z兲共x, y, z兲

z 苷 t共x, y兲S

r共u,

v兲

z 苷 t共x, y兲

⺢

FF 苷 P i ⫹ Q j

1. What is a vector ﬁeld? Give three examples that have physical

meaning.

2. (a) What is a conservative vector ﬁeld?

(b) What is a potential function?

3. (a) Write the deﬁnition of the line integral of a scalar function

along a smooth curve with respect to arc length.

(b) How do you evaluate such a line integral?

wire shaped like a curve if the wire has linear density

function .

(d) Write the deﬁnitions of the line integrals along of a

scalar function with respect to , , and .

(e) How do you evaluate these line integrals?

4. (a) Deﬁne the line integral of a vector ﬁeld along a smooth

curve given by a vector function .

(b) If is a force ﬁeld, what does this line integral represent?

integral of and the line integrals of the component func-

tions , , and ?

5. State the Fundamental Theorem for Line Integrals.

6. (a) What does it mean to say that is independent

of path?

(b) If you know that is independent of path, what can

you say about ?

7. State Green’s Theorem.

8. Write expressions for the area enclosed by a curve in terms

of line integrals around .

9. Suppose is a vector ﬁeld on .

(a) Deﬁne curl .

(b) Deﬁne div .F

⺢

F ⴢ dr

RQP

F 苷具P, Q, R 典

r共t兲C

zyxf

␳

共x, y兲

Determine whether the statement is true or false. If it is true, explain why.

If it is false, explain why or give an example that disproves the statement.

1. If is a vector ﬁeld, then div is a vector ﬁeld.

2. If is a vector ﬁeld, then curl is a vector ﬁeld.

3. If has continuous partial derivatives of all orders on , then

4. If has continuous partial derivatives on and is any

circle, then .

ⵜf ⴢ dr 苷 0

C⺢

ⵜf 兲苷 0div共curl

⺢

5. If and in an open region , then is

conservative.

If is a sphere and is a constant vector ﬁeld, then

8. There is a vector ﬁeld such that

curl F 苷 x i ⫹ y j ⫹ z k

F ⴢ dS 苷 0

⫺C

f 共x, y兲 ds 苷 ⫺x

f 共x, y兲 ds

FDP

苷 Q

F 苷 P i ⫹ Q j

TRUE-FALSE QUIZ

1142

||||

CHAPTER 17 VECTOR CALCULUS

1. A vector ﬁeld , a curve , and a point are shown.

(a) Is positive, negative, or zero? Explain.

(b) Is positive, negative, or zero? Explain.

2–9 Evaluate the line integral.

2. ,

is the arc of the parabola from (0, 0) to (1, 1)

3. ,

: , , ,

4. , is the ellipse with

counterclockwise orientation

5. , is the arc of the parabola

from to

6. ,

is given by ,

7. ,

is the line segment from , to

8. , where and is given by

9. , where and

is given by ,

10. Find the work done by the force ﬁeld

in moving a particle from the

point to the point along

(a) a straight line

(b) the helix , ,

11–12 Show that is a conservative vector ﬁeld. Then ﬁnd a func-

tion such that .

11.

12.

F共x, y, z兲苷 sin y

i ⫹ x cos y j ⫺ sin z k

F共x, y兲苷共1 ⫹ xy兲e

i ⫹ 共e

⫹ x

兲 j

F 苷 ∇ff

z 苷 3sin ty 苷 tx 苷 3 cos t

共0,

␲

兾2, 3兲共3, 0, 0兲

F共x, y, z兲苷 z i ⫹ x j ⫹ y k

0 艋 t 艋 1r共t兲苷 t

i ⫹ t

j ⫺ t

F共x, y, z兲苷 e

i ⫹ xz j ⫹ 共x ⫹ y兲 kx

F ⴢ dr

0 艋 t 艋

␲

r共t兲苷 sin t

i ⫹ 共1 ⫹ t兲

CF共x, y兲苷 xy i ⫹ x

F ⴢ dr

共3, 4, 2兲共1, 0, ⫺1兲C

xy dx ⫹ y

dy ⫹ yz dz

0 艋 t 艋 1r共t兲苷 t

i ⫹ t

j ⫹ t

xy dx ⫹ e

dy ⫹ xz dz

共0, 1兲共0, ⫺1兲

x 苷 1 ⫺ y

dx ⫹ x

⫹ 9y

苷 36Cx

y dx ⫹ 共x ⫹ y

兲 dy

0 艋 t 艋

␲

z 苷 3 sin ty 苷 3 cos tx 苷 tC

yz cos x ds

y 苷 x

x ds

div F共P兲

F ⴢ dr

PCF

13–14 Show that is conservative and use this fact to evaluate

along the given curve.

13. ,

: ,

14. ,

is the line segment from to

15. Verify that Green’s Theorem is true for the line integral

, where consists of the parabola

from to and the line segment from to

16. Use Green’s Theorem to evaluate ,

where is the triangle with vertices , , and

17. Use Green’s Theorem to evaluate ,

where is the circle with counterclockwise

orientation.

18. Find curl and div if

19. Show that there is no vector ﬁeld such that

20. Show that, under conditions to be stated on the vector ﬁelds

and ,

21. If is any piecewise-smooth simple closed plane curve

and and are differentiable functions, show that

22. If and are twice differentiable functions, show that

23. If is a harmonic function, that is, , show that the line

integral is independent of path in any simple

region .

24. (a) Sketch the curve with parametric equations

(b) Find .

25. Find the area of the part of the surface that lies

above the triangle with vertices , , and .

26. (a) Find an equation of the tangent plane at the point

to the parametric surface S given by

, ⫺3 艋

v 艋 30 艋 u 艋 3r共u, v兲苷 v

i ⫺ uv j ⫹ u

共4, ⫺2, 1兲

共1, 2兲共1, 0兲共0, 0兲

z 苷 x

⫹ 2y

2xe

dx ⫹ 共2x

⫹ 2y cot z兲 dy ⫺ y

csc

0 艋 t 艋 2

␲

z 苷 sin ty 苷 sin tx 苷 cos t

x f

dx ⫺ f

ⵜ

f 苷 0f

ⵜ

共 ft兲苷 f ⵜ

t ⫹ tⵜ

f ⫹ 2ⵜf ⴢ ⵜt

f 共x兲 dx ⫹ t共y兲 dy 苷 0

curl共F ⫻ G兲苷 F div G ⫺ G div F ⫹ 共G ⴢ ⵜ兲F ⫺ 共F ⴢ ⵜ 兲G

curl G 苷 2x i ⫹ 3yz j ⫺ xz

F共x, y, z兲苷 e

⫺x

sin y

i ⫹ e

⫺y

sin z j ⫹ e

⫺z

sin x k

⫹ y

苷 4C

y dx ⫺ xy

共1, 3兲.共1, 0兲共0, 0兲C

1 ⫹ x

dx ⫹ 2xy

共⫺1, 1兲

共1, 1兲共1, 1兲共⫺1, 1兲

y 苷 x

dx ⫺ x

共4, 0, 3兲共0, 2, 0兲C

F共x, y, z兲苷 e

i ⫹ 共xe

⫹ e

兲 j ⫹ ye

0 艋 t 艋 1r共t兲苷共t ⫹ sin

␲

t兲 i ⫹ 共2t ⫹ cos

␲

t兲

F共x, y兲苷共4x

⫺ 2xy

兲 i ⫹ 共2x

y ⫺ 3x

⫹ 4y

兲

F ⴢ dr

EXERCISES

CHAPTER 17 REVIEW

||||

1143

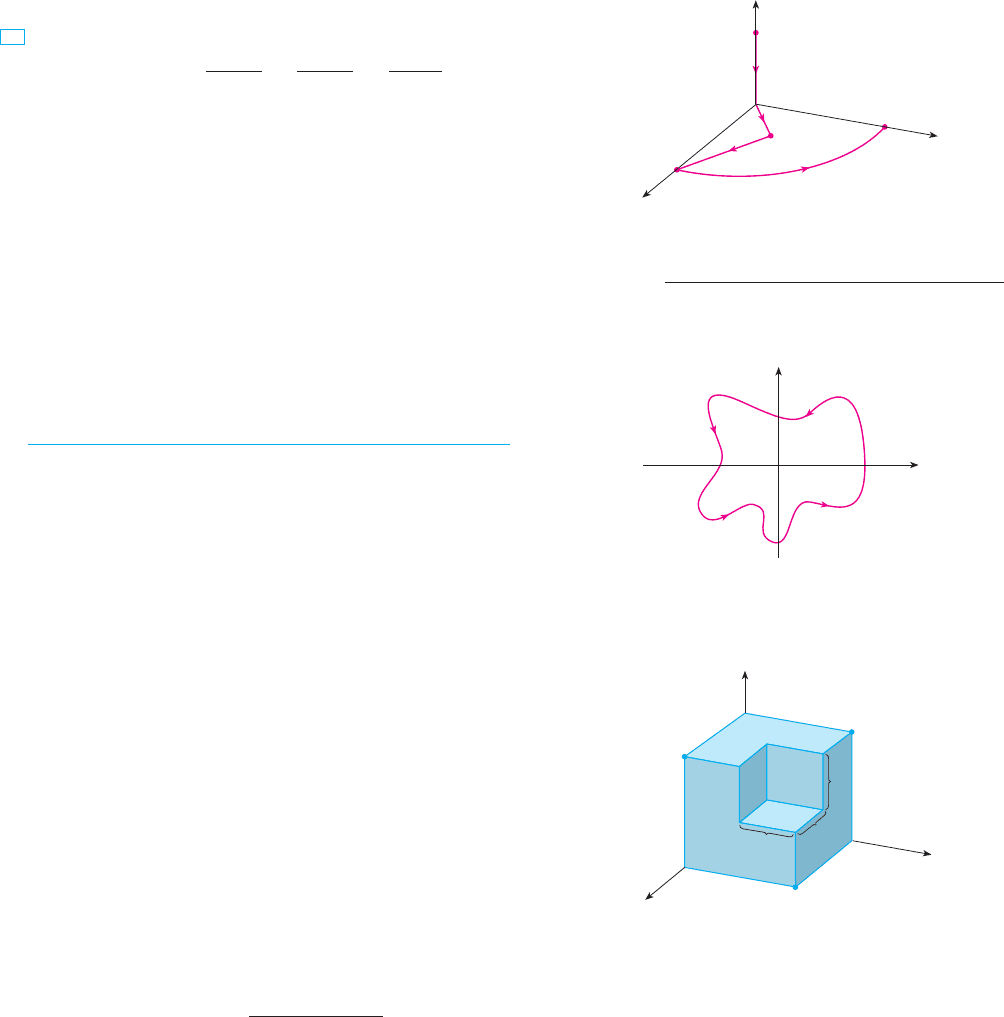
Evaluate , where is the curve with initial point

and terminal point shown in the ﬁgure.

38. Let

Evaluate , where is shown in the ﬁgure.

39. Find , where and is

the outwardly oriented surface shown in the ﬁgure (the

boundary surface of a cube with a unit corner cube removed).

40. If the components of have continuous second partial deriva-

tives and is the boundary surface of a simple solid region,

show that .

41. If is a constant vector, , and is an ori-

ented, smooth surface with a simple, closed, smooth,

positively oriented boundary curve , show that

2a ⴢ dS 苷

共a ⫻ r兲 ⴢ dr

Sr 苷 x i ⫹ y j ⫹ z ka

curl F ⴢ dS 苷 0

(0, 2, 2)

(2,0,2)

(2, 2, 0)

SF共x, y, z兲苷 x i ⫹ y j ⫹ z kxx

F ⴢ n dS

䊊

F ⴢ dr

F共x, y兲苷

共2x

⫹ 2xy

⫺ 2y兲 i ⫹ 共2y

⫹ 2x

y ⫹ 2x兲 j

⫹ y

(0,0,2)

(0,3,0)

(1,1,0)

(3,0,0)

共0, 3, 0兲共0, 0, 2兲

F ⴢ dr

;

(b) Use a computer to graph the surface and the tangent

plane found in part (a).

of .

(d) If

ﬁnd correct to four decimal places.

27–30 Evaluate the surface integral.

27. , where is the part of the paraboloid

that lies under the plane

28. , where is the part of the plane

that lies inside the cylinder

29. , where and is

the sphere with outward orientation

30. , where and is the

part of the paraboloid below the plane

with upward orientation

31. Verify that Stokes’ Theorem is true for the vector ﬁeld

, where is the part of the

paraboloid that lies above the -plane and

has upward orientation.

32. Use Stokes’ Theorem to evaluate , where

, is the part of the

sphere that lies above the plane , and

is oriented upward.

33. Use Stokes’ Theorem to evaluate , where

, and is the triangle with

vertices , , and , oriented counter-

clockwise as viewed from above.

34. Use the Divergence Theorem to calculate the surface integral

, where and is the

surface of the solid bounded by the cylinder and

the planes and .

35. Verify that the Divergence Theorem is true for the vector

ﬁeld , where is the unit ball

36. Compute the outward ﬂux of

through the ellipsoid .

37. Let

F共x, y, z兲苷共3x

yz ⫺ 3y兲 i ⫹ 共x

z ⫺ 3x兲 j ⫹ 共x

y ⫹ 2z兲 k

⫹ 9y

⫹ 6z

苷 36

F共x, y, z兲苷

x i ⫹ y j ⫹ z k

共x

⫹ y

⫹ z

兲

3兾2

⫹ y

⫹ z

艋 1

EF共x, y, z兲苷 x i ⫹ y j ⫹ z k

z 苷 2z 苷 0

⫹ y

苷 1

SF共x, y, z兲苷 x

i ⫹ y

j ⫹ z

kxx

F ⴢ dS

共0, 0, 1兲共0, 1, 0兲共1, 0, 0兲

CF共x, y, z兲苷 xy i ⫹ yz j ⫹ z x k

F ⴢ dr

z 苷 1x

⫹ y

⫹ z

苷 5

SF共x, y, z兲苷 x

yz i ⫹ yz

j ⫹ z

curl F ⴢ dS

xyz 苷 1 ⫺ x

⫺ y

SF共x, y, z兲苷 x

i ⫹ y

j ⫹ z

z 苷 1z 苷 x

⫹ y

SF共x, y, z兲苷 x

i ⫹ xy j ⫹ z kxx

F ⴢ dS

⫹ y

⫹ z

苷 4

SF共x, y, z兲苷 x z i ⫺ 2y j ⫹ 3x k

F ⴢ dS

⫹ y

苷 4z 苷 4 ⫹ x ⫹ y

共x

z ⫹ y

z兲

z 苷 4

z 苷 x

⫹ y

Sxx

z dS

F ⴢ dS

F共x, y, z兲苷

1 ⫹ x

i ⫹

1 ⫹ y

j ⫹

1 ⫹ z

CAS

1144

||||

CHAPTER 17 VECTOR CALCULUS

1145

1. Let be a smooth parametric surface and let be a point such that each line that starts

at intersects at most once. The solid angle subtended by at is the set of lines

starting at and passing through . Let be the intersection of with the surface of

the sphere with center and radius . Then the measure of the solid angle (in steradians) is

deﬁned to be

Apply the Divergence Theorem to the part of between and to show that

where is the radius vector from to any point on , , and the unit normal vector is

directed away from .

This shows that the deﬁnition of the measure of a solid angle is independent of the radius

of the sphere. Thus the measure of the solid angle is equal to the area subtended on a unit

sphere. (Note the analogy with the deﬁnition of radian measure.) The total solid angle sub-

tended by a sphere at its center is thus steradians.

2. Find the positively oriented simple closed curve for which the value of the line integral

is a maximum.

3. Let be a simple closed piecewise-smooth space curve that lies in a plane with unit normal

vector and has positive orientation with respect to . Show that the plane area

enclosed by is .

;

4. Investigate the shape of the surface with parametric equations

. Start by graphing the surface from several points of view. Explain the

appearance of the graphs by determining the traces in the horizontal planes , ,

and .

5. Prove the following identity:

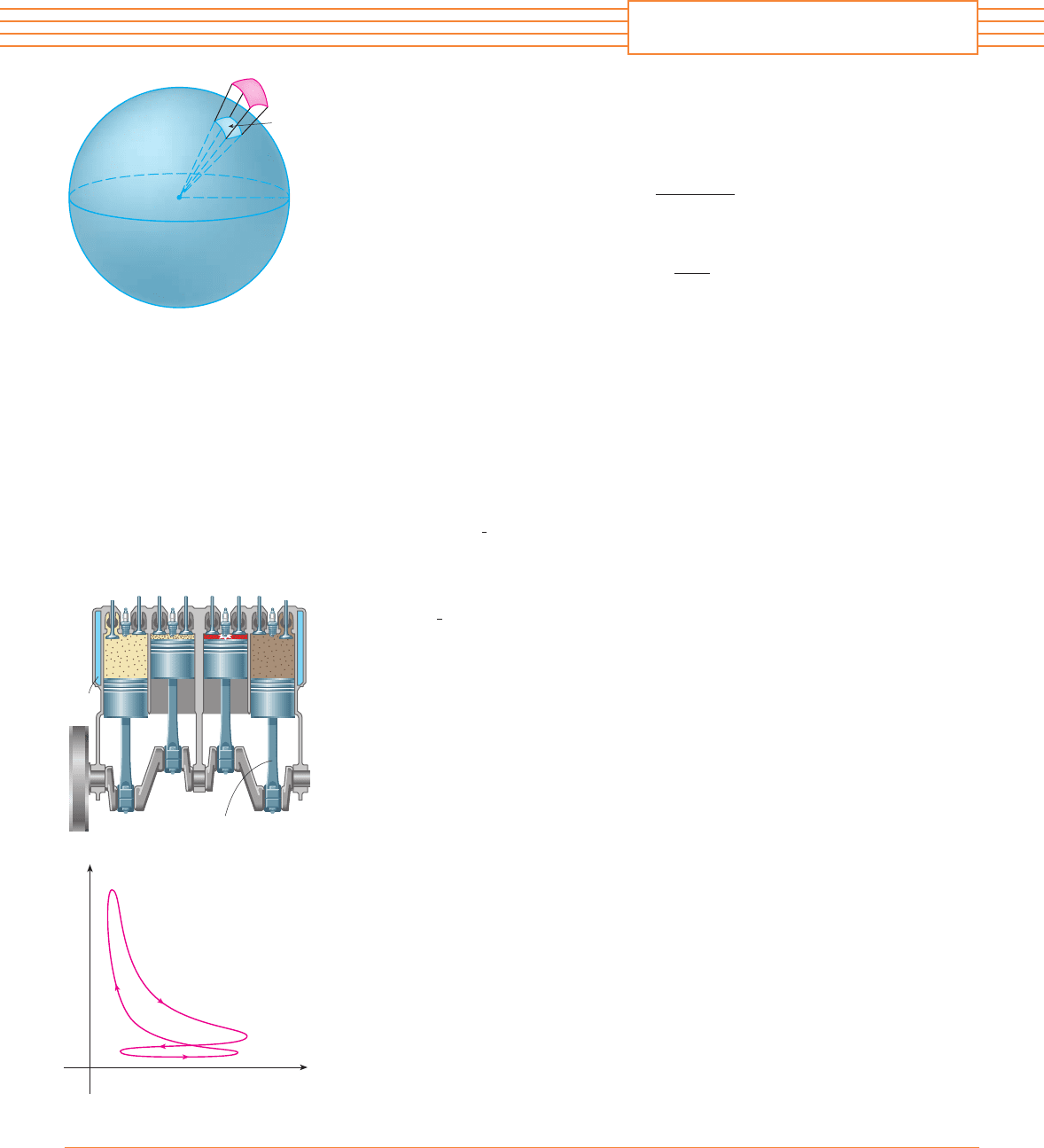
6. The ﬁgure depicts the sequence of events in each cylinder of a four-cylinder internal combus-

tion engine. Each piston moves up and down and is connected by a pivoted arm to a rotating

crankshaft. Let and be the pressure and volume within a cylinder at time , where

gives the time required for a complete cycle. The graph shows how and vary

through one cycle of a four-stroke engine. During the intake stroke (from ① to ②) a mixture

of air and gasoline at atmospheric pressure is drawn into a cylinder through the intake valve

as the piston moves downward. Then the piston rapidly compresses the mix with the valves

closed in the compression stroke (from ② to ③) during which the pressure rises and the vol-

ume decreases. At ③ the sparkplug ignites the fuel, raising the temperature and pressure at

almost constant volume to ④. Then, with valves closed, the rapid expansion forces the piston

downward during the power stroke (from ④ to ⑤). The exhaust valve opens, temperature and

pressure drop, and mechanical energy stored in a rotating ﬂywheel pushes the piston upward,

forcing the waste products out of the exhaust valve in the exhaust stroke. The exhaust valve

closes and the intake valve opens. We’re now back at ① and the cycle starts again.

(a) Show that the work done on the piston during one cycle of a four-stroke engine is

, where is the curve in the -plane shown in the ﬁgure.

[Hint: Let be the distance from the piston to the top of the cylinder and note that

the force on the piston is , where is the area of the top of the piston. Then

, where is given by . An alternative approach is

to work directly with Riemann sums.]

(b) Use Formula 17.4.5 to show that the work is the difference of the areas enclosed by the

two loops of .C

r共t兲苷 x共t兲 i, a 艋 t 艋 bC

W 苷 x

F ⴢ dr

AF 苷 AP共t兲 i

x共t兲

PVCW 苷

P dV

VPa 艋 t 艋 b

tV共t兲P共t兲

ⵜ共F ⴢ G兲苷共F ⴢ ⵜ兲G ⫹ 共G ⴢ ⵜ兲F ⫹ F ⫻ curl G ⫹ G ⫻ curl F

z 苷 ⫾

z 苷 ⫾1z 苷 0

z 苷 sin共u ⫹

v兲

y 苷 sin

v,x 苷 sin u,

共bz ⫺ cy兲 dx ⫹ 共cx ⫺ az兲 dy ⫹ 共ay ⫺ bx兲 dz C

nn 苷具a, b, c 典

共y

⫺ y兲 dx ⫺ 2x

␲

nr 苷

ⱍ

SPr

ⱍ

⍀共S 兲

ⱍ

苷

r ⴢ n

SS共a兲⍀共S 兲

ⱍ

⍀共S 兲

ⱍ

苷

area of S共a兲

⍀共S 兲S共a兲SP

PS⍀共S 兲SP

PROBLEMS PLUS

S(a)

FIGURE FOR PROBLEM 1

Flywheel

Crankshaft

Connecting rod

Water

FIGURE FOR PROBLEM 6

1146

The basic ideas of differential equations were explained in Chapter 10; there we concen-

trated on ﬁrst-order equations. In this chapter we study second-order linear differential

equations and learn how they can be applied to solve problems concerning the vibrations

of springs and the analysis of electric circuits. We will also see how inﬁnite series can be

used to solve differential equations.

Most of the solutions of the differential equation

resemble sine functions when is negative but they all look like

exponential functions when is large.x

y⬙⫹4y 苷 e

SECOND-ORDER

DIFFERENTIAL EQUATIONS

SECOND-ORDER LINEAR EQUATIONS

A second-order linear differential equation has the form

where , , , and are continuous functions. We saw in Section 10.1 that equations of

this type arise in the study of the motion of a spring. In Section 18.3 we will further pur-

sue this application as well as the application to electric circuits.

In this section we study the case where , for all , in Equation 1. Such equa-

tions are called homogeneous linear equations. Thus the form of a second-order linear homo-

geneous differential equation is

If for some , Equation 1 is nonhomogeneous and is discussed in Section 18.2.

Two basic facts enable us to solve homogeneous linear equations. The ﬁrst of these says

that if we know two solutions and of such an equation, then the linear combination

is also a solution.

THEOREM If and are both solutions of the linear homogeneous

equation (2) and and are any constants, then the function

is also a solution of Equation 2.

PROOF Since and are solutions of Equation 2, we have

and

Therefore, using the basic rules for differentiation, we have

Thus is a solution of Equation 2. My 苷 c

⫹ c

苷 c

共0兲 ⫹ c

共0兲苷 0

苷 c

关P共x兲y

⬙⫹Q共x兲y

⬘⫹R共x兲y

兴 ⫹ c

关P共x兲y

⬙⫹Q共x兲y

⬘⫹R共x兲y

兴

苷 P共x兲共c

⬙⫹c

⬙兲 ⫹ Q共x兲共c

⬘⫹c

⬘兲 ⫹ R共x兲共c

⫹ c

兲

苷 P共x兲共c

⫹ c

兲⬙⫹Q共x兲共c

⫹ c

兲⬘⫹R共x兲共c

⫹ c

兲

P共x兲y⬙⫹Q共x兲y⬘⫹R共x兲y

P共x兲y

⬙⫹Q共x兲y

⬘⫹R共x兲y

苷 0

P共x兲y

⬙⫹Q共x兲y

⬘⫹R共x兲y

苷 0

y共x兲苷 c

共x兲 ⫹ c

共x兲

共x兲y

共x兲

y 苷 c

⫹ c

xG共x兲苷 0

P共x兲

⫹ Q共x兲

⫹ R共x兲y 苷 0

xG共x兲苷 0

GRQP

P共x兲

⫹ Q共x兲

⫹ R共x兲y 苷 G共x兲

18.1

1147

The other fact we need is given by the following theorem, which is proved in more

advanced courses. It says that the general solution is a linear combination of two linearly

independent solutions and This means that neither nor is a constant multiple

of the other. For instance, the functions and are linearly dependent,

but and are linearly independent.

THEOREM If and are linearly independent solutions of Equation 2, and

is never 0, then the general solution is given by

where and are arbitrary constants.

Theorem 4 is very useful because it says that if we know two particular linearly inde-

pendent solutions, then we know every solution.

In general, it is not easy to discover particular solutions to a second-order linear equa-

tion. But it is always possible to do so if the coefﬁcient functions , , and are constant

functions, that is, if the differential equation has the form

where , , and are constants and .

It’s not hard to think of some likely candidates for particular solutions of Equation 5 if

we state the equation verbally. We are looking for a function such that a constant times

its second derivative plus another constant times plus a third constant times is equal

to 0. We know that the exponential function (where is a constant) has the prop-

erty that its derivative is a constant multiple of itself: . Furthermore, .

If we substitute these expressions into Equation 5, we see that is a solution if

But is never 0. Thus is a solution of Equation 5 if is a root of the equation

Equation 6 is called the auxiliary equation (or characteristic equation) of the differen-

tial equation . Notice that it is an algebraic equation that is obtained

from the differential equation by replacing by , by , and by .

Sometimes the roots and of the auxiliary equation can be found by factoring. In

other cases they are found by using the quadratic formula:

We distinguish three cases according to the sign of the discriminant .b

⫺ 4ac

苷

⫺b ⫺

⫺ 4ac

苷

⫺b ⫹

⫺ 4ac

1yry⬘r

y⬙

ay⬙⫹by⬘⫹cy 苷 0

⫹ br ⫹ c 苷 0

ry 苷 e

共ar

⫹ br ⫹ c兲e

苷 0

⫹ bre

⫹ ce

苷 0

y 苷 e

y⬙ 苷 r

y⬘ 苷 re

ry 苷 e

yy⬘y⬙

a 苷 0cba

ay⬙⫹by⬘⫹cy 苷 0

RQP

y共x兲苷 c

共x兲 ⫹ c

共x兲

P共x兲

t共x兲苷 xe

f 共x兲苷 e

t共x兲苷 5x

f 共x兲苷 x

1148

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

CASE I

In this case the roots and of the auxiliary equation are real and distinct, so

and are two linearly independent solutions of Equation 5. (Note that is not a

constant multiple of .) Therefore, by Theorem 4, we have the following fact.

If the roots and of the auxiliary equation are real and

unequal, then the general solution of is

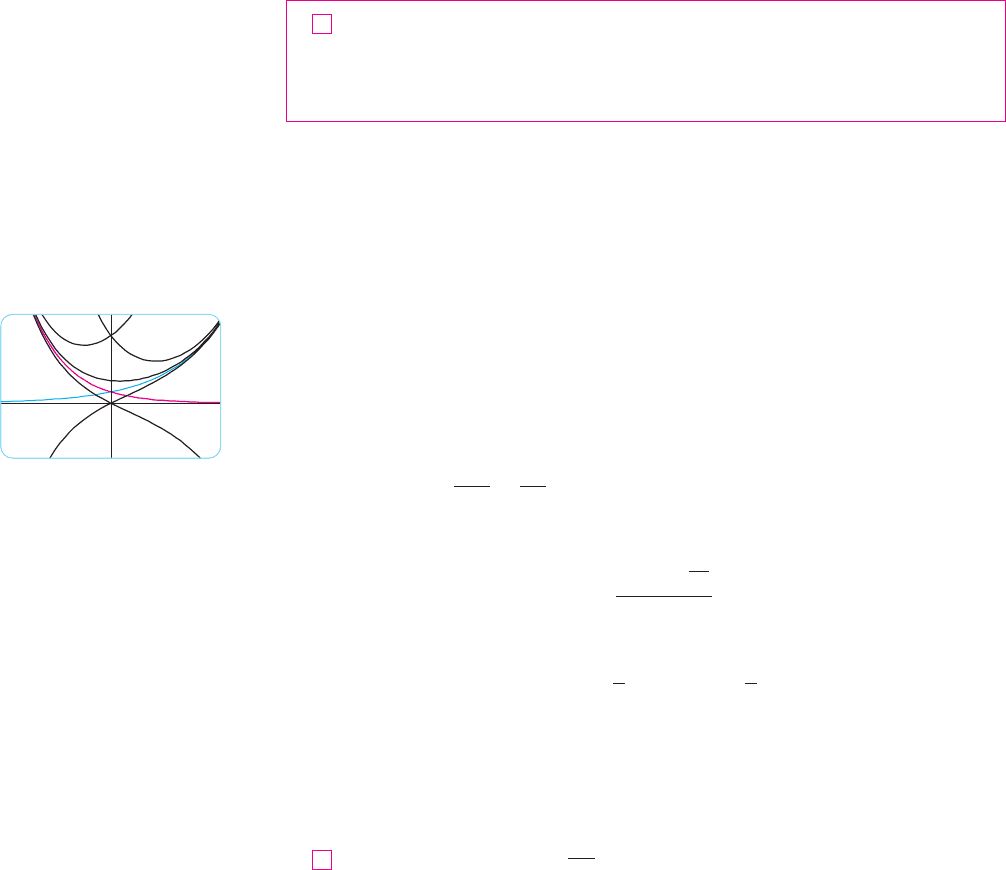
EXAMPLE 1 Solve the equation .

SOLUTION The auxiliary equation is

whose roots are , . Therefore, by (8), the general solution of the given differen-

tial equation is

We could verify that this is indeed a solution by differentiating and substituting into the

differential equation. M

EXAMPLE 2 Solve .

SOLUTION To solve the auxiliary equation , we use the quadratic formula:

Since the roots are real and distinct, the general solution is

CASE II

In this case ; that is, the roots of the auxiliary equation are real and equal. Let’s

denote by the common value of and Then, from Equations 7, we have

We know that is one solution of Equation 5. We now verify that is also

a solution:

苷 0共e

兲 ⫹ 0共xe

兲苷 0

苷共2ar ⫹ b兲e

⫹ 共ar

⫹ br ⫹ c兲xe

⬙⫹by

⬘⫹cy

苷 a共2re

⫹ r

兲 ⫹ b共e

⫹ rxe

兲 ⫹ cxe

苷 xe

苷 e

2ar ⫹ b 苷 0sor 苷 ⫺

苷 r

⫺ 4ac 苷 0

y 苷 c

(

⫺1⫹

)

x兾6

⫹ c

(

⫺1⫺

)

x兾6

r 苷

⫺1 ⫾

⫹ r ⫺ 1 苷 0

⫹

⫺ y 苷 0

y 苷 c

⫹ c

⫺3x

⫺3r 苷 2

⫹ r ⫺ 6 苷共r ⫺ 2兲共r ⫹ 3兲苷 0

y⬙⫹y⬘⫺6y 苷 0

y 苷 c

⫹ c

ay⬙⫹by⬘⫹cy 苷 0

⫹ br ⫹ c 苷 0r

苷 e

⫺ 4ac ⬎ 0

SECTION 18.1 SECOND-ORDER LINEAR EQUATIONS

||||

1149

_1 1

5f+g

f+5g

f-g

g-f

f+g

FIGURE 1

N In Figure 1 the graphs of the basic solutions

and of the differential

equation in Example 1 are shown in blue and

red, respectively. Some of the other solutions,

linear combinations of and , are shown

in black.

t共x兲苷 e

⫺3x

f 共x兲苷 e

The ﬁrst term is 0 by Equations 9; the second term is 0 because is a root of the auxiliary

equation. Since and are linearly independent solutions, Theorem 4 pro-

vides us with the general solution.

If the auxiliary equation has only one real root , then the

general solution of is

EXAMPLE 3 Solve the equation .

SOLUTION The auxiliary equation can be factored as

so the only root is . By (10), the general solution is

CASE III

In this case the roots and of the auxiliary equation are complex numbers. (See Appen-

dix G for information about complex numbers.) We can write

where and are real numbers. [In fact, , .] Then,

using Euler’s equation

from Appendix G, we write the solution of the differential equation as

where , . This gives all solutions (real or complex) of the dif-

ferential equation. The solutions are real when the constants and are real. We summa-

rize the discussion as follows.

If the roots of the auxiliary equation are the complex num-

bers , , then the general solution of

y 苷 e

␣

共c

cos

␤

x ⫹ c

sin

␤

x兲

ay⬙⫹by⬘⫹cy 苷 0r

苷

␣

⫺ i

␤

苷

␣

⫹ i

␤

⫹ br ⫹ c 苷 0

苷 i共C

⫺ C

兲c

苷 C

⫹ C

苷 e

␣

共c

cos

␤

x ⫹ c

sin

␤

x兲

苷 e

␣

关共C

⫹ C

兲 cos

␤

x ⫹ i共C

⫺ C

兲 sin

␤

x兴

苷 C

␣

共cos

␤

x ⫹ i sin

␤

x兲 ⫹ C

␣

共cos

␤

x ⫺ i sin

␤

x兲

y 苷 C

⫹ C

苷 C

共

␣

⫹i

␤

兲x

⫹ C

共

␣

⫺i

␤

兲x

␪

苷 cos

␪

⫹ i sin

␪

␤

苷

4ac ⫺ b

兾共2a兲

␣

苷 ⫺b兾共2a兲

␤

␣

苷

␣

⫺ i

␤

苷

␣

⫹ i

␤

⫺ 4ac

⬍

y 苷 c

⫺3x兾2

⫹ c

⫺3x兾2

r 苷 ⫺

共2r ⫹ 3兲

苷 0

⫹ 12r ⫹ 9 苷 0

4y⬙⫹12y⬘⫹9y 苷 0

y 苷 c

⫹ c

ay⬙⫹by⬘⫹cy 苷 0

rar

⫹ br ⫹ c 苷 0

苷 xe

苷 e

1150

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

N Figure 2 shows the basic solutions

and in

Example 3 and some other members of the

family of solutions. Notice that all of them

approach 0 as .x l ⬁

t共x兲苷 xe

⫺3x兾2

f 共x兲苷 e

⫺3x兾2

FIGURE 2

_2 2

5f+g

f+5g

f-g

g-f

f+g

EXAMPLE 4 Solve the equation .

SOLUTION The auxiliary equation is . By the quadratic formula, the roots

are

By (11), the general solution of the differential equation is

INITIAL-VALUE AND BOUNDARY-VALUE PROBLEMS

An initial-value problem for the second-order Equation 1 or 2 consists of ﬁnding a solu-

tion of the differential equation that also satisﬁes initial conditions of the form

where and are given constants. If , , , and are continuous on an interval and

there, then a theorem found in more advanced books guarantees the existence

and uniqueness of a solution to this initial-value problem. Examples 5 and 6 illustrate the

technique for solving such a problem.

EXAMPLE 5 Solve the initial-value problem

SOLUTION From Example 1 we know that the general solution of the differential equa-

tion is

Differentiating this solution, we get

To satisfy the initial conditions we require that

From (13), we have and so (12) gives

Thus the required solution of the initial-value problem is

EXAMPLE 6 Solve the initial-value problem

SOLUTION The auxiliary equation is , or , whose roots are . Thus

, , and since , the general solution is

Since y⬘共x兲苷 ⫺c

sin x ⫹ c

cos x

y共x兲苷 c

cos x ⫹ c

sin x

苷 1

␤

苷 1

␣

苷 0

⫾ir

苷 ⫺1r

⫹ 1 苷 0

y⬘共0兲苷 3y共0兲苷 2y⬙⫹y 苷 0

y 苷

⫹

⫺3x

苷

⫹

苷 1

苷

y⬘共0兲苷 2c

⫺ 3c

苷 0

y共0兲苷 c

⫹ c

苷 1

y⬘共x兲苷 2c

⫺ 3c

⫺3x

y共x兲苷 c

⫹ c

⫺3x

y⬘共0兲苷 0y共0兲苷 1y⬙⫹y⬘⫺6y 苷 0

P共x兲苷 0

GRQPy

y⬘共x

兲苷 y

y共x

兲苷 y

y 苷 e

共c

cos 2x ⫹ c

sin 2x兲

r 苷

6 ⫾

36 ⫺ 52

苷

6 ⫾

⫺16

苷 3 ⫾ 2i

⫺ 6r ⫹ 13 苷 0

y⬙⫺6y⬘⫹13y 苷 0

SECTION 18.1 SECOND-ORDER LINEAR EQUATIONS

||||

1151

N Figure 3 shows the graphs of the solu-

tions in Example 4, and

, together with some linear

combinations. All solutions approach 0

as .x l ⫺⬁

t共x兲苷 e

sin 2x

f 共x兲苷 e

cos 2x

FIGURE 3

_3 2

f-g

f+g

N Figure 4 shows the graph of the solution of the

initial-value problem in Example 5. Compare with

Figure 1.

FIGURE 4

_2 2