Stewart J. Calculus

Подождите немного. Документ загружается.

In general, the even coefﬁcients are given by

and the odd coefﬁcients are given by

The solution is

In Example 2 we had to assume that the differential equation had a series solu-

tion. But now we could verify directly that the function given by Equation 8 is indeed a

solution.

Unlike the situation of Example 1, the power series that arise in the solution of

Example 2 do not deﬁne elementary functions. The functions

and y

共x兲苷 x ⫹

兺

⬁

n苷1

1 ⴢ 5 ⴢ 9 ⴢ ⭈⭈⭈ ⴢ 共4n ⫺ 3兲

共2n ⫹ 1兲!

2n⫹1

共x兲苷 1 ⫺

⫺

兺

⬁

n苷2

3 ⴢ 7 ⴢ ⭈⭈⭈ ⴢ 共4n ⫺ 5兲

共2n兲!

NOTE 3

NOTE 2

苷 ⫹ c

冉

x ⫹

兺

⬁

n苷1

1 ⴢ 5 ⴢ 9 ⴢ ⭈⭈⭈ ⴢ 共4n ⫺ 3兲

共2n ⫹ 1兲!

2n⫹1

冊

y 苷 c

冉

1 ⫺

⫺

兺

⬁

n苷2

3 ⴢ 7 ⴢ ⭈⭈⭈ ⴢ 共4n ⫺ 5兲

共2n兲!

冊

苷 ⫹ c

冉

x ⫹

⫹

1 ⴢ 5

⫹

1 ⴢ 5 ⴢ 9

⫹

1 ⴢ 5 ⴢ 9 ⴢ 13

⫹⭈⭈⭈

冊

苷 c

冉

1 ⫺

⫺

3 ⴢ 7

⫺

3 ⴢ 7 ⴢ 11

⫺⭈⭈⭈

冊

y 苷 c

⫹ c

x ⫹ c

⫹ c

⫹⭈⭈⭈

2n⫹1

苷

1 ⴢ 5 ⴢ 9 ⴢ ⭈⭈⭈ ⴢ 共4n ⫺ 3兲

共2n ⫹ 1兲!

苷 ⫺

3 ⴢ 7 ⴢ 11 ⴢ ⭈⭈⭈ ⴢ 共4n ⫺ 5兲

共2n兲!

Put n 苷 7: c

苷

8 ⴢ 9

苷

1 ⴢ 5 ⴢ 9 ⴢ 13

Put n 苷 6: c

苷

7 ⴢ 8

苷 ⫺

3 ⴢ 7 ⴢ 11

Put n 苷 5: c

苷

6 ⴢ 7

苷

1 ⴢ 5 ⴢ 9

5! 6 ⴢ 7

苷

1 ⴢ 5 ⴢ 9

Put n 苷 4: c

苷

5 ⴢ 6

苷 ⫺

3 ⴢ 7

4! 5 ⴢ 6

苷 ⫺

3 ⴢ 7

1172

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

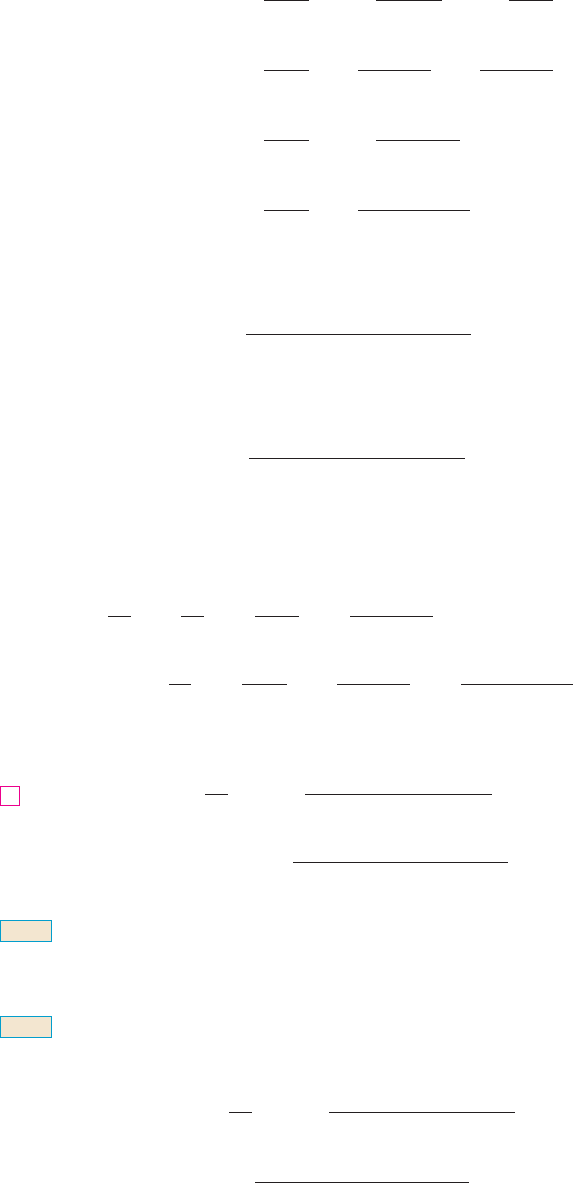
are perfectly good functions but they can’t be expressed in terms of familiar functions. We

can use these power series expressions for and to compute approximate values of the

functions and even to graph them. Figure 1 shows the ﬁrst few partial sums

(Taylor polynomials) for , and we see how they converge to . In this way we can

graph both and in Figure 2.

If we were asked to solve the initial-value problem

we would observe from Theorem 12.10.5 that

This would simplify the calculations in Example 2, since all of the even coefﬁcients would

be 0. The solution to the initial-value problem is

y共x兲苷 x ⫹

兺

⬁

n苷1

1 ⴢ 5 ⴢ 9 ⴢ ⭈⭈⭈ ⴢ 共4n ⫺ 3兲

共2n ⫹ 1兲!

2n⫹1

苷 y⬘共0兲苷 1c

苷 y共0兲苷 0

y⬘共0兲苷 1y共0兲苷 0y⬙⫺2xy⬘⫹y 苷 0

NOTE 4

共x兲

, T

, ...

CHAPTER 18 REVIEW

||||

1173

11. ,,

12. The solution of the initial-value problem

is called a Bessel function of order 0.

(a) Solve the initial-value problem to ﬁnd a power series

expansion for the Bessel function.

;

(b) Graph several Taylor polynomials until you reach one that

looks like a good approximation to the Bessel function on

the interval .关⫺5, 5兴

y⬘共0兲苷 0y共0兲苷 1x

y⬙⫹xy⬘⫹x

y 苷 0

y⬘共0兲苷 1y共0兲苷 0y⬙⫹x

y⬘⫹xy 苷 0

1–11 Use power series to solve the differential equation.

1. 2.

5. 6.

10. ,,y⬘共0兲苷 0y共0兲苷 1y⬙⫹x

y 苷 0

y⬘共0兲苷 0y共0兲苷 1y⬙⫺xy⬘⫺y 苷 0

y⬙ 苷 xy

共x ⫺ 1兲y⬙⫹y⬘ 苷 0

y⬙ 苷 yy⬙⫹xy⬘⫹y 苷 0

共x ⫺ 3兲y⬘⫹2y 苷 0y⬘ 苷 x

y⬘ 苷 xyy⬘⫺y 苷 0

EXERCISES

18.4

_15

_2.5 2.5

›

ﬁ

FIGURE 1

T¸

T¡¸

FIGURE 2

REVIEW

CONCEPT CHECK

(b) What is the complementary equation? How does it help

solve the original differential equation?

works.

(d) Explain how the method of variation of parameters works.

4. Discuss two applications of second-order linear differential

equations.

5. How do you use power series to solve a differential equation?

1. (a) Write the general form of a second-order homogeneous

linear differential equation with constant coefﬁcients.

(b) Write the auxiliary equation.

the differential equation? Write the form of the solution for

each of the three cases that can occur.

2. (a) What is an initial-value problem for a second-order differ-

ential equation?

(b) What is a boundary-value problem for such an equation?

3. (a) Write the general form of a second-order nonhomogeneous

linear differential equation with constant coefﬁcients.

Determine whether the statement is true or false. If it is true, explain why.

If it is false, explain why or give an example that disproves the statement.

1. If and are solutions of , then is also

a solution of the equation.

2. If and are solutions of , then

is also a solution of the equation.c

⫹ c

y⬙⫹6y⬘⫹5y 苷 xy

⫹ y

y⬙⫹y 苷 0y

3. The general solution of can be written as

4. The equation has a particular solution of the form

苷 Ae

y⬙⫺y 苷 e

y 苷 c

cosh x ⫹ c

sinh x

y⬙⫺y 苷 0

TRUE-FALSE QUIZ

1–10 Solve the differential equation.

10.

11–14 Solve the initial-value problem.

11. ,,

12. ,,

13. ,,

14. ,,

15. Use power series to solve the initial-value problem

y⬘共0兲苷 1y共0兲苷 0y⬙⫹xy⬘⫹y 苷 0

y⬘共0兲苷 2y共0兲苷 19y⬙⫹y 苷 3x ⫹ e

⫺x

y⬘共0兲苷 1y共0兲苷 0y⬙⫺5y⬘⫹4y 苷 0

y⬘共0兲苷 1y共0兲苷 2y⬙⫺6y⬘⫹25y 苷 0

y⬘共1兲苷 12y共1兲苷 3y⬙⫹6y⬘ 苷 0

⬍

␲

兾2

⫹ y 苷 csc x

⫺

⫺ 6y 苷 1 ⫹ e

⫺2x

⫹ 4y 苷 sin 2x

⫺ 2

⫹ y 苷 x cos x

⫹

⫺ 2y 苷 x

⫺ 4

⫹ 5y 苷 e

4y⬙⫹4y⬘⫹y 苷 0

y⬙⫹3y 苷 0

y⬙⫹4y⬘⫹13y 苷 0

y⬙⫺2y⬘⫺15y 苷 0

16. Use power series to solve the equation

17. A series circuit contains a resistor with , an inductor

with H, a capacitor with F, and a 12-V bat-

tery. The initial charge is C and the initial current

is 0. Find the charge at time t.

18. A spring with a mass of 2 kg has damping constant 16, and a

force of N keeps the spring stretched m beyond its

natural length. Find the position of the mass at time if it

starts at the equilibrium position with a velocity of m兾s.

19. Assume that the earth is a solid sphere of uniform density with

mass and radius mi. For a particle of mass

within the earth at a distance from the earth’s center, the

gravitational force attracting the particle to the center is

where is the gravitational constant and is the mass of the

earth within the sphere of radius .

(a) Show that .

(b) Suppose a hole is drilled through the earth along a diame-

ter. Show that if a particle of mass is dropped from rest

at the surface, into the hole, then the distance of

the particle from the center of the earth at time is given by

where .

harmonic motion. Find the period T.

(d) With what speed does the particle pass through the center

of the earth?

苷 GM兾R

苷 t兾R

y⬙共t兲苷 ⫺k

y共t兲

y 苷 y共t兲

苷

⫺GMm

苷

⫺GM

mR 苷 3960M

2.4

0.212.8

Q 苷 0.01

C 苷 0.0025L 苷 2

⍀R 苷 40

y⬙⫺xy⬘⫺2y 苷 0

EXERCISES

1174

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

APPENDIXES

A Numbers, Inequalities, and Absolute Values

B Coordinate Geometry and Lines

C Graphs of Second-Degree Equations

D Trigonometry

E Sigma Notation

F Proofs of Theorems

G Complex Numbers

H Answers to Odd-Numbered Exercises

NUMBERS, INEQUALITIES, AND ABSOLUTE VALUES

Calculus is based on the real number system. We start with the integers:

Then we construct the rational numbers, which are ratios of integers. Thus any rational

number can be expressed as

Examples are

(

Recall that division by is always ruled out, so expressions like and are undeﬁned.

)

Some real numbers, such as , can’t be expressed as a ratio of integers and are therefore

called irrational numbers. It can be shown, with varying degrees of difﬁculty, that the fol-

lowing are also irrational numbers:

The set of all real numbers is usually denoted by the symbol . When we use the word

number without qualiﬁcation, we mean “real number.”

Every number has a decimal representation. If the number is rational, then the corre-

sponding decimal is repeating. For example,

(The bar indicates that the sequence of digits repeats forever.) On the other hand, if the

number is irrational, the decimal is nonrepeating:

If we stop the decimal expansion of any number at a certain place, we get an approxima-

tion to the number. For instance, we can write

where the symbol is read “is approximately equal to.” The more decimal places we

retain, the better the approximation we get.

The real numbers can be represented by points on a line as in Figure 1. The positive

direction (to the right) is indicated by an arrow. We choose an arbitrary reference point ,

called the origin, which corresponds to the real number . Given any convenient unit of

measurement, each positive number is represented by the point on the line a distance of

units to the right of the origin, and each negative number is represented by the point

units to the left of the origin. Thus every real number is represented by a point on the

line, and every point on the line corresponds to exactly one real number. The number

associated with the point is called the coordinate of and the line is then called a coor-PP

⫺xx

⬇

␲

⬇ 3.14159265

␲

苷 3.141592653589793...

苷 1.414213562373095...

157

495

苷 0.317171717...苷 0.317

苷 1.285714285714...苷 1.285714

苷 0.5000...苷 0.50

苷 0.66666...苷 0.6

⺢

log

2sin 1⬚

␲

0.17 苷

100

46 苷

⫺

where m and n are integers and n 苷 0r 苷

..., ⫺3, ⫺2, ⫺1, 0, 1, 2, 3, 4, . . .

||||

APPENDIX A NUMBERS, INEQUALITIES, AND ABSOLUTE VALUES

dinate line, or a real number line, or simply a real line. Often we identify the point with

its coordinate and think of a number as being a point on the real line.

The real numbers are ordered. We say is less than and write if is a pos-

itive number. Geometrically this means that lies to the left of on the number line.

(Equivalently, we say is greater than and write .) The symbol (or )

means that either or and is read “ is less than or equal to .” For instance,

the following are true inequalities:

In what follows we need to use set notation. A set is a collection of objects, and these

objects are called the elements of the set. If is a set, the notation means that is

an element of , and means that is not an element of . For example, if repre-

sents the set of integers, then but . If and are sets, then their union

is the set consisting of all elements that are in or (or in both and ). The inter-

section of and is the set consisting of all elements that are in both and . In

other words, is the common part of and . The empty set, denoted by ∅, is the set

that contains no element.

Some sets can be described by listing their elements between braces. For instance, the

set consisting of all positive integers less than 7 can be written as

We could also write in set-builder notation as

which is read “ is the set of such that is an integer and .”

INTERVALS

Certain sets of real numbers, called intervals, occur frequently in calculus and correspond

geometrically to line segments. For example, if , the open interval from to con-

sists of all numbers between and and is denoted by the symbol . Using set-builder

notation, we can write

Notice that the endpoints of the interval—namely, and —are excluded. This is indicated

by the round brackets and by the open dots in Figure 2. The closed interval from to

is the set

Here the endpoints of the interval are included. This is indicated by the square brackets

and by the solid dots in Figure 3. It is also possible to include only one endpoint in an inter-

val, as shown in Table 1.

关兴

关a, b兴苷兵x

ⱍ

a 艋 x 艋 b其

a共兲

共a, b兲苷兵x

ⱍ

⬍

b其

共a, b兲ba

baa

⬍

7xxA

A 苷兵x

ⱍ

x is an integer and 0

⬍

7其

A 苷兵1, 2, 3, 4, 5, 6其

TSS 傽 T

TSS 傽 TTS

TSTSS 傼 T

␲

僆 Z⫺3 僆 Z

ZSaa 僆 SS

aa 僆 SS

2 艋 2

艋 2

⬍

2⫺3 ⬎⫺

␲

⬍

7.4

⬍

7.5

baa 苷 ba

⬍

b 艌 aa 艋 bb ⬎ aab

b ⫺ aa

⬍

bba

FIGURE 1

1234_1_2_3

_2.63

„

APPENDIX A NUMBERS, INEQUALITIES, AND ABSOLUTE VALUES

||||

FIGURE 2

Open interval (a,b)

FIGURE 3

Closed interval [a,b]

a b

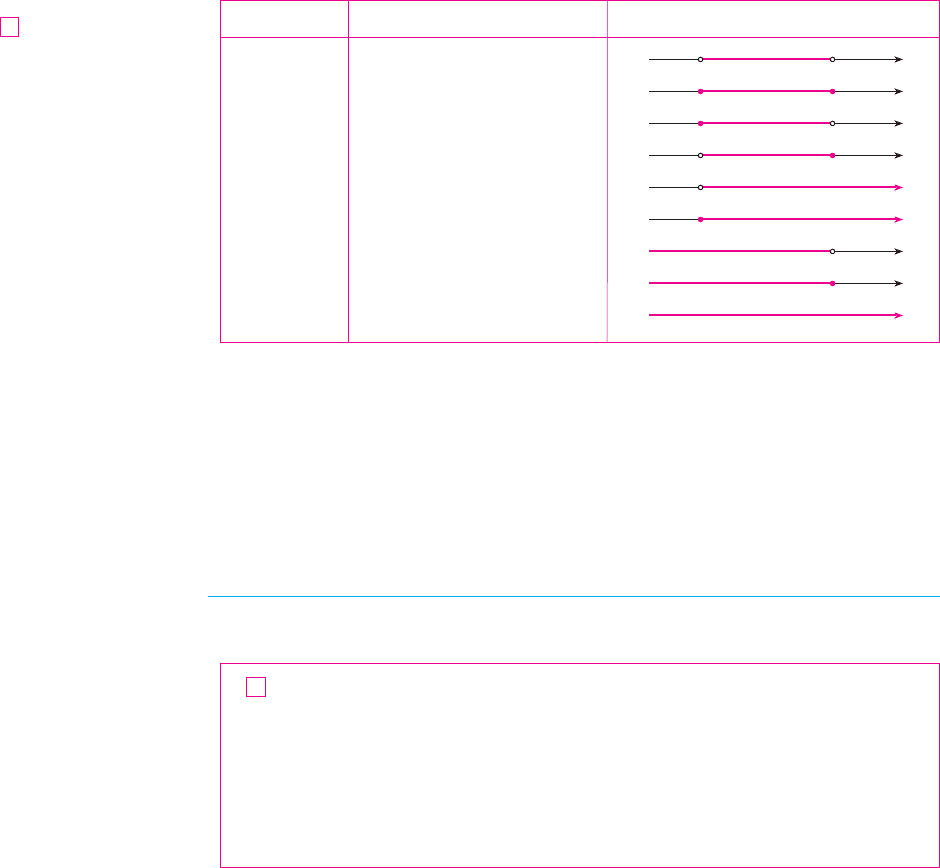
TABLE OF INTERVALS

We also need to consider inﬁnite intervals such as

This does not mean that (“inﬁnity”) is a number. The notation stands for the set

of all numbers that are greater than , so the symbol simply indicates that the interval

extends indeﬁnitely far in the positive direction.

INEQUALITIES

When working with inequalities, note the following rules.

RULES FOR INEQUALITIES

If , then .

2. If and , then .

3. If and , then .

4. If and , then .

5. If , then .

Rule 1 says that we can add any number to both sides of an inequality, and Rule 2 says

that two inequalities can be added. However, we have to be careful with multiplication.

Rule 3 says that we can multiply both sides of an inequality by a positive number, but

Rule 4 says that if we multiply both sides of an inequality by a negative number, then we

reverse the direction of the inequality. For example, if we take the inequality and

multiply by , we get , but if we multiply by , we get . Finally, Rule 5

says that if we take reciprocals, then we reverse the direction of an inequality (provided

the numbers are positive).

EXAMPLE 1 Solve the inequality .

SOLUTION The given inequality is satisﬁed by some values of but not by others. To solve

an inequality means to determine the set of numbers for which the inequality is true.

This is called the solution set.

1 ⫹ x

⬍

7x ⫹ 5

⫺6 ⬎⫺10⫺26

⬍

102

⬍

1兾a ⬎ 1兾b0

⬍

ac ⬎ bcc

⬍

bcc ⬎ 0a

⬍

a ⫹ c

⬍

b ⫹ dc

⬍

a ⫹ c

⬍

b ⫹ ca

⬍

⬁a

共a, ⬁兲⬁

共a, ⬁兲苷兵x

ⱍ

x ⬎ a其

||||

APPENDIX A NUMBERS, INEQUALITIES, AND ABSOLUTE VALUES

Notation Set description Picture

(set of all real numbers)⺢共⫺⬁, ⬁兲

兵x

ⱍ

x 艋 b其共⫺⬁, b兴

兵x

ⱍ

⬍

b其共⫺⬁, b兲

兵x

ⱍ

x 艌 a其关a, ⬁兲

兵x

ⱍ

x ⬎ a其共a, ⬁兲

兵x

ⱍ

⬍

x 艋 b其共a, b兴

兵x

ⱍ

a 艋 x

⬍

b其关a, b兲

兵x

ⱍ

a 艋 x 艋 b其关a, b兴

兵x

ⱍ

⬍

b其共a, b兲

N Table 1 lists the nine possible types of inter-

vals. When these intervals are discussed, it is

always assumed that .a

⬍

First we subtract 1 from each side of the inequality (using Rule 1 with ):

Then we subtract from both sides (Rule 1 with ):

Now we divide both sides by

(

Rule 4 with

)

These steps can all be reversed, so the solution set consists of all numbers greater than

. In other words, the solution of the inequality is the interval . M

EXAMPLE 2 Solve the inequalities .

SOLUTION Here the solution set consists of all values of that satisfy both inequalities.

Using the rules given in (2), we see that the following inequalities are equivalent:

(add 2)

(divide by 3)

Therefore the solution set is . M

EXAMPLE 3 Solve the inequality .

SOLUTION First we factor the left side:

We know that the corresponding equation has the solutions 2 and 3.

The numbers 2 and 3 divide the real line into three intervals:

On each of these intervals we determine the signs of the factors. For instance,

Then we record these signs in the following chart:

Another method for obtaining the information in the chart is to use test values. For

instance, if we use the test value for the interval , then substitution in

gives

⫺ 5共1兲 ⫹ 6 苷 2

⫺ 5x ⫹ 6

共⫺⬁, 2兲x 苷 1

x ⫺ 2

⬍

0 ? x

⬍

2 ? x 僆共⫺⬁, 2兲

共3, ⬁兲共2, 3兲共⫺⬁, 2兲

共x ⫺ 2兲共x ⫺ 3兲苷 0

共x ⫺ 2兲共x ⫺ 3兲艋 0

⫺ 5x ⫹ 6 艋 0

关2, 5兲

2 艋 x

⬍

6 艋 3x

⬍

4 艋 3x ⫺ 2

⬍

4 艋 3x ⫺ 2

⬍

(

⫺

, ⬁

)

⫺

x ⬎⫺

苷 ⫺

c 苷 ⫺

⫺6

⫺6x

⬍

c 苷 ⫺7x7x

⬍

7x ⫹ 4

c 苷 ⫺1

APPENDIX A NUMBERS, INEQUALITIES, AND ABSOLUTE VALUES

||||

FIGURE 4

y=≈-5x+6

234

N A visual method for solving Example 3 is to

use a graphing device to graph the parabola

(as in Figure 4) and observe

that the curve lies on or below the -axis when

.2 艋 x 艋 3

y 苷 x

⫺ 5x ⫹ 6

Interval

⫺⫺ ⫹

⫹⫺ ⫺

⫹⫹ ⫹ x ⬎ 3

⬍

共x ⫺ 2兲共x ⫺ 3兲x ⫺ 3x ⫺ 2

The polynomial doesn’t change sign inside any of the three intervals, so we

conclude that it is positive on .

Then we read from the chart that is negative when . Thus

the solution of the inequality is

Notice that we have included the endpoints 2 and 3 because we are looking for values of

such that the product is either negative or zero. The solution is illustrated in Figure 5. M

EXAMPLE 4 Solve .

SOLUTION First we take all nonzero terms to one side of the inequality sign and factor the

resulting expression:

As in Example 3 we solve the corresponding equation and use the

solutions , , and to divide the real line into four intervals ,

, , and . On each interval the product keeps a constant sign as shown

in the following chart:

Then we read from the chart that the solution set is

The solution is illustrated in Figure 6.

ABSOLUTE VALUE

The absolute value of a number , denoted by , is the distance from to on the real

number line. Distances are always positive or , so we have

For example,

In general, we have

ⱍ

苷 ⫺a if a

⬍

ⱍ

苷 a if a 艌 0

ⱍ

3 ⫺

␲

ⱍ

苷

␲

⫺ 3

ⱍ

⫺ 1

ⱍ

苷

⫺ 1

ⱍ

苷 0

ⱍ

⫺3

ⱍ

苷 3

ⱍ

苷 3

for every number a

ⱍ

艌 0

ⱍ

兵x

ⱍ

⫺4

⬍

0 or x ⬎ 1其苷共⫺4, 0兲傼共1, ⬁兲

共1, ⬁兲共0, 1兲共⫺4, 0兲

共⫺⬁, ⫺4兲x 苷 1x 苷 0x 苷 ⫺4

x共x ⫺ 1兲共x ⫹ 4兲苷 0

x共x ⫺ 1兲共x ⫹ 4兲 ⬎ 0 orx

⫹ 3x

⫺ 4x ⬎ 0

⫹ 3x

⬎ 4x

兵x

ⱍ

2 艋 x 艋 3其苷关2, 3兴

共x ⫺ 2兲共x ⫺ 3兲艋 0

⬍

3共x ⫺ 2兲共x ⫺ 3兲

共⫺⬁, 2兲

⫺ 5x ⫹ 6

||||

APPENDIX A NUMBERS, INEQUALITIES, AND ABSOLUTE VALUES

023

FIGURE 5

Interval x

⫺⫺ ⫺ ⫺

⫺⫺ ⫹ ⫹

⫹⫺ ⫹ ⫺

⫹⫹ ⫹ ⫹ x ⬎ 1

⬍

⫺4

⬍

⫺4

x共x ⫺ 1兲共x ⫹ 4兲x ⫹ 4x ⫺ 1

FIGURE 6

N Remember that if is negative, then

is positive.

⫺aa

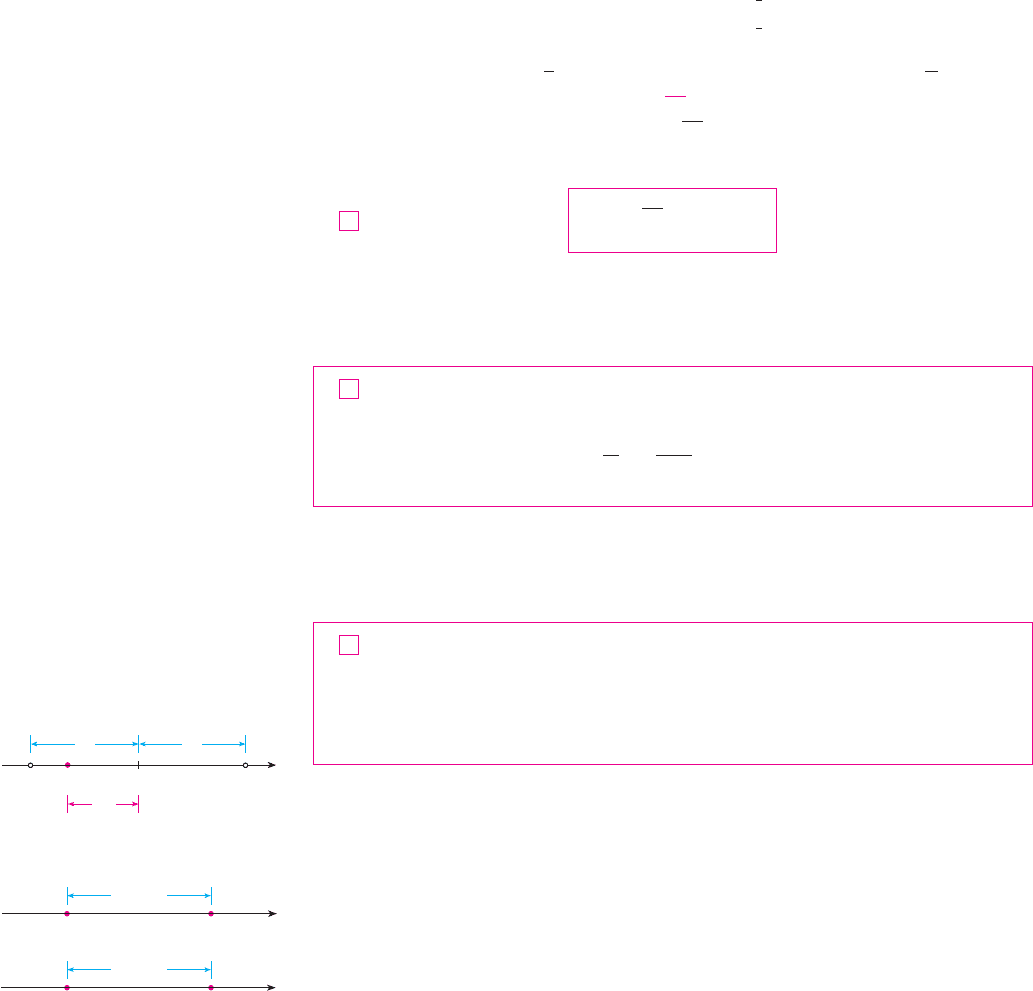
APPENDIX A NUMBERS, INEQUALITIES, AND ABSOLUTE VALUES

||||

a a

|x|

FIGURE 7

|a-b|

FIGURE 8

Length of a line segment=|a-b|

EXAMPLE 5 Express without using the absolute-value symbol.

SOLUTION

Recall that the symbol means “the positive square root of.” Thus means

and . Therefore, the equation is not always true. It is true only when

. If , then , so we have . In view of (3), we then have the

equation

which is true for all values of .

Hints for the proofs of the following properties are given in the exercises.

PROPERTIES OF ABSOLUTE VALUES Suppose and are any real numbers and

is an integer. Then

1. 2. 3.

For solving equations or inequalities involving absolute values, it’s often very helpful

to use the following statements.

Suppose . Then

4. if and only if

5. if and only if

6. if and only if or

For instance, the inequality says that the distance from to the origin is less

than , and you can see from Figure 7 that this is true if and only if lies between and .

If and are any real numbers, then the distance between and is the absolute value

of the difference, namely, , which is also equal to . (See Figure 8.)

EXAMPLE 6 Solve .

SOLUTION By Property 4 of (6), is equivalent to

So or . Thus or . Mx 苷 1x 苷 42x 苷 22x 苷 8

2x ⫺ 5 苷 ⫺3or2x ⫺ 5 苷 3

ⱍ

2x ⫺ 5

ⱍ

苷 3

ⱍ

2x ⫺ 5

ⱍ

苷 3

ⱍ

b ⫺ a

ⱍⱍ

a ⫺ b

ⱍ

baba

a⫺axa

ⱍ

⬍

⫺ax ⬎ a

ⱍ

⬎ a

⫺a

⬍

ⱍ

⬍

x 苷 ⫾a

ⱍ

苷 a

a ⬎ 0

ⱍ

苷

ⱍ

共b 苷 0兲

冟

苷

ⱍ

苷

ⱍ

ⱍⱍ

ⱍ

苷

ⱍ

苷 ⫺a⫺a ⬎ 0a

⬍

0a 艌 0

苷 as 艌 0s

苷 r

r 苷 s

苷

再

3x ⫺ 2

2 ⫺ 3x

if x 艌

if x

⬍

ⱍ

3x ⫺ 2

ⱍ

苷

再

3x ⫺ 2

⫺共3x ⫺ 2兲

if 3x ⫺ 2 艌 0

if 3x ⫺ 2

⬍

ⱍ

3x ⫺ 2

ⱍ