Stewart J. Calculus
Подождите немного. Документ загружается.

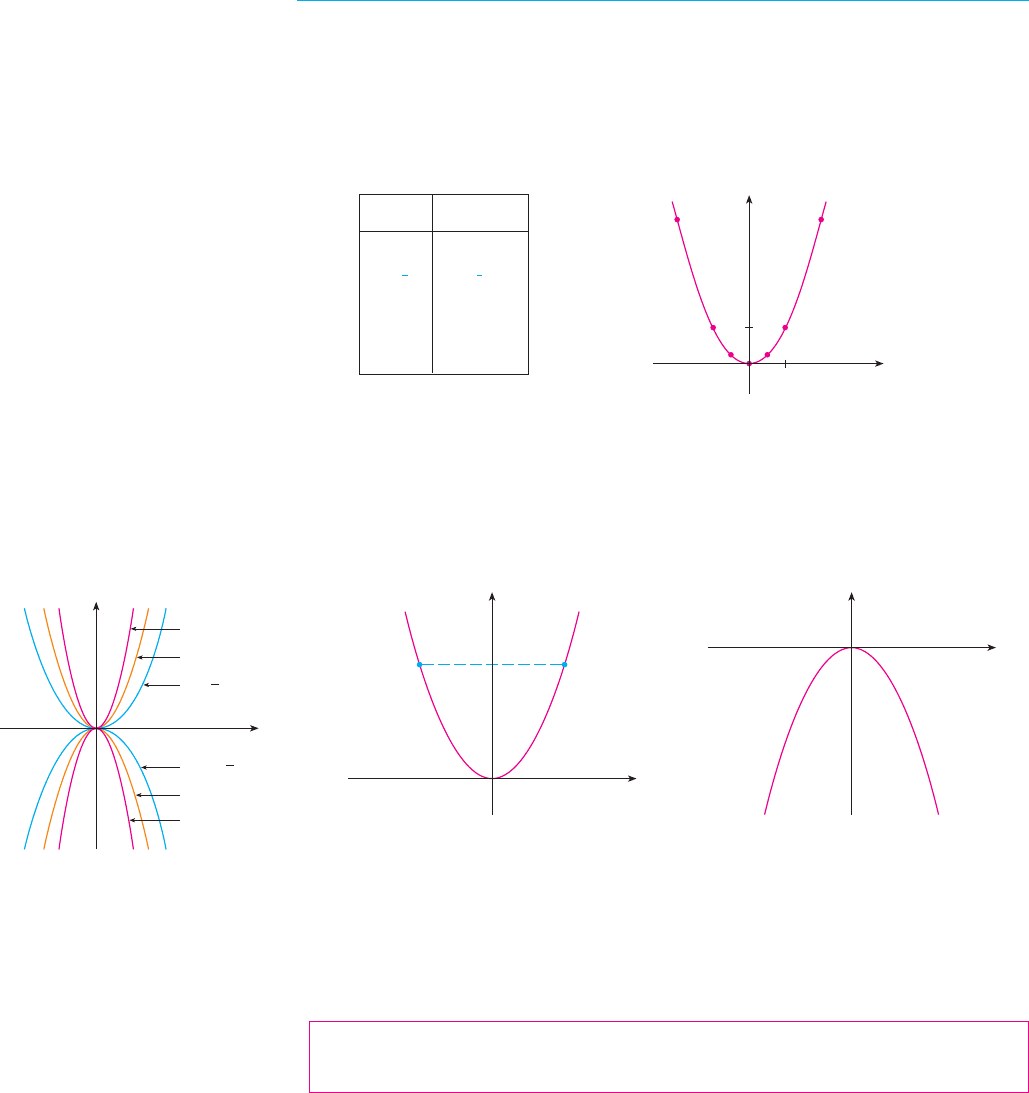
PARABOLAS
The geometric properties of parabolas are reviewed in Section 10.5. Here we regard a
parabola as a graph of an equation of the form .
EXAMPLE 3 Draw the graph of the parabola .
SOLUTION We set up a table of values, plot points, and join them by a smooth curve to
obtain the graph in Figure 3.
. M
Figure 4 shows the graphs of several parabolas with equations of the form for
various values of the number . In each case the vertex, the point where the parabola
changes direction, is the origin. We see that the parabola opens upward if
and downward if (as in Figure 5).
Notice that if satisfies , then so does . This corresponds to the geo-
metric fact that if the right half of the graph is reflected about the -axis, then the left half
of the graph is obtained. We say that the graph is symmetric with respect to the y-axis.
The graph of an equation is symmetric with respect to the -axis if the equation is
unchanged when is replaced by .
If we interchange and in the equation , the result is , which also rep-
resents a parabola. (Interchanging and amounts to reflecting about the diagonal line
.) The parabola opens to the right if and to the left if
.
(Seea
⬍
0a ⬎ 0x 苷 ay
2
y 苷 x
yx
x 苷 ay
2
y 苷 ax
2
yx
⫺xx
y
y
共⫺x, y兲y 苷 ax
2
共x, y兲
FIGURE 5
x
0
y
(_x,y) (x,y)
x
0
y
(a) y=a≈, a>0 (b) y=a≈, a<0
y
x
y=2≈
y=≈
y=_≈
y=_2≈
y=≈
1
2
y=_≈
1
2
FIGURE 4
a
⬍
0
a ⬎ 0y 苷 ax
2
a
y 苷 ax
2
FIGURE 3
0
y
1
x
1
y=≈
y 苷 x
2
y 苷 ax
2
⫹ bx ⫹ c
A18
||||
APPENDIX C GRAPHS OF SECOND-DEGREE EQUATIONS
x
00
1
4
9⫾3
⫾2
⫾1
1
4
⫾
1
2
y 苷 x
2

Figure 6.) This time the parabola is symmetric with respect to the -axis because if
satisfies , then so does .
The graph of an equation is symmetric with respect to the -axis if the equation is
unchanged when is replaced by .
EXAMPLE 4 Sketch the region bounded by the parabola and the line .
SOLUTION First we find the points of intersection by solving the two equations. Substituting
into the equation , we get , which gives
so or . Thus the points of intersection are and , and we draw
the line passing through these points. We then sketch the parabola by
referring to Figure 6(a) and having the parabola pass through and . The
region bounded by and means the finite region whose boundaries are
these curves. It is sketched in Figure 7. M
ELLIPSES
The curve with equation
where and are positive numbers, is called an ellipse in standard position. (Geometric
properties of ellipses are discussed in Section 10.5.) Observe that Equation 2 is unchanged
if is replaced by or is replaced by , so the ellipse is symmetric with respect to
both axes. As a further aid to sketching the ellipse, we find its intercepts.
The x-intercepts of a graph are the -coordinates of the points where the graph
intersects the -axis. They are found by setting in the equation of the graph.
The y-intercepts are the -coordinates of the points where the graph intersects the
-axis. They are found by setting in its equation.
If we set in Equation 2, we get and so the -intercepts are . Setting
, we get , so the -intercepts are . Using this information, together with
symmetry, we sketch the ellipse in Figure 8. If , the ellipse is a circle with radius .aa 苷 b
⫾byy
2
苷 b
2
x 苷 0
⫾axx
2
苷 a
2
y 苷 0
x 苷 0y
y
y 苷 0x
x
⫺yy⫺xx
ba
x
2
a
2
⫹
y
2
b
2
苷 1
2
y 苷 x ⫺ 2x 苷 y
2
共1, ⫺1兲共4, 2兲
x 苷 y
2
y 苷 x ⫺ 2
共1, ⫺1兲共4, 2兲⫺1y 苷 2
0 苷 y
2
⫺ y ⫺ 2 苷 共y ⫺ 2兲共y ⫹ 1兲
y ⫹ 2 苷 y
2
x 苷 y
2
x 苷 y ⫹ 2
y 苷 x ⫺ 2x 苷 y
2
⫺yy
x
FIGURE 6
x
0
y
x
0
y
(a) x=a¥, a>0 (b) x=a¥, a<0
共x, ⫺y兲x 苷 ay
2
共x, y兲x
APPENDIX C GRAPHS OF SECOND-DEGREE EQUATIONS
||||
A19
FIGURE 7
x
0
y
1
2
4
y=x-2
x=¥
(1,_1)
(4,2)
0
x
y
(0,b)
(0,_b)
(a,0)
(_a,0)
FIGURE 8
≈
a@
¥
b@
+ =1
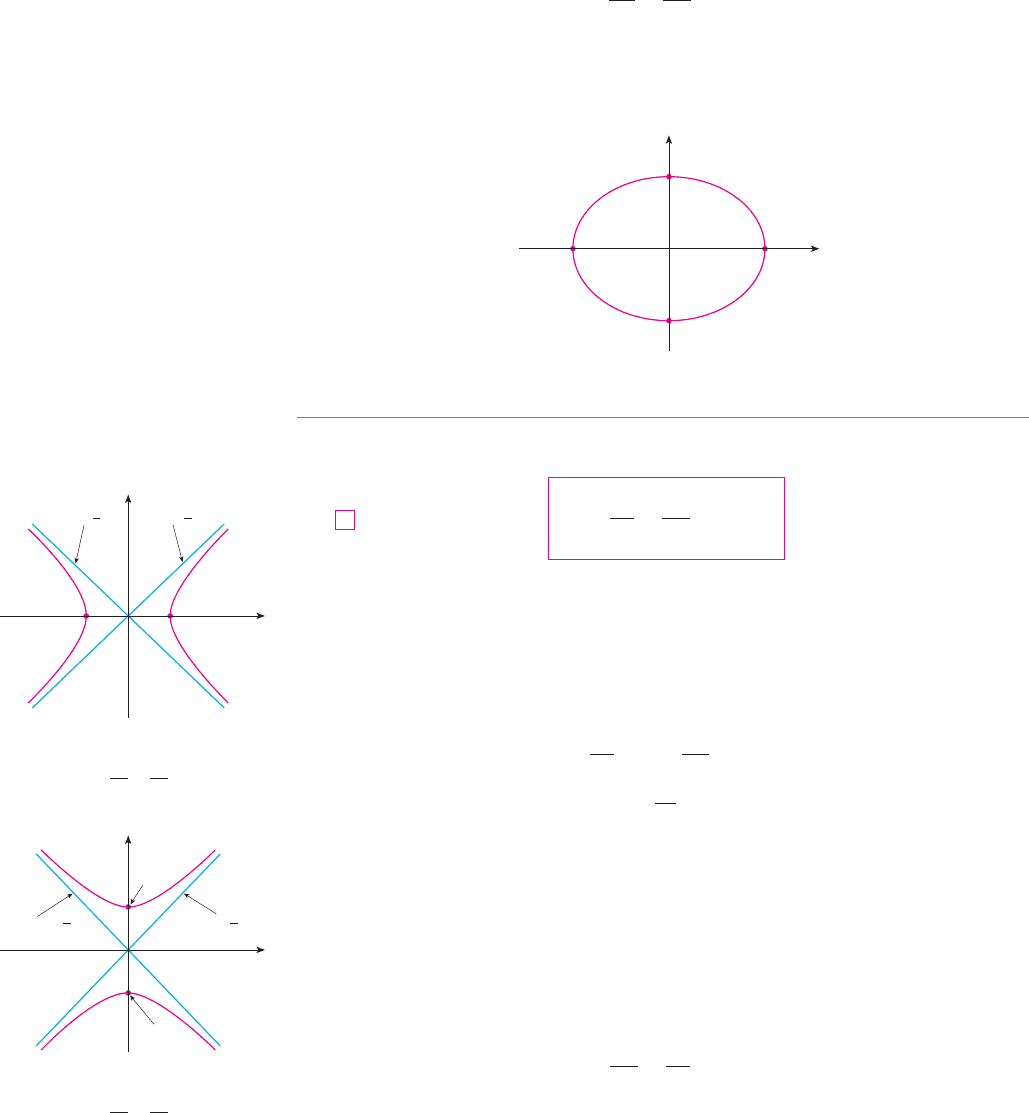
EXAMPLE 5 Sketch the graph of .
SOLUTION We divide both sides of the equation by 144:
The equation is now in the standard form for an ellipse (2), so we have , ,
, and . The -intercepts are ; the -intercepts are . The graph is
sketched in Figure 9.
M
HYPERBOLAS
The curve with equation
is called a hyperbola in standard position. Again, Equation 3 is unchanged when is
replaced by or is replaced by , so the hyperbola is symmetric with respect to both
axes. To find the -intercepts we set and obtain and . However, if
we put in Equation 3, we get , which is impossible, so there is no -inter-
cept. In fact, from Equation 3 we obtain
which shows that and so . Therefore we have or .
This means that the hyperbola consists of two parts, called its branches. It is sketched in
Figure 10.
In drawing a hyperbola it is useful to draw first its asymptotes, which are the lines
and shown in Figure 10. Both branches of the hyperbola
approach the asymptotes; that is, they come arbitrarily close to the asymptotes. This
involves the idea of a limit, which is discussed in Chapter 2. (See also Exercise 55 in
Section 4.5.)
By interchanging the roles of and we get an equation of the form
which also represents a hyperbola and is sketched in Figure 11.
y
2
a
2
⫺
x
2
b
2
苷 1
yx
y 苷 ⫺共b兾a兲xy 苷 共b兾a兲x
x 艋⫺ax 艌 a
ⱍ
x
ⱍ
苷
s
x
2
艌 ax
2
艌 a
2
x
2
a
2
苷 1 ⫹
y
2
b
2
艌 1
yy
2
苷 ⫺b
2
x 苷 0
x 苷 ⫾ax
2
苷 a
2
y 苷 0x
⫺yy⫺x
x
x
2
a
2
⫺
y
2
b
2
苷 1
3
0
x
y
(0,3)
(4,0)
(_4,0)
(0,_3)
FIGURE 9
9≈+16¥=144
⫾3y⫾4xb 苷 3a 苷 4
b
2
苷 9a
2
苷 16
x
2
16
⫹
y
2
9
苷 1
9x
2
⫹ 16y
2
苷 144
A20
||||
APPENDIX C GRAPHS OF SECOND-DEGREE EQUATIONS
0
y
x
(_a,0)
(a,0)
y=_x
b
a
y=x
b
a
FIGURE 10
The hyperbola - =1
≈
a@
¥
b@
FIGURE 11
The hyperbola - =1
¥
a@
≈
b@
y
0
x
(0,a)
(0,_a)
y=_ x
a
b
y=x
a
b
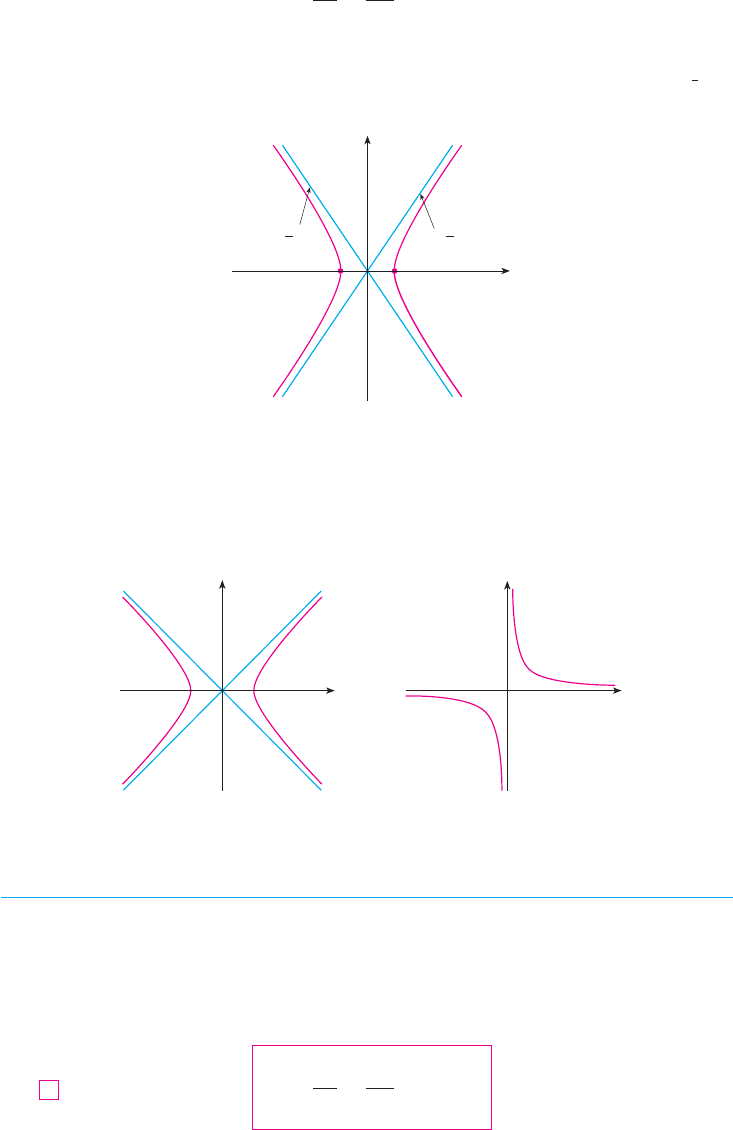
EXAMPLE 6 Sketch the curve .
SOLUTION Dividing both sides by 36, we obtain
which is the standard form of the equation of a hyperbola (Equation 3). Since ,
the -intercepts are . Since , we have and the asymptotes are .
The hyperbola is sketched in Figure 12.
M
If , a hyperbola has the equation (or ) and is called an
equilateral hyperbola [see Figure 13(a)]. Its asymptotes are , which are perpendi-
cular. If an equilateral hyperbola is rotated by , the asymptotes become the - and
-axes, and it can be shown that the new equation of the hyperbola is , where is a
constant [see Figure 13(b)].
SHIFTED CONICS
Recall that an equation of the circle with center the origin and radius is , but
if the center is the point , then the equation of the circle becomes
Similarly, if we take the ellipse with equation
x
2
a
2
⫹
y
2
b
2
苷 1
4
共x ⫺ h兲
2
⫹ 共y ⫺ k兲
2
苷 r
2
共h, k兲
x
2
⫹ y
2
苷 r
2
r
FIGURE 13
Equilateral hyperbolas
(a) ≈-¥=a@ (b) xy=k (k>0)
0
y
x
0
y
x
y=xy=_x
kxy 苷 ky
x45⬚
y 苷 ⫾x
y
2
⫺ x
2
苷 a
2
x
2
⫺ y
2
苷 a
2
b 苷 a
FIGURE 12
The hyperbola 9≈-4¥=36
0
y
(_2,0)
(2,0)
x
y=x
3
2
y=_x
3
2
y 苷 ⫾
(
3
2
)
xb 苷 3b
2
苷 9⫾2x
a
2
苷 4
x
2
4
⫺
y
2
9
苷 1
9x
2
⫺ 4y
2
苷 36
APPENDIX C GRAPHS OF SECOND-DEGREE EQUATIONS
||||
A21
A22
||||
APPENDIX C GRAPHS OF SECOND-DEGREE EQUATIONS
and translate it (shift it) so that its center is the point , then its equation becomes
(See Figure 14.)
Notice that in shifting the ellipse, we replaced by and by in Equation 4
to obtain Equation 5. We use the same procedure to shift the parabola so that its
vertex (the origin) becomes the point as in Figure 15. Replacing by and by
, we see that the new equation is
EXAMPLE 7 Sketch the graph of the equation .
SOLUTION First we complete the square:
In this form we see that the equation represents the parabola obtained by shifting
so that its vertex is at the point . The graph is sketched in Figure 16.
M
FIGURE 16
y=2≈-4x+1
x
0
y
1
321
(1,_1)
共1, 1兲y 苷 2x
2
y 苷 2共x
2
2x兲 1 苷 2共x 1兲
2
1
y 苷 2x
2
4x 1
FIGURE 15
y
0x
(h,k)
y=a(x-h)@+k
y=a≈
y 苷 a共x h兲
2
kory k 苷 a共x h兲
2
y k
yx hx共h, k兲
y 苷 ax
2
y kyx hx
FIGURE 14
(0, 0)
y
(x-h,y-k)
(h,k)
(x,y)
x
¥
b@
≈
a@
+=1
(x-h)@
a@
(y-k)@
b@
+=1
b
a
h
b
k
a
共x h兲
2
a
2
共y k兲
2
b
2
苷 1
5
共h, k兲
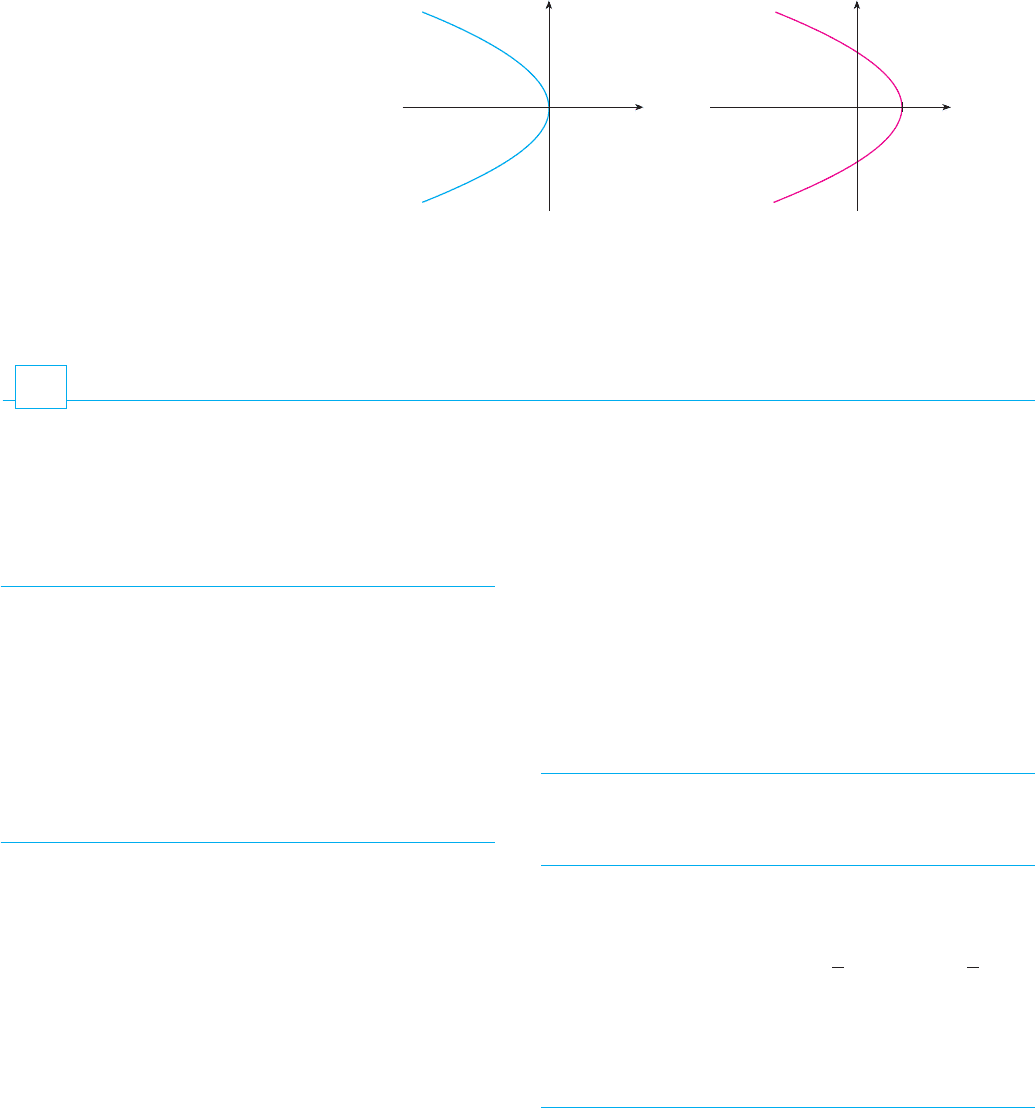
EXAMPLE 8 Sketch the curve .
SOLUTION This time we start with the parabola (as in Figure 6 with )
and shift one unit to the right to get the graph of . (See Figure 17.)
M
FIGURE 17
(a) x=_¥
0
y
x
(b) x=1-¥
x
1
0
y
x 苷 1 y
2
a 苷 1x 苷 y
2
x 苷 1 y
2
APPENDIX C GRAPHS OF SECOND-DEGREE EQUATIONS
||||
A23
15. 16.
17. 18.
19. 20.
21. 22.
23. 24.
25.
26.
27. 28.
29. 30.
31.
32.
33–34 Sketch the region bounded by the curves.
33. , 34. ,
35. Find an equation of the parabola with vertex that
passes through the points and .
36. Find an equation of the ellipse with center at the origin that
passes through the points and .
37– 40 Sketch the graph of the set.
37. 38.
39. 40.
兵共x, y兲
ⱍ
x
2
4y
2
4其兵共x, y兲
ⱍ
y x
2
1其
兵共x, y兲
ⱍ
x
2
y
2
4其兵共x, y兲
ⱍ
x
2
y
2
1其
(
2, 5
s
5
兾3
)(
1, 10
s
2
兾3
)
共3, 3兲共1, 3兲
共1, 1兲
x 2y 苷 2y 苷 4 x
2
y 苷 x
2
y 苷 3x
4x
2
9y
2
16x 54y 61 苷 0
x
2
4y
2
6x 5 苷 0
y
2
2x 6y 5 苷 0x 苷 4 y
2
x
2
y
2
4x 3 苷 0y 苷 x
2
6x 13
16x
2
9y
2
36y 苷 108
9共x 1兲
2
4共y 2兲
2
苷 36
y 苷 x
2
2xxy 苷 4
2x
2
5y
2
苷 109y
2
x
2
苷 9
9x
2
25y
2
苷 225x 苷 y
2
1
y 苷 x
2
24x
2
y
2
苷 1
25x
2
4y
2
苷 10016x
2
25y
2
苷 400
1– 4 Find an equation of a circle that satisfies the given conditions.
1. Center , radius
2. Center , radius
3. Center at the origin, passes through
4. Center , passes through
5–9 Show that the equation represents a circle and find the
center and radius.
5.
6.
7.
8.
9.
10. Under what condition on the coefficients , , and does the
equation represent a circle?
When that condition is satisfied, find the center and radius of
the circle.
11–32 Identify the type of curve and sketch the graph. Do not plot
points. Just use the standard graphs given in Figures 5, 6, 8, 10,
and 11 and shift if necessary.
11. 12.
13. 14.
x 苷 2y
2
x
2
4y
2
苷 16
y
2
x
2
苷 1y 苷 x
2
x
2
y
2
ax by c 苷 0
cba
2x
2
2y
2
x y 苷 1
16x
2
16y
2
8x 32y 1 苷 0
x
2
y
2
x 苷 0
x
2
y
2
6y 2 苷 0
x
2
y
2
4x 10y 13 苷 0
共4, 6兲共1, 5兲
共4, 7兲
10共2, 8兲
5共3, 1兲
EXERCISES
C
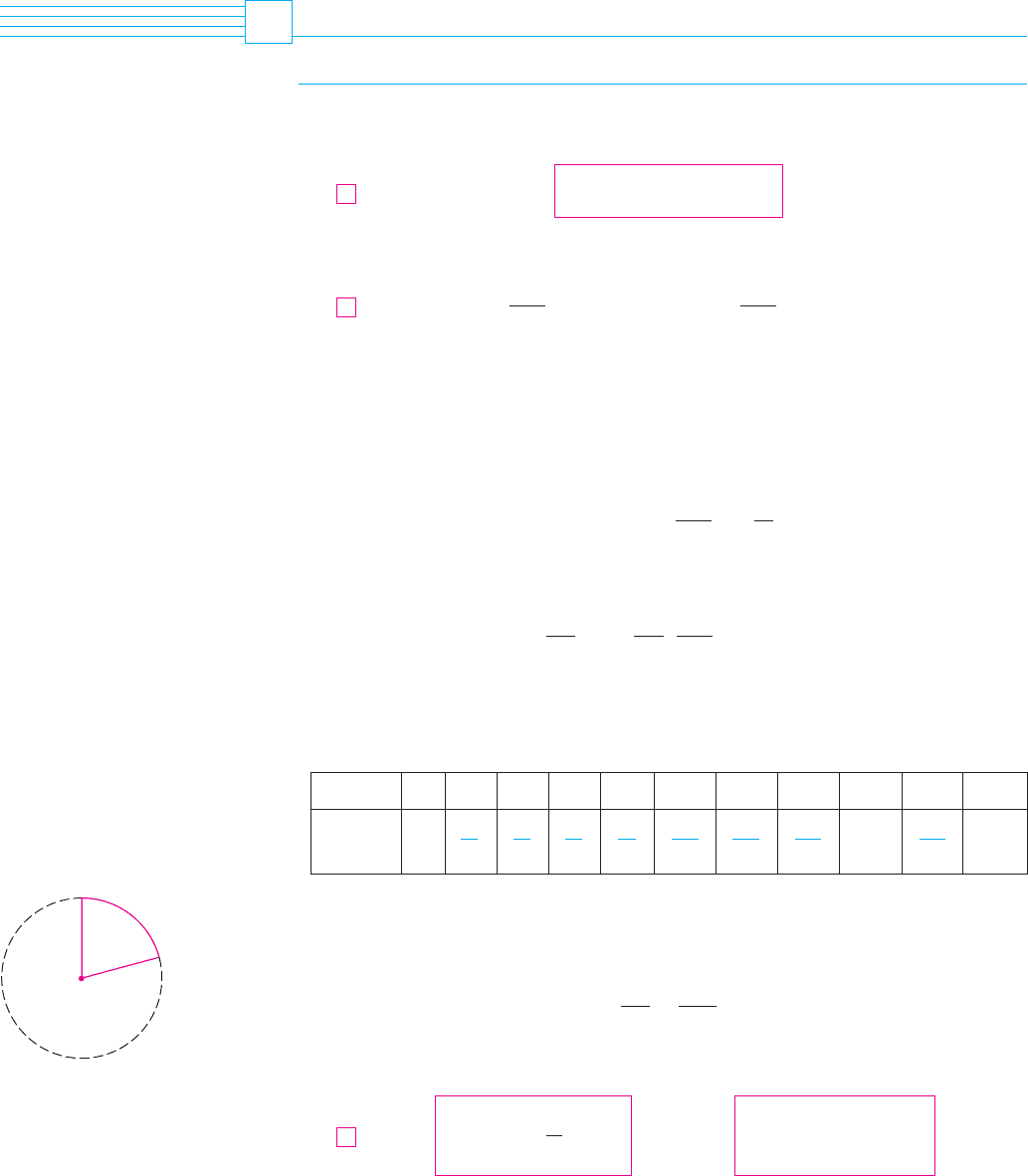
TRIGONOMETRY
ANGLES
Angles can be measured in degrees or in radians (abbreviated as rad). The angle given by
a complete revolution contains , which is the same as rad. Therefore
and
EXAMPLE 1
(a) Find the radian measure of . (b) Express rad in degrees.
SOLUTION
(a) From Equation 1 or 2 we see that to convert from degrees to radians we multiply by
. Therefore
(b) To convert from radians to degrees we multiply by . Thus
M
In calculus we use radians to measure angles except when otherwise indicated. The fol-
lowing table gives the correspondence between degree and radian measures of some com-
mon angles.
Figure 1 shows a sector of a circle with central angle and radius subtending an arc
with length . Since the length of the arc is proportional to the size of the angle, and since
the entire circle has circumference and central angle , we have
Solving this equation for and for , we obtain
Remember that Equations 3 are valid only when is measured in radians.
a 苷 r
苷
a
r
3
a
2
苷
a
2
r
2
2
r
a
r
5
4
rad 苷
5
4
冉
180
冊
苷 225
180兾
60 苷 60
冉
180
冊
苷
3
rad
兾180
5
兾460
1 苷
180
rad ⬇ 0.017 rad1 rad 苷
冉
180
冊
⬇ 57.3
2
rad 苷 180
1
2
360
D
A24
||||
APPENDIX D TRIGONOMETRY
Degrees 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
Radians 0 2
3
2
5
6
3
4
2
3
2
3
4
6
r
r
a
¨
FIGURE 1

In particular, putting in Equation 3, we see that an angle of 1 rad is the angle sub-
tended at the center of a circle by an arc equal in length to the radius of the circle (see
Figure 2).
EXAMPLE 2
(a) If the radius of a circle is 5 cm, what angle is subtended by an arc of 6 cm?
(b) If a circle has radius 3 cm, what is the length of an arc subtended by a central angle
of rad?
SOLUTION
(a) Using Equation 3 with and , we see that the angle is
(b) With cm and rad, the arc length is
M
The standard position of an angle occurs when we place its vertex at the origin of a
coordinate system and its initial side on the positive -axis as in Figure 3. A positive angle
is obtained by rotating the initial side counterclockwise until it coincides with the termi-
nal side. Likewise, negative angles are obtained by clockwise rotation as in Figure 4.
Figure 5 shows several examples of angles in standard position. Notice that different
angles can have the same terminal side. For instance, the angles , , and
have the same initial and terminal sides because
and rad represents a complete revolution.
FIGURE 5
Angles in standard position
y
x
0
¨=_
5π
4
0
y
x
¨=
11π
4
0
y
x
¨=
3π
4
0
y
x
¨=_
π
2
0
y
x
¨=1
2
3
4
2
苷
11
4
3
4
2
苷
5
4
11
兾45
兾43
兾4
0
y
x
¨
initial side
terminal
side
FIGURE 3 ¨˘0
0
y
x
¨
initial side
terminal side
FIGURE 4 ¨<0
x
a 苷 r
苷 3
冉
3
8
冊
苷
9
8
cm
苷 3
兾8r 苷 3
苷
6
5
苷 1.2 rad
r 苷 5a 苷 6
3
兾8
a 苷 r
APPENDIX D TRIGONOMETRY
||||
A25
r
r
r
1
ra
d
FIGURE 2
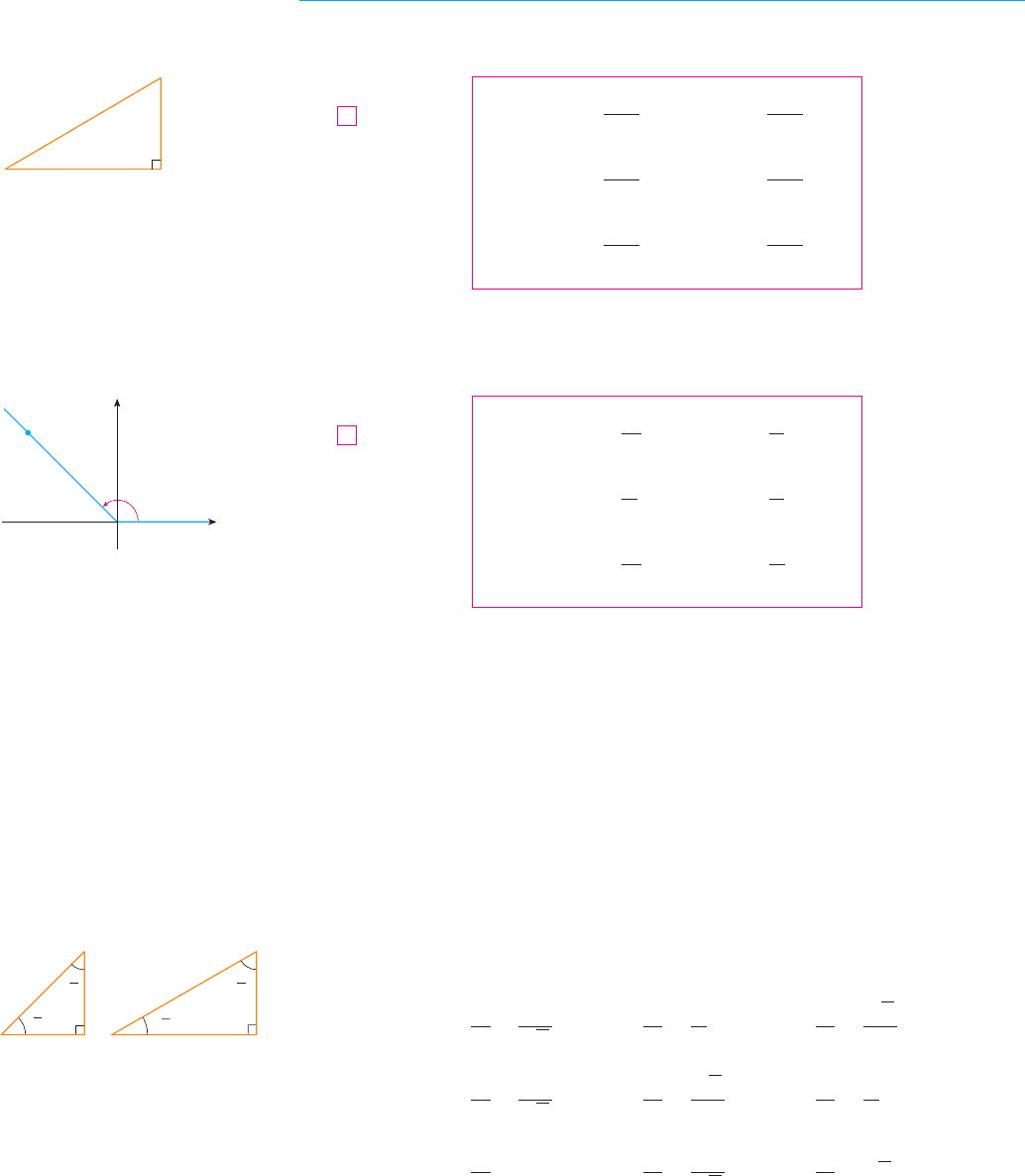
THE TRIGONOMETRIC FUNCTIONS
For an acute angle the six trigonometric functions are defined as ratios of lengths of sides
of a right triangle as follows (see Figure 6).
This definition doesn’t apply to obtuse or negative angles, so for a general angle in
standard position we let be any point on the terminal side of and we let be the
distance as in Figure 7. Then we define
Since division by 0 is not defined, and are undefined when and
and are undefined when . Notice that the definitions in (4) and (5) are consis-
tent when is an acute angle.
If is a number, the convention is that means the sine of the angle whose radian
measure is . For example, the expression implies that we are dealing with an angle
of 3 rad. When finding a calculator approximation to this number, we must remember to
set our calculator in radian mode, and then we obtain
If we want to know the sine of the angle we would write and, with our calculator
in degree mode, we find that
The exact trigonometric ratios for certain angles can be read from the triangles in Fig-
ure 8. For instance,
tan
4
苷 1 tan
6
苷
1
s
3
tan
3
苷
s
3
cos
4
苷
1
s
2
cos
6
苷
s
3
2
cos
3
苷
1
2
sin
4
苷
1
s
2
sin
6
苷
1
2
sin
3
苷
s
3
2
sin 3 ⬇ 0.05234
sin 33
sin 3 ⬇ 0.14112
sin 3
sin
y 苷 0cot
csc
x 苷 0sec
tan
cot
苷
x
y
tan
苷
y
x
sec
苷
r
x
cos
苷
x
r
csc
苷
r
y
sin
苷
y
r
5
ⱍ
OP
ⱍ
r
P共x, y兲
cot
苷
adj
opp
tan
苷
opp
adj
sec
苷
hyp
adj
cos
苷
adj
hyp
csc
苷
hyp
opp
sin
苷
opp
hyp
4
A26
||||
APPENDIX D TRIGONOMETRY
opposite
hypotenuse
adjacent
¨
FIGURE 6
P(x,y)
O
y
x
r
¨
FIGURE 7
1
1
2œ
„
π
4
π
4
1
2
π
3
œ
„
3
π
6
FIGURE 8
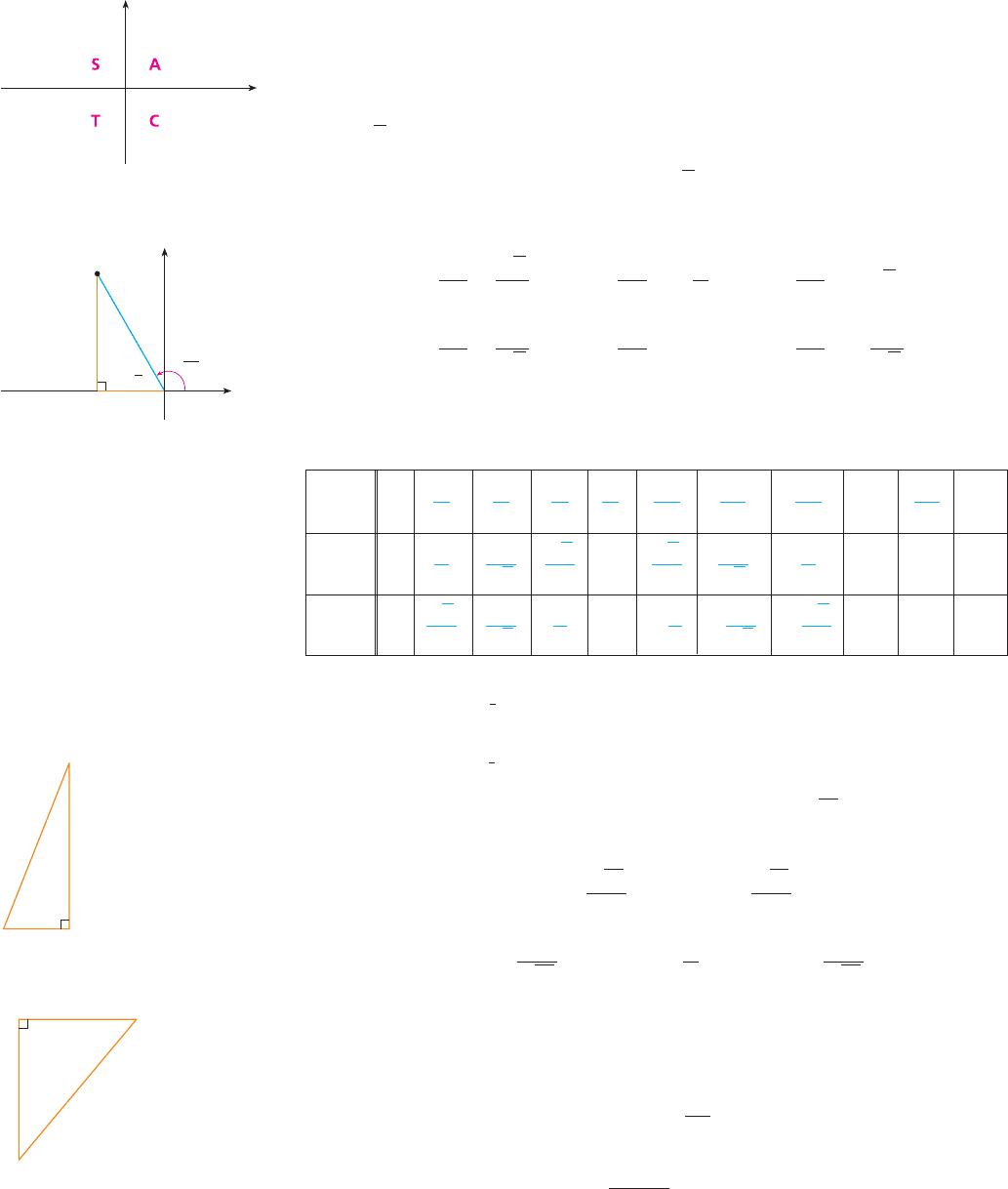
The signs of the trigonometric functions for angles in each of the four quadrants can be
remembered by means of the rule “All Students Take Calculus” shown in Figure 9.
EXAMPLE 3 Find the exact trigonometric ratios for .
SOLUTION From Figure 10 we see that a point on the terminal line for is
. Therefore, taking
in the definitions of the trigonometric ratios, we have
M
The following table gives some values of and found by the method of
Example 3.
EXAMPLE 4 If and , find the other five trigonometric functions
of .
SOLUTION Since , we can label the hypotenuse as having length 5 and the
adjacent side as having length 2 in Figure 11. If the opposite side has length , then the
Pythagorean Theorem gives and so , . We can now use
the diagram to write the other five trigonometric functions:
M
EXAMPLE 5 Use a calculator to approximate the value of in Figure 12.
SOLUTION From the diagram we see that
Therefore M
x 苷
16
tan 40
⬇ 19.07
tan 40 苷
16
x
x
cot
苷
2
s
21
sec
苷
5
2
csc
苷
5
s
21
tan
苷
s
21
2
sin
苷
s
21
5
x 苷
s
21
x
2
苷 21x
2
4 苷 25
x
cos
苷
2
5
0
兾2cos
苷
2
5
cos
sin
csc
2
3
苷
2
s
3
sec
2
3
苷 2 cot
2
3
苷
1
s
3
sin
2
3
苷
s
3
2
cos
2
3
苷
1
2
tan
2
3
苷
s
3
r 苷 2 y 苷
s
3
x 苷 1
P
(
1,
s
3
)
苷 2
兾3
苷 2
兾3
APPENDIX D TRIGONOMETRY
||||
A27
0
01 00
10 011
s
3
2
1
s
2
1
2
1
2
1
s
2
s
3
2
cos
1
1
2
1
s
2
s
3
2
s
3
2
1
s
2
1
2
sin
2
3
2
5
6
3
4
2
3
2
3
4
6
0
y
x
sin¨>0
tan¨>0
all ratios>0
cos¨>0
FIGURE 9
y
0x
2π
3
π
3
2
œ
„
3
1
P{_1, œ
„
3}
FIGURE 10
16
40°
x
FIGURE 12
5
2
¨
x=œ„„21
FIGURE 11
