Stewart J. Calculus

Подождите немного. Документ загружается.

A38

||||

APPENDIX E SIGMA NOTATION

35.

36. Find the number such that .

37. Prove formula (b) of Theorem 3.

38. Prove formula (e) of Theorem 3 using mathematical

induction.

39. Prove formula (e) of Theorem 3 using a method similar to that

of Example 5, Solution 1 [start with .

40. Prove formula (e) of Theorem 3 using the following method

published by Abu Bekr Mohammed ibn Alhusain Alkarchi in

about

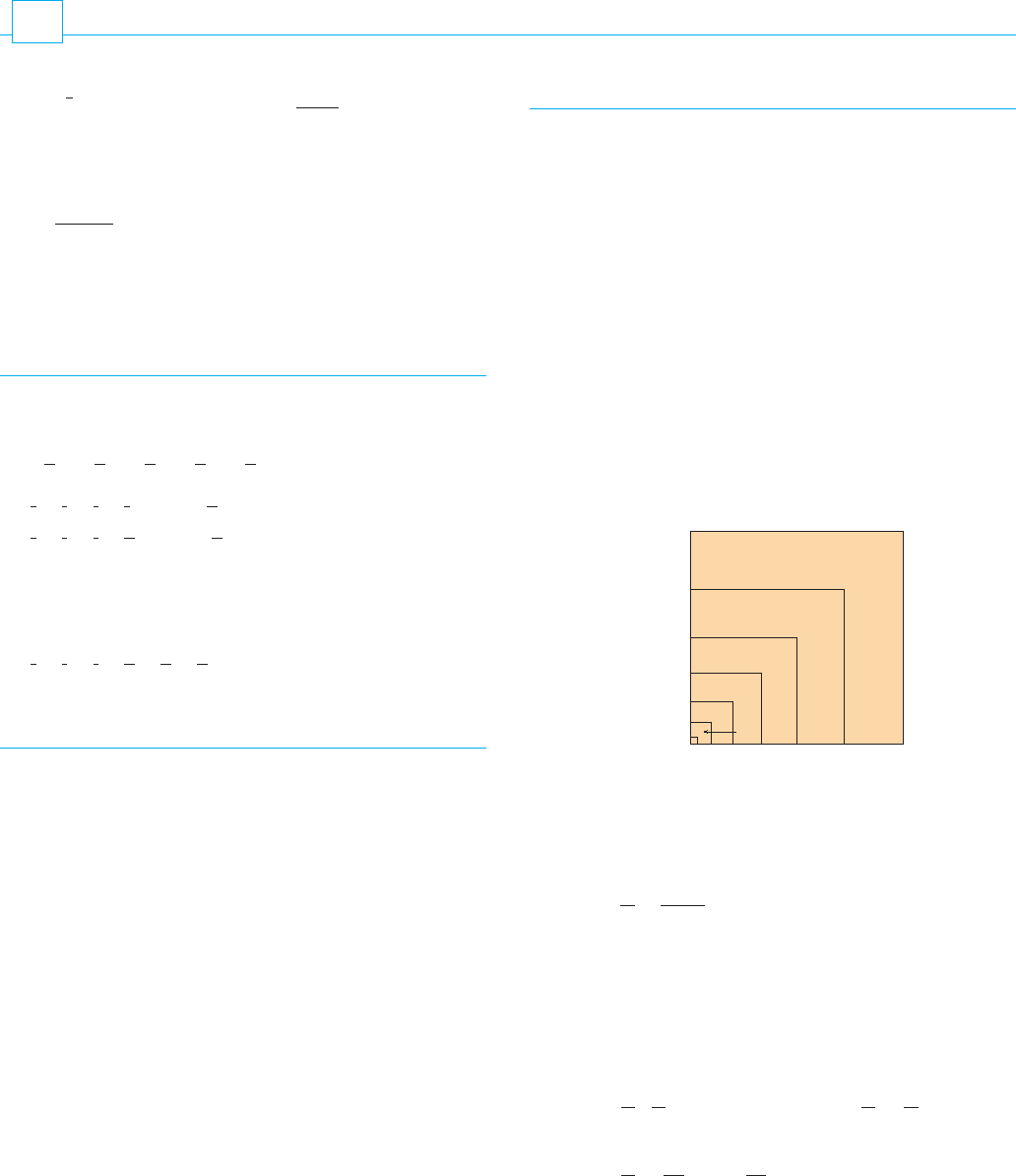
AD 1010. The ﬁgure shows a square in which

sides and have been divided into segments of lengths ,

, ,..., Thus the side of the square has length

so the area is . But the area is also the sum of the

areas of the n “gnomons” , ,..., shown in the ﬁgure.

Show that the area of is and conclude that formula (e) is

true.

41. Evaluate each telescoping sum.

(a) (b)

42. Prove the generalized triangle inequality:

43– 46 Find the limit.

43. 44.

45. lim

n l 

兺

i苷1

冋冉

冊

 5

冉

冊册

lim

n l 

兺

i苷1

冋冉

冊

 1

册

lim

n l 

兺

i苷1

冉

冊

冟

兺

i苷1

冟



兺

i苷1

ⱍ

兺

i苷1

共a

 a

i1

兲

兺

i苷3

冉



i  1

冊

兺

100

i苷1

共5

 5

i1

兲

兺

i苷1

关i

 共i  1兲

兴

12 3 4 5

...

nBA

G™

G£

G¢

G∞

.

.

关n共n  1兲兾2兴

n共n  1兲兾2n.32

1ADAB

ABCD

共1  i 兲

 i

兴

兺

i苷1

i 苷 78n

兺

i苷1

共i

 i  2兲

1–10 Write the sum in expanded form.

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11– 20 Write the sum in sigma notation.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21–35 Find the value of the sum.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

31. 32.

33. 34.

兺

i苷1

i共i  1兲共i  2兲

兺

i苷1

共i  1兲共i  2兲

兺

i苷1

共3  2i 兲

兺

i苷1

共i

 3i  4兲

兺

i苷1

共2  5i 兲

兺

i苷1

兺

i苷2

3i

兺

i苷0

共2

 i

兲

兺

100

i苷1

兺

n苷1

共1兲

兺

k苷0

cos k



兺

j苷1

j1

兺

i苷3

i共i  2兲

兺

i苷4

共3i  2兲

1  x  x

 x

共1兲

x  x

 x

x



1  2  4  8  16  32

1  3  5  7 共2n  1兲

2  4  6  8 2n











1  2  3  4 10

兺

i苷1

f 共x

兲 x

兺

n1

j苷0

共1兲

兺

n3

j苷n

兺

i苷1

兺

k苷5

兺

k苷0

2k  1

2k  1

兺

i苷4

兺

i苷4

兺

i苷1

i  1

兺

i苷1

EXERCISES

APPENDIX F PROOFS OF THEOREMS

||||

A39

48. Evaluate .

49. Evaluate .

50. Evaluate .

兺

i苷1

冋

兺

j苷1

共i  j 兲

册

兺

i苷1

共2i  2

兲

兺

i苷1

i1

46.

47. Prove the formula for the sum of a ﬁnite geometric series with

ﬁrst term and common ratio :

兺

i苷1

i1

苷 a  ar  ar

ar

n1

苷

a共r

 1兲

r  1

r 苷 1a

lim



兺

i苷1

冋冉

1 

冊

 2

冉

1 

冊册

PROOFS OF THEOREMS

In this appendix we present proofs of several theorems that are stated in the main body of

the text. The sections in which they occur are indicated in the margin.

SECTION 2.3 LIMIT LAWS Suppose that is a constant and the limits

and

exist. Then

1. 2.

3. 4.

PROOF OF LAW 4 Let be given. We want to ﬁnd such that

In order to get terms that contain and , we add and subtract

as follows:

(Triangle Inequality)

We want to make each of these terms less than .

Since , there is a number such that

Also, there is a number such that if , then

and therefore

ⱍ

t共x兲

ⱍ

苷

ⱍ

t共x兲  M  M

ⱍ



ⱍ

t共x兲  M

ⱍ



ⱍ



1 

ⱍ

t共x兲  M

ⱍ



ⱍ

x  a

ⱍ





 0

ⱍ

t共x兲  M

ⱍ





(

1 

ⱍ

)

then0



ⱍ

x  a

ⱍ





 0lim

x l a

t共x兲苷 M

兾2

苷

ⱍ

f 共x兲  L

ⱍⱍ

t共x兲

ⱍ



ⱍ

ⱍⱍ

t共x兲  M

ⱍ



ⱍ

关 f 共x兲  L兴t共x兲

ⱍ



ⱍ

L关t共x兲  M兴

ⱍ

苷

ⱍ

关 f 共x兲  L兴t共x兲  L关t共x兲  M 兴

ⱍ

f 共x兲t共x兲  LM

ⱍ

苷

ⱍ

f 共x兲t共x兲  Lt共x兲  Lt共x兲  LM

ⱍ

Lt共x兲

ⱍ

t共x兲  M

ⱍⱍ

f 共x兲  L

ⱍ

f 共x兲t共x兲  LM

ⱍ



then0



ⱍ

x  a

ⱍ





 00

M 苷 0lim

x l a

f 共x兲

t共x兲

苷

lim

关 f 共x兲t共x兲兴苷 LMlim

x l a

关cf共x兲兴苷 cL

lim

x l a

关 f 共x兲  t共x兲兴苷 L  Mlim

x l a

关 f 共x兲  t共x兲兴苷 L  M

lim

x l a

t共x兲苷 Mlim

x l a

f 共x兲苷 L

Since , there is a number such that

Let min . If , then we have ,

, and , so we can combine the inequalities to obtain

This shows that . M

PROOF OF LAW 3 If we take in Law 4, we get

(by Law 7) M

PROOF OF LAW 2 Using Law 1 and Law 3 with , we have

PROOF OF LAW 5 First let us show that

To do this we must show that, given , there exists such that

Observe that

We know that we can make the numerator small. But we also need to know that the

denominator is not small when is near . Since , there is a number

such that, whenever , we have

and therefore



ⱍ



ⱍ

t共x兲

ⱍ

苷

ⱍ

M  t共x兲  t共x兲

ⱍ



ⱍ

M  t共x兲

ⱍ



ⱍ

t共x兲

ⱍ

t共x兲  M

ⱍ



ⱍ



ⱍ

x  a

ⱍ





 0

lim

x l a

t共x兲苷 Max

冟

t共x兲



冟

苷

ⱍ

M  t共x兲

ⱍ

Mt共x兲

ⱍ

冟

t共x兲



冟



then0



ⱍ

x  a

ⱍ





 00

lim

x l a

t共x兲

苷

苷 lim

x l a

f 共x兲  共1兲 lim

x l a

t共x兲苷 lim

x l a

f 共x兲  lim

x l a

t共x兲

lim

关 f 共x兲  t共x兲兴苷 lim

关 f 共x兲  共1兲t共x兲兴苷 lim

f 共x兲  lim

共1兲t共x兲

c 苷 1

苷 c lim

x l a

f 共x兲

苷 lim

x l a

c ⴢ lim

x l a

f 共x兲

lim

x l a

关cf共x兲兴苷 lim

x l a

关t共x兲f 共x兲兴苷 lim

x l a

t共x兲 ⴢ lim

x l a

f 共x兲

t共x兲苷 c

lim

x l a

f 共x兲t共x兲苷 LM









苷 





(

1 

ⱍ

)

(

1 

ⱍ

)



ⱍ



(

1 

ⱍ

)

ⱍ

f 共x兲t共x兲  LM

ⱍ



ⱍ

f 共x兲  L

ⱍⱍ

t共x兲

ⱍ



ⱍ

ⱍⱍ

t共x兲  M

ⱍ



ⱍ

x  a

ⱍ







ⱍ

x  a

ⱍ







ⱍ

x  a

ⱍ







ⱍ

x  a

ⱍ





兵



其



苷

ⱍ

f 共x兲  L

ⱍ





(

1 

ⱍ

)

then0



ⱍ

x  a

ⱍ





 0lim

x l a

f 共x兲苷 L

A40

||||

APPENDIX F PROOFS OF THEOREMS

This shows that

and so, for these values of ,

Also, there exists such that

Let min . Then, for , we have

It follows that . Finally, using Law 4, we obtain

THEOREM If for all in an open interval that contains (except

possibly at ) and

and

then .

PROOF We use the method of proof by contradiction. Suppose, if possible, that .

Law 2 of limits says that

Therefore, for any , there exists such that

In particular, taking (noting that by hypothesis), we have a

number such that

then

Since for any number , we have

then

which simpliﬁes to

then

But this contradicts . Thus the inequality must be false. Therefore

. M

L  M

L  Mf 共x兲  t共x兲

t共x兲



f 共x兲0



ⱍ

x  a

ⱍ





关t共x兲  f 共x兲兴  共M  L兲



L  M0



ⱍ

x  a

ⱍ





aa 

ⱍ

关t共x兲  f 共x兲兴  共M  L兲

ⱍ



L  M0



ⱍ

x  a

ⱍ





 0

L  M  0 苷 L  M

ⱍ

关t共x兲  f 共x兲兴  共M  L兲

ⱍ



then0



ⱍ

x  a

ⱍ





 00

lim

x l a

关t共x兲  f 共x兲兴苷 M  L

L  M

L  M

lim

x l a

t共x兲苷 Mlim

x l a

f 共x兲苷 L

axf 共x兲  t共x兲

苷 lim

f 共x兲 lim

t共x兲

苷 L ⴢ

苷

lim

f 共x兲

t共x兲

苷 lim

f 共x兲

冉

t共x兲

冊

lim

x l a

1兾t共x兲苷 1兾M

冟

t共x兲



冟

苷

ⱍ

M  t共x兲

ⱍ

Mt共x兲

ⱍ



 苷 



ⱍ

x  a

ⱍ





兵



其



苷

ⱍ

t共x兲  M

ⱍ



then0



ⱍ

x  a

ⱍ





 0

ⱍ

Mt共x兲

ⱍ

苷

ⱍ

ⱍⱍ

t共x兲

ⱍ



ⱍ

ⴢ

ⱍ

苷

ⱍ

t共x兲

ⱍ



ⱍ

then0



ⱍ

x  a

ⱍ





APPENDIX F PROOFS OF THEOREMS

||||

A41

THE SQUEEZE THEOREM If for all in an open interval that

contains (except possibly at ) and

then

PROOF Let be given. Since , there is a number such that

if then

that is,

if then

Since , there is a number such that

then

that is,

then

Let min . If , then and ,

In particular,

and so . Therefore . M

SECTION 2.5 THEOREM If is continuous at and , then

PROOF Let be given. We want to ﬁnd a number such that

Since is continuous at , we have

and so there exists such that

Since , there exists such that

ⱍ

t共x兲 ⫺ b

ⱍ

⬍

␦

then0

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

⬎ 0lim

x l a

t共x兲苷 b

ⱍ

f 共y兲 ⫺ f 共b兲

ⱍ

⬍

␧then0

⬍

ⱍ

y ⫺ b

ⱍ

⬍

␦

⬎ 0

lim

y l b

f 共y兲苷 f 共b兲

ⱍ

f 共t共x兲兲 ⫺ f 共b兲

ⱍ

⬍

␧then0

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

⬎ 0␧⬎0

lim

x l a

f 共t共x兲兲苷 f 共b兲

lim

x l a

t共x兲苷 bbf

lim

x l a

t共x兲苷 L

ⱍ

t共x兲 ⫺ L

ⱍ

⬍

␧

L ⫺␧

⬍

t共x兲

⬍

L ⫹␧

L ⫺␧

⬍

f 共x兲艋 t共x兲艋 h共x兲

⬍

L ⫹␧

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

兵

␦

其

␦

苷

L ⫺␧

⬍

h共x兲

⬍

L ⫹␧0

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

ⱍ

h共x兲 ⫺ L

ⱍ

⬍

␧0

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

⬎ 0lim

x l a

h共x兲苷 L

L ⫺␧

⬍

f 共x兲

⬍

L ⫹␧0

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

ⱍ

f 共x兲 ⫺ L

ⱍ

⬍

␧0

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

⬎ 0lim

x l a

f 共x兲苷 L␧⬎0

lim

x l a

t共x兲苷 L

lim

x l a

f 共x兲苷 lim

x l a

h共x兲苷 L

xf 共x兲艋 t共x兲艋 h共x兲

A42

||||

APPENDIX F PROOFS OF THEOREMS

Combining these two statements, we see that whenever we have

, which implies that . Therefore we have proved

that . M

SECTION 3.4 The proof of the following result was promised when we proved that

THEOREM If , then .

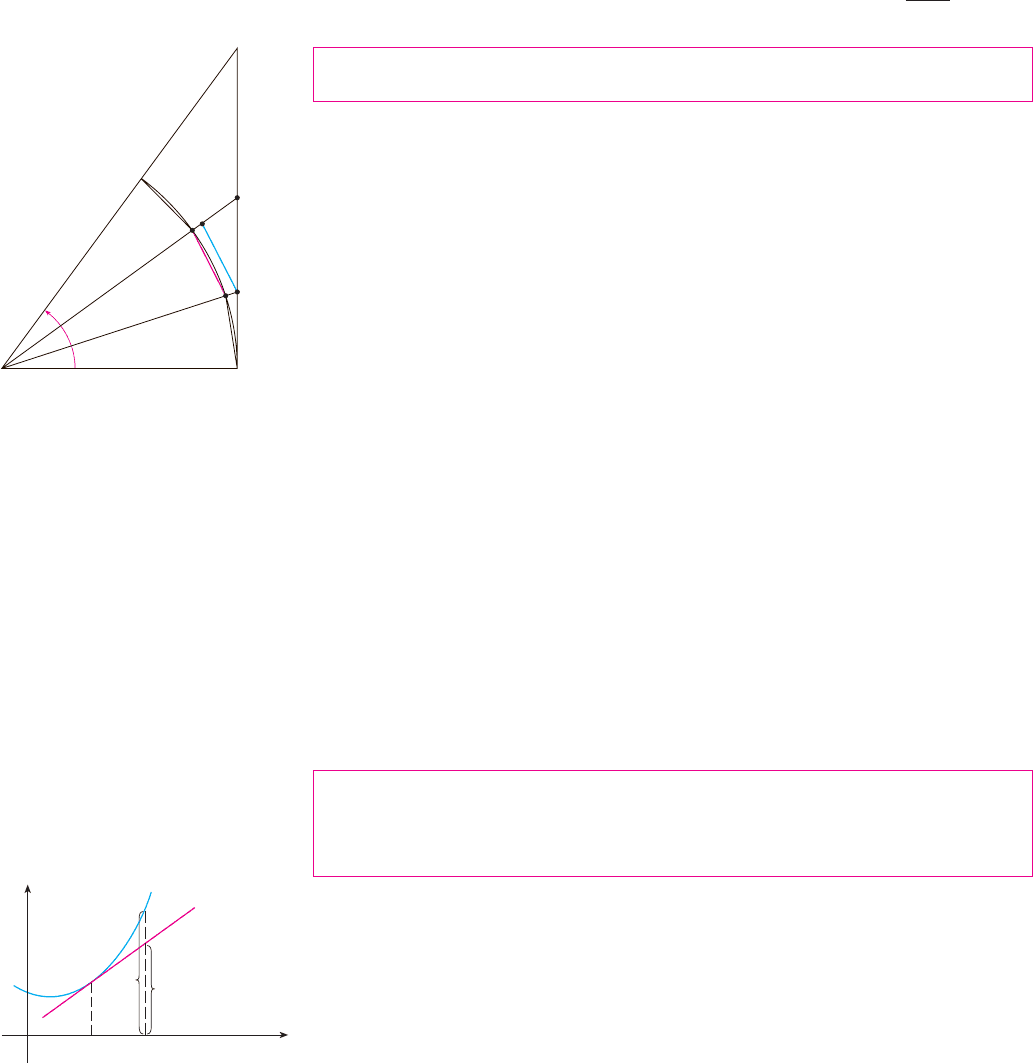
PROOF Figure 1 shows a sector of a circle with center , central angle , and radius 1.

Then

We approximate the arc by an inscribed polygon consisting of equal line segments

and we look at a typical segment . We extend the lines and to meet in the

points and . Then we draw as in Figure 1. Observe that

and so . Therefore we have

If we add such inequalities, we get

where is the length of the inscribed polygon. Thus, by Theorem 2.3.2, we have

But the arc length is deﬁned in Equation 9.1.1 as the limit of the lengths of inscribed

polygons, so

SECTION 4.3 CONCAVITY TEST

(a) If for all in , then the graph of is concave upward on .

(b) If for all in , then the graph of is concave downward on .

PROOF OF (a) Let be any number in . We must show that the curve lies above

the tangent line at the point . The equation of this tangent is

So we must show that

whenever . (See Figure 2.)共x 苷 a兲x 僆 I

f 共x兲 ⬎ f 共a兲 ⫹ f ⬘共a兲共x ⫺ a兲

y 苷 f 共a兲 ⫹ f ⬘共a兲共x ⫺ a兲

共a, f 共a兲兲

y 苷 f 共x兲Ia

IfIxf ⬙共x兲

⬍

IfIxf ⬙共x兲 ⬎ 0

␪

苷 lim

⬁

艋 tan

␪

lim

⬁

艋 tan

␪

⬍

ⱍ

苷 tan

␪

ⱍ

⬍

ⱍ

⬍

ⱍ

⬔RTS ⬎ 90⬚

⬔RTO 苷 ⬔PQO

⬍

90⬚

RT 储 PQSR

ADOQOPPQ

nAB

ⱍ

苷

ⱍ

tan

␪

苷 tan

␪

艋 tan

␪

⬍

␪

⬍

␲

兾2

lim

␪

l 0

sin

␪

苷 1

lim

x l a

f 共t共x兲兲苷 f 共b兲

ⱍ

f 共t共x兲兲 ⫺ f 共b兲

ⱍ

⬍

␧

ⱍ

t共x兲 ⫺ b

ⱍ

⬍

␦

⬍

ⱍ

x ⫺ a

ⱍ

⬍

␦

APPENDIX F PROOFS OF THEOREMS

||||

A43

AO1

FIGURE 1

FIGURE 2

f(a)+fª(a)(x-a)

y=ƒ

First let us take the case where . Applying the Mean Value Theorem to on the

interval , we get a number , with , such that

Since on , we know from the Increasing/Decreasing Test that is increasing

on . Thus, since , we have

and so, multiplying this inequality by the positive number , we get

Now we add to both sides of this inequality:

But from Equation 1 we have . So this inequality becomes

which is what we wanted to prove.

For the case where we have , but multiplication by the negative

number reverses the inequality, so we get (2) and (3) as before.

SECTION 7.1 THEOREM If is a one-to-one continuous function deﬁned on an interval

, then its inverse function is also continuous.

PROOF First we show that if is both one-to-one and continuous on , then it must

be either increasing or decreasing on . If it were neither increasing nor decreasing,

then there would exist numbers , , and in with such that

does not lie between and . There are two possibilities: either (1) lies

between and or (2) lies between and . (Draw a picture.) In

case (1) we apply the Intermediate Value Theorem to the continuous function to get a

number between and such that . In case (2) the Intermediate Value

Theorem gives a number between and such that . In either case we

have contradicted the fact that is one-to-one.

Let us assume, for the sake of deﬁniteness, that is increasing on . We take any

number in the domain of and we let ; that is, is the number in

such that . To show that is continuous at we take any such

that the interval is contained in the interval . Since is increasing,

it maps the numbers in the interval onto the numbers in the interval

and reverses the correspondence. If we let denote the

smaller of the numbers and , then the interval

is contained in the interval and so is mapped

into the interval by . (See the arrow diagram in Figure 3.) We have

therefore found a number such that

ⱍ

⫺1

共y兲 ⫺ f

⫺1

共y

兲

ⱍ

⬍

␧then

ⱍ

y ⫺ y

ⱍ

⬍

␦

⬎ 0

⫺1

共x

⫺␧, x

⫹␧兲

共 f 共x

⫺␧兲, f 共x

⫹␧兲兲共y

⫺

␦

, y

⫹

␦

兲

␦

苷 f 共x

⫹␧兲 ⫺ y

␦

苷 y

⫺ f 共x

⫺␧兲

␦

⫺1

共 f 共x

⫺␧兲, f 共x

⫹␧兲兲

共x

⫺␧, x

⫹␧兲

f共a, b兲共x

⫺␧, x

⫹␧兲

␧⬎0y

⫺1

f 共x

兲苷 y

共a, b兲

⫺1

共y

兲苷 x

⫺1

共a, b兲f

f 共c兲苷 f 共x

兲x

f 共c兲苷 f 共x

兲x

f 共x

兲f 共x

兲

f 共x

兲f 共x

兲

f 共x

兲x

⬍

共a, b兲x

共a, b兲

共a, b兲f

⫺1

共a, b兲

x ⫺ a

f ⬘共c兲

⬍

f ⬘共a兲x

⬍

f 共x兲 ⬎ f 共a兲 ⫹ f ⬘共a兲共x ⫺ a兲

f 共x兲苷 f 共a兲 ⫹ f ⬘共c兲共x ⫺ a兲

f 共a兲 ⫹ f ⬘共a兲共x ⫺ a兲

⬍

f 共a兲 ⫹ f ⬘共c兲共x ⫺ a兲

f 共a兲

f ⬘共a兲共x ⫺ a兲

⬍

f ⬘共c兲共x ⫺ a兲

x ⫺ a

f ⬘共a兲

⬍

f ⬘共c兲

⬍

f ⬘If ⬙⬎0

f 共x兲 ⫺ f 共a兲苷 f ⬘共c兲共x ⫺ a兲

⬍

xc关a, x兴

fx ⬎ a

A44

||||

APPENDIX F PROOFS OF THEOREMS

This shows that and so is continuous at any number in

its domain. M

SECTION 12.8 In order to prove Theorem 12.8.3, we ﬁrst need the following results.

THEOREM

If a power series converges when (where ), then it converges

whenever .

2. If a power series diverges when (where ), then it diverges

whenever .

PROOF OF 1 Suppose that converges. Then, by Theorem 12.2.6, we have

. According to Deﬁnition 12.1.2 with , there is a positive integer

such that whenever . Thus, for , we have

If , then , so is a convergent geometric series. Therefore,

by the Comparison Test, the series is convergent. Thus the series is

absolutely convergent and therefore convergent. M

PROOF OF 2 Suppose that diverges. If is any number such that , then

cannot converge because, by part 1, the convergence of would imply the

convergence of . Therefore diverges whenever . M

THEOREM For a power series there are only three possibilities:

1. The series converges only when .

2. The series converges for all .

3. There is a positive number such that the series converges if and

diverges if .

PROOF Suppose that neither case 1 nor case 2 is true. Then there are nonzero numbers

and such that converges for and diverges for . Therefore the set

is not empty. By the preceding theorem, the series diverges if

, so for all . This says that is an upper bound for the set .

Thus, by the Completeness Axiom (see Section 12.1), has a least upper bound . If

, then , so diverges. If , then is not an upper bound for

and so there exists such that . Since , converges, so by the

preceding theorem converges. M

冘

b 僆 Sb ⬎

ⱍ

b 僆 SS

ⱍ

ⱍⱍ

ⱍ

⬍

冘

x 僆 S

ⱍ

⬎ R

ⱍ

x 僆 S

ⱍ

艋

ⱍ

ⱍⱍ

ⱍ

⬎

ⱍ

S 苷兵x

ⱍ

冘

converges其

x 苷 dx 苷 b

冘

ⱍ

⬎ R

ⱍ

⬍

x 苷 0

冘

ⱍ

⬎

ⱍ

冘

ⱍ

⬎

ⱍ

冘

⬁

n苷N

ⱍ

冘

ⱍ

x兾b

ⱍ

x兾b

ⱍ

⬍

ⱍ

⬍

ⱍ

苷

冟

苷

ⱍ

冟

⬍

冟

n 艌 Nn 艌 N

ⱍ

⬍

␧ 苷 1lim

n l ⬁

苷 0

冘

ⱍ

⬎

ⱍ

d 苷 0x 苷 d

冘

ⱍ

⬍

ⱍ

b 苷 0x 苷 b

冘

⫺1

lim

y l y

⫺1

共y兲苷 f

⫺1

共y

兲

x¸

y¸

ff–!

f(x¸-∑) f(x¸+∑)

x¸-∑ x¸+∑

∂¡ ∂™

}

{

}

{

}

{

FIGURE 3

APPENDIX F PROOFS OF THEOREMS

||||

A45

THEOREM For a power series there are only three possibilities:

1. The series converges only when .

2. The series converges for all .

3. There is a positive number such that the series converges if and

diverges if .

PROOF If we make the change of variable , then the power series becomes

and we can apply the preceding theorem to this series. In case 3 we have con-

vergence for and divergence for . Thus we have convergence for

and divergence for . M

SECTION 15.3 CLAIRAUT’S THEOREM Suppose is deﬁned on a disk that contains the point

. If the functions and are both continuous on , then .

PROOF For small values of , , consider the difference

Notice that if we let , then

By the Mean Value Theorem, there is a number between and such that

Applying the Mean Value Theorem again, this time to we get a number between

and such that

Combining these equations, we obtain

If , then , so the continuity of at gives

Similarly, by writing

and using the Mean Value Theorem twice and the continuity of at , we obtain

It follows that . Mf

共a, b兲苷 f

共a, b兲

lim

h l 0

⌬共h兲

苷 f

共a, b兲

共a, b兲f

⌬共h兲苷关 f 共a ⫹ h, b ⫹ h兲 ⫺ f 共a, b ⫹ h兲兴 ⫺ 关 f 共a ⫹ h, b兲 ⫺ f 共a, b兲兴

lim

h l 0

⌬共h兲

苷 lim

共c, d兲 l 共a, b兲

共c, d兲苷 f

共a, b兲

共a, b兲f

共c, d兲 l 共a, b兲h l 0

⌬共h兲苷 h

共c, d兲

共c, b ⫹ h兲 ⫺ f

共c, b兲苷 f

共c, d兲h

b ⫹ h

bdf

t共a ⫹ h兲 ⫺ t共a兲苷 t⬘共c兲h 苷 h关 f

共c, b ⫹ h兲 ⫺ f

共c, b兲兴

a ⫹ hac

⌬共h兲苷 t共a ⫹ h兲 ⫺ t共a兲

t共x兲苷 f 共x, b ⫹ h兲 ⫺ f 共x, b兲

⌬共h兲苷关 f 共a ⫹ h, b ⫹ h兲 ⫺ f 共a ⫹ h, b兲兴 ⫺ 关 f 共a, b ⫹ h兲 ⫺ f 共a, b兲兴

h 苷 0h

共a, b兲苷 f

共a, b兲Df

共a, b兲

ⱍ

x ⫺ a

ⱍ

⬎ R

ⱍ

x ⫺ a

ⱍ

⬍

ⱍ

⬎ R

ⱍ

⬍

冘

u 苷 x ⫺ a

ⱍ

x ⫺ a

ⱍ

⬎ R

ⱍ

x ⫺ a

ⱍ

⬍

x 苷 a

冘

共x ⫺ a兲

A46

||||

APPENDIX F PROOFS OF THEOREMS

SECTION 15.4 THEOREM If the partial derivatives and exist near and are continu-

ous at , then f is differentiable at .

PROOF Let

According to (15.4.7), to prove that f is differentiable at we have to show that we

can write in the form

where and as .

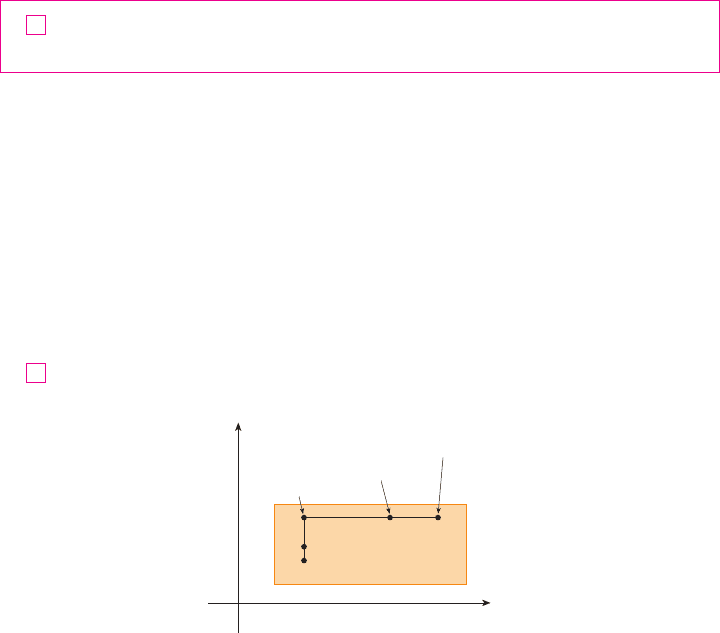
Referring to Figure 4, we write

Observe that the function of a single variable

is deﬁned on the interval and . If we apply the Mean

Value Theorem to , we get

where is some number between and . In terms of , this equation becomes

This gives us an expression for the ﬁrst part of the right side of Equation 1. For the

second part we let . Then is a function of a single variable deﬁned on

the interval and . A second application of the Mean Value

Theorem then gives

where is some number between and . In terms of , this becomes

f 共a, b ⫹⌬y兲 ⫺ f 共a, b兲苷 f

共a, v兲 ⌬y

fb ⫹⌬ybv

h共b ⫹⌬y兲 ⫺ h共b兲苷 h⬘共v兲 ⌬y

h⬘共y兲苷 f

共a, y兲关b, b ⫹⌬y兴

hh共y兲苷 f 共a, y兲

f 共a ⫹⌬x, b ⫹⌬y兲 ⫺ f 共a, b ⫹⌬y兲苷 f

共u, b ⫹⌬y兲 ⌬x

fa ⫹⌬xau

t共a ⫹⌬x兲 ⫺ t共a兲苷 t⬘共u兲 ⌬x

t⬘共x兲苷 f

共x, b ⫹⌬y兲关a, a ⫹⌬x兴

t共x兲苷 f 共x, b ⫹⌬y兲

FIGURE 4

(a,√)

(a,b+Îy)

(a+Îx,b+Îy)

(u,b+Îy)

(a,b)

⌬z 苷关 f 共a ⫹⌬x, b ⫹⌬y兲 ⫺ f 共a, b ⫹⌬y兲兴 ⫹ 关 f 共a, b ⫹⌬y兲 ⫺ f 共a, b兲兴

共⌬x, ⌬y兲 l 共0, 0兲␧

l 0␧

⌬z 苷 f

共a, b兲 ⌬x ⫹ f

共a, b兲 ⌬y ⫹␧

⌬x ⫹␧

⌬y

⌬z

共a, b兲

⌬z 苷 f 共a ⫹⌬x, b ⫹⌬y兲 ⫺ f 共a, b兲

共a, b兲共a, b兲

共a, b兲f

APPENDIX F PROOFS OF THEOREMS

||||

A47