Stewart J. Calculus

Подождите немного. Документ загружается.

EXAMPLE 1 A spring with a mass of 2 kg has natural length m. A force of N

is required to maintain it stretched to a length of m. If the spring is stretched to a

length of m and then released with initial velocity 0, ﬁnd the position of the mass at

any time .

SOLUTION From Hooke’s Law, the force required to stretch the spring is

so . Using this value of the spring constant , together with

in Equation 1, we have

As in the earlier general discussion, the solution of this equation is

We are given the initial condition that . But, from Equation 2,

Therefore . Differentiating Equation 2, we get

Since the initial velocity is given as , we have and so the solution is

DAMPED VIBRATIONS

We next consider the motion of a spring that is subject to a frictional force (in the case of

the horizontal spring of Figure 2) or a damping force (in the case where a vertical spring

moves through a ﬂuid as in Figure 3). An example is the damping force supplied by a

shock absorber in a car or a bicycle.

We assume that the damping force is proportional to the velocity of the mass and acts

in the direction opposite to the motion. (This has been conﬁrmed, at least approximately,

by some physical experiments.) Thus

where is a positive constant, called the damping constant. Thus, in this case, Newton’s

Second Law gives

⫹ c

⫹ kx 苷 0

苷 restoring force ⫹ damping force 苷 ⫺kx ⫺ c

damping force 苷 ⫺c

x共t兲苷

cos 8t

苷 0x⬘共0兲苷 0

x⬘共t兲苷 ⫺8c

sin 8t ⫹ 8c

cos 8t

苷 0.2

x共0兲苷 c

.x共0兲苷 0.2

x共t兲苷 c

cos 8t ⫹ c

sin 8t

⫹ 128x 苷 0

m 苷 2kk 苷 25.6兾0.2 苷 128

k共0.2兲苷 25.6

0.7

25.60.5

1162

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

Schwinn Cycling and Fitness

FIGURE 3

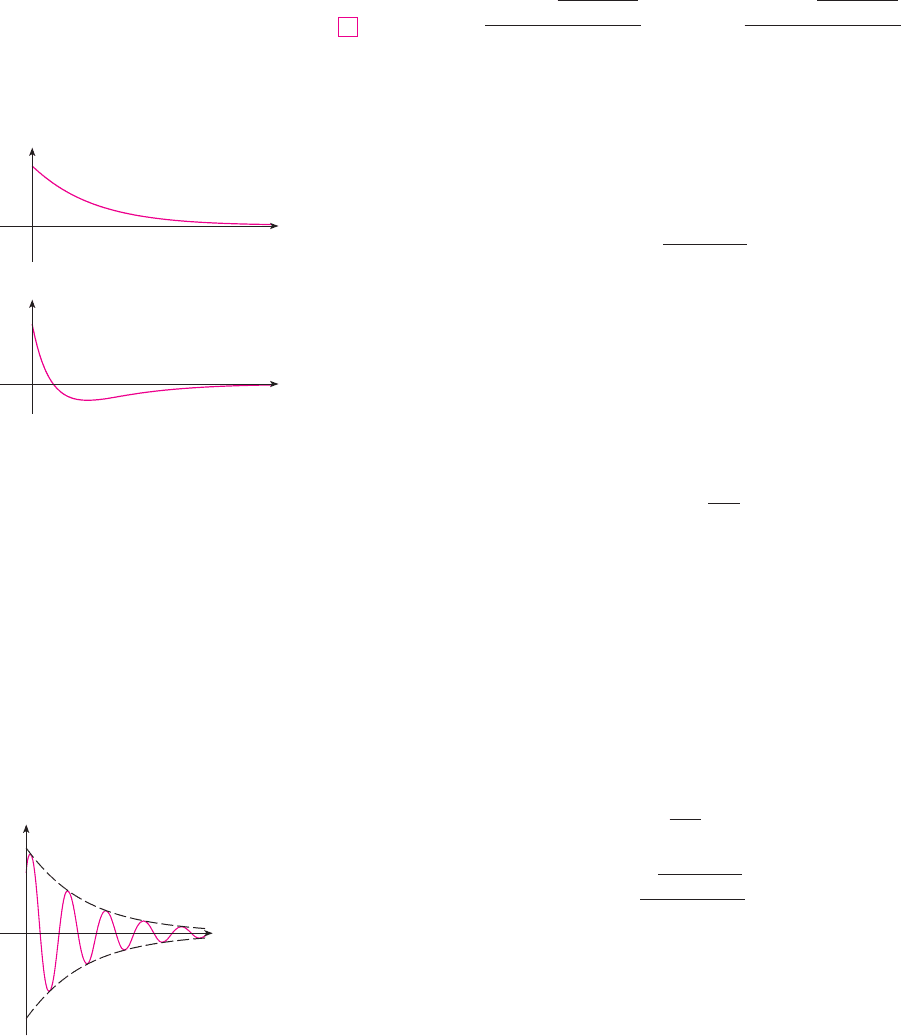
Equation 3 is a second-order linear differential equation and its auxiliary equation is

. The roots are

According to Section 18.1 we need to discuss three cases.

CASE I (overdamping)

In this case and are distinct real roots and

Since , , and are all positive, we have , so the roots and given by

Equations 4 must both be negative. This shows that as . Typical graphs of

as a function of are shown in Figure 4. Notice that oscillations do not occur. (It’s pos-

sible for the mass to pass through the equilibrium position once, but only once.) This is

because means that there is a strong damping force (high-viscosity oil or grease)

compared with a weak spring or small mass.

CASE II (critical damping)

This case corresponds to equal roots

and the solution is given by

It is similar to Case I, and typical graphs resemble those in Figure 4 (see Exercise 12), but

the damping is just sufﬁcient to suppress vibrations. Any decrease in the viscosity of the

ﬂuid leads to the vibrations of the following case.

CASE III (underdamping)

Here the roots are complex:

where

The solution is given by

We see that there are oscillations that are damped by the factor . Since and

, we have so as . This implies that as

that is, the motion decays to 0 as time increases. A typical graph is shown in Figure 5.

t l ⬁;x l 0t l ⬁e

⫺共c兾2m兲t

l 0⫺共c兾2m兲

⬍

0m ⬎ 0

c ⬎ 0e

⫺共c兾2m兲t

x 苷 e

⫺共c兾2m兲t

共c

cos

␻

t ⫹ c

sin

␻

t兲

␻

苷

4mk ⫺ c

冎

苷 ⫺

⫾

␻

⫺ 4mk

⬍

x 苷共c

⫹ c

t兲e

⫺共c兾2m兲t

苷 r

苷 ⫺

⫺ 4mk 苷 0

⬎ 4mk

t l ⬁x l 0

⫺ 4mk

⬍

ckmc

x 苷 c

⫹ c

⫺ 4 mk ⬎ 0

苷

⫺c ⫺

⫺ 4mk

苷

⫺c ⫹

⫺ 4mk

⫹ cr ⫹ k 苷 0

SECTION 18.3 APPLICATIONS OF SECOND-ORDER DIFFERENTIAL EQUATIONS

||||

1163

FIGURE 4

Overdamping

FIGURE 5

Underdamping

x=Ae–

(c/2m)t

x=_Ae–

(c/2m)t

EXAMPLE 2 Suppose that the spring of Example 1 is immersed in a ﬂuid with

damping constant . Find the position of the mass at any time if it starts from the

equilibrium position and is given a push to start it with an initial velocity of m兾s.

SOLUTION From Example 1, the mass is and the spring constant is , so the

differential equation (3) becomes

The auxiliary equation is with roots

and , so the motion is overdamped and the solution is

We are given that , so . Differentiating, we get

Since , this gives or . Therefore

FORCED VIBRATIONS

Suppose that, in addition to the restoring force and the damping force, the motion of the

spring is affected by an external force . Then Newton’s Second Law gives

Thus, instead of the homogeneous equation (3), the motion of the spring is now governed

by the following nonhomogeneous differential equation:

The motion of the spring can be determined by the methods of Section 18.2.

⫹ c

⫹ kx 苷 F共t兲

苷 ⫺kx ⫺ c

⫹ F共t兲

苷 restoring force ⫹ damping force ⫹ external force

F共t兲

x 苷 0.05共e

⫺4t

⫺ e

⫺16t

兲

苷 0.0512c

苷 0.6c

苷 ⫺c

x⬘共0兲苷 ⫺4c

⫺ 16c

苷 0.6

x⬘共t兲苷 ⫺4c

⫺4t

⫺ 16c

⫺16t

⫹ c

苷 0x共0兲苷 0

x共t兲苷 c

⫺4t

⫹ c

⫺16t

⫺16

⫺4r

⫹ 20r ⫹ 64 苷共r ⫹ 4兲共r ⫹ 16兲苷 0

⫹ 20

⫹ 64x 苷 0

⫹ 40

⫹ 128x 苷 0

k 苷 128m 苷 2

0.6

tc 苷 40

1164

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

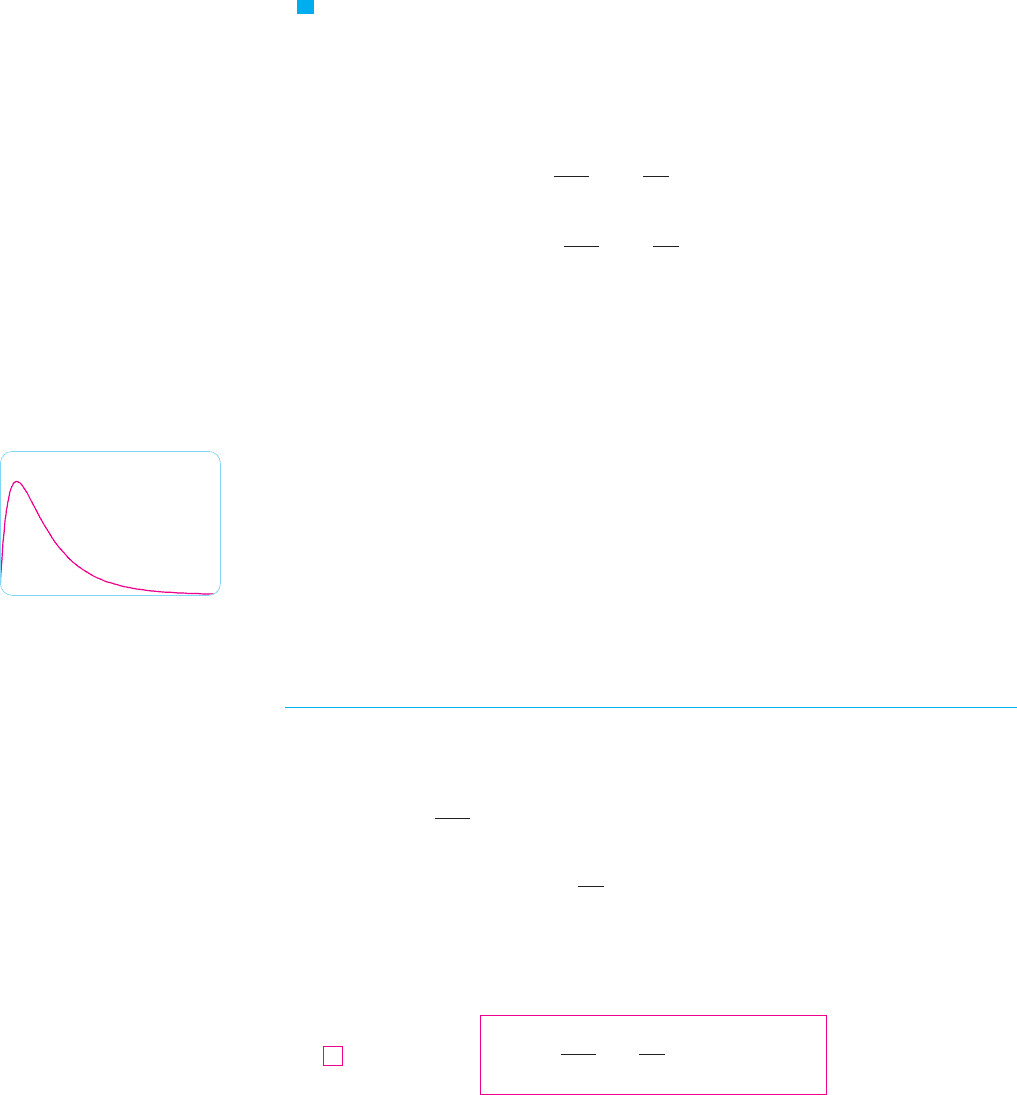
N Figure 6 shows the graph of the position func-

tion for the overdamped motion in Example 2.

FIGURE 6

0.03

1.5

A commonly occurring type of external force is a periodic force function

In this case, and in the absence of a damping force ( ), you are asked in Exercise 9 to

use the method of undetermined coefﬁcients to show that

If , then the applied frequency reinforces the natural frequency and the result is

vibrations of large amplitude. This is the phenomenon of resonance (see Exercise 10).

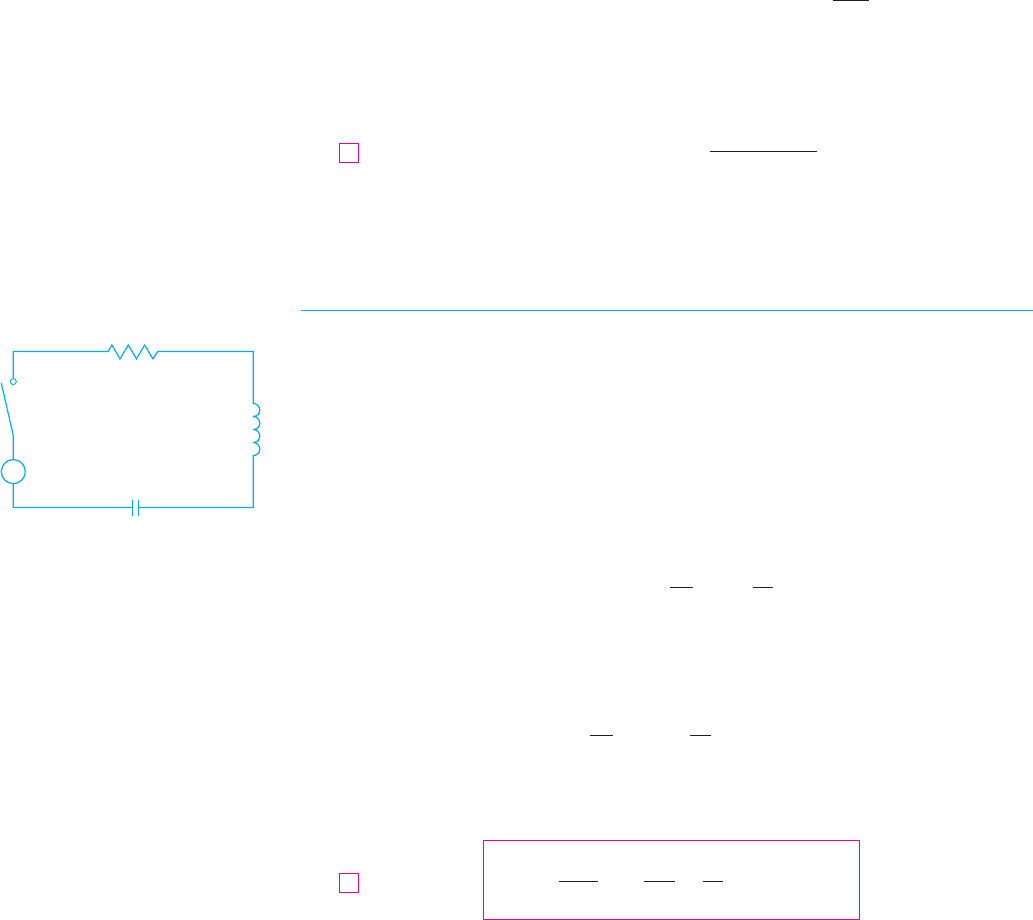
ELECTRIC CIRCUITS

In Sections 10.3 and 10.5 we were able to use ﬁrst-order separable and linear equations to

analyze electric circuits that contain a resistor and inductor (see Figure 5 on page 618 or

Figure 4 on page 641) or a resistor and capacitor (see Exercise 29 on page 643). Now that

we know how to solve second-order linear equations, we are in a position to analyze the

circuit shown in Figure 7. It contains an electromotive force (supplied by a battery or

generator), a resistor , an inductor , and a capacitor , in series. If the charge on the

capacitor at time is , then the current is the rate of change of with respect

to : . As in Section 10.5, it is known from physics that the voltage drops across

the resistor, inductor, and capacitor are

respectively. Kirchhoff’s voltage law says that the sum of these voltage drops is equal to

the supplied voltage:

Since , this equation becomes

which is a second-order linear differential equation with constant coefﬁcients. If the charge

and the current are known at time 0, then we have the initial conditions

and the initial-value problem can be solved by the methods of Section 18.2.

Q⬘共0兲苷 I共0兲苷 I

Q共0兲苷 Q

⫹ R

⫹

Q 苷 E共t兲

I 苷 dQ兾dt

⫹ RI ⫹

苷 E共t兲

I 苷 dQ兾dtt

QQ 苷 Q共t兲t

CLR

␻

苷

␻

x共t兲苷 c

cos

␻

t ⫹ c

sin

␻

t ⫹

m共

␻

⫺

␻

兲

cos

␻

c 苷 0

where

␻

苷

␻

苷

k兾m

F共t兲苷 F

cos

␻

SECTION 18.3 APPLICATIONS OF SECOND-ORDER DIFFERENTIAL EQUATIONS

||||

1165

FIGURE 7

switch

A differential equation for the current can be obtained by differentiating Equation 7

with respect to and remembering that :

EXAMPLE 3 Find the charge and current at time in the circuit of Figure 7 if

, H, F, , and the initial charge and

current are both 0.

SOLUTION With the given values of , , , and , Equation 7 becomes

The auxiliary equation is with roots

so the solution of the complementary equation is

For the method of undetermined coefﬁcients we try the particular solution

Then

Substituting into Equation 8, we have

Equating coefﬁcients, we have

The solution of this system is and , so a particular solution is

and the general solution is

苷 e

⫺20t

共c

cos 15t ⫹ c

sin 15t兲 ⫹

697

共21 cos 10t ⫹ 16 sin 10t兲

Q共t兲苷 Q

共t兲 ⫹ Q

共t兲

共t兲苷

697

共84 cos 10t ⫹ 64 sin 10t兲

B 苷

697

A 苷

697

⫺16A ⫹ 21B 苷 0 ⫺400A ⫹ 525B 苷 0

21A ⫹ 16B 苷 4 525A ⫹ 400B 苷 100

共525A ⫹ 400B兲 cos 10t ⫹ 共⫺400A ⫹ 525B兲 sin 10t 苷 100 cos 10t

⫹ 625共A cos 10t ⫹ B sin 10t兲苷 100 cos 10t

共⫺100A cos 10t ⫺ 100B sin 10t兲 ⫹ 40共⫺10A sin 10t ⫹ 10B cos 10t兲

⬙共t兲苷 ⫺100A cos 10t ⫺ 100B sin 10t

⬘共t兲苷 ⫺10A sin 10t ⫹ 10B cos 10t

共t兲苷 A cos 10t ⫹ B sin 10t

共t兲苷 e

⫺20t

共c

cos 15t ⫹ c

sin 15t兲

r 苷

⫺40 ⫾

⫺900

苷 ⫺20 ⫾ 15i

⫹ 40r ⫹ 625 苷 0

⫹ 40

⫹ 625Q 苷 100 cos 10t

E共t兲CRL

E共t兲苷 100 cos 10tC 苷 16 ⫻ 10

⫺4

L 苷 1R 苷 40 ⍀

⫹ R

⫹

I 苷 E⬘共t兲

I 苷 dQ兾dtt

1166

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

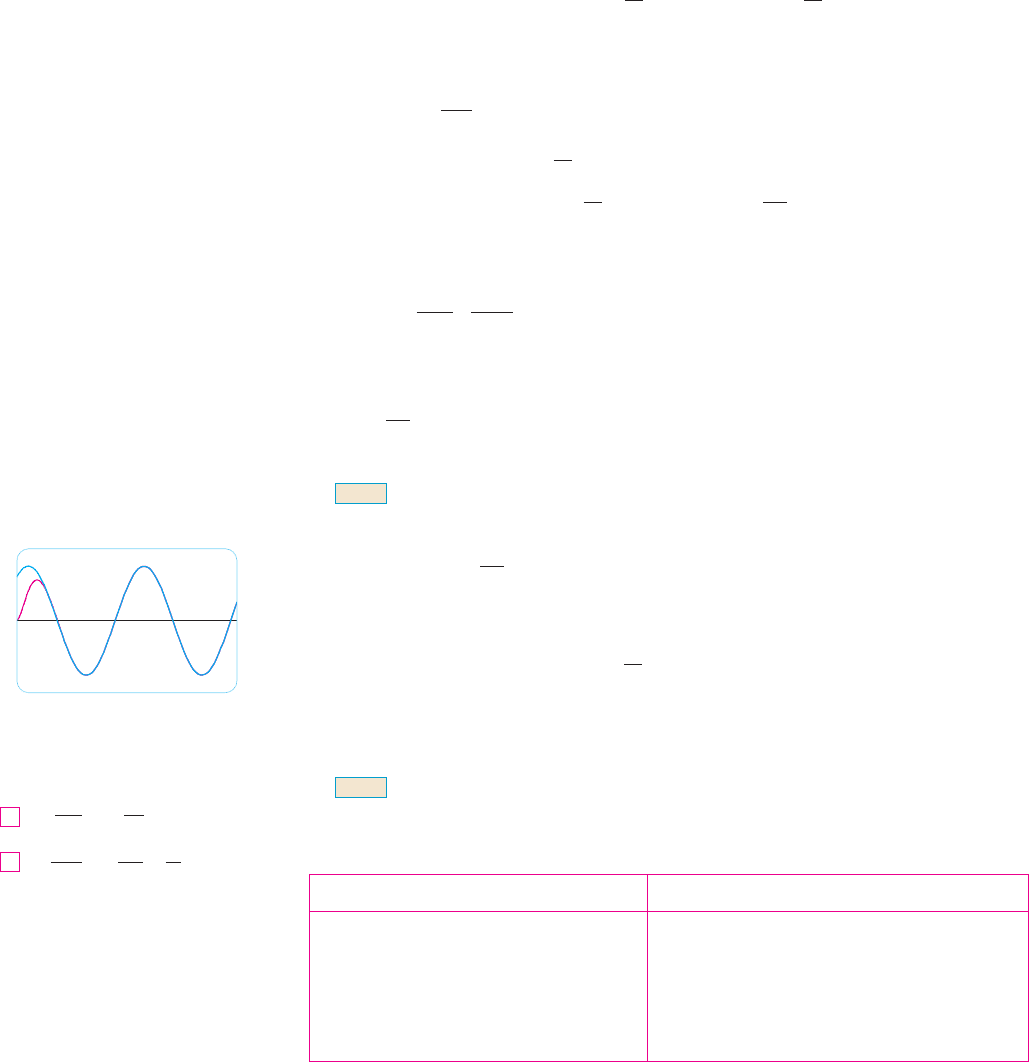
Imposing the initial condition , we get

To impose the other initial condition, we ﬁrst differentiate to ﬁnd the current:

Thus the formula for the charge is

and the expression for the current is

In Example 3 the solution for consists of two parts. Since as

and both and are bounded functions,

So, for large values of ,

and, for this reason, is called the steady state solution. Figure 8 shows how the graph

of the steady state solution compares with the graph of in this case.

Comparing Equations 5 and 7, we see that mathematically they are identical.

This suggests the analogies given in the following chart between physical situations that,

at ﬁrst glance, are very different.

We can also transfer other ideas from one situation to the other. For instance, the steady

state solution discussed in Note 1 makes sense in the spring system. And the phenomenon

of resonance in the spring system can be usefully carried over to electric circuits as elec-

trical resonance.

NOTE 2

共t兲

Q共t兲⬇Q

共t兲苷

697

共21 cos 10t ⫹ 16 sin 10t兲

as t l ⬁Q

共t兲苷

2091

⫺20t

共⫺63 cos 15t ⫺ 116 sin 15t兲 l 0

sin 15tcos 15tt l ⬁

⫺20t

l 0Q共t兲

NOTE 1

I共t兲苷

2091

关e

⫺20t

共⫺1920 cos 15t ⫹ 13,060 sin 15t兲 ⫹ 120共⫺21 sin 10t ⫹ 16 cos 10t兲兴

Q共t兲苷

697

冋

⫺20t

共⫺63 cos 15t ⫺ 116 sin 15t兲 ⫹ 共21 cos 10t ⫹ 16 sin 10t兲

册

苷 ⫺

464

2091

I共0兲苷 ⫺20c

⫹ 15c

⫹

640

697

苷 0

⫹

697

共⫺21 sin 10t ⫹ 16 cos 10t兲

I 苷

苷 e

⫺20t

关共⫺20c

⫹ 15c

兲 cos 15t ⫹ 共⫺15c

⫺ 20c

兲 sin 15t兴

苷 ⫺

697

Q共0兲苷 c

⫹

697

苷 0

Q共0兲苷 0

SECTION 18.3 APPLICATIONS OF SECOND-ORDER DIFFERENTIAL EQUATIONS

||||

1167

FIGURE 8

0.2

_0.2

0 1.2

⫹ R

⫹

Q 苷 E共t兲

⫹ c

⫹ kx 苷 F共t兲

Spring system Electric circuit

x displacement Q charge

velocity current

m mass L inductance

c damping constant R resistance

k spring constant elastance

external force electromotive forceE共t兲F共t兲

1兾C

I 苷 dQ兾dtdx兾dt

1168

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

12. Consider a spring subject to a frictional or damping force.

(a) In the critically damped case, the motion is given by

. Show that the graph of crosses the

-axis whenever and have opposite signs.

(b) In the overdamped case, the motion is given by

where . Determine a condition

on the relative magnitudes of and under which the

graph of crosses the -axis at a positive value of .

A series circuit consists of a resistor with , an

inductor with H, a capacitor with F, and a

12-V battery. If the initial charge and current are both 0, ﬁnd

the charge and current at time t.

14. A series circuit contains a resistor with , an induc-

tor with H, a capacitor with F, and a 12-V

battery. The initial charge is C and the initial cur-

rent is 0.

(a) Find the charge and current at time t.

;

(b) Graph the charge and current functions.

15. The battery in Exercise 13 is replaced by a generator produc-

ing a voltage of . Find the charge at time t.

16. The battery in Exercise 14 is replaced by a generator pro-

ducing a voltage of .

(a) Find the charge at time t.

;

(b) Graph the charge function.

Verify that the solution to Equation 1 can be written in the

form .

18. The ﬁgure shows a pendulum with length L and the angle

from the vertical to the pendulum. It can be shown that , as a

function of time, satisﬁes the nonlinear differential equation

where is the acceleration due to gravity. For small values of

we can use the linear approximation and then the

differential equation becomes linear.

(a) Find the equation of motion of a pendulum with length

1 m if is initially 0.2 rad and the initial angular velocity

is .

(b) What is the maximum angle from the vertical?

complete one back-and-forth swing)?

(d) When will the pendulum ﬁrst be vertical?

(e) What is the angular velocity when the pendulum is

vertical?

␪

兾dt 苷 1 rad兾s

␪

sin

␪

⬇

␪

⫹

sin

␪

苷 0

␪

x共t兲苷 A cos共

␻

t ⫹

␦

兲

17.

E共t兲苷 12 sin 10t

Q 苷 0.001

C 苷 0.005L 苷 2

⍀R 苷 24

C 苷 0.002L 苷 1

⍀R 苷 20

13.

ttx

⬎ r

x 苷 c

⫹ c

x 苷 c

⫹ c

1. A spring has natural length and a mass. A force of

is needed to keep the spring stretched to a length of .

If the spring is stretched to a length of and then released

with velocity , ﬁnd the position of the mass after seconds.

2. A spring with an mass is kept stretched beyond its

natural length by a force of . The spring starts at its equi-

librium position and is given an initial velocity of . Find

the position of the mass at any time .

A spring with a mass of 2 kg has damping constant 14, and

a force of 6 N is required to keep the spring stretched m

beyond its natural length. The spring is stretched 1 m beyond

its natural length and then released with zero velocity. Find the

position of the mass at any time t.

4. A force of 13 N is needed to keep a spring with a 2-kg mass

stretched 0.25 m beyond its natural length. The damping con-

stant of the spring is .

(a) If the mass starts at the equilibrium position with a

velocity of , ﬁnd its position at time .

;

(b) Graph the position function of the mass.

5. For the spring in Exercise 3, ﬁnd the mass that would produce

critical damping.

6. For the spring in Exercise 4, ﬁnd the damping constant that

would produce critical damping.

;

7. A spring has a mass of 1 kg and its spring constant is .

The spring is released at a point 0.1 m above its equilibrium

position. Graph the position function for the following values

of the damping constant c: 10, 15, 20, 25, 30. What type of

damping occurs in each case?

;

8. A spring has a mass of 1 kg and its damping constant is

The spring starts from its equilibrium position with a

velocity of 1 m兾s. Graph the position function for the follow-

ing values of the spring constant k: 10, 20, 25, 30, 40. What

type of damping occurs in each case?

Suppose a spring has mass and spring constant and let

. Suppose that the damping constant is so small

that the damping force is negligible. If an external force

is applied, where , use the method

of undetermined coefﬁcients to show that the motion of the

mass is described by Equation 6.

10. As in Exercise 9, consider a spring with mass , spring con-

stant , and damping constant , and let .

If an external force is applied (the applied

frequency equals the natural frequency), use the method of

undetermined coefﬁcients to show that the motion of the mass

is given by .

11. Show that if , but is a rational number, then the

motion described by Equation 6 is periodic.

␻

兾

␻

苷

␻

x共t兲苷 c

cos

␻

t ⫹ c

sin

␻

t ⫹ 共F

兾共2m

␻

兲兲t sin

␻

F共t兲苷 F

cos

␻

苷

k兾m

c 苷 0k

␻

苷

␻

F共t兲苷 F

cos

␻

苷

k兾m

c 苷 10.

k 苷 100

t0.5 m兾s

c 苷 8

0.5

1 m兾s

32 N

0.4 m8-kg

1.1 m

1 m25 N

5-kg0.75 m

EXERCISES

18.3

SERIES SOLUTIONS

Many differential equations can’t be solved explicitly in terms of ﬁnite combinations of

simple familiar functions. This is true even for a simple-looking equation like

But it is important to be able to solve equations such as Equation 1 because they arise from

physical problems and, in particular, in connection with the Schrödinger equation in quan-

tum mechanics. In such a case we use the method of power series; that is, we look for a

solution of the form

The method is to substitute this expression into the differential equation and determine the

values of the coefﬁcients This technique resembles the method of undeter-

mined coefﬁcients discussed in Section 18.2.

Before using power series to solve Equation 1, we illustrate the method on the simpler

equation in Example 1. It’s true that we already know how to solve this equa-

tion by the techniques of Section 18.1, but it’s easier to understand the power series

method when it is applied to this simpler equation.

EXAMPLE 1 Use power series to solve the equation .

SOLUTION We assume there is a solution of the form

We can differentiate power series term by term, so

In order to compare the expressions for and more easily, we rewrite as follows:

Substituting the expressions in Equations 2 and 4 into the differential equation, we

obtain

兺

⬁

n苷0

关共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

⫹ c

兴x

苷 0

兺

⬁

n苷0

共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

⫹

兺

⬁

n苷0

苷 0

y⬙ 苷

兺

⬁

n苷0

共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

y⬙y⬙y

y⬙ 苷 2c

⫹ 2 ⭈ 3c

x ⫹⭈⭈⭈苷

兺

⬁

n苷2

n共n ⫺ 1兲c

n⫺2

y⬘ 苷 c

⫹ 2c

x ⫹ 3c

⫹⭈⭈⭈苷

兺

⬁

n苷1

n⫺1

y 苷 c

⫹ c

x ⫹ c

⫹ c

⫹⭈⭈⭈苷

兺

⬁

n苷0

y⬙⫹y 苷 0

, c

, . . . .

y 苷 f 共x兲苷

兺

⬁

n苷0

苷 c

⫹ c

x ⫹ c

⫹ c

⫹⭈⭈⭈

y⬙⫺2xy⬘⫹y 苷 0

18.4

SECTION 18.4 SERIES SOLUTIONS

||||

1169

N By writing out the ﬁrst few terms of (4), you

can see that it is the same as (3). To obtain (4),

we replaced by and began the sum-

mation at 0 instead of 2.

n ⫹ 2n

If two power series are equal, then the corresponding coefﬁcients must be equal. There-

fore the coefﬁcients of in Equation 5 must be 0:

Equation 6 is called a recursion relation. If and are known, this equation allows

us to determine the remaining coefﬁcients recursively by putting in

succession.

By now we see the pattern:

Putting these values back into Equation 2, we write the solution as

Notice that there are two arbitrary constants, and

苷 c

兺

⬁

n苷0

共⫺1兲

共2n兲!

⫹ c

兺

⬁

n苷0

共⫺1兲

2n⫹1

共2n ⫹ 1兲!

苷 ⫹ c

冉

x ⫺

⫹

⫺

⫹⭈⭈⭈⫹共⫺1兲

2n⫹1

共2n ⫹ 1兲!

⫹⭈⭈⭈

冊

苷 c

冉

1 ⫺

⫹

⫺

⫹⭈⭈⭈⫹共⫺1兲

共2n兲!

⫹⭈⭈⭈

冊

y 苷 c

⫹ c

x ⫹ c

⫹ c

⫹⭈⭈⭈

For the odd coefficients, c

2n⫹1

苷共⫺1兲

共2n ⫹ 1兲!

For the even coefficients, c

苷共⫺1兲

共2n兲!

Put n 苷 5: c

苷 ⫺

6 ⴢ 7

苷 ⫺

5! 6 ⴢ 7

苷 ⫺

Put n 苷 4: c

苷 ⫺

5 ⴢ 6

苷 ⫺

4! 5 ⴢ 6

苷 ⫺

Put n 苷 3: c

苷 ⫺

4 ⴢ 5

苷

2 ⴢ 3 ⴢ 4 ⴢ 5

苷

Put n 苷 2: c

苷 ⫺

3 ⴢ 4

苷

1 ⴢ 2 ⴢ 3 ⴢ 4

苷

Put n 苷 1: c

苷 ⫺

2 ⴢ 3

Put n 苷 0: c

苷 ⫺

1 ⴢ 2

n 苷 0, 1, 2, 3, . . .

n 苷 0, 1, 2, 3, . . .c

n⫹2

苷 ⫺

共n ⫹ 1兲共n ⫹ 2兲

共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

⫹ c

苷 0

1170

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

We recognize the series obtained in Example 1 as being the Maclaurin series

for and . (See Equations 12.10.16 and 12.10.15.) Therefore we could write the

solution as

But we are not usually able to express power series solutions of differential equations in

terms of known functions.

EXAMPLE 2

Solve .

SOLUTION

We assume there is a solution of the form

Then

and

as in Example 1. Substituting in the differential equation, we get

This equation is true if the coefﬁcient of is 0:

We solve this recursion relation by putting successively in Equation 7:

Put n 苷 3: c

苷

4 ⴢ 5

苷

1 ⴢ 5

2 ⴢ 3 ⴢ 4 ⴢ 5

苷

1 ⴢ 5

Put n 苷 2: c

苷

3 ⴢ 4

苷 ⫺

1 ⴢ 2 ⴢ 3 ⴢ 4

苷 ⫺

Put n 苷 1: c

苷

2 ⴢ 3

Put n 苷 0: c

苷

⫺1

1 ⴢ 2

n 苷 0, 1, 2, 3, . . .

n 苷 0, 1, 2, 3, . . .c

n⫹2

苷

2n ⫺ 1

共n ⫹ 1兲共n ⫹ 2兲

共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

⫺ 共2n ⫺ 1兲c

苷 0

兺

⬁

n苷0

关共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

⫺ 共2n ⫺ 1兲c

兴x

苷 0

兺

⬁

n苷0

共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

⫺

兺

⬁

n苷1

2nc

⫹

兺

⬁

n苷0

苷 0

兺

⬁

n苷0

共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

⫺ 2x

兺

⬁

n苷1

n⫺1

⫹

兺

⬁

n苷0

苷 0

y⬙ 苷

兺

⬁

n苷2

n共n ⫺ 1兲c

n⫺2

苷

兺

⬁

n苷0

共n ⫹ 2兲共n ⫹ 1兲c

n⫹2

y⬘ 苷

兺

⬁

n苷1

n⫺1

y 苷

兺

⬁

n苷0

y⬙⫺2xy⬘⫹y 苷 0

y共x兲苷 c

cos x ⫹ c

sin x

sin xcos x

NOTE 1

SECTION 18.4 SERIES SOLUTIONS

||||

1171

兺

⬁

n苷1

2nc

苷

兺

⬁

n苷0

2nc

Openmirrors.com