Stewart J. Calculus

Подождите немного. Документ загружается.

the initial conditions become

Therefore the solution of the initial-value problem is

A boundary-value problem for Equation 1 or 2 consists of ﬁnding a solution of the

differential equation that also satisﬁes boundary conditions of the form

In contrast with the situation for initial-value problems, a boundary-value problem does

not always have a solution. The method is illustrated in Example 7.

EXAMPLE 7 Solve the boundary-value problem

SOLUTION The auxiliary equation is

whose only root is . Therefore the general solution is

The boundary conditions are satisﬁed if

The ﬁrst condition gives , so the second condition becomes

Solving this equation for by ﬁrst multiplying through by , we get

Thus the solution of the boundary-value problem is

SUMMARY: SOLUTIONS OF ay

⬘⬘⬘⬘ ⫹⫹

⬘⬘ ⫹⫹

⫽⫽

y 苷 e

⫺x

⫹ 共3e ⫺ 1兲xe

⫺x

苷 3e ⫺ 11 ⫹ c

苷 3e

⫺1

⫹ c

⫺1

苷 3

苷 1

y共1兲苷 c

⫺1

⫹ c

⫺1

苷 3

y共0兲苷 c

苷 1

y共x兲苷 c

⫺x

⫹ c

⫺x

r 苷 ⫺1

共r ⫹ 1兲

苷 0orr

⫹ 2r ⫹ 1 苷 0

y共1兲苷 3y共0兲苷 1y⬙⫹2y⬘⫹y 苷 0

y共x

兲苷 y

y共x

兲苷 y

y共x兲苷 2 cos x ⫹ 3sin x

y⬘共0兲苷 c

苷 3y共0兲苷 c

苷 2

1152

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

Roots of General solution

y 苷 e

␣

共c

cos

␤

x ⫹ c

sin

␤

x兲r

, r

complex:

␣

⫾ i

␤

y 苷 c

⫹ c

苷 r

y 苷 c

⫹ c

, r

real and distinct

⫹ br ⫹ c 苷 0

N The solution to Example 6 is graphed in

Figure 5. It appears to be a shifted sine curve

and, indeed, you can verify that another way of

writing the solution is

where tan

␾

苷

y 苷

13 sin共x ⫹

␾

兲

FIGURE 5

_2π

2π

N Figure 6 shows the graph of the solution of

the boundary-value problem in Example 7.

FIGURE 6

_1 5

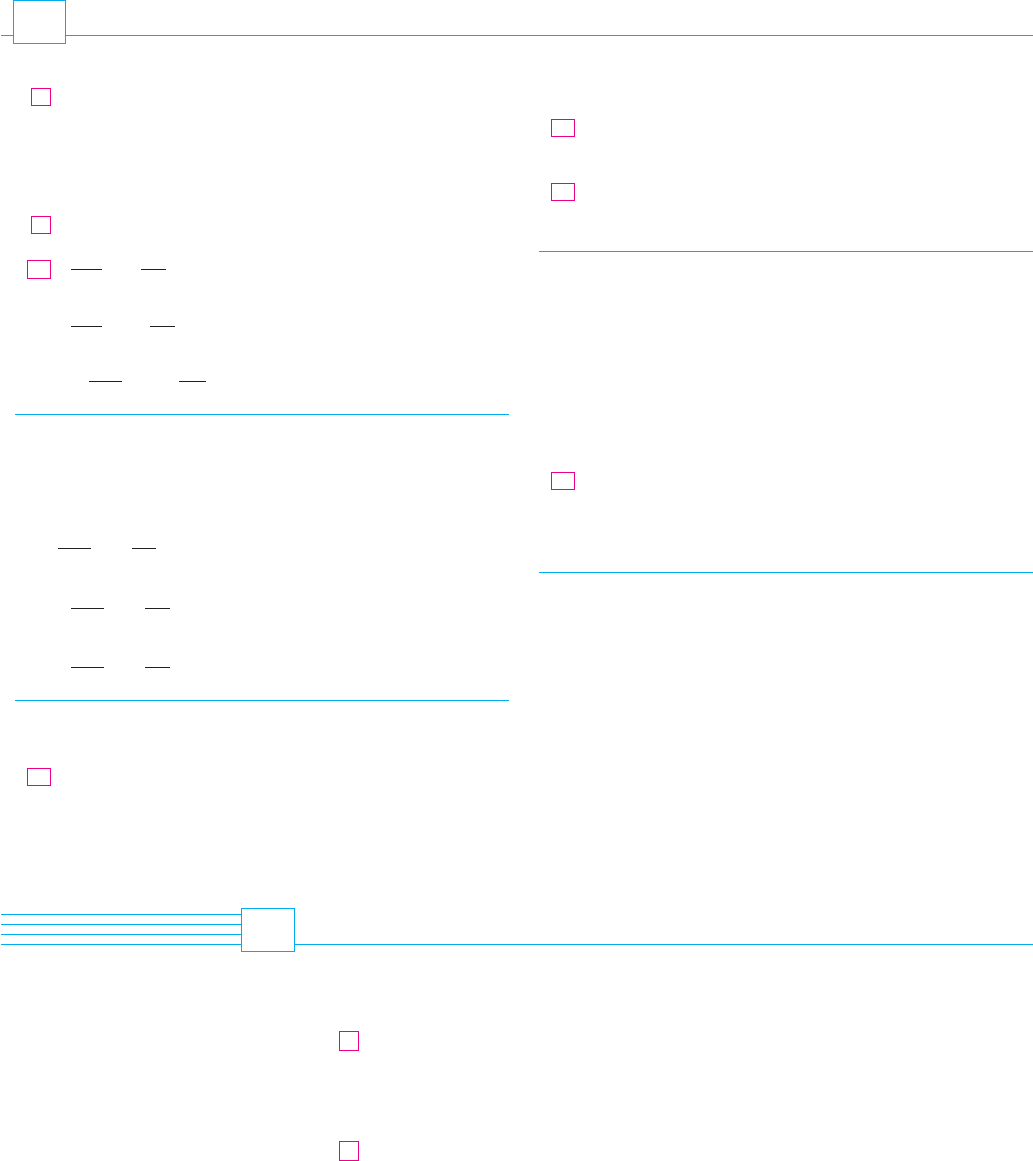
SECTION 18.2 NONHOMOGENEOUS LINEAR EQUATIONS

||||

1153

19. ,,

20. ,,

22. ,,

24. ,,

25–32 Solve the boundary-value problem, if possible.

25. ,,

26. ,,

27. ,,

28. ,,

29. ,,

31. ,,

32. ,,

33. Let be a nonzero real number.

(a) Show that the boundary-value problem ,

, has only the trivial solution for

the cases and .

(b) For the case , ﬁnd the values of for which this

problem has a nontrivial solution and give the corre-

sponding solution.

34. If , , and are all positive constants and is a solution

of the differential equation , show that

.lim

x l ⬁

y共x兲苷 0

ay⬙⫹by⬘⫹cy 苷 0

y共x兲cba

␭

⬎ 0

␭

⬍

␭

苷 0

y 苷 0y共L兲苷 0y共0兲苷 0

y⬙⫹

␭

y 苷 0

y共

␲

兲苷 1y共0兲苷 09y⬙⫺18y⬘⫹10y 苷 0

y共

␲

兾2兲苷 1y共0兲苷 2y⬙⫹4y⬘⫹13y 苷 0

y共1兲苷 0y共0兲苷 1y⬙⫺6y⬘⫹9y 苷 0

30.

y共

␲

兲苷 2y共0兲苷 1y⬙⫺6y⬘⫹25y 苷 0

y共

␲

兲苷 5y共0兲苷 2y⬙⫹100y 苷 0

y共3兲苷 0y共0兲苷 1y⬙⫺3y⬘⫹2y 苷 0

y共1兲苷 2y共0兲苷 1y⬙⫹2y⬘ 苷 0

y共

␲

兲苷 ⫺4y共0兲苷 34y⬙⫹y 苷 0

y⬘共1兲苷 1y共1兲苷 0y⬙⫹12y⬘⫹36y 苷 0

y⬘共0兲苷 1y共0兲苷 2y⬙⫹2y⬘⫹2y 苷 0

23.

y⬘共

␲

兲苷 2y共

␲

兲苷 0y⬙⫺2y⬘⫹5y 苷 0

y⬘共

␲

兾4兲苷 4y共

␲

兾4兲苷 ⫺3y⬙⫹16y 苷 0

21.

y⬘共0兲苷 4y共0兲苷 12y⬙⫹5y⬘⫺3y 苷 0

y⬘共0兲苷 ⫺1.5y共0兲苷 14y⬙⫺4y⬘⫹y 苷 0

1–13 Solve the differential equation.

3. 4.

5. 6.

7. 8.

10.

12.

13.

;

14 –16 Graph the two basic solutions of the differential equation

and several other solutions. What features do the solutions have in

common?

14.

15.

16.

17–24 Solve the initial-value problem.

18. ,,y⬘共0兲苷 3y共0兲苷 1y⬙⫹3y 苷 0

y⬘共0兲苷 ⫺4y共0兲苷 32y⬙⫹5y⬘⫹3y 苷 0

17.

⫹ 6

⫹ y 苷 0

⫺ 2

⫺ 3y 苷 0

⫹ 4

⫹ 20y 苷 0

100

⫹ 200

⫹ 101P 苷 0

⫹ 12

⫹ 5y 苷 0

⫹ 2

⫺ y 苷 0

11.

y⬙⫹3y⬘ 苷 0y⬙⫺4y⬘⫹13y 苷 0

y⬙⫺4y⬘⫹y 苷 0y⬘ 苷 2y⬙

25y⬙⫹9y 苷 09y⬙⫺12y⬘⫹4y 苷 0

y⬙⫺8y⬘⫹12y 苷 0y⬙⫹16y 苷 0

y⬙⫹4y⬘⫹4y 苷 0y⬙⫺y⬘⫺6y 苷 0

EXERCISES

18.1

NONHOMOGENEOUS LINEAR EQUATIONS

In this section we learn how to solve second-order nonhomogeneous linear differential equa-

tions with constant coefﬁcients, that is, equations of the form

where , , and are constants and is a continuous function. The related homogeneous

equation

is called the complementary equation and plays an important role in the solution of the

original nonhomogeneous equation (1).

ay⬙⫹by⬘⫹cy 苷 0

Gcba

ay⬙⫹by⬘⫹cy 苷 G共x兲

18.2

THEOREM The general solution of the nonhomogeneous differential equation

(1) can be written as

where is a particular solution of Equation 1 and is the general solution of the

complementary Equation 2.

PROOF All we have to do is verify that if is any solution of Equation 1, then is a

solution of the complementary Equation 2. Indeed

We know from Section 18.1 how to solve the complementary equation. (Recall that the

solution is , where and are linearly independent solutions of Equa-

tion 2.) Therefore Theorem 3 says that we know the general solution of the nonhomoge-

neous equation as soon as we know a particular solution . There are two methods for

ﬁnding a particular solution: The method of undetermined coefﬁcients is straightforward

but works only for a restricted class of functions . The method of variation of parameters

works for every function but is usually more difﬁcult to apply in practice.

THE METHOD OF UNDETERMINED COEFFICIENTS

We ﬁrst illustrate the method of undetermined coefﬁcients for the equation

where ) is a polynomial. It is reasonable to guess that there is a particular solution

that is a polynomial of the same degree as because if is a polynomial, then

is also a polynomial. We therefore substitute a polynomial (of the

same degree as ) into the differential equation and determine the coefﬁcients.

EXAMPLE 1 Solve the equation .

SOLUTION The auxiliary equation of is

with roots , . So the solution of the complementary equation is

Since is a polynomial of degree 2, we seek a particular solution of the form

Then and so, substituting into the given differential equation, we

have

共2A兲 ⫹ 共2Ax ⫹ B兲 ⫺ 2共Ax

⫹ Bx ⫹ C 兲苷 x

⬙ 苷 2Ay

⬘ 苷 2Ax ⫹ B

共x兲苷 Ax

⫹ Bx ⫹ C

G共x兲苷 x

苷 c

⫹ c

⫺2x

⫺2r 苷 1

⫹ r ⫺ 2 苷共r ⫺ 1兲共r ⫹ 2兲苷 0

y⬙⫹y⬘⫺2y 苷 0

y⬙⫹y⬘⫺2y 苷 x

共x兲苷ay⬙⫹by⬘⫹cy

yGy

G共x

ay⬙⫹by⬘⫹cy 苷 G共x兲

苷 c

⫹ c

苷 t共x兲 ⫺ t共x兲苷 0

苷共ay⬙⫹by⬘⫹cy兲 ⫺ 共ay

⬙⫹by

⬘⫹cy

兲

a共y ⫺ y

兲⬙⫹b共y ⫺ y

兲⬘⫹c共y ⫺ y

兲苷 ay⬙⫺ay

⬙⫹by⬘⫺by

⬘⫹cy ⫺ cy

y ⫺ y

y共x兲苷 y

共x兲 ⫹ y

共x兲

1154

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

Polynomials are equal when their coefﬁcients are equal. Thus

The solution of this system of equations is

A particular solution is therefore

and, by Theorem 3, the general solution is

If (the right side of Equation 1) is of the form , where and are constants,

then we take as a trial solution a function of the same form, , because the

derivatives of are constant multiples of .

EXAMPLE 2 Solve .

SOLUTION The auxiliary equation is with roots , so the solution of the com-

plementary equation is

For a particular solution we try . Then and . Substi-

tuting into the differential equation, we have

so and . Thus a particular solution is

and the general solution is

If is either or , then, because of the rules for differentiating the

sine and cosine functions, we take as a trial particular solution a function of the form

EXAMPLE 3 Solve .

SOLUTION We try a particular solution

Then y

⬙ 苷 ⫺A cos x ⫺ B sin xy

⬘ 苷 ⫺A sin x ⫹ B cos x

共x兲苷 A cos x ⫹ B sin x

y⬙⫹y⬘⫺2y 苷 sin x

共x兲苷 A cos kx ⫹ B sin kx

C sin kxC cos kxG共x兲

y共x兲苷 c

cos 2x ⫹ c

sin 2x ⫹

共x兲苷

A 苷

13Ae

苷 e

9Ae

⫹ 4共Ae

兲苷 e

⬙ 苷 9Ae

⬘ 苷 3Ae

共x兲苷 Ae

共x兲苷 c

cos 2x ⫹ c

sin 2x

⫾2ir

⫹ 4 苷 0

y⬙⫹4y 苷 e

共x兲苷 Ae

kCCe

G共x兲

y 苷 y

⫹ y

苷 c

⫹ c

⫺2x

⫺

x ⫺

共x兲苷 ⫺

⫺

x ⫺

C 苷 ⫺

B 苷 ⫺

A 苷 ⫺

2A ⫹ B ⫺ 2C 苷 02A ⫺ 2B 苷 0⫺2A 苷 1

⫺2Ax

⫹ 共2A ⫺ 2B兲x ⫹ 共2A ⫹ B ⫺ 2C兲苷 x

SECTION 18.2 NONHOMOGENEOUS LINEAR EQUATIONS

||||

1155

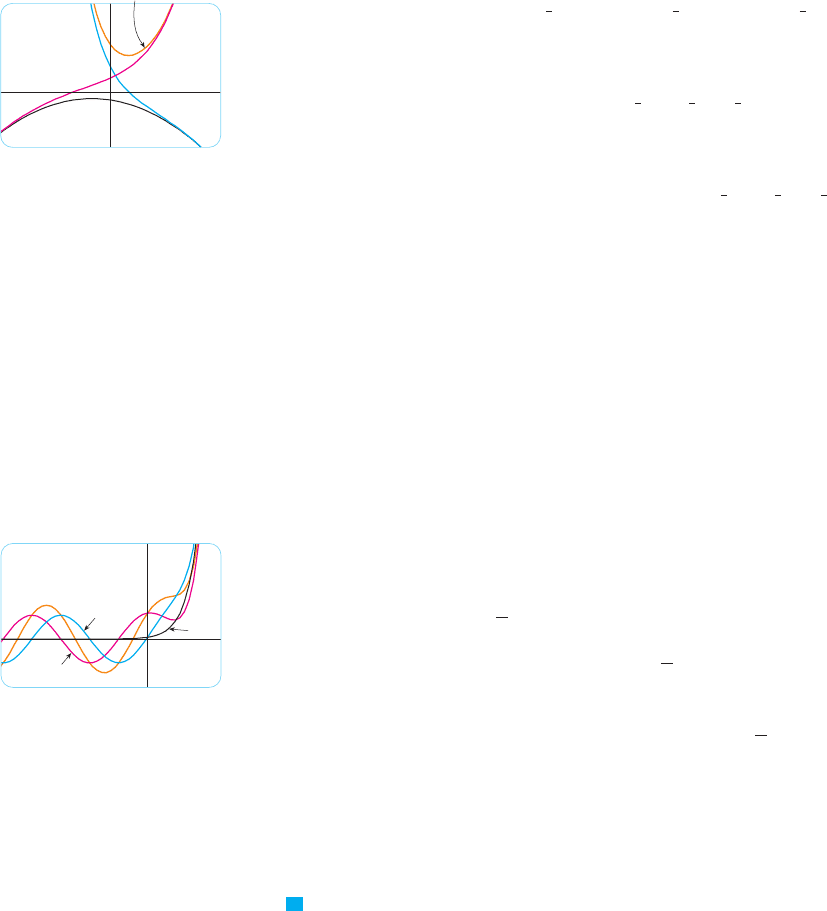
N Figure 1 shows four solutions of the differen-

tial equation in Example 1 in terms of the partic-

ular solution and the functions

and .t共x兲苷 e

⫺2x

f 共x兲苷 e

FIGURE 1

_3 3

+3g

+2f

+2f+3g

N Figure 2 shows solutions of the differential

equation in Example 2 in terms of and the

functions and .

Notice that all solutions approach as

and all solutions (except ) resemble sine

functions when is negative.x

x l ⬁⬁

t共x兲苷 sin 2xf 共x兲苷 cos 2x

FIGURE 2

_4 2

+f+g

so substitution in the differential equation gives

This is true if

The solution of this system is

so a particular solution is

In Example 1 we determined that the solution of the complementary equation is

. Thus the general solution of the given equation is

If is a product of functions of the preceding types, then we take the trial solu-

tion to be a product of functions of the same type. For instance, in solving the differential

equation

we would try

If is a sum of functions of these types, we use the easily veriﬁed principle of super-

position, which says that if and are solutions of

respectively, then is a solution of

EXAMPLE 4 Solve .

SOLUTION The auxiliary equation is with roots , so the solution of the com-

plementary equation is . For the equation we try

Then , , so substitution in the equation

gives

or 共⫺3Ax ⫹ 2A ⫺ 3B兲e

苷 xe

共Ax ⫹ 2A ⫹ B兲e

⫺ 4共Ax ⫹ B兲e

苷 xe

⬙ 苷共Ax ⫹ 2A ⫹ B兲e

⬘ 苷共Ax ⫹ A ⫹ B兲e

共x兲苷共Ax ⫹ B兲e

y⬙⫺4y 苷 xe

共x兲苷 c

⫹ c

⫺2x

⫾2r

⫺ 4 苷 0

y⬙⫺4y 苷 xe

⫹ cos 2x

ay⬙⫹by⬘⫹cy 苷 G

共x兲 ⫹ G

共x兲

⫹ y

ay⬙⫹by⬘⫹cy 苷 G

共x兲ay⬙⫹by⬘⫹cy 苷 G

共x兲

G共x兲

共x兲苷共Ax ⫹ B兲 cos 3x ⫹ 共Cx ⫹ D兲 sin 3x

y⬙⫹2y⬘⫹4y 苷 x cos 3x

G共x兲

y共x兲苷 c

⫹ c

⫺2x

⫺

共cos x ⫹ 3sin x兲

苷 c

⫹ c

⫺2x

共x兲苷 ⫺

cos x ⫺

sin x

B 苷 ⫺

A 苷 ⫺

⫺A ⫺ 3B 苷 1and⫺3A ⫹ B 苷 0

共⫺3A ⫹ B兲 cos x ⫹ 共⫺A ⫺ 3B兲 sin x 苷 sin x

共⫺A cos x ⫺ B sin x兲 ⫹ 共⫺A sin x ⫹ B cos x兲 ⫺ 2共A cos x ⫹ B sin x兲苷 sin x

1156

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

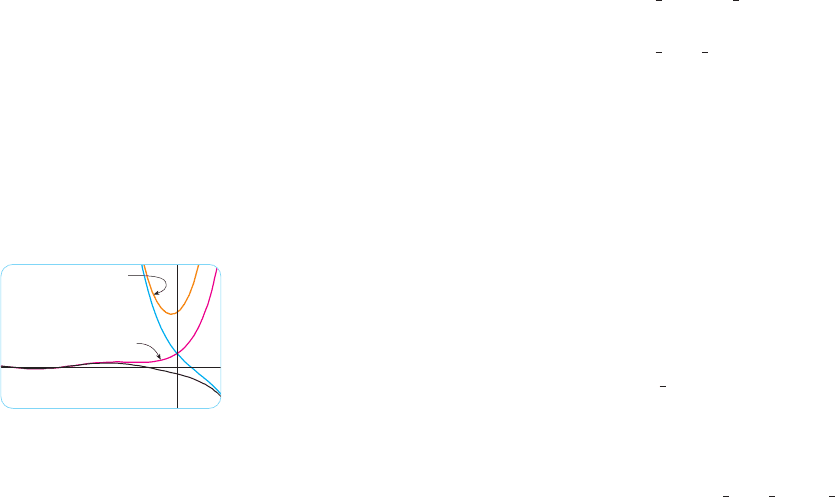
Thus and , so , , and

For the equation , we try

Substitution gives

Therefore , , and

By the superposition principle, the general solution is

Finally we note that the recommended trial solution sometimes turns out to be a solu-

tion of the complementary equation and therefore can’t be a solution of the nonhomoge-

neous equation. In such cases we multiply the recommended trial solution by (or by

if necessary) so that no term in is a solution of the complementary equation.

EXAMPLE 5 Solve .

SOLUTION The auxiliary equation is with roots , so the solution of the com-

plementary equation is

Ordinarily, we would use the trial solution

but we observe that it is a solution of the complementary equation, so instead we try

Then

Substitution in the differential equation gives

⬙⫹y

苷 ⫺2A sin x ⫹ 2B cos x 苷 sin x

⬙共x兲苷 ⫺2A sin x ⫺ Ax cos x ⫹ 2B cos x ⫺ Bx sin x

⬘共x兲苷 A cos x ⫺ Ax sin x ⫹ B sin x ⫹ Bx cos x

共x兲苷 Ax cos x ⫹ Bx sin x

共x兲苷 A cos x ⫹ B sin x

共x兲苷 c

cos x ⫹ c

sin x

⫾ir

⫹ 1 苷 0

y⬙⫹y 苷 sin x

共x兲

y 苷 y

⫹ y

苷 c

⫹ c

⫺2x

⫺

(

x ⫹

)

⫺

cos 2x

共x兲苷 ⫺

cos 2x

⫺8D 苷 0⫺8C 苷 1

⫺8C cos 2x ⫺ 8D sin 2x 苷 cos 2x

⫺4C cos 2x ⫺ 4D sin 2x ⫺ 4共C cos 2x ⫹ D sin 2x兲苷 cos 2x

共x兲苷 C cos 2x ⫹ D sin 2x

y⬙⫺4y 苷 cos 2x

共x兲苷

(

⫺

x ⫺

)

B 苷 ⫺

A 苷 ⫺

2A ⫺ 3B 苷 0⫺3A 苷 1

SECTION 18.2 NONHOMOGENEOUS LINEAR EQUATIONS

||||

1157

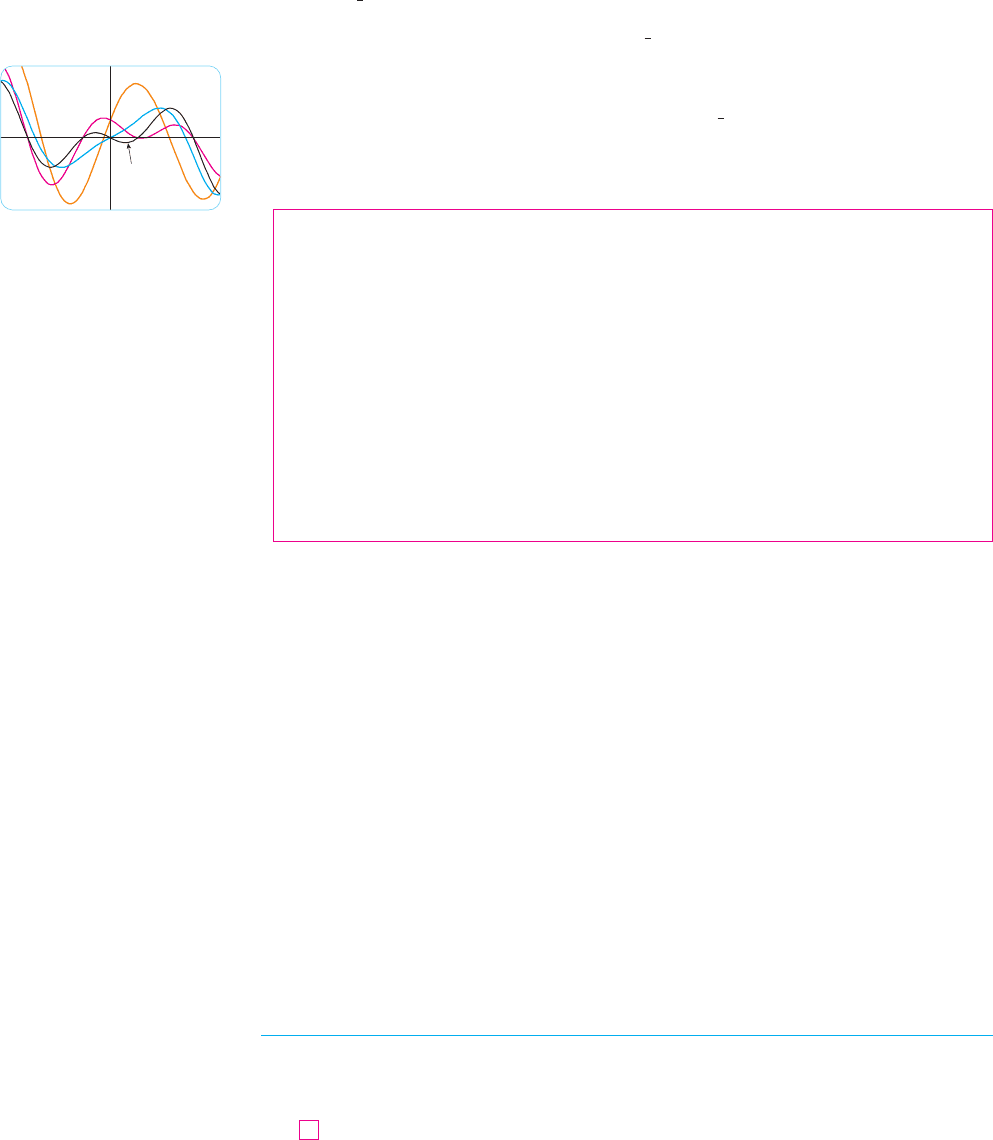
N In Figure 3 we show the particular solution

of the differential equation in

Example 4. The other solutions are given in terms

of and .t共x兲苷 e

⫺2x

f 共x兲苷 e

苷 y

⫹ y

FIGURE 3

_4 1

+2f+g

so , , and

The general solution is

We summarize the method of undetermined coefﬁcients as follows:

SUMMARY OF THE METHOD OF UNDETERMINED COEFFICIENTS

If , where is a polynomial of degree , then try ,

where is an th-degree polynomial (whose coefﬁcients are determined by

substituting in the differential equation).

2. If or , where is an th-degree

polynomial, then try

where and are th-degree polynomials.

Modiﬁcation: If any term of is a solution of the complementary equation,

multiply by (or by if necessary).

EXAMPLE 6 Determine the form of the trial solution for the differential equation

SOLUTION Here has the form of part 2 of the summary, where , , and

. So, at ﬁrst glance, the form of the trial solution would be

But the auxiliary equation is , with roots , so the solution

of the complementary equation is

This means that we have to multiply the suggested trial solution by . So, instead, we

use

THE METHOD OF VARIATION OF PARAMETERS

Suppose we have already solved the homogeneous equation and writ-

ten the solution as

where and are linearly independent solutions. Let’s replace the constants (or parame-

ters) and in Equation 4 by arbitrary functions and . We look for a particu-u

共x兲u

共x兲c

y共x兲苷 c

共x兲 ⫹ c

共x兲

ay⬙⫹by⬘⫹cy 苷 0

共x兲苷 xe

共A cos 3x ⫹ B sin 3x兲

共x兲苷 e

共c

cos 3x ⫹ c

sin 3x兲

r 苷 2 ⫾ 3ir

⫺ 4r ⫹ 13 苷 0

共x兲苷 e

共A cos 3x ⫹ B sin 3x兲

P共x兲苷 1

m 苷 3k 苷 2G共x兲

y⬙⫺4y⬘⫹13y 苷 e

cos 3x

nRQ

共x兲苷 e

Q共x兲 cos mx ⫹ e

R共x兲 sin mx

nPG共x兲苷 e

P共x兲 sin mxG共x兲苷 e

P共x兲 cos mx

nQ共x兲

共x兲苷 e

Q共x兲nPG共x兲苷 e

P共x兲

y共x兲苷 c

cos x ⫹ c

sin x ⫺

x cos x

共x兲苷 ⫺

x cos x

B 苷 0A 苷 ⫺

1158

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

FIGURE 4

_2π 2π

N The graphs of four solutions of the differential

equation in Example 5 are shown in Figure 4.

lar solution of the nonhomogeneous equation of the form

(This method is called variation of parameters because we have varied the parameters

and to make them functions.) Differentiating Equation 5, we get

Since and are arbitrary functions, we can impose two conditions on them. One con-

dition is that is a solution of the differential equation; we can choose the other condition

so as to simplify our calculations. In view of the expression in Equation 6, let’s impose the

condition that

Then

Substituting in the differential equation, we get

But and are solutions of the complementary equation, so

and Equation 8 simpliﬁes to

Equations 7 and 9 form a system of two equations in the unknown functions and .

After solving this system we may be able to integrate to ﬁnd and and then the partic-

ular solution is given by Equation 5.

EXAMPLE 7 Solve the equation , .

SOLUTION The auxiliary equation is with roots , so the solution of

is . Using variation of parameters, we seek a solution

of the form

Then

Set

⬘

sin x ⫹ u

⬘

cos x 苷 0

⬘ 苷共u

⬘ sin x ⫹ u

⬘ cos x兲 ⫹ 共u

cos x ⫺ u

sin x兲

共x兲苷 u

共x兲 sin x ⫹ u

共x兲 cos x

sin x ⫹ c

cos xy⬙⫹y 苷 0

⫾ir

⫹ 1 苷 0

⬍

␲

兾2y⬙⫹y 苷 tan x

⬘u

⬘

a共u

⬘y

⬘⫹u

⬘y

⬘兲苷 G

⬙⫹by

⬘⫹cy

苷 0anday

⬙⫹by

⬘⫹cy

苷 0

共ay

⬙⫹by

⬘⫹cy

兲 ⫹ u

共ay

⬙⫹by

⬘⫹cy

兲 ⫹ a共u

⬘y

⬘⫹u

⬘y

⬘兲苷 G

a共u

⬘y

⬘⫹u

⬘y

⬘⫹u

⬙⫹u

⬙兲 ⫹ b共u

⬘⫹u

⬘兲 ⫹ c共u

⫹ u

兲苷 G

⬙ 苷 u

⬘y

⬘⫹u

⬘y

⬘⫹u

⬙⫹u

⬙

⬘y

⫹ u

⬘y

苷 0

⬘ 苷共u

⬘y

⫹ u

⬘y

兲 ⫹ 共u

⬘⫹u

⬘兲

共x兲苷 u

共x兲 y

共x兲 ⫹ u

共x兲 y

共x兲

ay⬙⫹by⬘⫹cy 苷 G共x兲

SECTION 18.2 NONHOMOGENEOUS LINEAR EQUATIONS

||||

1159

Then

For to be a solution we must have

Solving Equations 10 and 11, we get

(We seek a particular solution, so we don’t need a constant of integration here.) Then,

from Equation 10, we obtain

(Note that for .) Therefore

and the general solution is

My共x兲苷 c

sin x ⫹ c

cos x ⫺ cos x ln共sec x ⫹ tan x兲

苷 ⫺cos x ln共sec x ⫹ tan x兲

共x兲苷 ⫺cos x sin x ⫹ 关sin x ⫺ ln共sec x ⫹ tan x兲兴 cos x

⬍

␲

兾2sec x ⫹ tan x ⬎ 0

共x兲苷 sin x ⫺ ln共sec x ⫹ tan x兲

⬘ 苷 ⫺

sin x

cos x

⬘ 苷 ⫺

sin

cos x

苷

cos

x ⫺ 1

cos x

苷 cos x ⫺ sec x

共x兲苷 ⫺cos xu

⬘ 苷 sin x

⬘共sin

x ⫹ cos

x兲苷 cos x tan x

⬙⫹y

苷 u

⬘

cos x ⫺ u

⬘

sin x 苷 tan x

⬙ 苷 u

⬘ cos x ⫺ u

⬘ sin x ⫺ u

sin x ⫺ u

cos x

1160

||||

CHAPTER 18 SECOND-ORDER DIFFERENTIAL EQUATIONS

;

11–12 Graph the particular solution and several other solutions.

What characteristics do these solutions have in common?

11. 12.

13–18 Write a trial solution for the method of undetermined

coefﬁcients. Do not determine the coefﬁcients.

13.

14.

15.

17.

y⬙⫹4y 苷 e

⫹ x sin 2x

18.

y⬙⫹2y⬘⫹10y 苷 x

⫺x

cos 3x

y⬙⫹3y⬘⫺4y 苷共x

⫹ x兲e

16.

y⬙⫹9y⬘ 苷 1 ⫹ xe

y⬙⫹9y⬘ 苷 xe

⫺x

cos

␲

y⬙⫹9y 苷 e

⫹ x

sin x

y⬙⫹4y 苷 e

⫺x

y⬙⫹3y⬘⫹2y 苷 cos x

1–10 Solve the differential equation or initial-value problem

using the method of undetermined coefﬁcients.

8. ,,

10. ,,

y⬘共0兲苷 0y 共0兲苷 1y⬙⫹y⬘⫺2y 苷 x ⫹ sin 2x

y⬘共0兲苷 1y共0兲苷 2y⬙⫺y⬘ 苷 xe

y⬘共0兲苷 2y共0兲苷 1y⬙⫺4y 苷 e

cos x

y⬘共0兲苷 0y共0兲苷 2y⬙⫹y 苷 e

⫹ x

y⬙⫹2y⬘⫹y 苷 xe

⫺x

y⬙⫺4y⬘⫹5y 苷 e

⫺x

y⬙⫹6y⬘⫹9y 苷 1 ⫹ x

y⬙⫺2y⬘ 苷 sin 4x

y⬙⫹9y 苷 e

y⬙⫹3y⬘⫹2y 苷 x

EXERCISES

18.2

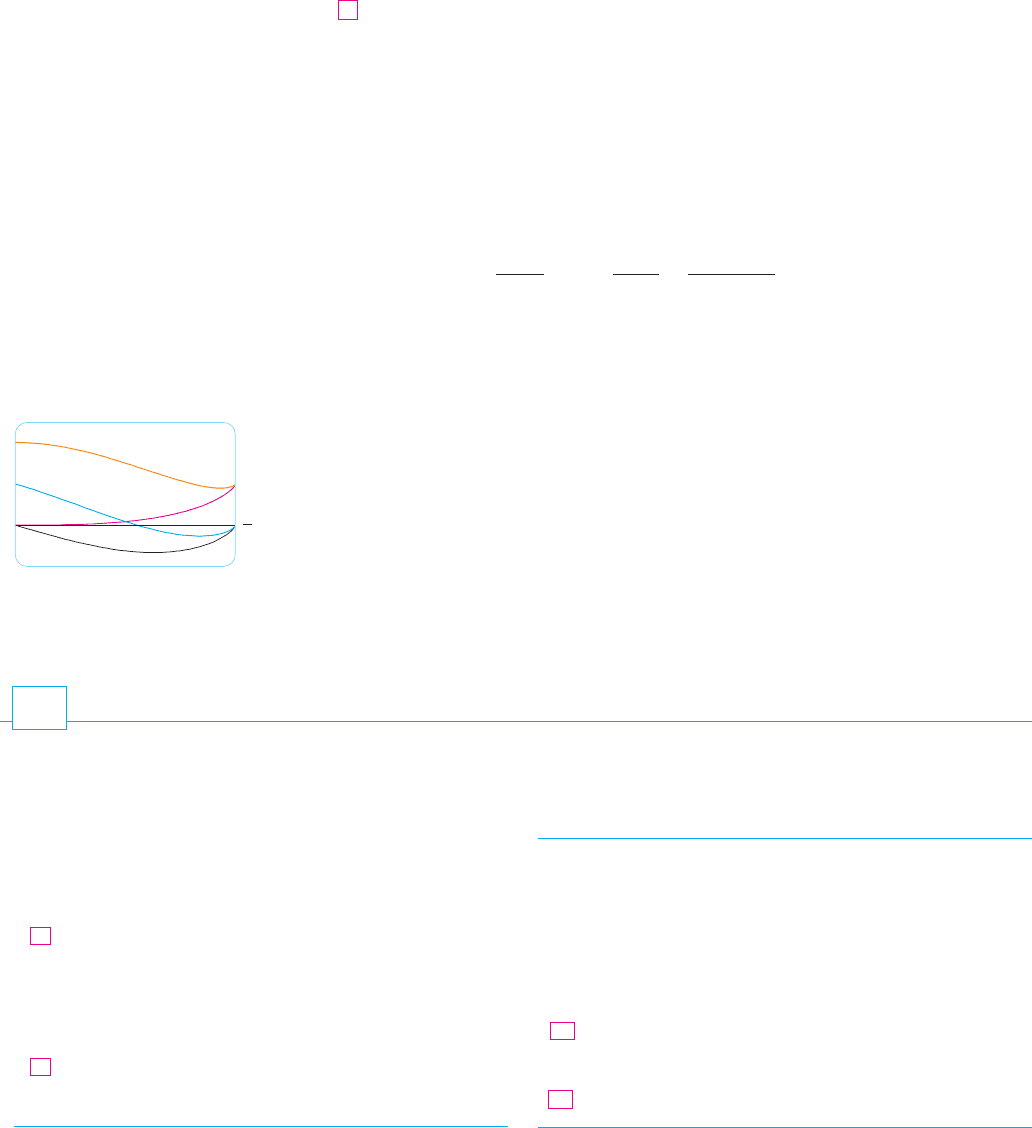
FIGURE 5

2.5

N Figure 5 shows four solutions of the

differential equation in Example 7.

SECTION 18.3 APPLICATIONS OF SECOND-ORDER DIFFERENTIAL EQUATIONS

||||

1161

24. ,

26.

27.

28.

y⬙⫹4y⬘⫹4y 苷

⫺2x

y⬙⫺2y⬘⫹y 苷

1 ⫹ x

y⬙⫹3y⬘⫹2y 苷 sin共e

兲

y⬙⫺3y⬘⫹2y 苷

1 ⫹ e

⫺x

25.

⬍

␲

兾2y⬙⫹y 苷 sec

19–22 Solve the differential equation using (a) undetermined coef-

ﬁcients and (b) variation of parameters.

19. 20.

22.

23–28 Solve the differential equation using the method of

variation of parameters.

23. ,0

⬍

␲

兾2y⬙⫹y 苷 sec

y⬙⫺y⬘ 苷 e

y⬙⫺2y⬘⫹y 苷 e

21.

y⬙⫺2y⬘⫺3y 苷 x ⫹ 24y⬙⫹y 苷 cos x

APPLICATIONS OF SECOND-ORDER DIFFERENTIAL EQUATIONS

Second-order linear differential equations have a variety of applications in science and

engineering. In this section we explore two of them: the vibration of springs and electric

circuits.

VIBRATING SPRINGS

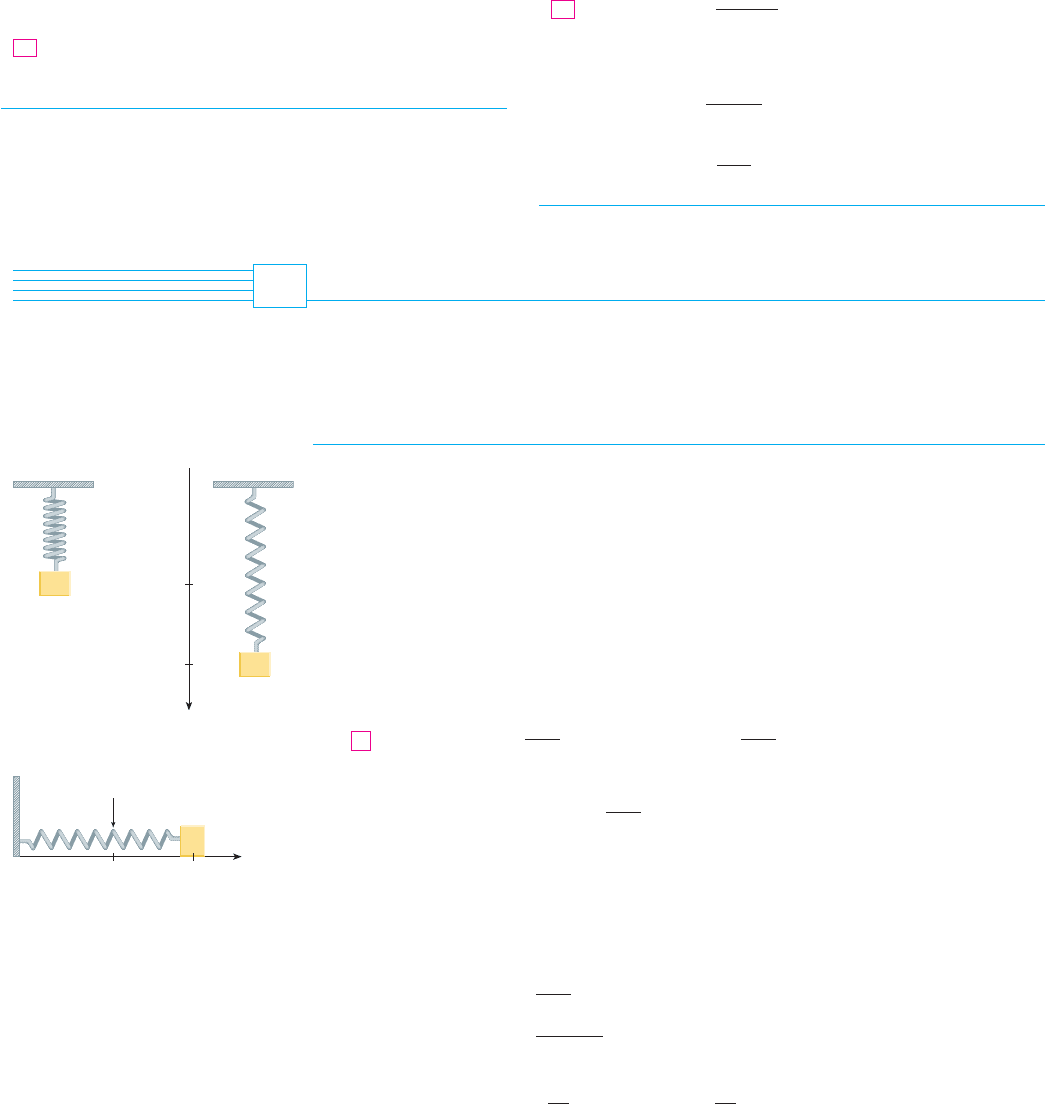
We consider the motion of an object with mass at the end of a spring that is either ver-

tical (as in Figure 1) or horizontal on a level surface (as in Figure 2).

In Section 6.4 we discussed Hooke’s Law, which says that if the spring is stretched (or

compressed) units from its natural length, then it exerts a force that is proportional to :

where is a positive constant (called the spring constant). If we ignore any external resist-

ing forces (due to air resistance or friction) then, by Newton’s Second Law (force equals

mass times acceleration), we have

This is a second-order linear differential equation. Its auxiliary equation is

with roots , where . Thus the general solution is

which can also be written as

where (frequency)

(amplitude)

(See Exercise 17.) This type of motion is called simple harmonic motion.

共

␦

is the phase angle兲sin

␦

苷 ⫺

cos

␦

苷

A 苷

⫹ c

␻

苷

k兾m

x共t兲苷 A cos共

␻

t ⫹

␦

兲

x共t兲苷 c

cos

␻

t ⫹ c

sin

␻

苷

k兾m

r 苷 ⫾

␻

⫹ k 苷 0

⫹ kx 苷 0orm

苷 ⫺kx

restoring force 苷 ⫺kx

18.3

FIGURE 2

FIGURE 1

equilibrium position

equilibrium

position