Stewart J. Calculus
Подождите немного. Документ загружается.

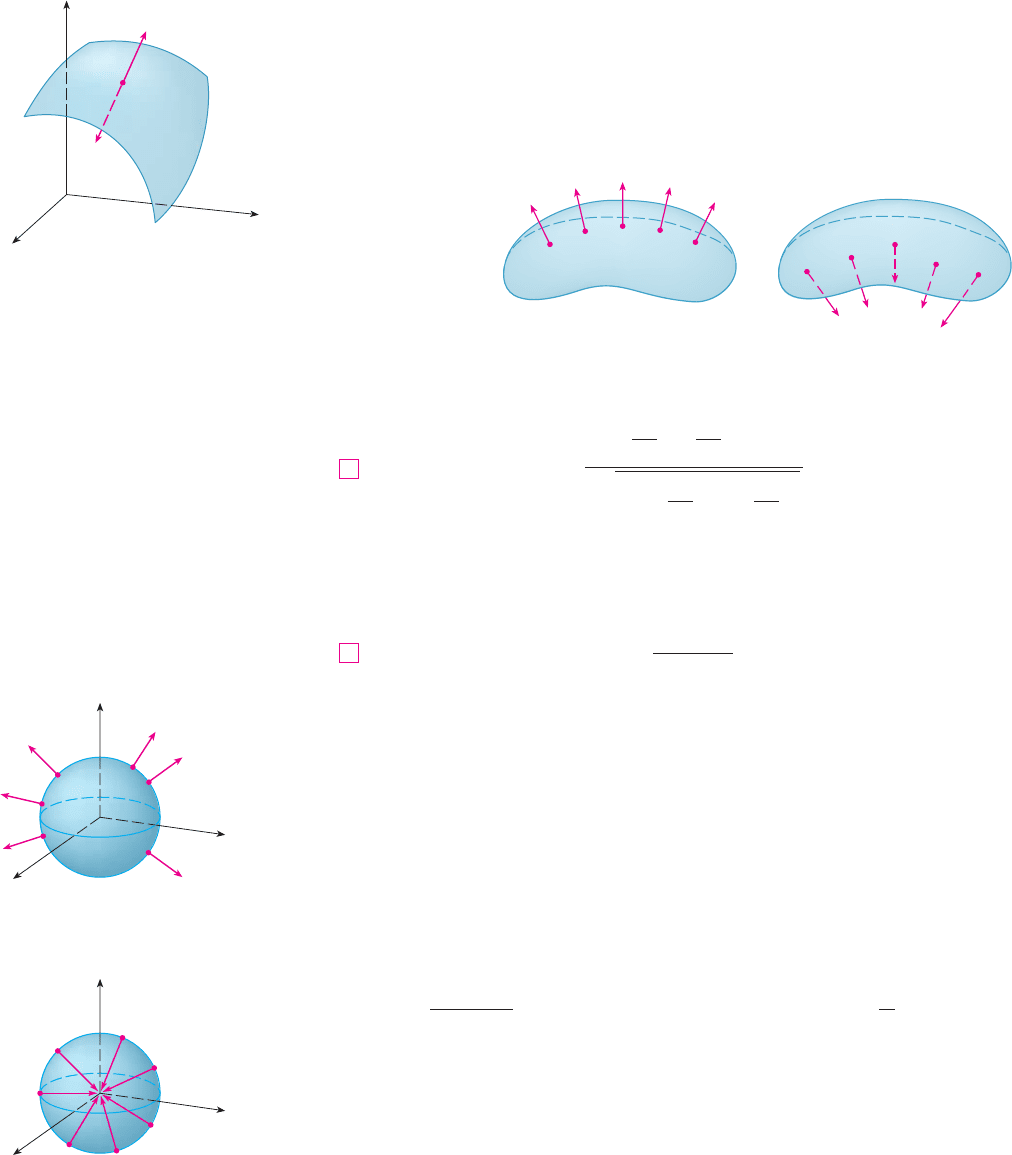
From now on we consider only orientable (two-sided) surfaces. We start with a surface
that has a tangent plane at every point on (except at any boundary point). There
are two unit normal vectors and at . (See Figure 6.)
If it is possible to choose a unit normal vector at every such point so that
varies continuously over , then is called an oriented surface and the given choice of
provides with an orientation. There are two possible orientations for any orientable sur-
face (see Figure 7).
For a surface given as the graph of , we use Equation 3 to associate with
the surface a natural orientation given by the unit normal vector
Since the -component is positive, this gives the upward orientation of the surface.
If is a smooth orientable surface given in parametric form by a vector function
, then it is automatically supplied with the orientation of the unit normal vector
and the opposite orientation is given by . For instance, in Example 4 in Section 17.6 we
found the parametric representation
for the sphere . Then in Example 10 in Section 17.6 we found that
and
So the orientation induced by is defined by the unit normal vector
Observe that points in the same direction as the position vector, that is, outward from the
sphere (see Figure 8). The opposite (inward) orientation would have been obtained (see
Figure 9) if we had reversed the order of the parameters because .
For a closed surface, that is, a surface that is the boundary of a solid region , the
convention is that the positive orientation is the one for which the normal vectors point
outward from , and inward-pointing normals give the negative orientation (see Figures 8
and 9).
E
E
r
r
苷 r
r
n
n 苷
r
r
ⱍ
r
r
ⱍ
苷 sin
cos
i sin
sin
j cos
k 苷
1
a
r共
,
兲
r共
,
兲
ⱍ
r
r
ⱍ
苷 a
2
sin
r
r
苷 a
2
sin
2
cos
i a
2
sin
2
sin
j a
2
sin
cos
k
x
2
y
2
z
2
苷 a
2
r共
,
兲 苷 a sin
cos
i a sin
sin
j a cos
k
n
n 苷
r
u
r
v
ⱍ
r
u
r
v
ⱍ
6
r共u, v兲
S
k
n 苷
t
x
i
t
y
j k
冑
1
冉
t
x
冊
2
冉
t
y
冊
2
5
tz 苷 t共x, y兲
n
n
n
n
n
n
n
n
n
n
FIGURE 7
The two orientations
of an orientable surface
S
nSS
n共x, y, z兲n
共x, y, z兲n
2
苷 n
1
n
1
S共x, y, z兲S
1122
||||
CHAPTER 17 VECTOR CALCULUS
FIGURE 6
n¡
n™
0
y
z
x
0
FIGURE 8
Positive orientation
FIGURE 9
Negative orientation
y
z
x
y
z
x

SURFACE INTEGRALS OF VECTOR FIELDS
Suppose that is an oriented surface with unit normal vector , and imagine a fluid with
density and velocity field flowing through . (Think of as an imagi-
nary surface that doesn’t impede the fluid flow, like a fishing net across a stream.) Then the
rate of flow (mass per unit time) per unit area is . If we divide into small patches ,
as in Figure 10 (compare with Figure 1), then is nearly planar and so we can approxi-
mate the mass of fluid crossing in the direction of the normal per unit time by the
quantity
where , , and are evaluated at some point on . (Recall that the component of the vec-
tor in the direction of the unit vector is .) By summing these quantities and tak-
ing the limit we get, according to Definition 1, the surface integral of the function
over :
and this is interpreted physically as the rate of flow through .
If we write , then is also a vector field on and the integral in Equation 7
becomes
A surface integral of this form occurs frequently in physics, even when is not , and is
called the surface integral (or flux integral) of over .
DEFINITION If is a continuous vector field defined on an oriented surface
with unit normal vector , then the surface integral of over S is
This integral is also called the flux of across .
In words, Definition 8 says that the surface integral of a vector field over is equal to
the surface integral of its normal component over (as previously defined).
If is given by a vector function , then is given by Equation 6, and from Def-
inition 8 and Equation 2 we have
where is the parameter domain. Thus we have
yy
S
F ⴢ dS 苷
yy
D
F ⴢ 共r
u
r
v
兲 dA
9
D
苷
yy
D
冋
F共r共u, v兲兲 ⴢ
r
u
r
v
ⱍ
r
u
r
v
ⱍ
册
ⱍ
r
u
r
v
ⱍ
dA
yy
S
F ⴢ dS 苷
yy
S
F ⴢ
r
u
r
v
ⱍ
r
u
r
v
ⱍ
dS
nr共u, v兲S
S
S
SF
yy
S
F ⴢ dS 苷
yy
S
F ⴢ n dS
Fn
SF
8
SF
vF
yy
S
F ⴢ n dS
⺢
3
FF 苷
v
S
yy
S
v ⴢ n dS 苷
yy
S
共x, y, z兲v共x, y, z兲 ⴢ n共x, y, z兲 dS
7
S
v ⴢ n
v ⴢ nn
v
S
ij
nv
共
v ⴢ n兲A共S
ij
兲
nS
ij
S
ij
S
ij
S
v
SSv共x, y, z兲
共x, y, z兲
nS
SECTION 17.7 SURFACE INTEGRALS
||||
1123
0
y
z
x
n
F=∏v
S
S
ij
FIGURE 10
N Compare Equation 9 to the similar expres-
sion for evaluating line integrals of vector fields
in Definition 17.2.13:
y
C
F ⴢ dr 苷
y
b
a
F共r共t兲兲 ⴢ r共t兲 dt

EXAMPLE 4 Find the flux of the vector field across the unit
sphere .
SOLUTION Using the parametric representation
we have
and, from Example 10 in Section 17.6,
Therefore
and, by Formula 9, the flux is
by the same calculation as in Example 1. M
If, for instance, the vector field in Example 4 is a velocity field describing the flow of a
fluid with density 1, then the answer, , represents the rate of flow through the unit
sphere in units of mass per unit time.
In the case of a surface given by a graph , we can think of and as param-
eters and use Equation 3 to write
Thus Formula 9 becomes
This formula assumes the upward orientation of ; for a downward orientation we multi-
ply by . Similar formulas can be worked out if is given by or .
(See Exercises 35 and 36.)
x 苷 k共y, z兲y 苷 h共x, z兲S1
S
yy
S
F ⴢ dS 苷
yy
D
冉
P
t
x
Q
t
y
R
冊
dA
10
F ⴢ 共r
x
r
y
兲 苷 共P i Q j R k兲 ⴢ
冉
t
x
i
t
y
j k
冊
yxz 苷 t共x, y兲S
4
兾3
苷
4
3
冉
since
y
2
0
cos
d
苷 0
冊
苷 0
y
0
sin
3
d
y
2
0
sin
2
d
苷 2
y
0
sin
2
cos
d
y
2
0
cos
d
y
0
sin
3
d
y
2
0
sin
2
d
苷
y
2
0
y
0
共2sin
2
cos
cos
sin
3
sin
2
兲
d
d
yy
S
F ⴢ dS 苷
yy
D
F ⴢ 共r
r
兲
dA
F共r共
,
兲兲 ⴢ 共r
r
兲 苷 cos
sin
2
cos
sin
3
sin
2
sin
2
cos
cos
r
r
苷 sin
2
cos
i sin
2
sin
j sin
cos
k
F共r共
,
兲兲 苷 cos
i sin
sin
j sin
cos
k
r共
,
兲 苷 sin
cos
i sin
sin
j cos
k 0
0
2
x
2
y
2
z
2
苷 1
F共x, y, z兲 苷 z i y j x k
1124
||||
CHAPTER 17 VECTOR CALCULUS
N Figure 11 shows the vector field in
Example 4 at points on the unit sphere.
F
FIGURE 11
y
x
z
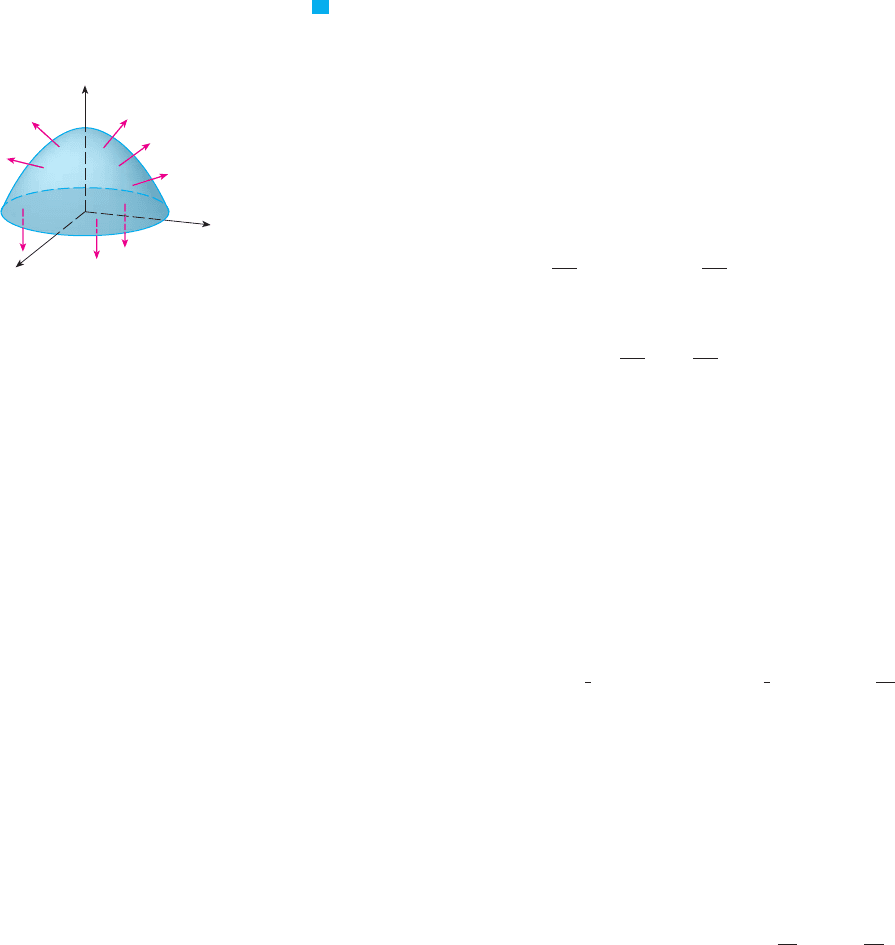
EXAMPLE 5 Evaluate , where and is the
boundary of the solid region enclosed by the paraboloid and the
plane .
SOLUTION consists of a parabolic top surface and a circular bottom surface . (See
Figure 12.) Since is a closed surface, we use the convention of positive (outward)
orientation. This means that is oriented upward and we can use Equation 10 with
being the projection of on the -plane, namely, the disk . Since
on and
we have
The disk is oriented downward, so its unit normal vector is and we have
since on . Finally, we compute, by definition, as the sum of the sur-
face integrals of over the pieces and :
M
Although we motivated the surface integral of a vector field using the example of fluid
flow, this concept also arises in other physical situations. For instance, if is an electric
field (see Example 5 in Section 17.1), then the surface integral
is called the electric flux of through the surface . One of the important laws of electro-SE
yy
S
E ⴢ dS
E
yy
S
F ⴢ dS 苷
yy
S
1
F ⴢ dS
yy
S
2
F ⴢ dS 苷
2
0 苷
2
S
2
S
1
F
xx
S
F ⴢ dSS
2
z 苷 0
yy
S
2
F ⴢ dS 苷
yy
S
2
F ⴢ 共k兲 dS 苷
yy
D
共z兲 dA 苷
yy
D
0 dA 苷 0
n 苷 kS
2
苷
y
2
0
(
1
4
cos
sin
)
d
苷
1
4
共2
兲 0 苷
2
苷
y
2
0
y
1
0
共r r
3
4r
3
cos
sin
兲
dr d
苷
y
2
0
y
1
0
共1 4r
2
cos
sin
r
2
兲
r dr d
苷
yy
D
共1 4xy x
2
y
2
兲
dA
苷
yy
D
关y共2x兲 x共2y兲 1 x
2
y
2
兴
dA
yy
S
1
F ⴢ dS 苷
yy
D
冉
P
t
x
Q
t
y
R
冊
dA
t
y
苷 2y
t
x
苷 2xS
1
R共x, y, z兲 苷 z 苷 1 x
2
y
2
Q共x, y, z兲 苷 xP共x, y, z兲 苷 y
x
2
y
2
1xyS
1
D
S
1
S
S
2
S
1
S
z 苷 0
z 苷 1 x
2
y
2
E
SF共x, y, z兲 苷 y i x j z kxx
S
F ⴢ dS
V
SECTION 17.7 SURFACE INTEGRALS
||||
1125
S™
S¡
FIGURE 12
y
z
x

statics is Gauss’s Law, which says that the net charge enclosed by a closed surface is
where is a constant (called the permittivity of free space) that depends on the units used.
(In the SI system, .) Therefore, if the vector field in
Example 4 represents an electric field, we can conclude that the charge enclosed by is
.
Another application of surface integrals occurs in the study of heat flow. Suppose the
temperature at a point in a body is . Then the heat flow is defined as the
vector field
where is an experimentally determined constant called the conductivity of the sub-
stance. The rate of heat flow across the surface in the body is then given by the surface
integral
EXAMPLE 6 The temperature in a metal ball is proportional to the square of the
distance from the center of the ball. Find the rate of heat flow across a sphere of
radius with center at the center of the ball.
SOLUTION Taking the center of the ball to be at the origin, we have
where is the proportionality constant. Then the heat flow is
where is the conductivity of the metal. Instead of using the usual parametrization of
the sphere as in Example 4, we observe that the outward unit normal to the sphere
at the point is
and so
But on we have , so . Therefore the rate of heat
flow across is
M
苷 2aKCA共S兲 苷 2aKC共4
a
2
兲 苷 8KC
a
3
yy
S
F ⴢ dS 苷
yy
S
F ⴢ n dS 苷 2aKC
yy
S
dS
S
F ⴢ n 苷 2aKCx
2
y
2
z
2
苷 a
2
S
F ⴢ n 苷
2KC
a
共x
2
y
2
z
2
兲
n 苷
1
a
共x i y j z k兲
共x, y, z兲x
2
y
2
z
2
苷 a
2
K
F共x, y, z兲 苷 K u 苷 KC共2x i 2y j 2z k兲
C
u共x, y, z兲 苷 C共x
2
y
2
z
2
兲
a
S
u
V
yy
S
F ⴢ dS 苷 K
yy
S
∇u ⴢ dS
S
K
F 苷 K ∇u
u共x, y, z兲共x, y, z兲
Q 苷 4
0
兾3
S
FC
2
兾Nⴢ m
2
0
⬇ 8.8542 10
12
0
Q 苷
0
yy
S
E ⴢ dS
11
S
1126
||||
CHAPTER 17 VECTOR CALCULUS
SECTION 17.7 SURFACE INTEGRALS
||||
1127
13. ,
is the part of the paraboloid that lies inside the
cylinder
14. ,
is the part of the sphere that lies
inside the cylinder and above the -plane
,
is the hemisphere ,
16. ,
is the boundary of the region enclosed by the cylinder
and the planes and
17. ,
is the part of the cylinder that lies between the
planes and in the first octant
18. ,
is the part of the cylinder between the planes
and , together with its top and bottom disks
19–30 Evaluate the surface integral for the given vector
field and the oriented surface . In other words, find the flux of
across . For closed surfaces, use the positive (outward) orientation.
, is the part of the
paraboloid that lies above the square
, and has upward orientation
20. ,
is the helicoid of Exercise 10 with upward orientation
21. ,
is the part of the plane in the first octant and
has downward orientation
22. ,
is the part of the cone beneath the plane
with downward orientation
23. ,
is the part of the sphere in the first octant,
with orientation toward the origin
24. ,
is the hemisphere , , oriented in the
direction of the positive -axis
,
consists of the paraboloid , ,
and the disk ,
26. , S is the surface ,
, , with upward orientation0 y 10 x 1
z 苷 xe
y
F共x, y, z兲 苷 xy i 4x
2
j yz k
y 苷 1x
2
z
2
1
0 y 1y 苷 x
2
z
2
S
F共x, y, z兲 苷 y j z k
25.
y
y 0x
2
y
2
z
2
苷 25S
F共x, y, z兲 苷 xz i x j y k
x
2
y
2
z
2
苷 4S
F共x, y, z兲 苷 x i z j y k
z 苷 1z 苷
s
x
2
y
2
S
F共x, y, z兲 苷 x i y j z
4
k
x y z 苷 1S
F共x, y, z兲 苷 xz e
y
i xze
y
j z k
S
F共x, y, z兲 苷 y i x j z
2
k
0 y 10 x 1,
z 苷 4 x
2
y
2
SF共x, y, z兲 苷 xy i yz j z x k
19.
S
FSF
xx
S
F ⴢ dS
z 苷 2z 苷 0
x
2
y
2
苷 9S
xx
S
共x
2
y
2
z
2
兲
dS
x 苷 3x 苷 0
y
2
z
2
苷 1S
xx
S
共z x
2
y兲 dS
x y 苷 5x 苷 0y
2
z
2
苷 9
S
xx
S
xz dS
z 0x
2
y
2
z
2
苷 4S
xx
S
共x
2
z y
2
z兲
dS
15.
xyx
2
y
2
苷 1
x
2
y
2
z
2
苷 4S
xx
S
y
2
dS
x
2
z
2
苷 4
y 苷 x
2
z
2
S
xx
S
y dS
1. Let be the boundary surface of the box enclosed by the
planes , , , , , and . Approx-
imate by using a Riemann sum as in Defini-
tion 1, taking the patches to be the rectangles that are the
faces of the box and the points to be the centers of the
rectangles.
2. A surface consists of the cylinder , ,
together with its top and bottom disks. Suppose you know that
is a continuous function with
Estimate the value of by using a Riemann sum,
taking the patches to be four quarter-cylinders and the top
and bottom disks.
3. Let be the hemisphere , and
suppose is a continuous function with
, and .
By dividing into four patches, estimate the value of
.
Suppose that , where is a
function of one variable such that . Evaluate
, where is the sphere .
5–18 Evaluate the surface integral.
,
is the part of the plane that lies above the
rectangle
6. ,
is the triangular region with vertices (1, 0, 0), (0, 2, 0),
and (0, 0, 2)
7. ,
is the part of the plane that lies in the
first octant
8. ,
is the surface , ,
9. ,
is the surface with parametric equations , ,
,
10. ,
is the helicoid with vector equation
, ,
11. ,
is the part of the cone that lies between the
planes and
12. ,
is the surface , , 0 z 10 y 1x 苷 y 2z
2
S
xx
S
z dS
z 苷 3z 苷 1
z
2
苷 x
2
y
2
S
xx
S
x
2
z
2
dS
0
v
0 u 1r共u, v兲 苷 u cos v i u sin v j v k
S
xx
S
s
1 x
2
y
2
dS
0 u 1, 0
v
兾2z 苷 u cos v
y 苷 u sin vx 苷 u
2
S
xx
S
yz
dS
0 y 10 x 1z 苷
2
3
共x
3兾2
y
3兾2
兲S
xx
S
y dS
x y z 苷 1S
xx
S
yz dS
S
xx
S
xy dS
关0, 3兴 关0, 2兴
z 苷 1 2x 3yS
xx
S
x
2
yz dS
5.
x
2
y
2
z
2
苷 4Sxx
S
f 共x, y, z兲 dS
t共2兲 苷 5
t
f 共x, y, z兲 苷 t
(
s
x
2
y
2
z
2
)
4.
xx
H
f 共x, y, z兲 dS
H
f 共3, 4, 5兲 苷 12f 共3, 4, 5兲 苷 8, f 共3, 4, 5兲 苷 9
f 共3, 4, 5兲 苷 7,f
x
2
y
2
z
2
苷 50, z 0H
S
ij
xx
S
f 共x, y, z兲 dS
f 共0, 0, 1兲 苷 4f 共0, 1, 0兲 苷 3f 共1, 0, 0兲 苷 2
f
1 z 1x
2
y
2
苷 1S
P
ij
*
S
S
ij
xx
S
e
0.1共xyz兲
dS
z 苷 6z 苷 0y 苷 4y 苷 0x 苷 2x 苷 0
S
EXERCISES
17.7
39. (a) Give an integral expression for the moment of inertia
about the -axis of a thin sheet in the shape of a surface
if the density function is .
(b) Find the moment of inertia about the -axis of the funnel
in Exercise 38.
40. Let be the part of the sphere that lies
above the plane . If has constant density , find
(a) the center of mass and (b) the moment of inertia about
the -axis.
41. A fluid has density and flows with velocity
, where and are measured in
meters and the components of in meters per second. Find
the rate of flow outward through the cylinder ,
.
42. Seawater has density and flows in a velocity field
, where and are measured in meters and
the components of in meters per second. Find the rate of
flow outward through the hemisphere ,
.
43. Use Gauss’s Law to find the charge contained in the solid
hemisphere , , if the electric field is
44. Use Gauss’s Law to find the charge enclosed by the cube
with vertices if the electric field is
The temperature at the point in a substance with con-
ductivity is . Find the rate of
heat flow inward across the cylindrical surface ,
.
46. The temperature at a point in a ball with conductivity is
inversely proportional to the distance from the center of the
ball. Find the rate of heat flow across a sphere of radius
with center at the center of the ball.
47. Let be an inverse square field, that is, for
some constant , where . Show that the
flux of across a sphere with center the origin is inde-
pendent of the radius of .S
SF
r 苷 x i y j z kc
F共r兲 苷 cr兾
ⱍ
r
ⱍ
3
F
aS
K
0 x 4
y
2
z
2
苷 6
u共x, y, z兲 苷 2y
2
2z
2
K 苷 6.5
共x, y, z兲
45.
E共x, y, z兲 苷 x i y j z k
共1, 1, 1兲
E共x, y, z兲 苷 x i y j 2z k
z 0x
2
y
2
z
2
a
2
z 0
x
2
y
2
z
2
苷 9
v
zy,x,v 苷 y i x j
1025 kg兾m
3
0 z 1
x
2
y
2
苷 4
v
zy,x,v 苷 z i y
2
j x
2
k
870 kg兾m
3
z
kSz 苷 4
x
2
y
2
z
2
苷 25S
z
Sz
I
z
27. ,
is the cube with vertices
28. , is the boundary of the region
enclosed by the cylinder and the planes
and
29. , is the boundary of the
solid half-cylinder ,
30. ,
is the surface of the tetrahedron with vertices ,
, , and
31. Evaluate correct to four decimal places, where is
the surface , , .
32. Find the exact value of , where is the surface in
Exercise 31.
33. Find the value of correct to four decimal places,
where is the part of the paraboloid that
lies above the -plane.
34. Find the flux of
across the part of the cylinder that lies above
the -plane and between the planes and with
upward orientation. Illustrate by using a computer algebra
system to draw the cylinder and the vector field on the same
screen.
35. Find a formula for similar to Formula 10 for the
case where is given by and is the unit normal
that points toward the left.
36. Find a formula for similar to Formula 10 for the
case where is given by and is the unit normal
that points forward (that is, toward the viewer when the axes
are drawn in the usual way).
Find the center of mass of the hemisphere
, if it has constant density.
38. Find the mass of a thin funnel in the shape of a cone
, , if its density function is
.
共x, y, z兲 苷 10 z
1 z 4z 苷
s
x
2
y
2
z 0
x
2
y
2
z
2
苷 a
2
,
37.
nx 苷 k共y, z兲S
xx
S
F ⴢ dS
ny 苷 h共x, z兲S
xx
S
F ⴢ dS
x 苷 2x 苷 2xy
4y
2
z
2
苷 4
F共x, y, z兲 苷 sin共xyz兲 i x
2
y j z
2
e
x兾5
k
CAS
xy
z 苷 3 2x
2
y
2
S
xx
S
x
2
y
2
z
2
dS
CAS
Sxx
S
x
2
yz dS
CAS
0 y 10 x 1z 苷 xy
S
xx
S
xyz dS
CAS
共0, 0, 1兲共0, 1, 0兲共1, 0, 0兲
共0, 0, 0兲S
F共x, y, z兲 苷 y i 共z y兲 j x
k
0 x 20 z
s
1 y
2
SF共x, y, z兲 苷 x
2
i y
2
j z
2
k
x y 苷 2
y 苷 0x
2
z
2
苷 1
SF共x, y, z兲 苷 x i y j 5 k
共1, 1, 1兲S
F共x, y, z兲 苷 x i 2y j 3z k
1128
||||
CHAPTER 17 VECTOR CALCULUS
STOKES’ THEOREM
Stokes’ Theorem can be regarded as a higher-dimensional version of Green’s Theorem.
Whereas Green’s Theorem relates a double integral over a plane region to a line integral
around its plane boundary curve, Stokes’ Theorem relates a surface integral over a surface
to a line integral around the boundary curve of (which is a space curve). Figure 1 shows SS
D
17.8

an oriented surface with unit normal vector . The orientation of induces the positive
orientation of the boundary curve C shown in the figure. This means that if you walk in
the positive direction around with your head pointing in the direction of , then the sur-
face will always be on your left.
STOKES’ THEOREM Let be an oriented piecewise-smooth surface that is bounded
by a simple, closed, piecewise-smooth boundary curve with positive orientation.
Let be a vector field whose components have continuous partial derivatives on
an open region in that contains . Then
Since
Stokes’ Theorem says that the line integral around the boundary curve of of the tangen-
tial component of is equal to the surface integral of the normal component of the curl
of .
The positively oriented boundary curve of the oriented surface is often written as
, so Stokes’ Theorem can be expressed as
There is an analogy among Stokes’ Theorem, Green’s Theorem, and the Fundamental
Theorem of Calculus. As before, there is an integral involving derivatives on the left side
of Equation 1 (recall that is a sort of derivative of ) and the right side involves the
values of only on the boundary of .
In fact, in the special case where the surface is flat and lies in the -plane with
upward orientation, the unit normal is , the surface integral becomes a double integral,
and Stokes’ Theorem becomes
This is precisely the vector form of Green’s Theorem given in Equation 17.5.12. Thus we
see that Green’s Theorem is really a special case of Stokes’ Theorem.
Although Stokes’ Theorem is too difficult for us to prove in its full generality, we can
give a proof when is a graph and , , and are well behaved.
PROOF OF A SPECIAL CASE OF STOKES’ THEOREM We assume that the equation of is
, where has continuous second-order partial derivatives and is a simple
plane region whose boundary curve corresponds to . If the orientation of is
upward, then the positive orientation of corresponds to the positive orientation of .
(See Figure 2.) We are also given that , where the partial deriva-
tives of , , and are continuous.RQP
F 苷 P i Q j R k
C
1
C
SCC
1
Dt共x, y兲 僆 D
z 苷 t共x, y兲,S
CSFS
y
C
F ⴢ dr 苷
yy
S
curl F ⴢ dS 苷
yy
S
共curl F兲 ⴢ k dA
k
xyS
SF
Fcurl F
yy
S
curl F ⴢ dS 苷
y
S
F ⴢ dr
1
S
S
F
F
S
yy
S
curl F ⴢ dS 苷
yy
S
curl F ⴢ n dSand
y
C
F ⴢ dr 苷
y
C
F ⴢ T ds
y
C
F ⴢ dr 苷
yy
S
curl F ⴢ dS
S⺢
3
F
C
S
nC
Sn
SECTION 17.8 STOKES’ THEOREM
||||
1129
S
y
z
x
C
0
n
n
FIGURE 1
N Stokes’ Theorem is named after the Irish
mathematical physicist Sir George Stokes
(1819–1903). Stokes was a professor at Cam-
bridge University (in fact he held the same
position as Newton, Lucasian Professor of
Mathematics) and was especially noted for his
studies of fluid flow and light. What we call
Stokes’ Theorem was actually discovered by
the Scottish physicist Sir William Thomson
(1824–1907, known as Lord Kelvin). Stokes
learned of this theorem in a letter from Thomson
in 1850 and asked students to prove it on an
examination at Cambridge University in 1854.
We don’t know if any of those students was
able to do so.
FIGURE 2
0
D
C
S
z=g(x,y)
C¡
n
y
z
x

Since is a graph of a function, we can apply Formula 17.7.10 with replaced by
. The result is
where the partial derivatives of , , and are evaluated at . If
is a parametric representation of , then a parametric representation of is
This allows us, with the aid of the Chain Rule, to evaluate the line integral as follows:
where we have used Green’s Theorem in the last step. Then, using the Chain Rule again
and remembering that , , and are functions of , , and and that is itself a func-
tion of and , we get
Four of the terms in this double integral cancel and the remaining six terms can be
arranged to coincide with the right side of Equation 2. Therefore
M
y
C
F ⴢ dr 苷
yy
S
curl F ⴢ dS
冉
P
y
P
z
z
y
R
y
z
x
R
z
z
y
z
x
R
2
z
y x
冊册
dA
y
C
F ⴢ dr 苷
yy
D
冋冉
Q
x
Q
z
z
x
R
x
z
y
R
z
z
x
z
y
R
2
z
x y
冊
yx
zzyxRQP
苷
yy
D
冋
x
冉
Q R
z
y
冊
y
冉
P R
z
x
冊册
dA
苷
y
C
1
冉
P R
z
x
冊
dx
冉
Q R
z
y
冊
dy
苷
y
b
a
冋冉
P R
z
x
冊
dx
dt
冉
Q R
z
y
冊
dy
dt
册
dt
苷
y
b
a
冋
P
dx
dt
Q
dy
dt
R
冉
z
x
dx
dt
z
y
dy
dt
冊册
dt
y
C
F ⴢ dr 苷
y
b
a
冉
P
dx
dt
Q
dy
dt
R
dz
dt
冊
dt
a t bz 苷 t共x共t兲, y共t兲兲y 苷 y共t兲x 苷 x共t兲
CC
1
a t by 苷 y共t兲x 苷 x共t兲
共x, y, t共x, y兲兲RQP
苷
yy
D
冋
冉
R
y
Q
z
冊
z
x
冉
P
z
R
x
冊
z
y
冉
Q
x
P
y
冊册
dA
yy
S
curl F ⴢ dS
2
curl F
FS
1130
||||
CHAPTER 17 VECTOR CALCULUS
EXAMPLE 1 Evaluate , where and is the
curve of intersection of the plane and the cylinder . (Orient to
be counterclockwise when viewed from above.)
SOLUTION The curve (an ellipse) is shown in Figure 3. Although could be
evaluated directly, it’s easier to use Stokes’ Theorem. We first compute
Although there are many surfaces with boundary C, the most convenient choice is the
elliptical region S in the plane that is bounded by . If we orient upward,
then has the induced positive orientation. The projection of on the -plane is the
disk and so using Equation 17.7.10 with , we have
M
EXAMPLE 2 Use Stokes’ Theorem to compute the integral , where
and is the part of the sphere that
lies inside the cylinder and above the -plane. (See Figure 4.)
SOLUTION To find the boundary curve we solve the equations and
. Subtracting, we get and so (since ). Thus is the
circle given by the equations , . A vector equation of is
so
Also, we have
Therefore, by Stokes’ Theorem,
M 苷
s
3
y
2
0
0 dt 苷 0
苷
y
2
0
(
s
3
cos t sin t
s
3
sin t cos t
)
dt
yy
S
curl F ⴢ dS 苷
y
C
F ⴢ dr 苷
y
2
0
F共r共t兲兲 ⴢ r共t兲 dt
F共r共t兲兲 苷
s
3
cos t i
s
3
sin t j cos t sin t k
r共t兲 苷 sin t i cos t j
0 t 2
r共t兲 苷 cos t i sin t j
s
3
k
Cz 苷
s
3
x
2
y
2
苷 1
Cz 0z 苷
s
3
z
2
苷 3x
2
y
2
苷 1
x
2
y
2
z
2
苷 4C
xyx
2
y
2
苷 1
x
2
y
2
z
2
苷 4SF共x, y, z兲 苷 xz i yz j xy k
xx
S
curl F ⴢ dS
V
苷
1
2
共2
兲 0 苷
苷
y
2
0
冋
r
2
2
2
r
3
3
sin
册
0
1
d
苷
y
2
0
(
1
2
2
3
sin
)
d
苷
y
2
0
y
1
0
共1 2r sin
兲
r dr d
y
C
F ⴢ dr 苷
yy
S
curl F ⴢ dS 苷
yy
D
共1 2y兲 dA
z 苷 t共x, y兲 苷 2 yx
2
y
2
1
xySDC
SCy z 苷 2
curl F 苷
ⱍ
i
x
y
2
j
y
x
k
z
z
2
ⱍ
苷 共1 2y兲 k
x
C
F ⴢ drC
Cx
2
y
2
苷 1y z 苷 2
CF共x, y, z兲 苷 y
2
i x j z
2
kx
C
F ⴢ dr
V
SECTION 17.8 STOKES’ THEOREM
||||
1131
FIGURE 3
C
S
y+z=2
D
0
y
z
x
FIGURE 4
0
S
≈+¥+z@=4
C
≈+¥=1
y
z
x
