Stewart J. Calculus
Подождите немного. Документ загружается.


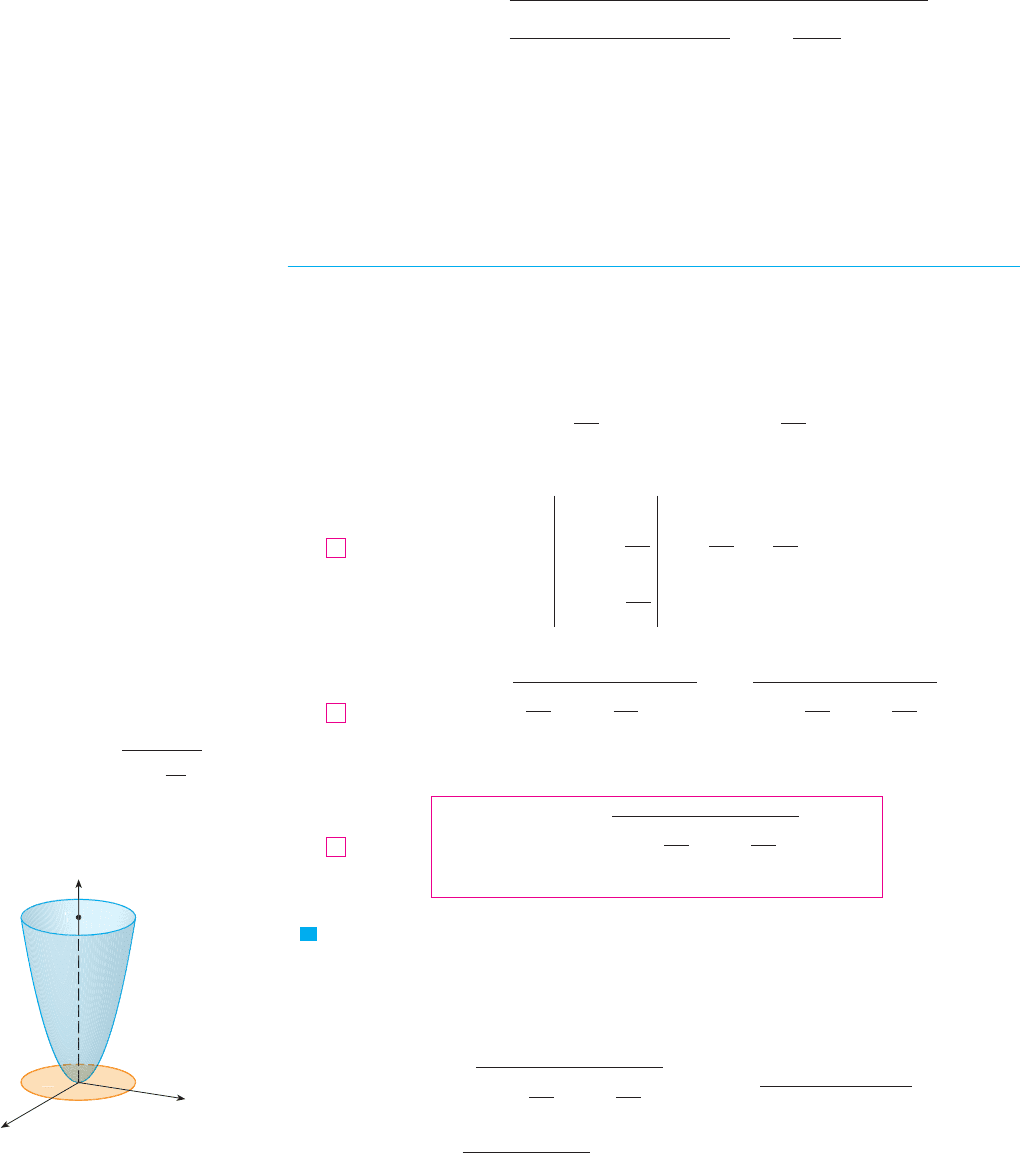
Figure 14(a) shows how the two edges of the patch that meet at can be approximated
by vectors. These vectors, in turn, can be approximated by the vectors and
because partial derivatives can be approximated by difference quotients. So we approxi-
mate by the parallelogram determined by the vectors and . This parallelo-
gram is shown in Figure 14(b) and lies in the tangent plane to at The area of this
parallelogram is
and so an approximation to the area of is
Our intuition tells us that this approximation gets better as we increase the number of sub-
rectangles, and we recognize the double sum as a Riemann sum for the double integral
. This motivates the following definition.
DEFINITION If a smooth parametric surface is given by the equation
and is covered just once as ranges throughout the parameter domain ,
then the surface area of is
where
EXAMPLE 10 Find the surface area of a sphere of radius .
SOLUTION In Example 4 we found the parametric representation
where the parameter domain is
We first compute the cross product of the tangent vectors:
苷 a
2
sin
2
cos
i a
2
sin
2
sin
j a
2
sin
cos
k
r
r
苷
ⱍ
i
x
x
j
y
y
k
z
z
ⱍ
苷
ⱍ
i
a cos
cos
a sin
sin
j
a cos
sin
a sin
cos
k
a sin
0
ⱍ
D 苷
兵
共
,
兲
ⱍ
0
,0
2
其
z 苷 a cos
y 苷 a sin
sin
x 苷 a sin
cos
a
r
v
苷
x
v
i
y
v
j
z
v
kr
u
苷
x
u
i
y
u
j
z
u
k
A共S兲 苷
yy
D
ⱍ
r
u
r
v
ⱍ
dA
S
D共u, v兲S
共u, v兲 僆 Dr共u, v兲 苷 x共u, v兲 i y共u, v兲 j z共u, v兲 k
S
6
xx
D
ⱍ
r
u
r
v
ⱍ
du dv
兺
m
i苷1
兺
n
j苷1
ⱍ
r
u
* r
v
*
ⱍ
u v
S
ⱍ
共u r
u
*兲 共v r
v
*兲
ⱍ
苷
ⱍ
r
u
* r
v
*
ⱍ
u v
P
ij
.S
v r
v
*u r
u
*S
ij
v r
v
*u r
u
*
P
ij
1112
||||
CHAPTER 17 VECTOR CALCULUS
FIGURE 14
Approximating a patch
by a parallelogram
(b)
Î√r
*
√
Îur
*
u
(a)
P
ij
S
ij
Thus
since for . Therefore, by Definition 6, the area of the sphere is
M
SURFACE AREA OF THE GRAPH OF A FUNCTION
For the special case of a surface with equation , where lies in and
has continuous partial derivatives, we take and as parameters. The parametric equations
are
so
and
Thus we have
and the surface area formula in Definition 6 becomes
EXAMPLE 11 Find the area of the part of the paraboloid that lies under
the plane .
SOLUTION The plane intersects the paraboloid in the circle , . There-
fore the given surface lies above the disk with center the origin and radius 3. (See
Figure 15.) Using Formula 9, we have
苷
yy
D
s
1 4共x
2
y
2
兲 dA
A 苷
yy
D
冑
1
冉
z
x
冊
2
冉
z
y
冊
2
dA 苷
yy
D
s
1 共2x兲
2
共2y兲
2
dA
D
z 苷 9x
2
y
2
苷 9
z 苷 9
z 苷 x
2
y
2
V
A共S兲 苷
yy
D
冑
1
冉
z
x
冊
2
冉
z
y
冊
2
dA
9
ⱍ
r
x
r
y
ⱍ
苷
冑
冉
f
x
冊
2
冉
f
y
冊
2
1 苷
冑
1
冉
z
x
冊
2
冉
z
y
冊
2
8
r
x
r
y
苷
ⱍ
i
1
0
j
0
1
k
f
x
f
y
ⱍ
苷
f
x
i
f
y
j k
7
r
y
苷 j
冉
f
y
冊
kr
x
苷 i
冉
f
x
冊
k
z 苷 f 共x, y兲y 苷 yx 苷 x
yx
fD共x, y兲z 苷 f 共x, y兲S
苷 a
2
y
2
0
d
y
0
sin
d
苷 a
2
共2
兲2 苷 4
a
2
A 苷
yy
D
ⱍ
r
r
ⱍ
dA 苷
y
2
0
y
0
a
2
sin
d
d
0
sin
0
苷
s
a
4
sin
4
a
4
sin
2
cos
2
苷 a
2
s
sin
2
苷 a
2
sin
ⱍ
r
r
ⱍ
苷
s
a
4
sin
4
cos
2
a
4
sin
4
sin
2
a
4
sin
2
cos
2
SECTION 17.6 PARAMETRIC SURFACES AND THEIR AREAS
||||
1113
N Notice the similarity between the surface area
formula in Equation 9 and the arc length formula
from Section 9.1.
L 苷
y
b
a
冑
1
冉
dy
dx
冊
2
dx
F
I
G
URE 1
5
9
9
9
9
9
9
x
z
y
3
D

Converting to polar coordinates, we obtain
M
The question remains whether our definition of surface area (6) is consistent with the
surface area formula from single-variable calculus (9.2.4).
We consider the surface obtained by rotating the curve , , about
the -axis, where and is continuous. From Equations 3 we know that para-
metric equations of are
To compute the surface area of we need the tangent vectors
Thus
and so
because . Therefore the area of is
This is precisely the formula that was used to define the area of a surface of revolution in
single-variable calculus (9.2.4).
苷 2
y
b
a
f 共x兲
s
1 关 f 共x兲兴
2
dx
A 苷
yy
D
ⱍ
r
x
r
ⱍ
dA 苷
y
2
0
y
b
a
f 共x兲
s
1 关 f 共x兲兴
2
dx d
Sf 共x兲 0
苷
s
关 f 共x兲兴
2
关1 关 f 共x兲兴
2
兴
苷 f 共x兲
s
1 关 f 共x兲兴
2
ⱍ
r
x
r
ⱍ
苷
s
关 f 共x兲兴
2
关 f 共x兲兴
2
关 f 共x兲兴
2
cos
2
关 f 共x兲兴
2
sin
2
苷 f 共x兲 f 共x兲 i f 共x兲 cos
j f 共x兲 sin
k
r
x
r
苷
ⱍ
i
1
0
j
f 共x兲 cos
f 共x兲 sin
k
f 共x兲 sin
f 共x兲 cos
ⱍ
r
苷 f 共x兲 sin
j f 共x兲 cos
k
r
x
苷 i f 共x兲 cos
j f 共x兲 sin
k
S
0
2
a x bz 苷 f 共x兲 sin
y 苷 f 共x兲 cos
x 苷 x
S
f f 共x兲 0x
a x by 苷 f 共x兲S
苷 2
(
1
8
)
2
3
共1 4r
2
兲
3兾2
]
0
3
苷
6
(
37
s
37
1
)
A 苷
y
2
0
y
3
0
s
1 4r
2
r dr d
苷
y
2
0
d
y
3
0
r
s
1 4r
2
dr
1114
||||
CHAPTER 17 VECTOR CALCULUS
5.
6.
;
7–12 Use a computer to graph the parametric surface. Get a printout
and indicate on it which grid curves have constant and which have
constant.
7.
8.
9.
,,0
v 2
1 u 1r共u, v兲 苷 具u cos v, u sin v, u
5
典
1
v 11 u 1,r共u, v兲 苷 具u v, u
2
, v
2
典,
1 u 1, 1
v 1r共u, v兲 苷 具u
2
1, v
3
1, u v 典,
v
u
r共s, t兲 苷 具s sin 2t, s
2
, s cos 2t典
r共s, t兲 苷 具s, t, t
2
s
2
典
1–2 Determine whether the points and lie on the given surface.
1.
2.
3–6 Identify the surface with the given vector equation.
4. ,0 v 2r共u, v兲 苷 2 sin u i 3 cos u j v
k
r共u,
v兲 苷 共u v兲 i 共3 v兲 j 共1 4u 5v兲 k
3.
P共3, 1, 5兲, Q共1, 3, 4兲
r共u,
v兲 苷 具u v, u
2
v, u v
2
典
P共7, 10, 4兲, Q共5, 22, 5兲
r共u,
v兲 苷 具2u 3v, 1 5u v, 2 u v 典
QP
EXERCISES
17.6

19–26 Find a parametric representation for the surface.
The plane that passes through the point and
contains the vectors and
20. The lower half of the ellipsoid
21. The part of the hyperboloid that lies to the
right of the -plane
22. The part of the elliptic paraboloid that lies
in front of the plane
The part of the sphere that lies above the
cone
24. The part of the sphere that lies between
the planes and
25. The part of the cylinder that lies between the
planes and
The part of the plane that lies inside the cylinder
27–28 Use a computer algebra system to produce a graph that
looks like the given one.
27. 28.
;
29. Find parametric equations for the surface obtained by rotating
the curve , , about the -axis and use them
to graph the surface.
;
30. Find parametric equations for the surface obtained by rotating
the curve , , about the -axis and
use them to graph the surface.
;
31. (a) What happens to the spiral tube in Example 2 (see Fig-
ure 5) if we replace by and by ?
(b) What happens if we replace by and
by ?
;
32. The surface with parametric equations
where and , is called a Möbius
strip. Graph this surface with several viewpoints. What is
unusual about it?
0
2
1
2
r
1
2
z 苷 r sin共
兾2兲
y 苷 2 sin
r cos共
兾2兲
x 苷 2 cos
r cos共
兾2兲
sin 2u
sin ucos 2ucos u
cos usin usin ucos u
y2 y 2x 苷 4y
2
y
4
x0 x 3y 苷 e
x
3
0
_3
_3
0
0
5
z
y
x
0
_1
_1
1
0
1
0
_1
z
y
x
CAS
x
2
y
2
苷 1
z 苷 x 3
26.
x 苷 5x 苷 0
y
2
z
2
苷 16
z 苷 2z 苷 2
x
2
y
2
z
2
苷 16
z 苷
s
x
2
y
2
x
2
y
2
z
2
苷 4
23.
x 苷 0
x y
2
2z
2
苷 4
xz
x
2
y
2
z
2
苷 1
2x
2
4y
2
z
2
苷 1
i j ki j k
共1, 2, 3兲
19.
10. ,
,
11. ,, ,
,
12. ,,
13–18 Match the equations with the graphs labeled I–VI and
give reasons for your answers. Determine which families of grid
curves have constant and which have constant.
14. ,
15.
16. ,
,
17. ,,
18. ,,
y
x
x
y
y
z
z
x
z
z
x
y
III
V
x
y
z
IV
III
VI
y
z
x
z 苷 uy 苷 共1
ⱍ
u
ⱍ
兲sin vx 苷 共1
ⱍ
u
ⱍ
兲cos v
z 苷 sin
3
vy 苷 sin
3
u cos
3
vx 苷 cos
3
u cos
3
v
z 苷 3u 共1 u兲 sin v
y 苷 共1 u兲共3 cos v兲 sin 4
u
x 苷 共1 u兲共3 cos v兲 cos 4
u
r共u,
v兲 苷 sin v i cos u sin 2v j sin u sin 2v k
u
r共u, v兲 苷 u cos v i u sin v j sin u k
r共u,
v兲 苷 u cos v i u sin v j v k
13.
vu
z 苷 u sin
vy 苷 u cos u cos vx 苷 u sin u cos v
兾2 v
兾20 u 2
z 苷 sin 2u sin 4vy 苷 cos u sin 4vx 苷 sin v
0.1 v 6.20 u 2
r共u, v兲 苷 具cos u sin v, sin u sin v, cos v ln tan共v兾2兲典
SECTION 17.6 PARAMETRIC SURFACES AND THEIR AREAS
||||
1115
51. (a) Use the Midpoint Rule for double integrals (see Sec-
tion 16.1) with six squares to estimate the area of the
surface , , .
(b) Use a computer algebra system to approximate the
surface area in part (a) to four decimal places. Compare
with the answer to part (a).
52. Find the area of the surface with vector equation
, ,
. State your answer correct to four decimal
places.
53. Find the exact area of the surface ,
, .
54. (a) Set up, but do not evaluate, a double integral for the area
of the surface with parametric equations ,
, , , .
(b) Eliminate the parameters to show that the surface is an
elliptic paraboloid and set up another double integral for
the surface area.
;
(c) Use the parametric equations in part (a) with and
to graph the surface.
(d) For the case , , use a computer algebra
system to find the surface area correct to four decimal
places.
(a) Show that the parametric equations ,
, , , ,
represent an ellipsoid.
;
(b) Use the parametric equations in part (a) to graph the ellip-
soid for the case , , .
(c) Set up, but do not evaluate, a double integral for the sur-
face area of the ellipsoid in part (b).
56. (a) Show that the parametric equations ,
, , represent a hyperboloid
of one sheet.
;
(b) Use the parametric equations in part (a) to graph the
hyperboloid for the case , , .
(c) Set up, but do not evaluate, a double integral for the sur-
face area of the part of the hyperboloid in part (b) that lies
between the planes and .
Find the area of the part of the sphere that
lies inside the paraboloid .
58. The figure shows the surface created when the cylinder
intersects the cylinder . Find the
area of this surface.
z
y
x
x
2
z
2
苷 1y
2
z
2
苷 1
z 苷 x
2
y
2
x
2
y
2
z
2
苷 4z
57.
z 苷 3z 苷 3
c 苷 3b 苷 2a 苷 1
z 苷 c sinh uy 苷 b cosh u sin
v
x 苷 a cosh u cos v
c 苷 3b 苷 2a 苷 1
0
v 2
0 u
z 苷 c cos uy 苷 b sin u sin v
x 苷 a sin u cos v
55.
b 苷 3a 苷 2
CAS
b 苷 3
a 苷 2
0
v 2
0 u 2z 苷 u
2
y 苷 bu sin v
x 苷 au cos v
0 y 11 x 4
z 苷 1 2x 3y 4y
2
CAS
0 v 2
0 u
r共u, v兲 苷 具cos
3
u cos
3
v, sin
3
u cos
3
v, sin
3
v 典
CAS
CAS
0 y 40 x 6z 苷 1兾共1 x
2
y
2
兲
33–36 Find an equation of the tangent plane to the given para-
metric surface at the specified point. If you have software that
graphs parametric surfaces, use a computer to graph the surface
and the tangent plane.
,, ;
34. ,, ;
35. ;
36. ;
37–47 Find the area of the surface.
The part of the plane that lies in the
first octant
38. The part of the plane that lies inside the
cylinder
39. The surface , ,
40. The part of the plane with vector equation
that is given by
,
The part of the surface that lies within the cylinder
42. The part of the surface that lies above the
triangle with vertices , , and
43. The part of the hyperbolic paraboloid that lies
between the cylinders and
44. The part of the paraboloid that lies inside the
cylinder
45. The part of the surface that lies between the
planes , , , and
46. The helicoid (or spiral ramp) with vector equation
, ,
The surface with parametric equations , ,
, ,
48– 49 Find the area of the surface correct to four decimal places
by expressing the area in terms of a single integral and using your
calculator to estimate the integral.
48. The part of the surface that lies inside the
cylinder
49. The part of the surface that lies above the disk
50. Find, to four decimal places, the area of the part of the
surface that lies above the square
. Illustrate by graphing this part of the surface.
ⱍ
x
ⱍ
ⱍ
y
ⱍ
1
z 苷 共1 x
2
兲兾共1 y
2
兲
CAS
x
2
y
2
4
z 苷 e
x
2
y
2
x
2
y
2
苷 1
z 苷 cos共x
2
y
2
兲
0
v 20 u 1z 苷
1
2
v
2
y 苷 uvx 苷 u
2
47.
0 v
0 u 1r共u, v兲 苷 u cos v i u sin v j v k
z 苷 1z 苷 0x 苷 1x 苷 0
y 苷 4x z
2
y
2
z
2
苷 9
x 苷 y
2
z
2
x
2
y
2
苷 4x
2
y
2
苷 1
z 苷 y
2
x
2
共2, 1兲共0, 1兲共0, 0兲
z 苷 1 3x 2y
2
x
2
y
2
苷 1
z 苷 xy
41.
0 v 10 u 1
r共u,
v兲 苷 具1 v, u 2v, 3 5u v 典
0 y 10 x 1z 苷
2
3
共x
3兾2
y
3兾2
兲
x
2
y
2
苷 9
2x 5y z 苷 10
3x 2y z 苷 6
37.
u 苷 0, v 苷
r共u, v兲 苷 uv i u sin v j v cos u k
u 苷 1,
v 苷 0r共u, v兲 苷 u
2
i 2u sin v j u cos v k
u 苷 1,
v 苷 1z 苷 uvy 苷 v
2
x 苷 u
2
共2, 3, 0兲z 苷 u vy 苷 3u
2
x 苷 u v
33.
1116
||||
CHAPTER 17 VECTOR CALCULUS
SECTION 17.7 SURFACE INTEGRALS
||||
1117
å
¨
0
(x, y, z)
(b, 0, 0)
z
x
y
59. Find the area of the part of the sphere that
lies inside the cylinder .
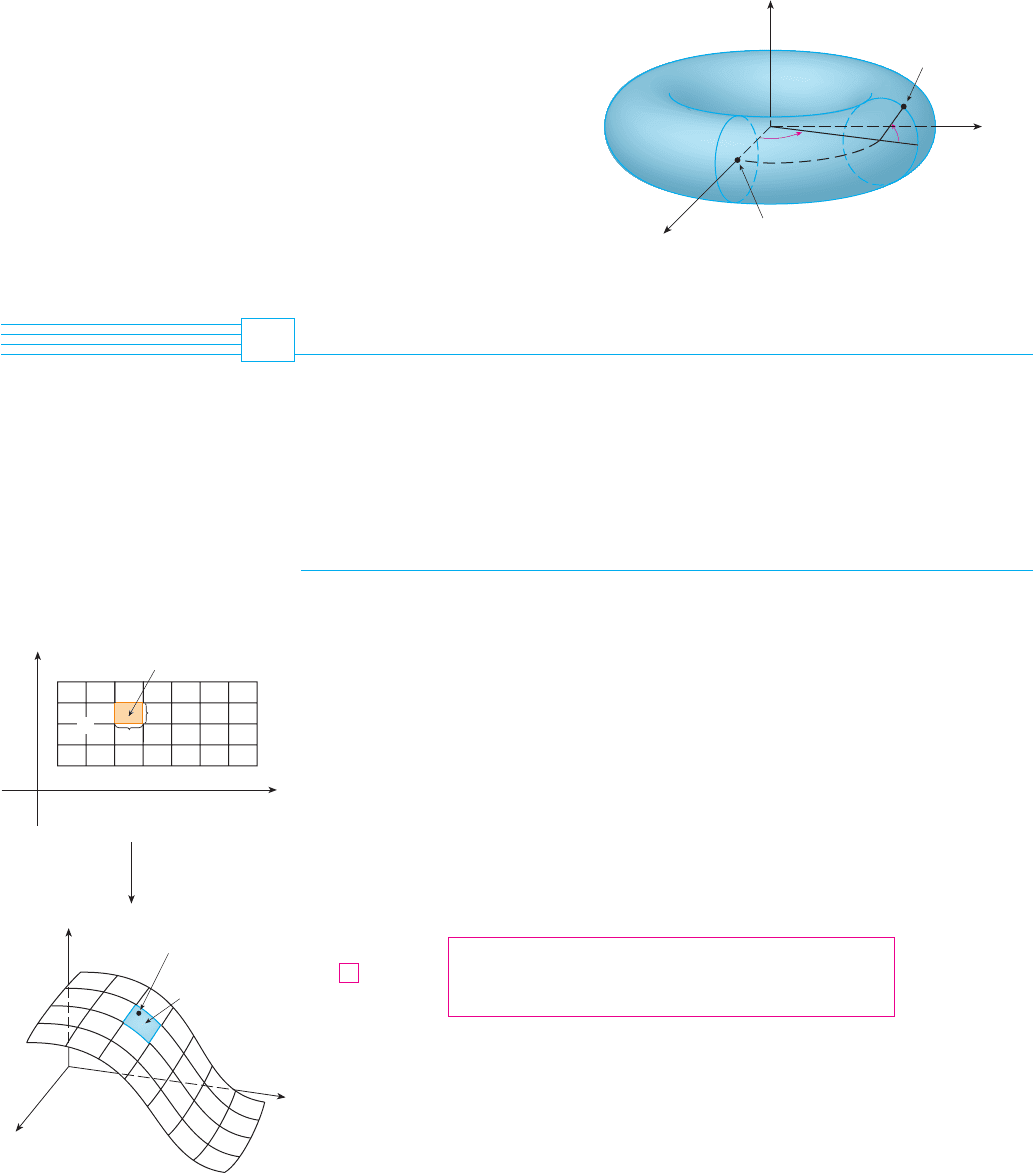
60. (a) Find a parametric representation for the torus obtained
by rotating about the -axis the circle in the -plane with
center and radius . [Hint: Take as parame-
ters the angles and shown in the figure.]
;
(b) Use the parametric equations found in part (a) to graph
the torus for several values of a and b.
(c) Use the parametric representation from part (a) to find the
surface area of the torus.
a
b共b, 0, 0兲
xzz
x
2
y
2
苷 ax
x
2
y
2
z
2
苷 a
2
SURFACE INTEGRALS
The relationship between surface integrals and surface area is much the same as the rela-
tionship between line integrals and arc length. Suppose is a function of three variables
whose domain includes a surface . We will define the surface integral of over in such
a way that, in the case where , the value of the surface integral is equal to the
surface area of . We start with parametric surfaces and then deal with the special case
where is the graph of a function of two variables.
PARAMETRIC SURFACES
Suppose that a surface has a vector equation
We first assume that the parameter domain is a rectangle and we divide it into subrect-
angles with dimensions and . Then the surface is divided into corresponding
patches as in Figure 1. We evaluate at a point in each patch, multiply by the area
of the patch, and form the Riemann sum
Then we take the limit as the number of patches increases and define the surface integral
of f over the surface S as
Notice the analogy with the definition of a line integral (17.2.2) and also the analogy with
the definition of a double integral (16.1.5).
To evaluate the surface integral in Equation 1 we approximate the patch area by the
area of an approximating parallelogram in the tangent plane. In our discussion of surface
area in Section 17.6 we made the approximation
S
ij
⬇
ⱍ
r
u
r
v
ⱍ
u v
S
ij
yy
S
f 共x, y, z兲 dS 苷 lim
m, n l
兺
m
i苷1
兺
n
j苷1
f 共P
ij
*
兲 S
ij
1
兺
m
i苷1
兺
n
j苷1
f 共P
ij
*
兲 S
ij
S
ij
P
ij
*
fS
ij
SvuR
ij
D
共u, v兲 僆 Dr共u, v兲 苷 x共u, v兲 i y共u, v兲 j z共u, v兲 k
S
S
S
f 共x, y, z兲 苷 1
SfS
f
17.7
FIGURE 1
0
√
u
R
ij
Î√
Îu
0
z
y
x
P
*
ij
S
S
ij
D
r

1118
||||
CHAPTER 17 VECTOR CALCULUS
N We assume that the surface is covered only
once as ranges throughout . The value
of the surface integral does not depend on the
parametrization that is used.
D共u,
v兲
N Here we use the identities
Instead, we could use Formulas 64 and 67 in
the Table of Integrals.
sin
2
苷 1 cos
2
cos
2
苷
1
2
共1 cos 2
兲
where
are the tangent vectors at a corner of . If the components are continuous and and
are nonzero and nonparallel in the interior of D, it can be shown from Definition 1, even
when D is not a rectangle, that
This should be compared with the formula for a line integral:
Observe also that
Formula 2 allows us to compute a surface integral by converting it into a double inte-
gral over the parameter domain . When using this formula, remember that is
evaluated by writing , , and in the formula for .
EXAMPLE 1 Compute the surface integral , where is the unit sphere
.
SOLUTION As in Example 4 in Section 17.6, we use the parametric representation
that is,
As in Example 10 in Section 17.6, we can compute that
Therefore, by Formula 2,
M
Surface integrals have applications similar to those for the integrals we have previously
considered. For example, if a thin sheet (say, of aluminum foil) has the shape of a surface
苷
1
2
[
1
2
sin 2
]
0
2
[
cos
1
3
cos
3
]
0
苷
4
3
苷
y
2
0
1
2
共1 cos 2
兲
d
y
0
共sin
sin
cos
2
兲
d
苷
y
2
0
y
0
sin
2
cos
2
sin
d
d
苷
y
2
0
cos
2
d
y
0
sin
3
d
yy
S
x
2
dS 苷
yy
D
共sin
cos
兲
2
ⱍ
r
r
ⱍ
dA
ⱍ
r
r
ⱍ
苷 sin
r共
,
兲 苷 sin
cos
i sin
sin
j cos
k
0
2
0
z 苷 cos
y 苷 sin
sin
x 苷 sin
cos
x
2
y
2
z
2
苷 1
Sxx
S
x
2
dS
f 共x, y, z兲z 苷 z共u, v兲y 苷 y共u, v兲x 苷 x共u, v兲
f 共r共u, v兲兲D
yy
S
1 dS 苷
yy
D
ⱍ
r
u
r
v
ⱍ
dA 苷 A共S兲
y
C
f 共x, y, z兲 ds 苷
y
b
a
f 共r共t兲兲
ⱍ
r共t兲
ⱍ
dt
yy
S
f 共x, y, z兲 dS 苷
yy
D
f 共r共u, v兲兲
ⱍ
r
u
r
v
ⱍ
dA
2
r
v
r
u
S
ij
r
v
苷
x
v
i
y
v
j
z
v
kr
u
苷
x
u
i
y
u
j
z
u
k

and the density (mass per unit area) at the point is , then the total mass
of the sheet is
and the center of mass is , where
Moments of inertia can also be defined as before (see Exercise 39).
GRAPHS
Any surface with equation can be regarded as a parametric surface with para-
metric equations
and so we have
Thus
and
Therefore, in this case, Formula 2 becomes
Similar formulas apply when it is more convenient to project onto the -plane or
-plane. For instance, if is a surface with equation and is its projection on
the -plane, then
EXAMPLE 2 Evaluate , where is the surface , , .
(See Figure 2.)
SOLUTION Since
z
y
苷 2yand
z
x
苷 1
0 y 20 x 1z 苷 x y
2
Sxx
S
y dS
yy
S
f 共x, y, z兲 dS 苷
yy
D
f
(
x, h共x, z兲, z
)
冑
冉
y
x
冊
2
冉
y
z
冊
2
1 dA
xz
Dy 苷 h共x, z兲Sxz
yzS
yy
S
f 共x, y, z兲 dS 苷
yy
D
f
(
x, y, t共x, y兲
)
冑
冉
z
x
冊
2
冉
z
y
冊
2
1 dA
4
ⱍ
r
x
r
y
ⱍ
苷
冑
冉
z
x
冊
2
冉
z
y
冊
2
1
r
x
r
y
苷
t
x
i
t
y
j k
3
r
y
苷 j
冉
t
y
冊
kr
x
苷 i
冉
t
x
冊
k
z 苷 t共x, y兲y 苷 yx 苷 x
z 苷 t共x, y兲S
z 苷
1
m
yy
S
z
共x, y, z兲 dSy 苷
1
m
yy
S
y
共x, y, z兲 dSx 苷
1
m
yy
S
x
共x, y, z兲 dS
共x, y, z 兲
m 苷
yy
S
共x, y, z兲 dS
共x, y, z兲共x, y, z兲S
SECTION 17.7 SURFACE INTEGRALS
||||
1119
FIGURE 2
y
x
z

Formula 4 gives
M
If is a piecewise-smooth surface, that is, a finite union of smooth surfaces ,
that intersect only along their boundaries, then the surface integral of over is defined
by
EXAMPLE 3 Evaluate , where is the surface whose sides are given by the
cylinder , whose bottom is the disk in the plane , and
whose top is the part of the plane that lies above .
SOLUTION The surface is shown in Figure 3. (We have changed the usual position of
the axes to get a better look at .) For we use and as parameters (see Example 5
in Section 17.6) and write its parametric equations as
where
Therefore
and
Thus the surface integral over is
苷
1
2
[
3
2
2 sin
1
4
sin 2
]
0
2
苷
3
2
苷
1
2
y
2
0
关1 2 cos
1
2
共1 cos 2
兲兴
d
苷
y
2
0
y
1cos
0
z dz d
苷
y
2
0
1
2
共1 cos
兲
2
d
yy
S
1
z dS 苷
yy
D
z
ⱍ
r
r
z
ⱍ
dA
S
1
ⱍ
r
r
z
ⱍ
苷
s
cos
2
sin
2
苷 1
r
r
z
苷
ⱍ
i
sin
0
j
cos
0
k
0
1
ⱍ
苷 cos
i sin
j
0 z 1 x 苷 1 cos
and0
2
z 苷 zy 苷 sin
x 苷 cos
z
S
1
S
S
S
2
z 苷 1 xS
3
z 苷 0x
2
y
2
1S
2
x
2
y
2
苷 1
S
1
Sxx
S
z dS
V
yy
S
f 共x, y, z兲 dS 苷
yy
S
1
f 共x, y, z兲 dS
yy
S
n
f 共x, y, z兲 dS
SfS
n
S
2
, ...,S
1
S
苷
s
2
(
1
4
)
2
3
共1 2y
2
兲
3兾2
]
0
2
苷
13
s
2
3
苷
y
1
0
dx
s
2
y
2
0
y
s
1 2y
2
dy
苷
y
1
0
y
2
0
y
s
1 1 4y
2
dy dx
yy
S
y dS 苷
yy
D
y
冑
1
冉
z
x
冊
2
冉
z
y
冊
2
dA
1120
||||
CHAPTER 17 VECTOR CALCULUS
FIGURE 3
0
S¡(≈+¥=1)
S™
S£ (z=1+x)
x
z
y
Since lies in the plane , we have
The top surface lies above the unit disk and is part of the plane . So,
taking in Formula 4 and converting to polar coordinates, we have
Therefore
M
ORIENTED SURFACES
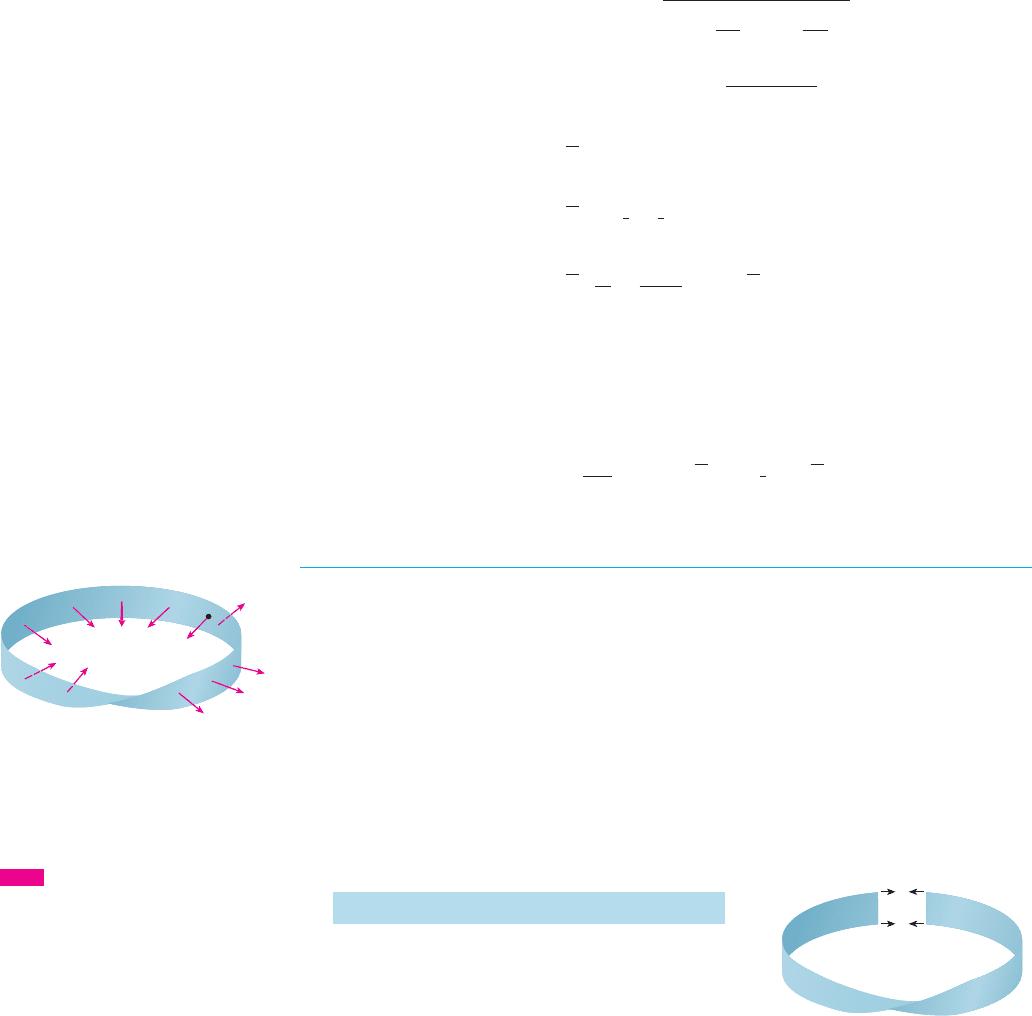
To define surface integrals of vector fields, we need to rule out nonorientable surfaces such
as the Möbius strip shown in Figure 4. [It is named after the German geometer August
Möbius (1790–1868).] You can construct one for yourself by taking a long rectangular
strip of paper, giving it a half-twist, and taping the short edges together as in Figure 5.
If an ant were to crawl along the Möbius strip starting at a point , it would end up on
the “other side” of the strip (that is, with its upper side pointing in the opposite direction).
Then, if the ant continued to crawl in the same direction, it would end up back at the
same point without ever having crossed an edge. (If you have constructed a Möbius strip,
try drawing a pencil line down the middle.) Therefore a Möbius strip really has only
one side. You can graph the Möbius strip using the parametric equations in Exercise 32 in
Section 17.6.
FIGURE 5
Constructing a Möbius strip
A
B
D
C
A
B
C
D
P
P
苷
3
2
0
s
2
苷
(
3
2
s
2
)
yy
S
z dS 苷
yy
S
1
z dS
yy
S
2
z dS
yy
S
3
z dS
苷
s
2
冋
2
sin
3
册
0
2
苷
s
2
苷
s
2
y
2
0
(
1
2
1
3
cos
)
d
苷
s
2
y
2
0
y
1
0
共r r
2
cos
兲
dr d
苷
y
2
0
y
1
0
共1 r cos
兲
s
1 1 0
r dr d
yy
S
3
z dS 苷
yy
D
共1 x兲
冑
1
冉
z
x
冊
2
冉
z
y
冊
2
dA
t共x, y兲 苷 1 x
z 苷 1 xDS
3
yy
S
2
z dS 苷
yy
S
2
0 dS 苷 0
z 苷 0S
2
SECTION 17.7 SURFACE INTEGRALS
||||
1121
FIGURE 4
A Möbius strip
P
Visual 17.7 shows a Möbius strip
with a normal vector that can be moved
along the surface.
TEC
