Сталл Д. Вестрам Э. Зинке Г. Химическая термодинамика органических соединений

Подождите немного. Документ загружается.

102

Часть

Основы

термодинамики

III. Термохимия

103

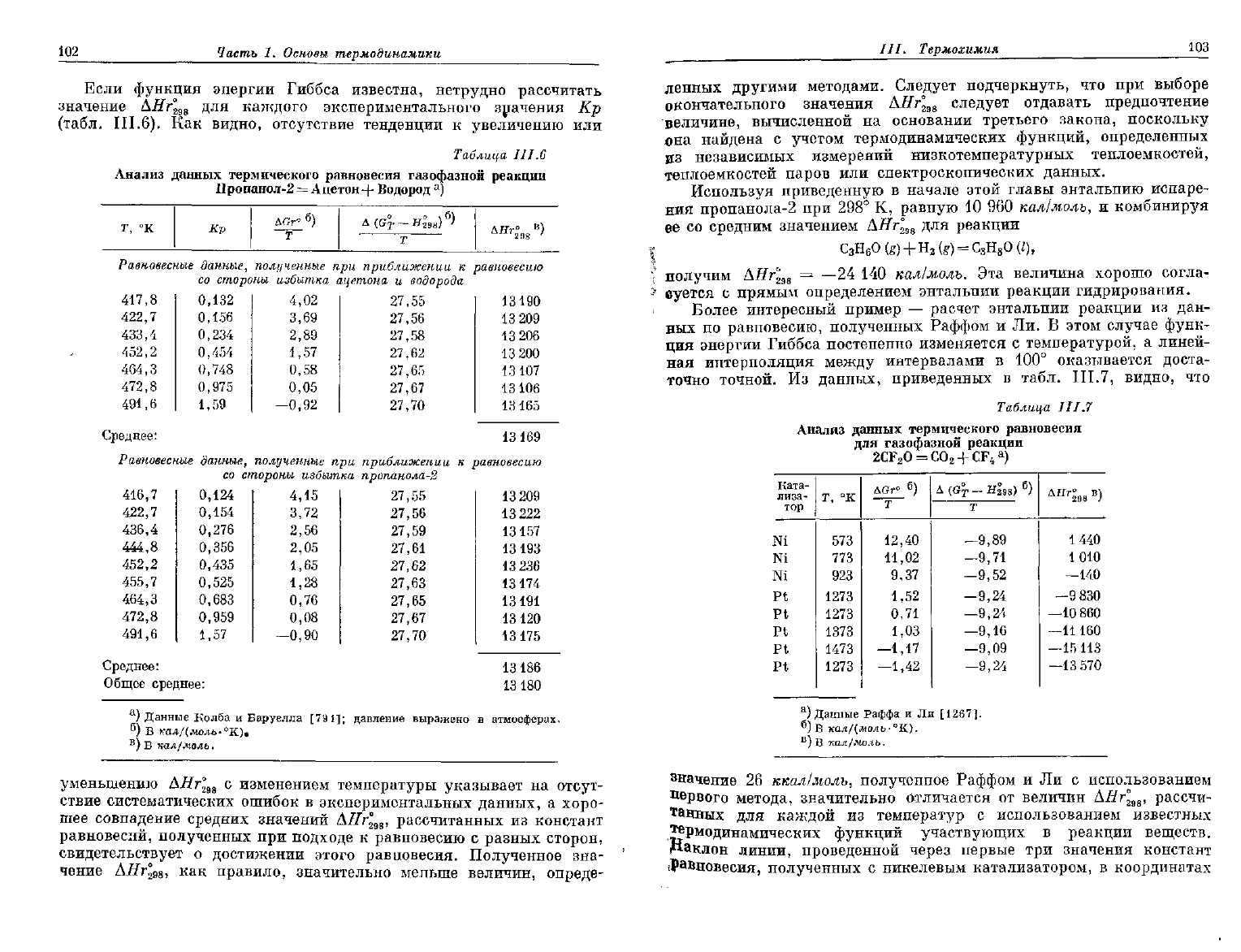
Если

функция энергии Гиббса известна, нетрудно рассчитать

значение

AHr"

29S

для

каждого экспериментального значения

Кр

(табл. II 1.6).

Как

видно, отсутствие тенденции

увеличению

или

Таблица

III.6

Анализ

данных

термического

равновесия

газофазноЁ

реакции

Пропанол-2

Ацетон+Водород

)

г,

°к

Равновесные

417,8

422,7

433,4

452,2

464,3

472,8

491,6

Среднее:

Равновесные

416,7

422,7

436,4

444,8

452,2

455,7

464,3

472,8

491,6

Среднее:

Кр

данные,

AGr«

)

полученные

при

(в°

В°

298

)

приближении

со

стороны

избытка

ацетона

водорода

0,132

0,156

0,234

0,454

0,748

0,975

1,59

данные,

4,02

3,69

2,89

1,57

0,58

0,05

—0,92

полученные

при

со

стороны

избытка

0,124

0,154

0,276

0,356

0,435

0,525

0,683

0,959

1,57

Общее

среднее:

)

Данные

4,15

3,72

2,56

2,05

1,65

1,28

0,76

0,08

—0,90

27,55

27,56

27,58

27,62

27,65

27,67

27,70

A*rj,

»)

равновесию

13190

209

206

200

13107

13106

13165

13169

приближении

равновесию

пропанола-2

27,55

27,56

27,59

27,61

27,62

27,63

27,65

27,67

27,70

Колба

Баруелла

[791];

давление

выражено

)

кал/(моль-°К).

)

кал/моль.

209

222

13157

13193

236

13174

13191

13120

13175

13186

13180

атмосферах.

уменьшению

&Нг°

изменением температуры указывает

на

отсут-

ствие систематических ошибок

экспериментальных данных,

хоро-

шее совпадение средних значений

АНг°

рассчитанных

из

констант

равновесий,

полученных

при

подходе

равновесию

разных сторон,

свидетельствует

достижении этого равновесия. Полученное

зна-

чение

АНг°

298

ка

правило, значительно меньше величин, опреде-

другими методами.

Следует

подчеркнуть,

что при

выборе

окончательного значения

АНг°

2яв

следует

отдавать предпочтение

величине,

вычисленной

на

основании третьего закона, поскольку

;

она

найдена

учетом

термодинамических функций, определенных

из

независимых измерений низкотемпературных теплоемкостей,

теплоемкостей паров

или

спектроскопических данных.

Используя приведенную

начале этой главы энтальпию испаре-

ния

пропанола-2

при

298°

К,

равную

10 960

кал/молъ,

комбинируя

•

ее со

средним значением

AHrl

для

реакции

г получим Л#Г2

= —24 140

кал/молъ.

Эта

величина хорошо согла-

> суется

прямым определением энтальпии реакции гидрирования.

Более интересный пример

—

расчет энтальпии реакции

из дан-

ных

по

равновесию, полученных Раффом

и Ли. В

этом

случае

функ-

ция

энергии Гиббса постепенно изменяется

температурой,

линей-

ная

интерполяция

между

интервалами

в 100°

оказывается доста-

точно точной.

Из

данных, приведенных

табл.

III.7,

видно,

что

Таблица

III.7

Анализ

данных

термического

равновесия

для

газофазной

реакции

Ката-

лиза-

тор

°K

573

773

923

1273

1373

1473

1273

AGr°

)

12,40

11,02

9,37

1,52

0,71

1,03

-1,17

-1,42

д (

Hlas)

)

—9,89

—9,71

—9,52

—9,24

—9,16

—9,09

—9,24

АНГ

298

)

1440

1010

—140

—9

830

—10

860

—11160

—15113

—13

570

)

Данные

Раффа

Ли

[12671.

)в

кал/(.моль-°К).

)

кал/моль.

значение

ккал/молъ,

полученное Раффом

и Ли с

использованием

первого метода, значительно Отличается

от

величин

АНг°

рассчи-

танных

для

каждой

из

температур

использованием известных

2*рмодинамических функций

участвующих

реакции веществ.

Даклон линии, проведенной через первые

три

значения констант

равновесия,

полученных

никелевым катализатором,

координатах

104

Часть

Основы

термодинамики

Kp —

ЦТ, заметно отличается

от

наклона прямой, проходящей

через остальные пять экспериментальных точек, полученных

с платиновым катализатором при значительно более высокой темпе-

ратуре. Как видно

из

приведенных данных, константы равновесия

реакции,

изученной Раффом

Ли, при низких температурах очень

малы, поэтому

их

трудно измерить достаточно точно. Кроме того,

не

исключено, что при этих температурах полностью

не

достигалось

состояние равновесия. Поэтому наиболее достоверным

из

всех

зна-

чений

АНг°

2ю

приведенных

табл.

III.7,

следует

считать значение,

рассчитанное

из

пяти последних констант равновесия,

т. е.

Д#г£

(g)

—12

± 3

ккал/моль.

Комбинируя

полученное значение

энтальпией образования двуоки-

си

углерода

четырехфтористого

углерода

для

энтальпии образо-

вания

карбонилфторида, получим

ДЯУ£

(g)

—

152j5

± 3

ккал/моль.

Это значение хорошо согласуется

величиной —153

0,20 ккал/моль,

найденной

Вартенбергом

[1572]

из теплоты реакции гидролиза

Следует

отметить,

что

использованная Дузом

[360] для

расчета

энтальпии

образования газообразного CF

O величина

AHrl

ккал/моль

привела

ошибочному значению

AHf

(g), равному

—169 ккал/моль. Таким образом, применение функции энергии

Гиббса позволяет получить из равновесных данных такую полезную

информацию,

какую

не

могут

дать достаточно надежно

два

первых

описанных

метода.

Определение

энтальпий образования другими

методами

Для определения энтальпий образования некоторых молекул

можно использовать

ряд

специальных методов. Так, Гейдон

[461]

Герцберг [590] предложили применять

для

определения энергий

диссоциации

двухатомных

молекул спектроскопические данные.

Комбинируя

величины энергий диссоциации

энтальпий образо-

вания

газообразных одноатомных элементов, нетрудно рассчитать

энтальпии

образования

двухатомных

молекул. Методы определения

свободных энергий свободных радикалов описаны Шварцем [1462].

Глава

РАСЧЕТ

ЭНТРОПИИ

Второй закон термодинамики

Второй закон термодинамики позволяет ввести новую функцию

состояния

—

энтропию. Этот термин, предложенный Клаузиусом

[231]

1865

г.,

происходит

от

греческого троя'т! (что

переводе озна-

чает «поворачивать

кругом»

или «изменять»)

используется

крат-

кой

формулировке второго закона термодинамики, данной Клау-

зиусом: «Энтропия вселенной стремится

максимуму»

Матема-

тическое выражение второго закона термодинамики

помощью

линейных

интегралов

для

обратимых

необратимых процессов

может быть представлено

виде

•£«

2»

j ^

Actual

Это выражение можно сформулировать следующим образом: при

. переходе системы

из

состояния

1 в

состояние

линейный интеграл

от

&Q/T

для

обратимых процессов зависит только

от

исходного

конечного состояний системы

и по

своей величине больше соот-

ветствующего интеграла для любого реального процесса, связанного

с необратимым переходом системы

из

состояния

1 в

состояние

Под

обратимым процессом подразумевают такой процесс,

который

протекает под действием бесконечно малой движущей силы

(таким

образом, изменение направления процесса происходит

при

бесконечно малом изменении этой силы). Обратимые процессы

протекают бесконечно медленно

поэтому являются гипотетически-

*Ш» предельными случаями реальных

или

самопро-

извольных процессов, которые характеризуются конечными

Движущими силами

скоростями. Наличие конечных движущих

^^ Клаузиус,

как

известно, неправильно трактовал второй закон термо-

динамики

как абсолютный закон природы.

настоящее время бесспорно доказа-

ек

ъГл!

Нет

никаких

оснований переносить законы термодинамики

статистиче-

ски

физики

конечных изолированных систем на бесконечную во времени

про-

странстве вселенную. Правильно сформулированный постулат Клаузиуса гла-

что единственным результатом любой совокупности процессов

не

может

переход теплоты

от

менее нагретого тела

более нагретому. Подробнее

см., например:

В. Г.

Левич, Курс теоретической

физики,

т. I,

изд-во

:а

», М. 1969.

—

Прим.

перев.

106

Часть

Основы

термодинамики

сил реальных процессов в свою очередь приводит к их неэффектив-

ности,

обусловленной потерей энергии системы за счет трения.

Как

следует

из приведенного выражения (IV. 1), с математической

точки зрения 1/Т является интегрирующим множите-

лем определенного (или интегрируемого) или неоп-

ределенного дифференциала 8Q. Второй закон термодина-

мики

позволяет построить абсолютную термодинамическую шкалу

температур (Т).

Знак

неравенства в выражении

(IV.1)

служит осно-

вой

для оценки термодинамического равновесия и различия

между

обратимыми и необратимыми процессами, в то время как знак равен-

ства позволяет ввести новую термодинамическую

функцию

— энтропию, определяемую как

S*—St

указать способ ее расчета. В дифференциальной форме

(IV.2)

В этом выражении нижний индекс rev указывает на то, что величину

AS можно вычислить только на основании теплот обратимых процес-

сов.

Изменение

энтропии при нагревании системы

Если

система нагревается при постоянном объеме, то dQ

CvdT\ii

CvdT

Если

аналогичный процесс протекает при постоянном давлении,

то dQ

CpdT

(IV.3)

Из

приведенных соотношений видно, что размерность энтропии

совпадает с размерностью теплоемкости, т. е. равна калориям на

моль на

градус

Кельвина

[кал/(молъ-°К)].

В практических расчетах

энтропийную единицу часто обозначают э. е. Интегри-

рование выражения

(IV.3)

по температуре

дает

CpdT

(IV.4)

IV.

Расчет

энтропии

107

Энтропия

смешения

Шоттки

и Вагнер

[1291]

показали, что энтропия смешения невзаи-

модействующих компонентов раствора или невзаимодействующих

идеальных газов * может быть представлена выражением

где и

— число молей, a N

— мольная доля г-х частиц. Энтропия

образования

1 моля смеси идеальных газов равна

Д5=—Д

2(^

In по-

следовательно, в

случае

бинарной смеси, для которой

пЛ^

) = 1,38

кал/(молъ-°К)

Энтропия

фазовых переходов

Изменения

энтропии, связанные с такими фазовыми переходами.

как

энантиотропные твердофазные превращения, плавление, субли-

мация

или испарение, можно легко вычислить из выражения (IV.2),

поскольку они не зависят от температуры. Используя в качестве

примера расчет энтропии процесса плавления, находим

АНт ,

ТЛ

- д.

(IVb)

Вследствие ограничений, налагаемых обратимыми процессами [выра-

жение (IV.2)], расчет изменений энтропии фазовых переходов

будет

правилен только при условии, если все рассматриваемые фазы

находятся в равновесии. Для Я,-фазовых переходов или фазовых

переходов по Шоттки, которые характеризуются неизотермическим

изменением

энтальпии, необходимо учитывать соответствующий

интеграл от теплоемкости.

Влияние давления на энтропию

Изменение

давления влияет на величину энтропии газа, что

необходимо учитывать в термодинамических расчетах. Как показано

гл. V, нетрудно получить уравнение

связывающее зависимость энтропии от давления при постоянной

температуре с зависимостью объема от температуры при постояннол1

Давлении. Из этого уравнения

следует,

что

, При этом предполагают, что давление каждого газа до смешения равно

конечному

давлению газовой смеси

108

Часть

Основы

термодинамики

IV.

Расчет

энтропии

109

или

для

конечного изменения энтропии вещества

при

изменении

давления

от

начального

до

конечного

Р2

Нетрудно заметить,

что в

случае

идеального газа (PV — RT)

\~dfl

~Р~'

Подстановка этого значения

выражение

(IV.8)

дает

(IV.9)

Таким

образом, поскольку сжатие газа приводит

увеличению

его упорядоченности, при возрастании давления от

до

энтропия

газа уменьшается

на

величину

— Si.

Так, например, если давле-

ние

пара хлорбензола при

298,15°

К составляет

И,5мм

рт. ст. [1432],

то уменьшение энтропии

при

сжатии хлорбензола

от

давления

11,5

мм рт.

ст.

до

давления

760 мм рт.

ст.

при

этой темпера-

туре

составит

—1,9873In-jj-g=—8,328

кал/(моль-°К).

При

рассмотрении свойств реального газа «необходимо подставить

выражение

(IV.8)

уравнение состояния реального газа. Такие

уравнения

могут

иметь достаточно сложный

вид

(см., например,

Барроу [76]

Уелтнер

Питцер

[1588])

Так, дифференцирование

уравнения состояния Бертло приводит

выражению

РТс

"J-

дТ)р~

Р L

~32"

PcW

при

подстановке которого

уравнение

(IV.8)

получим

dP_

(IV.10)

Рассмотрим реальный газ, находящийся при начальном давлении

Pi,

дадим ему расшириться

до

некоторого давления

настолько

малого,

что для

всех

практических расчетов поведение газа

при

этом давлении можно рассматривать

как

идеальное. Затем снова

сожмем этот идеальный газ до давления Р±.

этом процессе величина

—

энтропия реального газа, величина

—

энтропия идеального

газа

стандартном состоянии (5

го

). Из уравнения (IV. 10)

соответ-

ствующего уравнения

для

идеального газа получим

27 RTc

Q р

РсТ»

Pi.

(IV. 11)

* См. также

Э. А.

Мелвин-Хьюа

Физическая химия,

ч. 2,

ИЛ.

1962.—

Прим.

перев.

вличина

S° — Si

представляет собой изменение энтропии

гипоте-

яческом

процессе перехода реального газа при давлении

состо-

яние

идеального газа при

том же

самом давлении.

Эту

величину

асто называют поправкой

на

неидеальность

'аза.

Для циклопентана Астон,

Финк

Шуман [35] приводят значения

Jc, равное

520°

К,

и Рс,

равное 44,2 атм. Используя эти данные,

Рлвторы

[35]

рассчитали по (IV. 11) значение поправки на неидеаль-

1вость циклопентана

при 1 атм,

которая оказалась равной

10,084

кал/(молъ

-°К).

Третий закон термодинамики

, Значения энтропии при температурах, близких

абсолютному

яулю, необходимы

для

решения практических

теоретических

термохимических задач,

это

значительной степени стимулировало

появление

дополнительного постулата,

так

называемого третьего

вакона

термодинамики.

1906

г.

Нернст

[1053]

пришел

выводу,

что изменение энтропии химической реакции вблизи абсолютного

Вуля

пренебрежимо мало.

1912

г.

Планк

[1168]

показал, что кри-

оталлическая решетка индивидуального вещества при абсолютном

ауле

характеризуется максимальной степенью упорядоченности

связи

этим должна обладать нулевой энтропией. Симон

[1350]

позднее Уилкс

[1613]

рассмотрели развитие этой концепции

начиная

тепловой теоремы Нернста

и до

наших дней. Тепловая

«ворема Нернста

и ее

практическое использование были подробно

обсуждены Астоном [30]. Льюис

Ренделл [860] раскрыли квантово-

механическую природу этого постулата

указали

на его

примени-

мость

химическим системам:

«Если энтропию каждого элемента

некотором кристаллическом

состоянии

принять равной нулю при температуре

0°

К,

то

каждое

вещество при определенной температуре

будет

обладать некоторым

конечным

положительным значением энтропии; однако при темпе-

ратуре

абсолютного нуля энтропия может оказаться равной нулю.

Такая

ситуация имеет место

случае

совершенных кристаллических

веществ».

Третий закон термодинамики был подтвержден многочисленными

химическими

физическими исследованиями, причем вещества,

энтропия

которых при абсолютном нуле

не

равнялась нулю, обла-

дали вполне объяснимыми отклонениями

от

совершенного кристал-

лического состояния. Анализ значений энтропии органических

веществ был проведен Вестрамом и Мак-Каллохом [1598]. Как

следо-

вало ожидать, газы, жидкости, метастабильные стеклообразные

Фазы,

вещества

замороженной разупорядоченностью

растворы

не

Подчиняются

третьему закону; нулевой энтропией обладают вещества,

•Сходящиеся

во

внутреннем термодинамическом равновесии

при

110

Часть

Основы

термодинамики

IV.

Расчет

энтропии

111

0° К.

Те

вещества, которые при

0° К не

образуют упорядоченных

кристаллических твердых фаз,

не

имеют S°

= 0 *. В

качестве при

мера веществ,

не

обладающих нулевой энтропией, можно привести

смеси цис-

ттграис-изомеров, оптически активные изомерные веще

ства, образующие твердые растворы,

разупорядоченные твердые

фазы.

«Абсолютное»

значение энтропии совершенного кристалли-

ческого вещества при температуре

Т° К

можно вычислить, интегри-

руя выражение

(IV.4)

пределах

от

нуля

до ГК и

подставляя

S°

= 0.

Строго говоря, для расчета энтропии смесей при

0° К

необ-

ходимо использовать выражения типа (IV.5). Однако

простых

химических реакциях соотношения изотопов

ядерных спиновых

состояний

не меняются, поэтому обычно такими вкладами

энтропию

(и

энергию Гиббса) пренебрегают.

таблицах, как правило, приво

дят практические значения энтропии, используемые

химической

термодинамике.

Все

энтропии, приведенные

данной книге, явля

ются практическими.|'

Вычисление энтропии

на

основе третьего закона

термодинамики

Для вычисления абсолютных значений энтропии обычно необхо-

димы экспериментальные значения теплоемкости

интервале

от 0°

до исследуемой температуры. Поскольку измерение теплвемкосги

вблизи абсолютного нуля представляет значительные эксперимен-

тальные трудности,

литературе практически

отсутствуют

значения

теплоемкостей ниже

4—10°

К. Значение энтропии

этой области

часто определяют методом экстраполяции, подставляя уравнение

теплоемкости Дебая (II.7)

выражение (IV.4).

В табл. П.6 (см. приложение) приведены значения

9в и

соответ-

ствующие им энтропии.

табл. П.1 приведены экстраполированные

значения

измеренных теплоемкостей 1,2,4-триметилбензола, рассчи-

танные

предположении пяти степеней свободы

и 8j =

103,7°.

Таким

образом,

/Т

для 15°

равно 6,91,

и для

каждой степени

свободы #15

0,146

кал/(молъ-°К).

таком

случае

суммарная

энтропия

при 15°

равна

0,729

кал/(молъ

-°К),

что

хорошо согла-

суется

со

значением, приведенным Патнамом

Килпатриком [1208].

Выше было показано, что данные по теплоемкостям можно экстра-

полировать

помощью комбинации функций Дебая

Эйнштейна,

а именно

80,5

\ , „„ /155

* Этот вопрос был подробно рассмотрен

работе

А. В.

Фроста «Расчет

химических равновесий газовых реакций» [Успехи химии,

445 (1933)]

связи

с, использованием третьего закона термодинамики

для

расчетов химических

равновесий.—

Прим.

перев.

„обходимые значения 8

и Э

нетрудно рассчитать, используя табл. П.3

sll.6,

приведенные

приложении.

Для

15° К

[в

кал/(моль

-°К)1

иеем:

5,366

дает

для

-^-=10,333 дает

для

0,838

0,004

Суммарная

рассчитанная энтропия при 15° К

0,842

Эта величина примерно

на

10% превышает значение, вычислен-

по

эмпирическому

методу,

использованному Патнамом

Кил-

атриком.

Общее выражение

для

энтропии

Используя приведенные выше термодинамические соотношения,

5щее выражение для расчета температурной зависимости энтропии

вщества, находящегося

стандартном состоянии

характеризую-

вгося энантиотропным превращением при температуре

Tt,

точкой

навления

Tm и

нормальной точкой кипения

Tb,

можно предста-

гь

виде

1000

=^0+

1 ft ^

Cp(l)dT

AHm

о°к

тъ

Ср (I) dT

1000

(g) dT

(IV.12)

ть

Вычисление энтропии по данным

низкогпемпературных теплоемкостей

Энтропии

чистых кристаллических веществ можно рассчитать

Ио

данным измерения теплоемкостей. Значения теплоемкостей, полу-

денные

помощью криогенных

газовых калориметров различных

*Идов,

описанных

в гл. II,

позволяют рассчитать энтропию

и ее

процессе фазовых переходов.

низкотемпературном калориметре, аналогичном описанному

, Гатри, Скотт, Хаббард, Катц, Мак-Каллох, Гросс, Уильямсон

Паддингтон [551] определили теплоемкость жидкого

твердого

на,

его

энтальпии плавления

испарения,

также давление

теплоемкость газообразного фурана. Полученные данные

112

Часть

Основы

термодинамики

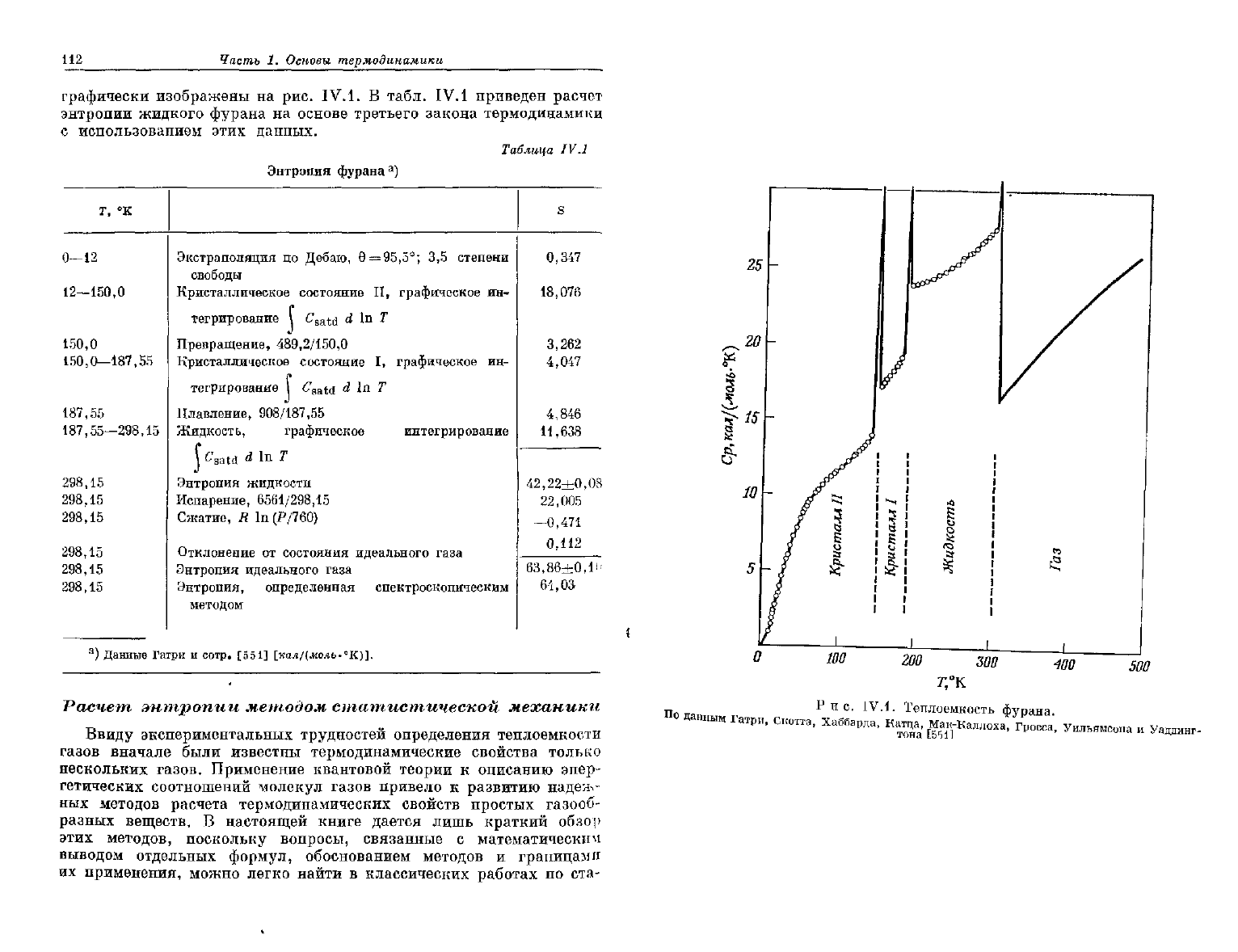
графически изображены

на

рис. IV. 1.

табл. IV.

приведен расчет

энтропии

жидкого фурана

на

основе третьего закона термодинамики

с использованием этих данных.

Таблица

IV.1

Энтропия

фурана

)

Т, "К

0—12

12—150,0

150,0

150,0—187,55

187,55

187,55—298,15

298,15

Экстраполяция

по

Дебаю,

6 =

95,5°;

3,5

степени

свободы

Кристаллическое

состояние

И,

графическое ин-

тегрирование

In T

Превращение,

489,2/150,0

Кристаллическое

состояние

графическое

ин-

тегрирование

atd

d In T

Плавление,

908/187,55

Жидкость,

графическое интегрирование

satd

In T

Энтропия

жидкости

Испарение,

6561/298,15

Сжатие,

In (P/760)

Отклонение

от

состояния идеального газа

Энтропия

идеального газа

Энтропия,

определенная спектроскопическим

методом

0,347

18,076

3,262

4,047

4,846

11,638

42,22±0,08

22,

—0,

,005

,471

,112

63,86+0,

К'

61,03

) Данные Гатри

сотр.

[551]

[кал/(моль-°К)].

Расчет энтропии методом статистической механики

Ввиду

экспериментальных трудностей определения теплоемкости

газов вначале были известны термодинамические свойства только

нескольких газов. Применение квантовой теории

описанию энер-

гетических соотношений молекул газов привело

развитию надеж-

ных методов расчета термодинамических свойств простых газооб-

разных веществ.

настоящей книге дается лишь краткий обзор

этих методов, поскольку вопросы, связанные

математическим

выводом отдельных формул, обоснованием методов

границами

их применения, можно легко найти

классических работах

по

ста-

Т°К

Рис. IV.1.

Теплоемкость фурана

Данным

Гатри, Скотта, Хаббарда, Катца, Мак-Каллоха, Гросса

тона

[551]

Уильямсона

Уаддинг-

8^-831

114

Часть

Основы

термодинамики

тистической механике

статистической термодинамике [436,

602,

603,

842, 942, 1036, 1292,

1619]

Различные

возможные энергетические состояния молекулы обыч-

но

большой степенью точности можно рассматривать

как

незави-

симые.

Кроме того, можно вычислить распределение энергии

между

такими

состояниями молекулы

помощью математических соотно-

шений,

называемых функциями распределения.

Соответствующее суммирование

по

всем функциям распределения

позволяет вычислить термодинамические характеристики газа.

Так,

абсолютную энтропию всей молекулы (<Stot) можно представить

виде

суммы энтропии поступательного движения молекулы

энтро-

пии

вращательного движения всей молекулы

энтропии внут-

реннего вращения

) и

энтропии колебательного движения <S\,t,

(IV.13)

IV.

Расчет

энтропии

115

Рассмотрим методы расчета каждого энтропийного составляющего.

Энтропия

поступательного движения

Сакур

[1273]

1911

г.

предложил выражение

для

расчета энтро-

пии

моноатомного газа, хорошо согласующееся

эксперименталь-

ными

данными. Любая газообразная молекула обладает только тремя

поступательными степенями свободы, поэтому одно

и то же

выражение

дает

поступательный вклад

энтропию любой молекулы.

Поступательная энтропия равна

/гй In М+з/

Д In T+R In

V+5/

+ С,

где

М —

молекулярный

вес

газа,

Т —

абсолютная температура,

—

мольный объем,

R —

постоянная идеального газа, отнесенная

на

один моль,

и С —

константа

для

всех

веществ. Спустя го \

Тетроде

[1480]

показал,

что

константа

имеет

вид

Д1п

=—16,0412

кал'(моль-°К),

где к — константа идеального газа, отнесенная

одной молекуле.

h — постоянная Планка,

а N

— число Авогадро. Комбинируя

два

при-

веденных выражения, получим уравнение Сакура —Тетроде:

—11,0731

кал/(молъ-°К),

(IV. И)

* См. также'

В. М.

Грязное,

А. В.

Фрост,

Статистические методы расчета

термодинамических величин, изд-во Всесоюзного химического общества

им.

Д. И.

Менделеева, М., 1949;

И. Н.

Годнее,

Вычисление термодинамически

функций

по

молекулярным данным, Гостехтеоретиздат, М., 1956;

А. Г.

Самойло-

вич, Термодинамика

статистическая физика, Гостехтеоретиздат,

М.,

1955

Прим.

перев.

которое

случае

идеального газа при температуре

298,15°

давле-

Гнии

1 атм

принимает

вид

5^=6,8637

log ДГ+25,8182

кал/(молъ-°К).

(IV.15)

Энтропия

вращения

Для определения термодинамических функций молекул необхо-

димо знать моменты инерции вокруг центра массы молекулы,

как

^двухатомной, линейной многоатомной, так

нелинейной. Для такого

расчета требуются атомные массы, межатомные расстояния

валент-

**ные

углы

молекуле. Большая часть этих данных обычно опреде-

| ляется методом электронной дифракции. Анализ данных, полученных

| втим методом начиная

середины

1954 г., был

проведен Уиландом

11602].

Им

были составлены специальные таблицы, содержащие

, сведения

длинах связи

углах

для

более

чем 600

органических

молекул. Величины, приведенные

табл.

IV.2,

получены усредне-

нием

измеренных значений

для

данной длины связи или валентного

„угла молекулы, взятых

из

каталога Уиланда. Эти величины можно

использовать

для

аппроксимации

структур

неисследованных

, молекул.

Для

расчета моментов инерции линейных молекул необходимо

определить только положение центра массы молекулы

провести

Суммирование моментов инерции каждого атома, поскольку момент

инерции

i-го

атома равен

где

di —

расстояние

(в

сантиметрах)

от £-го

атома

до

центра массы

молекулы,

а т

—

масса атома

граммах. Линейная молекула может

Вращаться вокруг

двух

перпендикулярных осей, поэтому

ее

моменты

инерции

будут

равны

друг

другу:

/„=/,=2

см,

). (

-i

)

Методы расчета моментов инерции нелинейных многоатомных

молекул более сложны. Впервые они были рассмотрены Хиршфель-

Дером [608]. Хиршфельдер предложил метод,

суть

которого сводится

следующему.

Из данных

по

массам,

углам

расстояниям строится

пространственная диаграмма,

помощью которой определяется

положение каждого атома относительно

трех

координатных осей

У и г.

Затем для каждого атома записываются картезианские коор-

динаты

, y

и z, и

вычисляется произведение

трех

главных момен-

тов инерции, равное детерминанту:

[

— D —

Е1

—D

В —F

\=ABC—AF2—CD2—2DEF—BE2,

—E—F

С\

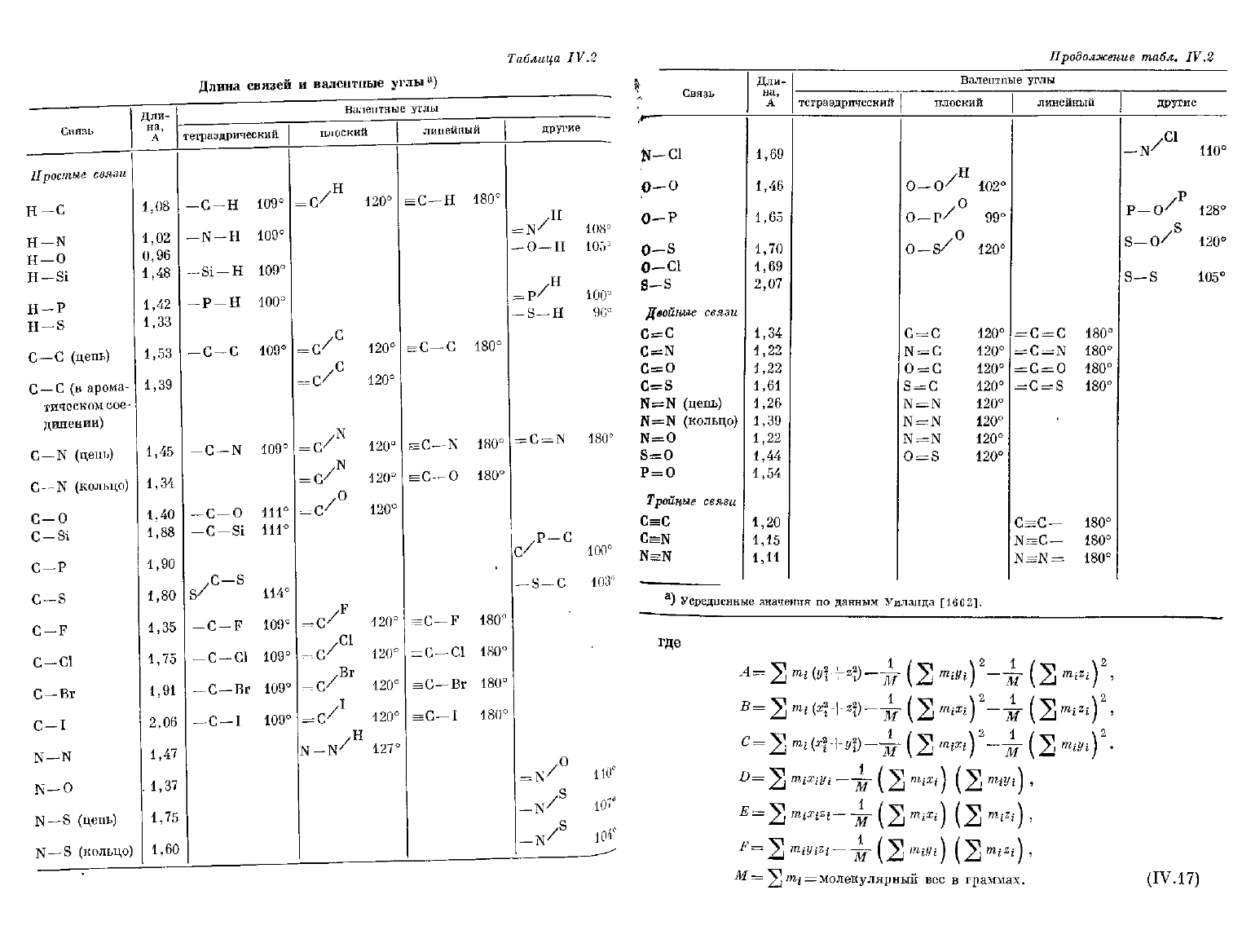
Таблица IV

Связь

Простые

связи

Н-С

H-N

н-о

— Si

Н-Р

H-S

—С (цепь)

— С (в арома-

тическом сое-

динении)

—N (цепь)

—N (кольцо)

С-0

—Si

С-Р

C-S

C-F

С-С1

С—Вг

С—I

N—N

— О

—S (цепь)

— S (кольцо)

Дли-

на,

1,08

1,02

0,96

1,48

1,42

1,33

1,53

1,39

1,45

1,34

1,40

1,88

1,90

1,80

1,35

1,75

1,91

2,06

1,47

1,37

1,75

1,60

Длина

связей

тетраэдрический

—

С —Н

-N-H

—

Si —H

—

Р-Н

—

С-С

—

С —N

-С-0

—

С —Si

—S

—

—F

-C-Cl

—

С—Вг

—

С—I

109°

100°

109°

111°

114°

109°

валентные

углы

)

Валентны

плоский

С/ 120°

120°

С/ 120°

120°

С/ 120°

= С/ 120°

= С

120°

/С1

= С

120°

Вг

= С/ 120°

= 0^ 120°

N — N^ 127°

углы

линейный

=с—н

=с—с

=С—N

=С—О

=С—F

=С—С1

=С—Вг

=С

—I

180°

другие

.н

-о-н

=р/

—

S— Н

C = N

,Р

— С

—

S—С

—

-N/

108°

105°

100°

9G°

180°

100°

103°

110°

лГ\1

10'

—--"

Продолжение

табл.

IV.2

^ Связь

K-ci

o-o

O-P

o-s

0—Cl

s-s

Двойные

связи

c=c

C=N

c=o

c=s

N=N

(цепь)

N=N

(кольцо)

N=O

S=O

= O

Тройные

связи

CsC

C=N

N=N

Дли-

на,

1,69

1,46

1,65

1,70

1,69

2,07

1,34

1,22

1,61

1,26

1,39

1,22

1,44

1,54

1,20

1,15

1,11

Валентные

углы

тетраэдрический

плоский

/Н

О — 0

о—р/

/О

О —S/

с=с

N = C

о=с

s=c

= N

N=N

o=s

102°

99°

120°

линейный

=c=c

C = N

=c=o

=c=s

•

c^c—

N=C—

N=N

180°

другие

/Cl

—

W 110°

P—O

128°

S— Q/ 120°

S—S 105°

) Усредненные значения

по

данным Уиланда [1602].

где

M =

пц = молекулярный вес в граммах.

(IV.17)

118

Часть

Основы

термодинамики

Обычно удобнее выражать массы в граммах и расстояния

ангстремах (10~

см) и обозначать такие моменты инерции

штрихом, например /'. Тогда

1' I'

IV.

Расчет

энтропии

119

/*=•

откуда

6,023-1023.(108)2

6,0231-10

218,504.104'

(IV.18)

Другим фактором, который необходимо учитывать при вычисле-

нии

энтропии, является число симметрии а. В современных расчетах

число симметрии разбивают на два слагаемых: на число симметрии

молекулы в целом (e

) и число симметрии вращающейся части

молекулы (а

). Полное число симметрии (o

) является произведе-

нием

всех

чисел симметрии молекулы

Число

симметрии а

можно определить как число положений,

которые может занимать жесткая многоатомная молекула, совпадая

при

вращении со своей первоначальной конфигурацией. Например,

для молекулы окиси

углерода

С = О o

= 1. Для молекулы СО,

О = С = О a

= 2. Для такой тетраэдрической молекулы, как моле-

кула метана СН

, сг

= 12, поскольку для каждой из четырех ориен-

тации

молекулы

существует

три собственные ориентации метильнои

группы. Для молекулы хлористого метила Н

СС1 a

= 3, посколь-

ку для одной ориентации молекулы можно указать три ориентации

метильнои группы, т. е. 1 «3.

Если

часть молекулы способна вращаться относительно осталь-

ной

ее части, то симметрия вращающейся части может внести допол-

нительные нефиксированные положения. Это приводит к необходи-

мости введения второго числа симметрии (о>). Так, например, жест-

кая

молекула этана Н

С — СН

может вращаться вокруг оси, пер-

пендикулярной

связи G — С, поэтому обладает двумя одинаковыми

положениями.

В то же время вращение молекулы может происходить

вокруг связи С — С на

360°

через три одинаковых положения.

Таким

образом, a

= 2-3 = 6. Помимо этого, одна метильная

группа может вращаться на

360°

вокруг второй неподвижной метиль-

нои

группы, проходя через три одинаковых положения, так что

= 3. Таким образом, o

= 18. Для молекулы разветвленного

углеводорода с числом метальных групп, равным п,

существует

различных положения метильных групп в молекуле, поэтому о> =

. Например, молекула неопентана С

обладает o

= 12

(как

и у метана) и тремя дополнительными положениями каждой

из

четырех метильных групп, так что сг

= З

и сг* = 972.

Аминогруппа (например,

CNH

)

обладает структурой пирамиды

имеет а

, равное 1. Группа С — О — Н нелинейна и обладает

Таблица

IV .3

Числа симметрии

Молекула

Бензол

Толуол

Этилбензол

о-Ксилол

ж-Ксилол

тг-Ксилол

1,3,5-Триметилбензол

Гексаметилбензол

Фенол

Анилин

Тиофенол

Вифенил

729

°t

162

8748

Литера-

тура

[1477]

[14771

[1477]

[577]

[392]

[391]

[1319]

[725]

— 1. В табл. IV.3 приведены числа симметрии для некоторых

ароматических молекул.

Для линейной газообразной молекулы вклад в энтропию, обуслов-

ленный

вращением всей молекулы, равен

(

iv.2O)

Подстановка соответствующих констант в это уравнение приводит

выражению

758[l1) l04 кал/(молъ.°К).

Для нелинейной газообразной молекулы вклад в энтропию от вра-

щения

всей молекулы составляет

Подстановка констант в это уравнение

дает

or=2,2879

lg (I

.Ю117) -4,5758 Ig а

6,8637

Г-0,0332

ка)

(IV.22)

Энтропия

внутреннего вращения

Вений

МИМ

ВраЩеНИЯВСеЙмолекулы

для

многих газообразных соеди-

rDvmr

еобх

°Д

имо

Учитывать внутреннее вращение

двух

или более

*J"UB

молекуле. Вклад в энтропию за счет свободного вращения

120

Часть

Основы

термодинамики

одной

группы молекулы равен

+ In

Подставляя

значения соответствующих констант

выражая

(момент

вращения

фрагмента вокруг

его оси) в

г-см

получим

[в

кал/(моль -°К)]

S°

3,0348—4,5758

lg a

2,2879

• 1038)

2,2879

lg Т.

(IV.23)

Если

внутреннее вращение заторможено, удобно использовать

таб-

лицы,

предложенные Питцером

[1156]

Питцером

Гуинном

[1162]

приведенные

приложении (табл. П.7— П. 10).

случае симметрич-

ных волчков

для

расчета параметра

HQf

можно использовать урав-

нение

(11.11), подставляя

= о

Величину уменьшения энтропии

вследствие влияния потенциального барьера

находят

таблицах.

Если

учитывать вклад свободного вращения

по

уравнению (IV.23),

приведенные таблицы также можно использовать

для

несимметрич-

ных волчков, центр тяжести которых лежит вблизи

оси

вращения.

Несимметричный

волчок обычно связан

атомом углерода, который

свою очередь тетраэдрически связан

тремя другими группами,

поэтому

при

полном повороте преодолевает

три

максимума потен-

циальной

энергии.

первом приближении обычно полагают,

что эти

максимумы равны.

таком случае нетрудно вычислить параметр

HQf,

используя выражение

(11.11)

при в

= 3и

заимствуя величину

уменьшения

энтропии

за

счет потенциального барьера

V из

таблиц

Питцера

Гуинна.

Для

вычисления вкладов

энтропию

за

счет

заторможенного вращения внутренних ротаторов

был

предложен

ряд

других

методов, например метод Халфорда [563]. Этот метод

представлен

табл.

П.12 и

легко может быть использован

для

расчета.

Энтропия

колебания

Эйнштейн

на

основе

тех же

теоретических предпосылок,

из

кото-

рых было выведено уравнение

(II.6),

получил следующее выражение

для вклада каждого гармонического осциллятора

энтропию:

(IV.24)

В этом выражении х = hca/kT, h — постоянная Планка, со — волно-

вое число колебательного движения (т. е. значение, обратное длине

волны, выраженное в см-

), к — постоянная Больцмана, Т — абсо-

лютная температура. Значения этой функции приведены в табл. П.З

(см.

приложение). Для многоатомной молекулы суммирование вкла-

дов от каждой нормальной координатной частоты с соответствующими

энтропийными

составляющими поступательного и вращательного

движения дает полную энтропию молекулы. Рассмотрим несколько

примеров, иллюстрирующих применение приведенных выше урав-

нений.

IV. Расчет энтропии

121

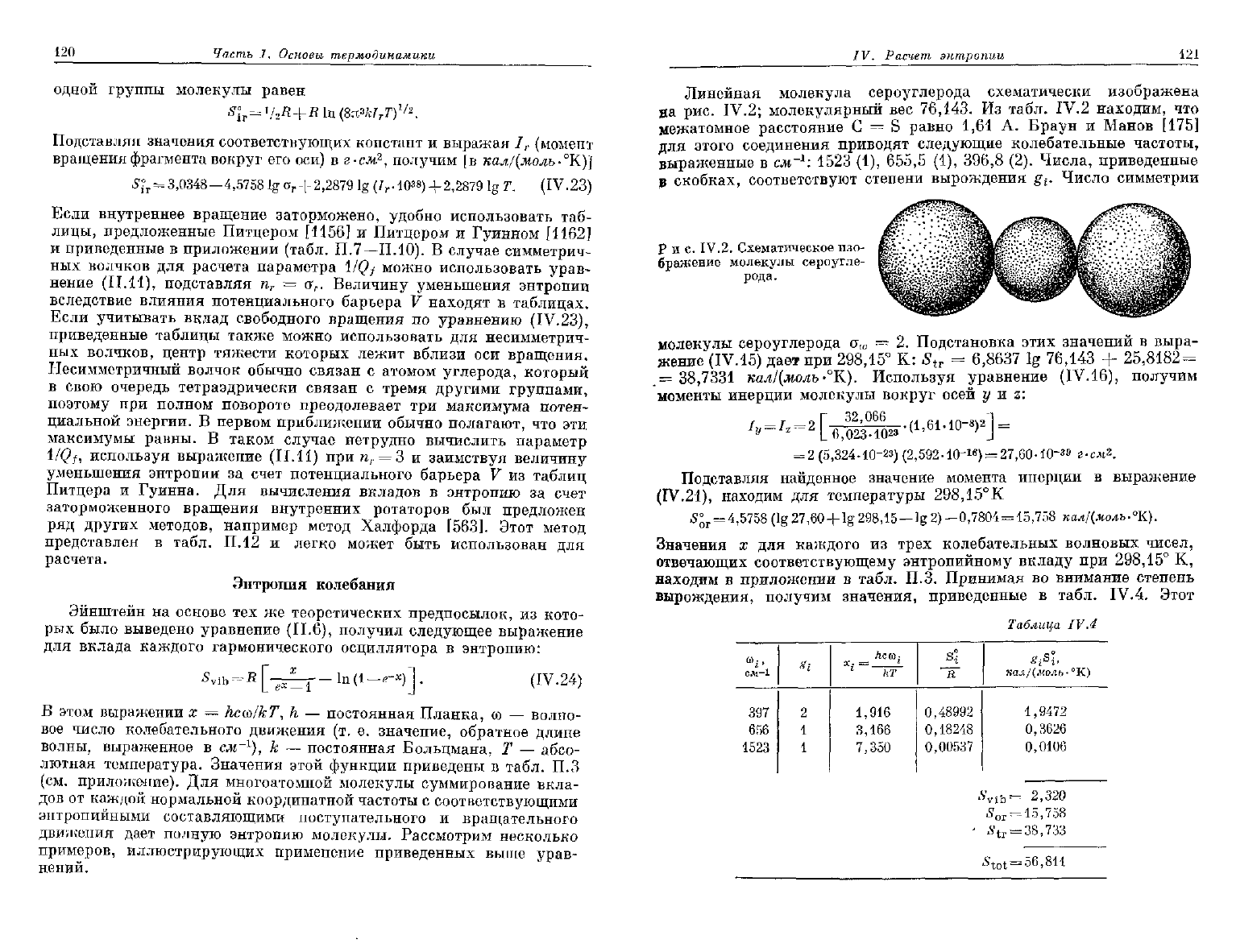
Линейная

молекула сероуглерода схематически изображена

|яа

рис. IV.2; молекулярный вес 76,143. Из табл. IV.2 находим, что

|межатомное расстояние С = S равно 1,61 А. Браун и Манов [175]

|для этого соединения приводят следующие колебательные частоты,

[выраженные в см-

: 1523 (1),

655,5

(1),

396,8

(2). Числа, приведенные

[в скобках, соответствуют степени вырождения g

. Число симметрии

Рис.

IV.2.

Схематическое

изо-

бражение

молекулы

сероугле-

рода.

иолекулы сероуглерода a

= 2. Подстановка этих значений в выра-

жение

(IV.15)

дает при

298,15°

К: S

6,8637

76,143

25,8182

38,7331

кал/'(моль -°К). Используя уравнение (IV.16), получим

моменты инерции молекулы вокруг осей у и z:

(5,324-10-23) (2,592-10-")

27,60-10"

г-смР-.

Подставляя найденное значение момента инерции в выражение

(IV.21), находим для температуры

298,15°

5°

4,5758

(lg27,60

+ lg

298,15—lg

2)-0,7804

15,758 кал/(молъ.°К).

Значения

х для каждого из трех колебательных волновых чисел,

отвечающих соответствующему энтропийному вкладу при

298,15°

К,

находим в приложении в табл. П.З. Принимая во внимание степень

вырождения, получим значения, приведенные в табл. IV.4. Этот

Таблица

IV.4

см-1

397

656

1523

he Ш;

,916

,166

,350

,48992

,18248

,00537

кал/(моль

•

°К)

1,9472

0,3626

0,0106

о Р9П

i b

•—" *

d£\j

ОГ

15,758

38,733

tot

56,811