Сталл Д. Вестрам Э. Зинке Г. Химическая термодинамика органических соединений
Подождите немного. Документ загружается.


40
Часть
1.
Основы
термодинамики
II.
Теплоемкость
и
энтальпия
фазовых
переходов
41
В этом выражении величина и равна hvlkT = в
Е
/Т, где h ~-
постоянная
Планка, а к — константа Больцмана, или газовая посто-
янная,
отнесенная к одному атому. Величина Э
Е
— характеристи-
ческая константа (температура Эйнштейна) вещества. Выраже-
ние
(П.6) при Т = 0
дает
Си, равное нулю; при Т = оо значение Cv
достигает максимального значения, равного 3R.
В 1910 г. Нернст и сотрудники, измеряя теплоемкости веществ
при
очень низких температурах, показали, что теплоемкость при
температурах, близких к 0° К, действительно стремится к нулю.
Однако наблюдаемая экспериментально зависимость Cv от темпе-
ратуры в значительной степени отличалась от найденной теорети-
чески из формулы
(И.6).
В 1912 г. Дебай [315] и независимо Борн и Карман [147] полу-
чили новое теоретическое выражение зависимости теплоемкости
от температуры, лучше описывающее экспериментальные значения
теплоемкостей при низких температурах, чем уравнение Эйнштейна.
В своей модели Дебай рассматривал одноатомный изотропный кри-
сталл как некоторый упругий континуум, состоящий из набора Зп
осцилляторов, характеризующихся определенным спектром частот,
И
ограниченным
некоторой максимальной частотой
v
max
.
б
р
Используя
теорию колебаний, Дебай получил следующее выражение для тепло-
емкости
упругого
твердого кристалла при постоянном объеме:
Су = 9Л —-
(И.7)
где x = hv
max
/kT = Q
D
/T, a u = hv/kT. Выражение (II.7) можно пред-
ставить в более компактном виде
(П.8)
где /
D
— функция теплоемкости по Дебаю, общая для
всех
веществ.
Параметр Q
D
является характеристической константой (температу-
рой
Дебая) для данного вещества. Функция Дебая хорошо описывает
экспериментальные значения теплоемкостей большого числа простых
веществ, но применима лишь к тем простым молекулам, для которых
можно определить необходимые численные значения колебательных
частот. Отсутствие необходимых экспериментальных данных для
колебательных частот многоатомных молекул не позволяет в настоя-
щее время рассчитывать теплоемкости многоатомных кристалли-
ческих веществ на основании моделей Эйнштейна и Дебая.
Уравнения теплоемкости Эйнштейна (П-6) и Дебая (II.7) содер-
жат универсальную
газовую
постоянную R и получены для одно-
атомных твердых тел, атомы которых колеблются в
трех
направле-
ниях
или, как говорят, обладают тремя колебательными степенями
свободы. Приведенные в приложении таблицы П. 1 и П. 4 содержат
рассчитанные значения функций теплоемкостей Эйнштейна
и
Дебая,
деленные
на R и
отнесенные
к
одной колебательной степени свободы.
Приведенные
в
этих таблицах значения функций теплоемкостей
Эйнштейна
и
Дебая остаются справедливыми
при
изменении вели-
чины
экспериментального значения
R. При
вычислении теплоем-
костей конкретных веществ приведенные функции теплоемкостей
должны быть умножены
на
соответствующее число степеней
сво-
боды.
На рис. II.4 для
сравнения приведены
две
функции теплоем-
костей,
вычисленные
для
различных характеристических колеба-
тельных частот.
1,U
0,8
0,6
0,4
0,2
if
-//
/' А
к
/
1 //
i //
/
у/
^
-i
^^-
1
**
l
v
l
*
30C
^.
-'""''
1
| _| —
т~~~
| |
200
400
600
800 1000
Рис.
II.4. Сравнение функций теплоемкостей по Дебаю ( ) и по Эйнштейну
( ), вычисленных для различных характеристических частот.
Поскольку
разница
между
Ср и Cv для молекулярных кристаллов
становится неразличимой вблизи температур порядка 30° К, функ-
цию
теплоемкости Дебая можно использовать для экстраполяции
измеренных значений Ср к абсолютному нулю. Келли и Кинг [738],
рассмотрев ход наблюдаемых значений Ср ряда неорганических
веществ при низких температурах, предложили для экстраполяции
опытных данных так называемый метод проб и ошибок, основанный
на
соответствующих комбинациях функций Дебая и Эйнштейна.
Для аналогичной экстраполяции теплоемкостей органических соеди-
нений
многие авторы использовали только одну функцию Дебая.
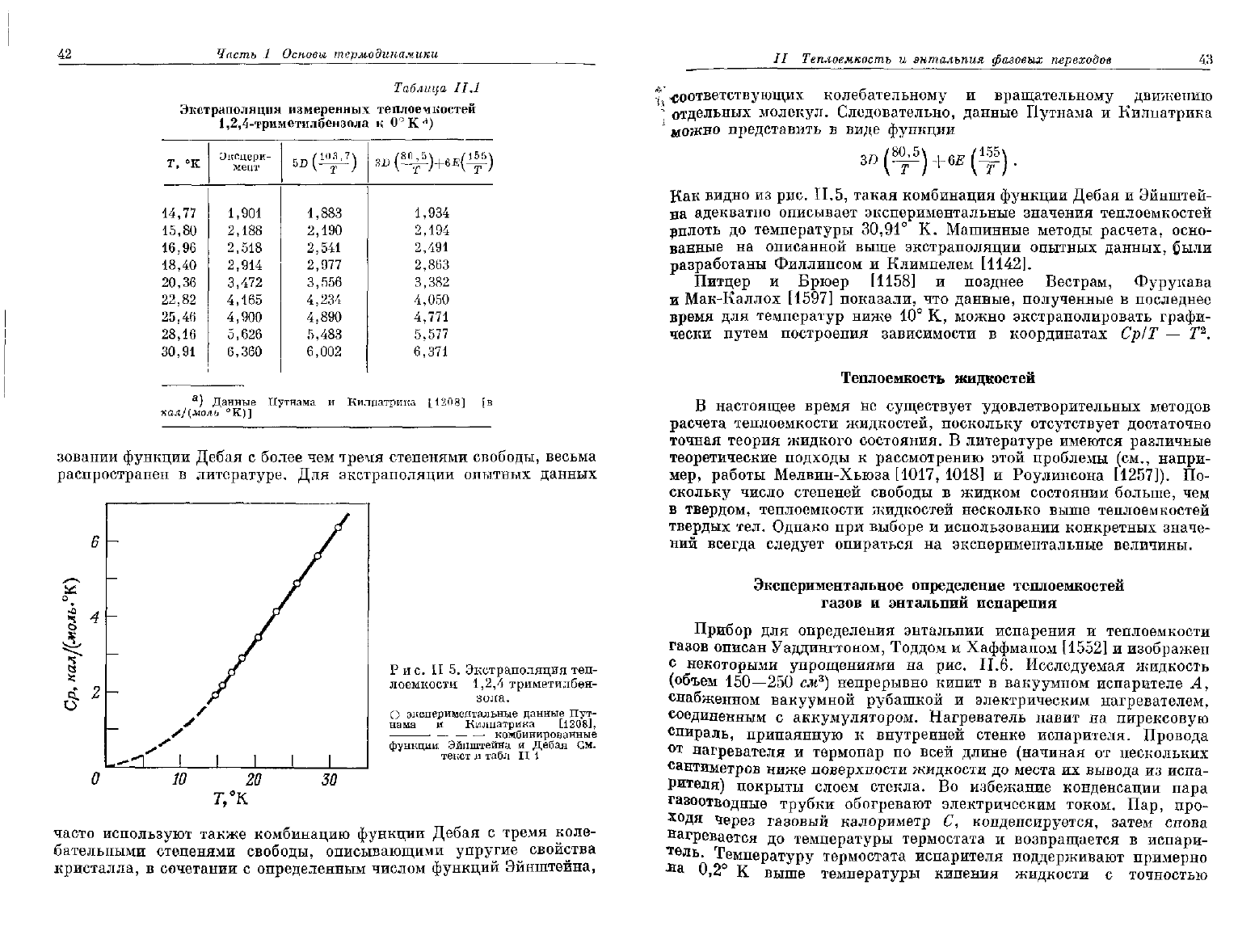
Иутнам и Килпатрик
[1208]
измерили низкотемпературную тепло-
емкость 1,2,4-триметилбензола; значения, полученные ими, при-
ведены в табл. II. 1. С помощью метода проб и ошибок Путнам и Кил-
патрик
пришли к выводу, что их экспериментальные значения можно
экстраполировать к 0° К, основываясь на том, что значения теплоем-
костей,
вычисленные в предположении пяти степеней свободы
и
«D =
103,7,
совпадают с первыми шестью экспериментальными
начениями
теплоемкостей. Подобный эмпирический
подход
к вычис-
ению теплоемкости вблизи абсолютного нуля, основанный на исполь-
42
Часть
1
Основы
термодинамики
Таблица
II.1
Экстраполяция
измеренных
теплоемкостей
Г, °К
14,77
15,80
16,96
18,40
20,36
22,82
25,46
28,16
30,91
1,2,4-триметилбензола
Экспери-
мент
1,901
2,188
2,518
2,914
3,472
4,165
4,900
5,626
6,360
5Х
Ч
т )
1,883
2,190
2,541
2,977
3,556
4,234
4,890
5,483
6,002
к
0°
/8
K
d
)
0.5\ /<155\
т
)' V т /
1,934
2,194
2,491
2,863
3,382
4,050
4,771
5,577
6,371
а
)
Данные Путнама и
Килпатрика
[1208] [в
кал}(моль
°К)]
зовании
функции Дебая с более чем тремя степенями свободы, весьма
распространен в литературе. Для экстраполяции опытных данных
Рис.
II 5.
Экстраполяция
теп-
лоемкости
1,2,4
триметилбен-
зола.
О экспериментальные данные Пут-
нама
и
Килпатрика
[1208],
—
комбинированные
функции
Эйнштейна и Дебая См.
текст
и табл II 1
30
т,°к
часто используют также комбинацию функции Дебая с тремя коле-
бательными степенями свободы, описывающими
упругие
свойства
кристалла, в сочетании с определенным числом функций Эйнштейна,
//
Теплоемкость
и энтальпия
фазовых
переходов
43
i
-соответствующих колебательному и вращательному движению
"
отдельных молекул. Следовательно, данные Путнама и Килпатрика
можно представить в виде функции
Как
видно из рис. П.5, такая комбинация функции Дебая и Эйнштей-
на
адекватно описывает экспериментальные значения теплоемкостей
вплоть до температуры
30,91°
К. Машинные методы расчета, осно-
ванные
на описанной выше экстраполяции опытных данных, были
разработаны Филлипсом и Климпелем [1142].
Питцер
и Брюер
[1158]
и позднее Вестрам, Фурукава
и Мак-Каллох
[1597]
показали, что данные, полученные в последнее
время для температур ниже 10° К, можно экстраполировать графи-
чески
путем построения зависимости в координатах Ср/Т — Т
2
.
Теплоемкость жидкостей
В настоящее время не
существует
удовлетворительных методов
расчета теплоемкости жидкостей, поскольку
отсутствует
достаточно
точная теория жидкого состояния. В литературе имеются различные
теоретические подходы к рассмотрению этой проблемы (см., напри-
мер,
работы Мелвин-Хьюза
[1017,
1018] и Роулинсона [1257]). По-
скольку число степеней свободы в жидком состоянии больше, чем
в
твердом, теплоемкости жидкостей несколько выше теплоемкостей
твердых
тел. Однако при выборе и использовании конкретных значе-
ний
всегда
следует
опираться на экспериментальные величины.
Экспериментальное определение теплоемкостей
газов и
энтальпий
испарения
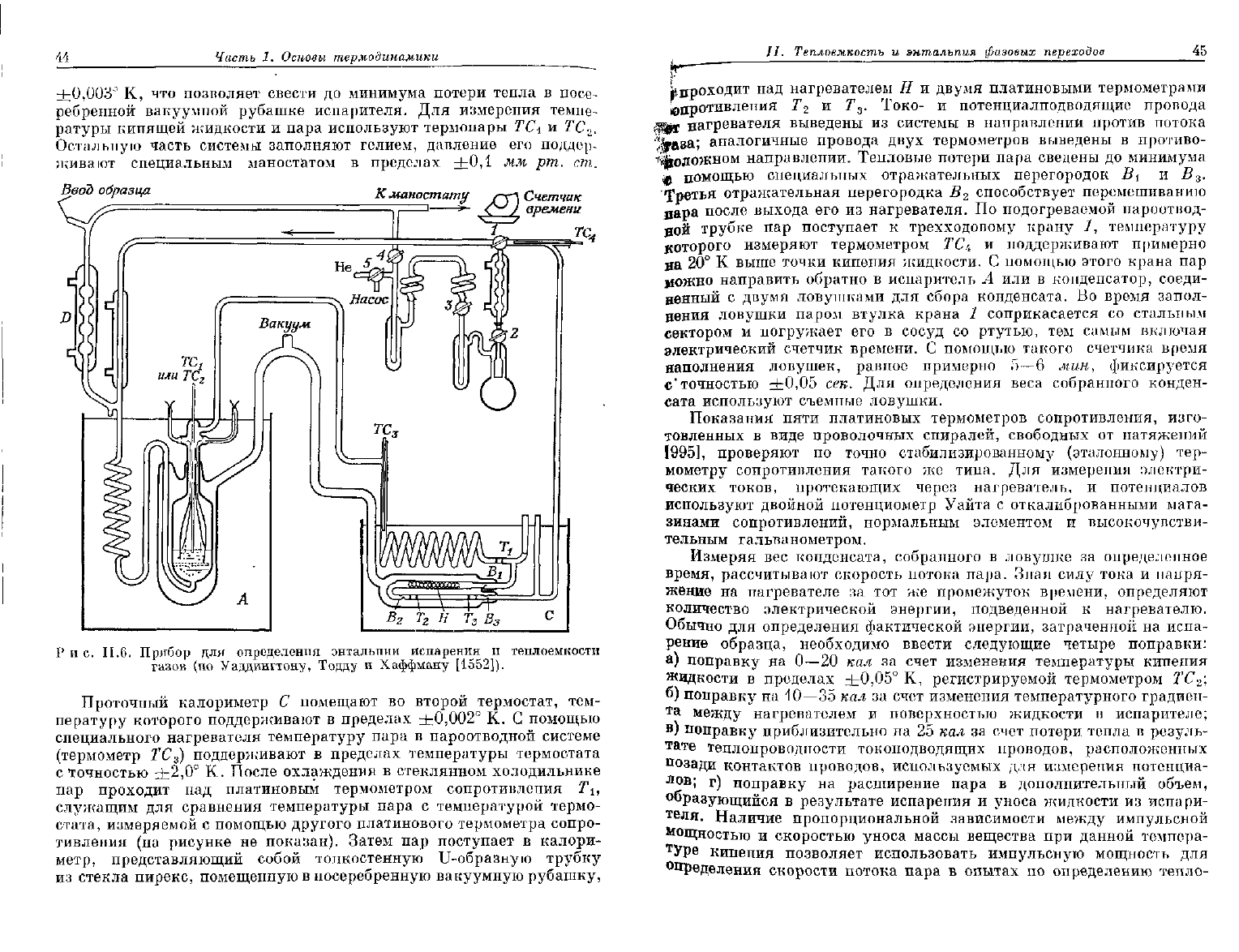
Прибор
для определения энтальпии испарения и теплоемкости
газов описан Уаддингтоном, Тоддом и Хаффманом
[1552]
и изображен
с некоторыми упрощениями на рис. II.6. Исследуемая жидкость
(объем
150—250
еж
3
) непрерывно кипит в вакуумном испарителе А,
снабженном вакуумной рубашкой и электрическим нагревателем,
соединенным
с аккумулятором. Нагреватель навит на пирексовую
спираль,
припаянную к внутренней стенке испарителя. Провода
от нагревателя и термопар по всей длине (начиная от нескольких
сантиметров ниже поверхности жидкости до места их вывода из испа-
рителя) покрыты слоем стекла. Во избежание конденсации пара
газоотводные трубки обогревают электрическим током. Пар, про-
ходя
через газовый калориметр С, конденсируется, затем снова
нагревается до температуры термостата и возвращается в испари-
тель. Температуру термостата испарителя поддерживают примерно
Ла
0,2° К выше температуры кипения жидкости с точностью
44
Часть
1.
Основы
термодинамики
±0,003°
К, что
позволяет свести
до
минимума потери тепла
в
посе-
ребренной
вакуумной рубашке испарителя.
Для
измерения темпе-
ратуры кипящей жидкости
и
пара используют термопары
ТС\ и ТС
2
.
Остальную часть системы заполняют гелием, давление
его
поддер-
живают специальным маностатом
в
пределах
±0,1 мм pm. ст.
Ввод образца
Кманостату s-ул Счетчик
^э
*- v'V
времени
Рис.
П.6.
Прибор
для
определения энтальпии испарения
и
теплоемкости
газов
(по
Уаддингтону,
Тодду
и
Хаффману [1552]).
Проточный
калориметр
С
помещают
во
второй термостат,
тем-
пературу которого поддерживают
в
пределах
±0,002°
К.
G помощью
специального нагревателя температуру пара
в
пароотводной системе
(термометр
TC
S
)
поддерживают
в
пределах температуры термостата
с точностью ±2,0°
К.
После охлаждения
в
стеклянном холодильнике
пар
проходит
над
платиновым термометром сопротивления
Т\,
служащим
для
сравнения температуры пара
с
температурой термо-
стата, измеряемой
с
помощью
другого
платинового термометра сопро-
тивления
(на
рисунке
не
показан). Затем
пар
поступает
в
калори-
метр, представляющий собой тонкостенную U-образную
трубку
из
стекла пирекс, помещенную
в
посеребренную вакуумную рубашку,
//.
Теплоемкость
и
энтальпия
фазовых
переходов
45
проходит
над
нагревателем
Н и
двумя платиновыми термометрами
эП
ротивления
Т
2
и Т
3
.
Токо-
и
потенциалподводящие провода
нагревателя выведены
из
системы
в
направлении против потока
%аза; аналогичные провода
двух
термометров выведены
в
противо-
положном направлении. Тепловые потери пара сведены
до
минимума
ф помощью специальных отражательных перегородок
В\ и В
3
.
Третья отражательная перегородка
В
2
способствует перемешиванию
дара после выхода
его из
нагревателя.
По
подогреваемой пароотвод-
ной
трубке
пар
поступает
к
трехходовому
крану
1,
температуру
которого измеряют термометром
ГС
4
и
поддерживают примерно
да
20° К
выше точки кипения жидкости.
С
помощью этого крана
пар
можно направить обратно
в
испаритель
А или в
конденсатор, соеди-
ненный
с
двумя ловушками
для
сбора конденсата.
Во
время запол-
нения
ловушки паром втулка крана
1
соприкасается
со
стальным
сектором
и
погружает
его в
сосуд
со
ртутью,
тем
самым включая
электрический
счетчик времени.
С
помощью такого счетчика время
наполнения
ловушек, равное примерно
5—6 мин,
фиксируется
с'точностью ±0,05
сек. Для
определения веса собранного конден-
сата используют съемные ловушки.
Показания
пяти платиновых термометров сопротивления, изго-
товленных
в
виде проволочных спиралей, свободных
от
натяжений
[995], проверяют
по
точно стабилизированному (эталонному)
тер-
мометру сопротивления такого
же
типа.
Для
измерения электри-
ческих токов, протекающих через нагреватель,
и
потенциалов
используют двойной потенциометр Уайта
с
откалиброванными мага-
зинами
сопротивлений, нормальным элементом
и
высокочувстви-
тельным гальванометром.
Измеряя
вес
конденсата, собранного
в
ловушке
за
определенное
время,
рассчитывают скорость потока пара.
Зная
силу тока
и
напря-
жение
на
нагревателе
за тот же
промежуток времени, определяют
количество электрической энергии, подведенной
к
нагревателю.
Обычно
для
определения фактической энергии, затраченной
на
испа-
рение
образца, необходимо ввести следующие четыре поправки:
а) поправку
на
0—20
кал за
счет изменения температуры кипения
жидкости
в
пределах ±0,05°
К,
регистрируемой термометром
ТС
2
',
б) поправку
на
10—35
кал за
счет изменения температурного градиен-
та
между
нагревателем
и
поверхностью жидкости
в
испарителе;
в) поправку приблизительно
на 25 кал за
счет потери тепла
в
резуль-
тате
теплопроводности токоподводящих проводов, расположенных
позади контактов проводов, используемых
для
измерения потепциа-
лов
!
г)
поправку
на
расширение пара
в
дополнительный объем,
образующийся
в
результате
испарения
и
уноса жидкости
из
испари-
теля. Наличие пропорциональной зависимости
между
импульсной
мощностью
и
скоростью уноса массы вещества
при
данной темпера-
туре
кипения позволяет использовать импульсную мощность
для
°пределения скорости потока пара
в
опытах
по
определению тепло-

46
Часть
1.
Основы
термодинамики
емкостей. При такой температуре эта пропорциональность не зависит
от скорости потока и продолжительности эксперимента.
Для определения кажущихся значений теплоемкостей пара изме-
ряют температуру газового калориметра при фиксированной подаче
энергии
на нагреватель и четырех или более значениях скоростей
потока. Независимые величины кажущихся значений теплоемкости
58,0
Я57,5\-
157,0
46,5
46,0
466,10°K
357,10°К
jy
Термометр
3 ^**^ ^^•"•"^
^S^^^^
Термометр
Z
i
Термометр
3 ^ "
Термометр
Z
1 1
10 15
l/F, мин
/моль
20
Рис.
II.7. Кажущиеся значения теплоемкости гептана как функция скорости
потока пара (по Уаддингтону,
Тодду
и Хаффману [1552]).
при
различных скоростях потока получают, измеряя показания тер-
мометров сопротивления Т
2
и Т
3
. Зависимость кажущейся теплоем-
кости
от скорости потока, построенная в координатах Ср — MF
(где F — скорость потока),
дает
прямую линию в пределах
±0,05%
(рис.
П.7). Экстраполяция этой зависимости к нулевому значению
скорости газового потока
дает
поправку на тепловые потери, кото-
рые
даже
при самых высоких температурах и малых скоростях пото-
ка
не превышают 2%.
В начале опыта с помощью термометров сопротивления Т
и
Т
2
и
Т
3
измеряют температуру потока пара при отключенном нагрева-
теле
Н; затем нагревателю сообщается измеренное количество
энер-
гии,
и после достижения теплового равновесия повторно измеряется
температура термометрами Ti, Т
2
и Т
3
. Незначительные колебания
в
скорости потока вызывают изменения температуры в пределах
//.
Теплоемкость
и
энтальпия
фазовых
переходов
47
v
* ±0,003 до ±0,008°. Для каждого термометра определяют разность
'^температур (например, Т
2
,
]1Па1
— Г
2
,
initial)
До и после подвода
энергии
и стараются уменьшить ошибки, связанные с различиями
в
калибровке термометров и влиянием эффекта Джоуля — Томсона,
обусловленного перепадом давления при прохождении пара череа
калориметр. Для
учета
температурного коэффициента эффекта
Джоуля — Томсона вводят соответствующую поправку, отвечающую
изменению
температуры газа на 8°. Этот эффект составляет примерно
0,03% общего теплового эффекта. Совпадение средних значений тем-
пературы ряда экспериментов свидетельствует об отсутствии влияния
величины AT на кажущиеся значения теплоемкостей. В процессе
эксперимента
перепад давления
между
испарителем и калориметром
составляет от 1 до 35 мм и достигает максимального значения для
самой большой скорости газового потока и самой низкой температуры
эксперимента.
Для
учета
перепада давления вводится соответствую-
щая
поправка, которая по величине не превышает 0,1% и связана
с измеряемой величиной
(АС
Р
/АР)
Т
.
Значения теплоемкости, совпа-
дающие в пределах 0,05% со средним значением, находят из вели-
чин
AT, определенных с помощью термометров Т
2
или Т
3
.
Поправка
для приведения величины теплоемкости Ср при 1
апгм
к
теплоемкости при нулевом давлении (Ср°) (т. е. к теплоемкости
вещества в состоянии идеального газа) определяется из эксперимен-
тальных данных при
двух
или более давлениях, отвечающих одной
и
той же температуре, путем построения графика в координатах
Ср — Р и экстраполяции полученной зависимости к нулевому дав-
лению.
Такой прием позволяет получить значения Ср° и
(АСр/АР)
т
и
служит для нахождения уравнения состояния вещества.
В табл. П.2 приведены типичные экспериментальные данные no-
теплоемкости газообразного к-гептана, полученные Уаддингтоном,.
Таблица
II.2
Теплоемкость
газообразного
гептана
а
)
195,5
391,2
597.7
760,0
0,0
а
) Данные
кал/(моль-"К).
35'
46
46
47
45
Г,10
140
515
22
77
373
47,
48,
48,
48,
47,
Уаддингтона,
,15
805
095
410
66
51
Г
400
50,
50,
51,
50,
Тодда
°к
,40
555
930
08
37
и
43^
53
54
54
53
i,35
965
200
30
85
Хаффмана
466
57
57,
57,
57,
[156
,10
075
215
27
00
2]
в

48
Часть
1.
Основы
термодинамики
Тоддом
и
Хаффмаыом [1552]. Определенное ими значение энтальпии
испарения
и
соответствующие поправки обсуждаются
в
этой главе
несколько
позднее.
Расчет теплоемкостеи газов на основе
статистической механики
Роль
статистической механики
в
теоретическом обосновании мето-
дов расчета термических свойств газов аналогична роли актуарной
статистики. Исходя
из
законов статистической механики нельзя
предсказать время жизни отдельной частицы; можно лишь оценить
среднее время жизни большого числа частиц. При использовании
мощного аппарата статистической механики необходимо, во-первых,
знать,
можно
ли
применять
для
описания распределения энергии
частицы по различным степеням свободы
и
распределения
энергии
между
молекулами законы классической механики или пове-
дение частиц системы нужно рассматривать
с
точки зрения кванто-
вой
механики,
и,
во-вторых, необходимо знать способы усреднения
или
распределения энергии
между
различными состояниями частиц.
Несмотря
на то что
квантовая механика лучше описывает энергети-
ческие свойства молекул,
в
некоторых
случаях,
когда энергетиче-
ские
уровни молекул полностью возбуждены
и
расстояния
между
дискретными уровнями малы по сравнению
с
величиной кТ, класси-
ческая механика позволяет также достаточно точно рассчитать термо-
динамические свойства веществ. Статистический расчет можно значи-
тельно упростить, если рассматривать координаты
и
моменты раз-
личных степеней свободы молекулы как независимые,
а
рассматри-
ваемым молекулам приписать свойства частиц идеального газа.
В классической кинетической теории газов для вычисления
энер-
гии
и
теплоемкости используют принцип классической механики
о
равномерном распределении энергии
по
степеням свободы, согласно которому вследствие беспо-
рядочных столкновений частиц происходит постоянное перераспре-
деление энергии,
в
результате
чего
на
каждую ступень свободы при-
ходится одна и та же доля энергии, равная
RTI2
на
1
моль. Этот вывод
строго вытекает
из
уравнений статистической механики (см., напри-
мер,
работы Астона [30], Толмана [1513], Майера
и
Майера
[942]
и
Фаулера
и
Гугенгейма [436]).
В
таком
случае
вклад
в
теплоемкость
будет
составлять
£4
Выражение для кинетической энергии поступательного движения
молекулы, отвечающее одной степени свободы, можно представить
в
виде E
tr
/n
=
1
/
2
m
(и,)
2
или как
квадратичную функцию момента
количества движения
(p
t
=
mv
t
), например
Е
R
ln
=
(pi)
2
/2m. Отсю-
да
следует,
что минимальное мольное значение кинетической энергии,
//.
Теплоемкость
и
энтальпия
фазовых
переходов
49
гриходящееся на одну степень свободы, составляет
RTI2.
Поскольку
'число степеней свободы одноатомной газообразной молекулы равно
слу координат, необходимых
для
описания положения центра
;массы
в
пространстве
(х, у и z в
картезианских координатах
или
и
Э, ф в
полярных координатах),
то
для одноатомной молекулы
их число равно трем
и
отвечает трем возможным направлениям
поступательного движения
в
пространстве. Энергия поступательного
•движения
и
теплоемкости
Cv и Ср
одного моля такого идеального
газа
будут
равны
—
—
4-Я —
—
У
2 2
Значения
теплоемкостей, полученные для гелия на основе класси-
ческой теории, согласуются
с
экспериментальными величинами, опре-
деленными
для
интервала температур
в
несколько
градусов
Кель-
8ина вблизи абсолютного нуля,
и,
таким образом, подтверждают
применимость
классической теории теплоемкостей
при
таких
тем-
пературах, когда можно пренебречь влиянием квантовых эффектов.
Энергия
вращательного движения по своей природе также являет-
ся
кинетической,
т. е.
F
_
(Рог)
2
ог
"~
2/ '
где
р
от
—
момент количества движения,
а /
— момент инерции вокруг/
оси
вращения. Индекс
«or»
означает свободное вращение всей моле/
кулы. Поскольку энергия вращения также является квадратичной
функцией
момента, любой вид вращения всей молекулы
будет
давать
вклад, равный
RT/2
кал/моль,
в
общую энергию молекулы.
• Энергия простого гармонического осциллятора представляет
собой
сумму
двух
квадратичных членов: одного, содержащего момент
движения
р
х
, и
другого,
связанного
с
координатой смещения
х. т. е.
V1D
~~
2m ' 2 '
Щв
f —
силовая постоянная. Таким образом, первый член выраже-
ния
представляет собой кинетическую,
а
второй
—
потенциальную
энергию колебательного движения. Отсюда
следует,
что
каждая
колебательная степень свободы
дает
вклад
в
общую энергию моле-
кулы, равный (RT/2)
X 2, или RT
кал/молъ.
Общее число степеней
свободы, необходимых
для
полного описания нелинейных много-
атомных молекул, содержащих
п
атомов, составляет Зге. Три
из
них
описывают движение центра тяжести молекулы
и
являются посту-
пательными степенями свободы; три, отвечающие ориентации моле-
кулы как целого,— вращательными
и
остальные Зге
— 6 —
колеба-
тельными. Полная теплоемкость такой молекулы
при
постоянном
объеме, согласно принципу равномерного распределения энергии,
"УДет
равна (Зге
— 3) R. Для
линейных молекул число вращатель-
ных
и
колебательных степеней свободы равно соответственно
двум
4—831
50
Часть
1.
Основы
термодинамики
О
и
(Зге — 5); в таком
случае
теплоемкость линейной молекулы при
постоянном
объеме
будет
составлять (Зп — 5/2) R. Для двухатомной
молекулы Cv = 1I2R. Анализ данных по теплоемкостям газов пока-
зывает, что найденные экспериментально теплоемкости, как правило,
меньше,
чем вычисленные по приведенным формулам, и лишь при
высоких температурах они приближаются к расчетным величинам.
Расхождение объясняется в основном тем, что не учитывалась кван-
товая природа вещества, и это осо-
у бенно сказывается на колебатель-
ной
энергии молекул. В дополне-
ние
следует
подчеркнуть, что откло-
нение
от точной квадратичной
зависимости в выражении для
энергии
даже
при высоких темпе-
ратурах
неизбежно приводит к не-
выполнению
принципа равномер-
ного распределения энергии по
степеням свободы. Подобные от-
клонения,
например,
будут
вызы-
вать осцилляторы, не являющиеся
строго гармоническими. И
нако-
нец,
следует
учитывать наличие
в
молекулах заторможенного внут-
реннего вращения.
Методику расчета теплоемко-
стей удобно рассмотреть на ряде
примеров,
начиная с простых и кончая более сложными молекулами.
Квантовый
подход
для оценки энергии колебательного движения
будет
использоваться по мере необходимости для получения вели-
чин,
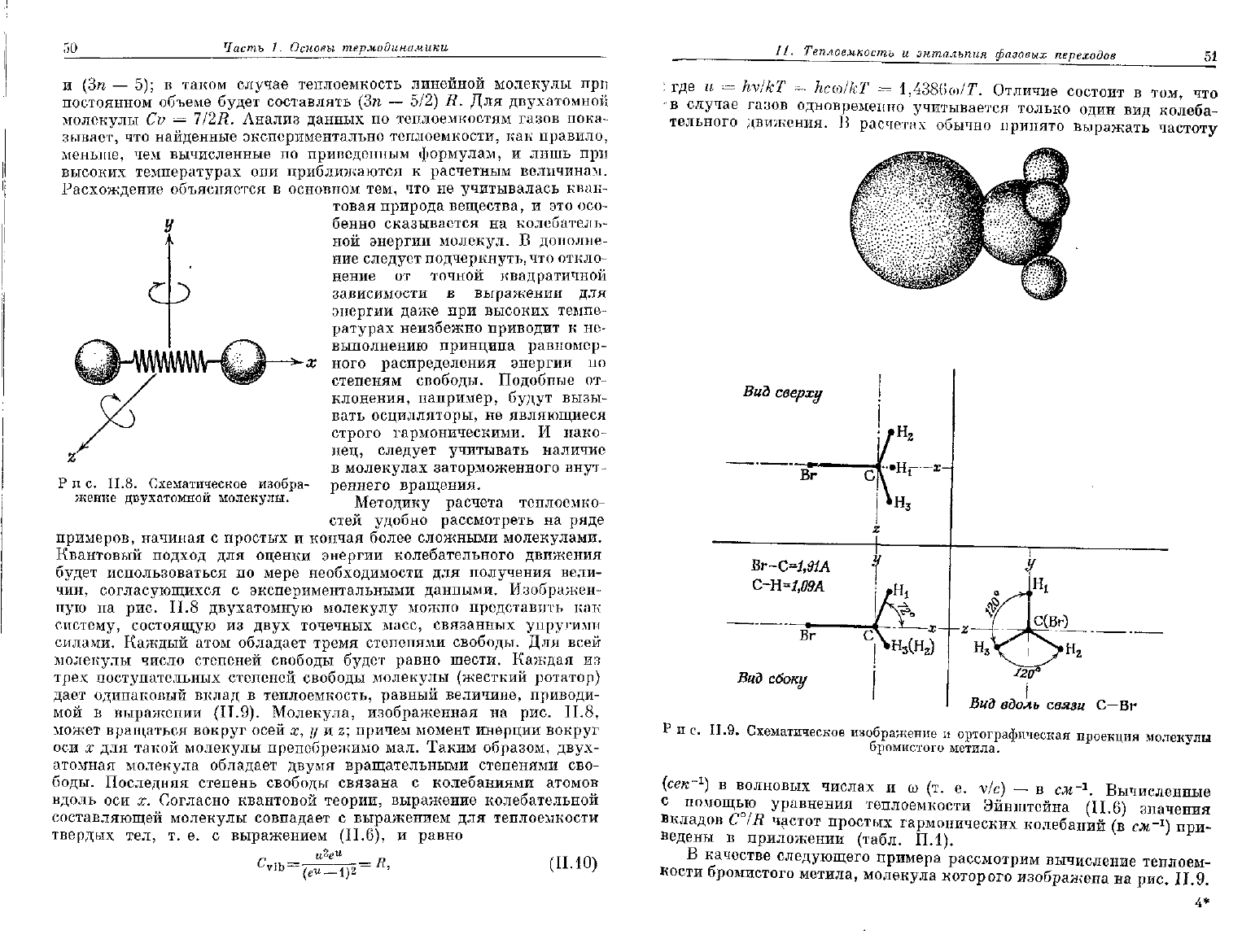
согласующихся с экспериментальными данными. Изображен-
ную на рис. II.8
двухатомную
молекулу можно представить как
систему, состоящую из
двух
точечных масс, связанных упругими
силами.
Каждый атом обладает тремя степенями свободы. Для всей
молекулы число степеней свободы
будет
равно шести. Каждая из
трех
поступательных степеней свободы молекулы (жесткий ротатор)
дает
одинаковый вклад в теплоемкость, равный величине, приводи-
мой
в выражении
(П.9).
Молекула, изображенная на рис. П.8,
может вращаться вокруг осей х, у и z; причем момент инерции вокруг
оси
х для такой молекулы пренебрежимо мал. Таким образом,
двух-
атомная молекула обладает двумя вращательными степенями сво-
боды. Последняя степень свободы связана с колебаниями атомов
вдоль оси х. Согласно квантовой теории, выражение колебательной
составляющей молекулы совпадает с выражением для теплоемкости
твердых тел, т. е. с выражением
(II.6),
и равно
//.
Теплоемкость
и
энтальпия
фазовых
переходов
51
Р
и с. П.8. Схематическое изобра-
жение двухатомной молекулы.
—1)2"
где и = hv/kT = hcalkT =
l,4386oi/7\
Отличие состоит в том, что
в
случае
газов одновременно учитывается только один вид колеба-
тельного движения. В расчетах обычно принято выражать частоту
Вид
сверху
/20°
Вид
вдоль
связи
С—Вг
Р
и с. II.9. Схематическое изображение и ортографическая проекция молекулы
бромистого метила.
(сек-
1
) в волновых числах и со (т. е. vie) — в см-
1
. Вычисленные
-.с помощью уравнения теплоемкости Эйнштейна (И.6) значения
вкладов
C°IR
частот простых гармонических колебаний (в см-
1
) при-
ведены в приложении (табл. П.1).
', В качестве следующего примера рассмотрим вычисление теплоем-
кости
бромистого метила, молекула которого изображена на рис. 11.9.
4*
52
Часть
1.
Основы
термодинамики
Каждые три поступательные и три вращательные степени свободы
этой
молекулы
дают
вклад в теплоемкость при постоянном объеме,
равный
2>RI2
кал/(моль-°К.);
вклады остальных колебательные
степеней свободы, число которых равно (3x5) — 6 = 9, вы-
числяются из спектроскопических данных. Вейсман, Бернштейн,
Россер,
Майстер и Клевеленд
[1584]
исследовали инфракрасные
спектры этой молекулы в области частот от 400 до
4000
см*
1
и опре-
делили следующие фундаментальные частоты (в см'
1
) и их мульти-
плетность (в скобках): 611 (1), 955 (2), 1305 (1), 1444 (2),
2972
(1),
3057
(2). Обычно говорят, что степень свободы обладает мульти-
плетностью g
t
, если g
t
степеням свободы соответствует одинаковая
частота колебаний.
Бромистый
метил обладает тремя дважды вырожденными часто-
тами, поэтому вклад в теплоемкость этих
трех
частот необходимо
удвоить. Вклад колебательных степеней свободы в теплоемкость
определяется для каждой из приведенных выше частот или непосред-
ственно,
или путем интерполяций по данным табл. П.1 (см. прило-
жения).
Величины этих вкладов при
300°
К приведены в табл. П.З.
Таблица II.3
II.
Теплоемкость
и
энтальпия
фазовых
переходов
53
со
г
, сж-1
611
955
1305
1444
2972
3057
Si
1
2
1
2
1
2
C°/R
0,5116
0,4392
0,0762
0,0948
0,0001
0,0002
Вклад колебательных степеней сво-
боды
Вклад поступательных и вращатель-
ных
степеней свободы всей моле-
кулы
Переход от Со к Ср
1,122
3,000
1,000
5,122
Суммарное рассчитанное значение
Cp'^JR
для идеального газо-
образного СН
3
Вг равно 5,122 X
1,9873
= 10,18
кал/(моль-°К).
Иногда,
помимо рассмотренных выше поступательной, враща-
тельной и колебательной энергий, необходимо учитывать энергию
внутреннего вращения, т. е. энергию, связанную с вращением групп
атомов в молекуле вокруг некоторой валентной связи. Если энергия
вращения
группы атомов в молекуле намного меньше энергии потен-
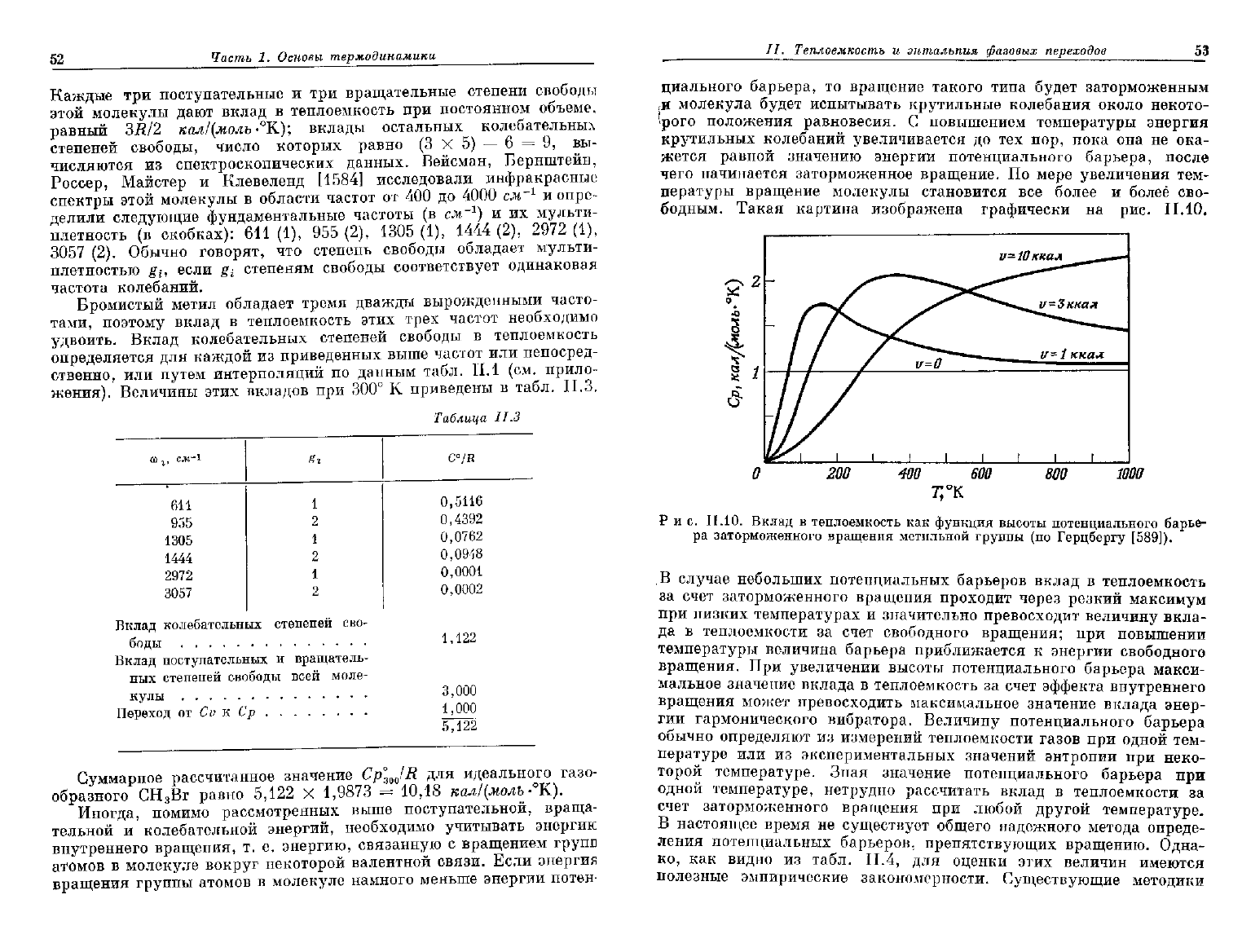
циального барьера, то вращение такого типа
будет
заторможенным
я
молекула
будет
испытывать крутильные колебания около некото-
рого положения равновесия. С повышением температуры энергия
крутильных колебаний увеличивается до тех пор, пока она не ока-
жется равной значению энергии потенциального барьера, после
чего начинается заторможенное вращение. По мере увеличения тем-
пературы вращение молекулы становится все более и более сво-
бодным. Такая картина изображена графически на рис. 11.10.
v-10
•""•'
800
1000
[р
и с.
11.10.
Вклад в теплоемкость как
функция
высоты потенциального барье-
ра
заторможенного вращения метильной группы (по Герцбергу [589]).
,В
случае
небольших потенциальных барьеров вклад в теплоемкость
за счет заторможенного вращения проходит через резкий максимум
при
низких температурах и значительно превосходит величину вкла-
да в теплоемкости за счет свободного вращения; при повышении
температуры величина барьера приближается к энергии свободного
вращения.
При увеличении высоты потенциального барьера макси-
мальное значение вклада в теплоемкость за счет эффекта внутреннего
вращения
может превосходить максимальное значение вклада
энер-
гии
гармонического вибратора. Величину потенциального барьера
обычно определяют из измерений теплоемкости газов при одной тем-
пературе или из экспериментальных значений энтропии при
неко-
торой температуре.
Зная
значение потенциального барьера при
одной
температуре, нетрудно рассчитать вклад в теплоемкости за
;
счет заторможенного вращения при любой
другой
температуре.
,
В настоящее время не
существует
общего надежного метода опреде-
|
ления потенциальных барьеров, препятствующих вращению. Одна-
[ ко, как видно из табл. II.4, для оценки этих величин имеются
i
полезные эмпирические закономерности. Существующие методики
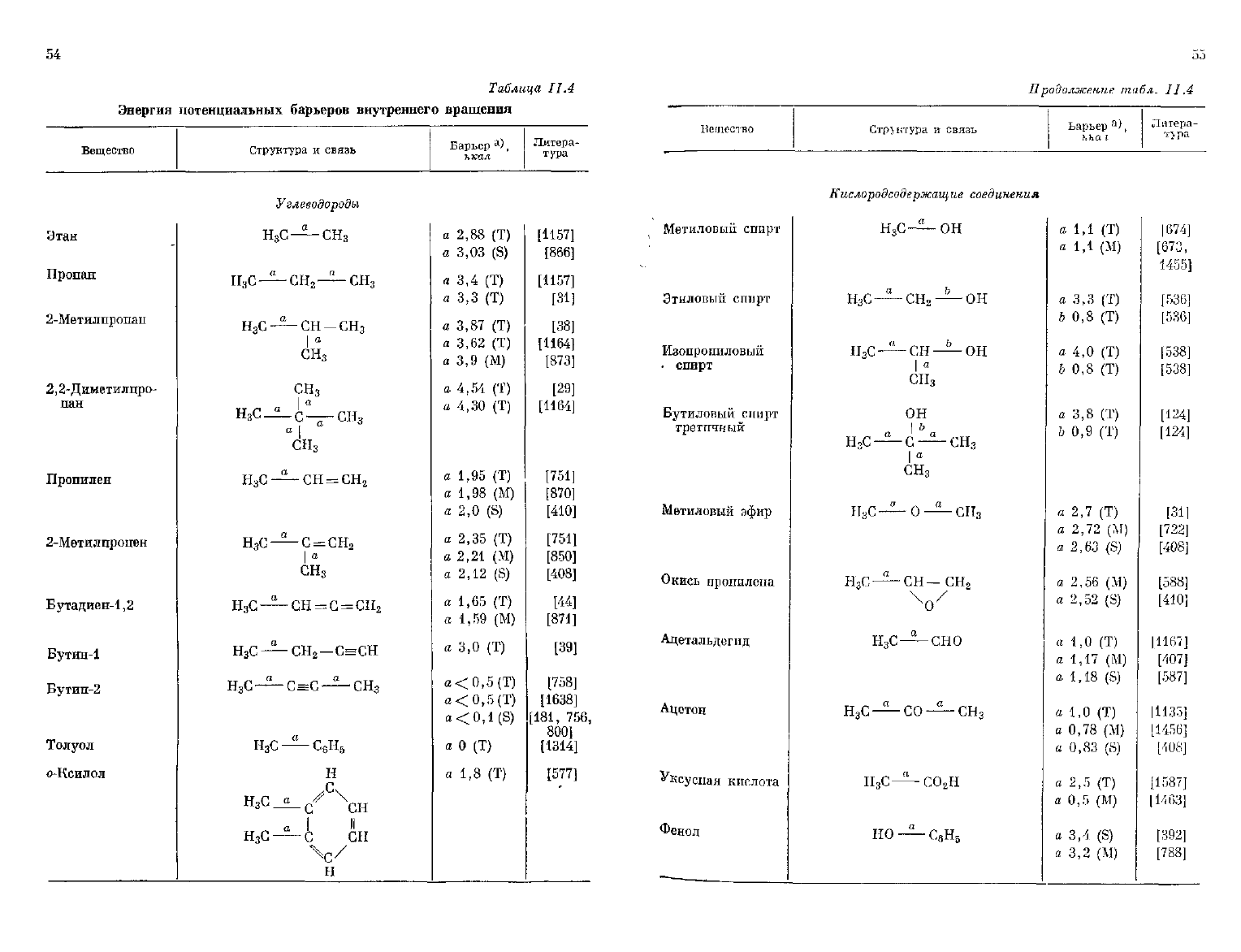
54
Таблица
II.-
Энергия
потенциальных
барьеров
внутреннего
вращения
Продолжение табл. II.4
Вещество
Структура
и
связь
Углеводороды,
Барьер
а
),
Литера-
тура
Этан
Пропан
2-Метилпропан
2,2-Диметилпро-
пан
Пропилен
2-Метилпропен
Бутадиен-1,2
Бутин-1
Бутин-2
Толуол
о-Ксилол
н
3
а
3
н
3
с-
Н
3
С
°
н
3
с-
н
3
с-
н
3
с-^
нг
а
*1
3
L.
(X
н
3
с
н
3
с_
н
3
с-
а
3
а
\а
СН
3
СН
3
|а
Г
1
РТТ
V
а
ЬН
3
(7
1
сн
3
а
сп си
—
с=сн
2
а
СН
3
-сн=с=сн
2
-СН
2
—
СЕ=СН
(X
с
в
н
5
н
—
с
/
си
~\
с
/
сн
н
а 2,88 (Т)
а 3,03 (S)
а 3,4 (Т)
а 3,3 (Т)
а 3,87 (Т)
а 3,62 (Т)
а 3,9 (М)
а 4,54 (Т)
а 4,30 (Т)
а 1,95 (Т)
а 1,98 (М)
а 2,0 (S)
а 2,35 (Т)
а 2,21 (М)
а 2,12 (S)
а 1,65 (Т)
а 1,59 (М)
а 3,0 (Т)
а<0,5(Т)
а<0,5(Т)
a<0,l(S)
а 0 (Т)
а 1,8 (Т)
[1157]
[866]
[1157]
[31]
[38]
[1164]
[873]
[29]
[1164]
[751]
[870]
[410]
[751]
[850]
[408]
[44]
[871]
[39]
[758]
[1638]
[181,
756,
800]
[1314]
[577]
к
1
Вещество Структура
и
связь
Ьарьер
а
),
Кислородсодержащие соединения
Литера-
Метиловый спирт
Этиловый спирт
Изопро
пи
ловый
. спирт
Бутиловый спирт
третичный
Метиловый эфир
Окись пропилена
Ацетальдегид
Ацетон
Уксусная
кислота
Фенол
Н
3
С-^-ОН
а
Ь
т г п РТТ ("1ТТ
rl
3
vj
^11
2
Uxl
ТТ
О
П
' РТТ АТТ
H
3
L
Ы1 (JH
1
а
сн
3
он
1
ь
\
а
сн
3
а а
ТТ
Г
1
ЛТТ Г*ТТ
XI3^-J liJl ^-П-2
Н
3
С-^-СНО
а а
Н
3
С
СО
2
Н
НО
СвН
5
а 1,1 (Т)
а 1,1 (М)
a
3,3 (Т)
Ъ
0,8 (Т)
а 4,0 (Т)
6 0,8 (Т)
а 3,8 (Т)
Ь
0,9 (Т)
а 2,7 (Т)
a
2,72 (М)
а 2,63 (S)
a
2,56 (М)
а 2,52 (S)
о
1,0 (Т)
a
1,17 (М)
a
1,18 (S)
а 1,0 (Т)
a
0,78 (М)
a
0,83 (S)
а 2,5 (Т)
a
0,5 (М)
a
3,4 (S)
a
3,2 (М)
[674]
[673,
1455]
[536]
[536]
[538]
[538]
[124]
[124]
[31]
[722]
[408]
[588]
[410]
[1167]
[407]
[587]
[1135]
[1456]
[408]
[1587]
[1463]
[392]
[788]

56
57
Вещество
Метантиол
Этантиол
2-Пропантиол
2-М етил-2-пропан-
тиол
Метилсульфид
Тиофенол
Продолжение
табл.
II .4
Структура
и
связь
Барьер
а
),
Серусодержащие
соединения
SH
SH
Н
3
С
\
СН
3
SH
—С-2
\а
СН
3
a 2,10 (T)
a 2,09 (S)
a 2,18 (M)
a 2,13 (M)
a 0(T)
Азотсодержащие
соединения
Литера-
тура
a
a
a
b
a
b
a
b
1,27
1,27
3,31
1,64
3,95
1,39
5,10
1,36
(T)
(M)
(T)
(T)
(T)
(T)
(T)
(T)
[1271,
1316]
[790]
[962]
[962]
[955]
[955]
[963]
[963;
[958]
[408]
[354]
[1143]
[1319]
Метиламин
Диметиламин
Триметиламин
N-Метилметилен-
имин
Нитрометан
H
3
C-^-NH
2
ТТ ГЛ ^
-ЦТТТ
ЛТТ
H
3
U
JNrl
СН
3
и
г ° тчт
а
гн
Н
3
Ь
JN ЬНз
сн
3
НзС-^-N
=СН
2
HaC-^-NO,
а 1,98 (М)
а 3,46 (Т)
а 3,28 (S)
а 4,27 (Т)
а 4,40 (М)
а 4,41 (S)
1,97 (М)
а 0 (Т)
а 0 (М)
[1346]
[32]
[408]
[42]
[872]
[408]
[12771
[964]
[1466]
Вещество
Метилнитрат
2-Метилпиридин
З-Метилпиридин
Анилин
Структура
и
связь
H-jC-^-O
—NO
2
Н
3
С—C
6
H
4
N
H
3
C-^C
5
H
4
N
H
2
N
CgHs
Продолжение
табл.
II.4
Барьер
а
),
ккал
а 0 (Т)
а 2,3 (М)
Ъ 0 (Т)
Ъ 9,1 (М)
аО (Т)
а 0 (Т)
а 3,43 (Т)
а 3,54 (S)
Литера
тура
[524]
[330]
[524]
[330]
[1315]
[1310]
[579]
[391]
Этил фтористый
1,1-Дифторэтан
1,1,1-Трифторэтан
Гексафторэтан
Бензотрифторид
, Этил хлористый
i
1,1-Дихлорэтан
1,1.1-Трихлорэтан
* Этил бромистый
• Этил йодистый
Галогенсодержащие
соединения
н
3
с-
CH
2
F
Н
3
С-
н
3
с-
F
3
C-
F
3
C-
Н
3
С
—
-CHF
2
CF3
CF
3
Н
3
С-
Н
3
С-
Н
3
С-
Н
3
С-
СНС1
2
-ССЬ
СН
2
1
а 3,33 (S)
а 3,30 (М)
а 3,18 (М)
а 3,21 (S)
а 3,34 (Т)
а 3,20 (Т)
а 3,04 (S)
а 3,96 (Т)
а 0 (Т)
а 3,7 (Т)
а 3,69 (М)
а 3,69 (S)
а 3,75 (Т)
а 3,75 (S)
а 2,7 (Т)
а 2,8 (S)
а 3,68 (М)
а 3,2 (М)
[1274]
[586]
[586]
[407]
[1402]
[1270]
[204]
[673]
[1301]
[518]
[1296]
[410]
[862]
[302]
[1261]
[377]
[430]
[723]
) Обозначения
(Т), (S) и (М)
соответствуют величинам потенциальных барьеров,
по-
'
лученным
на
основе термических данных, данных
в
области далекой инфракрасной спектро-
'
Скопии
и
микроволновой спектроскопии соответственно.
В
таблице приведены ссылки
на
оригинальные работы
по
определению величин барьеров
на
основе термических данных,
J
однако некоторые значения несколько изменены
в
целях соответствия более правильным
•
отнесениям колебательных частот
или
моментов инерции.

58
Часть
1.
Основы
термодинамики
термодинамического расчета, весьма
грубые
для оценки небольших
значений
потенциальных барьеров, вполне применимы для вычисле-
ния
высоких потенциальных барьеров.
Кистяковский
и Райе [758] определили теплоемкость газообраз-
ного диметилацетилена, молекула которого схематически изображена
на
рис. 11.11. Значительное удаление атомов водорода метильных
групп
друг
от
друга
обеспечивает свободное вращение одной метиль-
ной
группы относительно
другой
в этой молекуле. Для молекулы
диметилацетилена Кистяковский и Райе [758] получили следующие
Рис.
11.11.
Схематическое
изображение
молекулы
ди-
метилацетилена.
значения
фундаментальных частот (в см'
1
) и их мультиплетностей
(в
скобках): 213 (2), 371 (2), 725 (1), 1029 (2), 1050 (2), 1126 (1), 1380
(2),
1448 (2), 1468 (2),
2270
(1), 2916 (1),
2966
(2),
2976
(3). Изученная
молекула содержит 10 атомов и нелинейна, поэтому она обладает
(3
X 10) — 6 = 24 колебательными степенями свободы. При
отсут-
ствии потенциального барьера каждой степени свободного
внутреннего вращения можно приписывать значения энергии
и
теплоемкости, равные соответственно E
ir
= RT/2 и С
1Г
= Л/2 =
=
0,994
кал/(моль
-°К).
Вклад поступательной и вращательной энергии всей молекулы
в
теплоемкость диметилацетилена составит 3.R. Полное значение
теплоемкости диметилацетилена при
336,07°
К
будет
определяться
суммой вкладов, приведенных в табл. П.5.
Таким
образом, вычисленное значение
С;?ззб,07
диметилацети-
лена в состоянии идеального газа равно
10,211
X
1,9873
=
=
20,29
кал/(молъ
-°К). Эта величина в пределах ошибок экспери-
мента согласуется со значением Ср° = 20,21
кал/'(моль
-°К), полу-
ченным
Кистяковским и Райсом, и указывает на наличие заметного
свободного вращения метильных групп в молекуле диметилацетилена.
Вандеркуи и Де Врис
[1527]
измерили теплоемкость газообраз-
ного 1,1,1-трифторэтана, молекула которого изображена на рис. 11.12
и
для температуры
300°
К нашли значение Cv, равное 16,83 ±
±0,18
кал/'(моль
-"К).
Нилсен, Классен и Смит
[1070]
исследовали
спектр частот этой молекулы и определили следующие фундаменталь-
ные
частоты колебаний (в см~
х
) и их мультиплетности (в скобках):
238 (1), 365 (2), 541 (2), 603 (1), 830 (1), 969 (2), 1232 (2), 1278 (1),
//.
Теплоемкость
и
энтальпия
фазовых
переходов
59
Таблица
II 5
со,,
сж-1
213
317
725
1029
1050
1126
1380
1448
1468
2270
2916
2966
2976
Si
2
2
1
2
2
1
2
2
2
1
1
2
3
CJR
1,8674
1,6287
0,4732
0,4862
0,5614
0,1905
0,1905
0,1569
0,1479
0,0057
0,0006
0,0010
0,0014
Вклад колебательной энергии
Вклад энергии поступательного
движения и вращения всей мо-
лекулы .... ...
Переход от Cv к Ср
Вклад энергии внутреннего враще-
ния
молекулы
5,711
3,000
1,000
0,500
10,211
1408 (1), 1443 (2),
2978
(1),
3036
(2). Эта нелинейная молекула содер-
жит восемь атомов и обладает (3x8) — 6 = 18 колебательными
степенями
свободы. Нилсен, Классен и Смит отнесли частоту 238 (1)
к
частоте крутильных колебаний вокруг связи С — С. В данном рас-
чете
это предположение
будет
рассмотрено и обсуждено несколько
позднее. Остальные вклады в теплоемкость этой молекулы при
300°
К
приведены в табл. И.6.
Таким
образом, Cv равно 7,413 X
1,9872
=
14,731
кал/'(моль
-°К).
Из
сравнения вычисленных и найденных величин
следует,
что рас-
считанное значение меньше экспериментального на величину, рав-
ную 16,83 — 14,73 = 2,10
кал/(молъ-°К).
Эту разность можно рас-
сматривать как вклад в теплоемкость за счет заторможенного враще-
ния
групп атомов вокруг центральной связи С — С с
учетом
сил,
Действующих
между
ними. Действительно, величина 2,10
кал/(молъ
X
* К) значительно больше величины 1,782
кал/(молъ
-°К), рассчи-
танной
для частоты крутильных колебаний, равной 238 см"
х
, а также
более
чем в два раза превышает вклад в теплоемкость за счет свобод-
ного внутреннего вращения и объясняется взаимодействием групп
"-utg и
—СН
3
в молекуле 1,1,1-трифторэтана.
