Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

407

– [389–416] 13.3.2008 2:46PM

is derived from the convectively driven radial

motion and that differential rotation cannot con-

tribute to it.

A toroidal field line would be drawn out by

the helical motion, as in Fig. 24.6(c), resulting in

a field loop out of the plane of the diagram. Such

a field loop is of poloidal form, but for generation

of a large-scale poloidal field, such as the Earth’s

dipole field, non-zero average helicity is required.

It is possible that this arises by a systematic

latitude dependence of upwelling and down-

welling convection, especially an asymmetry

between the hemispheres, but non-linear effects

arising from narrow upwelling with a broad-

scale return flow would achieve the same result.

A dynamo that relies on generation of a toroidal

field from a poloidal one by the !-effect and

regeneration of the poloidal field by the -effect

is referred to as an –! dynamo. Dynamos that

rely on the -effect for both stages are also pos-

sible and are termed 

dynamos. It is possible

for an 

dynamo, driven entirely by a repeated

pattern of small-scale motions, as in turbulence,

to generate a large-scale field.

Simple mechanical models have been useful

in understanding how a self-exciting dynamo

can operate. They include computer calculations

of the behaviour of the coupled disc dynamo in

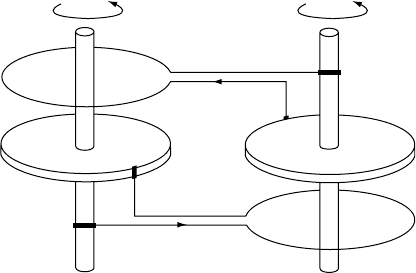
Fig. 24.7, which was analysed by Rikitake (1966).

Each of the discs rotates in an axial field pro-

duced by a coil carrying a current driven by the

other disc. Rotation in the field generates an

e.m.f. between the perimeter and the axis, pro-

viding the current that causes the axial field

in the other disc. Self-excitation occurs when

current generation overcomes ohmic dissipation

by an adequate combination of size, speed and

loop conductance. The model is symmetrical

with respect to polarities of the currents and

fields. If a particular combination of currents,

and consequent fields, is self-exciting, then this

is equally true when both currents (and fields)

are reversed. Instability, including spontaneous

current reversals, has been found with certain

combinations of model parameters. Such time-

varying behaviour depends on the loop induc-

tances as well as the other model characteristics.

A practical realization of the principle of

coupled disc dynamos was a laboratory model

constructed by Lowes and Wilkinson (1963,

1968). The geometry of this device is illustrated

in Fig. 24.8(a). Two metal cylinders were rotated

at controlled speeds within cavities in a metal

block, to which they were connected electrically

by filling the gaps with mercury. No electrical or

magnetic excitation was deliberately intro-

duced, but ferromagnetic material was used for

both the cylinders and the block, so that self-

excitation could occur at attainable rotation

speeds. The performance of the early version

of the Lowes–Wilkinson model is illustrated in

Fig. 24.8(b). The slight excitation at low speeds is

attributed to residual magnetism in the metal,

but the onset of self-excitation occurred quite

sharply when a critical combination of rotation

speeds was reached. A later, more sophisticated

version of the model demonstrated instabilities,

with spontaneous oscillations and reversals

of the measured field. Use of ferromagnetic

material in the Lowes–Wilkinson dynamo was

necessary to suppress field diffusion sufficiently

to allow dynamo action with a reasonable size

and speed of the apparatus. The free space per-

meability 

in the equation for magnetic dif-

fusivity (Eq. (24.44)) is replaced by the much

higher permeability of the magnetic material.

However, ferromagnetism has no relevance

Disc 1 Disc 2

FI G U R E 24.7 A simple mechanical analogue of the

geomagnetic dynamo mechanism. This shows two

interconnected disc dynamos. A single disc dynamo,

which uses its current output to produce its own axial

magnetic field, is self-excited if it has sufficient rotational

speed. An interconnected pair, as shown here, may

show more complicated effects, including spontaneous

field reversals.

24.5 THE DYNAMO MECHANISM 407

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

408

– [389–416] 13.3.2008 2:46PM

to the Earth’s core where the permeability is

insignificantly different from 

. Progress on

more recent laboratory experiments, with non-

magnetic media, mostly liquid sodium, has been

discussed in a special journal issue (R¨adler

and C

ebers, 2002). A significance of such experi-

ments is that, by using a conducting liquid

of low viscosity, the role of turbulence can

be examined in a way that is not possible in

numerical dynamos.

The theoretical approach to self-exciting

dynamo action in a fluid conducting sphere

took an important step forwards with the

model by Bullard and Gellman (1954). They

applied the principle of –! dynamo action by

representing poloidal and toroidal fields, with

their associated motion, as spherical harmonics

feeding one another. This work was influential

in focussing attention on several features that

became central to discussions of the dynamo:

the necessity for a toroidal field, which is not

observable, poloidal–toroidal field interaction

and differential rotation within the core. The

success of their approach was limited by lack

of convergence of their harmonic series. This

fact is interesting in view of the evidence that

the spatial spectrum may be white and that the

various harmonics cannot occur independently,

with energy fed down the harmonic chain. The

Bullard and Gellman approach pioneered kine-

matic dynamo modelling, that is the develop-

ment of models in which the motion is

specified and the electromagnetic consequen-

ces are calculated. The disc dynamo and the

Lowes–Wilkinson laboratory model formally

come into this category, although with less

Earth-like geometry.

Fully dynamic numerical modelling, with fluid

motion impelled by buoyancy and self-adjusted by

the mutual control of the motion and the field,

became possible with very large and fast com-

puters. There are different ideas about assump-

tions and approximations (Glatzmaier and

Roberts, 1995a,b; Kuang and Bloxham, 1997;

Takahashi et al. 2005) that yield internal motions

and field patterns that may be quite different

from one another in detail, but they generally

give quite Earth-like behaviour, with dominant

dipole fields. Kono and Roberts (2002) reviewed

the various approaches. Dominance of the dipole

field is evidently a feature of the terrestrial sit-

uation but, as modelling reported by Busse

(2002) shows, different physical conditions may

lead to quadrupole dominated dynamos. This

appears to be the case in Uranus and Neptune.

In using the models to judge what is important in

the physical assumptions, by comparing them

with observations of the Earth’s field, we are

limited by the fact that the fine details are

obscured by our distance from the source. Also

our direct observations extend over a very short

time, compared with the time scales of geomag-

netic effects, and we turn to paleomagnetic evi-

dence, discussed in Chapter 25.

100

150

= 277.5 rad s

–1

(rad s

–1

)

ext

(10

–4

(b)

(a)

FI G U R E 24.8 (a) Arrangement of rotating cylinders in

the Lowes and Wilkinson (1963, 1968) laboratory model of

geomagnetic dynamo action. The cylinders are enclosed

in a metal block with which they are electrically continuous.

(b) Externally observed field as a function of the speed of

cylinder 1, with cylinder 2 maintained at a fixed speed.

408 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

409

– [389–416] 13.3.2008 2:46PM

First, we note that the fluid viscosity of the

outer core is almost certainly quite low, within a

factor 10 or so of the viscosity of water (Poirier,

1988; Dobson, 2002). This means that viscous

forces are very weak compared with the

Coriolis force of rotation and in this situation

convective motion tends to break up into quasi-

independent columns (Taylor columns) parallel

to the rotation axis, with little viscous interac-

tion between them. The ‘tangent cylinder’, a

cylindrical surface parallel to the axis and just

enclosing the inner core, assumes particular sig-

nificance. Although not a physical boundary, in

many models it effectively isolates core motion

in polar regions (within the tangent cylinder)

from the rest of the outer core. But molecular

viscosity may not really be relevant to the

motion of a magnetically controlled fluid, in

which eddy viscosity has a much higher value

and is anisotropic, being controlled by the field.

The possibility that the tangent cylinder has

an observable surface expression is examined

by Olson and Aurnou (1999). What evidence

do we have for Taylor columns in the core?

Correlated ‘flux bundles’ in opposite hemi-

spheres (Bloxham, 2002) are probably an indica-

tion of their existence. A related question is the

rotation of the inner core. Differential rotation

within the outer core, with the inner core rotat-

ing slightly faster than the mantle, is a feature of

several theories and was drawn to attention by

the model of Glatzmaier and Roberts (1996).

Reports that it is observed seismologically are

discussed in Section 24.6, but the Kuang and

Bloxham (1997) model gives inner core rotation

that may be either faster or slower at different

times and gravitational interaction between the

inner core and the mantle complicates the pic-

ture (Section 24.6).

Reversals of the dipole are a common feature

of the models and the mechanism is of particular

interest. In the model of Takahashi et al. (2005)

reversals appear to be initiated by flux patches

that start at low latitudes and migrate to higher

latitudes. The latitude migration of sunspots

with their intense fields, during the 22-year sun-

spot cycle of solar field reversals, appears similar

although it occurs in the opposite direction. But

terrestrial field reversals are very irregular and

have a long-term frequency variation that is sug-

gestive of mantle control (Jones, 1977; McFadden

and Merrill, 1984 – see Section 25.4). It is feas-

ible that flux patches of the kind seen in the

Takahashi et al. (2005) model would be triggered

by thermal structure in the D

layer at the base of

the mantle. Variations in this structure on the

-year time scale of mantle convection appear

to offer a plausible explanation for the very var-

iable rate of reversals (Section 25.4).

The intervals between reversals, typically sev-

eral hundred thousand years, are much longer

than the duration of the reversal process, which

may be 5000 years or even less. The inner core

may have a stabilizing effect, inhibiting reversals

(Hollerbach and Jones, 1995), because the mag-

netic flux in the inner core can change only by

diffusion and its relaxation time, about 1600

years, is longer than the reorganization times

plotted in Fig. 24.4.

Although many details of the dynamo remain

obscure, or subject to different theories, the gen-

eral principles are not in doubt. Any sufficiently

large-scale and complicated motion of a fluid

conductor will generate a field. Like any other

state, the zero field state is unstable and cannot

occur if conditions favour field generation. It is

useful to anticipate two results of paleomagnet-

ism (Chapter 25) by appealing to Curie’s princi-

ple of symmetry, according to which no effect

can have lower symmetry than the combination

of its causes. If we assume that, apart from the

effect of rotation, the core and the composi-

tional and thermal gradients within it are spheri-

cally symmetrical, then the rotational axis must

be a symmetry axis in the operation of the

dynamo, and the only one. Curie’s principle

requires that, averaged over a sufficient multiple

of its relaxation time, the magnetic axis must

coincide with the rotational axis. This is recog-

nized as the axial dipole hypothesis in paleomag-

netism (Section 25.3). Moreover, nothing in the

dynamo distinguishes the two opposite direc-

tions of the axis. As we now know from paleo-

magnetism (Section 25.4) the field may have

either polarity with equal probability. Curie’s

principle is discussed in the context of inner

core anisotropy in Section 17.9, where it is

pointed out that in geophysical or geological

24.5 THE DYNAMO MECHANISM 409

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

410

– [389–416] 13.3.2008 2:46PM

contexts of this kind it must be applied in a

statistical sense. An analogy is a turbulent

stream, in which individual drops of water

have highly variable motions, but with sufficient

averaging, either over all the drops or over time

for one drop, are seen to move steadily down-

stream. Provided this statistical approach is

adopted, the symmetry principle is a powerful

constraint on our physical theories.

24.6 The westward drift and

inner core rotation

The historical record of the secular variation in

western Europe extends back to about 1600. The

400 years of data from London (Fig. 25.3) appear

as a rotation of the field direction about the

inclined dipole field. Bullard et al. (1950) noted

that this is consistent with a westward drift of

the non-dipole features (Fig. 24.1) past any point

of observation. It gives the impression that

the westward drift is a permanent feature of

the secular variation and it was interpreted by

Bullard as a bodily motion of the outer part of the

core relative to the mantle. The spectrum of the

length of day observations (Sections 7.4 and 7.5)

indicates a relaxation time for establishment of

rotational equilibrium between the core and

mantle that is a few decades at most and this is

incompatible with prolonged differential rota-

tion. For this reason, Bullard postulated that

the mantle was somehow coupled to the deeper

seated dipole field and that the westward drift

was a direct indication of differential rotation

within the core. There is a fundamental difficulty

with this interpretation. Electromagnetic cou-

pling of the core and mantle is due to the field

at the outer boundary of the core and, to the

extent that the frozen flux principle applies,

the entire field moves with the outermost part

of the core. The mantle cannot be coupled inde-

pendently to a deep feature of the field, which

can enter the mantle only through the surface

layer of the core. An obvious, but contrived,

explanation is that we do not see all of the field

at core level and that the westward drifting

long wavelengths are compensated by unseen

finer scale features with a net eastward drift.

Subsequent extension of the record by archeo-

magnetic measurements to span 2000 years, as

in Fig. 25.3, shows that the simple cyclic pattern

is characteristic only of the last few hundred

years and not the earlier period. But a systematic

drift, even for a few hundred years, has appeared

paradoxical.

Figure 25.3 represents the field in a small

local area, whereas the drift of the features in

Fig. 24.1 is global. Moreover, the non-dipole field

is not only drifting but its pattern is changing, so

that Fig. 25.3 is not a conclusive argument

against the significance of the drift. If the core–

mantle coupling coefficient, K

¼3.2 10

Nms

(Eq. (7.33)), is correctly estimated from the spec-

trum of length of day observations, with a relax-

ation time of about 8 years, and the westward

drift is D! ¼0.188/year ¼1.0 10

10

rad s

1

, the

energy dissipation by a bodily drift at this rate

would be K

¼3 10

W. This is small enough

to present no difficulty, energy-wise, but it

would preclude differential rotation lasting for

hundreds of years. The essential difficulty with

the drift is in devising a mechanism to maintain

it against the electromagnetic coupling that

would establish equilibrium between the rota-

tions of the mantle and the top of the core. A

gravitational interaction, considered below,

appears to be the only possibility.

Independent evidence for differential rotation

is faster rotation (super-rotation) of the inner

core. This was drawn to attention by the model

of Glatzmaier and Roberts (1995a,b) and seismo-

logical evidence was first presented by Song and

Richards (1996) (see also Section 17.9). The basis

of their observation is that the inner core is not

completely homogeneous and is anisotropic,

with an anisotropy axis close to but not coincid-

ing with the rotational axis, so that any rotation

of the inner core, relative to the mantle, gives a

time-dependence to the travel times of seismic

waves with paths that enter the core. The effect

is small and its interpretation requires detailed

information on the structure of the inner core.

The rate of relative rotation was estimated by

Song and Richards (1996) to be about 18/year,

comparable to the value for the Glatzmaier and

Roberts (1996a,b) model, although that varied

410 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

411

– [389–416] 13.3.2008 2:46PM

with time, as did the relative rotation for the

Kuang and Bloxham (1997) model. Further stud-

ies yielded both widely differing rotation rates

and refutations (Su et al., 1996; Creager, 1997;

Souriau et al., 1997; Laske and Masters, 2003). A

later, more secure estimate is 0.3 to 0.58/year

(Zhang et al., 2005).

Meanwhile, Buffett (1996) suggested that

inner core super-rotation might not be expected,

because of gravitational coupling to heterogene-

ities in the lower mantle. The idea is that the

gravity field of the heterogeneities would cause

the development of topography on the inner

core boundary and that this would be ‘locked’

to the gravity field that caused it. While it is

plausible that the gravitational torques would

be strong enough if such topography exists, its

development requires special conditions. If the

inner core, starting from nothing and growing at

0.3 mm/year (1200 km in 4 billion years), is rotat-

ing at (say) 0.58/year, it would have grown by

5 cm in radius in the 180 years required for a

908 rotation, and this is far too little to represent

significant topography. The rotation would smear

out any tendency to uneven growth at locations

fixed relative to the mantle. The required top-

ography could develop only if the inner core is

soft enough to deform in response to the gravita-

tional forces, which would then resist, but not

stop, the rotation, because the deformation

would continuously readjust, a process analo-

gous to tidal friction (Section 8.3). The possibility

of a drag by gravitational interaction with the

mantle threw a lifeline to Bullard’s notion of

coupling of the mantle to the deep core, allowing

rotation of the top of the core, relative to the

mantle, and therefore a westward drift, to persist

indefinitely. It appears that the top of the core

has been rotating more slowly than the mantle

for several hundred years, but that this is a con-

sequence of the coupling of the mantle to the

inner core and is probably not a permanent fea-

ture. The inner core is coupled to irregular

motion in the inner part of the outer core, so

that the westward drift may come and go accord-

ing to variations in the convective pattern very

deep in the core (see also Section 17.9).

Inner core rheology is important also to the

interpretation of its anisotropy, which Yoshida

et al. (1996) explained by preferential deposition

of solid in equatorial regions and anelastic relax-

ation of the inner core towards equilibrium

ellipticity. The anisotropy is due to crystalline

alignment caused by the continuing slow defor-

mation. This means that the inner core is contin-

uously relaxing from a state of excess ellipticity.

If the excess can be reliably observed then the

relaxation time and the implied viscosity can be

estimated. Such an estimate would impose a

tight constraint on the theory of gravitational

locking (Buffett, 1997).

We are led to a tentative conclusion that the

relative motion of the inner core and mantle is

variable but that ‘super-rotation’ predominates.

Nevertheless, gravitational coupling may exert a

drag on the inner core rotation and provide a

torque on the mantle sufficient to allow a persis-

tent westward drift in spite of the opposite elec-

tromagnetic torque imposed by the top of the

core. If this is so, then it raises doubt about the

validity of the core–mantle coupling coefficient

(Eq. (7.33)), which assumes only electromagnetic

coupling of the core and mantle.

24.7 Dynamo energy and the

toroidal field

In Section 24.2 we suggest that the rms strength

of the poloidal field in the core is about

11.8 10

nT. This corresponds to a magnetic

energy density

ðE=VÞ

Poloidal

¼ B

=2

¼ 0:55 J m

3

: (24:47)

For any plausible speed of core motion, this is

much greater than the kinetic energy,

ðE=VÞ

Kinetic

¼ v

=2 ¼ 8  10

4

3

; (24:48)

assuming  ¼10

kg m

3

and v ¼4 10

4

1

If the energy of the toroidal field is added,

the difference is even greater. These numbers

demonstrate that mechanical inertia has little

influence on the dynamo mechanism and that

the inertia of the system is due to the magnetic

field (a magnetic field imparts inertia to the elec-

tric current producing it). The convective forces

driving core motion work directly against the

24.7 DYNAMO ENERGY AND THE TOROIDAL FIELD 411

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

412

– [389–416] 13.3.2008 2:46PM

magnetic forces and kinetic energy is irrelevant.

Also, the molecular viscosity is very low, allow-

ing us to conclude that the convective energy

calculated in Section 22.7 is converted almost

entirely to magnetic energy, which is dissipated

by ohmic heating, with no other limitation or

inefficiency. Thus, by subtracting the ohmic dis-

sipation by the poloidal field from the estimated

total convective power, we have an estimate of

the dissipation by the toroidal field. From this we

can estimate the ratio of toroidal to poloidal field

strengths.

Consider first a current of uniform density i

circulating about the magnetic axis in a sphere of

radius a. Its dipole moment is (Problem 24.2)

m ¼

i: (24:49)

If we take a as the core radius with m given by

Eq. (24.2), then we require i ¼ 4: 3  10

4

2

The ohmic dissipation is i

=

per unit volume,

that is the total dipole field dissipation is





Dipole



256



¼ 1:3  10

W: ð24:50Þ

We can use this as a guide to the total dissipation.

The spectrum of the field, as represented

by Fig. 24.2, leads to the conclusion that the

rms field strength of all harmonic components

of degree l, taken together, is independent of l

up to a limit which we assess as l

max

¼136. If

the higher degree components were identified

with independent current loops of correspond-

ing sizes, then the required currents would be

inversely proportional to loop size. But this is not

relevant. The current loops are linked in a net-

work, with a continuity of magnetic flux passing

between them. The field at any point is due not

just to an adjacent loop, but to an inseparable

combination of them all, with flux paths having

some resemblance to the domains in ferromag-

netic material (Section 25.2). The result is that

a white field spectrum is produced by a white

current spectrum. So, we assume the rms cur-

rent density, and therefore ohmic dissipation,

by harmonics of degree l to be independent of

l for l 2.

The dipole field is stronger than the trend of

the other harmonics in Fig. 24.2 and Eq. (24.24)

by a factor of about 6 in spectral energy (or

ﬃﬃﬃ

rms field strength). If the rms current density is

the same for all higher harmonics, they each

dissipate 2.5 10

W. If there is a total of n har-

monics, the total dissipation is





Poloidal

¼



Dipole

1 þ

n  1



¼ 2:6  10

W; ð24 :51Þ

where n ¼136 is adopted from Section 24.2.

If the toroidal field is about ten times as strong

as the observed poloidal field, making it about

5 10

nT (5 mT), it is comparable to the esti-

mate of the radial field at the inner core boun-

dary, 7.2 10

nT, by Mathews et al. (2002) from

the electromagnetic coupling required to

explain observations of nutations. Oscillatory

motions of the Earth driven by gravitational

interactions with other bodies, termed nuta-

tions, have amplitudes and phases that are

influenced by the internal motions that they

cause. As an example, the nutation accompany-

ing precession is referred to in Section 7.2 and

indicated in Fig. 7.6. The flux linkage between

the inner and outer cores must be dominated

by the toroidal field, which has, at that level,

strong radial components penetrating the inner

core. This is to be expected because the inner

core is a slightly better conductor than the outer

core and would carry the necessary currents.

Thus, the nutation calculations indicate a toroi-

dalfield10timesasstrongasthepoloidalfield,

implying ohmic dissipation 100 times as great,

that is 3 10

W. This is the dynamo power

requirement assumed i n Section 21.4.

It remains to re-examine the role of preces-

sion as a core energy source. In Section 22.7 we

mention the estimate of the present energy dis-

sipation in the core by precessional torques,

6 10

W. This is lost in the uncertainties in

our calculation of core energy, but that may

have been less true in the remote past, when

the Moon was closer and the Earth was rotating

faster and so was more elliptical. Our reason for

re-opening the question here is to assess the

412 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

413

– [389–416] 13.3.2008 2:46PM

plausibility of a significant energy contribution

to the dynamo early in the life of the Earth.

First, we consider the present situation, fol-

lowing some of the arguments of Stacey (1973).

The rate of change in the orientation of the

Earth’s rotational axis on its precessional path is

2p sin /,where ¼23.458 is the angle between

the rotational axis and the ecliptic pole, around

which it rotates in a period  ¼25 800 years. The

core axis must keep up with this, but only

the necessary torque comes from the lunar and

solar gravitational interactions, because the core

is denser and therefore less elliptical than the

Earth as a whole. So, core–mantle interaction

must provide a torque sufficient to change the

orientation of the angular momentum axis of

the core at a rate

0:25  2p sin = ¼ 7:7  10

13

rad s

1

: (24:52)

If the core rotation axis is left behind by an angle

 then its rotation is misaligned by this angle

relative to the symmetry axis of the cavity. The

mantle exerts a precessional torque on the core,

in the manner of Toomre’s marble analogy in

Section 7.5, and the angular rate of its preces-

sional motion is fe!, where e ¼2.45 10

3

is the

ellipticity of the cavity, ! is the rotation rate and

f 0.7 is a factor to allow for the elastic distortion

of the cavity. We assume this to have the same

value as the factor f in Eq. (7.24) that accounts for

the lengthening of the Chandler wobble period.

This motion causes the core axis to move to a

wider angle of precession, as in Fig. 7.6, with 

self adjusted so that the torque exerted by the

mantle makes up for the deficiency in the luni-

solar torques. The two axes precess together,

separated by the small angle . Thus

fe! ¼ 7:7  10

13

rad s

1

; (24:53)

requiring

 ¼ 6:1  10

6

rad: (24:54)

Equation (24.54) gives the misalignment of

the core and mantle axes with the assumption

that the coupling is entirely inertial. The dissipa-

tion implied by this angle if electromagnetic

coupling is superimposed is

dE=dt ¼ K

ð!Þ

¼ 6:4  10

W; (24:55)

where K

is the coupling coefficient given by

Eq. (7.33). The addition of dissipative coupling

introduces the lag angle d in Fig. 7.6. It is

essential to the argument that the coupling is

mainly inertial because, if it were entirely dis-

sipative, the angular separation of axes would

be much larger and cause dissipation of about

8 terawatts.

Now we are in a position to assess the effect

of faster early precession. By Eq. (7.11), the angu-

lar rate of precession, O, varies as (C A)/R

where R is the distance to the Moon and (C A)

/ !

. Thus O / !/R

and the product (fe! )in

Eq. (24.53) is increased by this factor. But, like

(C A), e is proportional to !

, so, with f assumed

to be constant, !

 / !/R

,or

! / 1=!R

: (24:56)

Then, by Eq. (24.55), the dissipation varies as

1/!

. We do not need to consider the Moon

to be closer than 30 Earth radii (half of the

present distance). With conservation of angular

momentum in the Earth–Moon system, this

means a 10 hour rotation period, that is !

greater than at present by a factor 2.4. With

these numbers, the dissipation in Eq. (24.55)

would be increased by a factor 11 to about

7 10

W. Bearing in mind that this is mechan-

ical, not thermal, energy, it is big enough to be

interesting. Precession could have provided a

significant contribution to dynamo power

early in the life of the Earth, when the inner

core was small, or non-existent, and composi-

tional convection ineffective, although some

ohmic dissipation would have occurred in the

mantle.

The westward drift has sometimes been attrib-

uted to the small angular difference between

the core and mantle rotational axes, but the

value of  in Eq. (24.54) is quite inadequate.

The equilibrium difference between the rotation

rates is D!/! ¼1 cos 

/2 ¼2 10

11

, giving

D! ¼1.5 10

15

rad s

1

¼2.7 10

6

degrees/

year. A westward drift of 0.28/year would require

 ¼0.18 and then Eq. (24.55) would give an

energy dissipation of 5 10

24.7 DYNAMO ENERGY AND THE TOROIDAL FIELD 413

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

414

– [389–416] 13.3.2008 2:46PM

24.8 Magnetic fields of other planets

Magnetic fields have been sought on the Moon

and planets (Table 24.2). The giant planets all

have active dynamos, made possible by the con-

version of their light gaseous components to

metallic forms by the very high internal pres-

sures. Table 24.2 lists estimated dipole moments

and corresponding mean surface field strengths,

but in several cases, especially Uranus and

Neptune, the field is far from dipolar and these

numbers must be taken as no more than an

indication. Among the terrestrial planets, and

including the Moon, the Earth is exceptional.

Their fields are all much weaker and, with the

probable exception of Mercury, require no

appeal to currently active dynamos, but are

apparently due to magnetizations of their crusts

by former fields. In the case of Venus, the crust is

too hot to retain magnetic remanence, and it

probably has no field at all. Mars is an oxidized

planet with a high iron oxide content of its crust.

It has a strong crustal magnetization, giving an

irregular field for which the estimated dipole

moment is irrelevant as there is evidently no

dynamo. The magnetic pattern is apparent at

satellite altitudes and includes magnetic stripes

(Connerney et al., 1999), apparently similar to

those on the ocean floors. This is intriguing

evidence not just of an early dynamo, now extin-

guished, but also of magnetic reversals and man-

tle convection of plate tectonic form. All of the

terrestrial planets and the Moon have cores that

are still at least partly liquid and they would

almost certainly have had dynamos early in

their lives, a conclusion reached by Stevenson

(2003) in a review of planetary magnetism.

The magnetic field of Mercury is of particular

interest and merits more detailed attention. Its

strength is in the middle of the range of the

planetary fields, being much stronger than the

fields of the planets that clearly lack dynamos

but very weak compared with the fields of the

Earth and giant planets that certainly have dyna-

mos. The evidence that the large core of Mercury

is still at least partly liquid (Margot et al., 2007)

allows the possibility of an active dynamo, but an

explanation in terms of crustal magnetization

has not been totally abandoned (Aharonson

et al., 2004). The hypothesis that the field is a

fossil relic of an early dynamo faces several diffi-

culties. First, there is the problem that a uniform

crust magnetized by an internal dipole would

itself have no dipole moment. The magnetiza-

tion of the equatorial crust would be opposite

to that in the polar regions and precisely cancel

it. But, on a planet so close to the Sun, the crust

would not be magnetically homogeneous. The

equatorial crust would be hot, possibly suffi-

ciently so to demagnetize it thermally over geo-

logical time, leaving the polar regions to give a

net dipole moment. Even so, the field strength

is high enough to demand abnormally mag-

netic rock, or else a remarkably strong former

dynamo. Mars has a strongly magnetic crust but

its field is very weak compared with that of

Mercury, and Mercury is evidently in a reduced

state with little iron oxide in its mantle or crust.

Moreover, we could hardly expect the field to

remain as a steady dipole, systematically mag-

netizing the whole crust over a very long time. It

would have drifted and probably reversed, giving

scattered magnetization, as seen on Mars. Thus,

crustal magnetization cannot be regarded as a

serious candidate source for the field of Mercury.

We now consider the energy implications

of a currently active dynamo in Mercury. Being

a small planet, with gravity correspondingly

Table 24.2 Magnetic fields of planets. Data

from Ness (1994) with a later revision for

Mars

Planet

Dipole

moment

(Am

) Dynamo?

Surface field

(nT)

Mercury 5 10

Probably 475

Venus <4 10

No <2.5

Earth 8 10

Yes 41 455

Moon <1 10

No <0.26

Mars 1 10

No 3.5

Jupiter 1.6 10

Yes 650 000

Saturn 4.7 10

Yes 32 850

Uranus 3.8 10

Yes 32 170

Neptune 2.0 10

Yes 18 560

414 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

415

– [389–416] 13.3.2008 2:46PM

weaker than in the Earth, the thermodynamic

efficiency of thermal convection is lower, as is

also the energy that might be available from

compositional separation. There is, however, a

compensating advantage: it means a smaller

adiabatic temperature gradient and less conduc-

tive heat loss. We can examine the balance of

these effects by adjusting the core analysis in

Sections 21.4, 22.6 and 22.7 to parameters appro-

priate to the core of Mercury. To focus on a

plausible situation we adopt a Mercury core

model investigated by Stanley et al. (2005), with

an inner core that has grown to 0.8 of the core

radius. This has the advantage that, if composi-

tional convection still operates, it maximizes the

ratio of compositional to thermal energies,

allowing for dynamo action with a minimum

cooling rate (as pointed out for the Earth’s core

in Section 22.7). We may wonder whether, at

such an advanced stage of inner core develop-

ment (55% of the core mass solidified), the outer

core can still accommodate more rejected solute.

But we find that, if it does so, then what Stanley

et al. (2005) refer to as a thin shell dynamo is

energetically viable.

Using the model of Mercury in Table 1.2,

with the core equation of state parameters

in Table 5 of Stacey and Davis (2004), the core

properties at the core–mantle boundary pressure

of Mercury (6.8 GPa) are:  ¼1.74, K

¼158 GPa,

g ¼4.09 m s

2

,  ¼6890 kg m

3

and T ¼2200 K

(by adiabatic extrapolation from the melting

point at the inner core boundary, 383 km deeper).

Applying these values to Eq. (19.55), we estimate

the adiabatic temperature variation at the top of

thecoretobedT/dz ¼6.83 10

4

1

. We need

to estimate also the thermal conductivity, by

applying the Wiedemann–Franz law (Eq. (19.63)),

as in the case of the Earth’s core (Section 24.4). At

the lower pressure of Mercury the modification of

electron band structure by pressure is much less

than in the case of the Earth and, for pure iron,

the resistivity is nearer to the zero pressure liquid

iron value (1.35 mO m). With a small pressure

effect and adding impurity resistivity, as for the

Earth’s core, a calculation similar to that in

Section 24.4 gives 2.4 mO m for the Mercury core,

making it a slightly better electrical conductor

than the Earth’s core. But, in calculating the

thermal conductivity by Eq. (19.63), the lower

temperature in Mercury more than compensates

for this difference and, with a small lattice con-

tribution we estimate  ¼25 W m

1

.With

this value we calculate the conducted heat flux

at the top of the core:

dQ =dt ¼ 4pr

dT=dz ¼ 7:85  10

W: (24:57)

As in the Earth, the conducted heat is a base

load on core energy sources. It amounts to

1.1 10

J over 4.5 10

years. We can compare

this number with the heat provided by core cool-

ing and latent heat of inner core solidification,

ignoring for the moment the possibilities of com-

positional convection and radiogenic heat. The

calculation is essentially the same as that for the

Earth in Section 21.3, replacing the numbers

with those appropriate for Mercury. The specific

heat of Mercury’s core is somewhat smaller

than for the Earth’s core because, at the lower

temperature, there is a smaller electron contri-

bution, although the density of electron states

is higher at the lower pressure (Eq. (19.17)). Also,

in the smaller planet, less gravitational energy

is released by contraction. Allowing for these

effects, referred to the core–mantle boundary

temperature as the core cools adiabatically,

the effective heat capacity, that is the heat

lost per degree cooling of the boundary, is

2.3 10

1

. By an analysis similar to that for

the Earth’s core, leading to Eq. (21.19), the cor-

e–mantle boundary temperature drop accompa-

nying development of the inner core to 0.8 core

radii is 185 K, giving a heat release of 4.3 10

To this we add the latent heat of solidification by

Eq. (21.11). The inner core mass, 1.24 10

kg,

is assumed to have the same mean atomic

weight as the Earth’s inner core (m ¼50.16),

so that n ¼2.47 10

. The temperature at

the solidifying interfa ce varies from 3020 K

to 2430 K as the inner core grows and the

weighted average is close to the simple aver-

age, 2700 K. Using the Gr ¨uneisen parameter

(Eq. (19.1)) to calculate the K

term, and

Eq. (19.54) for the volume change accompany-

ing solidification, we estimate the latent he at

release to be

L ¼ T

nR ln 2ð1 þ 2T

Þ¼5:1  10

J; (24:58)

24.8 MAGNETIC FIELDS OF OTHER PLANETS 415

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

416

– [389–416] 13.3.2008 2:46PM

making the total heat release by cooling and

freezing 9.4 10

We see that, with no allowance for composi-

tional separation or radiogenic heat, the heat

released during inner core formation does not

fall far short of the conducted heat in the life of

the planet. It is a much larger fraction of the

conducted heat than in the case of the Earth’s

core but, of course, that is a consequence of the

fact that the Earth’s inner core is only 5% of

the total core mass, whereas for Mercury we

are considering 55%. Thus, a dynamo driven ther-

mally, with an inner core age significantly less

than that of the planet, is plausible. Although the

average thermodynamic efficiency is modest

(7%), so is the energy demand by the weak

dynamo. Compositional separation may also

have a role, although we suggest in Section 1.14

that, since Mercury is a reduced planet, we would

not expect a large oxygen content in its core. But a

modest compositional energy would permit con-

sideration of an inner core no younger than the

planet and still allow a weak dynamo. Planetary

dynamos are generally be lieved to require

rotation and the rotation of Mercury is very

slow, but we may wonder whether, in spite

of conventional disbelief, the solar tide has a

role. T he orbit of Mercury is very elliptical

(e ¼0.2056) and gives a strong 88 day radial

tide that takes effect as a modulation of the

176 day angular tide. Although we still know

rather little about Mercury, we conclude that

its magnetic field is most plausibly a ttributed

to a core dynamo.

The magnetizations of meteorites, and by

inference of the asteroids, are discussed in

Section 1.11. They are attributed to a former

strong solar magnetic field. Mention should

be made also of evidence for fields on Jupiter’s

satellite Ganymede and on the asteroids Gaspra

and Ida, but these remain to be interpreted.

Magnetic fields are ubiquitous, not just in the

Solar System but in the Universe generally.

Magnetohydrodynamic action occurs spontane-

ously in any conductor that is large enough and

has sufficient vorticity in its internal motion.

416 THE GEOMAGNETIC FIELD