Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

377

– [376–388] 13.3.2008 10:47AM

simple empirical expression to represent their

combined effect as a function of lithospheric

age. This is a subject of Section 23.2, in which

we show that a simple dimensional analysis indi-

cates that there is no systematic variation in

plate size with time or average convective

speed (Eq. (23.5)). This is not an intuitively

obvious result, but, as we point out in that sec-

tion, there appears to be no contradictory

evidence.

Returning to the problem of rheological con-

trol, the basic equation is Eq. (10.27), in which

the exponent n is unknown. Favoured values are

n ¼1 (linear rheology) and n ¼3 (non-linear) and

opinions differ over which is the more appropri-

ate value for the mantle. We examine both alter-

natives, but the problem of choosing a value of n

is compounded with the uncertainty over the

value of the parameter g, which is a measure of

the activation energy of creep. Together they

control the cooling rate, that is, the difference

between the heat loss and radiogenic heat, so we

treat them both as unknown and use the present

radiogenic heat,

, as a controlled variable to

investigate the relationship between them and

the cooling history.

The continental crust, which is rich in radio-

active elements, has grown with time and its

separation from the mantle has progressively

reduced the mantle content of these elements.

We assume that this differentiation process has

occurred at a rate proportional to the speed of

convection, and therefore to the rate of mantle

heat loss, being much slower now than several

billion years ago. In integrating the heat balance

equation (Eq. (23.14)) backwards in time, we

return the continental crust progressively to

the mantle. This has two effects. It gives an

increase in the mantle radiogenic heat, addi-

tional to the time-dependence arising from

radioactive decay, and it increases the surface

area of oceanic lithosphere by progressively

removing the continents.

Now we mention two effects that we do not

consider important and do not include in our

analysis for reasons that we explain: the loss of

mantle volatiles and latent heat of lava solidifi-

cation at ocean ridges. The significance of vola-

tile loss is that volatiles reduce viscosity (Fig. 2.3).

If this were important to mantle rheology it

could be allowed for by varying the activation

energy for creep in Eq. (10.22) by making the

parameter g a function of time or of integrated

heat loss. Such a calculation reverses the thermal

history: the mantle would be heating up. If this

effect exists it must be exceedingly small. From

the water contents of hot spot (plume) basalts,

referred to in Section 2.11, the mantle appears

still to hold at least half of its early inventory of

volatiles, and their weakening effect occurs at

small concentrations and is little affected by fur-

ther additions. The latent heat question is really

asking: are we correctly calculating the very

early heat loss at ocean ridges? As considered in

the following section, the total heat lost by the

oceanic lithosphere in its surface lifetime is

about 2.9 10

2

and dwarfs the latent heat

of any plausible depth of lava. Ridge lava poses

an interesting question of detail on ridge behav-

iour but does not materially affect the thermal

history of the mantle.

The core cooling history presents a com-

pletely different set of problems, a central one

being the question of its radioactivity. This has

been a subject of debate for several decades.

Section 2.8 summarizes the chemical arguments

and Stacey and Loper (2007) re-examine the phys-

ical argument. The case for radiogenic heat

arises from the conductive heat loss and there-

fore depends on core conductivity (Section 19.6),

which is calculated from the electrical con-

ductivity. The preferred model adopted in

Sections 21.4 and 22.7 has a small heat contribu-

tion by

K (0.2 terawatt at the present time) and

Section 23.5 examines the implications for core

cooling.

The extrapolation of the thermal regime of

the Earth back to about 4.5 billion years, as pre-

sented in this chapter, is based on physical pro-

cesses that are assumed to be smooth and

continuous. The starting point is an Earth that

has stabilized, following accretion and settling

out of the core, with a fully solidified mantle and

excess accretion energy lost to space. We reach

some robust conclusions that hardly depend on

assumptions. In particular, the thermal history is

virtually the same, whether linear or non-linear

rheology is assumed, and, although the cooling

23 . 1 P R EA M B LE 377

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

378

– [376–388] 13.3.2008 10:47AM

rate depends on what is assumed about the

radioactive content of the Earth, the surface

heat flux for the last four billion years hardly

does so.

23.2 The rate of heat transfer

to the oceans

The purpose of this section is to relate the ocean

floor heat flux to the speed of the mantle con-

vection that delivers this heat. The relationship

allows us to substitute heat flux for the convec-

tive strain rate in the creep law (Eq. (10.27)) and

so relate it to mantle temperature.

Approximately 3.4 km

/year of new ocean

lithosphere is produced at the ocean ridges

and, of course, the same area disappears at sub-

duction zones. With the total oceanic area of

3.1 10

the mean surface lifetime is 91

million years. Combining this with the average

heat flux from ocean floors, 0.101 W m

2

(Pollack et al., 1993), the average heat release

by oceanic lithosphere in its surface lifetime is

the product of these numbers, 2.9 10

2

The heat is transferred to the sea by a combina-

tion of thermal diffusion and hydrothermal

circulation and observations indicate that

hydrothermal cooling has more or less shut

down by the time the lithosphere has reached

an age of 50 or 70 million years, although we

suggest that internal hydrothermal circulation

may continue. The inference is that the sea

floor cracks, through which the water circul-

ates, become choked with sediment and this

must be at least partly true, but there is another

mechanism. As the lithosphere ages, so the

depth from which the water must draw heat

increases, reducing the temperature gradient

driving the water circulation and increasing

the viscous drag on its flow in the cracks. At

the same time the diffusion of heat is reduced

by the hydrothermal cooling of shallow layers,

invalidating Eqs. (20.7) and (20.9). Having no

theory of the overall cooling process, we assume

a simple empirical relationship and adjust it to

match the observations of heat flow and ocean

depth discussed in Section 20.2.

The required relationship must give enhanced

heat flux from young lithosphere, relative to the

1/2

variation in Eq. (20.7), but still allow signifi-

cant heat from ageing lithosphere. We represent

the observations by a simple power law for the

average heat flux per unit area,

q / t

a

: (23:1)

This gives the integrated heat in the lithospheric

life-time, ,

Q / 

1a

: (23:2)

The selected value of a is a compromise between

conflicting requirements. We emphasize the sta-

bilization of the depth curve for old lithosphere,

which gives the integrated heat flux and is less

dependent on details of the cooling model than

is the heat flux itself. This requires 0.5 < a < 1.0,

and we choose a ¼2/3, so that (1 a) ¼1/3 in

Eq. (23.2). This is assumed in the calculations

that follow, but we emphasize that it is not a

theoretical result. It is a simple empirical fit to

present day data, which we assume to be valid

also in the distant past. The total heat, Q, takes

time  to pass into the sea, so the average rate is

Q ¼Q/ / 

2/3

. This is calibrated by the present

average ocean floor heat flux,

¼0.101 W m

2

for an average lithospheric lifetime, t

¼91 10

years (2.87 10

s), that is

Q / 

a

(23:3)

Q ¼



ðÞ

2=3

: (23:4)

We must relate  to the speed of convection

and for this it is necessary to know how the plate

size varies. At the present time there is a wide

range of both plate sizes and speeds. Carlson et al.

(1983) reported a correlation, such that speed

was roughly proportional to the square root of

age at subduction, as might be expected if speed is

proportional to shrinkage, and therefore to neg-

ative buoyancy, by the diffusive model. But such

an argument cannot be extended to a similar

relationship between average plate size and

speed in the past because, with a variable mantle

temperature and viscosity, there was no

378 THERMAL HISTORY

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

379

– [376–388] 13.3.2008 10:47AM

constant relationship between plate speed and

driving stress. However, we can establish a gen-

eral rule for average plate size by a series of

substitutions, (i) to (iv), of proportionalities

between the quantities involved. We consider

the general case of arbitrary a in Eqs. (23.1)

and (23.2).

(i) Start with 

a

Q by Eq. (23.3).

(ii) Substitute for

Q by using the thermody-

namic result, from Chapter 22, that

Q / 

because the dissipation (stress strain

rate) is related to convected heat by a con-

stant efficiency, independent of convective

speed.

(iii) Substitute  / Q, because the convective

stress is proportional to the cumulative

cooling of a slab, and then substitute for Q

by Eq. (23.2).

(iv) Take strain rate

" / v, the plate speed, and

then write v ¼L/, where the plate size, L,is

identified as the distance from ridge source

to subduction zone.

These give



a

Q / 

" / Q

" / 

1a

" / 

1a

/ 

1a

L =ðÞ/L

a

(23:5)

We see that, by this line of reasoning, L is inde-

pendent of t and therefore of convective speed.

Thus we can relate convective speed to the heat

flux,

" / v / 

1

11a=

(23:6)

Q /

2=3

(23:7)

This result depends on the analysis, summar-

ized by Eq. (23.5), leading to the conclusion that

the mean plate size has not varied. It requires the

mean plate speed to have been greater in the past

and we can consider the implications, and the

possibility that contradictory evidence will come

to light. With fixed plate size, Eq. (23.3) or (23.7)

gives speed proportional to

3/2

. By the cooling

history in Section 23.4, 10

years ago this quan-

tity would have been greater than at present by

the factor 1.25. If we consider just the last 180

million year record of ocean floor magnetic

stripes, the factor is 1.04. Plate speeds differ

from one another now by much more than this

and there is no prospect that paleomagnetism

would be able to distinguish such variations in

the average.

Equation (23.7) refers to the ocean floor

heat flux per unit area. The total oceanic heat

flux,

, is therefore related to the present value,

1;0

,by

1;0

ðÞð

23=

; (23: 8)

where f is the fraction of the surface area of

the Earth occupied by oceans and, from Pollack

et al. (1993), we take the present values to be

¼0.606 and

1;0

¼3.10 10

W, being 0.101

2

, less radiogenic heat of the ocean crust.

Subscript 1 is introduced because there is a sec-

ond component of the heat flux, through the

continents.

The heat flux from the continents is largely

due to crustal radioactivity, which must be dis-

counted in calculating the mantle cooling. We

estimate the total crustal radiogenic heat as

8.2 10

W. But there is also a flux of heat

through the continents from the mantle and in

Section 20.3 this is estimated to be 0.025 W m

2

Thus we add to Eq. (23.8) a second component of

the mantle heat loss, proportional to the fraction

(1  f) of the surface area A that is occupied by

continents,

¼ð1  f ÞA  0:025 W m

2

¼ 1:275  10

ð1  f ÞW: (23:9)

At the present time this is 11% of the total heat

flux from the Earth and the fraction decreases

backwards in time. For a reason considered in

Section 9.3, we make the simple assumption

that continental structure, in particular its

thickness, remains essentially the same through

time. This means that the area is proportional to

the total mass of continental material that has

accumulated and that the heat flux per unit area

through it from the mantle has varied rather

little, although its own radiogenic heat has

decreased with time. This is a simplifying

approximation, but it affects only a small com-

ponent of the heat flux. The total heat lost by the

23.2 THE RATE OF HEAT TRANSFER TO THE OCEANS 379

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

380

– [376–388] 13.3.2008 10:47AM

mantle is the sum of Eqs. (23.8) and (23.9), less a

steady component,

¼3.5 10

W, which we

attribute to the core and assume to be conveyed

to the surface by plumes operating independ-

ently of the plate tectonic mechanism of mantle

convection. Thus we write the mantle heat

loss as

Q ¼



: (23:10)

The fraction f of the surface area occupied by

oceans has decreased with time as continental

material separated from the mantle. This is a

consequence of convection and the rate has not

been constant with time. We assume that it has

been proportional to the rate of convective heat

transport from the mantle, that is, to

Q by

Eq. (23.10). This means that the area of the con-

tinents at any time is proportional to the inte-

grated heat flux since the origin of the Earth at

t ¼T. Thus we can write

1  fðÞ1  f

ðÞ¼1  fðÞ0:394 ¼

t

T

;



(23:11)

where Q

t

T

is the integrated mantle heat over

the period from T ¼4.5 10

years to t years

ago and superscript zero means t ¼0. But

T

¼ Q

t

T

þ Q

t

; so that Eq. (23.11) can be writ-

ten in a more convenient form:

¼ 1 þ

 1



t

T

¼ 1 þ 0:65

t

T

: (23:12)

The calculation is iterative because Q

T

is a prod-

uct of the calculation and is repeatedly adjusted

in seeking a solution. There is another role for

the factor f. The ratio (1 f)/(1 f

) is the fraction

of the present continental crust that has been

emplaced at any time. Thus the fraction still in

the mantle was

f  f

1  f

t

T

: (23:13)

This time-dependent fraction of the radiogenic

heat identified with the composition of the

present crust is added to the mantle radiogenic

heat. It means that we assume all of the radio-

genic heat to have been in the mantle 4.5 10

years ago.

23.3 The heat balance equation

and mantle rheology

The rate at which the mantle loses heat is the

difference between the heat lost to the surface,



, and radiogenic heating,

tðÞ. It is written

as a heat balance equation,



tðÞ



; (23:14)

where 

¼7.4 10

1

is the heat capacity,

defined as the heat lost per degree fall in the

potential temperature, T

, as in Section 21.3.

For this purpose the heat lost to the surface is

only the heat lost by the mantle and excludes

core heat, although the core heat is included in

the surface heat flux calculation in Section 23.2

and subtracted in Eq. (23.10). Without any

detailed knowledge of the two functions on

the right-hand side of Eq. (23.14), we have a

qualitative assessment of thermal history.

tðÞ

is a decreasing function of time, t, and



decreases as temperature falls, because it is con-

trolled by convection, which slows up as the

mantle stiffens. If we suppose the mantle to be

in thermal balance, with dT

/dt ¼0, then in the

moderately recent past

would have been

stronger and the mantle would have been heat-

ing up. Since, in that case, it would have been

cooler, the convected heat loss,

Q , would have

been smaller, reinforcing the temperature

change. By this hypothesis the Earth started

cool and has been heating up until now, making

the present time unique, with a cooler Earth in

both the past and the future. This is not plausi-

ble. The Earth started hot and, by Eq. (23.14), it is

still cooling and will continue to do so.

The function Q

(t) is a sum of the exponential

decays of the four thermally important isotopes

½f

expðl

tÞþf

expðl

tÞ

þf

expðl

tÞþf

expðl

tÞ; (23:15)

where f

, f

are the fractional contributions

to the present radiogenic heat,

, and t is time

relative to the present, that is negative for past

time. These fractions rely on an assessment of

composition. We assume the Th/U ratio to be 3.7

380 THERMAL HISTORY

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

381

– [376–388] 13.3.2008 10:47AM

for both the mantle and crust, but that the K/U

ratio is 2800 for the mantle but 13 000 for the

crust. With these relative concentrations and the

energies in Table 21.2 we obtain the fractional

contributions in Table 23.1. We do not have a

secure value for the present mantle radiogenic

heat,

. In the following section we adopt

20 10

W as a preferred value but investigate

the implications of alternatives. Equation (23.15)

applies also to the crust, with the alternative

fractions in Table 23.1 and

¼8.2 10

in this case. The crustal radioactivity is progres-

sively added to the mantle in the backwards

integration, according to Eq. (23.13).

Now we consider the second term on the right-

hand side of Eq. (23.14), that is the mantle heat

loss. The present value,

, is the total rate of heat

loss by the Earth, 44.2 10

W, less 8.2 10

of crustal radiogenic heat and 3.5 10

Wof

core heat, as discussed in Section 23.5, leaving

¼32.5 10

W (Table 21.4). Fortuitously, this

almost coincides with the ocean floor heat flux, as

reported by Pollack et al. (1993), with near cancel-

lation of the core heat conveyed to the ocean

floors and mantle heat conducted through the

continents. With substitutions for

and

Eq. (23.8) and (23.9) and f/f

by Eq. (23.12) or

(23.13), Eq. (23.10) gives

ðÞ¼

1 þ 0:65

t

T



2=3

1 

t

T





(23:16)

To use Eq. ((23.16)), we need another relation-

ship between

Q and

". This is obtained by

combining the creep law (Eq. (10.27)) with pro-

portionality (ii) in Eq. (23.5), that is

Q / 

rewritten as







: (23:17)

In Eq. (10.27) B is constant and although  varies

with depth its variation with time (or temper-

ature) is slight enough to neglect, so the equation

can be rewritten relative to present conditions

(subscripted zero),





exp gT





; (23:18)

where T is understood to be T

and T

¼1700 K is

its present value. Combined with Eq. (23.17) this

gives



nþ1

exp gT





; (23:19)

which we use to substitute for

Þð in

Eq. (23.16) by rewriting as



2=3

2n=3 nþ1ðÞ

exp

2gT

3 n þ 1ðÞ





;

(23:20)

so that

Q ¼

1 þ 0:65

t

T



3 nþ1ðÞ

exp

2gT

3 n þ 1ðÞ







1þ

t

T





: ð23:21Þ

This is the equation for

ðÞrequired in

Eq. (23.14). Together with the relationship for

mantle radiogenic heat, with component 1 for

the present mantle composition and 2 for the

present crust, which is progressively added to

the mantle in the backward integration

t

T

; (23:22)

it allows Eq. (23.4) to be integrated numerically.

For each of a range of values of

, and n ¼1

or n ¼3, Eq. (23.14) is integrated to find

(by iteration) values of the parameter g in

Table 23.1 Fractions of present radiogenic

heat attributed to four isotopes

Isotope

Decay constant

l (year

1

)

Mantle

heat

fraction

Crustal

heat

fraction

238

U 1.551 25 10

10

0.4566 0.3892

235

U 9.8485 10

10

0.0197 0.0167

232

Th 4.9475 10

11

0.4763 0.4062

K 5.544 10

10

0.0474 0.1878

23.3 THE HEAT BALANCE EQUATION AND MANTLE RHEOLOGY 381

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

382

– [376–388] 13.3.2008 10:47AM

Eq. (23.21) that give an extrapolation back to

¼2399 K at t ¼4.5 10

years. This is

the assumed starting temperature, constrained

by matching it to the mantle solidus at the

core–mantle boundary, where it is assumed to

coincide with the core temperature at that

time. The results are plotted in Fig. 23.1. We

need to note that we are using a creep equation

that applies to material at a specified temper-

ature with an identifiable melting point,

but both T and T

have wide ranges in the

mantle. We use the potential temperature, T

to represent the mantle as a whole, and no

error or difficulty would arise if the ratio of

temperature to melting point were the same

everywhere but that is not the case. The ratio

T/T

decreases with depth over most of the

mantle range and this is reflected in the viscosity

variation. So, we appeal to the concept of

averaged or notional values of both T and T

recognizing that this compromises the meaning

(and numerical value) of the parameter g in

Eqs. (10.27) and (23.21). But an exponential

dependence of rheology on temperature, as in

Eq. (10.27), is unavoidable, so, although we

cannot impose theoretical values of quantities

such as g or T

, we can reach some important

general conclusions that are not sensitive

to them.

23.4 Thermal history of the mantle

Integration of Eq. (23.14) requires an assumption

about starting conditions, that is, the notional

mantle temperature 4.5 10

years ago. The only

thing known for sure about conditions at that

time is that they were changing very rapidly and

simple extrapolations back from the present can-

not convey any information about the accretion

process. We are considering the evolution of the

Earth from the stage when it had stabilized suf-

ficiently for cooling to be controlled by convec-

tion in a solidified mantle, with no significant

continuing accretion, loss of volatiles to space or

extended separation of the core. The starting

point is assumed to be early enough for there

to be no thermal boundary layer at the base of

the mantle, attributable to greater cooling of the

mantle than of the core. Thus, referred to the

core–mantle boundary temperature, core and

mantle thermal histories start from the same

Mantle heat flux

10 20 30

McDonough and Sun

29.5

Turcotte and Schubert

Mantle radiogenic heat (10

Laboratory range

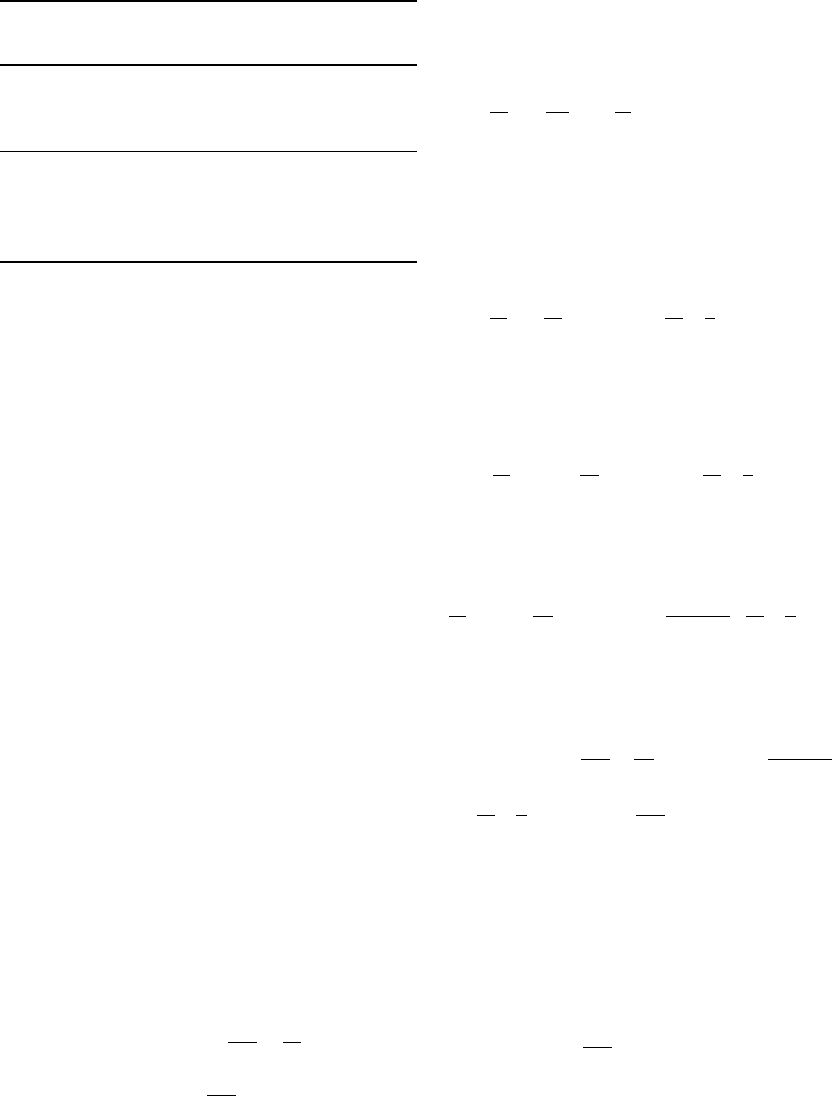
FI G U R E 23.1 Mutual dependence of

the mantle radiogenic heat,

, and

the rheological parameter, g, for two

values of n, n ¼1 for linear (Newtonian)

rheology and n ¼3 for non-linear

rheology. Values of

are indicated

for compositions by McDonough and

Sun (1995) and Turcotte and Schubert

(2002).

382 THERMAL HISTORY

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

383

– [376–388] 13.3.2008 10:47AM

point. A different assumption is possible. We

could suppose that the core retained more of

the accretion energy, and started much hotter

than the mantle, so that there would have been a

strong thermal boundary layer at the base of the

mantle from the beginning. However, in our

thermal history model the mantle starts at its

solidus temperature, so if the core were much

hotter it would have melted the mantle to a

considerable depth, allowing it to convect so

rapidly that the excess core heat would have

been quickly removed, bringing the Earth to

the starting point that we assume, with the man-

tle at its solidus temperature.

Core cooling (Section 23.5) is constrained by

the requirement that the inner core has existed

for most of the life of the Earth. By Eq. (21.14), this

means a decrease in core–mantle boundary (CMB)

temperature no more than 200 K. Since we argue

that the mantle has cooled by about 1000 K more

than this, it is useful to have some corroboration

of the slow CMB cooling. In a consideration of

melting points of mantle minerals, Boehler

(2000) concluded that ‘The extrapolated solidus

of the lower mantle intersects the geotherm at

the core–mantle boundary ...’. He pointed out

that this is consistent with the identification of

ultra low velocity zones (ULVZs) at the base of the

mantle as pockets of partial melt. The enormous

accretion energy (Table 21.1) ensured that the

Earth started hot, but any molten stage would

have lost heat very rapidly, leaving the mantle

at its solidus temperature, which is therefore

the starting point for convective cooling con-

trolled by solid state creep (Eq. 10.27). Thus

Boehler’s conclusion invites the supposition that

the core–mantle boundary has not cooled at all.

But a growing inner core, so important to the

dynamo (Section 22.7), disallows this. Mao et al.

(2006) presented an alternative explanation for

ULVZs. They observed that the post-perovskite

phase (ppv), to which perovskite is converted at

the base of the mantle, readily absorbs iron and

that iron-rich ppv has acoustic velocities compat-

ible with ULVZs, without appealing to partial

melting. We suppose that heterogeneities in the

mantle, especially in the D

layer at its base, give a

range of solidus temperatures and that a better

average value to assume for the starting point of

the mantle cooling calculation is 100 K to 200 K

higher than the present CMB temperature.

Taking this to be 3931 K and extrapolating adia-

batically to P ¼0, we have an initial mantle poten-

tial temperature, T

¼2399 K. This is a notional

temperature for the application of Eqs. (10.27)

and (23.14) to the mantle as a whole. It is also

the notional melting point for the purpose of

these equations, that is we assume the mantle to

start at its melting point. In Eq. (23.21) we see that

this is not a critical assumption because T

appears in a single adjustable constant with the

rheological parameters g and n, which are not

well constrained.

We treat the parameters n and g in Eqs. (10.27)

and (23.21) and

in Eq. (23.15) as adjustable,

but they are related in the sense that if one is

fixed then integration of the model to the

assumed starting conditions at t ¼4.5 10

years constrains the others. Geochemical argu-

ments, largely derived from observed radio-

activity in meteorites and in the crust, favour

 20  10

W. This is the value obtained

from the pyrolite model of McDonough and

Sun (1995). We adopt it for our preferred

model, although we argue for a different K/U

ratio (Table 23.1) so the assumption is rather

arbitrary. We note the much higher estimate of

the mantle content of radioactive isotopes

quoted by Turcotte and Schubert (2002, Table

4.2, p. 137), 29.5 10

W, and consider both

this case and an intermediate value, 24 10

W, as alternatives to the preferred model.

The mutual constraint on values of

, n and

g is illustrated by Fig. 23.1. The first thing to

notice is that the value of n makes little differ-

ence to the relationship between

and g. For

both n ¼1 and n ¼3, if g is within the range of

laboratory observations, then

must have a

high value, quite close to the present mantle

heat loss,

¼ 32: 5  10

W, making the

present cooling rate very slow with very rapid

early cooling. Much smaller values of g are

required if the radiogenic heat comes within

the range of the geochemical estimates. Neither

of the estimates of radiogenic heat marked on

Fig. 23.1 can be regarded as secure, which is the

reason for considering also the intermediate

value, 24 10

23.4 THERMAL HISTORY OF THE MANTLE 383

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

384

– [376–388] 13.3.2008 10:47AM

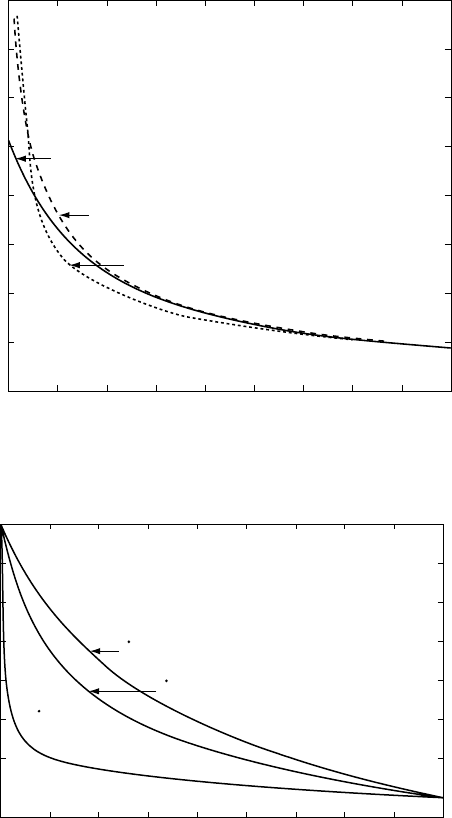
Figure 23.2 is a plot of the variation with time

of the total heat flux from the Earth for the three

models. On this scale the differences between

plots for n ¼1 and n ¼3 do not show and for

most of the life of the Earth the heat loss curves

are not very different. The big difference occurs

only in the first 100 million years. This is a con-

sequence of the constraint imposed by matching

the models to the present rate of heat loss,

44.2 10

W. The temperature curves (Fig. 23.3)

differ according to the fraction of the heat

loss that is made up by radioactivity, but in this

case also the n ¼1 and n ¼3 curves differ too

little to show separately. For the 29.5 10

model the present mantle cooling rate is 10 K/

billion years, corresponding to 16 K/billion years

at the core–mantle boundary, less than the esti-

mated core cooling rate. This appears unlikely

because the mantle must have cooled faster than

the core to allow any core cooling at all, and so

far as we understand the mechanism this trend

would not have reversed. We consider the

1.02.03.0

Time before present (10

years)

4.0

= 29.5 x 10

Global heat flux (10

24 x 10

x 10

FI G U R E 23.2 The geothermal flux for three

values of mantle radiogenic heat. This is the

total, with crust and core heat added to the

mantle heat flux. Differences between curves

for alternative values of n are not noticeable

on this scale. The rate of heat loss is not very

dependent on parameters of the cooling

theory for most of the life of the Earth. The

major difference occurs very early.

2400

1800

2000

2200

1.02.03.04.0

Mantle potential temperature (K)

Time before present (10

)

29.5

x 10

Mantle cooling (right hand scale)

FI G U R E 23.3 Mantle temperature

variation as a function of time for three

values of radiogenic heat. Rapid early

cooling is a feature of all models, more so

for those with stronger radioactive heating.

384 THERMAL HISTORY

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

385

– [376–388] 13.3.2008 10:47AM

24 10

W model to represent an upper bound

on mantle radiogenic heat. For this, and the pre-

ferred 20 10

W model, the cooling curves of

Fig. 23.3 are not very different and offer nothing

that would distinguish them observationally.

We note from Fig. 23.1 that the preferred

model requires a value of g differing by a factor

of two from the laboratory range, and accept that

the laboratory values are not appropriate to the

application of Eq. (10.27) to the mantle as a

whole. This is not surprising, as the model

assumes a uniform homologous temperature,

T/T

, although it varies with depth. A more

complete model might allow for this, but we

see that it would have little influence on the

conclusions. In Eq. (23.21) T

is coupled with g

and n in a composite parameter, 2gT

/3(n þ1),

and does not enter the calculations independ-

ently. Uncertainties in g and n are certainly

greater than the uncertainty in T

and, as

Fig. 23.1 illustrates, the essential conclusions of

the cooling model hardly depend on the value of

n. They are, therefore, not very dependent on the

naivety of the assumption about T

. Although

details are uncertain, we see in these models

common features that we regard as secure.

Mantle convection governed by an exponential

dependence of viscosity on temperature, as in

Eq. (10.27), gives a plausible thermal history

that is almost independent of whether the rheol-

ogy is linear or non-linear. The rate of terrestrial

heat loss depends significantly on the assumed

radiogenic heat only in the first 10

years or so,

when validity of the model can be questioned

anyway. For all models early cooling is fastest,

giving a substantial thermal boundary layer at

the base of the mantle for most of the life of the

Earth. Mantle radiogenic heat is not well deter-

mined, but the preferred estimate, 20 10

is unlikely to err by more than 4 10

W. If we

specify both the present rate of heat loss and

radiogenic heat then the thermal history follows

almost independently of assumptions about

physical properties. The essential physics is

embodied in the two obvious principles, strongly

temperature-dependent rheology and decaying

radiogenic heat, with little ambiguity in the tem-

perature variation and virtually none in the ter-

restrial heat flux.

Table 23.2 summarizes numerical details of the

preferred model, with 20 10

W of mantle radio-

genic heat and a core heat loss of 3.5 10

as discussed in Section 23.5. This extends some

of the discussion in Chapter 21, in which it is

pointed out that radiogenic heat accounts for

little more than half of the total heat loss in the

life of the Earth (Table 21.1). The fraction of the

Earth’s heat loss that is attributed to radioactiv-

ity is known as the Urey ratio. Its present value,

for our model, is 0.64. Over the life of the Earth

the ratio is 0.57, so it has varied rather little. The

longevity of

232

Th ensures that in the distant

future it dominates the radiogenic heat and it

may be surprising that the radiogenic heat still

to be released exceeds the heat released so far in

the life of the Earth. Internal heat will maintain

tectonic activity until conduction suffices to

carry the mantle heat flux and that state will

not be reached for more than 10

years.

23.5 Cooling history of the core

The cooling of the core is controlled by the prop-

erties of the mantle and the behaviour of

the thermal boundary layer at its base (D

Thermal processes in the core are consequences,

Table 23.2 Numerical details of the

thermal history model with 20 10

Wof

mantle radiogenic heat

Present radiogenic heat

Mantle 20 10

Crust 8.2 10

Core 0.2 10

Total 28.4 10

Present rate of heat loss

Mantle 32.5 10

Crust 8.2 10

Core 3.5 10

Total 44.2 10

Radiogenic heat in 4.5 10

years 7.6 10

Total heat loss in 4.5 10

years 13.4 10

Residual (stored) heat 13.3 10

Radiogenic heat now to t ¼1 10.9 10

23.5 COOLING HISTORY OF THE CORE 385

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

386

– [376–388] 13.3.2008 10:47AM

not causes, of the heat loss. This was the basis of

an argument by Stacey and Loper (1984) that the

heat flux from the core is stabilized to a more or

less steady value by a balance between compet-

ing effects in the boundary layer. Heat is

removed from the core by a convective process

that we identify with plumes of hot, low viscosity

material that flows rapidly up narrow channels

in the mantle. But all convective processes are

slowed by the cooling and stiffening of the man-

tle. The competing effect is the relatively faster

cooling of the mantle than the core, which

increases the temperature increment across the

boundary layer, causing an increase in the heat

flux into it which compensates for the general

stiffening. Although we cannot expect this com-

pensation to be more than approximate, it is

essential to understanding what happens in the

core. The point is that it is the heat flux that is

stabilized and not the rate of change in temper-

ature. We now consider how these are related.

Table 21.5 distinguishes several contribu-

tions to core energy that vary differently

with time. We ignore, for the moment, the

contributions by radioactivity and precession

and divide the first five entries in the table

into heat Q

¼20.23 10

J, resulting from

cooling at a rate proportional to dT/dt, and

¼13.91 10

J, arising from latent heat and

compositional separation, which contribute at a

rate proportional to dV/dt, where V is the inner

core volume. dV/dt and dT/dt are related by

Eq. (22.41). Since r / V

1/3

, we can rewrite this as

1=3

dV=dt / dT=dt; (23:23)

which we can integrate, without regard to the

time dependence, from V ¼0atT ¼T

to V at

temperature T. Substituting present values, V

and T

to eliminate the proportionality constant,



 T

: (23:24)

By differentiating we relate the time

dependences of V and T

 T



dT

 T



: (23:25)

The extremes of this relationship are dV/dt !0at

(T ¼T

, V ¼0) and dV/dt ! (3/2)V

/(T

T

)at

(T ¼T

, V ¼V

We identify V/ V

with the fraction of heat Q

released, so dQ

/dt varies from zero to (3/2)(Q

DT)(dT/dt), where DT ¼98.4 K is the tempera-

ture drop accompanying inner core formation.

The variation in Q

is linear in temperature, so

/dt ¼(Q

/DT)(dT/dt). Thus the total rate of

heat release at any stage is

Q ¼

 T



T

dT



: (23:26)

From the values of Q

and Q

above, the frac-

tion contributed by the Q

term varies from

zero to 0.508 as the inner core grows from noth-

ing to its present size. If, as we suppose, the

mantle control keeps

Q approximately constant

then dT/dt decreases by a factor 2 during inner

core growth. But this does not compensate

for the low thermodynamic efficiency of the Q

sources (0.15), compared with the Q

sources

(0.50). Maintenance of constant dynamo power

requires a decrease in the core-to-mantle heat

flux with time to offset the increasing thermody-

namic efficiency with the greater contribution

by inner core growth. By the cooling calculation

presented here, inner core formation began

early, at least 3.5 Ga ago, and has become pro-

gressively more important as its increasing con-

tribution to dynamo power compensated for a

decreasing cooling rate.

The core-to-mantle heat flux implied by this

calculation, about 3.5 terawatt, has some obser-

vational support because it corresponds to the

plume heat flux inferred from Sleep’s (1990) esti-

mate of the buoyancy of hot spot ‘swells’. This

identifies the hot spots with plumes originating

at the base of the mantle and carrying up the

core heat. Most other estimates of the core–man-

tle heat flux are higher, typically 10 tW. Even

with 1 to 2 tW of radiogenic heat, as often

assumed, this would mean core cooling faster

than mantle cooling for all of the mantle cooling

models in the previous section (see Problem

23.3). But the mantle must have cooled much

more than the core to leave a thermal boundary

layer at its base and it would be difficult to devise

386 THERMAL HISTORY