Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C20.3D

–

347

– [337–347] 13.3.2008 10:39AM

This can be used directly for any regular oscilla-

tion that can be Fourier analysed, and, in princi-

ple, could be used for irregular variations, but a

better method is to represent surface tempera-

ture changes by a sum (or integral) of a sequence

of steps, each of which propagates downwards

in the manner of Eq. (20.3). This is an example of

an inverse problem for which the forward solu-

tion (calculation of a deep temperature profile

from a known surface temperature variation) is

straightforward and trial solutions can be repeat-

edly adjusted to find surface variations that best

reproduce the observed profile. This is the trial-

and-error method first applied by V. Cermak.

Although more sophisticated inversion proce-

dures are now used, they do not give identical

results and there is no unambiguous ‘best’

method.

Strengths and limitations of the method are

indicated by the hypothetical examples in

Fig. 20.6, which shows temperature increments

as functions of depth for five surface thermal

impulses, all of magnitude T

and different dura-

tions. The curves for impulses starting either 100

or 1000 years ago and continuing to the present

time are simply plots of the complementary

error function, that is (1 erf x), where erf x is

given by Eq. (20.4). Note that they are scaled in

depth by a factor

10 with respect to one

another. For the purpose of calculation the 20

to 120-year plot assumes an impulse T

that

began 120 years ago and continues to the present

time but with a superimposed impulse T

, can-

celling it 20 years ago. The 100 to 200-year and

200 to 300-year plots are calculated similarly. All

these curves are normalized to the arbitrary

impulse magnitude T

.IfT

¼10 K the approxi-

mate magnitude of the steady gradient against

which such effects must be observed is shown by

the broken line.

As is apparent in Fig. 20.6, temperature var-

iations that are brief compared with the times

that have elapsed since they occurred are

smeared out and become insignificant in a bore-

hole profile. All of the curves can be re-scaled for

times differing by any factor f from those plotted

by re-scaling depth by a factor

f. This means

that gradients change by 1/

f, and since it is

gradient variations that are sought, because

they must be distinguished from the background

gradient, resolution decreases with increasing

age. In reviewing the results of numerous mea-

surements, Pollack and Huang (2000) empha-

sized that temperature profiles from individual

boreholes are subject to various disturbances

and are not useful, but that systematic variations

in numerous holes from a limited region reliably

represent variations in surface temperature for

that region.

The most obvious variation is a warming for

the last 150 years, accelerating in the last 50

years, which is seen everywhere, most notice-

ably at high latitudes. An earlier cool period is

consistent with a ‘little ice age’ from about 1500

to the mid nineteenth century, that probably had

two separated maxima, although that would be

difficult to see in the borehole data. The homo-

geneity of Greenland ice has allowed deep holes

there to give paleotemperature estimates

extending back as much as 25 000 years, to the

last glacial maximum, in spite of complications

arising from ice compression and glacial flow.

20.5 CLIMATIC EFFECTS 347

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

348

– [348–360] 13.3.2008 10:48AM

The global energy budget

21.1 Preamble

If the Earth’s internal heat were not maintained

by radioactivity, the present rate of heat loss,

44.2 10

W, would cause cooling at an average

rate of about 120 K per billion years. Even over

4.5 billion years, cooling at this rate would have

had only a moderate effect on the temperature of

the deep interior. Although radioactivity is the

dominant continuing source of internal energy,

it is only topping up the primordial heat gener-

ated by the Earth’s accretion. It is slowing the

cooling rate but is not the reason why the inte-

rior is hot. But radioactivity is decreasing slowly

with time and does not balance the heat loss. The

Earth is cooling at a rate determined by the dif-

ference between the surface heat flux and the

radiogenic heat. Mantle convection and tecton-

ics are slowing down as the Earth cools and the

rate of change is determined by this unbalance.

A substantial source of internal energy is nec-

essary also to maintain core convection, which

drives the geomagnetic dynamo. The Earth has

had a magnetic field for at least 3.5 billion years

and probably for its entire life. The power

requirement for dynamo action is probably less

than the drain on core energy by thermal con-

duction, and if the core has some radioactivity

then its effect is to compensate for the conduc-

tive heat loss. The necessity for this depends on

the core conductivity, which is still poorly

determined.

The first thing to note is that the gravitational

energy released in the original accretion of the

Earth dwarfs all other energy sources. This may be

calculated by building up the Earth in layers, start-

ing at the centre. When the radius has reached the

value r,withmassm, the gravitational potential at

the surface is Gm/r and when a further layer of

mass dm ¼4pr

dr is added there is a loss of grav-

itational potential energy

¼Gm dm=r ¼4pGmr dr; (21:1)

where m ¼ 4p

r

dr and G ¼6.67 10

11

1

2

is the gravitational constant. For a

spherical mass M and radius R this integrates to

¼fGM

=R; (21:2)

as in the calculation of solar energy in

Section 4.1, with f ¼3/5 if the density is uniform.

For a uniform body with the size and mass of the

Earth this gives 224 10

J, but with the cen-

tral concentration of mass in the real Earth there

is an additional energy release so that integra-

tion over the observed density profile gives

f ¼0.6654 and

¼249  10

J ð41:6  10

J=kgÞ: (21:3)

This is fortuitously close to the value for a sphere

with density inversely proportional to radius

(Problem 21.1), for which C/Ma

¼1/3

(Problem1.1(c)), closely representing the central

concentration of mass within the Earth.

However, there is no formal relationship

between moment of inertia and gravitational

energy. These energies are written as negative

because the zero of gravitational energy refers to

infinite separation of material, making all values of

negative, but in most of what follows we are

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

349

– [348–360] 13.3.2008 10:48AM

interested in the positive gravitational energy

released by aggregation or collapse of material.

The magnitude of the number in Eq. (21.3) is

emphasized by comparing it with the total

release of radiogenic heat in the life of the

Earth, 7.6 10

J (Table 21.1). If the energy

in Eq. (21.3) were supposed to be retained by

the Earth, it would correspond to an average

temperature exceeding 37 000 K. Almost all of it

was radiated away in the accretion process, but

retention of a small fraction sufficed to ensure

that the Earth started its life hot.

A consideration of gravitational energy also

makes it difficult to avoid the inference that

formation of the core accompanied accretion

and was not delayed until the Earth was essen-

tially complete. As pointed out in Section 5.4, the

energy released by core separation from an ini-

tially homogeneous Earth would be 16 10

sufficient to raise the temperature of the core by

6300 K. The gravitational instability of a homo-

geneous Earth, implied by these numbers, disal-

lows any serious suggestion that it ever existed.

These calculations are necessarily numerical,

with repeated iteration to the final version of

any model, using equations of state for core

and mantle materials to allow for their self-

compression (Stacey and Stacey, 1999). An inter-

esting by-product of the calculations is the

energy of compression, which is stored irretriev-

ably in the Earth as elastic strain energy. The

total is 15 10

J. In the core it averages 4.3 

Jkg

1

, and is comparable to the binding

energy of iron (at zero pressure) or to the energy

of a chemical explosive. In core processes involv-

ing redistribution of mass, as in the formation of

the inner core, stored strain energy accounts for

12% of the gravitational energy release; this frac-

tion produces neither heat nor dynamo power.

The principal continuing internal source of

energy is radioactivity, which is slowly decaying.

It yields about 28 10

Watthepresenttimebut

fourtimesasmuchwhentheEarthwasyoungand

twice as much when averaged over the life of the

Earth. Although it is an important contribution to

the total energy budget, it is not an overwhelming

one, as seen in the comparisons in Table 21.1.

Although the Earth is hot inside because of the

original accretion energy, two thirds of the cur-

rent heat loss is attributable to radioactivity. A

thermal history calculation (Chapter 23) is needed

to tie these estimates together.

21.2 Radiogenic heat

The thermally important elements in the Earth

are uranium, thorium and potassium, for which

heat outputs are listed in Table 21.2. Their con-

centrations in the Earth are very uneven and

many details remain obscure, but there are sev-

eral considerations that allow us to develop a

broad picture of their distributions. A compari-

son of the measured abundances in various geo-

logical materials is given in Table 21.3 with

estimated average concentrations in the major

components of the Earth. The thermal structure

and history of the Earth depend on these concen-

trations, but, conversely, arguments about ther-

mal history impose a constraint on the estimates

of radiogenic heat. In particular, the thermal

budget (Table 21.4) must balance.

A basic problem is to estimate the concentra-

tions of radioactive elements in the mantle,

Table 21.1 A comparison of global energies.

Allvaluesaregiveninunitsof10

J. The

first four entries give gravitational energy

release with the resulting elastic strain

energies subtracted. Strain energy is listed

separately, so that the total gravitational

energy release is the sum of the first five

items. Tidal dissipation is included in the

table but occurs mainly in the sea and does

not influence the thermal state of the solid

Earth

Accretion of a homogeneous mass 219.0

Core separation less strain energy 13.9

Inner core formation 0.09

Mantle differentiation 0.03

Elastic strain 15.8

Radiogenic heat in 4.5 10

years 7.6

Residual stored heat 13.3

Heat loss in 4.5 10

years 13.4

Present rotational energy 0.2

Tidal dissipation in 4.5 10

years 1.1

21 . 2 R A D I O G EN I C H E A T 349

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

350

– [348–360] 13.3.2008 10:48AM

where they cannot be directly observed. As evi-

dent from the numbers in Table 21.3, the ratio of

thorium to uranium is quite similar in a wide

range of rock types as well as meteorites.

Although lower Th/U ratios occur in mid-ocean

ridge basalts (MORB), it is reasonable to suppose

that the global balance of these elements has

preserved the meteorite ratio. Here the overall

mantle ratio is assumed to be 3.7. Estimates of

the potassium/uranium ratio are less secure.

Although both of these elements are strongly

concentrated in the crust, the evidence of

argon outgassing, considered below, indicates

that potassium is more strongly depleted in the

mantle than are uranium and thorium. We can-

not appeal to meteorite data for an estimate of

the global potassium content, because, being a

volatile element, it is certainly depleted in the

Earth relative to the meteorites. Even the mete-

orites show substantial variations, as do all of the

Table 21.2 Thermally important radioactive elements in the Earth

Isotope

Energy/atom

(MeV)

mW/kg of

isotope

mW/kg of

element

Estimated total

Earth content

(kg)

Total heat

(10

Total heat

4.5 10

ago

(10

238

U 47.7 95.0 94.35 12.86 10

12.21 24.5

235

U 43.9 562.0 4.05 0.0940 10

0.53 44.4

232

Th 40.5 26.6 26.6 47.9 10

12.74 15.9

K 0.71 30.0 0.003 50 7.77 10

2.72

——

33.0

——

(Total K) 28.2 117.8

These energies include all series decays to final daughter products. Average locally

absorbed energies are considered; neutrino energies are ignored.

Table 21.3 Average radiogenic heat in geological materials. These numbers may be compared

with the total heat flux per unit mass of the Earth, 7.4 10

12

Wkg

1

Material

Concentration (parts per million by

mass)

Heat production

12

Wkg

1

U Th K K/U

Igneous rocks granites 4.6 18 33 000 7 000 1050

alkali basalts 0.75 2.5 12 000 16 000 180

tholeitic basalts 0.11 0.4 1500 13 600 27

eclogites 0.035 0.15 500 14 000 9.2

peridotites, dunites 0.006 0.02 100 17 000 1.5

Meteorites carbonaceous chondrites 0. 020 0.070 400 20 000 5.2

ordinary chondrites 0.015 0.046 900 60 000 5.8

iron meteorites nil nil nil – <3 10

4

Moon Apollo samples 0.23 0.85 590 2 500 47

Global averages crust (2.8 10

kg) 1.2 4.5 15 500 13 000 29 3

mantle (4.0 10

kg) 0.025 0.087 70 2800 5.1

core nil nil 29 – 0.1

whole Earth 0.022 0.081 118 5400 4.7

350 THE GLOBAL ENERGY BUDGET

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

351

– [348–360] 13.3.2008 10:48AM

Solar System bodies that have been sampled

(Fig. 21.1).

Fisher (1975) drew attention to the fact that

argon and helium trapped in glassy (rapidly

cooled) submarine basalts indicated that the K/

U ratio of the mantle, from which they were

derived, may be as low as 1500. More recent

work, involving simultaneous measurements of

He,

Ar and of the non-radiogenic isotopes

and

Ar, which evidently remain in the Earth

from the original accretion, has given very vari-

able results which have not been untangled from

the problem of contamination by the rare gases,

especially

He, in marine sediment introduced

by the infall of cosmic dust. There is no compel-

ling reason to adopt a particular value for the

mantle average K/U ratio. Values in the range of

1500 to 6000 appear plausible and 2800 is

assumed in Tables 21.2 to 21.4.

An extreme lower bound on total terrestrial

potassium (4.7 10

kg) is imposed by the

in the atmosphere. This is only slightly greater

than the estimate of crustal potassium in

Table 21.3. A simple outgassing history is com-

patible with a total potassium content of the

Earth slightly less than twice this value

(Section 5.2). We have no comparable check on

the outgassing of

He from the Earth, as helium

rapidly escapes from the atmosphere to space.

It has been conventional to assume negligible

radioactivity in the core, essentially because it is

not found in meteoritic iron, but there is a long

history of suggestions that the core contains

potassium, associated with sulphur, which is

almost certainly present in both the outer and

inner cores. As we mention in Section 2.8, the

chemical argument for a substantial potassium

content in the core is not conclusive. Also, we

follow the conclusion of Wheeler et al. (2006)

that the uranium content of the core is negli-

gible. The physical case for core radioactivity is

based on the need for a heat source to compen-

sate for the conductive heat loss and that

requires an estimate of thermal conductivity

(Section 19.6). This is not known with sufficient

accuracy to be clear whether radiogenic heat is

needed, but current estimates favour a small

contribution and 0.2 terawatt of heat from

is included in Tables 21.3 to 21.5. This is the

A ¼0.2 model in Section 21.4.

Uranium and thorium are not readily separa-

ted by volatility or normal geochemical processes

and appear in meteorites, and by implication in

the Earth, in an almost constant ratio. This is

evidence that they are not fractionated relative

to other non-volatiles and so have approximately

meteoritic abundances in the Earth. With the

radiogenic heat that this implies and the total

heat required by thermal history calculations

(Chapter 23), we have an estimate of potassium

abundance independent of the evidence from

Ar/

He ratios in mantle-derived igneous rocks.

The numbers in Tables 21.3 and 21.4 satisfy these

conditions but give rather less potassium than

often suggested. We consider what the data in

Fig. 21.1 indicate. On this graph, materials having

equal concentrations of uranium lie on a line of

gradient unity. The ordinary and carbonaceous

chondrites are not far from such a line, encour-

aging the view that they have similar uranium

abundances. But the ordinary chondrites are

Table 21.4 The heat budget (all values in

units of 10

Income

Crustal radioactivity 8.2

Mantle radioactivity 20.0

Core radioactivity 0.2

Latent heat and

gravitational

energy released by

core evolution

1.0

Gravitational energy of

mantle differentiation

0.1

Gravitational energy

released by thermal

contraction

3.1

Tidal dissipation 0.1

TOTAL 32.7

Expenditure

Crustal heat loss 8.2

Mantle heat loss 32.5

Core heat loss 3.5

TOTAL 44.2

Net Loss of Heat 11.5

21 . 2 R A D I O G EN I C H E A T 351

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

352

– [348–360] 13.3.2008 10:48AM

systematically richer in potassium, so there was

evidently a processing of potassium that did not

affect uranium. Variations in potassium abun-

dance are commonly attributed to its volatility,

but this does not readily explain its enrichment

in ordinary chondrites, relative to the volatile-

rich carbonaceous chondrites. The data for ter-

restrial samples, Moon rocks and the available

Venus analyses are well removed from the trend

of the chondrite data in Fig. 21.1, but they are for

crustal materials, in which all of the radioactive

elements are concentrated. They have been sub-

jected to much more severe processing than the

chondrites and, in view of the wide disparity

between potassium concentrations in the differ-

ent types of chondrite, we conclude that none of

these data provide evidence of the total potas-

sium content of the Earth. Evidence of its outgas-

sing and the

Ar content of the atmosphere,

with the

Ar/

He ratios in glassy submarine

basalts, provide the clearest information that

we have.

21.3 Thermal contraction,

gravitational energy and the

heat capacity

The continued gradual cooling of the Earth is

accompanied by thermal contraction and conse-

quent release of gravitational energy. In thermal

history calculations this is allowed for by an

adjustment to the heat capacity; the gravita-

tional energy is added to the heat lost per degree

of cooling. The magnitude of the effect is the

subject of this section. Although for the purpose

of thermal history it is accounted for by the heat

Eucrites

Moon rocks

Carbonaceous

chondrites

Ocean

basalts

Land basalts

Earth

Tektites

Granodiorites

Granites

Ordinary

chrondrites

V10

Potassium concentration (ppm)

Mass ratio (K / U)

100

1000

Andesites

FI G U R E 21.1 Mass ratios, K/U, as a function of K concentrations, showing the separate groupings of crustal

rocks, ordinary and carbonaceous chondrites, eucrites (a class of achondrite), Moon rocks and three samples

from Venera probes 8, 9 and 10. Most of the data are from Eldridge et al. (1974). Values for the Venus samples are

from Keldysh (1977).

352 THE GLOBAL ENERGY BUDGET

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

353

– [348–360] 13.3.2008 10:48AM

capacity adjustment, we need to note that, in

balancing the energy budget, the gravitational

energy increases the difference between the

heat loss and the radiogenic heat. Geochemical

estimates of the mantle content of thermally

important elements (e.g. McDonough and Sun,

1995) give about 20 10

W at the present time

and thermal history calculations (Section 23.4)

indicate that this is reasonable, so we adopt it for

our thermal model. However, it could be in error

by 4 10

W and our estimate of the K/U ratio

differs from that by McDonough and Sun, so this

uncertainty carries through all our calculations.

The gravitational energy released by the con-

traction of any material element is readily calcu-

lated if it is assumed that the densities of all other

elements are unaffected, even though their posi-

tions may change. However, this is not what hap-

pens. When the Earth contracts by thermal

shrinkage of any component, the pressure is

increased throughout, so that the density

increases everywhere, adding to the shrinkage

and to the consequent gravitational energy

release. It is necessary to consider the Earth as a

whole and to allow for compression as well as

thermal shrinkage. A perturbation calculation

appears possible in principle, but the obvious,

direct way of doing this is to compare two inde-

pendently calculated, self-compressed models

with specified pressure–density relationships

for each of the components. Then it is found

that shrinkage of the mantle causes compression

and therefore gravitational energy release in

thecoreaswellasinthemantleitself,and

vice versa. Calculations of this kind were reported

by Stacey and Stacey (1999) in a sufficiently gen-

eral way to allow rescaling to any assumed con-

traction of the core or mantle, and the results are

applied here.

We seek a relationship between gravitational

energy release and the net energy loss, that is,

the ratio of the third and second terms in the

heat balance equation:

radiogenic heat þ net cooling þ gravitational

energy loss  compressional energy ¼ surface

heat flux: (21:4)

For this purpose mantle and core cooling must

be treated independently because their cooling

rates are not the same and the ratio of gravita-

tional energy loss to cooling is bigger in the case

of the core. The mantle case is simpler, being a

straightforward application of the Stacey and

Stacey (1999), results with only a minor influ-

ence of the core. We refer to the effective heat

capacity of the mantle as the loss of heat

required for the potential temperature of the

lower mantle to fall by one degree, and this

differs little from the potential temperature of

most of the upper mantle. The point of this def-

inition is that if the temperature gradient is

everywhere adiabatic, and remains so with cool-

ing, the decrease in temperature is proportional

to the absolute temperature. Since the potential

temperature, T

¼1700 K, is the temperature of

adiabatic extrapolation to zero pressure, mate-

rial at any higher pressure, being at a higher

temperature, T > T

, contributes more to the

heat loss than if uniform cooling is assumed.

Using the thermal model in Appendix G, the

effective heat capacity of the mantle is, without

considering thermal contraction,

Mantle : mhC

i¼

C

ðT=T

ÞdV

¼ 6:19  10

1

: (21:5)

Defined in this way, hC

i¼1537 J K

1

, com-

pared with C

1200 J K

1

, as calculated by

Eq. (19.4) and listed in Appendix G. A similar

calculation gives the corresponding thermal

contraction

Mantle : Vhi¼

ðT=T

ÞdV

¼ 2:12  10

1

: (21:6)

This corresponds to an effective expansion coef-

ficient hi¼23.4 10

6

1

, being the average

contraction for a one degree fall in potential

temperature.

From the results of the Stacey and Stacey

(1999) calculations we see that a uniform 1%

contraction of the mantle would release

5.90 10

J of gravitational energy, but that

0.75 10

J of this would become elastic strain

energy, leaving a net release of 5.15 10

With the value of hi calculated above, a 1%

contraction corresponds to a fall in potential

temperature of 427 K, so we have a gravitational

21.3 HEAT CAPACITY 353

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

354

– [348–360] 13.3.2008 10:48AM

contribution of 5.15 10

J/427 K ¼1.21 10

1

to the effective heat capacity, which,

added to Eq. (21.5), gives a total effective mantle

heat capacity



¼ 7:40  10

1

: (21:7)

This is used in the thermal history calculations in

Chapter 23. The numbers show that, of the net

heat loss by the mantle, approximately 20% is

gravitational energy, although this slightly over-

estimates the effect because  decreases with

depth and the deep mantle is weighted by the

factor T/T

in the gravity calculation.

In considering the cooling of the core, the

growth of the inner core introduces a complica-

tion, but we treat it as adding three independ-

ently calculable terms to the effective heat

capacity, attributed to latent heat of solidifica-

tion, gravitational energy of contraction due to

solidification and the gravitational energy

released by compositional separation of the

light outer core solute. Section 21.4 examines

the radial distribution of heat sources, but here

we estimate their global effects. We use the

core–mantle boundary temperature, T

CMB

,as

the reference, with the higher internal temper-

atures adiabatically related to it, as for T

in the

case of the mantle. We define the effective core

heat capacity as the net heat loss per degree fall

in T

CMB

For the general cooling and contraction, with-

out consideration of inner core development,

we have expressions analogous to Eqs. (21.5)

and (21.6):

Core : mhC

i¼1:80  10

1

; (21:8)

Vhi¼2:79  10

1

: (21:9)

Equation (21.9) corresponds to hi¼15.8 10

6

1

. By the Stacey and Stacey (1999) calculations

a 1% contraction of the core would release

5.36 10

J, less 0.73 10

J of strain energy,

leaving 4.63 10

J, and with the estimated hi

this would require T

CMB

to fall by (0.01/

15.8 10

6

)K¼634 K. Thus the gravitational

contribution to the heat capacity is 4.63 10

J/634 K ¼7.31 10

1

. This is added to

Eq. (21.8) to give an effective core heat capacity



¼ 2:53  10

1

; (21:10)

with no allowance for inner core development.

This is 40% greater than the heat capacity esti-

mated with neglect of gravitational energy.

The three additional energy contributions

mentioned above can be converted to notional

components of the heat capacity by dividing

them by the temperature change, expressed as

the fall in T

CMB

required for inner core forma-

tion. First we estimate the magnitudes of the

energies. The latent heat of inner core forma-

tion, L, is calculated from the entropy by

Eq. (19.53),

L ¼ T

S ¼ T

ðnR ln 2 þ K

VÞ; (21:11)

where n ¼M

/m is the number of moles of inner

core material, with total mass M

and mean

atomic weight m ¼50.16 by Table 2.1. It is con-

venient that the product hK

ivaries rather little

and we take an average from Appendices F and

hK

i¼hK

=ð1 þ TÞi

¼ 12:16  10

Pa K

1

: (21:12)

As in Section 19.4, we take the density change on

freezing of constant composition to be

200 kg m

3

(1.55% of the average inner core den-

sity), making DV ¼1.18 10

, and, with an

average boundary temperature during solidifica-

tion of 5050 K, these numbers give

L ¼ 6:36  10

J: (21:13)

The gravitational energy released by the con-

traction caused by freezing was calculated by

Stacey and Stacey (1999) for an assumed density

increment of 140 kg m

3

to be 4.123 10

J, less

0.515 10

J of strain energy. Revising these

values to a density increment of 200 kg m

3

obtain the net gravitational energy release by

solidification, 5.15 10

J. This is the global

energy release, some of which occurs in the

mantle. For the purpose of calculating the

energy balance of the core and the contribution

to dynamo power (Section 22.7), we require only

the fraction of this energy that is released in the

core, and write this as

¼ 3:14  10

J: (21:14)

354 THE GLOBAL ENERGY BUDGET

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

355

– [348–360] 13.3.2008 10:48AM

A simple calculation of the energy released

by compositional separation is given in

Section 22.6, but we can use the results of the

Stacey and Stacey (1999) calculation, with the

advantage that the effects of global contraction

and strain energy increase are included. The

compositional component of the density con-

trast between the inner and outer cores is

taken to be 620 kg m

3

, being a total density

difference of 820 kg m

3

, as estimated by

Masters and Gubbins (2003), less 200 kg m

3

for

solidification. Renormalizing the Stacey and

Stacey result to this density contrast, the global

energy release minus strain energy is 4.99 10

of which the fraction released in the core is

¼ 4:79  10

J: (21:15)

We relate the energy released by inner core

formation to its contribution to the global effec-

tive heat capacity by calculating the required

cooling. This is the difference between the

adiabatic and melting point gradients over

the pressure difference between the centre and

the present inner core boundary, but with

an adjustment for the increase in pressure

caused by the contraction. The principle is illus-

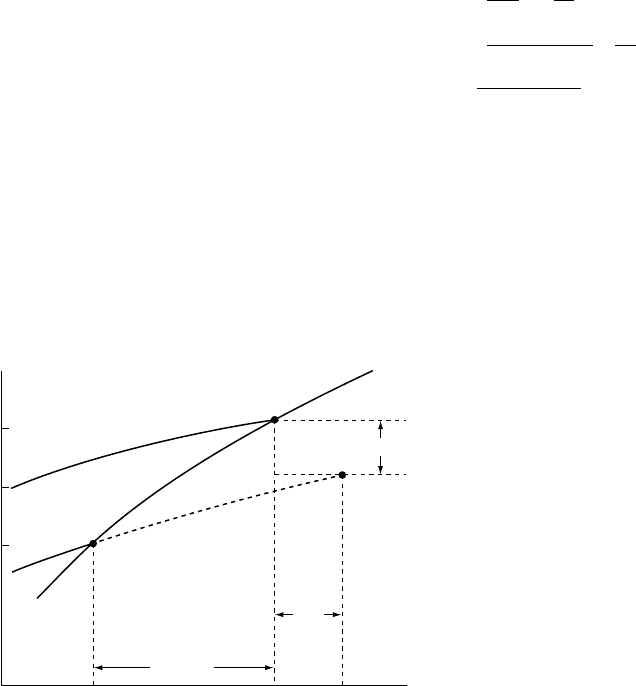
trated in Fig. 21.2. With the density increments

used above there are increments in central pres-

sure of 1.82 GPa and 4.41 GPa due to solidifica-

tion and compositional separation, giving

6.23 GPa together. There are also contributions

of 5.4 10

3

GPa K

1

by general core cooling

(referenced to T

CMB

) and 4.1 10

3

GPa K

1

per

degree change in T

, arising from thermal con-

traction of the mantle. These effects are all sub-

tracted from the present pressure difference

between the centre and the inner core boundary

(35.05 GPa by PREM) to obtain the pressure

change at the boundary as the inner core grows,

PðGPaÞ¼ð35:05  6:23Þþ5:4

 10

3

T

CMB

ðKÞþ4:1

 10

3

T

ðKÞ: (21:16)

The cooling is calculated from the difference

between the melting point gradient by Eq. (19.50)

and the adiabatic gradient by Eq. (19.19) over the

pressure range P given by Eq. (21.16), with

T ¼T

T

ICB







P

2Tð1 þ TÞ

ð1 þ 2TÞ



T



P

TP

ð1 þ 2TÞ

; (21:17)

with adiabatic extrapolation giving

T

CMB

=T

ICB

¼ T

CMB

ICB

¼ 0:787: (21:18)

Solution of these equations requires an assump-

tion about the mantle cooling (DT

in Eq. 21.16)

that occurs during inner core formation, but its

effect is small enough that no serious uncer-

tainty arises. We take DT

¼300 K. Then

Eqs. (21.16) to (21.18) give

Outer

Core

Inner

Core

ΔT

35 GPa

~5300

5173

5000

ICB

δP

Pressure

FI G U RE 21.2 Temperature–pressure

relationship for the inner core. The outer core

adiabat, T

, intersects the melting curve, T

at A and is extrapolated to the centre of the

Earth at C, pressure P

. The hotter adiabat at

commencement of inner core growth, T

meets T

at central pressure P

(at point B),

which is less than P

because the whole Earth

was then hotter and more dilated. Growth of

the inner core to its present size requires

cooling DT

at the centre of the Earth and

0.723 DT

at the core–mantle boundary.

21.3 HEAT CAPACITY 355

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

356

– [348–360] 13.3.2008 10:48AM

T

CMB

¼ 98:4K: (21:19)

Now we add to the effective heat capacity by

Eq. (21.10) the notional contributions by inner

core formation:

’

cTotal

¼ ’

þðL þ E

þ E

Þ=T

CMB

¼ 4:21  10

1

: (21:20)

This is the effective core heat capacity, averaged

over the duration of inner core formation. The

value in Eq. (21.10) must be used for the period, if

there was such early in the life of the Earth,

when there was no inner core. Sections 21.4

and 22.7 consider the radial variation of heat

sources. The values estimated here are global

totals, with separate identification of energy

released in the core that is needed in calculating

dynamo power and discounting the energy of

elastic compression.

We must note that the numbers in this sec-

tion present a simplification of the effective core

heat capacity, which increases with time as the

inner core grows. The value in Eq. (21.20) is an

average over the period of development of the

inner core and the fractional contribution of

(L þE

þE

) to the total has increased with

time. These terms are contributed by the growth

in inner core volume, which is not linear in core

temperature. This problem is referred to in

Section 22.7 and discussed in more detail in

Section 23.5.

21.4 Energy balance of the core

The energy estimates in Section 21.3 are now re-

examined to determine their distribution within

the core. A basic question is: how fast is it cool-

ing? We know that it must have been losing heat

fast enough to maintain dynamo action for

several billion years, and this requires three-

dimensional stirring of the outer core that keeps

the temperature gradient very close to adiabatic.

There is, therefore, a conducted heat flux at all

levels, and this is a base load on core energy that

must be supplied, whatever combination of ther-

mal and compositional driving forces is respon-

sible for the convection. The conducted heat

contributes nothing to dynamo action, which

requires additional energy, thermal, composi-

tional, gravitational, or some combination of

them to drive convection. The compositional

contribution is particularly important, being

mechanical energy of gravitational origin that

is 100% efficient in driving the dynamo (dis-

counting a small loss by diffusive mixing).

Thermal convection operates with a limited ther-

modynamic efficiency (12% to 25%, depending

on the distribution of the heat source) and

exhausts, as heat to the core–mantle boundary,

much more energy than it produces as convec-

tive power. With a strong compositional effect

the heat flux into the mantle may be less than

the conducted heat at the top of the core. In this

situation compositional convection carries back

down some of the conducted heat, a process that

we refer to as refrigerator action. It is needed only

over a limited depth range at the top of the core

and therefore a limited temperature range,

making it a very efficient process in the thermo-

dynamic sense of requiring little mechanical

energy for a large heat transfer.

We identify seven sources of energy in the

core. Table 21.5 gives their integrated contribu-

tions over the lifetime of the inner core, , which

may be less than the age of the Earth, 

.By

listing the total energies in this way we post-

pone, to Sections 22.7 and 23.5, consideration

of variations in the rates at which they are dis-

sipated. Here we consider average rates over

time , obtained by dividing the energies by .

The first five entries in the Q column of

Table 21.5 are discussed in Section 21.3.

Precessional dissipation is considered in

Section 7.5 and re-examined in Section 24.7 as a

possibly significant contributor to the dynamo

early in the life of the Earth. The entry in the

table, 0.20/

, corresponds to a mean dissipa-

tion rate of 0.014 terawatt, a little more than

twice our estimate of the present rate but only

20% of the very early rate. It is only a minor

contribution.

The least certain of the entries in Table 21.5 is

radioactivity. We follow the chemical argument

in Section 2.8 by assuming that any radiogenic

heat is due to

K, but allow the possibility that it

is zero. In the table it is represented by the

parameter A, which is the present heat output

356 THE GLOBAL ENERGY BUDGET