Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

367

– [361–375] 13.3.2008 10:48AM

surface is by conduction and makes no contribu-

tion to tectonic power.

The power calculation requires an assump-

tion about the distribution of heat sources. For

this purpose radiogenic heat and net cooling are

treated slightly differently. We assume radio-

genic heat to be distributed uniformly, so that

the heat generation per unit volume,

, is pro-

portional to density,

=M

¼ 5  10

12

Wkg

1

 ;

(22:19)

where, by the preferred model in Chapter 21,

¼ 20  10

W is the total radiogenic heat in

the mantle, mass M

¼4 10

kg. The heat loss

by cooling is proportional to temperature

because the temperature profile is assumed to

be adiabatic, with temperatures having constant

ratios as they decrease. This means that, as in the

calculation of the effective heat capacity

(Section 21.3), the rate of heat loss from unit

volume at temperature T is calculated from the

rate of change of the potential temperature, T

¼ 1:195C

: (22:20)

The factor 1.195 is the ratio of Eqs. (21.7)

and (21.5), arising from the gravitational contribu-

tion to the effective heat capacity. For the tem-

perature ratio we use the adiabatic one, as in

Eq. (22.17),

¼ exp

 K

ðÞdP

: (22:21)

The cooling rate is



Q 



¼ 1:69  10

15

1

¼ 53 K=10

years; (22:22)

where

Q ¼32.5 10

W is the total convected

heat loss,

¼ 20  10

W is the radiogenic

heat of our model, as in Section 23.4, and



¼7.4 10

1

(Eq. (21.7)). The heat flux

through any depth is the integral of

ðÞ

for the volume below that depth.

Integration of Eq. (22.17) gives the total power

of mantle convection. Assuming that all the heat is

convectively transported, this is E ¼8.03 10

There is a correction for the fact that the con-

ducted heat is not zero, although it is small.

By calculating the power that would be generated

by the conducted heat at each level if it were

convected, and integrating over the whole mantle,

we obtain the mechanical power loss due

to conduction, 0.3 10

W. Subtracting this

from the power estimated with neglect of conduc-

tion, we have a net convective (tectonic) power

of 7.7 10

W. This power is not generate d

uniformly through the mantle. Its distribution

is calculated by taking the incremental thermo-

dynamic efficiency for a radius range Dr,noting

that, by differentiating Eq. (22.1), d ¼dlnT,

Efficiency

0 1000 2000

3000

0.1

0.2

0.3

0.4

Depth (km)

FI G U R E 22.3 Thermodynamic efficiency

of convective heat transport to the surface

from depth z in the mantle as a function of z,

neglecting irreversibility of phase

transitions.

22 . 4 T E CT O N I C PO W ER 367

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

368

– [361–375] 13.3.2008 10:48AM

ðd=drÞr ¼ð@ ln T=@PÞ

ðdP=drÞr

¼ðg=K

Þr; (22:23)

and multiplying by the heat flux through that

radius. Figure 22.4 shows the result of this calcu-

lation, represented as power generation per unit

volume. The essential feature is the general

decrease in power generation with depth. This

is a consequence of the fact that power genera-

tion at any depth is proportional to the heat flux

and all of the deep heat is convected through the

shallow layers. Although there can be no precise

correspondence between the generation and dis-

sipation of convective power, there must be a

general correspondence and this necessarily

means that convection is less vigorous in the

lower mantle than in the upper mantle.

However, the whole lower mantle must be

involved because to lose heat it must be convect-

ing, but its convection is slower and this is con-

sistent with a higher viscosity.

The effect of the phase transitions on thermo-

dynamic efficiency is shown in Fig. 22.3 and their

contributions to convective power are indicated

in Fig. 22.4. Although the negative transition at

660 km depth has a greater entropy than the

shallower transitions, the heat flux through it

is less, reducing its effect on total power, relative

to the two positive transitions.

Referred to the heat flux to the surface, the

total convective power represents an efficiency

of 24%. This is higher than might be expected

from a glance at Fig. 22.3. The reason is that the

heat per unit volume from the lower mantle is

enhanced by the factor T/T

in Eq. (22.20). But, in

spite of the dominance of lower mantle heat, the

power generation in the lower mantle is much

weaker than in the upper mantle, because the

heat is transported over a small temperature

ratio within the lower mantle itself. Conversely,

all of the lower mantle heat passes up through

the entire upper mantle. If the upper mantle

were convecting alone, with no heat from the

lower mantle, the power generation would be

0.83 10

W, little more than 10% of the power

of whole mantle convection and insufficient

to account for the tectonic dissipation discussed

in Section 13.2. With lower mantle heat, the

upper mantle convective power is 5.3 10

obtained by integrating the convective power per

unit volume, plotted in Fig. 22.4.

22.5 Why are mantle phase

boundaries sharp?

Two observations on phase boundaries offer clues

to the manner of mantle convection: (i) over most

of the mantle, that is except in the limited areas of

strong subduction, the depths of the boundaries

are more or less uniform (say 10 km), and (ii) the

Power per unit volume (1×

–9

W m

–3

)

0 1000 2000

3000

Depth (km)

Δ E = 1.0 × 10

Δ E = + 0.8 × 10

ΔE = –1.0 × 10

FI G U R E 22.4 Convective power

generation per unit volume of the mantle as

a function of depth, showing its

concentration in the upper mantle. The

three phase transitions appear as

discontinuities that can be regarded as delta

functions in this figure, two positive and

one negative. Their contributions to the

total convective power are indicated.

368 THERMODYNAMICS OF CONVECTION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

369

– [361–375] 13.3.2008 10:48AM

boundaries are sharp enough to reflect short

period seismic waves, indicating that the depth

ranges over which the transitions at 410 km and

660 km occur are less than 2 km (Xu et al., 2003).

The implication of observation (i) is that subduc-

tion occurs in narrow bands and that the return

flow is a broad upwelling over the rest of the

mantle. Temperature contrasts between upgoing

and downgoing material are presumed to be sev-

eral hundred degrees and, by the values of z/T

in Table 22.1, this means boundary deflections of

tens of kilometres. Thus there is no evidence of

differential motion over most of the mantle and

it must all be doing the same thing – rising. The

subduction of cool slabs is compensated by a

broad-scale return flow.

Observation (ii), that the boundaries are

sharp, confirms that over most of the mantle

the vertical motion is slow, less than 1 cm per

year, compared with the plate speeds of several

centimetres per year. There are two reasons why

thicker phase boundaries might be expected. As

Solomatov and Stevenson (1994) pointed out,

under isothermal (equilibrium) conditions a sin-

gle mineral may undergo a phase transition at

sharply defined P–T conditions but this cannot

be true for the multi-component mineral mix of

the mantle. For the 660 km transition the

expected depth spread is nevertheless quite

small, and Solomatov and Stevenson addressed

more particularly the 410 km transition, for

which equilibrium thermodynamics predicts a

depth range much greater than 2 km. They

show that the narrowing of the transition can

be explained as a consequence of the fact that

phase transitions often do not occur under pre-

cisely equilibrium conditions but require nuclea-

tion under conditions of metastable overshoot.

For the 410 km transition they estimate this to

correspond to about 10 km in depth, which

would sharpen the transition sufficiently to

give the observed seismic reflections. Such an

overshoot would occur for transitions in both

directions and reduce by about 1% the thermody-

namic efficiency calculated in Section 22.2.

The other mechanism that causes thickening

of phase boundaries is directly relevant to our

ideas about the pattern of mantle convection. It

applies even to the transformation of a simple

single component if it occurs adiabatically, that

is too rapidly to allow isothermalization by ther-

mal diffusion. This is illustrated in Fig. 22.5 for

the case of an endothermic transition, as at

660 km. Consider material subducting on an

adiabat and meeting the boundary at A. As

soon as it does so it begins to transform to the

higher density phase, but this causes cooling and

the transformation goes to completion only

when a further increase in pressure suffices to

overcome the temperature drop, DT, at point B.

As long as both phases, are present the material

follows the Clapeyron path AB, and at greater

depths it resumes the normal adiabatic gradient.

Equation (22.14) gives DT, as listed in Table 22.1,

and the consequent depth range, Dz, is given by

z ¼ T= 





: (22:24)

Note that dT

/dz is negative for the case illus-

trated, but (@T/@z)

is always positive (unless

one considers materials with negative expansion

coefficients). The depth range over which this

occurs, as illustrated in Fig. 22.5, gives Dz,as

listed in Table 22.1. Since this is greater than

the transition zone thicknesses indicated by seis-

mology, we appeal to thermal diffusion to equal-

ize temperature and sharpen the transitions.

When thermal diffusion is allowed the tem-

perature profile takes the form illustrated in

Fig. 22.6, in which the phase transition is

restricted to the range CD. Outside this range

T (Adiabat)

FI G U R E 22.5 Temperature–depth relationship for rapid

(adiabatic) subduction through the transition at 660 km

depth, for which the transition temperature, T

decreases with pressure or depth.

22.5 WHY ARE MANTLE PHASE BOUNDARIES SHARP? 369

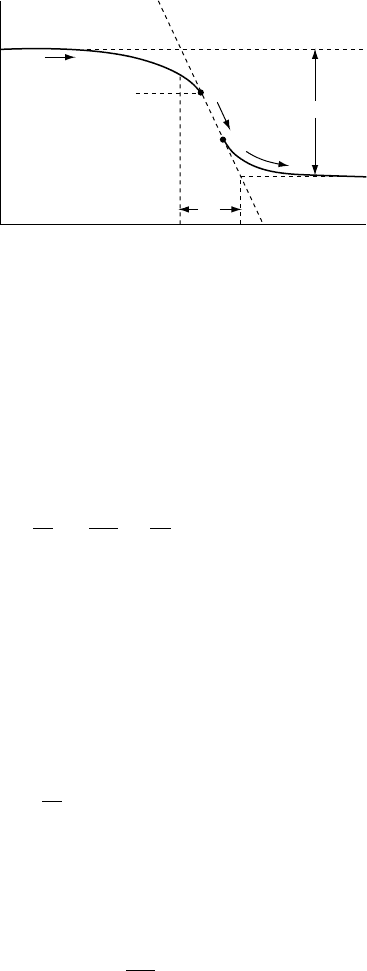
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

370

– [361–375] 13.3.2008 10:48AM

we add a term to the thermal diffusion equation

to account for the motion, at speed v. Ignoring

the small adiabatic temperature gradient,

¼ 

 v

; (22:25)

where  ¼/C

is thermal diffusivity.

Equation (22.25) represents the temperature at a

fixed point, with the material moving past, carry-

ing its temperature with it and so counteracting

the diffusion and producing a steady state in

which @T/@t ¼0 at any level. Then, for the

approach to point C we can integrate Eq. (22.25)

to give



¼ vðT  T

Þ; (22:26)

where boundary conditions @T/@z ¼0 and T ¼T

at z!1are applied. As long as C and D do not

meet, the boundary conditions at C, depth

þx), are @T/@z ¼dT

/dz and T ¼T



, where



¼ T

Þx:



(22:27)

Introducing this boundary condition to Eq. (22.26),

we have

 ¼ vx: (22:28)

The same applies to the lower bound of the

transition at D, which is displaced upwards by

distance x from z

. Thus, if x ¼(z

z

)/2 ¼Dz/2,

the layer shrinks to zero thickness. This applies

to speeds

v  2=z: (22:29)

With the values of Dz in Table 22.1 and assum-

ing diffusivity  ¼1.0 10

–6

1

, Eq. (22.29)

gives the listed values of v(critical), the convec-

tive speeds below which thermal diffusion

makes the boundaries sharp. It is evident that

the sharpness of phase boundaries, outside the

more confused subduction zones, imposes a

limit on convective speeds significantly lower

than the speeds of most of the surface plates.

This conclusion coincides with the convective

pattern favoured by the energy argument in

Section 13.2.

22.6 Compositional convection

in the core

Compositional convection was first recognized to

be important to core energetics and the dynamo

by S. I. Braginsky and confirmed by Gubbins

(1977) and Loper (1978a,b). In Section 21.4 it is

referred to as one of the components of the

core heat budget, but that is almost incidental

to its role in the dynamics and evolution of the

core. We give it a closer examination here. In

particular, we seek a simple analytical treatment

of this important effect. We make the conven-

tional assumption that the light core solute

rejected by the solidifying inner core mixes uni-

formly into the outer core, releasing gravita-

tional energy in the process The possibility that

this assumption is not completely valid is con-

sidered briefly in Section 23.5. In Section 21.4 the

energy is determined from models of the whole

Earth with and without an inner core. The value

so calculated, 5.63 10

J, includes elastic strain

energy and a small component released in the

mantle that must be subtracted, leaving

4.79 10

J as the energy relevant to the

dynamo. It recognizes that the mass rearrange-

ment modifies the gravity profile by increasing

the central density and causing a contraction

of the whole Earth, although the energy released

in the mantle by this process is less than 5%.

ΔT

FI G U R E 22.6 Effect of thermal diffusion at the 660 km

phase boundary. The small ambient adiabatic

temperature gradient is ignored here, so that the remote

temperature limits are T

and T

370 THERMODYNAMICS OF CONVECTION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

371

– [361–375] 13.3.2008 10:48AM

Nevertheless, we are interested to know how big

a fraction of the core energy release is attribut-

able to relative motion of materials with differ-

ent densities and not to the general contraction.

With the assumption that the material moves in

a fixed gravity profile a simple but realistic ana-

lytical calculation is possible.

As in Section 21.3, we take the compositional

component of the density contrast between

inner and outer cores to be 620 kg m

3

. In the

volume of the inner core this represents a mass

excess of 4.49 10

kg, referred to the outer

core density. The fraction of this that has been

drawn from the outer core is 0.949, being the

outer core fraction of the total mass of the core,

so that the mass drawn from the outer core and

deposited in the inner core is

m ¼ 4:26  10

kg: (22:30)

This is gravitationally equivalent to a mass defi-

ciency going the other way. We assume that the

inner and outer cores remain compositionally

homogeneous, so that this mass is drawn from

the outer core in proportion to the local density.

Similarly, its deposition in the inner core is pro-

portional to local density.

To calculate the energy released by this pro-

cess we need the gravity profile. This is reason-

ably represented by a power law,

g ¼ g

ðr=RÞ

: (22:31)

A least-square fit to the PREM outer core tabula-

tion gives x ¼0.8436, with g

¼10.78 m s

2

at the

core–mantle boundary radius, R. We use this

relationship in what follows, recognizing that it

is a simple analytical approximation and is not

exact but greatly simplifies the calculation. It

allows us to write the mass inside radius r as

mðrÞ¼gr

=G ¼ðg

=GÞr

xþ2

¼ M

ðr=RÞ

xþ2

; ð22:32Þ

where M

is the total core mass. We need the

fraction of this mass in the range r to (r þdr),

dm ¼ðx þ 2ÞM

xþ1

xþ2

; (22:33)

because this is the fraction of Dm (Eq. (22.30))

that originates in a range dr (between R and the

inner core radius, r

). We calculate first the

energy released by depositing Dm on the inner

core boundary. For this we need the gravitational

potential difference between r and r

V ¼

g dr ¼

dx ¼

xþ1

 r

xþ1



= x þ 1ðÞ:

(22:34)

Then the energy release is

¼ m

dmðrÞ

¼ m

ðx þ 2Þ

ðx þ 1Þ

ðr

xþ1

 r

xþ1

xþ2

¼ mg

ðx þ 2Þ

ðx þ 1Þ

2x þ 3



xþ1

ðx þ 2Þ



2xþ3

2xþ2

x þ 1

ðx þ 2Þð2x þ 3Þ



¼ 9:45  10

m ¼ 4:03  10

J: ð22:35Þ

The second stage of the integration is to dis-

tribute Dm through the inner core volume, but it

is useful to see Eq. (22.35) separately because for

an incremental Dm it gives the energy release at

the present stage of inner core formation. For the

total energy of inner core formation we add a

second integral, set up similarly, with

¼ðx þ 2Þ

xþ1

xþ2

dr; (22:36)

giving

mg

2x þ 3

xþ1

¼ 4:9  10

J: (22:37)

By this calculation the total compositional com-

ponent of the gravitational energy of inner core

formation is

E ¼ E

þ E

¼ 4:52  10

J; (22:38)

which is seen to be about 6% less than that calcu-

lated by the complete theory, after deduction of

the strain energy and the mantle energy release.

The difference can be attributed to a general

contraction associated with the chemical separa-

tion, because that is not allowed for in the

approximate calculation above.

The compositional separation energy shares

with precessional energy a physical distinction

from the other core energy sources listed in

Section 21.4, being mechanical energy, whereas

the others are thermal energies, from which

mechanical energy can be derived only with the

22.6 COMPOSITIONAL CONVECTION IN THE CORE 371

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

372

– [361–375] 13.3.2008 10:48AM

thermodynamic efficiency of a heat engine. The

simple way of identifying mechanical vs thermal

sources is to ask: can the processes be reversed,

in principle, simply by applying heat to the core?

If the answer is yes, then we must classify them as

thermal energy. For example, although the grav-

itational energy released by thermal contraction

may appear to be mechanical, if we could reheat

the core then the contraction would be reversed,

with no mechanical input and no more heat than

was extracted by the cooling. Thus we must count

the energy released by contraction as thermal.

Otherwise we would have a physical system vio-

lating the second law of thermodynamics. We can

re-examine the compositional energy in this light,

having noted that we can identify two contribu-

tions to it. Is the 6% that we attributed to general

contraction properly counted with the other 94%

as mechanical? By the reheating test the answer

must be yes. Being part of the separation process it

cannot be recovered by applying heat and it can

contribute to dynamo power with high efficiency.

22.7 Thermodynamic efficiency

of core convection and

dynamo power

There is no simple number to represent the effi-

ciency of core convection. We consider the

several components of core energy that have

different efficiencies and contribute in different

proportions according to the rate of core cooling.

The first distinction to make is between thermal

and compositional convection. We treat the

compositional effect as 100% efficient, although

some energy may be lost in turbulent mixing.

The efficiency of thermal convection depends

on the depth distribution of the heat sources,

being greatest for the latent heat, which is

derived entirely from the inner core boundary

(ICB). The heat from cooling of the inner core is

also treated as coming from the ICB. We calcu-

late here the thermodynamic efficiencies of the

several energy sources discussed in Section 21.4

and apply them to the calculation of convective

power, as summarized in Table 21.5. We recog-

nize the distinction between  and 

(Eqs. (22.1)

and (22.2)) by calculating  for each process, but

in Eq. (21.22) effectively convert the total to 

by allowing for the re-use of ohmic heat.

Conduction is treated as a negative component

of convective power in the sense of reducing the

power that would be generated if all of the heat

flux were convected.

The convective energy of each thermal

source is calculated by taking the heat originat-

ing in the range dr, at temperature T, multiply-

ing by the efficiency of its convective transport

to the core–mantle boundary, (1 T

CMB

/T ), and

integrating over the volume of the outer core. As

in the calculation of heat capacity, T

CMB

is the

reference temperature and an adiabatic temper-

ature gradient is maintained so that cooling is

everywhere proportional to absolute tempera-

ture and the thermal contribution by an element

at temperature T is multiplied by T/T

CMB

relative

to its normal heat capacity, C

. The cooling and

freezing components of the heat budget are each

accompanied by global contraction and conse-

quent release of gravitational energy. Some of

this energy is released in the mantle but only

the core component is included in Table 21.5.

As pointed out in Section 22.6, this energy must

be treated as thermal for the purpose of calculat-

ing the efficiency with which it generates con-

vective power, and not as mechanical energy.

Radiogenic heat is assumed to be propor-

tional to density, to accord with compositional

homogeneity, making it more concentrated at

greater depth. This gives it a slightly higher

thermodynamic efficiency than a volumetrically

uniform source, which is assumed in the case

of ohmic heat. Precessional dissipation, being

assumed to be 100% efficient, requires no infor-

mation about how it is converted to ohmic heat.

As discussed in Section 22.6, the energy released

by compositional convection is calculated by

assuming complete compositional mixing, that,

is the light solute is distributed according to local

density. Since it is released at the inner core

boundary, this means a somewhat smaller

energy release than if volumetrically uniform

mixing were assumed. In Section 23.5 we note

the suggestion that the mixing may not be uni-

form, but that the light ingredient rises to form a

gravitationally stable layer at the top of the core,

372 THERMODYNAMICS OF CONVECTION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

373

– [361–375] 13.3.2008 10:48AM

releasing much more energy. Seismological evi-

dence for such a layer would be needed to justify

that assumption here.

Although, in a formal thermodynamic sense,

conduction is a process of zero efficiency, it is

convenient to the present discussion to treat it as

having negative efficiency. The efficiency that it

would have if the conducted heat were convec-

tively transported gives an implied power which

is subtracted from the total power obtained by

assuming all heat to be convected. This is a sim-

ple way of accounting for the radial distribution

of the loss of convective power, as may be

inferred from Fig. 21.3, even without allowing

for the efficiency factor. The ‘inefficiency’ of

conduction may be considered modified by

refrigerator action (Section 22.8), but we treat

the refrigerator efficiency ( f in Table 21.5) sepa-

rately. It depends on the depth range over which

conducted heat exceeds the total heat flux. For

the two models represented in Figs. 21.3 and

21.4, f ¼0.091 (for A ¼0) and 0.043 (for A ¼0.2).

We identify as dynamo energy all of the

convective energy that is not either lost by

conduction or consumed in refrigerator action.

This means that we assume viscosity, ,tobe

negligible, although there are no useful direct

observations. Estimates of  for the core from

geophysical observations cover an extremely

wide range (Secco, 1995) but are only upper

bounds. Estimates based on liquid metal physics

(Poirier, 1988; Dobson, 2002) agree that a value

below 1 Pa s can be confidently assumed.

Assuming this value, we can estimate the viscous

dissipation by internal motion at 4 10

4

1

as indicated by the geomagnetic secular varia-

tion (Section 24.3), in cells of radius 80 km,

the smallest viable size suggested in

Section 24.2. This corresponds to a shear rate

"  5  10

9

1

. The corresponding dissipation

is 

2:5  10

17

3

, compared with 2 

9

3

attributed to ohmic dissipation. As we

point out in Section 24.7, the kinetic energy of

core motion is very small compared with the mag-

netic energy. The convective forces work directly

against the magnetic field and do not establish

significant kinetic energy, so, with negligible vis-

cosity, the convective power is converted directly

to magnetic field energy with no losses. Thus, we

identify the convective energies in Eqs. (21.23) and

(21.24) as dynamo energy and divide by the inner

core lifetime, , to obtain the mean dynamo power

for this period, as plotted in Fig. 21.4.

The mean power plotted in Fig. 21.4, and the

equations in Section 21.4 on which it is based,

ignore the variations with time of the convective

driving forces. We now take a closer look at this.

The obvious variation is that of the radiogenic

heat, which, being attributed to

K (half life 1.25

billion years), was more than ten times as strong

early in the life of the Earth. The dynamo energy

of the non-radioactive model (A ¼0) in Fig. 21.4 is

only marginally adequate, and we recognize the

dynamo as a robust feature of the Earth, for

which marginal viability is unconvincing. We

therefore refer to the 0.2 terawatt model as a

preferred model. In this case the early radiogenic

heat would have been 2 terawatts, which has no

dramatic effect on the thermal history calcula-

tion in Section 23.5. However, 2 terawatt models,

as have been suggested on account of higher

assumed conductivity, would release 20 tera-

watts in the early core and this is difficult to

rationalize with the thermal history.

Dissipation by precessional torques would

also have been stronger in the past. Although,

by our estimate it was never a major contributor

to core energy, being mechanical energy it could

be almost 100% efficient for dynamo action,

although there must be some ohmic dissipation

in the mantle. By a calculation presented in

Section 24.7, we estimate that it would have

provided about 7 10

W to the early dynamo,

a partial offset to the variation in compositional

convective energy that we now examine.

In the Q column of Table 21.5 compositional

separation appears as a significant but far from

dominant source of heat, but its high efficiency

makes it the biggest contributor to the E column

of the table. But the relative proportions of the

entries in this column change with time. The

rates of energy release by latent heat and compo-

sitional separation are proportional to the rate of

growth of the inner core volume, but the heat

release by general cooling is proportional to

the rate of change in temperature. The ratio of

these two rates depends on the inner core size.

Lister and Buffett (1995) pointed out that the

22.7 DYNAMO POWER 373

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

374

– [361–375] 13.3.2008 10:48AM

compositional and freezing contributions were

smaller when the inner core was small. We show

here how this arises and consider the consequen-

ces in Section 23.5.

Both the adiabatic and melting point gra-

dients are proportional to the pressure gradient

and therefore to gravity. In the inner core range

this is almost proportional to radius, as it would

be exactly in a uniform sphere. Thus dT/dr / r,

and as the boundary temperature changes with

time, t, so the temperature of the boundary

varies with its radius as

ICB

=dt /rdr=dt: (22:39)

But the inner core volume varies as

dV=dt ¼ 4p r

dr=dt; (22:40)

so that

dV=dt / rdT

ICB

=dt: (22:41)

To a sufficient approximation for this purpose

ICB

CMB

and we can substitute dT

ICB

/dt ¼(T

ICB

CMB

)dT

CMB

/dt in Eq. (22.41) to identify it with

the cooling rate, as considered in the discussion

of heat capacity (Section 21.3). The rate at which

growth of the inner core contributed to dynamo

power is proportional to its radius and would

have begun gradually. There was no sudden

onset and therefore no discontinuity for which

evidence could be sought in the paleomagnetic

record.

We need to consider the variation in dynamo

power over time in the light of Eq. (22.41). The

rate at which the core loses heat to the mantle is

controlled by the physical properties and con-

vective processes in the mantle, particularly

the D

boundary layer. Stacey and Loper (1983)

argued that it is stabilized by two competing

effects: as the mantle cools and stiffens, so it

slows all convective processes, but it cools faster

than the core and it is the temperature differ-

ence that drives the core-to-mantle heat flux. If

we accept that it is the heat flux from the core

that is controlled in this way and not the rate of

change in temperature, then without any change

in the heat flux the cooling rate slows as the

inner core grows. This occurs irrespective of

radioactivity because the effective heat capacity

of the core increases with the inner core size. But

if there were ever no inner core, then, in the

absence of the very efficient convective pro-

cesses represented by items 3, 4 and 5 in

Table 21.5, the dynamo could not have been

maintained without a much greater contribution

by items 1, 2, 6 and 7 than would be required to

maintain a constant heat flux. This problem is

pursued further in Section 23.5 with the conclu-

sion that the constant heat flux argument

appears satisfactory for the last 2 billion years

but not for the earlier period.

In Section 23.5 we refer also to the sugges-

tion that the light solute rejected by the inner

core may become concentrated at the top of the

core, releasing much more gravitational energy

than with uniform mixing. However, a seismo-

logical indication that this is so would be

needed to make it the basis of a core energy

calculation.

22.8 Refrigerator action in the core

In Sections 21.4 and 22.7 (see also Table 21.5) we

refer to refrigerator action as a feature of the

core energy balance. We now add a note on

how this arises and what it means from a thermo-

dynamic perspective. As a simple example con-

sider a large fluid body of negligible viscosity,

and with no heat sources, in a container which

is perfectly insulating. We introduce a stirring

mechanism strong enough to maintain an adia-

batic temperature gradient. Upward conduction

of heat would tend to reduce this gradient,

but since it is maintained by stirring there is a

continuous flow of heat. It cannot escape from

the top of the container and is carried down,

against the temperature gradient, by the stirring

action. This is refrigerator action, which

requires mechanical power equal to the power

that would be generated by upward convection

of the same heat. This power would be

released as heat in the fluid, causing a general

temperature rise.

As Fig. 21.3 indicates, it is possible for con-

ducted heat to exceed the total heat flux in the

outermost part of the core and in this case t he

difference must be carried down mechanically.

374 THERMODYNAMICS OF CONVECTION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

375

– [361–375] 13.3.2008 10:48AM

This can be accomplished b y compositional con-

vection. The energy available for dynamo action

isreducedbyanamountthatdependsonhow

far the heat must be transported, being deter-

mined by the temperature range over which i t is

transported. The ratio of the mechanical power

required to the heat transp orted is the factor f

in Eq. (21.22) and Table 21.5. Thus, for the

A ¼0.2 t erawatt model in Fig. 21.3, f ¼0.043,

but for the A ¼0 model, with no radioactivity,

the heat must be carried down t o greater depths

and f ¼0.091.

22.8 REFRIGERATORACTIONINTHECORE 375

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C23.3D

–

376

– [376–388] 13.3.2008 10:47AM

Thermal history

23.1 Preamble

A thermal history of the mantle can be calculated

almost independently of the core. The logic for

this is that core heat is carried up through

the mantle by narrow, buoyant plumes that

have only a weak interaction with the plate

tectonic convection process that cools the

mantle. The converse is not true. The core is

cooled by loss of heat into a thermal boundary

layer at the base of the mantle and so depends

on the temperature difference between the

core and the deep mantle, 100 to 200 km

above the boundary, as well as on mantle

rheology. The boundary layer must have devel-

oped, that is, the mantle must have cooled

substantially, before significant core cooling

could occur.

Mantle rheology also controls the cooling

of the mantle itself, but it is a mutual control.

Tozer (1972) drew attention to the fact that the

strong dependence of viscosity on temperature

(Eq. (10.27)) has a stabilizing effect on both. If the

mantle were to become too cool and viscous to

convect at the ‘normal’ rate, convection would

slow until radioactive heating caught up. But this

does not mean that the heat loss is in equili-

brium with the heat source, because the source

is not constant. With diminishing radiogenic

heat, convection slows down and this means

that the mantle is cooling, as is most convinc-

ingly demonstrated by a consideration of the

heat balance equation (Eq. (23.14)). Application

of this equation shows that the rate at which

radiogenic heat decreases is an important con-

trol on thermal history.

The other basic principle that we apply is

referred to in Section 13.3: convection is driven

by sources of buoyancy, positive or negative,

generated at boundaries. This means that we

need a quantitative description of the process

of surface heat loss. As discussed in Chapter 20,

this is quite different in continental and oceanic

areas. Both must be accounted for. The conti-

nents move about and conduct heat to the sur-

face, but are otherwise non-participants in

convection and act as blankets on the 40% of

the surface area that they cover. This is an area

of 2 10

, in which we include the sub-

merged continental margins. Of greater interest

to the subject of this chapter is the 3.1 10

of oceanic crust/lithosphere, which is a thermal

boundary layer and acts as the exhaust of the

mantle heat engine. It loses heat to the sea

until it reaches a subduction zone and returns

to the mantle, to be replaced by fresh, hot litho-

sphere at an ocean ridge. Heat is lost from the

oceanic lithosphere by a combination of thermal

diffusion and circulation of sea water in cracks.

These processes vary differently with time. The

hydrothermal circulation decreases in impor-

tance with increasing age of the lithosphere.

This means that, in extrapolating backwards in

time to periods of more rapid convection and

shorter residence time of oceanic lithosphere,

the relatively greater importance of hydrother-

mal circulation must be recognized. But the two

effects are not independent and there is no

theory of the total process, so we introduce a