Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

397

– [389–416] 13.3.2008 2:46PM

scale has a straightforward explanation as the size

of the smallest magnetically controlled vortex

in the core motion. We therefore identify it with

the upper bound of the spatial spectrum of the

field at core level, corresponding to harmonic

degree l ¼136, and model the core surface field

by current loops of all radii down to this limit.

Although the dipole field (l ¼1) is not as dom-

inant at core level as it is at the surface, its strength

is clearly above the trend of the higher harmonics

(Fig. 24.2, open circle). The difference is more than

a statistical effect, indicating that the dipole field

has a special role in the geodynamo, so that we

give it separate consideration in calcula ting the

total rms field strength at core level. The quadru-

pole (l ¼2) field is lower than the trend and this,

too, probably has a physical cause in the dynamo,

but it is not separately identified in the numbers

that follow. The relationship between these field

components is considered in a more general way

in Sections 25.3 and 25.4, using evidence of a

fundamental distinction between harmonics that

are symmetric or antisymmetric about the equa-

tor. Omitting the dipole term, the downward-

continued core field at the core–mantle boundary

has a spectrum represented by the upper line in

Fig. 24.2 and given by

ðCMBÞ¼1:085  10

ð0:959Þ

: (24:24)

This may be used to calculate the total rms field

strength,

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

, for any range of harmonics.

With an independent calculation for the dipole

field from the l ¼1 coefficients in Table 24.1, the

sums of all field components of differently selected

groups of harmonics (added in quadrature) are

rms

ðCMBÞ¼2:61  10

nT for l ¼ 1;

4:90  10

nT for l ¼ 2 to 136;

5:55  10

nT for l ¼ 1 to 136:

By this estimate the poloidal field strength at core

level is about 5.5 10

nT (5.5 Gauss). If we con-

sider the spectrum to be white 100 km or so inside

thecorethenahighervalue,11.810

nT,

applies. This number is derived from observations

of the poloidal field, but it cannot be the total field

in the core. Dynamo theory requires, in addition

to the observed poloidal field (a field with poles),

toroidal fields that are confined to the source

region and are not observable in principle. The

simplest toroidal field would be found in the mate-

rial of a ring on which a current-carrying coil is

uniformly wound. With care in winding the coil in

layers progressing both backwards and forwards,

so that there is no current component along the

toroidal ring, the field is confined to it, forming a

closed loop with no poles. From coupling of the

inner core to nutations, the strength of the radial

field penetrating it was estimated by Mathews

et al. (2002) to be 7.2 10

nT. We interpret this

as the total field strength within the core, includ-

ing the toroidal field, because the inner core is a

slightly better conductor than the outer core

(Section 24.4) and can support the currents

responsible for the toroidal field. On this basis,

the toroidal field is about five times as strong as

the poloidal field (see Section 24.7).

24.3 The secular variation and

the electrical conductivity

of the mantle

The slow variation in the geomagnetic field,

driven by the changing pattern of motion in the

core, is referred to as the secular variation. These

changes occur on a time scale that extends from 1

year or so upwards, into the range of the varia-

tions caused by solar disturbances, which include

an 11-year period related to the sunspot cycle.

However, most of the extra-terrestrial effects are

more rapid than any observable changes in the

core field and no serious confusion arises.

As mentioned in Section 24.1, the historical

record is too short to display some of the geo-

magnetic phenomena that have been recognized

from the study of paleomagnetism. However, for

the past few hundred years, and especially the

last 50 years, we have a far more detailed picture

of the behaviour of the field than could ever be

expected for the remote past. This section is

concerned primarily with the interpretation of

the historical observations. Barton (1989) has

given an overall review and a detailed analysis

of the changing pattern of the field at core level

24.3 SECULAR VARIATION AND MANTLE CONDUCTIVITY 397

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

398

– [389–416] 13.3.2008 2:46PM

is reported by Bloxham et al. (1989). Yukutake

(1989) has summarized the relevant theories.

The time-variations of the spherical harmonic

coefficients of the field,

g and

h (Table 24.1b), are

tabulated only up to degree 8, that is for features

with surface wavelengths of 5000 km or greater.

Uncertainties in higher degree terms are too great

for them to be meaningful. The corresponding

wavelength limit at core level is 2700 km. It is

evident from the table that even for 5 l 8the

values of

g and

h are very small and are not pre-

cisely determined. Nevertheless, they suffice to

give an idea of the relative rates of change of

features of different sizes. A quantity analogous

to R

(Eq. (24.22)), but using the rates of change of

the harmonic coefficients, is

¼ðl þ 1Þ

m¼0







; (24:25)

and we can define a reorganization time 

for

the degree l components of the field,



¼ R

ðÞ

1= 2

: (24:26)

We expect the reorganization times, 

,tobe

systematically related to the dimensions of

current loops in the core that would produce

the different harmonic features of the field.

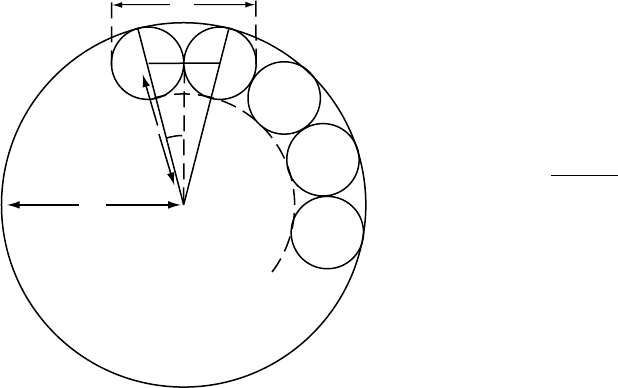
Consider the geometry of Fig. 24.3, which

represents a series of circular current loops,

each of cross-sectional radius d/4, fitted into the

core, radius R

. We have

sin  ¼

d=4

 d=4

; (24:27)

and if there are l current loops, that is l pairs of

small circles in a complete circumference, then

4 ¼ 2p=l (24:28)

and the variation of loop diameter with har-

monic degree, l,is

d ¼ 4R

1 þ 1= sin p=2l

ðÞ½

1

: (24:29)

For current loops of a particular shape and con-

ductivity, the electromagnetic relaxation times

vary as the square of the linear dimensions

(Eq. (24.43)), so we might expect the degree reor-

ganization times (Eq. (24.26)) to vary as



/ d

: (24:30)

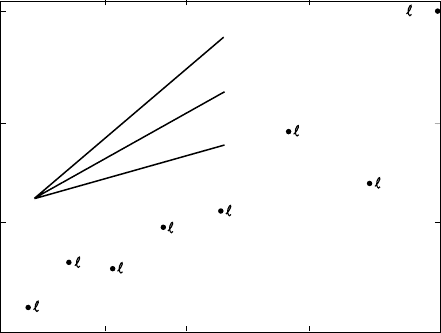
Figure 24.4 is a plot of 

vs d,bothonlogarithmic

scales, permitting the reasonableness of Eq. (24.30)

to be judged by eye. The l ¼1(dipole)termstands

above the trend and l ¼2 below it. This appears to

have fundamental significance and to be related to

the dynamo mechanism, with magnetic energy

fed from l ¼2tol ¼1. Indeed, the trend for all

the odd l harmonics is systematically above that

for the even l terms. McFadden et al. (1988) model

the secular variation in a way that distinguishes

dipole and quadrupole ‘families’ of harmonics by

their symmetry about the equator, and in

Section 25.3 we refer to paleomagnetic evidence

for this distinction. The non-dipole field is not

simply fluctuating noise superimposed on the

dipole but an essential feature of the dynamo.

With respect to the approximate validity of

Eq. (24.30), ignoring the odd/even difference, we

can take a linear regression of log  vs log d to

compare the gradient with the value 2 suggested

by electromagnetic relaxation. Using all eight

values the gradient is 2.5 0.5 (one standard

deviation). If the dipole (l ¼1) is omitted, then

the gradient is 1.7 0.4, and if both l ¼1 and l ¼2

– d /4)

/ 4

FI G U R E 24.3 Geometry used to calculate the

relationship between the size, d, and number, l,of

current loops that can be fitted into the perimeter of the

core (Eq. 24.29). The current loops are toroids, each

represented by a pair of small circles.

398 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

399

– [389–416] 13.3.2008 2:46PM

terms are omitted the gradient is 2.4 0.3. But

the notion of a simple relaxation process cannot

be valid. The values of  are smaller by a factor 10

than the relaxation times for loops of the sizes

modelled. The changes in field structure are not

controlled by magnetic diffusion (or, equiva-

lently, ohmic dissipation) but indicate the rate

of rearrangement of the field by core motion.

This is the frozen flux principle, by which a

moving conductor carries the field with it. For

this reason we refer to  as a ‘reorganization

time’ and not as a relaxation time.

A more detailed illustration of the frozen flux

principle is presented by Bloxham et al. (1989),

who deduced the pattern of secular variation at

the core–mantle boundary from the observed

surface field at a series of dates spanning the

historical record. They followed particular fea-

tures of the field in time, using as the definition

of their boundaries the surrounding null-flux

contours where the vertical component of the

field is zero. These boundaries move about, but

if the frozen flux principle applies then the total

flux within a boundary remains constant.

Bloxham et al. (1989) concluded that, although

some diffusion is observable, it is a secondary

effect. The frozen flux condition gives a valid

representation of the observed secular variation.

A finer scale of unresolved features must be

superimposed but does not affect this conclu-

sion. With the frozen flux condition the secular

variation can be used to infer the motion of the

core surface. Eymin and Hulot (2005) applied

satellite data to this problem, concluding that

some strong vortices were apparent, but that

unseen fine-scale features of the field have

important effects.

In Section 24.1 we mention that a westward

drift has been a prominent feature of the secular

variation for the duration of the historical

record. However, when we examine archeomag-

netic and paleomagnetic data spanning several

thousand years a different picture emerges.

A paleomagnetic perspective on secular varia-

tion and the westward drift is presented in

Section 25.3. Before extensive paleomagnetic

data became available and theories were con-

strained only by the historical record, a west-

ward drift of features of the field by about 0.2 8/

year, as found by Bullard et al. (1950), was gener-

ally supposed to be a permanent feature. This has

appeared paradoxical because the frozen flux

principle locks the field lines to the outermost

part of the core and electromagnetic coupling

would bring it to rotational equilibrium with

the mantle in a decade or so. An attempt to

explain the westward drift in terms of propagat-

ing hydromagnetic waves, first suggested by

Hide (1966) remains of interest, whatever the

duration of the drift. Braginsky (1991) empha-

sized the role in dynamo theory of travelling

disturbances subject to magnetic, Archimedean

(buoyancy) and Coriolis pressures and known by

their acronym, MAC waves. The assumption is

1000

300

100

0.3 0.4 0.5 0.7 1.0

Current loop diameter / Core diameter

Field reorganization time, τ (years)

τ ∝ d

= 4

= 1

FI G U R E 24.4 A plot of field

reorganization time, 

, for harmonics

of degree l (Eq. (24.26)), against the

diameters of current loops in the outer

core that would be responsible for these

harmonics of the field (Eq. (24.29)). The

field data used are those in Table 24.1.

Numbers against the data points give

the harmonic degrees.

24.3 SECULAR VARIATION AND MANTLE CONDUCTIVITY 399

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

400

– [389–416] 13.3.2008 2:46PM

that they propagate along the toroidal magnetic

field, B

, in the core, and that this is much stron-

ger than the observed poloidal field. In the

approximation that the Archimedean pressure

is neglected, the wave is known as a magneto-

geostrophic mode and, for wavelength l, has a

phase speed

MAC

 pB

=

!l; (24:31)

where  10

kg m

3

is the local density, ! ¼

7.292 10

5

1

is the Earth’s rotational speed,

and the characteristic dimension l/2 corres-

ponds to the features that are seen to drift,

that is at least 4 10

m (4000 km). A wave with

wavelength-dependent speed given by Eq. (24.31)

is strongly dispersive. Applying Eq. (16.49), the

group speed is

MAC

¼ 2V

MAC

 2pB

=

!l; (24:32)

which is the speed of observable features. For a

drift speed of 0.28/year or 4 10

4

1

at the

core surface, B

 0.02 T (200 Gauss), that is 30 to

40 times as strong as the poloidal field. This

explanation faces two difficulties. No strong dis-

persion is observed – the Bullard et al. (1950)

analysis concluded that different harmonic com-

ponents of the field drifted at the same rate. Also,

the energy requirement of a dynamo maintain-

ing a 0.02 T field is implausibly high. So, we seek

another explanation for the persistence of the

westward drift in the historical record. The only

obvious possibility appears to be gravitational

coupling of the inner core to the deep mantle

(Section 24.6).

As we mention in Section 24.1, electrical con-

duction in the mantle influences our observa-

tions of the field. For the purpose of this

discussion the mantle is solid and stationary,

with only a passive role as the seat of induced

electric currents, and it has a much lower con-

ductivity than the core. The effect is essentially

the same as the frozen flux principle, as applied

to the core, in that the induced currents oppose

motion of the field relative to the material of the

conductor. The fixity of the mantle means that it

resists changes to the field in it. This is Lenz’s law

of electromagnetic induction. In the case of an

oscillatory field, the frequency of oscillation

determines how effectively it penetrates the

conductor. This is the skin effect. The amplitude

of oscillation is reduced by a factor 1/e at a depth

termed the skin depth, which is a function of

frequency and conductivity. There is also a

phase delay. For a plane wave, of angular fre-

quency !, entering a semi-infinite medium of

conductivity , the variation with depth z of its

amplitude and phase are given by

B ¼ B

z

sinð!t  zÞ; (24:33)

where

 ¼ 1=z

¼ 

!=2ðÞ

(24:34)

and z

is the skin depth.

The trends in the data plotted in Figs. 24.2 and

24.4 give no indication that the more rapid com-

ponents of the secular variation (larger l or

smaller ) are noticeably attenuated by mantle

conduction. The conductivity is not high enough

to influence the observation of changes occurring

over periods of 30 years or more. Evidence that

changes occurring in a period of about 1 year can

penetrate the mantle arose from an event in

1969–70, when there was a widespread, probably

global, impulsive change in the secular variation,

although possibly not synchronous everywhere.

It is referred to as the 1969 geomagnetic jerk. It is

best displayed in plots of time derivatives of the

eastward component of the field (Y ), because this

is least affected by external disturbances. At many

observatories there was a sharp change in dY/dt,

suggesting a discontinuity in d

Y/dt

. ‘Sharp’ in

this context means that it occurred within about a

year. Noise of external origin precludes any pos-

sibility of seeing more rapid effects if they were to

occur. The jerk is surprising, both because it

imposes a bound on mantle conductivity that is

lower than previously supposed and because it is

difficult to understand how a global change in

core motions could occur so rapidly. It was some

years before the possibility of an external influ-

ence was securely discounted, but the internal

origin is not now in doubt (Courtillot and

LeMou¨el, 1984). There is some evidence of earlier

jerks, although less well documented.

As we note below, the mantle conduct-

ivity increases sharply at the 660 km phase boun-

dary and so we concentrate attention on the

400 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

401

– [389–416] 13.3.2008 2:46PM

transmission of a jerk through the more highly

conducting lower mantle, depth range

Dz 2200 km. Consider the attenuation in ampli-

tude, jBj, of a field component oscillating with

angular frequency ! ¼p/year ¼10

7

1

to repre-

sent the spectrum of the jerk, as it propagates

upwards, ignoring its phase. By Eq. (24.33), over

the range dz the variation is

d Bjj

Bjj

¼dz ¼

!=2ðÞ

dz; (24:35)

and integrating over a total depth range Dz,

lnð B

Þ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



!=2

z



¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



!=2

h

1=2

iz: (24:36)

If we take jBj/B

¼0.5, that is a 50% attenuation of

the signal, then h

1/2

i¼1.78 S

1/2

1/2

,thatisan

average lower mantle conductivity of 3.2 S m

1

Although this is a simplified, plane wave approx-

imation to a spherical situation and assumes a

uniform conductivity, it gives a reasonable order

ofmagnitudeestimateoftheaveragelowerman-

tle conductivity.

A complementary approach to mantle con-

ductivity is to observe the effect of electromag-

netic signals originating in upper atmospheric

disturbances. Surface field variations are super-

positions of external (inducing) and internal

(induced) field variations. Being internal, the

induced field can be represented by a potential

with the spherical harmonic form of Eq. (24.14)

or the terms with unprimed coefficients in

Eq. (C.11) of Appendix C. The inducing (external)

fields must be represented by the primed coeffi-

cients C

and S

in Eq. (C.11). The difference

appears in the radial dependences. The potential

itself is not observable, but its derivatives, the

field components north (X), east (Y) and down-

wards (Z) are all recorded. Differentiating

Eq. (C.11), ignoring the summation, that is con-

sidering only the zonal harmonic l (with m ¼0),

and then substituting r ¼a for observations on

the surface,

X ¼ð1=rÞð@V=@Þ

¼ð1=a

ÞðC

þ C

Þð@P

ðcos Þ=@Þ; ð24:37Þ

Z ¼ð@V=@rÞ

¼ð1=a

Þ½ðl þ 1ÞC

þ lC

P

ðcos Þ: ð24:38Þ

The different radial dependences of the primed

and unprimed terms give opposite signs to the

terms in Eq. (24.38), but the same signs in

Eq. (24.37), allowing the ratio C /C

to be obtained

from Z/X. This is the principle by which Gauss

demonstrated that the main field is of internal

origin, but we are considering here disturbance

fields for which the internal components (the

unprimed coefficients) must be explained by cur-

rents induced in the Earth by the external com-

ponents. The radial variation in conductivity is

obtained from the frequency variation of the

ratio of internal to external fields.

In the approximation that the Earth is spheri-

cally symmetrical, the harmonic components of

inducing and induced fields correspond, but

there are complications. Field disturbances dur-

ing magnetic storms are different on the sunlit

and dark sides of the Earth. With sufficiently

extensive data this can be accommodated by

spherical harmonic analysis, but the induced

field is subject to a phase delay, as in

Eq. (24.33), and the Earth is rotating. The diurnal

variation is particularly useful in this connec-

tion, because it has a very specific frequency,

and there is a smaller but still well observed

semi-diurnal variation, but these appear as

waves propagating around the Earth, requiring

a slightly different analysis. Greatest penetration

is achieved with the longest period disturbances,

which are essential to the estimation of lower

mantle conductivity, but beyond a few months

become confused with the secular variation. This

limits the reliable information to the top part of

the lower mantle, where a conductivity of about

1Sm

1

is inferred. This is consistent with the

average lower mantle value estimated above

from the 1969 jerk.

We conclude that there is no dramatic radial

variation in lower mantle conductivity, but tem-

per this conclusion by noting the possibility of

lateral heterogeneity, especially at the base of

the mantle (layer D

). This is recognized in the

conductivity profile in Fig. 24.5. A widely can-

vassed suggestion is that the deep mantle

24.3 SECULAR VARIATION AND MANTLE CONDUCTIVITY 401

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

402

– [389–416] 13.3.2008 2:46PM

under the Pacific Ocean is so much more con-

ducting than the mantle elsewhere that it limits

the penetration of the secular variation and

the non-dipole field over a wide area c entred

on Hawaii (the Pa cific ‘dipole window’). The

evidence is reviewed by Merrill et al. (1996,

pp. 259–261), who c onclude that the suggestion

arises from a misinterpretation of paleomag-

netic data and that the secular variation

recorded by Hawaiia n lavas is no different

from that seen elsewhere. We note an argument

by Buffett (1992) that a layer of metallic con-

ductivity, with a thickness of a few hundred

metres, at the base of the mantle would explain

a phase lag in nutational motion. A complete

layer of very high conductivity appears improb-

able and patches are more likely. They could

have strong electromagnetic interaction with

unseen fine-scale features of the field (or

account for ‘standing’ features) b ut be small

enough to have little influence on the global

secular variation. This possibility is allowed

in Fig. 24. 5.

The mantle has a conductivity that is very

low compared with that of metals, including

the core. It must be classified as a semi-conductor.

A feature of semi-conductors is an exponential

dependence of conductivity on temperature.

This was exploited by Dobson and Brodholt

(2000) to infer that there is no major jump

in temperature from the upper mantle to the

lower mantle, unless the mineralogy has been

misunderstood. This conclusion disallows the

hypothesis of separate convective circulations

in the upper and lower mantles because that

would require a thermal boundary layer between

them.

24.4 Electrical conductivity

of the core

As far as we can tell, the Earth has always had a

magnetic field, certainly for at least 3.5 billion

years of its 4.5 billion year life. The geomagnetic

dynamo is a robust feature and requires a core

conductivity that is high enough to ensure that

the dynamo is much more than marginally sta-

ble. The outer, fluid core must be a metallic con-

ductor. There is no doubt or difficulty about this

because available cosmochemical and geochem-

ical evidence (Section 2.8) points to iron as the

major core constituent. A necessary conclusion

is that the thermal conductivity of the core is

also characteristic of a metal, because thermal

and electrical conductivities are linked by the

Wiedemann–Franz law (Eq. (19.63)). There is,

therefore, a continuous conductive heat loss by

the core and this imposes a requirement on core

energy sources that has provoked a vigorous

debate over the need for a radioactive heat

source. Stevenson (2003) pointed out that con-

ductive heat loss is the most serious limitation

on planetary dynamos. The chemical argument

for potassium in the core is a subject of doubt

(Section 2.8), and implicitly assumes that there is

a strong physical argument for the need for it as

a heat source. But that depends on the conduc-

tive heat loss and therefore on the estimate of

conductivity, which is also seriously uncertain.

Stacey and Loper (2007) argue that core conduc-

tivity is lower than has generally been supposed,

perhaps low enough to avoid completely the

need to assume radiogenic heat. The energy

problem is a subject of Sections 21.4 and 22.7.

Conducting patches

Crypto-oceans

Core (σ

= 2.76 x 10

S m

–1

)

0 1000 2000 3000

Depth (km)

–2

Conductivity, σ

(S m

–1

)

FI G U R E 24.5 Electrical conductivity of the mantle.

402 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

403

– [389–416] 13.3.2008 2:46PM

First, we consider the conductivity require-

ment of the dynamo. In Section 24.5 this is repre-

sented in terms of the dimensionless parameter,

magnetic Reynolds number

¼ Lv



; (24:39)

where L is the scale size of motion at speed v,



¼4p 10

7

1

is the permeability of free

space and 

is conductivity. Dynamo action is

favoured by increasing the size, speed of motion

and conductivity; R

is a product of all three. The

argument leading to Eq. (24.45) (below) indicates

that, for a sphere of radius L, a self-sustaining

dynamo requires R

> p

 10. This is also the

factor by which estimated electromagnetic relax-

ation times exceed the reorganization times for

harmonic components of the field plotted in

Fig. 24.4. We assume this limiting condition to

apply to the smallest viable current loops in the

core and that their size is indicated by the

160 km thick surface layer suggested by the spa-

tial spectrum of the field in Section 24.2, that is,

loops of cross-sectional radius 80 km. Putting

L ¼80 km in Eq. (24.39), with v ¼4 10

4

1

as indicated by the speed of core fluid motion in

the secular variation study by Bloxham et al.

(1989), we have 

 2.5 10

1

. Although

rough and simplistic, this is a reasonable esti-

mate of core conductivity and happens to be

the mean of the values at the top and bottom of

the outer core, as estimated below.

By the standard of metals, iron is a poor con-

ductor. If the core were made of copper, with a

conductivity more than 10 times higher, then

core energy would be conductively dissipated

too fast to permit dynamo action. In extrapolat-

ing the conductivity of iron to core conditions, it

is helpful to understand the reason for the differ-

ence between copper and iron. An isolated cop-

per atom has a single electron in its highest (4s)

occupied state, with all inner shells filled, includ-

ing a full complement of ten 3d electrons. When

the atoms are combined in a metal, interactions

between them spread the energy levels into

bands, corresponding to the discrete shells of

individual atoms. The lowest bands are filled

to an energy level, known as the Fermi level,

and the higher states are left vacant, except for

thermal excitation of electrons between states

within an energy range of order kT at the Fermi

level. In metallic copper all the 3d states remain

below the Fermi level and, as for the filled elec-

tron shells of insulators, cannot participate in

conduction. The 4s band in copper is half-filled,

with one electron per atom in the two available

states. With the Fermi level in the middle of

the 4s band, electrons close to it can readily

change states, making copper a good conductor.

The effective number of these mobile electrons

decreases with pressure, as the band spread

increases.

Iron has three fewer electrons per atom than

copper and its 3d band is only partly filled, with

the more widely spread, overlapping 4s band

also partly filled. Both 4s and 3d electrons are

available to contribute to conduction. Although

the available 3d electrons are more numerous,

with a high density of states at the Fermi level,

they are more tightly bound and much less

mobile. Conduction is dominated by the 4s elec-

trons. It is limited by the scattering of electrons

by phonons (lattice vibrations) or crystal irregu-

larities, such as those caused by impurity atoms.

The probability that an electron, accelerated by a

field, will be scattered by any of these effects

depends on the number of alternative states

into which it can be scattered. For the 4s elec-

trons in iron this number is greatly enhanced by

the high density of 3d states. This is the reason for

the high resistivity of iron, relative to copper.

At low temperatures the effect of the 3d states is

reduced by ferromagnetic alignment of their

spins, invalidating any direct extrapolation from

laboratory pressure–temperature conditions to

the core. But the properties of iron at high tem-

perature are well known, although extrapolation

to core pressures requires some idea of the very

different behaviour of the 4s and 3d states.

Experimental observations are also a subject

of difficulty. Recent theories have been con-

strained by shock wave observations on iron

and its alloys with Ni and Si up to pressures

in the core range, but measurements on iron by

Bi et al. (2002) have given much higher resistiv-

ities than earlier reports. Their samples were

encapsulated in sapphire to avoid what they

argued was a defect in earlier experiments,

with the metal samples encapsulated in epoxy,

24.4 ELECTRICAL CONDUCTIVITY OF THE CORE 403

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

404

– [389–416] 13.3.2008 2:46PM

which becomes conducting at a pressure of

about 50 GPa. Shunting by epoxy biases low

the apparent resistivity. This report prompted a

re-examination of the theoretical arguments

(Stacey and Loper, 2007).

The scattering of electrons by thermal vibra-

tions can be regarded as a response to instanta-

neous deformation or irregularity of a crystal

lattice. This increases with temperature but

decreases with pressure, which reduces the

amplitude of atomic vibration. Thermal disorder

is essentially the same as that causing melting,

and so we expect the effect of scattering on resis-

tivity to be almost constant on the melting curve.

Stacey and Anderson (2001) gave this argument a

mathematical basis, concluding that it implies

constant resistivity on the melting curve.

However, this conclusion can apply only to elec-

tronically simple metals, such as copper, and not

to iron, which has overlapping bands with differ-

ent properties. In a simple metal with a single

conduction band, the number of electrons avail-

able for electrical conduction, those within

about kT of the Fermi level, is proportional to

the density of states at that level. But the proba-

bility of scattering, being proportional to the

number of available states into which an elec-

tron can be scattered, depends on the same num-

ber. Thus, to first order, conductivity does not

depend on the density of states, provided it is

high enough to give metallic conduction, and so

is not materially affected by the increasing

spread of the band by compression. In iron the

4s states, which dominate conduction, are spread

much more than the 3d states and the effective

number of conduction electrons decreases faster

with pressure than the number of states into

which they can be scattered. For this reason, pres-

sure reduces the conductivity of iron more than

it does for metals such as copper, in which all

electrons at the Fermi level are of the same kind.

A calculation by Bukowinsky and Knopoff (1977)

indicated that at four-fold compression the entire

4s band would be above the Fermi level, in which

case the conductivity would be very low, being

due to 3d electrons only, but this is well beyond

the terrestrial pressure range and is relevant only

because it indicates a trend. Stacey and Loper

(2007) made the simple assumption that the 4s

states follow a relationship with the form of

Eq. (19.17), but that the density of 3d states is

much less affected by compression. On this basis

they applied this equation as a multiplying factor

to the resistivity of pure iron, as calculated by

assuming that it is constant on the melting

curve, and obtained 2.72 mO matthetopofthe

outer core and 3.75 mO matthebottom.

The addition of impurity atoms to a solid

metal introduces static irregularities to its lat-

tice, causing an increment in resistivity that

is independent of temperature and, for small

concentrations, proportional to the impurity

concentration. Thus, at atmospheric pressure a

constant impurity contribution to resistivity

becomes a decreasing proportion of the total

as the resistivity increases with temperature. It

is often supposed that the impurity effect can

be neglected at high temperatures. However,

although pressure reduces the thermal effect, it

does not reduce the effect of impurity disorder,

but, as experiments by Bridgman (1957) showed,

increases it. With a sufficient impurity concen-

tration the normal decrease in resistivity with

pressure may be masked, and pressure and

temperature both cause increased resistivity.

Systematic measurements by Bridgman on a

variety of iron alloys at pressures up to 10 GPa

appear still to be the most relevant data that

we have. They show that, for a variety of alloy-

ing elements, the break-even concentration, at

which pressure has no effec t on the resistivity

of iron alloys at constant temperature, is about

14 atomic %. This is comparable to the concen-

tration of light elements required to explain

the core density (Section 2.8), so the effect of

pressure on impurity resistivity in the core is

probably slight, and we adopt the Stacey and

Anderson (2001) v alue, 0.90 mO m.

Adding the impurity effect to the pure iron

resistivity estimated above, we have a t otal

resistivity of 3.62 mO m at the top of the core

and 4.65 mO m at the bottom of the outer core.

Corresponding conductivities are 2.76 10

1

and 2.15 10

1

. For the inner core,

with less impurity resistivity, the estimated con-

ductivity is about 2.7 10

1

. As we note

in Section 19.6, application of Eq. (19.63), with a

small lattice contribution, gives thermal

404 THE GEOMAGNETIC FIELD

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

405

– [389–416] 13.3.2008 2:46PM

conductivities 28.3 W m

1

at the top of the

core and 29.3 W m

1

at the bottom of the

outer core. These values are used in assessing

the core energy balance in Section 22.7, but it

must be admitted that they are insecure. The

electrical conductivity of the core is a prime

target for further study.

24.5 The dynamo mechanism

Merrill et al. (1996, Chapters 8 and 9) give a com-

prehensive review of dynamo principles; this

section selects salient features for comment.

The underlying physics of the geodynamo is

summarized in Fig. 24.6. The central idea is the

frozen flux principle, illustrated by Fig. 24.6(a),

which we have referred to in Sections 24.1

and24.3.Aswementioninconnectionwith

Eq. (24.39), and now consider more closely, if the

combination of conductivity and the scale size

and speed of motion (the magnetic Reynolds

number, R

, Eq. (24.39)) is high enough, then

the field and the fluid move together. There is

no inhibition to flow of fluid along field lines

because that generates no electromagnetic

forces; it is motion across field lines that is

opposed by electromagnetic induction (Lenz’s

law). The motion would be completely prevented

only in a superconductor, and in a normal

conductor some diffusion of the field through

the conductor occurs, generating electric cur-

rents that cause ohmic dissipation of energy.

Dynamo action is possible only if the frozen

flux principle prevails over field diffusion. As

we demonstrate below, this requirement is sat-

isfied if R

exceeds about 10. An important point

that is illustrated by Fig. 24.6(a) is that magnetic

energy is created. The intensity of the field is

represented by the closeness of the field lines,

which is increased in the shear zone, where the

total field is a vector superposition of the origi-

nal field (upwards in the diagram) and a trans-

verse field generated by the motion.

For dynamo action to be effective, the process

of field regeneration, represented by Fig. 24.6(a),

must be rapid enough to overcome the diffusion

of the field out of the conductor. We can repre-

sent the two processes by time constants. For the

regeneration process the time constant is



¼ L=v; (24:40)

where L is the scale of velocity shear with speed

v, that is field lines can be moved over a distance

L in the time 

if the relative speed is v. This must

be less than the time constant 



for decay of the

field by diffusion out of the conductor, that is, by

ohmic dissipation,





¼ B=ðdB=dtÞ; (24:41)

where (dB/dt) is the rate of free decay of an

unmaintained field, for example in a stationary

(a)

(b)

(c)

FI G U R E 24.6 Basic physics of the dynamo mechanism, following the ideas of W. M. Elsasser. (a) A velocity shear

perpendicular to a magnetic field in a fluid conductor deforms and intensifies the field. Field intensity is represented

by the closeness of the field lines. (b) Differential rotation between the inner and outer parts of the outer core draws

out the field lines of an initial poloidal field to produce an additional toroidal field in the shear zone. This is referred to

as the !-effect because it depends on differential rotation (at speed !). (c) A toroidal field, B

, is drawn out by a

convective upwelling (at speed v

) and, in the absence of rotation, would follow the dotted line. The Coriolis effect

gives the fluid a helical motion, with rotational component v

(anticlockwise in the northern hemisphere), deforming

the field loop out of the plane of the diagram. This is the basis of the -effect, generating a poloidal field from a

toroidal one.

24.5 THE DYNAMO MECHANISM 405

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C24.3D

–

406

– [389–416] 13.3.2008 2:46PM

conductor. Thus, a necessary condition for

dynamo action is





: (24:42)

The free decay time-constant, 



, is an un-

ambiguous quantity only for specific field pat-

terns that maintain their forms as they decay

in strength. We have a special interest in com-

paring the value of 



for the dipole field with

the observed reorganization time, 

1180

years, given by Equation (24.26). Parkinson

(1983, pp. 114–116) derived an expression for





for the simplest dipole field pattern due to

currents in a uniform sphere of radius a and

conductivity 



1

¼ 



¼ða=pÞ

=

; (24:43)

where



¼ 1=



(24:44)

is referred to as magnetic diffusivity. Unlike R

this is a material property; its value in the core

averages about 3.2 m

1

. To emphasize that this

is a diffusion problem we point out that if 

is replaced by thermal diffusivity,  ¼k/rC

(Eq. (20.2)), then Eq. (24.43) gives the relaxation

time for cooling of a sphere by thermal diffusion

(Problem 19.2, Appendix J). The relationship

between dissipation and magnetic energy

depends on the current pattern and Eq. (24.43)

applies to a pattern that remains constant as it

decays. Substituting values of 

and a for the core

in Eq. (24.43), we obtain 

1

¼3.9 10

s ¼12 200

years. This is ten times the longest observed field

reorganization time constant 

,asplottedin

Fig. 24.4, satisfying Eq. (24.42).

Comparing 



, by Eq. (24.43), with 

,by

Eq. (24.40) with L ¼a, the inequality in

Eq. (24.42) becomes





av > p

: (24:45)

The quantity on the left-hand side of this equ-

ation is the magnetic Reynold’s number, R

(Eq. (24.39)), with L identified as the radius of

the sphere. As may be verified by substituting

units or dimensions of its component parame-

ters, it is a dimensionless number. The precise

value that it must exceed to make a viable

dynamo depends on geometrical details of the

regenerative flow and boundary conditions and

Equation (24.45) is only an approximate relation-

ship. The competition between regeneration

and diffusion is represented in a general way by

the magnetic induction equation

@B=@t ¼ 

B þrðv  BÞ: (24:46)

The first term in this equation represents field

diffusion and the second gives its interac-

tion with material velocity that allows regenera-

tion. Although electric currents are necessarily

involved, and can be calculated from the B field,

they do not appear in this equation, which sim-

plifies dynamo calculations. Even so, Eq. (24.46)

must be combined with expressions for the buoy-

ancy and rotational forces driving v and the com-

bination is not amenable to analytical solution.

Numerical methods are required.

Two kinds of motion in the core are usually

distinguished. The simpler to visualize is differ-

ential rotation, caused by the tendency of con-

vecting fluid to conserve its angular momentum

as it moves radially in response to buoyancy

forces. This causes the inner part of the core to

rotate with a higher angular velocity than the

outer part and the shearing motion draws out

the lines of a poloidal field to produce an addi-

tional toroidal field, as in Fig. 24.6(b). This mech-

anism is known as the omega (!) effect. Although

differential rotation within the core is central to

dynamo theory, the supposition that it is steady is

too simple and it may even reverse. Implications

are considered further in Section 24.6. The con-

vective radial motion is needed to regenerate the

initial poloidal field from the toroidal one, by the

second process, the alpha () effect, discussed by

Roberts and Gubbins (1987) and Roberts (1987).

An essential feature of the motion that drives the

-effect is its helicity, that is its spiral nature.

Material drawn into an upwelling motion is

deflected by the Earth’s rotation (the Coriolis

effect), causing cyclonic motion, as in the atmos-

phere (Fig. 24.6(c)). In the northern hemisphere

rising material rotates anti-clockwise when

viewed from above and the sign of this helicity

is reversed for sinking fluid. Both signs are oppo-

site in the southern hemisphere. It is important

to recognize that the energy for dynamo action

406 THE GEOMAGNETIC FIELD