Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

417

– [417–437] 13.3.2008 10:45AM

Rock magnetism and paleomagnetism

25.1 Preamble

Paleomagnetism (ancient magnetism) is the

study of the pre-history of the Earth’s magnetic

field, extending the record from the 400 years of

direct observation to almost 4 billion years. It

relies on the fact that many rocks retain indef-

initely the remanent magnetism that is induced

in them during their formation, and so record

the direction and, with less certainty, the

strength of the inducing field. That rocks have

magnetic properties has been known since

ancient times. By the late nineteenth century

measurement methods had become sensitive

enough to observe remanence in a wide range

of rock types. However, they were not used to

infer the history of the Earth’s field. Even the

discovery by P. David and B. Brunhes early in

the twentieth century of rocks with magnetic

remanence opposite to the Earth’s field did not

attract attention commensurate with its signifi-

cance for another 50 years. The study of rock

magnetism began to develop rapidly in the

1950s, when the revolutionary discoveries of

paleomagnetism were appearing and the need

for a fundamental understanding had become

urgent. The two principal landmark publications

in the early development of our understanding

are Nagata (1953) and N

eel (1955). Dunlop and

Ozdemir (1997) present a comprehensive state-

ment of physical principles.

Two particularly important developments in

our study of the Earth have resulted from paleo-

magnetism. We know how the geomagnetic field

behaves on a billion-year time scale and we can

trace the movements of surface features of the

Earth, originally referred to as continental drift

and now as plate tectonics. The crucial link is

that, averaged over 10

years or more, the Earth’s

magnetic and geographic (rotational) axes coin-

cide. This is known as the geocentric axial dipole

(GAD) hypothesis. It follows that, with appropri-

ate care in averaging, paleomagnetic measure-

ments give the latitude and orientation (with

respect to north) of a body of rock at the time

of its formation. For rocks with ages exceeding a

few tens of millions of years, the magnetizations

are found to be incompatible with their present

latitudes and orientations. Initially it was sup-

posed that the observations could be explained

by ‘polar wander’, that is, coherent motion of the

whole of the Earth’s surface relative to the rota-

tion axis, but systematically different polar

wander paths for different continents could be

interpreted only by relative motion. Continental

drift, postulated in the 1800s but considered

seriously only by a small minority of Earth scien-

tists until the early 1950s, rapidly became the

conventional wisdom and a great scientific revo-

lution was in progress.

Another vital discovery of paleomagnetism

that became a cornerstone of plate tectonics is

the sequence of polarity reversals of the mag-

netic field. At the ocean ridges, the upwelling

centres of mantle convection, fresh igneous

crust is produced, becoming magnetized as it

cools. It then moves away from the ridges,

producing stripes of alternating magnetic polar-

ity in the oceanic crust that have a spacing

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

418

– [417–437] 13.3.2008 10:45AM

characteristic of the reversal sequence. These

allow the rate of sea floor spreading to be deter-

mined from marine magnetic surveys. Reversals

themselves present interesting questions for

dynamo theory. Why is the frequency of rever-

sals so variable? Does the dipole field disappear

during a reversal, leaving only the non-dipole

field, or does an equatorial dipole remain? If so,

why does the equatorial dipole appear to have

preferred orientations?

25.2 Magnetic properties of

minerals and rocks

Magnetic properties of materials are dominated

by the intrinsic magnetic moments of electrons

(electron spin). In a few materials the electron

spins on neighbouring atoms interact to cause

mutual alignment and, when large numbers of

atoms have parallel magnetic moments, we say

that the material is spontaneously magnetized.

In bulk magnetic material, the regions of

spontaneous magnetization, termed magnetic

domains, are normally arranged in patterns to

make the magnetic field follow closed loops, so

that no total magnetic moment is observed.

This is referred to as the demagnetized state.

Application of an external field aligns the

domains and the alignment may remain, wholly

or partly, after the external field is removed.

The material then has a magnetic remanence.

The remanence that is induced in rocks by the

Earth’s magnetic field during their formation is,

in many cases, stable enough to be measured

millions or billions of years later. This is the

basis of paleomagnetism.

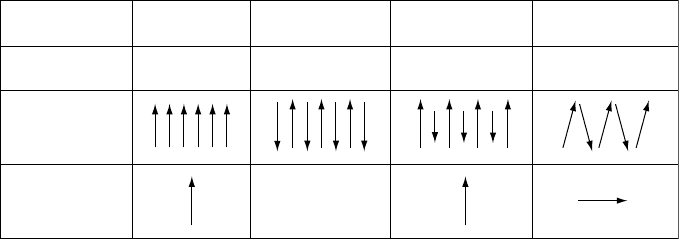
There are several kinds of electron spin inter-

action, with different magnetic effects, illus-

trated in Fig. 25.1. The term ferromagnetism

(iron-like magnetism) is loosely applied to

the first, third and fourth of the patterns in the

figure, all of which give spontaneous magnetiza-

tions. True ferromagnetism, in which all neigh-

bouring magnetic moments are aligned parallel,

is restricted to a few metals and alloys. It is

observed in the metal constituents of meteorites

and lunar samples, but not in terrestrial rocks.

Strongly magnetic minerals are all of the ferri-

magnetic type, in which neighbouring moments

are aligned antiparallel, as in antiferromagnet-

ism, but unequal numbers or strengths give a net

magnetization. Ferrimagnetism refers to the

magnetism of ferrites, which are oxides of iron

and other metals that are of commercial interest

as insulating magnetic materials. Magnetite

(Fe

) is a ferrite. Its solid solutions with ulvo-

spinel (Fe

TiO

), known as titanomagnetites, are

the most important magnetic minerals in igne-

ous rocks. They are sometimes found also in

sediments produced from eroded igneous rocks.

The spontaneous alignment of electron spins

in a ferromagnetic or ferrimagnetic material

is an example of a cooperative phenomenon,

which means that the probability of any one of

them being aligned depends on the alignments

of its neighbours and thus on the average of the

Ferromagnetic Antiferromagnetic Ferrimagnetic

Canted

antiferromagnetic

Interaction Type

Examples

Atomic magnetic

moments

Net spontaneous

magnetization

Zero

Fe, Co, Ni NiO, MnO

Magnetite (Fe

)

Hematite (Fe

)

FI G U R E 25.1 The four most important patterns of mutual alignment of magnetic moments of atoms, caused by

interactions of their electron spins.

418 ROCK MAGNETISM AND PALEOMAGNETISM

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

419

– [417–437] 13.3.2008 10:45AM

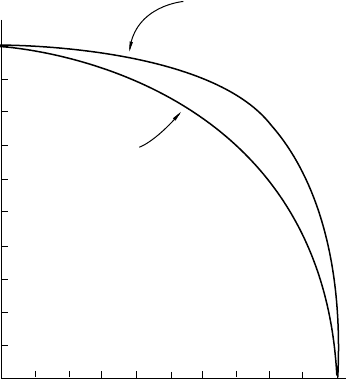
whole assembly. As temperature is raised, the

misaligning influence of thermal agitation

increases, until a critical temperature is reached

and spontaneous magnetization rapidly disap-

pears. This is the Curie point, above which all

these materials are paramagnetic, i.e. weakly

magnetic, with no remanence possible. The vari-

ation of spontaneous magnetization with tem-

perature for magnetite is compared with that

for iron in Fig. 25.2.

The iron ions in magnetite are a mixture of

3þ

and Fe

2þ

in the ratio 2:1, with the moments

of the Fe

3þ

ions oppositely aligned so that the net

spontaneous magnetization is that of the Fe

2þ

ions. When igneous rocks are weathered, the

magnetite is oxidized to make all of the

iron trivalent. The product may be maghemite

(Fe

), which is a ferrimagnetic mineral struc-

turally similar to magnetite. But maghemite is

only metastable and converts to hematite

(Fe

), which has a weak (parasitic) ferromag-

netism due to the canting of its equal and nearly

opposite atomic magnetic moments (Fig. 25.1).

Hematite is the principal magnetic mineral

in sedimentary rocks. Although only weakly

magnetic, its remanence is often very stable.

Hematite may also be formed, not directly or

via maghemite, but via a hydrated oxide, goe-

thite (FeOOH), which has properties similar to

those of hematite. Also encountered, especially

in sedimentary and metamorphic rocks, are

ferrimagnetic iron sulphides, pyrrhotite and

greigite.

Magnetic properties, such as the stability of

remanence, depend on grain size, crystal imper-

fections, impurities and stresses. The smallest

grains of any material are single domains, that

is, they have the same direction of spontaneous

magnetization throughout. They are perma-

nently magnetized to saturation. The magnetic

moment of a grain may be deflected by an

applied field, but the only possible change in its

remanence is from one preferred, or easy, direc-

tion of magnetization to another, usually the

opposite direction. At low temperatures, reversal

of the magnetic moment requires a high mag-

netic field and so single domains may have

high magnetic stability, but, being small,

they are subject to thermal agitation. This can

cause repeated spontaneous reversal of their

moments and the stability is then lost. This phe-

nomenon is referred to as superparamagnetism.

A material in which it occurs has a high magnetic

susceptibility, that is it has a strong induced

magnetization when exposed to a field, but can-

not retain remanence. We refer to it below in

connection with thermoremanence, the process

by which superparamagnetic grain moments are

stabilized by cooling.

Large grains are subdivided into domains,

each of which is magnetized to saturation, geo-

metrically arranged to form paths of magnetic

flux closure. This structure avoids the appear-

ance of surfaces of magnetic polarity either inter-

nally or on grain surfaces and so minimizes the

magnetic energy. (For a review of ferromagnetic

domain theory, see Kittel (1949).) The domain

walls, separating domains with different direc-

tions of magnetization, have a progressive rota-

tion of spin orientation and, in magnetite, are

about 0.1 mm thick. This is a critical size for

domain structures. Magnetite grains smaller

than this cannot accommodate a domain wall.

Spontaneous subdivision into domains occurs

0.5

0 0.5 1

/ m

Magnetite

= 0.51 × 10

–1

(273K)

0.48

–1

Iron

= 1.74 × 10

–1

= 853 K

= 1043 K

FI G U R E 25.2 Temperature dependences of

spontaneous magnetization, m

, for magnetite and iron.

Values are normalized to zero temperature values, m

and temperatures are normalized to the Curie points, 

25.2 MAGNETIC PROPERTIES OF MINERALS AND ROCKS 419

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

420

– [417–437] 13.3.2008 10:45AM

only for larger grains. The weak spontaneous

magnetization of hematite allows much larger

single domains. Changes in magnetization of

multidomain grains occur mainly by movements

of domain walls, enlarging domains that are

favourably oriented with respect to an external

field at the expense of their neighbours. This is

an easier process than the coherent changes in

direction of whole domains and so large multi-

domain grains tend to be magnetically soft and

therefore of little interest to paleomagnetism.

For materials such as magnetite, true single

domain grains are smaller than about 0.1 mmin

size and true multidomains, with no observable

single-domain-like properties, are larger than

10 mmto20mm. There is a wide intermediate

range, for which grains are too large to be single

domains, but nevertheless have properties that

resemble them and are clearly incompatible

with the theory of multidomains. We refer to

them as pseudo-single-domain (PSD) grains.

Most of the stable remanence that is of interest

to paleomagnetism is attributed to them. So, an

understanding of PSD properties is important to

the subject, but they can be accounted for by a

wide range of ferromagnetic domain structures

and there is no single theory. We illustrate the

problem considering the simple case of a grain

with just two domains, with opposite magnet-

izations, separated by a domain wall, within

which the electron spin alignments have a pro-

gressive rotation from one alignment to the

other.

If the grain is perfectly symmetrical, with the

two domains equal in size, then the grain has a

magnetic moment perpendicular to them, aris-

ing from the magnetization within the domain

wall. This domain wall moment can be reversed

but not removed by any demagnetization proc-

ess (except heating above the Curie point). Also,

precise symmetry (equal domains) is unlikely to

occur, because of both irregular grain shape and

internal strains. Magnetization is accompanied

by magnetostriction, the small change in crystal

lattice spacing arising from an interaction of the

electron spins with the electron orbits. This

means that the domain wall involves strain

energy and interacts with various crystal defects,

which also cause strain energy. Minima in total

energy occur for domain wall positions con-

trolled by the distribution of imperfections. The

wall may jump between them, a phenomenon

well observed as Barkhausen noise in larger mag-

netic systems, in which magnetization changes

are observed to occur in erratic jerks. Except in

the unusual case of perfect symmetry there is a

minimum component of the net moment in the

direction of one or other of the domains. So, even

in this simple case, we see that there are two

components of PSD magnetization, arising

from domain wall moments and Barkhausen

discreteness.

Irregular grain surfaces and resulting compli-

cated patterns of flux closure domains must also

contribute to PSD moments. The important

result of all these effects is that, unless the grains

are so large that PSD effects are masked by much

larger domains, they have minimum magnetic

moments that respond to external fields in a

manner similar to single domains. Most impor-

tantly, being larger than true single domains,

they are less sensitive to thermal agitation. The

most stable magnetizations are of the PSD type.

When a rock containing magnetic minerals is

cooled in a magnetic field it becomes magne-

tized as soon as the temperature falls below the

Curie point, 

. However, if the field is removed

when the temperature is below but still close to



the magnetization disappears. The domains

are still spontaneously magnetized, but thermal

agitation rearranges and realigns them, causing

statistical cancellation in the case of small grains

or rearrangement of domains to give flux closure

in large grains. After cooling in a field to a block-

ing temperature, several tens of degrees below



, magnetization may remain after removal of

the field. This is thermoremanent magnetiza-

tion, often abbreviated to its acronym, TRM.

Each of the magnetic constituents of a rock,

and perhaps even the individual domain walls,

has a blocking temperature, below which ther-

mal activation is ineffective and TRM becomes

frozen in. Further cooling causes an increase in

the TRM, according to the increase in spontane-

ous magnetization and, more importantly, an

increase in its stability, that is, its ability to resist

changes over a very long time. For small induc-

ing fields the strength of thermoremanence is

420 ROCK MAGNETISM AND PALEOMAGNETISM

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

421

– [417–437] 13.3.2008 10:45AM

directly proportional to the field strength.

Igneous rocks with natural remanent magnetiza-

tion (NRM) that is thermoremanent in origin are

favoured for determinations of the intensity of

the ancient geomagnetic field.

The long-term stability of thermoremanence

is crucial to paleomagnetism. It is most easily

understood in terms of the single domain theory

of N

eel (1955). An isolated single domain of a

material, such as magnetite, is anisotropic; its

magnetic energy is a function of the direction

of its magnetization. It is spontaneously mag-

netized in one of the so-called easy directions,

between which there are energy barriers that

can be overcome either by application of a strong

field or by thermal activation. Anisotropy arises

from crystalline effects and also from grain

shape. Unless a grain is almost equidimensional,

the shape effect is stronger and has the effect of

making the longest axis the easy direction,

because that minimizes the external energy of

its field. The twooppositedirectionsareequivalent

and, if an energy barrier, E, separates them, then

the probability, dP, that a thermal impulse will

reverse the magnetization in time dt is

dP ¼ 

expðE=kT Þdt; (25:1)

where 

, termed the attempt frequency, is of

order 10

Hz.

Now consider a single domain grain that is

cooling from a high temperature, with the ther-

mally activated reversals of its magnetization

becoming progressively more sluggish. If the

cooling rate is represented by a characteristic

time, , for cooling through a few degrees,

which would be 100 s in a laboratory experi-

ment, then the blocking temperature, T

, is the

value of T in Eq. (25.1) at which (dP/dt)  1. Thus

we can write

E=kT

¼ lnð

Þ25:3: (25:2)

Further cooling has two effects. (E/kT) increases

with decreasing T, but there is also an increase in

E, which, for the case of shape anisotropy, is

proportional to the square of the spontaneous

magnetization. By ignoring the variation in E we

overestimate dP/dt at any lower temperature, T

that is

dP=dt



expð25:3T

Þ: (25:3)

We are interested in high blocking tempera-

tures, which give greatest stability. Assuming

¼ 750 K, 100 K below the Curie point of mag-

netite, and T

¼ 300 K, Eq. (25.3) gives dP/dt <

3.4 10

19

Hz, which corresponds to a relaxa-

tion time exceeding 9 10

years.

We see how it is possible for magnetic rema-

nence to be stable over geological time, but even

rocks with high magnetic stability include com-

ponents with lower stability. The less stable com-

ponents may gradually acquire magnetizations

subsequent to rock formation, at times when

the field was different, a phenomenon termed

magnetic viscosity. Viscous magnetization may

be enhanced by mild reheating that is insuffi-

cient to affect the primary remanence, but intro-

duces a disturbing secondary magnetization.

Secondary magnetizations are softer than the

primary remanence and their removal by partial

demagnetization in an alternating field (in

zero ambient field), ‘AF cleaning’, is a standard

method of revealing the primary remanence.

Partial thermal demagnetization is also useful

as it retraces, in reverse, the acquisition of ther-

moremanence, allowing identification of the

blocking temperatures of different components.

Heating experiments of this kind require cross-

checks to discard observations that are affected

by chemical changes.

Above their blocking temperatures, single

domains are superparamagnetic. For a magnetic

moment  in a field B, alignment with B is fav-

oured by the Boltzmann factor exp(B/kT), or

exp(B/kT) for the opposite alignment. The

average magnetization is proportional to the dif-

ference between these factors. Relative to the

saturation magnetization, m

(all moments

aligned parallel), this is

expðB=kTÞexpðB=kTÞ

expðB=kTÞþexpðB=kTÞ

¼ tanh

B



: (25:4)

P. Langevin generalized this expression to

describe ordinary paramagnetism, for which 

is very much smaller, being the value for a single

atom, and the magnetization is correspondingly

25.2 MAGNETIC PROPERTIES OF MINERALS AND ROCKS 421

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

422

– [417–437] 13.3.2008 10:45AM

weaker. The Langevin expression is simply an

integral over all orientations of grain moments

with respect to the field. Hence the term ‘super-

paramagnetism’ for the behaviour of sponta-

neously magnetized but thermally randomized

single domains. Cooling through the blocking

temperature freezes in the superparamagnetic

moment, which becomes thermoremanence.

The only change with further cooling is an

increase in remanence in proportion to the

increasing spontaneous magnetizations of the

domains.

Equation (25.4) would apply to an assembly

of single domains with their axes parallel to

the inducing field, but is readily integrated over a

randomly oriented distribution, as in the Langevin

theory. The tanh form is characteristic of single

domain behaviour. For small fields (B kT), ther-

moremanence is proportional to the inducing

field, but it begins to saturate in much lower fields

than does multidomain remanence. In spite of the

fact that true single domains are probably rare in

rocks, the single domain theory is of greater

interest than multidomain theory because it

is a reasonable description also for pseudo-single

domains, which are the carriers of the most

stable remanence.

When an igneous rock is eroded and its frag-

ments are deposited in water, the magnetic

grains may carry remanent moments from

their earlier history and, if the water is very

still, they may be partly aligned by the ambient

field at the site of deposition. The resulting sedi-

ment acquires detrital remanent magnetization

(DRM), but true DRM is generally transient. The

subsequent realignment of grains during sedi-

ment consolidation is accompanied by a stronger

post-depositional remanence. This, too, is lost if

there are chemical changes. Then new magnetic

minerals are formed, that may be hematite in an

oxidizing environment or pyrrhotite in a reduc-

ing environment with available sulphur. They

acquire chemical remanent magnetization

(CRM), the remanence resulting from chemical

formation in a field. This is normal in sedimen-

tary rocks. Also, in some igneous rocks, such as

sea-floor basalt with prolonged water percola-

tion, the remanence may be more chemical

than thermoremanent in origin. CRM is similar

in stability to TRM and equally useful for paleo-

magnetic direction studies, provided the time of

its acquisition is reasonably well known, but not

for paleointensities (Section 25.5).

25.3 Secular variation and the axial

dipole hypothesis

Although the natural magnetizations of rocks

and archeological samples record both the direc-

tions and intensities of the fields in which they

were formed, the directions can be determined

more easily and more reliably than the inten-

sities. If a large fraction of a primary remanence

survives the process of magnetic cleaning to

remove secondary magnetizations, then the pri-

mary direction is accurately determined. The

interpretation of intensity is less straightfor-

ward. Additional experiments, involving heat-

ing, are required and chemical changes caused

by heat make the interpretation both more diffi-

cult and more prone to error. For this reason,

studies of the intensity of the ancient field have

proceeded more or less independently of the

directional studies. This section is concerned

with the directional information and paleointen-

sities are considered in Section 25.5.

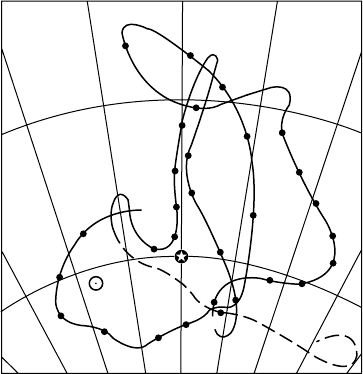
Magnetic field directions obtained from the

remanence in pottery kilns for which the last

firings have been carbon-dated are plotted in

Fig. 25.3. This extends the historical record of

the secular variation in Britain to about 2000

years. It is a plot of magnetic inclination vs decli-

nation, known as a Bauer plot, after L. A. Bauer,

who first represented secular variation in this

way. Such a graph is a series of spot measure-

ments of the field in a particular area. It is sat-

isfactory to compare in this way observations

made over distances up to about 1000 km,

because the strong features of the field are larger

than this (Fig. 24.1). The record has been

extended back to 10 000 years, although with

slightly less precision, using thin slices of lake

sediment (Turner and Thompson, 1981; Creer

and Tucholka, 1982), and shows a similar char-

acter for the whole period. If the field were due

only to an axial dipole at the centre of the Earth

422 ROCK MAGNETISM AND PALEOMAGNETISM

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

423

– [417–437] 13.3.2008 10:45AM

then the direction would be that of the star in the

centre of the figure. The figure shows, and more

extended data confirm that, although the field

drifts about, it is constrained not to wander too

far from that direction and the wandering is

centred on it. The present, tilted dipole field

gives the direction indicated by the open circle,

which is clearly displaced from the centre of the

figure.

Another way to represent paleomagnetic

directions is to plot the virtual or apparent pole

positions, assuming the observed field to be due

to a dipole. If each of the spot measurements

used to produce Fig. 25.3 had, instead, been

used to calculate a virtual pole position, then

the virtual magnetic pole would have traced

out a similar-looking path. But there would be a

subtle difference, because the pole position is

calculated from inclination by Eq. (24.11),

which is not linear. Thus, the mean of the inde-

pendently determined virtual pole positions

would not coincide precisely with the pole

obtained from the mean direction in Fig. 25.3.

Differences of this kind have become important

to the fine details of the paleomagnetic record

and will be considered further presently.

As data sets such as that in Fig. 25.3 are

extended to longer periods, so it becomes even

clearer that the average field direction is that of

an axial dipole, not just for a single site, but for

all sites. There is a limit to the time span that can

be considered in this way because the slow pro-

cesses of polar wander and continental drift

(Section 25.5) eventually spread the paleo-poles

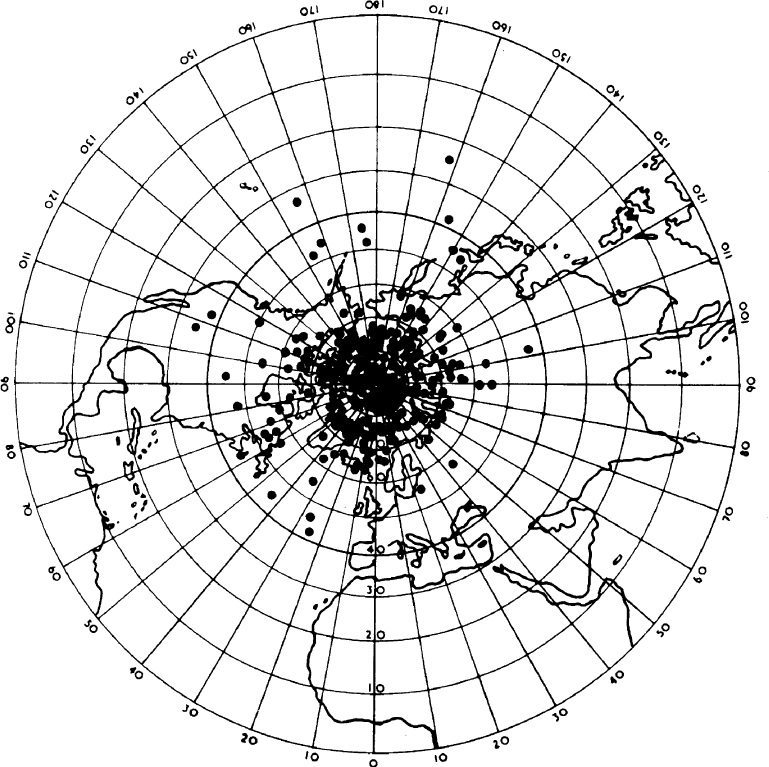
around the globe. However, even up to 20 mil-

lion years ago, the scatter of virtual pole posi-

tions appears centred on the present geographic

pole. Figure 25.4 is a plot of pole positions

obtained from igneous rocks younger than

20 million years. The points are spot measure-

ments of the field directions for the brief periods

when the rocks were cooling. Although they were

obtained from many places, and so are not points

on a single virtual pole path, they are from many

similar paths and the effect is the same. For the

purpose of plotting Fig. 25.4, the polarity of the

field is ignored. It has reversed many times in

the past 20 million years and whichever pole

happened to be in the northern hemisphere is

plotted. Reversals are considered in Section 25.4.

The conclusion that the averaged geomag-

netic field is that of a dipole at the centre of the

Earth, with its axis coinciding with the geo-

graphic axis, is an important fundamental result

in paleomagnetism. It is of interest in dynamo

theory, but its great impact has been in establish-

ing continental drift. Suitably averaged paleo-

magnetic poles are not just average magnetic

poles, they are also geographic poles. Thus the

wander of the magnetic pole, viewed over hun-

dreds of millions of years, traces the rotation

axis, relative to surface features where paleo-

magnetic samples are obtained. This application

is pursued in Section 25.6.

With close examination of observations, the

axial dipole hypothesis is seen as a good approx-

imation, but not exact. Curie’s principle of sym-

metry, which we refer to in Section 24.5, gives

confidence to the expectation that, averaged

over a sufficient time, the field is symmetrical

about the rotation axis. But this allows an axial

60°

70°

20°

W0° 20°

1900

1800

1700

1500

1400

1200

1300

200

300

400

100

500

1100

1000

900

600

800

700

Declination

Inclination

FI G U R E 25.3 Secular variation of the magnetic field in

Britain, plotted as inclination vs declination as a function

of time. The record of direct observations from about 1600

is extended back by archeomagnetic measurements,

with dates given by numbers on the curves.

Archeomagnetic data are from a plot by Tarling (1989).

The direction of the field of a geocentric axial dipole is

shown by the star and the direction corresponding to the

present, inclined dipole is represented by the open circle.

25.3 THE AXIAL DIPOLE HYPOTHESIS 423

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

424

– [417–437] 13.3.2008 10:45AM

quadrupole and higher terms, as long as they are

axial, and does not even demand a dominant

dipole. Remoteness of our observations from

the source of the field makes a spatial spectrum

with the general form of Fig. 24.2 almost inevi-

table, so from the perspective of paleomagnet-

ism the axial dipole hypothesis looks safe, but

we have a reason for enquiring how good an

approximation it is, apart from the fact that we

rely on it to interpret paleomagnetic data.

Theories agree that core motion within the

tangent cylinder, parallel to the rotation axis and

enclosing the inner core, is semi-isolated from

the convective motion in the rest of the outer

core. If this has a surface expression in the pat-

tern of the field, it would be most obvious as an

axial quadrupole, systematically related to the

dipole. The present field does not provide a suf-

ficient test for a systematic quadrupole and sta-

tistics of a much longer record are needed to

examine this possibility. From a study of paleo-

magnetic data for the last five million years,

Constable and Parker (1988) concluded that

there is a consistent axial quadrupole, repre-

sented by a harmonic coefficient g

that is

about 6% of the axial dipole term, g

, and

FI G U R E 25.4 Paleomagnetic pole positions obtained from igneous rocks up to 20 million years old. Reproduced,

by permission, from Tarling (1971).

424 ROCK MAGNETISM AND PALEOMAGNETISM

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

425

– [417–437] 13.3.2008 10:45AM

reverses with the dipole. Merrill et al. (1996,

Table 6.2) give 3.8%. This is evidently a robust

result, in spite of the difference between these

estimates, and their dependence on assumptions

about the statistical behaviour of the field, a

point that we return to below. Selecting only

the g

and g

terms in Eq. (24.14), differentiating

to obtain the radial and circumferential compo-

nents of the field by Eqs. (24.19) and (24.17) and

taking the ratio, the dip angle is given by

tan I ¼



cos  þ 3g

cos ð

cos

 

sin  þ 3g

sin  cos 

(25:5)

The apparent colatitude inferred by supposing

that this magnetic inclination is due to the axial

dipole alone is obtained by Eq. (24.11). The differ-

ence between this apparent colatitude and the

true colatitude is plotted in Fig. 25.5 for the ratio

¼ 0.06, as estimated by Constable and

Parker (1988).

Figure 25.5 is a plot of what Wilson (1970) was

first to identify as a systematic ‘far-sidedness’ of

paleomagnetic poles. The magnetically inferred

colatitude exceeds the true colatitude by a small

angle, so that, from all directions, the pole

appears to be slightly further away than it really

is. Of course, such conclusions are possible only

by analysing data from rocks that are young

enough for polar wander/continental drift to be

insignificant. As Fig. 25.5 shows, the apparent

polar displacement is sensibly constant over

most of the Earth’s surface. With the 6% assump-

tion it is between 2.08 and 2.68 for the colatitude

range 288 to 908, which is almost 90% of the area

and excludes only the little sampled polar

regions. The far-sidedness has no obvious lati-

tude dependence. For it to be a systematic effect

it is necessary for g

and g

to have the same

sign, reversing together, and for the other

harmonics to be averaged out by sufficient sam-

pling to allow a 28 deflection to be recognized as

statistically significant. The scatter of paleomag-

netic directions is much greater than this so the

procedure for averaging the secular variation

requires close scrutiny.

A basic problem is that a pole position

is calculated from magnetic inclination by

Eq. (24.11), which is non-linear. Merrill et al.

(1996, Section 6.4) discuss the statistical argu-

ments that have been used to deal with this

problem. A random distribution of field direc-

tions about a mean does not produce a random

distribution of inferred poles or vice versa. To

illustrate this point, consider a site where the

magnetic dip angle corresponding to an axial

dipole is 458, but a pair of measurements give

308 and 608, representing symmetrical scatter,

arising from local, non-dipole field variations.

The colatitude is  ¼ ctn

1

(

tan 458) ¼ 63.48,

but, assuming a dipole field in each case, the two

observations correspond to 73.98 and 49.18 and

so to an average of 61.58. This bias would indi-

cate near-sidedness and so give an underestimate

of observed far-sidedness. Conversely, if the scat-

ter of field directions is due to a randomly

wandering pole, that would produce a spurious

far-sided effect. Magnetizations at colatitude 458

due to poles at 308 and 608 would have inclina-

tions of 73.98 and 49.18, averaging 61.58 and indi-

cating a pole at 47.48, far-sided by 2.48. But, if

measurements are made on a sediment that

does the averaging, then it is the vector average

40 60

Far sidedness (degrees)

Quadrupole

effect

Apparent

pole averaging

Colatitude (degrees)

FI G U R E 25.5 Apparent angular displacement of the

pole (far-sidedness) as a function of latitude due to a 6%

quadrupole field by Eq. (25.5) (solid line), compared with

the effect of taking averages of magnetic inclination for a

dipole field transiently deflected to 158 from the true

pole (broken line). This illustrates the need for care in

statistical averaging of secular variation if small effects,

such as the quadrupole field, are to be discerned.

25.3 THE AXIAL DIPOLE HYPOTHESIS 425

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C25.3D

–

426

– [417–437] 13.3.2008 10:45AM

field that is observed and not a simple average of

directions. Assuming a similar dipole strength

for both pole positions, by Eq. (24.10) the nearer

pole gives a field of 1.8B

and the more remote

one a field of 1.3B

, biasing the average direction

to the nearer pole and giving an average inclina-

tion of 63.48. Since this corresponds to the true

latitude of 458, the sedimentary weighted aver-

age compensates for the bias introduced by the

non-linearity of Eq. (24.11).

We may suppose that drift of the non-dipole

field past a site would cause angular dispersion

of the field direction that is properly averaged at

the site before calculation of the pole position,

but that components of the secular variation

caused by the equatorial dipole, and variations

in the strength of the axial dipole, require aver-

aging of the pole positions corresponding to spot

measurements of the field. This suggests a

decrease in the scatter of apparent pole positions

with the latitude of observation, because the

dipole field is stronger at high latitudes, reduc-

ing the scattering effect of the non-dipole field.

However, the opposite latitude variation is

observed, so it is evident that we cannot separate

dipole and non-dipole effects in this way.

McFadden et al. (1988) argued that a more

useful procedure is to consider separately the

symmetric and antisymmetric harmonic compo-

nents of the field. This refers to symmetry about

the equator. The axial dipole, represented by g

is antisymmetric, but the axial quadrupole, g

,is

symmetric. These are the leading members of

two ‘families’ of harmonics, which have been

referred to as the dipole and quadrupole types,

but this is misleading because g

and h

, which

represent the equatorial dipole, are symmetric

and belong to the quadrupole family with g

.In

terms of harmonic order, l, and degree, m (see

Appendix C), the distinction is between an anti-

symmetric family, for which (l m) is odd, and a

symmetric family with even (l m). From an

examination of the harmonic components of

the present field, McFadden et al. (1988) observed

that the scatter of directions from an axial dipole

field attributable to the symmetric components

is independent of latitude, but that antisymmet-

ric components cause scatter approximately pro-

portional to latitude. The combination gives the

observed increase with latitude. The conclusion

is that correction for paleomagnetic scatter

should involve two terms, one constant and

one proportional to the apparent latitude of a

measurement. While this approach allows a

more rigorous assessment of the significance of

the quadrupole field, it does not completely

solve the problem of paleomagnetic scatter.

But we can note that it involves an error of 28

to 38 at most, and that this is very small com-

pared with the angular variations observed in

paleomagnetism.

This discussion prompts a reconsideration of

the distinction between odd and even harmon-

ics. It suggests that, for the purpose of dynamo

theory, the fundamental distinction is between

odd or even (l m), rather than odd or even l.

Merrill et al. (1996) refer to a discussion by P. H.

Roberts and M. Stix of –! dynamos of the

Bullard and Gellman type (Section 24.5), point-

ing out that, if the core velocity field is symmet-

rical about the equator, then the !-effect, caused

by differential rotation, is also symmetrical, but

that the -effect, which depends on helicity, is

opposite in the two hemispheres. In this situa-

tion, the odd and even families of harmonics

may be generated independently, interacting

only to the extent that the pattern of core motion

is asymmetrical. Even if core motion is too irreg-

ular for such a clear separation, a difference

between the within-family and between-family

interactions must have a fundamental implica-

tion for the behaviour of the field. This argument

is considered in the following section in connec-

tion with reversals. The separation of the

harmonic components of the field into antisym-

metric and symmetric families refers to the

observed, poloidal field.

Merrill et al. (1996) discount the significance

of an axial octupole term, g

, but Kent and

Smethurst (1998) reported evidence that paleo-

magnetic data from the period before 250 mil-

lion years ago suggest g

 0.25. Unlike the

situation in the last five million years, the con-

tinents have been redistributed since (and dur-

ing) that time so it is not possible (without a

much larger coherent continent than actually

exists) to isolate such an effect from polar wander/

continental drift. Only a statistical argument is

426 ROCK MAGNETISM AND PALEOMAGNETISM