Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

357

– [348–360] 13.3.2008 10:48AM

in terawatts. The expression in the table is the

integral over time , with a numerical factor to

give the integrated heat in units of 10

J, as for

other entries in the table. We consider two mod-

els, with A ¼0.2 terawatt and A ¼0.

The major item of heat loss listed in

Table 21.5, 54.0/

, is the conducted heat at the

top of the core, being 3.79 10

W for time ,

assuming a conductivity of 28.3 W m

1

(Section 19.6) and an adiabatic temperature gra-

dient (Eqs. (19.55) and (19.56)). Arguments about

the energy balance of the core, and the need to

consider radioactivity, are critically dependent

on this heat loss, and therefore on the conduc-

tivity. Most discussions have assumed a higher

value. The nature of the problem is seen by not-

ing that if the inner core has existed for most of

the life of the Earth ( 

), then the sources in

the Q column of Table 21.5 balance the heat loss

only with a radiogenic contribution, refrigerator

action, or both. Since refrigeration consumes

convective power that would otherwise be avail-

able for the dynamo (the fQ

entry in the E

column of the table), its availability is limited.

To determine the efficiency factor f with which it

operates we need to know the radial variation of

the core heat flux.

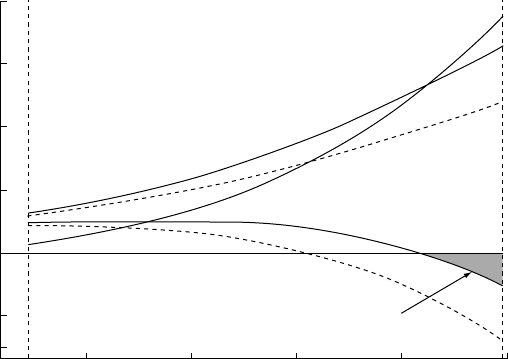
The heat flux within the core is plotted in

Fig. 21.3 for the two models considered, with

and without radiogenic heat. Conducted heat

diminishes strongly with depth mainly because

the adiabatic temperature gradient decreases

(Eq. 19.55). The total heat flux through any radius

is the total heat originating within it and varies

less with radius than the conducted heat, both

because of the latent heat of inner core solid-

ification and because the deep parts cool faster

in maintaining the adiabatic gradient. In the fig-

ure we see that the total heat comfortably

exceeds the conducted heat deep in the core

but that for both models the conducted heat is

greater in the outer part. Convected heat, shown

as the difference, is negative at the top of the

core (shaded for the A ¼ 0.2 model in Fig. 21.3),

where the adiabatic temperature gradient must

be maintained by reversed convection, that is

refrigerator action, the principle of which is dis-

cussed in Section 22.8. The refrigerator power

required is the product of heat carried down

and an efficiency, f, determined by the tempera-

ture range over which it operates. f is the Carnot

efficiency with which the same heat would gen-

erate power if convected upwards. For the A ¼0.2

model f ¼0.043. For the A ¼0 model not only

must more heat be transferred downwards but

the depth and temperature ranges are greater

and f ¼0.091. With these values of f we can

examine the models to see whether the refrige-

rator action leaves eno ugh conv ective energy

for a viable dynamo.

Table 21.5 Summary of components of the core energy balance during the lifetime  of the

inner core. Q gives energy sources and E the corresponding convective energies, which are

related to Q by thermodynamic efficiencies. 

is the age of the Earth and A is the present rate of

radiogenic heating by

K in terawatts. For a discussion of refrigerator action see Section 22.8

Sources Q (10

J) Efficiency E (10

Heat capacity Cooling 17.75 0.139 2.47

Contraction 2.52 0.135 0.34

Freezing Latent heat 6.36 0.252 1.60

Contraction 2.76 0.190 0.52

Compositional separation 4.79 1.00 4.79

Precession 0.20 /

1.00 0.20 /

Radioactivity 5.69A[exp(2.5 /

) 1] 0.127 0.723A[exp(2.5 /

) 1]

Losses

Conduction 54.0 /

0.119 6.43 /

Refrigerator action Q

f fQ

21.4 ENERGY BALANCE OF THE CORE 357

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

358

– [348–360] 13.3.2008 10:48AM

The sources and losses in the Q column of

Table 21.5 must balance. With A in terawatts

and other numerical values adjusted so that all

terms are expressed in units of 10

J, as in the

table,

34:14 þ 5:69A½expð2:5 =

Þ1¼53:8=

 Q

(21:21)

Now we need also the entries in the E column

of the table. These are convective energies

related to corresponding entries in the Q col-

umn by thermodynamic efficiencies discussed

in Section 22.7. The sum of all the E entries

(subtracting the negative terms) is the energy,

, available for the dynamo. But the dynamo

itself generates heat by ohmic dissipation; by

assuming it to be uniformly distributed through

the core we assign an efficiency of 0.122 to its

generation of further dynamo power. This

cannot be counted as a heat source but it

means that we equate the available energy not

to E

but to (1 0.122) E

. Thus, in units of

J as before,

0:878E

¼ 9:72 þ 0:723A½expð2:5=

Þ1

 6:23=

 fQ

: (21:22)

Substituting for Q

by Eq. (21.21) we obtain an

expression for dynamo power in terms of A, 

and f. For the two cases considered, (A ¼0,

f ¼0.091) and (A ¼0.2, f ¼0.043),

A ¼ 0 : E

¼ 14:61  12:67=

; (21:23)

A ¼ 0:2 : E

¼ 12:66  9:73=

þ0:2204½expð2:5=

Þ1: (21:24)

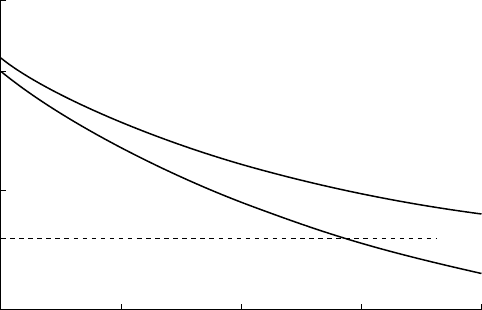
Dividing E

by , we have the average dynamo

power for the lifetime, , of the inner core as a

function of  for each of the models, as plotted in

Fig. 21.4. The broken line in the figure shows the

estimated dynamo power requirement from

Section 24.7, 0.3 terawatt. Remembering that we

have deferred to Sections 22.7 and 23.5 the varia-

tions of core heat flux and dynamo power with

time, the figure shows the average power over

the inner core lifetime and not a time variation

of the power. The essential conclusion from this

figure is that the assumed core conductivity,

 ¼28.3 W m

1

at the top of the core and vary-

ing little with depth, marks a boundary between

alternative core models, with and without radio-

activity. With a lower conductivity there would be

no reason to consider radioactivity, but a higher

value would make it difficult to avoid. The uncer-

tainty in  is the central doubt around which the

current debate about core physics revolves, as

reviewed by Nimmo et al. (2004).

3500

300025001500 20001100

Radius (km)

–1.5

4.0

3.0

2.0

1.0

–1.0

Average heat flux (terawatt)

Refrigerator action

Convected heat

= 0.2 terawatt)

Conducted heat

Convected heat (A

= 0)

Total heat

= 0.2 terawatt)

Total heat

= 0)

Mantle

Inner core

FI G U R E 21.3 Radial variation of

the average core heat flux over the

life of the Earth for two models,

both of which assume that the

inner core began to form very

early. Conducted heat, calculated

assuming a thermal conductivity

which varies from 28.3 W m

1

at the top to 29.3 W m

1

at the

bottom of the outer core, exceeds

the plotted total heat flux in the

outermost part of the core for both

models. The difference is plotted

as convected heat, the negative

range indicating how much heat is

carried down by refrigerator

action, driven by compositional

convection. The model with 0.2

terawatt of present radiogenic heat

from

K(theA ¼0.2 model) is

shown by solid lines and the non-

radioactive model by broken lines.

358 THE GLOBAL ENERGY BUDGET

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

359

– [348–360] 13.3.2008 10:48AM

21.5 Minor components of the

energy budget

By ‘minor components’ we mean contributions

that may be geophysically interesting and are

included in Table 21.4, but are smaller than the

uncertainties in the major components and are

not discussed elsewhere in this chapter. We con-

sider two: tidal friction and mantle differentia-

tion. Others that we can think of, such as

absorption of cosmic neutrinos, are certainly

insignificant.

The tidal energy dissipation, calculated from

the slowing rotation in Section 8.3, with a small

allowance for the increasing orbital energy of

the Moon, is 3.7 10

W. Most of this is due to

marine tides and has no impact on the solid

Earth. The internal dissipation can be estimated

from the elastic strain energy of the solid tide, of

which a fraction, 2p/Q

, is lost per tidal cycle by

anelastic effects. We adopt the value of Q

¼280

for shear deformation of the mantle at tidal fre-

quencies obtained by Ray et al. (2001), who com-

bined satellite observations of the total tidal

deformation of the Earth, as deduced from its

gravitational effect, with altimeter data on the

deformation of the ocean surface. Although

measuring a small effect as a difference between

much larger ones, they claimed 25% accuracy.

Their tidal Q

value appears high compared

with what might be expected from extrapolation

from seismic frequencies, but it is the only

direct observation. The tidal strain of the solid

Earth, estimated from the Love number h

(Section 10.5), is " ¼5 10

8

so the strain energy

"

V ¼2 10

J, with rigidity modulus,

 ¼176 GPa, averaged over the volume, V,of

the mantle. With Q

¼280, the fraction of this

energy that is dissipated each tidal cycle (12.4

hours or 44 700 s) is 2.25%, giving a rate of

1.0 10

W, about 2.7% of the total tidal dissi-

pation but of little consequence to the present

thermal state of the Earth. However, it could

have exceeded 10

W very early in the history

of the Earth, when the Moon was closer and the

Earth was rotating faster.

The crust is a light differentiate that has sep-

arated from the mantle, releasing gravitational

energy in the process. We consider only the con-

tinental crust, which has progressively accumu-

lated, and not the oceanic crust, which is

continuously recycled back into the mantle.

The continental crust, volume V ¼8 10

is less dense than the underlying mantle by an

average D ¼470 kg m

3

, so that VD ¼3.8 10

kg. The average gravitational potential through

which this mass has moved depends on whether

the crust is believed to have been derived uni-

formly from the whole mantle or only from

the upper mantle. We calculate each case and

adopt a compromise, because the upper mantle

appears to have been more affected. It is conven-

ient to the calculation that the density profile of

4.5

4.03.53.02.5

Inner core lifetime (10

Years)

0.3

1.3

1.0

0.5

Mean dynamo power (terawatt)

A = 0

= 0.2 terawatt

FIG U R E 21.4 Average dynamo power

over the inner core lifetime, t,asa

function of t for models with 0.2

terawatt of radiogenic heat from

Kat

the present time and no radiogenic

heat (A ¼0). The broken line indicates

the power requirement for a

geomagnetic field of the present

strength.

21.5 MINOR COMPONENTS OF THE ENERGY BUDGET 359

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C21.3D

–

360

– [348–360] 13.3.2008 10:48AM

the Earth happens to give almost constant grav-

ity, g 10 m s

2

, over the whole depth of the

mantle (see Appendix F). Since at radius r,

g ¼Gm(r)/r

, the mass inside r is

mðr Þ¼ðg=GÞr

; (21:25)

where G ¼6.67 10

11

1

2

is the gravita-

tional constant, so that, in this approximation,

(g/G) is constant. It allows a simple calculation of

the average gravitational potential difference

between radius r

and the surface at r

, weighted

according to the distribution of mass in this

range. By Eq. (21.23) the mass in the range r to

r þdr is a fraction of the mass M between r

and

, given by

dm=M ¼ 2rdr=ðr

 r

Þ; (21:26)

and its gravitational potential relative to the

surface is g(r

r), so that the gravitational

energy released by separation of the mass differ-

ence VD uniformly from the mass in the range

to r

E ¼

Vg

ðr

 r

ðr

 rÞr dr

¼ Vg



3ðr

þ r



: (21: 27)

For the two cases, separation from the whole

mantle or from the upper mantle, the values of

this energy are 4.9 10

J and 1.2 10

Accretion of the continental crust is a conse-

quence of convection, which was faster in the

past than at present. We assume that the rate of

accretion is proportional to the rate of convec-

tive heat transport, calculated in Chapter 23, and

that the present rate is half of the average over

the life of the Earth. On this basis the present

rates of energy release for the two cases are

1.7 10

W and 4.3 10

W. We should prob-

ably add an energy of accumulation of dense

differentiates in the D

layer, but have no quan-

titative estimate and presume it to be smaller. In

Tables 21.1 and 21.4 we take rounded averages of

the alternative estimates.

360 THE GLOBAL ENERGY BUDGET

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

361

– [361–375] 13.3.2008 10:47AM

Thermodynamics of convection

22.1 Preamble

We have a good measure of the rate of heat loss

from the solid Earth to the atmosphere and

oceans, 44.2 10

W (Pollack et al. 1993).

Although the final stage is observed as conduc-

tion through the crust and hydrothermal circu-

lation of sea water through young ocean floor,

most of the heat comes from the deep interior.

Thermal diffusion in a body the size of the Earth

is too slow to have cooled the lower mantle

noticeably in its lifetime. The deep heat is trans-

ported upwards by hot material, driven by

the buoyancy of its thermal dilation relative to

the cooler material that sinks to replace it. The

global scale motion is evident at the surface as

tectonic activity, including continental drift and

earthquakes, with volcanism as a side effect.

Chapter 13 considers the stresses involved in

this process and relates them to the mechanical

energy derived from convection. The calculation

of the energy is presented in this chapter. It is an

application of classical thermodynamics.

The mechanical power of convection is the

product of heat transport and a thermodynamic

efficiency that we can calculate in two ways.

First, we recognize that the mantle is a heat

engine in the classical thermodynamic sense

and that we can apply the Carnot theorem to

derive the mechanical power of convection with-

out an explicit consideration of the forces

involved. Then, we relate the conclusion more

directly to the driving forces of convection, as

outlined in Chapter 13, by calculating the

efficiency from the buoyancy forces acting on

the rising and falling limbs of a convective cell.

The two calculations are complementary. The

mechanical model shows not only how convec-

tive power is generated, but that its efficiency is

that of a Carnot cycle operating over an adiabatic

temperature ratio between its heat source and

sink. We point out here that this is a completely

general result. We are calculating the power that

is inevitably generated, not merely may be gen-

erated, and show that no more power is possible,

in principle. This is a fundamental theorem on

which a discussion of tectonics must be based, as

well as being an essential consideration in the

thermal history of the mantle (Section 23.4).

The thermodynamic theorem is first pre-

sented in a special, limited form by applying

physical restrictions that make the principle

easy to see, and then we show that the restric-

tions can be removed without affecting the con-

clusions. We consider a homogeneous layer with

an adiabatic temperature gradient. As pointed

out in Section 19.5, such a layer is neutrally buoy-

ant and a steeper gradient would be required to

make it convect, but we can nevertheless postu-

late that a parcel of material at the bottom of the

layer is given an infinitesimal amount of heat

which it carries up and releases at the top. By

making the heat infinitesimal we can ignore the

thermodynamically irreversible processes of

heat conduction into and out of the parcel and

treat them as isothermal. Then, by allowing the

parcel to return to its original position and tem-

perature, we take it round a Carnot cycle

between two adiabats and two isotherms. In

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

362

– [361–375] 13.3.2008 10:47AM

fact, the return path is not really necessary

because the parcel considered and the material

it displaces by its return are identical. So, we can

appeal to the standard theorem that the mechan-

ical energy, W, generated by the cycle, being the

area of a loop in a P–V diagram, is the heat input,

, multiplied by a thermodynamic efficiency, ,

given by

 ¼

 T

¼ 1 

; (22:1)

where T

and T

are the temperatures of the heat

source and sink at the bottom and top of the

layer (assumed to be the equilibrium tempera-

tures at those levels). By restricting the applied

temperature increment to an infinitesimal

value, and the temperature profile of the

medium to be precisely adiabatic, we can adopt

the ideal Carnot efficiency, given by Eq. (22.1). In

the following section we show how this is gener-

alized to arbitrary temperature increments and

gradients.

22.2 Thermodynamic efficiency,

buoyancy forces and

convective power

Conservation of energy (the first law of thermo-

dynamics) means that the heat exhausted to the

sink is

¼ Q

 W; (22:2)

so that we can write Eq. (22.1) in a less familiar

form,



 T

 1 ¼



1  

: (22:3)

A reason for interest in 

, the efficiency referred

to the heat exhausted to the sink, rather than the

conventional , referred to the source, is that in

the case of the Earth we observe the heat

exhausted at the surface. The mechanical

power generated is consumed in deforming and

so heating the mantle, being thereby put back

into the heat source, although not necessarily

distributed in the same way, and effectively

reduces the net heat input to Q

. Note that it is

not the difference in the temperatures of the

heat source and sink that appears in the effi-

ciency, it is their ratio.

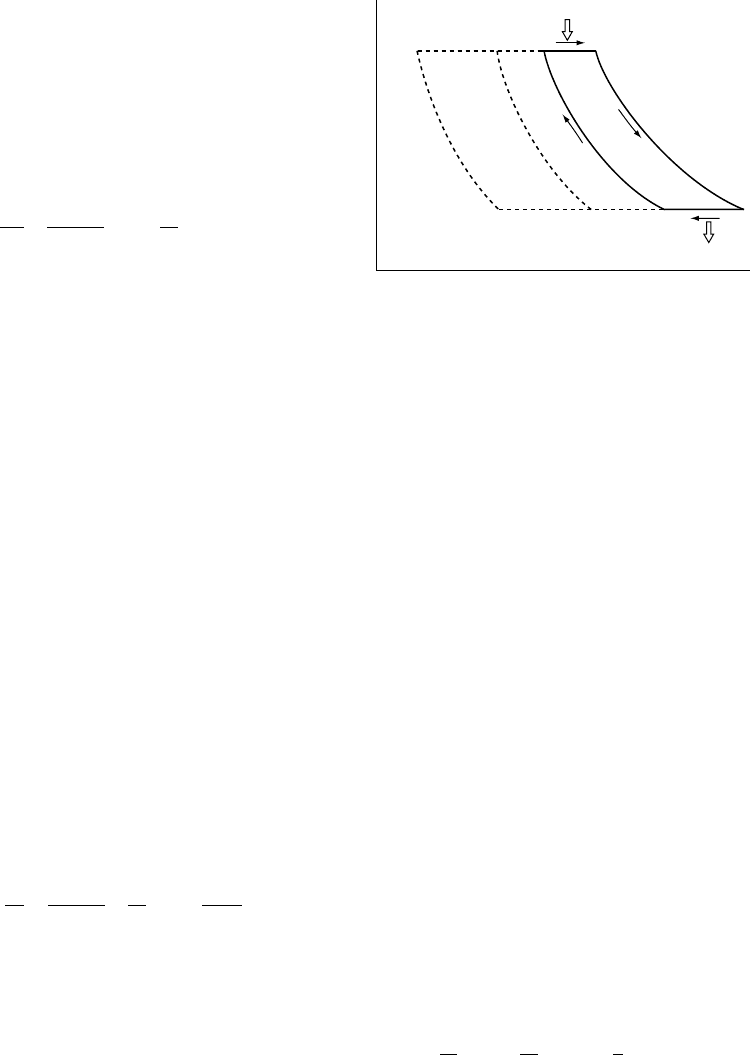
We can extend the loop with an indefinite

number of adjacent loops, each of which is a

Carnot cycle, as in Fig. 22.1. The limbs at pres-

sures P

and P

then involve finite temperature

changes and cannot be regarded as isotherms,

but each point at P

is adiabatically related to a

point at P

and gives an efficiency corresponding

to that section of the total loop. This is given by

the temperature ratio, calculated by Eq. (19.19),

which integrates to give





dP ¼







d: (22:4)

In general  and K

are temperature dependent

so that these component efficiencies are not all

equal, but the temperature variations in phys-

ical properties are quite small, especially at

FA'AB

CDD'E

FI G U R E 22.1 A thermodynamic cycle between

pressures P

and P

. The solid loop is of infinitesimal

width, involving infinitesimal heat input, Q

, on limb AB

and output, Q

, on limb CD. The temperature changes on

these limbs are, therefore, infinitesimal and they can be

treated as isothermal. The other two limbs are adiabats of

entropies S

and S

(also infinitesimally different),

making the loop ABCDA a Carnot cycle. When an adjacent

cycle, A

ADD

A is added, the limb DA is cancelled, but

temperatures T

and T

cannot be treated as equal to T

and T

. They are, however, adiabatically related to each

other in the same way as T

and T

. This allows a finite

extension of the loop to EF, with limbs FB and CE

involving finite temperature changes, but with each point

on FB adiabatically related to a point on CE by the same

pressure difference. The mechanical work done on one

cycle is the area of the loop on the P–V diagram.

362 THERMODYNAMICS OF CONVECTION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

363

– [361–375] 13.3.2008 10:47AM

high pressure, and there is no difficulty in cal-

culating the average efficiency for the complete

loop. Even a large temperature difference

between B and F (or C and E) in Fig. 22.1 does

not compromise the efficiency argument. Of

course, to get heat into the medium on limb

FB the source may need to be at a higher tem-

perature, and to get heat out on limb CE the

sink must certainly be at a lower temperature,

but these excess temperature differences con-

tribute nothing to the convective cycle per se.

They merely drive thermal diffusion, which is

thermodynamically irreversible and cannot

affect the calculated power or efficiency.

Convective power is determined by the adia-

batic temperature ratio, whatever higher ratio

actually drives the convection.

Now we can also ask whether it is necessary

for limbs BC and DA in Fig. 22.1 to be adiabats. If

they are not, then it means that heat leaks into or

out of the medium on these limbs. If it leaks from

one limb of the cycle to the other then it is

simply returned to its source and contributes

nothing to either heat transfer or convective

power. If it leaks into some non-participating

part of the medium then we do not have a closed

cycle and additional material must be brought

into the energy balance. Inevitably some of the

heat from the source, or equivalently coolness

from the sink, gets only part way round a cycle.

But, if we disallow time variations of the thermal

structure, this only means that part of the heat

participates in a shortened cycle, with its own

thermodynamic efficiency. This is directly rele-

vant to mantle convection for which it is conven-

ient to describe convection in terms of coolness

transported downwards by subducting slabs,

rather than heat transported upwards. The

assumption of a uniform distribution of heat

sources requires that the subducting coolness is

distributed through the mantle and does not all

end up at the bottom.

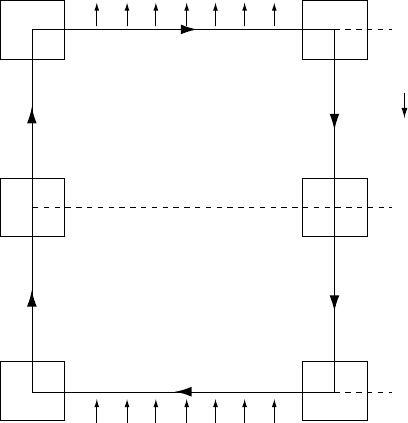
We now examine a mechanical model that is

more obviously related to the forces driving con-

vection in the Earth. The cycle ABCDA in Fig. 22.2

is the physical path of a mass m between depths

and z

and corresponds to the elementary

cycle shown by the solid line in Fig. 22.1. On

limb AB of the path it absorbs (or acquires by

its own radioactivity) heat Q

, so that the temper-

ature rises from T

to T

and

¼ mC

ðT

 T

Þ: (22:5)

As before, we assume initially that (T

T

)is

infinitesimal, but we allow the surrounding

medium to have any arbitrary temperature pro-

file. The assumption of an infinitesimal temper-

ature increment means that physical properties,

specific heat, C

, volume expansion coefficient,

, and Gr ¨uneisen parameter, , are taken as inde-

pendent of temperature over the small incre-

ment, although they may vary arbitrarily with

pressure. The mass element then rises from B to

C, cooling to temperature T

, and we make the

further assumption, removed later, that this

limb of the path is adiabatic. It loses heat on

limb CD, cooling to temperature T

, which is so

adjusted that with adiabatic recompression on

limb DA it returns to temperature T

The buoyancy forces at arbitrary depth z,at

positions X and Y in Fig. 22.2, are

¼ mgðT

 TÞ; (22:6)

FI G U R E 22.2 The physical path of an element of

material in a convective cycle.

22.2 EFFICIENCY AND CONVECTIVE POWER 363

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

364

– [361–375] 13.3.2008 10:47AM

¼ mgðT

 TÞ; (22:7)

where g is gravity and the surrounding ambient

temperature, T, is assumed to be the same at X

and Y. Then, since no mechanical work is done

on the horizontal limbs AB and CD, the net

work done by buoyancy forces over the whole

cycle is

W ¼

ðF

 F

Þdz ¼ m

gðT

 T

Þdz: (22:8)

This result does not depend on T and it is the

same whether the convection is considered to be

driven by upwelling at X or subduction at Y.

Since BC and DA are adiabats the entropy differ-

ence, DS, between any point on one and any

point on the other is the same. Thus

S ¼

dT ¼

dT (22:9)

and, with the assumption of an infinitesimal

temperature difference,

S ¼ mC

lnðT

ÞmC

ðT

 1Þ

¼ mC

lnðT

ÞmC

ðT

 1Þ

¼ Q

: (22:10)

Using this result to substitute for (T

T

)in

Eq. (22.8),

W ¼

gT

dz ¼

gT

dz: (22:11)

The integrand in Eq. (22.11) is the adiabatic tem-

perature gradient (see Eqs. (19.55) and (19.56)), so

we can write Eq. (22.11) in a form coinciding with

the conclusion of Section 22.1:

W ¼ Q

 T

¼ Q

1 



¼ Q

1  exp





d



;

 Q

1 









(22:12)

The efficiency,  ¼W/Q

, is calculated knowing

only the density variation and the Gr ¨uneisen

parameter. It is not necessary to know the tem-

peratures.  depends only the adiabatic temper-

ature ratio between the heat source and sink.

This is given by Eq. (22.4) and does not depend

on the actual temperatures unless the thermal

properties are temperature dependent.

As mentioned, the assumption of an infinites-

imal temperature increment is removed by con-

sidering a large number of infinitesimally

displaced cycles and allowing for the tempera-

ture variations of properties by taking the aver-

age efficiency over any temperature range. If we

postulate that limb BC or DA departs from adia-

bats by leakage of heat to or from the surround-

ing medium, then we must include additional

material in a more complicated cycle to main-

tain a closed system, and if heat leaks from X to Y

it is merely returned to the source at A and con-

tributes nothing. The rising and sinking limbs of

a convective cycle do not need to be adiabats. The

essential conclusion is that the thermodynamic

efficiency of convection, that is, the ratio of

mechanical power generated to the convective

heat transport, is the Carnot efficiency corre-

sponding to the adiabatic temperature ratio of

the heat source and sink. Excess temperature

gradients are required to make convection

occur, but they do not yield more power. They

drive the thermodynamically irreversible pro-

cess of conduction, by which heat enters and

leaves the convecting medium. This makes

numerical calculations simple because we need

only the thermal properties in Appendix G and

not the absolute temperatures. However, before

discussing numerical results, we consider a com-

plication arising from phase transitions.

22.3 Convection through phase

transitions

At depths between 200 km and 700 km, mineral

phase transitions complicate convection in ways

that have been subject to much debate. The tran-

sitions obey the Clausius–Clapeyron equation,

which is considered in the special case of melt-

ing in Section 19.4 (Eq. (19.40)), but is quite

general. We apply it here to the solid–solid tran-

sitions of mantle minerals, whose crystal

364 THERMODYNAMICS OF CONVECTION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

365

– [361–375] 13.3.2008 10:48AM

structures adjust to higher pressure forms at

depth. We write the variation with pressure of

the temperature of any transition, T

, in terms of

the volume and entropy changes of the transi-

tion by the Clausius–Clapeyron equation:

V

S

: (22:13)

The principle of LeChatelier demands that, for

any phase transition caused by increasing pres-

sure, the volume change, DV, is negative but the

entropy change, DS, may have either sign, and

both positive and negative values are observed

for mantle minerals. If DS is positive, that is the

higher pressure form has the higher entropy,

then the mineral absorbs heat in converting to

this form. The transition is referred to as endo-

thermic and if external heat is not supplied then

the mineral is cooled. The phase boundary at

660 km depth in the mantle is due to an endo-

thermic transition. Conversely, with positive DS,

we have an exothermic transition of the kind

occurring at 220 km and 410 km.

If convection proceeds adiabatically through a

transition, with no thermodynamic irreversi-

bility or thermal diffusion resulting from the

temperature change, then Eqs. (22.1) and (22.12)

still apply, where (T

T

)or(T

T

)now

include the temperature increment or decre-

ment of the phase transition. An exothermic

transition increases the adiabatic temperature

ratio between the heat source and sink, increas-

ing the thermodynamic efficiency of the convec-

tion, whereas an endothermic transition reduces

the temperature ratio and the efficiency. The

660 km transition has received particular atten-

tion because of its inhibiting effect on whole

mantle convection. Also, the assumption of per-

fect thermodynamic reversibility and neglect of

thermal diffusion are unrealistic, and all such

irreversible effects reduce the efficiency for all

transitions, whether endothermic or exother-

mic. The effect of thermal diffusion in this sit-

uation is considered in Section 22.5.

Table 22.1 gives basic numerical data for the

transitions that we must consider. The depths

and absolute densities as well as values of bulk

modulus that are needed for calculations are

taken from PREM, but the density increments,

D, do not coincide with the PREM values, being

estimated from mineralogical data, along with

the entropy increments, DS. Other thermal pro-

perties are taken from Appendix G. DT is the

temperature increment corresponding to DS,

that is

T ¼ TS=C

: (22:14)

It is a notional quantity, not directly observable,

but its significance is that it adds to or subtracts

from the adiabatic temperature difference

T

) in Eq. (22.12). Its magnitude, relative

to the total adiabatic temperature range of the

mantle, about 1100 K, is a measure of the impor-

tance of phase transitions to the total mechan-

ical energy generated by convection (5% to 8%,

see Table 22.1). However, the total energy does

not determine what happens locally. The detail

of what happens is of greatest interest in the case

of the endothermic 660 km transition, for which

DT is negative, because this presents an obstacle

to convection through it.

Also listed in Table 22.1 is the Clapeyron slope,

/dP, given by Eq. (22.13). From this we obtain

the ‘overshoot’, z, that is, the difference between

the depths at which the transition occurs in

upgoing and downgoing material, according to

their temperature difference, T. In the table

this is given as a ratio, that is, the depth of over-

shoot per degree temperature difference,

Table 22.1 Characteristics of mantle phase

transitions (olivine composition)

Depth (km) 220 410 660

D (kg m

3

) 212 94 301

DS (J K

1

) 40 35 þ49

DT (K)

(Eq. (22.14))

þ61 þ54 79

/dP (K MPa

1

) þ0.44 þ0.21 0.36

z/ T (m K

1

)

(Eq. (22.15))

þ69 þ135 70

 (MPa)

(dT ¼200K)

Dz (km)

(Eq. (22.24))

4.3 7.6 þ5.4

v(critical)(cm/year)

(Eq. (22.29))

1.47 0.83 1.17

22.3 CONVECTION THROUGH PHASE TRANSITIONS 365

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C22.3D

–

366

– [361–375] 13.3.2008 10:48AM

z

T

gdT

=dP

: (22:15)

Bina and Helffrich (1994) discuss the topography

of mantle phase boundaries that result from this

effect. For subducting material, which is sinking

because it is cooler and denser, T is negative, so

the 660 km phase boundary, for which dT

/dP is

negative, is depressed by 70 m per degree temper-

ature difference. This means 14 km if the subduct-

ing slab is 200 K cooler, on average, than its

surroundings. It pushes (or pulls) lower density

material into the higher density phase, producing

abuoyancyforce,(gzD) per unit cross section of

slab, opposing its subduction. To estimate the

stress we must subtract the driving force of ther-

mal shrinkage, g(T )z per unit cross section,

where  is the volume expansion coefficient. For

a temperature contrast T the net force per unit

area of the slab cross section is therefore

 ¼

T

ðdT

=dPÞ





 T



; (22:16)

where D is the density increment of the transi-

tion. Note that the second term in Eq. (22.16)

depends on the square of the temperature decre-

ment, T, because the thermal contraction and

the depth of penetration are each proportional

to T. However, the first term is dominant for any

plausible value of T.

We can refer to s, as calculated by Eq. (22.16),

as the virtual stress. It is a rough estimate of the

boundary stress caused by subduction through

an endothermic transition, but the actual stress

depends on geometrical factors, especially the

slab thickness relative to the depth overshoot.

If the initial maximum temperature deficit of

subducting material is 1000 K, with an average

of 500 K, diffusion of heat from the surrounding

mantle produces a thicker slab with T 200 K. A

value of stress, , for dT ¼200 K is given in

Table 22.1 for the 660 km transition. Even

acknowledging that we have probably overesti-

mated the stress by assuming a 100% olivine

composition of the subducting material, this

stress exceeds the average tectonic stress esti-

mated in Section 13.2. Thus, subduction through

this transition presents a mechanical problem.

Seismological evidence of horizontal deflections

of slabs and accumulations of subducted mate-

rial at the boundary is referred to in Chapter 12,

but some slabs appear to pass straight through.

Numerical simulations (e.g. Solheim and Peltier,

1994; Tackley et al., 1994) have suggested that

accumulated material may avalanche into the

lower mantle after a delay.

22.4 Thermodynamic efficiency

of mantle convection and

tectonic power

The mechanical power,



, generated by the con-

vection of heat,



, from a source at pressure P

a sink at pressure P

is given by rewriting

Eq. (22.12) in a more general way:

E ¼

ð@ ln T @P=

dP ¼

 K

dP:



(22:17)

We use this to calculate the tectonic power from

the distribution of heat sources. It is not neces-

sary to know the temperatures, but only adia-

batic ratios that are expressed in terms of

physical properties. The intervention of phase

transitions is handled by introducing discontinu-

ities in the adiabatic temperature profile accord-

ing to the entropies of the transitions in

Table 22.1:

T=T ¼  ln T ¼S=C

: (22:18)

There are several ways of representing the

results of such calculations. A straightforward

calculation of the thermodynamic efficiency of

convective heat transport between any two

depths is simply  ¼

Q by Eq. (22.17) and this

is the fundamental result. Figure 22.3 is a plot of

this efficiency for convection of heat to the sur-

face as a function of the depth from which it

originates. The efficiency corresponding to the

transport of heat between any two depths is the

difference between the values at those depths.

The calculations assume that convective heat

transport stops at the base of the lithosphere

and that heat loss from the lithosphere to the

366 THERMODYNAMICS OF CONVECTION