Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

327

– [314–336] 13.3.2008 2:45PM

determine the thermodynamic efficiency of con-

vection and hence the mechanical power that it

generates. Absolute temperatures or temperature

differences are not important. However, these

equations are valid only for a homogeneous

region and integration through phase transitions

requires additional information (Section 22.3).

One reason for presenting the summary of

thermodynamic relationships in Appendix E is

that adiabatic gradients and adiabatic variations

of physical properties are central to deep Earth

physics, but most conventional treatments of

thermodynamics emphasize isothermal varia-

tions. For some properties adiabatic and iso-

thermal derivatives are very different and this

becomes increasingly true as one takes progres-

sively higher derivatives. An important example

is the difference between the temperature varia-

tions of the adiabatic and isothermal bulk mod-

uli, K

and K

, as represented by 

¼(1/)(@lnK

@T)

and its more commonly quoted isothermal

analogue, 

¼(1/)(@lnK

/@T)

. 

exceeds 

by a

factor that varies from 1.6 to 2.0 in the lower

mantle. In this case it is crucial to assessment

of the effect of temperature on seismic veloc-

ities, as well as to the calculation of  by

Eq. (19.33), that the correct derivative be used.

Another reason for interest in the adiabatic

temperature gradient is its relationship to the

melting point gradient. As appears to have been

recognized first by King (1893), melting points

normally increase more rapidly with pressure

that the adiabatic temperature rise. King was

endeavouring to rationalize the observation that

the tidal rigidity of the Earth demanded solidity to

great depth whereas Kelvin’s pre-radioactivity cal-

culation of the cooling of the Earth (Section 4.2)

suggested that the melting point would be

reached at a depth no greater than a few tens of

kilometres. King concluded that the Earth would

have solidified from the inside outwards, with the

latent heat carried upwards convectively by a

fluid layer, a process that we now understand to

be occurring in the core (Sections 22.5 and 23.6).

The ratio of adiabatic and melting point gradients

is made quantitative by comparing Eqs. (19.19)

and (19.52), using corresponding bulk moduli,

given by Eqs. (19.51) and (E.1) of Appendix E, so

that at the melting point

ðdT

=dzÞ=ð@T=@zÞ

¼ 2ð1 þ T

Þ=ð1 þ 2 T

Þ;

(19:57)

which can never be less than unity. King’s (1893)

conclusion is a general one and all composition-

ally homogeneous layers in planets and satellites

must solidify from the inside outwards.

In Section 10.6 we note the role of T/T

termed homologous temperature, in controll-

ing the rheological properties of the mantle. It

appears that sudden failure in earthquakes is

restricted to regions where this ratio is less than

0.5 to 0.6. The inference is that, apart from a

shallow surface layer, the only parts of the mantle

where T/T

is below this limit are the subducting

slabs, and then only down to about 700 km. If this

is the reason for the complete absence of earth-

quakes in the lower mantle, then we can use the

temperature profile in Table G.2 (Appendix G) to

impose limits on the solidus temperature, T

Adiabatic extrapolation from the 660 km phase

transition gives a temperature near to the base

of the mantle of about 2750 K, ignoring the steep

temperature gradient right at the bottom. On this

basis, T

near to the bottom of the mantle is less

than about 4580 K. Our estimate of the core–

mantle boundary temperature is 3740 K, and in

Section 23.5 we suggest that it was only about

200 K hotter, that is 3940 K, when the mantle

had fully solidified. These numbers are compat-

ible if we assume that, like the core, the mantle

solidified from the inside outwards, with a

melting point gradient steeper than the adiabat.

But we note the evidence for partial melt in ultra-

low velocity zones (ULVZs) at the base of the man-

tle (Section 17.6). The surface layer of the core is

much too nearly isothermal to admit hot patches,

so the ULVZs imply compositional heterogeneity.

This could mean either patches of some low melt-

ing point material at the base of the mantle or

pockets of the post-perovskite phase that has

absorbed iron from the core (Mao et al., 2006).

19.6 Thermal conduction

Through most of the Earth temperature gradients

are close to adiabatic (Eqs. (19.55), (19.56)). There

is, therefore, a steady flux of conducted heat at all

19.6 THERMAL CONDUCTION 327

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

328

– [314–336] 13.3.2008 2:45PM

levels. In the mantle this is only about 3% of

the total heat flux, most of which is convective,

except in the thermal boundary layers at the

bottom and top. Conduction is important at the

base of the mantle, in layer D

, where it transfers

core heat into the mantle, and at the surface,

where heat diffuses from the lithosphere into

the atmosphere and oceans. It needs to be

considered also in the transition zone, where

there are temperature changes in the material

convectively transported through mantle phase

transitions (Sections 22.3 and 22.5) and in the

diffusion of heat into cool, subducting litho-

spheric slabs. Thermal conductivity in the core

is much higher and conducted heat is an impor-

tant component of the core energy budget

(Sections 21.4, 22.7 and 23.5).

In the crust and uppermost mantle the effect

of pressure on conductivity is slight enough to

neglect, so that measured conductivities of

familiar rocks and minerals provide a reasonable

estimate of the conductivity of the lithosphere.

Laboratory measurements give a range of values

for different rocks and minerals. We take

 ¼4.0 W m

1

from measurements on miner-

als in ultramafic rocks to be representative of the

uppermost mantle (Clauser and Huenges, 1995),

but only 2.5 Wm

1

for basaltic oceanic crust.

For the deep mantle, theory takes over and it is

very insecure. Lattice conduction, that is heat

transport by phonons or quantized lattice vibra-

tions, is controlled by several phonon scattering

mechanisms which depend on temperature and

pressure in different ways. Greatest attention in

the literature has been given to phonon–phonon

scattering, because this is amenable to theoret-

ical analysis. However, while it may be the pro-

cess controlling conduction in large, perfect

crystals, it gives estimates of conductivity much

higher than observed in ordinary materials.

Phonons are scattered also by crystal imperfec-

tions of all kinds and this is the dominant pro-

cess controlling conduction in minerals. Glasses

are an extreme case of imperfect crystals, having

dislocated liquid-type structures. As Kieffer et al.

(1976) demonstrated in the case of fused quartz,

conductivity is very much lower than for single

quartz crystals and both the temperature and

pressure effects are reversed. Minerals are rarely

simple, but are non-stoichimetric solid solutions

with a variety of atoms. In such materials pho-

non scattering is not observed to depend in any

regular way on temperature or pressure. In the

absence of contrary information we assume that

lattice conductivity has no strong variation with

depth in the mantle.

We have a rough check on this assumption

from the thickness of the D

layer. This layer is

hottest and therefore least viscous at the bottom,

so that the softened material is skimmed off into

buoyant convective plumes, with the bulk of the

mantle gradually collapsing on to the core to

replace it. If the temperature of the plume mate-

rial when it first starts rising is DT ¼1000 K

higher than the temperature of the surround-

ing mantle and the heat flux from the core is

dQ/dT ¼3.5 10

W, as estimated in Chapter 21,

then, with heat capacity per unit volume

(C

) ¼6.6 10

1

3

, the rate of removal of

material is

dV=dT ¼ðdQ =dTÞðC

TÞ¼530 m

1

: (19:58)

This material is removed from the crypto-

oceanic areas of D

(see Fig. 12.3). We have no

precise estimate of the fraction of the

core–mantle boundary that this represents, but

the average rate of collapse of the mantle on to

the core is v ¼3.5 10

12

1

(0.11 mm/year).

This is analogous to the ablation of meteorites

and spacecraft entering the atmosphere, with

heat diffusing inwards but the surface tempera-

ture maintained as material is removed. It gives

an exponential temperature profile with height h

above the boundary (Stacey and Loper, 1983),

varying as e

h/H

, where the scale height is

H ¼ =v (19:59)

and  ¼/C

is the thermal diffusivity. There is a

trade-off between conductivity and assumed boun-

dary layer thickness:  /H ¼2.3 10

5

2

1

so that, if H ¼200 km, then  ¼4.6 Wm

1

.This

is marginally below the lower mantle range, 5 to

12 Wm

1

, inferred by Manga and Jeanloz

(1997) from high pressure measurements on

MgO and Al

. We can note that, with this con-

ductivity and the boundary temperature gra-

dient of 5 K/km (1000 K over a profile with a

328 THERMAL PROPERTIES

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

329

– [314–336] 13.3.2008 2:45PM

scale height of 200 km), the heat flow into the

mantle is 3.5 10

W, as adopted above.

Although the numbers applied in this calcula-

tion are uncertain, they are mutually consistent,

so, on this basis, we have no reason for suppos-

ing that the deep mantle conductivity is signifi-

cantly different from the lithospheric value.

Another phenomenon that introduces a

measure of doubt about deep mantle conduction

is the radiative transfer of heat. This process

occurs in stellar interiors and was introduced to

geophysics by Clark (1957). If mantle minerals

are moderately transparent in the near infra-red

then radiation gives a contribution, 

, to con-

ductivity which, in the simple case of a ‘grey

body’, that is, one with opacity, ", independent

of wavelength, is (as Clark showed)

¼ð16=3Þn

T

="; (19:60)

where n is refractive index and  ¼5.67 

8

2

4

is the Stefan–Boltzmann constant.

" is defined as causing radiation intensity to

decrease with distance x from a source as

"x

, so that the unit of " is m

1

. It is important

in the lower mantle if "<10

1

, which repre-

sents a moderate transparency. However,

iron-bearing minerals, typical of the lower

mantle, are opaque because iron ions give

strong absorption bands in the infra-red as well

as optical ranges. There have been conflicting

opinions about whether these absorption bands

are shifted sufficiently by pressure to open a win-

dow of transparency in the lower mantle and

cause significant radiative heat transfer, but Gon-

charov et al. (2006) reported that conversion of the

iron ions in (Mg,Fe)O to a ‘low spin’ state (with

electron spin moments paired) increased the min-

eral opacity at lower mantle pressures.

Core conductivity is dominated by electrons,

not phonons. For a liquid, such as the outer core,

the structural disorder gives very strong phonon

scattering, as noted above, and lattice conduc-

tion is not important. Stacey and Anderson

(2001) suggested a value of 3.1 W m

1

about 10% of total conductivity. Calculation of

the much stronger electron contribution, 

relies on the Wiedemann–Franz relationship

between 

and the electrical conductivity, 



¼ L

T; (19:61)

where L ¼(pk/e)

/3 ¼2.443 10

8

W O K

2

known as the Lorenz number, k is Boltzmann’s

constant and e is the electron charge. Kittel

(1971) discussed the reason for the constant

value of L, the same for all metals, which is

that, except at very low temperatures, the scat-

tering of electrons by phonons or by lattice

defects does not depend on whether they are

accelerated by an electric field or are carrying

heat down a temperature gradient.

The electrical conductivity of the core is dis-

cussed in Section 24.4 with the conclusion that

it varies from 2.76 10

1

at the core–

mantle boundary to 2.15 10

1

just

above the inner core and 2.42 10

1

the inner core. Applying Eq. (19.61) to these val-

ues and adding 3.1 W m

1

of lattice conductiv-

ity, we have  ¼28.3 W m

1

at the top of the

outer core and 29.3 W m

1

at the bottom of

the outer core. These numbers are very uncertain

but for the purpose of our thermal calculations

we assume them to apply, with a depth variation

as listed in Table G.1 (Appendix G). In the inner

core we take  ¼36 Wm

1

19.7 Temperature dependences

of elastic moduli: thermal

interpretation of tomography

Equations (19.34) and (19.35) define the dimen-

sionless parameters 

and ", which are used

to represent the temperature dependences of

elasticities. 

is known as the adiabatic

Anderson–Gr ¨uneisen parameter, to distinguish

it from its more familiar but geophysically less

useful isothermal analogue, 

¼(1/K

)(@lnK

@lnT). It is thermodynamically related to other

familiar quantities by identities in Appendix E

and is calculated from Eq. (E.4), in which it may

be convenient to substitute Eq. (E.8),



¼ K

 1 þ q   C

¼ K

 1 þ q

 ;

(19:62)

with parameters defined in Table E.1. All of them

can be derived from an equation of state, with

19.7 TEMPERATURE AND TOMOGRAPHY 329

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

330

– [314–336] 13.3.2008 2:45PM

Eq. (19.33). The estimation of  by this equation

requires 

as well as K

so the calculation of 

Eq. (19.62) is iterative, but this is not a problem

because the 

term in Eq. (19.37) is much smaller

than K

. Calculation of q requires differentiation

of Eq. (19.33) and so assumes knowledge of K

that is the next derivative of the equation of

state. This emphasizes the point that for a useful

estimate of 

it is essential to use an equation of

state for which the derivatives satisfy the rele-

vant thermodynamic constraints. This restricts

the choice to Eqs. (18.28), (18.39) or (18.45), with

their integral and derivative forms.

There is no thermodynamic relationship for

" (Eq. (19.35)), corresponding to the identity

for

(Eq. (19.62)). Without this constraint " can-

not be determined with the same reliability as



. We appeal instead to Eq. (18.67). The numer-

ical values of the coefficients in Eq. (18.68) are

specific to the lower mantle adiabat, but

Eq. (18.67) must be equally valid for any adia-

bat, with an adjustment to (/K)

but the same

values of (/K)

and K

, as explained by Stacey

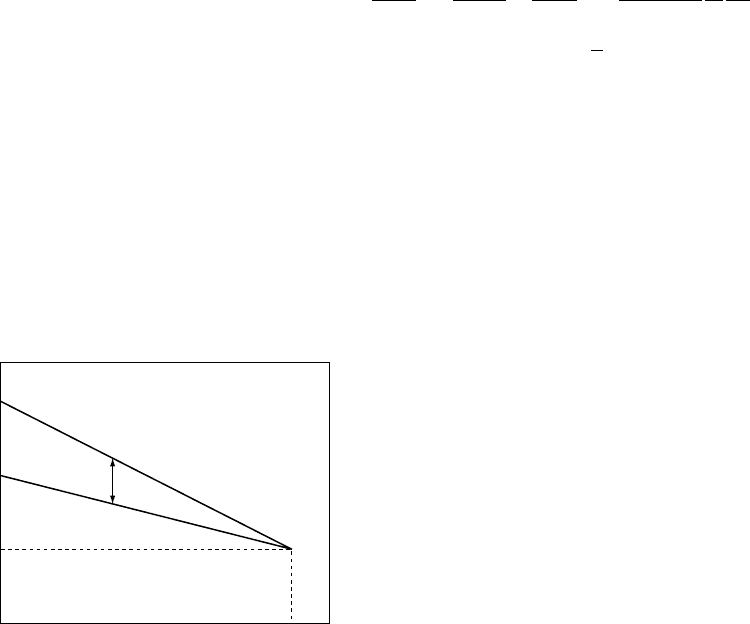
and Davis (2004, Section 12). A simple graph

(Fig. 19.3) shows how the difference in the

ratio (/K) between two adiabats, A–C and B–C,

varies with normalized pressure, P/K. From the

similar triangles, ABC and DEC, we have, with

Eq. (18.44),

ð=KÞ¼ð=KÞ

½ðP=KÞ

ðP=KÞ=ðP=KÞ

¼ ð=KÞ

ð1  K

P=KÞ: ð19:63Þ

Since AC and BC are adiabats, the entropy differ-

ence between any pair of points, such as D–E, is the

same as at A–B and can be related to the temper-

ature difference between the adiabats at any value

of P/K, allowing the variation of (/K)withtemper-

ature to be calculated from its variation at P ¼0.

This means that a laboratory observation of the

variation of (/K)

with T

can be combined with a

calculation of the temperature dependence of K at

arbitrary pressure, using 

(Eq. (19.62)), to give the

temperature dependence of . The resulting equa-

tion, derived by Stacey and Davis (2004), is

@ ln 



=KðÞ

@ ln K





dlnð=KÞ

1  K



: ð19:64Þ

A cautionary note must be applied to the use

of Eq. (19.64). There are two distinct mechanisms

that contribute to the temperature dependence

of . Equation (18.67) is derived from an argu-

ment about bond forces and it leads directly to

Eq. (19.64), but takes no account of an anelastic

effect that also contributes. The appeal to a labo-

ratory value of d(/K)

/dT

calibrates Eq. (19.64)

by the total effect, which includes a contribution

by anelasticity, unrelated to the derivation of the

equation. The problem was first drawn to atten-

tion by Karato (1993), who pointed out that ane-

lastic relaxation mechanisms that are thermally

activated cause a decrease in shear modulus with

temperature. Attenuation of seismic waves is

caused by a time or phase lag between stress

and strain (Section 10.5), which can have several

causes. Some of them are thermally activated

phenomena in which atomic displacements

must overcome potential barriers, for which

they must wait for suitable thermal impulses

(phonons). The probability of a big enough

impulse arriving in any time interval is repre-

sented by a frequency of occurrence

 ¼ 

expðE=kTÞ; (19:65)

where E is the barrier energy, k is Boltzmann’s

constant and 

is the ‘attempt frequency’ of the

Δ(μ

/K)

(μ

)

∞

ΔT

P/K

(P/K

)

∞

= 1/K

′

∞

Δ(μ

/K )

FI G U R E 19.3 The ratio of elastic moduli, /K, plotted

as a function of P/K for two close adiabats. The

difference, D(/K), decreases linearly with P/K, allowing

its temperature dependence to be calculated from the

zero pressure variation, d(/K)

/dT

330 THERMAL PROPERTIES

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

331

– [314–336] 13.3.2008 2:45PM

process, typically 10

to 10

Hz. Since this fre-

quency (or probability) increases with temper-

ature, the modulus decreases by an amount

that can be expressed in terms of the correspond-

ing damping of elastic waves. The effect is ana-

lysed in terms of the effect on shear wave speed

(details of the algebra are given by Stacey and

Davis, 2004, Appendix B), but can be expressed in

terms of the effect on . For a seismic shear wave

of frequency f,

ð@ ln =@ ln TÞ

Anelastic

¼ð2pQ

Þlnð

=f Þ; (19:66)

where Q is defined by Eq. (10.14) or (10.18) and

subscript S refers to shear waves. There is no

appreciable anelastic contribution to the tem-

perature dependence of K.

Equation (19.66) gives the maximum possi-

ble effect because it assumes that all of the

mechanisms that contribute to damping are

thermally activated and also that Q is independ-

ent of wave frequency. An increase in Q with

frequency gives a smaller effect. The maximum

effect, given by Eq. (19.66), is 20% of the total

(@/@T)

and probably 13% would be close to the

real contribution, but this is significant. In

allowing for it we note that there is a general

increase in Q

as well as T with depth in the

mantle, so that by Eq. (19.66) (@ln/@T)

Anelastic

decreases with depth as 1/Q

T. This is broadly

similar to the decrease with depth of the total

(@ ln /@T)

by Eq. (19.64). Thus the calibration of

this equation by laboratory observations of

(d(/K)/dT)

introduces no serious doubt about

the calculation of ".

Values of 

and " calculated by Eqs. (19.62)

and (19.64), with the definition " ¼(1/)(@ ln /

@T)

, are listed in Appendix G for the lower man-

tle. They are used to calculate the thermal con-

tribution to seismic velocity variations, for

comparison with tomographic observations.

Taking the equations for P- and S-wave speeds

(Chapter 16),

¼ð=Þ

1=2

; V

¼f½K þð4=3Þ=g

1=2

;

(19:67)

and differentiating with respect to T,

ð@ ln V

=@TÞ

¼ð=2Þð"  1Þ; (19:68)

ð@ ln V

=@TÞ

¼ð=2Þ½K

ð

 1Þ

þð4=3Þð"  1Þ=½K

þð4=3Þ:

(19:69)

We are interested also in the hydrodynamic

or ‘bulk sound’ velocity



¼ðV

ð4=3ÞV

1=2

¼ðK

=Þ

1=2

; (19:70)

for which

ð@ ln V



=@TÞ

¼ð=2Þð

 1Þ: (19:71)

This is not directly observable but is calcu-

lated from V

and V

. The significance is that its

temperature variation does not depend on " but

only on the better determined 

. Temperature

variations of the lower mantle velocities are

listed in Table 19.1.

Velocity heterogeneities are observed at all

depths in the mantle by seismic tomography

(Section 17.7). They are generally stronger in

the upper mantle, where subducting litho-

spheric slabs present strong contrasts in temper-

ature-dependent properties. The inference is

that in the lower mantle also the heterogeneities

reflect tectonics, present and past, with high

Table 19.1 Thermal variations of seismic

velocities in the lower mantle, with an

extrapolation to zero pressure

(km)

(qlnV

/qT)

(10

5

1

)

(qlnV

/qT)

(10

5

1

)

(qlnV

qlnV

)

(qlnV



qlnV

)

3480 2. 473 1.001 2.470 0.0492

3600 2. 561 1.050 2.440 0.0544

3630 2. 584 1.062 2.432 0.0574

3800 2. 714 1.136 2.388 0.0636

4000 2. 870 1.229 2.335 0.0739

4200 3. 042 1.334 2.280 0.0852

4400 3. 228 1.449 2.228 0.0967

4600 3. 451 1.595 2.164 0.1117

4800 3. 703 1.762 2.102 0.1276

5000 3. 990 1.960 2.036 0.1460

5200 4. 341 2.209 1.965 0.1677

5400 4. 760 2.518 1.890 0.1934

5600 5. 283 2.922 1.808 0.2254

5701 5. 543 3.154 1.758 0.2474

P ¼0 8.796 6.080 1.447 0.4315

19.7 TEMPERATURE AND TOMOGRAPHY 331

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

332

– [314–336] 13.3.2008 2:45PM

velocities marking cooler than average material.

However, we can use the calculations of 

and "

to show that temperature cannot be the only

cause and that compositional variations must

be invoked. Particular attention is given to ratios

of the velocity variations in Eqs. (19.68), (19.69)

and (19.71), for which knowledge of  is not

required,

ð@ ln V

=@ ln V

¼½1 þð4=3Þð=K

Þ=½ð

 1Þ=ð"  1Þ

þð4=3Þð=K

; ð19:72Þ

ð@ ln V



=@ ln V

¼ð

 1Þ=ð"  1Þ: (19:73)

In these equations we see two consequences

of the fact that 

decreases with depth,

approaching unity deep in the lower mantle, as

in the listing in Appendix G. By Eq. (19.73),

(@lnV

’

/@lnV

) becomes very small, but it remains

positive because, with these calculations, 

does

not fall below 1. Two groups reported negative

correlations between V

’

and V

(Robertson and

Woodhouse, 1996a,b; Su and Dziewonski, 1997).

A thermal explanation would require 

< 1, con-

trary to calculations using Eq. (19.62) (because

">1 is not in doubt). This is evidence of composi-

tional heterogeneity (see Section 17.8), a conclu-

sion that does not depend on knowledge of ". The

very small value of (

1)/(" 1) deep in the

lower mantle means also that, by Eq. (19.72),

(@ lnV

/@ lnV

)

is insensitive to the value of ".

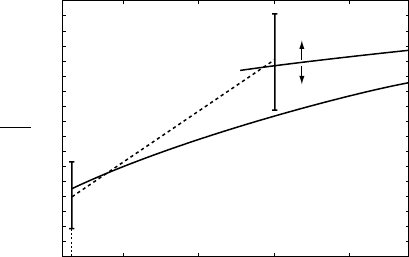
The observed variation in this ratio with depth

is broadly similar to the calculated variation

(Fig. 19.4), indicating that temperature varia-

tions account for a major part of it, although

not all. Unfortunately, insensitivity of critical

observations to the value of " prevents an obser-

vational check on the magnitude of the anelastic

effect.

19.8 Anharmonicity

The theory of specific heat, based on the principle

that lattice modes are harmonic oscillators

(Section 19.2), and the interpretation of thermal

expansion by Gr ¨uneisen’s theory (Section 19.3)

assume that if a material is held at constant

volume then the frequencies of its lattice modes

are independent of temperature or vibration

amplitude. This requires the oscillations to be

sinusoidal (harmonic) and that the atoms move

under the influence of interatomic forces propor-

tional to their displacements from equilibrium,

with potential energies proportional to squares

of the displacements. Although this is a useful

first approximation, as Fig. 18.4 illustrates, it

misses some of the important physics and we

need to consider the consequences of departures

from the harmonic assumption. Thermal expan-

sion and the strong pressure dependence of bulk

modulus are consequences of the asymmetry of

atomic potentials, as in Fig. 18.4, and are therefore

anharmonic effects. However, solid state and min-

eral physicists have generally made a distinction

between these two effects and other consequen-

ces of anharmonicity, such as departures from the

Dulong–Petit theory of specific heat (Section 19.2).

Acceptance of thermal expansion and pressure-

dependent elasticity, with neglect of temperature

variations of other thermal properties, such as

specific heat, is referred to as the quasi-harmonic

approximation (QHA), for reasons that are dis-

cussed below. The adequacy of QHA has been

vigorously debated by the mineral physics com-

munity. This section is concerned with the phys-

ical principles, following the argument of Stacey

and Isaak (2003), who interpreted the distinction

3.0

2.5

2.0

1.5

Robertson and

Woodhouse (1996)

Thermal effect

(Eq. 19.74)

> 1

< 1

= 1

Depth (km)

1000 1500

2000

2500

dlnV

FI G U R E 19.4 A comparison of the ratio of P-wave and

S-wave velocity variations in the lower mantle with

Eq. (19.72), using values of 

and " tabulated in

Appendix G.

332 THERMAL PROPERTIES

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

333

– [314–336] 13.3.2008 2:45PM

between QHA and full anharmonicity in terms

of derivatives of the atomic potential function

( in Fig. 18.4). QHA can be explained by non-

zero d

/dr

with neglect of the higher derivatives

that are required for temperature-dependent spe-

cific heat, etc. Stacey and Isaak termed this first-

order anharmonicity. The neglected higher-order

anharmonic effects are conventionally referred to

simply as anharmonicity.

The quasi-harmonic/anharmonic distinction is

blurred by the fact that there are two different

mechanisms involved. The asymmetry of atomic

potential functions referred to above causes what

we call type 1 or bond anharmonicity. This occurs

in all situations and is the only type of anharmo-

nicity in solids in which all atoms have neighbours

in opposite pairs. Asymmetry of crystal structures,

with bonds that do not occur in opposite pairs,

causes type 2 or structural anharmonicity. In this

case atomic oscillations would be anharmonic

even if individual atomic bonds were perfectly har-

monic. Then the two types are superimposed and

they have effects that are generally opposite in sign.

Consider first type 1 anharmonicity arising

from a linear oscillation of an atom between two

neighbours, as in Fig. 19.5(a). This is the situation

observed in minerals such as MgO, which has

cubic symmetry. It is a simplification that ignores

motion in perpendicular directions and corre-

lated motion of neighbours but it suffices for a

consideration of the effect of bond asymmetry on

atomic motion. For small displacements, x,of

atom B from its equilibrium position between

the fixed atoms A and C, we can write the poten-

tial energies of the two bonds as Taylor expan-

sions about the equilibrium atomic spacing, a,

ða  xÞ¼ðaÞ

ðaÞx þð1=2!Þ

ðaÞx

ð1=3!Þ

000

ðaÞx

þð1=4!Þ

ðaÞx

þ:

(19:74)

The total energy is the sum of the two potentials,

with subtraction of the equilibrium energy at

x ¼0,

E ¼ ða þ xÞþða  xÞ2ðaÞ

¼ 

ðaÞx

þð1=12Þ

ðaÞx

þ: (19:75)

Odd powers of x and odd derivatives of  are

eliminated by the symmetry. For very small x

this reduces to the energy for harmonic bonding,

¼

(a)x

, so that the departure from this sit-

uation is represented by

E=E

¼ 1 þð

ðaÞ=

ðaÞÞx

=12: (19:76)

In Fig. 19.6 this is plotted for the Born–Mie poten-

tial (Eq. (18.2) with just two terms and m ¼1,

n ¼5, to give K

¼4). For all plausible potential

ABC

a a

FI G U R E 19.5(a) Linear oscillation of an atom, B,

between neighbours A and C that are assumed fixed.

FI G U R E 19.5(b) Oscillation of an atom, B, in a crystal

with the diamond structure, having the four bonds to

each atom, directed to the corners of a tetrahedron. B

is displaced from equilibrium by a small distance, x,on

the line OBC, where O is the mid-point of an equilateral

triangle formed by neighbours A

, all equally

spaced from one another and from B.

E / E

0.1 0.2–0.2

0.6

0.8

0.7

0.9

1.2

1.4

1.3

1.1

Type 2

Type 1

–0.1

FI G U R E 19.6 Energies of atomic displacement

from equilibrium for geometries in Fig. 19.5(a), giving

type 1 (bond) anharmonicity (Eq. (19.76)), and Fig. 19.5(b),

giving type 2 (structural) anharmonicity (Eq. (19.82)).

19.8 ANHARMONICITY 333

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

334

– [314–336] 13.3.2008 2:45PM

functions 

is positive, giving an excess energy

relative to harmonic bonds. It has the effect of

driving atom B away from its extreme excur-

sions, reducing the time spent at large values of

x and therefore the mean potential energy of

thermal vibration. A result is a slight reduction

in specific heat, relative to the Dulong–Petit

limit (Eq. (19.3)). Anderson and Zou (1990)

observed this effect in MgO.

The geometry for calculation of type 2 anhar-

monicity is shown in Fig. 19.5(b) for the case of a

diamond structure. To isolate the type 2 effect

from a superimposed type 1 effect we assume

that all four of the bonds to the oscillating

atom, B, are perfectly harmonic, that is

 ¼ ðaÞþAðr  aÞ

; (19:77)

where A is a constant. Subtracting the energy at

equilibrium (x ¼0), the total potential energy at

displacement x is

E ¼ Aðr

 aÞ

þ 3Aðr

 aÞ

; (19:78)

where r

is simply (a x), but

¼½a

þ x

þ 2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð2=3Þ

ax

1=2

: (19:79)

Binomial expansion for small x gives

ðr

 aÞ

¼a

½ð2=3Þðx=aÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð2=27Þ

ðx=aÞ

ð7=36Þðx=aÞ

þ: ð19:80Þ

Substituting this in Eq. (19.78), we have

E=Aa

½3ðx=aÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð2=3Þ

ðx=aÞ

ð7=12Þðx=aÞ

þ

(19:81)

and, as for the type 1 calculation, we take the

ratio of total to harmonic energy,

E=E

¼ 1 þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð2=27Þ

ðx=aÞð7=36Þðx=aÞ

: (19:82)

The important feature of Eq. (19.82) is the

linear term. The potential energy is strongly

asymmetrical and so is quite different from the

type 1 effect, with which it is compared in

Fig. 19.6. Note that these are small departures

from the parabolic (harmonic) form and we are

considering x/a 1, so that the first terms in

Eqs. (19.75) and (19.81) are dominant and the

anharmonicity is a small superimposed effect.

For type 1 (bond) anharmonicity it depends on

the precise form of the atomic potential func-

tion, but all plausible forms give a result very

similar to that plotted in Fig. 19.6. As mentioned,

it gives a small decrease in C

with T,2%to3%for

MgO at 2000 K. When type 2 (structural) anhar-

monicity occurs, type 1 is superimposed but is

often masked by the type 2 effect. This depends

on crystal structure and is most obvious for the

tetrahedral bonding represented in Fig. 19.5(b)

and used to derive Eq. (19.82). This is common in

silicates because Si

4þ

ions favour tetrahedral

bonding to surrounding O

2

ions. It allows

atoms to vibrate towards ‘soft’ gaps in the crystal

structure, with correspondingly greater ampli-

tudes, causing C

to increase with temperature,

as observed in forsterite (Mg

SiO

) by Gillet et al.

(1991). Another consequence of ‘soft’ vibrations

is a lowered thermal expansion coefficient, as

considered below. This is particularly obvious

in crystals of Si and Ge, which have negative

coefficients over the limited temperature ranges

for which asymmetrically soft modes are most

significant, but the effect is quite general and

common (low pressure) silicates have low expan-

sion coefficients.

Although we tend to think of the thermal

expansion coefficient, , and in particular its

temperature dependence, as indicative of anhar-

monicity, this is not strictly correct.  is temper-

ature dependent even with the quasi-harmonic

assumption. The true indicator is the Gr ¨uneisen

parameter,  (Eq. (19.1)). For  we have a thermo-

dynamic identity,

ð@=@TÞ

¼ 

½q  1 ð@ ln C

=@ ln VÞ

ð1 þ 1=TÞ;

(19:83)

which does not vanish with the quasi-harmonic

assumption (because q ¼(@ ln /@ ln V)

6¼1), even

with the classical assumption that C

is constant.

On the other hand, as in Eq. (19.28),

ð@=@TÞ

¼ð1=TÞð@ ln C

=@ ln VÞ

: (19:84)

So, we examine the anharmonicity of  resulting

from the two bond geometries considered

above. The Mie–Gr ¨uneisen equation (Eq. (19.21))

can be taken to define  as the ratio of thermal

pressure to thermal energy per unit volume. The

effect on thermal energy of the two types of

334 THERMAL PROPERTIES

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

335

– [314–336] 13.3.2008 2:45PM

anharmonicity is represented by the energies of

atomic displacement in Eqs. (19.76) and (19.82).

We now seek expressions for the bond forces

that cause thermal pressure.

For the type 1, symmetrical situation in

Fig. 19.5(a), we need to calculate the average of

the forces exerted by B on A and C. It is important

to note that we cannot do this by differentiating

Eq. (19.75) because that gives the net force on B,

that is the difference between the two bond

forces, not the sum of them. We write Taylor

expansions for the individual bond forces in

the same way as Eq. (19.74) expands the energies,

noting that bond force is simply 



ðrÞ¼

ðaÞ

ðaÞx þð1=2!Þ

000

ðaÞx

ð1=3!Þ

ðaÞx

þð1=4!Þ

ðaÞx

: ð19:85Þ

Subtracting the non-thermal force, 

(a), the sum

of the two forces in Eq. (19.85) is

F ¼ 

000

ðaÞx

þð1=12Þ

ðaÞx

: (19:86)

Considering x to be the instantaneous displace-

ment in thermal vibration, we can take averages

of Eqs. (19.75) and (19.86) and then the ratio of

these equations is the ratio of thermal pressure

to thermal energy, that is . We have ignored

geometrical factors required for integration

over all bond orientations and so write this as a

proportionality:

 /



000

ðaÞ x





ðaÞ x





ðaÞ x



ðaÞ x



000

ðaÞ



ðaÞ



1 þ 

ðaÞ=

000

ðaÞ½x



=12 x



1 þ 

ðaÞ=

ðaÞ½x

hi=12 x

hi:

(19:87)

By separating the factor 

000

/

in this equation

we draw attention to the distinction between the

quasi-harmonic approximation (QHA) and the

higher anharmonic effects. QHA accepts positive

thermal expansion (>0) and is represented by



000

/

, but if the higher derivatives, 

and 

,are

assumed to be zero then  is independent of

vibration amplitude, or temperature. The second

fraction in this equation gives the anharmonic

temperature dependence. Stacey and Isaak

(2003) pointed out that, for a range of commonly

used potential functions and finite strain theories,

the ratios 

/

000

and 

/

are very similar. This

means that the anharmonic temperature depend-

ence of  is weaker than that of C

, which is

represented by the denominator of Eq. (19.87).

The anharmonicity of C

is better observed and,

particularly for type 1 structures, is found to be

quite small. That the anharmonicity of  is

smaller still makes it insignificant for type 1

bonding, especially under pressure, which suppres-

ses it.

In the asymmetrical, type 2 situation of

Fig. 19.5(b) we sum the bond forces resolved in

the direction of OBA, assuming individual bond

forces to be harmonic (Eq. (19.77)), as before, so

that 

¼2A(r  a). Writing the sum of the four

resolved forces and expanding binomially for

small x, we have a total force

F ¼ Aa½2 ðx=aÞ

ﬃﬃﬃ

ðx=aÞ

þð7=3Þðx=aÞ

ð25=36Þðx=aÞ

þ: ð19:88Þ

Now we can compare Eqs. (19.88) and (19.81) for an

idea of the effect on  of structural anharmonicity.

Strictly, we need time-averaged values, which

require numerical integration to handle the

non-harmonic oscillation, but as an approxima-

tion we assume that positive and negative x

occur equally often, so that odd powers of x

drop out in the averaging process, as for

Eqs. (19.75) and (19.86). Then we have

  a



ﬃﬃﬃ

ðx=aÞ



ðx=aÞ



ðx=aÞ

: (19:89)

With the assumed geometry  and hence  are

negative.

Equation (19.89) is not an estimate of  for

any real situation, but an indication of the funda-

mental reason why crystals with open structures,

most particularly those with tetrahedral bonding,

such as many common silicates, have low expan-

sion coefficients, and even negative coefficients

under special conditions. It is a consequence

of structural or type 2 anharmonicity. A three-

dimensional treatment, superposition of bond or

type 1 anharmonicity and rigorous integration of

atomic motion complicate the picture, but do not

change it fundamentally. A conclusion from

Eq. (19.89) is that structural anharmonicity allows

19.8 ANHARMONICITY 335

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C19.3D

–

336

– [314–336] 13.3.2008 2:45PM

a stronger temperature dependence of  than

does bond anharmonicity. This is seen in the

ratio of the x

and x

terms. However, all anhar-

monic effects diminish strongly with pressure,

both because vibration amplitudes become

decreasing fractions of atomic spacing and

because the structural effect decreases with

close-packing. Although anharmonicity may

appear to be a subtle effect that can be neglected

for many purposes, it has a central role in pheno-

mena such as the temperature dependences of

elastic moduli.

336 THERMAL PROPERTIES