Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

297

– [294–313] 13.3.2008 11:43AM

checks on the theories discussed in this chapter

as well as the composition and mineral structure

of the Earth. The several techniques each have

advantages and limitations. The first to be used

was hydrostatic compression in fluid-filled pres-

sure vessels, as in early work by P. W. Bridgman.

This still has an important role, in spite of more

recent developments of methods of attaining

much higher pressures, because it allows precise

measurements of acoustic velocities as functions

of pressure and therefore yields equation of state

derivatives, K

¼(@P/@ln)

and (@K

/@P)

at mod-

est pressures. It also offers the surety that pres-

sure is hydrostatic, which is not always

straightforward with higher pressure methods.

The next derivative, d

K/dP

, either isothermal or

adiabatic, is sometimes reported, although pres-

sure calibration is not generally precise enough

to make this useful.

Bridgman also experimented with the com-

pression of small, solid samples between tapered

anvils of very hard materials (sometimes crossed

anvils that required no special care in align-

ment). The modern use of diamond anvils pur-

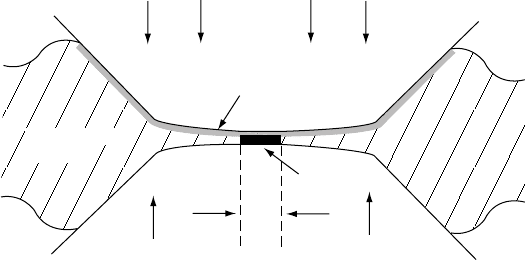
sues this idea with great success (Fig. 18.2),

thanks to the remarkable properties of diamond.

Pressures of a few hundred GPa (a few megabars)

have been achieved, although most experiments

have been restricted to a range below 100 GPa.

The transparency of diamond allows both sam-

ple observation and laser heating. Diamond is

reasonably transparent also to X-rays, permitting

in situ measurement of X-ray diffraction by the

very small samples and therefore determination

of both crystal structure and lattice spacing (and

hence density) at very high pressures. The

method has proved to be extremely versatile,

with care to ensure that pressure is reasonably

close to hydrostatic and that, in heating experi-

ments, temperature is uniform as nearly as

possible. As with other techniques, pressure cal-

ibration is problematic. But the small size and

relative simplicity of diamond anvil cells have

made them readily accessible and they are used

for a wide range of experiments in many

laboratories.

An early success in the application of dia-

mond anvils to mineral physics was a series of

experiments by Liu (1976), who heated a variety

of minerals by lasers to 1000 8C under strong

compression, showing that at a pressure corre-

sponding to the 660 km transition in the mantle

(23.5 GPa) these minerals were transformed pre-

dominantly to an orthorhombic perovskite

phase of (Mg,Fe)SiO

. Although such a transition

had been anticipated on the basis of similar tran-

sitions at lower pressures in chemical analogues,

the direct confirmation that it occurred in man-

tle silicates was a crucial step in our understand-

ing of the lower mantle. It also highlighted the

usefulness of diamond anvils in high pressure

mineralogy.

Some experiments require much larger speci-

men sizes than are possible with diamond anvils.

Static experiments on larger specimens use

multi-anvil presses with sample enclosures of

cubic or octahedral shape compressed by six or

eight rams driven by hydraulic pistons.

Specimens can be surrounded by relatively soft

material to ensure a close approximation to

hydrostatic compression and heated by internal

electric elements from which the massive

Ruby powder

50 µm

Stainless steel

gasket

Diamond

Sample

FIG U R E 18.2 Geometry of diamond

anvil cells in which pressures up to

250 GPa have been reached. Powdered

ruby fluoresces at a wavelength that

varies with pressure and is used for

pressure calibration, although not

generally to the highest pressures.

18.2 HIGH-PRESSURE EXPERIMENTS 297

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

298

– [294–313] 13.3.2008 11:43AM

pistons are insulated, with temperature moni-

tored by thermocouple. A particular use of such

apparatus is the production of high pressure

minerals, notably the perovskite mentioned

above, which is believed to be the dominant

component of the lower mantle but survives in

a metastable state at laboratory pressure and

temperature. After crystal growth at high pres-

sure and temperature it is quenched (cooled to

laboratory temperature while still at high pres-

sure) before decompression. Some other miner-

als, including Ca-silicate perovskite, which is

almost certainly a minor lower mantle constitu-

ent, do not survive decompression and must be

observed in situ in the high pressure apparatus.

The highest pressures are achieved transi-

ently in shock wave experiments. This method

is a by-product of atomic weapons development,

and the original application to terrestrial materi-

als was intended, at least partly, as a check on the

technique because the densities of these materi-

als at very high pressures were believed to be

known. Early results (McQueen and Marsh,

1966; McQueen et al., 1967) confirmed that

phase transitions converted familiar minerals

to denser forms, consistent with the lower man-

tle, but that the core could not be explained by

further phase transitions and must be inter-

preted as an alloy dominated by iron, with

minor addition(s) of lighter element(s).

Observations are made by high speed photogra-

phy of the motions of samples subjected to vio-

lent impacts by projectiles fired at them

(Fig. 18.3). Interpretation recognizes that shock

compression causes heating greater than adia-

batic compression. It must also be noted that

the compression is so sudden as to invite doubt

about how nearly specimens come to hydrostatic

and thermodynamic equilibrium. Anderson

(1995, Chapter 12) discusses the problems and

Stacey and Davis (2004) draw attention to doubt

about pressure calibration. It appears that shock

compression is a compromise between hydro-

static compression, described by K, and linear

compression, represented by the higher modu-

lus, . A plausible explanation is that stronger

(faster) shocks give less time for adjustment

towards a hydrostatic state, giving the impres-

sion of bulk modulus increasing faster with

pressure than it really does and leading to over-

estimates of pressure. Ignoring these doubts,

there is a reasonably simple interpretation of

compression in terms of the speeds of the

advance of a shock front through a specimen

and of the following shocked material.

Applying the principle that the mass of mate-

rial is conserved as the shock front advances

through it, at speed v relative to the uncom-

pressed material but speed (v u) relative to the

shock-compressed material, to which speed u is

imparted, we have

v

¼ðv  uÞ: (18:5)

By observing both v and u by high speed photog-

raphy the compression is measured:



¼ 1 



1

: (18:6)

The same observations give the pressure gener-

ated by the shock because this is equated to the

rate of change of momentum per unit area of

shock front,

P ¼ 

vu: (18:7)

That is, per unit time a mass (

v) per unit area is

given speed u. A series of observations with dif-

ferent shock intensities, produced by a range of

impactor speeds, gives a P() curve.

IMPACTOR

Shock front

Pressure, PP

= 0

FI G U R E 18.3 Geometry of shock wave propagation.

A high speed impact from the left initiates a shock wave

travelling at speed v through the initially stationary

sample. The shock-compressed material, density ,

moves at speed u < v. The unshocked material, density



, has not yet moved. The broken line indicates the

extent of the sample before impact.

298 FINITE STRAIN AND HIGH-PRESSURE EQUATIONS OF STATE

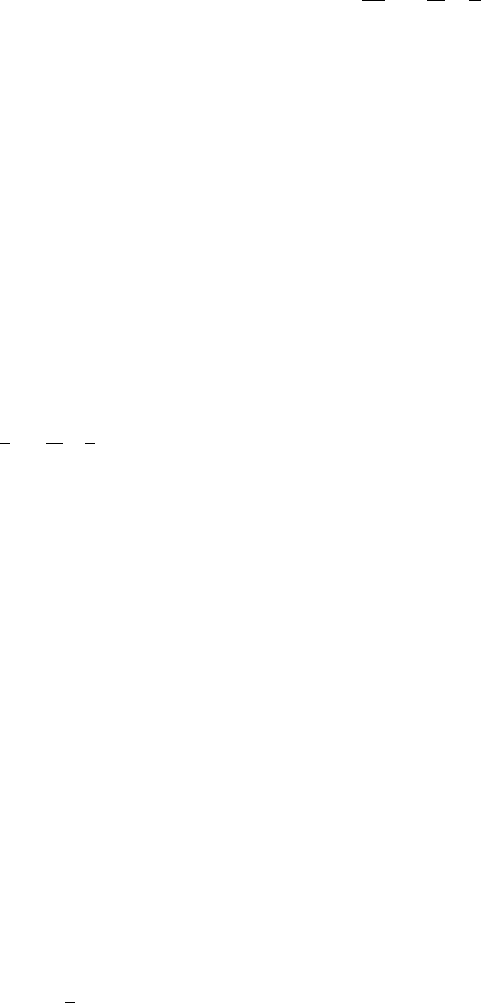
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

299

– [294–313] 13.3.2008 11:43AM

The compression is dynamic and is not, in

general, adiabatic. The heating can be calculated

by appealing to the conservation of energy

through a shock front, across which there is a

pressure difference P, causing acceleration of the

material to speed u. Since the pressure is exerted

by the compressed material, which advances at

speed u, the power per unit area of shock front is

Pu. This is equated to the rate at which energy is

imparted to the material, being the sum of

kinetic energy and increased internal energy,

Pu ¼ 

vðu

=2 þ U



 U



Þ: (18:8)



and U



are the internal energies per unit mass

in the compressed and uncompressed states, the

asterisk being introduced to distinguish these

quantities from the total internal energy U of

an arbitrary mass, which is the convention adop-

ted in Appendix E. With substitutions from

Eqs. (18.6) and (18.7), we have



 U







: (18:9)

This is the Hugoniot equation, named after one of

its original authors. A shock compression curve

along which internal energy varies in the manner

of this equation is referred to as a Hugoniot and

the subscript H emphasizes that this relationship

applies only to such compressions.

Equation (18.9) may be used to estimate either

adiabatic or isothermal compressions from

Hugoniot data. The calculation of an adiabat is

simpler and an isotherm can be calculated from

it by standard thermodynamics. From Table E.2

(Appendix E), (@U/@V)

¼P, so that the variation

of internal energy with adiabatic compression is



¼P



(18:10)

with subscript S to indicate adiabatic variations

and continuation of the asterisk for unit mass

parameters. Integrating Eq. (18.10) and combin-

ing it with Eq. (18.9), we have



 U



¼





ðV



 V



Þ; (18:11)

which is the difference between internal ener-

gies along an adiabat and a Hugoniot at the same

density, 1/V



. For constant volume changes we

have, from Table E.2,







; (18:12)

so that, in the reasonable approximation that the

Gr ¨uneisen parameter,  (Eq. (18.2)), is independ-

ent of temperature at constant volume,

 U

¼ðV=ÞðP

 P

Þ: (18:13)

Therefore the ‘correction’ of Hugoniot pressure

to an adiabat is given by

¼ P

1  =2ðÞ=

 1ðÞ½



: (18:14)

The integral in Eq. (18.14) assumes knowledge

of P

(), which it is the purpose of the calcula-

tion to determine, so use of this equation is iter-

ative. Calculation of an isotherm from Hugoniot

data, either directly or via an adiabat, assumes

knowledge of the variation of  with  by

an appeal to one of the theories in Sections 18.3

to 18.5.

18.3 The appeal to atomic potentials

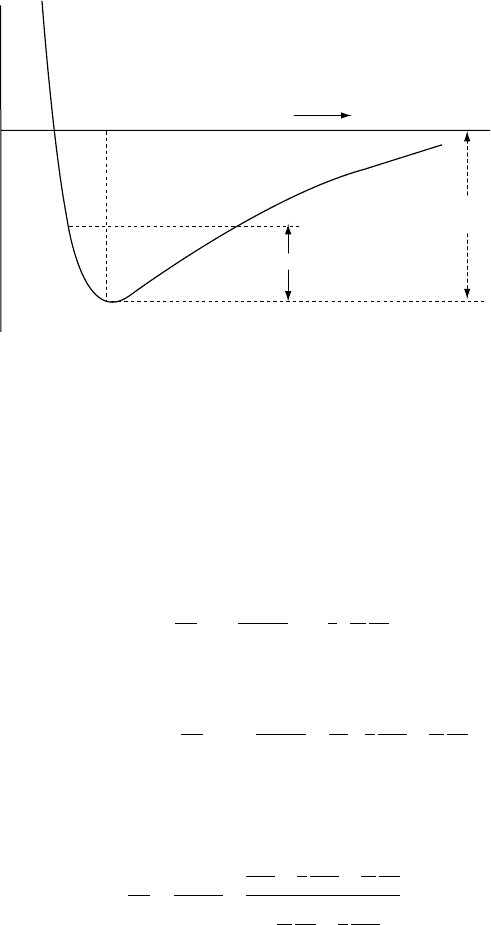
An atomic potential function is an expression for

the mutual potential energy, , of neighbouring

atoms as a function of their separation, r. Every

finite strain theory implies a potential function

with the general form of Fig. 18.4, the essential

feature of which is an asymmetry about the

potential minimum. It is easier to stretch atomic

bonds than to compress them. There are two

related consequences: bulk modulus increases

with pressure and materials normally expand

when heated. A finite strain theory is concerned

with the first of these effects, but it is closely

linked to theories of thermal properties, espe-

cially the Gr ¨uneisen parameter (Section 19.3).

There is a conceptual advantage in starting a

finite strain theory with a potential function; it

makes the underlying physical assumptions

clear and it leads naturally to the link with ther-

mal properties. Normal elasticity theory (infini-

tesimal strain theory) considers very small

18.3 THE APPEAL TO ATOMIC POTENTIALS 299

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

300

– [294–313] 13.3.2008 11:43AM

displacements from the minimum in Fig. 18.4. In

this range  varies as the square of displacement,

giving forces proportional to displacement and

therefore elastic moduli that can be treated as

constants. There is no unique representation of

 for extrapolation outside this range but only

numerous empirical potential functions that

have been used to represent the behaviour of

strongly compressed material. Computer models

(molecular dynamic calculations) can handle

analytically unmanageable potential functions,

but their validity still depends on assumed func-

tions There are two general forms, power law

potentials and functions incorporating exponen-

tials. They all have a minimum in ’ at r ¼a, the

equilibrium zero pressure spacing, at which

d/dr ¼0. Thus density variation is given by

=

¼ V

=V ¼ða=rÞ

; (18:15)

where subscript zero indicates zero pressure

values.

Consider a crystal with N atoms, each of

which has 6f neighbours and to each of which

it is bonded with energy . For a simple cubic

crystal f ¼1, for an atomic close-packed struc-

ture f ¼2 and for the diamond structure f ¼2/3.

Since each bond is shared by two atoms, the total

bond energy of the crystal is

E ¼ 3Nf : (18:16)

Let the volume of the crystal be

V ¼ Ngr

; (18:17)

where g is another dimensionless constant with

a value of unity for a simple cubic crystal. It is the

volume per atom, relative to a cube of side r;

it has a minimum value of 1=

ﬃﬃﬃ

for atomic

close-packed structures and a maximum value

of 8=3

ﬃﬃﬃ

for the diamond structure. Ignoring,

for the present, thermal effects, the pressure at

arbitrary atomic spacing, r,is

P ¼

¼

dE=dr

dV=dr

¼



d

(18:18)

and bulk modulus is

K ¼V

¼V

dP=dr

dV=dr





d

(18:19)

We are also interested in

dK=dr

dP=dr







d





(18:20)

because we wish to find functions  that match

the gradients of the K(P) curves for the deep

Earth. For some purposes we need higher deriv-

atives but it is generally more convenient to treat

each case specifically than to pursue the general

form. The algebra is simplified by noting that the

denominator of Eq. (18.20) has the form of K

(Eq. (18.19)), so that the next stage is obtained

by differentiating the product K(dK/dP).

Binding

Thermal energy

energy

FI G U R E 18.4 The form of an atomic

potential function, representing the

interaction energy of neighbouring atoms

as a function of their separation, r. The

equilibrium separation, a, is the result of a

balance between attractive and repulsive

forces. The increasing gradient with

decreasing r causes the bulk modulus

to increase with compression. Thermal

oscillation between A and B causes thermal

expansion by allowing greater bond

extensions than compressions.

300 FINITE STRAIN AND HIGH-PRESSURE EQUATIONS OF STATE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

301

– [294–313] 13.3.2008 11:43AM

The simplest potential functions are those

that represent  as a function of 1/r:

 ¼a

ða=rÞ

þ a

ða=rÞ

þ a

ða=rÞ

þ a

ða=rÞ

þ;

(18:21)

where a is the equilibrium spacing, a

, a

,...are

coefficients with the dimensions of energy and n,

m,... are dimensionless exponents, commonly

but not necessarily integers. There are numerous

variants. With just two terms and arbitrary m,

n (n > m so that a

is negative) we have the

potential proposed by G. Mie before the intro-

duction of quantum mechanics suggested differ-

ent forms. If m ¼1 to represent Coulomb

attraction it is known as the Born–Mie potential.

If m ¼6, n ¼12 we have the Lennard-Jones poten-

tial for dipole–dipole interactions. J. Bardeen

proposed a three-term potential with exponents

1, 2, 3 and the theory of Birch (1952) can be

represented by Eq. (18.21) with either 2, 3 or 4

terms having exponents 2, 4, 6, 8. With all four

terms it is referred to as the fourth-order theory,

although there cannot in principle be fewer than

two terms, so, with this nomenclature, there is

no first-order theory. With exponents that are all

multiples of 2, it is evident that Eq. (18.21) is a

polynomial in (/

)

2/3

so that repeated differen-

tiation is straightforward. Writing (/

) ¼x, dif-

ferentiating Eq. (18.21) with respect to x as far as

¼d

K/dP

and eliminating coefficients by sub-

stitution of zero pressure (x ¼1) values of K, K

and K

, the fourth-order Birch theory gives

P ¼dE=dV ¼ðx

ÞdE=dx

¼ð9=16ÞK

ðAx

5=3

þ Bx

7=3

 Cx

þ Dx

11=3

Þ;

(18:22)

where

A ¼K

þðK

 4ÞðK

 5Þþ59=9;

B ¼3K

þðK

 4Þð3K

 13Þþ129=9;

C ¼3K

þðK

 4Þð3K

 11Þþ105=9;

D ¼K

þðK

 4ÞðK

 3Þþ35=9:

(18:23)

For the third-order theory, a

and D are assumed

to be zero so that

¼ðK

 4ÞðK

 3Þ35=9;

simplifying A, B, C:

A ¼2ðK

 4Þþ8=3;

B ¼4ðK

 4Þþ8=3;

C ¼2ðK

 4Þ

¼ B  A:

(18:24)

For the second-order theory, with a

and C also

zero,

¼ 4; K

¼35=9; A ¼ B ¼ 8=3: (18:25)

Advantages and limitations of the Birch theory

and reasons for its prominence in geophysics are

discussed in Section 18.4.

Doubts about the fundamental validity of

equations with the power law form of Eq. (18.21)

arose as soon as quantum mechanics suggested

that at least the repulsive term of a potential

function should have an exponential form. Early

theoretical attempts to develop equations of this

form were based on studies of vibrational spectra

of diatomic molecules, first by P. N. Morse in 1929

and then by R. Rydberg in 1932. The Rydberg

potential, which now receives more attention, is

 ¼ A½1  f ð1  r=aÞexp½ð1  r=aÞ: (18:26)

Differentiation, as for the Birch theory above,

gives the corresponding finite strain equation,

P ¼ 3K

2=3

ð1  x

1=3

Þexp½ð1  x

1=3

Þ; (18:27)

where zero pressure conditions fix A and  ¼(3/2)

1). This equation was given strong support

by Vinet et al. (1987) and is sometimes referred

to as the Vinet equation, although it antedated

his work by many years. However, for appli-

cation to the pressures in the deep Earth the

Morse and Rydberg potentials share a crippling

shortcoming. In Section 18.6 we refer to the

thermodynamic requirement that a finite

strain theory must give a value of K

that exceeds

5/3 as P !1. This is the quantity K

which is

equal to the highest exponent of x in equations

such as 18.22 or 18.27. Equation (18.27) gives

¼2/3 and so fails the thermodynamic crite-

rion by a wide margin, but Stacey (2005) pointed

out that a very simple modification overcomes

this problem and gives sensible fits to terrestrial

18.3 THE APPEAL TO ATOMIC POTENTIALS 301

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

302

– [294–313] 13.3.2008 11:43AM

data. He suggested a generalized Rydberg equa-

tion with arbitrary K

P ¼ 3K

ð1  x

1=3

Þexp½ð1  x

1=3

Þ; (18:28)

where now

 ¼ð3=2ÞK

 3K

þ 1=2

¼3K

ð3=4ÞK

þ 1=12: (18: 29)

The approach to finite strain via potential

functions is fundamental and leads naturally

to the relationship to thermal properties

(Section 19.3). However, while it is useful to

remember that every finite strain theory implies

a potential function, the form of the required

function is not known precisely enough to

account adequately for properties that depend

on high derivatives of it. One such property is

¼d K/dP and especially its infinite pressure

asymptote, for which a thermodynamic argu-

ment in Section 18.6 leads to a lower bound,

5/3 (Eq. (18.56)). Most theories give fixed values

for this parameter, with a wide range, mostly

below this limit (Stacey, 2005, Table 1). A

quite different approach to finite strain,

designed to avoid this difficulty, is presented in

Section 18.5.

18.4 Finite strain approaches

To most geophysicists ‘finite strain’ means the

theory of Birch (1952) that leads to Eq. (18.22),

but from a quite different starting point. It origi-

nated from an attempt by Love (1927) to extend

conventional elasticity theory. This defines

strain as a fractional change in a dimension,

D l/l

, which is assumed to be infinitesimal. In

his extension of the theory to finite deformation,

Love imposed the mathematical requirement

that, when treated in three dimensions, strain

should appear invariant with rotations or inter-

changes of coordinate axes. His method of

achieving this was to define strain in terms of

the squares of the separations of material points.

Elastic shear strains are very small in all situa-

tions in the Earth, so we are interested in finite

strain only for the case of hydrostatic compres-

sion, with extension (or compression) the same

in all directions. Then, if the separation of two

material points is S

in the unstrained state and

becomes S in the strained state, the Love-defined

strain, "

, is given by

ðS=S

¼ 1 þ 2"

(18:30)

and the ratio of volumes in the strained and

unstrained states is

V=V

¼ðS=S

¼ð1 þ 2"

3=2

; (18:31)

so that

¼½ðV=V

2=3

 1=2: (18:32)

When strain energy is written as a polyno-

mial in "

, starting with "

, it is not convergent.

Prompted by a comment by F. D. Murnaghan,

Birch (1952) redefined strain relative to the

strained state, that is D l/l instead of D l/l

, and

found that this greatly improved the conver-

gence. For convenience in dealing with compres-

sion, Birch also reversed the sign of strain to

make it positive for compression. With these

changes the Birch-defined strain is

¼½ðV

=VÞ

2=3

 1=2 ¼½ð=

2=3

 1=2: (18:33)

is referred to as Lagrangian strain and "

Eulerian strain. In the limit of very small strains

both converge to the conventional definition in

elasticity theory (but with a sign difference). In

the Birch theory strain energy is written as a

polynomial in "

¼ c

þ c

þ (18:34)

with the implication that this is an infinite

series, but not usable beyond the "

term.

Substituting for "

by Eq. (18.33) and multiply-

ing out the terms, we see that Eq. (18.34) is a

polynomial in (/

)

2/3

and so is completely

equivalent to the 2, 4, 6, 8 power law potential

that gives Eq. (18.22). Although the Birch theory

is generally presented in terms of "

, this is

algebraically much less convenient than

Eq. (18.22).

The claim for convergence that made

Eq. (18.34) interesting to geophysicists is based

on the observation that for the second-order

theory (c

¼0, c

¼0) K

¼4 (Eq. 18.25) and this

is not far from the values for many minerals.

302 FINITE STRAIN AND HIGH-PRESSURE EQUATIONS OF STATE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

303

– [294–313] 13.3.2008 11:43AM

Thus, for these minerals c

 c

. However, when

lower mantle data are fitted to the Birch theory

they give c

 c

. Equation (18.34) is not intrinsi-

cally convergent but relies on "

1. Several

authors have drawn attention to difficulties

with the Birch theory. For example, if

Eq. (18.22) is fitted to lower mantle or core data

it gives negative D or, if the third order theory

(D ¼0) is used, it gives positive C, and in either

case this means negative pressure at strong com-

pressions. But the Birch theory survives because

the geophysical community has not been con-

vinced that there is anything better. So, we

draw attention to Eq. (18.28) and the theories in

Section 18.5.

Another strain-based theory was presented

by Poirier and Tarantola (1998), who pointed

out that there is no logical reason to define strain

relative to either strained or unstrained states. If

the concept of strain is used it should be defined

as a small increment in deformation relative to

the ambient state and integrated over the total

range. This gives the total strain as a logarithm of

the ratio of final and initial states, which, for

volume compression, is

¼ð1=3ÞlnðV=V

Þ: (18:35)

The factor 1/3 arises because strain is defined as a

change in a linear dimension. The subscript H

acknowledges that Poirier and Tarantola

referred to "

as Hencky strain, adopting the

definition from structural geology, in which it

represents large inelastic deformations. Writing

strain energy as a polynomial in "

, as for "

Eq. (18.34), they obtained their logarithmic finite

strain equation,

P ¼ xK

½ln x þð1=2ÞðK

 2Þðln xÞ

þ: (18:36)

This is the third-order equation, terminating at

. The fourth-order term is given by Stacey and

Davis (2004), but is doubtfully useful, justifying

the claim that Eq. (18.36) is more strongly con-

vergent than Eq. (18.22). Although, for most pur-

poses, the logarithmic equation is better than

the Birch equation, in the extreme pressure

limit it gives K

¼1 for all orders, falling short

of the thermodynamic lower bound, 5/3, dis-

cussed in Section 18.6.

18.5 Derivative equations

The equations discussed in Sections 18.3 and

18.4 have trouble with derivative properties, in

particular K

and especially its infinite pressure

asymptote, K

. In this section we consider equa-

tions that are derived by starting with physical

arguments about the behaviour of K

and inte-

grating to obtain P() relationships, instead of

working the other way. Most finite strain theo-

ries consider isothermal pressure derivatives,

but in geophysics adiabatic derivatives are

often more directly useful. Equations in this sec-

tion apply equally well to either and subscripts T

and S are dropped.

We can regard Murnaghan’s equation,

¼constant, as a special case and the precursor

to a class of equations that we refer to as K-

primed equations or derivative equations. With

d K/dP ¼K

, K ¼K

þK

P, integration gives

=

¼ðK=K

1=K

¼ð1 þ K

P=KÞ

1=K

: (18:37)

As Fig. 18.1 shows, this is a sufficiently good

approximation to be useful over moderate pres-

sure ranges and it is easy to apply. However,

closer inspection of the figure shows that the

gradients of the lower mantle and core graphs

decrease with pressure, that is K

is negative and

not zero as assumed by the Murnaghan equation.

Since the equations of the previous two sections

give negative K

, Murnaghan’s equation itself is

not a step forward, but is merely a pointer to a

new direction.

The first real insight on the behaviour of K

appears in a paper by Keane (1954). Keane recog-

nized that K

decreases from its zero pressure

value, K

, towards a finite limit, K

,asP !1.

Although he had no direct evidence of values of

, he argued that it must be bounded by limits

ðK

 1Þ > K

> K

=2; (18:38)

which we refer to as Keane’s rule. Evidence that

we now have strongly supports this rule

(Section 18.9). Derivation of a tighter limit is

one of the current challenges in finite strain

theory because if K

is known, or is related to

, then fitting of equations such as (18.28) or

18.5 DERIVATIVE EQUATIONS 303

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

304

– [294–313] 13.3.2008 11:43AM

those in this section requires one fewer fitting

constant and is correspondingly more secure. By

making the assumption that pressure is a quad-

ratic function of Birch strain (Eq. (18.33)), with

related coefficients, Keane derived the relation-

ship that we refer to as Keane’s equation:

¼ K

þðK

 K

ÞK

=K; (18:39)

which integrates to give

K=K

¼ 1 þðK

Þðx

 1Þ; (18:40)

P=K

¼ðK

0 2

Þðx

 1ÞðK

 1Þln x

(18:41)

with x ¼/

. In manipulating these equations it

is convenient to note the simple forms for higher

derivatives,

¼K

ðK

 K

Þ; (18:42)

000

¼ K

ðK

 K

Þð3K

 K

Þ: (18: 43)

Although Keane’s equation has been used very

occasionally its merit has not been widely recog-

nized. It is one of the equations to be taken

seriously.

The next step in development of K-primed

equations was recognition that

¼ðP=KÞ

1

; (18:44)

which is a universal algebraic feature of all equa-

tions for which K

is positive, as proved by

Stacey and Davis (2004). Although this is a stand-

ard condition of all potentially useful equations,

serious use of it is possible only if a finite strain

equation is written as a relationship between K

and (P/K), giving it a fixed end point at P !1.

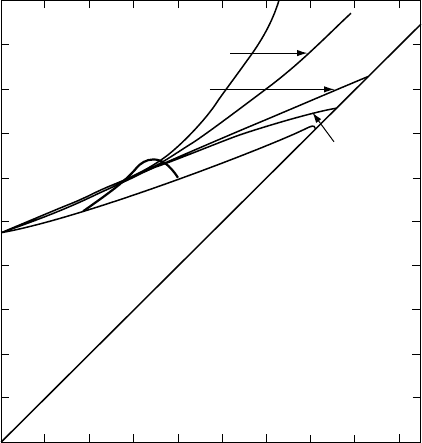
Several such equations have been tried. The most

successful is the ‘reciprocal K-primed equation’

1=K

¼ 1=K

þð1  K

ÞP=K: (18:45)

By writing it in this form Eq. (18.44) is automati-

cally incorporated. Eq. (18.45) is best represented

as a graph of 1/K

vs P/K, as in Fig. 18.5. On this

graph Eq. (18.45) is a straight line from 1/K

at P/K ¼0 to its intersection with Eq. (18.44),

which is marked ‘Infinite pressure limit’, a

straight line of gradient 1 through the origin,

along which the end points of all equations

must lie. Stacey and Davis (2004) presented a

method of integrating Eq. (18.45). Its integral

and derivative forms are

0.2

0.1

0.3

0.4

0.5

0.10 0.2 0.3 0.4

PREM

Birch 3

Infinite pressure limit

Birch 4

Rydberg

Keane

Reciprocal K

′

1/K

′

FI G U R E 18.5 Plots of 1/K

(¼dP/dK)vsP/K for

five equations fitted to the PREM model of

the lower mantle (for the radius range 3630 km

to 5600 km). Birch 4 (Eq. (18.23)); Birch 3

(Eq. (18.23) with three terms); Rydberg

(Eq. (18.27)); Keane (Eq. (18.39)); reciprocal

K-primed (Eq. (18.45)).

304 FINITE STRAIN AND HIGH-PRESSURE EQUATIONS OF STATE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

305

– [294–313] 13.3.2008 11:43AM

K=K

¼ð1  K

P=KÞ

K

;

(18:46)

lnð=

Þ¼ðK

Þlnð1  K

P=KÞ

ðK

 1ÞP=K; (18:47)

¼ðK

ÞðK

 K

Þ; (18:48)

000

¼ðK

ÞðK

 K

Þð3K

 2K

þ K

Þ:

(18:49)

Although Eqs. (18.39) and (18.45) appear very

different, in fact they are sufficiently similar that

we can choose between them only on the basis of

convenience of use. This is seen by comparing

the higher derivative relationships and noting

that Eqs. (18.42) and (18.48) become identical at

P ¼0, so that the relationship between K

, K

and K

is the same for both equations. For appli-

cations to laboratory compression data on mate-

rials that exist at P ¼0, and for which 

and K

are known, use of Eq. (18.41) is generally more

convenient. On the other hand, for an Earth

model such as PREM, with K tabulated but 

and K

to be estimated by extrapolation,

Eq. (18.45) has the advantage that P/K can be

treated as an observed quantity and Eq. (18.47)

can be fitted without involving K

, requiring

one fewer fitting constant and giving corre-

spondingly greater certainty. K

is then obtained

from Eq. (18.46), with K

and K

already fixed by

Eq. (18.47). Alternatively, K

can be fitted by

Eq. (18.46) without involving . Equation (18.45)

and its integral forms were used for the data fits

in Appendix F, referred to in Section 18.9.

The use of P/K as the pressure parameter in

the Eqs. (18.45) to (18.47) has other important

advantages. We refer to it as normalized pres-

sure. Unlike P itself, P/K ‘saturates’ at a finite

value with indefinitely strong compression, as

in Eq. (18.44). Properties such as the thermody-

namic Gr ¨uneisen parameter, that approach

finite limits at extreme pressure, are much bet-

ter related to P/K than to P or even . At the

bottom of the lower mantle the value of P/K is

half of its infinite pressure limit and throughout

the core it is much nearer to the infinite pressure

limit than to P/K ¼0. This means that a theoret-

ical restriction on the infinite pressure limit, as

considered in Section 18.6, is an important con-

straint on the very high pressure behaviour of an

equation of state. The divergence of alternative

equations is seen in Fig. 18.5; thermal properties

calculated from higher derivatives of these equa-

tions (Section 19.3) are very different and are

useful only if equations with satisfactorily con-

strained derivatives are applied.

We need to emphasize that all finite strain

theories are empirical, whether dressed up in

apparently sophisticated theoretical arguments

or not. There is no unique agreed theory, but a

choice must be made on the basis of plausibility

arguments and convenience of use in particular

applications. However, for the deep Earth the

choice is limited. Only the equations for which

is an adjustable parameter can give plausible

derivative properties. New theoretical con-

straints are urgently needed and Section 18.6

gives an indication of what may be possible.

18.6 Thermodynamic constraints

Many of the thermodynamic identities in

Appendix E connect elastic and thermal proper-

ties. They are often used in mineral physics to

assess the validity of approximations and

assumptions about material properties at high

pressures and temperatures. A particular exam-

ple that is central to the subject is the relation-

ship between the pressure dependence of

thermal expansion coefficient, , and the tem-

perature dependence of bulk modulus, K

ð@=@PÞ

¼ð1=K

Þð@K

=@TÞ

¼

;

(18:50)

where 

is one of the second derivative param-

eters defined in Table E.1. This is typical of the

conventional presentation of thermodynamic

relationships in that it considers isothermal

compression, both in (@/@P)

and in the use of

¼V(@P/@V)

. For application to geophysics

we are usually more interested in the variations

in properties on an adiabat, and one purpose of

the tables in Appendix E is to make adiabatic

properties as readily accessible as the more usu-

ally quoted isothermal ones.

18.6 THERMODYNAMIC CONSTRAINTS 305

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

306

– [294–313] 13.3.2008 11:43AM

In the limit of extreme pressure many of

these relationships simplify and the simplified

forms impose constraints that equations of state

must satisfy. This means that we are considering

the extrapolation of equations to P !1 and

need to be careful about the implications of the

extrapolation. The extrapolated values of mate-

rial properties at infinite pressure are simply

equation of state parameters. They are not

directly observable, even in principle, but are

coefficients of equations fitted to the observed

pressure range. If any familiar material were to

approach infinite compression it would undergo

phase transitions to exotic forms with quite dif-

ferent equations of state. Theoretical properties

and equation of state parameters of materials at

extreme pressure have no relevance to the pro-

perties of lower pressure phases. The extrapo-

lated properties must nevertheless satisfy

physical laws, in particular thermodynamic rela-

tionships, even though they refer to conditions

under which the material cannot exist. The laws

do not break down at the (P, T) conditions at

which another phase of lower free energy

appears. An obvious analogy is extrapolated

zero pressure properties, 

, K

, of materials

that do not survive decompression to P ¼0. They

are often quoted in high pressure mineral

physics and follow the conventional relation-

ships, but they are not the same as the properties

of the zero pressure phases of the same materi-

als. Infinite pressure extrapolation is no differ-

ent. We labour this point to allay any doubt

about the legitimacy of the important conclu-

sions that are derived from the extrapolation.

We are imposing constraints on parameters of

equations of state, in particular K

, which

appears in Eqs. (18.39) to (18.49). The practical

significance of this constraint is emphasized by

pointing out that in the core and the lower half

of the lower mantle K

is nearer to K

than it is to

. This applies quite generally to derivative

properties, including the Gr ¨uneisen parameter,

, (Eq. (18.2)). Deep in the Earth they are all much

closer to their infinite pressure extrapolations

than to zero pressure values.

Consider the product (T). This product

appears in many of the identities in

Appendix E, including Eqs. (E.1) to (E.3), which

relate adiabatic and isothermal bulk moduli

and their pressure derivatives. For solids and

liquids it is a small quantity, even at tempera-

tures of the Earth’s interior, and it decreases

with pressure. As we demonstrate, it vanishes

identically at P !1, simplifying these identities.

Equation (E.15) combines adiabatic derivatives

of g,  and T, from Table E.3, with substitutions

by other identities in Table E.4 and, like all of

the equations from which it is derived it is an

identity, without approximation. Noting the

proof by Stacey and Davis (2004) that if K

remains positive and finite then P !1 means

V !0, we can integrate Eq. (E.15) from P ¼0

(V ¼V

)toP ¼1(V ¼0),

ðTÞ

dðTÞ

Tð1 þ TÞ

¼ ln 1 þ

ðTÞ



 ln 1 þ

ðTÞ



ð

þ qÞ

: ð18:51Þ

(

þq ) must remain finite, so the volume inte-

gral in Eq. (18.51) is 1. The only way this can

be achieved is by (T)

¼0 identically. (Stacey

and Davis showed that the other apparent alter-

native, (d

þq )

¼0, implies the ideal gas equa-

tion, which is not relevant to solids.) Vanishing

(T) means not only K

¼K

but also

¼K

. Moreover, these equalities apply at

any temperature because the proof does not

depend on which adiabat is considered, so all

these quantities become independent of tem-

perature. Thus K

is an unambiguous equation

of state parameter, with the same value for all

adiabats and all isotherms of any particular

material. But it is a material constant, not a

universal one. We note that Eq. (E.14) is an

adiabatic derivative, so the integration that

gives Eq. (18.51) follows an adiabat. As we dis-

cuss below,  remains finite at V !0, and from

Table E.2,  ¼(@lnT/@lnV)

,soT !1 on an

adiabat as V !0. In spite of this (T) !0. Thus

 decreases more strongly than T increases, mak-

ing the product T vanish at V !0.

Now consider the definition of q:

q ¼ð@ ln =@ ln VÞ

: (18:52)

306 FINITE STRAIN AND HIGH-PRESSURE EQUATIONS OF STATE