Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

287

– [267–293] 13.3.2008 2:16PM

in the upper mantle without penetrating the

660 km discontinuity, but deeper high-velocity

anomalies suggest they have penetrated in the

past and that slab penetration may be episodic.

High velocities are observed beneath cratons

(the ancient continental cores), and low velo-

cities below mid-ocean ridges. Localized low-

velocity anomalies are observed under hot

spots to depths of several hundred km, but at

greater depth the picture is more blurred, prob-

ably because of a combination of lack of resolu-

tion, diffractive healing effects, and reduction of

the temperature sensitivity of P-wave velocity

with depth (Karato, 1993; Stacey and Davis,

2004, Table 4). Two major low-velocity regions

extending from the core into the upper

mantle are identified (Fig 17.14(a)), one beneath

the Pacific and one beneath Africa, and to the

south-west of it. They are referred to as the

‘Pacific and Africa super-plumes’, although

whether they actually represent upwelling mate-

rial or static velocity contrasts is debated. In that

they are surrounded by regions that are inferred

to have been fed by cold subducting material

in the past, they may just represent hotter

than average mantle. Alternatively, it has been

argued that topographic bulges above the super-

plumes are sustained by the dynamics of upward

flow. With improved tomographic resolution, it

appears that the Pacific super-plume may consist

of several plumes (Schubert et al., 2004).

In addition to velocity tomograms, attenua-

tion tomography gives variations in Q in the man-

tle (Gung and Romanowicz, 2004). Difficulties

with both observation and interpretation of Q

are discussed in Section 10.5. A general aim of

tomographic imaging is to identify features with

current or past tectonics, but this can be done

only tentatively with the detail available so far.

Generally, tomography has been based on

ray theory, which neglects diffraction effects.

We point out in Section 16.3 that, to take dif-

fraction into account, we must integrate over

the Fresnel volume sampled by the elementary

Huygens wavelets that make up a seismic wave.

Thetraveltimeofaseismicwaveisgivenbyray

theory as

T ¼

VðSÞ

; (17:34)

where S is distance measured along the ray and V

is velocity. Given a series of travel times, linking

various sources and receivers, Eq. (17.34) can be

used in a linear inversion to determine the dis-

tribution of V

1

. As discussed in Section 16.3, ray

theory is an infinite-frequency approximation

that applies to anomalies of dimension, a,

greater than the first Fresnel zone, a > ðlLÞ

1=2

where L is distance travelled and l is wavelength

(Eq. 16.14). For finite frequencies the relative

sizes of the anomaly and the Fresnel zone must

2.2

1.4

0.6

–0.6

–1.4

–2.2

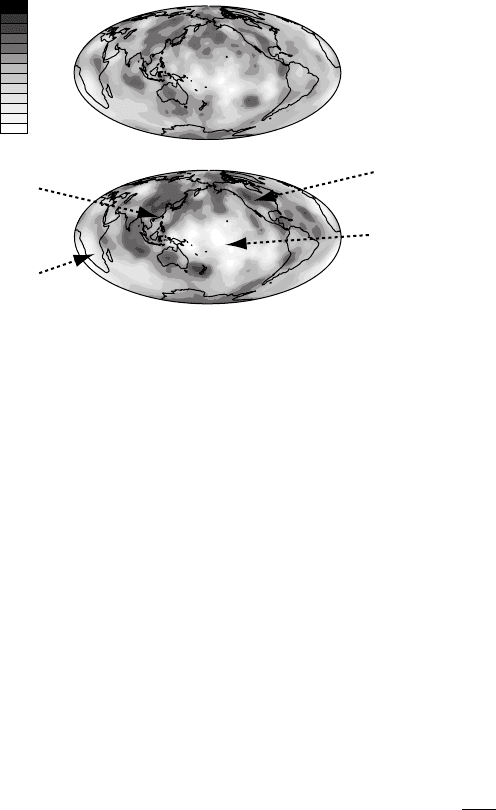
SB4L18-Lowermost Mantle

The lowermost mantle is dominated

by a ring of 'fast' material around the

Pacific and 'slow' material in the

Central Pacific and beneath Africa.

The fast regions are thought to be the

'graveyard of subducting slabs'.

graveyard of slabs

Central Pacific Super Plume

Great African

Plume

δ Vs/Vs

[%]

2425

2770 km

graveyard of slabs

FI G U R E 17.14(d) (Cont.)

17.8 LATERAL HETEROGENEITY: SEISMIC TOMOGRAPHY 287

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

288

– [267–293] 13.3.2008 2:16PM

be taken into account. In contrast to the simple,

essentially one-dimensional expression of

ray theory (Eq. 17.34), the travel time for a

finite-frequency wave is given by an integral

over the whole volume,

T ¼

1=VðrÞKðr;!ÞdV; (17:35)

where V(r) is the velocity distribution, K is a

kernel function that formally takes into account

the Fresnel volume effects described in

Section 16.3. Dahlen et al. (2000) give the

mathematical detail for computation of K.

Equation (17.35) recognizes that objects smaller

than the Fresnel zone have negligible effect on

travel time, and that diffractive healing dimin-

ishes travel time perturbations by features of

comparable size. Inversion of travel times

using Eq. (17.35), to obtain V(r), effectively

reverses diffractive healing and leads to tomo-

graphic anomalies that can be up to 60% stron-

ger than those obtained from ray theory

tomography (Montelli et al., 2004).

Large features, such as subducting slabs, are

well imaged by ray tomography, but smaller more

localized anomalies, associated with plumes at

depth, are better resolved using finite-frequency

tomography. In a recent tomographic inversion

by this method, Montelli et al. (2004) presented

evidence for six plumes that extend from the low-

ermost mantle, as well as several examples of

plumes apparently confined to the upper mantle.

Plumes are found to have apparent diameters of

several hundred kilometres. These are likely to be

the thermal halos of plumes with much narrower

rapidly flowing conduits where viscosity is lowest

(Loper and Stacey, 1983). The plume viscosity con-

trast is inferred to be about 10

:1. In the Montelli

et al. images the Pacific superplume appears as

several sub-plumes.

Interest in tomography arises primarily from

its usefulness as an indicator of mantle convection

and tectonics, present and past, but the interpre-

tation is not unique. Temperature variations of

the seismic velocities are derived from thermo-

dynamic arguments in Section 19.7 (see espe-

cially Eqs. (19.70), (19.71) and (19.73)), with

numerical values for the lower mantle listed

in Table 19.1. The ratio of the temperature sensi-

tivities of V

and V

has attracted particular

attention. (@lnV

/@lnV

)

depends quite strongly

on pressure, increasing from 1.7 to 2.5 over the

lower mantle range (column 4 of table 19.1),

and this is in general agreement with tomo-

graphic observations of V

and V

by Robertson

and Woodhouse (1996a) and Su and Dziewonski

(1997), indicating that the variations have a

thermal explanation. However, closer examina-

tion shows that this is not a sufficient explan-

ation. These data sets agree that when presented

as a comparison of S-wave anomalies with

variations in bulk sound velocity, V



,givenby

Eq. (19.72), they are seen to be negatively corre-

lated below about 2000 km depth or perhaps

uncorrelated (Kennett et al., 1998). The signifi-

cance of V



is that it does not depend on the

rigidity modulus, , but only on the bulk mod-

ulus K

(and ). The negative correlation, that is a

decrease in V



corresponding to an increase in V

and vice versa, can be interpreted as a thermal

effect only by supposing that K

decreases with

temperature more than does , and by Eq. (19.73)

that means 

< 1. 

is calculated by Eq. (19.64), a

thermodynamic identity, in terms of parameters

that are constrained by the equation of state

of the lower mantle (as detailed in Stacey and

Davis, 2004 and listed in Appendices F and G), by

which 

remains greater than unity throughout

the mantle (see Section 19.7). We must therefore

appeal to compositional variations in addition to

the thermal effects.

Forte and Mitrovica (2001) considered the

compositional variations of the lower mantle in

terms of the SiO

–FeO–MgO system with varying

proportions of these components. They used

seismic and modelling data to infer velocity

changes due to changes in the molar fraction of

iron, X

¼½FeO=ð½FeOþ½MgOÞ, and the molar

fraction of perovskite X

¼½Pv=ð½Pvþ½MwÞ,

where Pv refers to perovskite and Mw refers to

magnesiowustite. Then

 ln V

@ ln V

T þ

@ ln V

X

@ ln V

X

;

 ln V



@ ln V



T þ

@ ln V



X

@ ln V



X

(17:36)

288 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

289

– [267–293] 13.3.2008 2:16PM

With values of temperature derivatives at

radius 3600 km, 120 km above the core– mantle

boundary and the Forte–Mitrovica estimates of

compositional derivatives, these equations

become

 ln V

¼2:5 10

5

T  0:16 X

 0:22  X

;

 ln V



¼0:12 10

5

T þ 0:045 X

þ 0:048 X

(17:37)

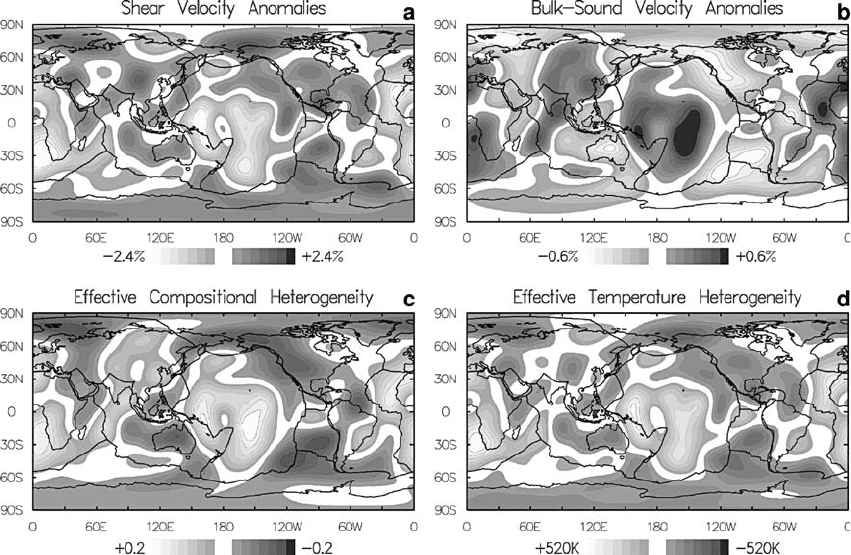
On this basis Forte and Mitrovica (2001)

mapped X

with maximum values of about

0.01 (Fig. 17.15). Assuming temperature varia-

tions of about 100 K, temperature has the dom-

inanteffectonV

in Eq. (17. 37) but V



is most

affected by compositional variations. This can

account for the negative correlation between



and V

. If this is the explanation, then

high temperatures are correlated with high

iron content, so that the thermal and composi-

tional effects on density are, at least partly,

compensating.

17.9 Seismic anisotropy

With rare exceptions, published tomographic

inversions have been based on the assumption

that that the velocity anomalies are isotropic.

This has been more a matter of necessity than a

fundamental requirement, because the data are

insufficient to resolve the extra parameters

required to describe anisotropy, but the perva-

siveness of anisotropy in the crust and upper

mantle suggests that interpretations based on iso-

tropy could be simplistic. Anisotropy is sought in

terms of variations in travel times of seismic

waves with direction and polarization and may

be due to alignment of intrinsically anisotropic

minerals or fabric made up of aligned elastic het-

erogeneities. If the fluctuations in anisotropy are

sufficiently random the region appears isotropic.

Crustal anisotropy is highly variable. On a small

(kilometre) scale, velocity variations can be very

large (as much as 20%), but on larger scales (tens of

FI G U R E 17.15 Tomographic shear and bulk sound velocity models compared with inferred temperature and

compositional variation at a radial distance of 3600 km (about 120 km above D

). (Forte and Mitrovica, 2001.)

17.9 SEISMIC ANISOTROPY 289

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

290

– [267–293] 13.3.2008 2:16PM

kilometres) the anisotropy appears to be almost

incoherent. By contrast, the uppermost mantle

exhibits long-wavelength coherent anisotropy,

probably caused by alignment of olivine crystals.

Olivine is highly anisotropic with orthorhombic

symmetry (see Tables 10.2a, b). When subjected

to finite shear deformation, fast directions align

in the direction of extension, and, in the case of

extreme shear, rotate to become parallel to the

shear plane itself.

A complete description of the effects of man-

tle fabric on seismic wave propagation requires a

full anisotropic tensor (Crampin, 1977), but

determination of all 21 components of the elas-

tic tensor (Chapter 10) is not feasible. Typically,

several parameters are obtained from a particu-

lar set of observations while the remaining coef-

ficients are constrained to be averaged isotropic

values. The resulting anisotropy parameters are

found to be in good agreement with laboratory

measurements on mantle rocks, such as ophio-

lites and xenoliths, which typically exhibit

P-wave anisotropy of about 8% and S-wave aniso-

tropy of 4% (Long and Christensen, 2000).

The reference Earth model (PREM, Dziewonski

and Anderson, 1981) describes the uppermost

195 km of the mantle as an anisotropic solid

with cylindrical symmetry about a vertical axis.

This is referred to as transverse isotropy, and

requires five depth-dependent elastic moduli.

The remainder of the PREM mantle is isotropic

with two moduli. Transverse isotropy was used

to model the observation that velocities of man-

tle Love waves are higher than those of mantle

Rayleigh waves. Azimuthal anisotropy has been

recognized in oceanic mantle since the 1960s

with the observations that P

-waves, critically

refracted in the mantle beneath the crust, travel

faster in the spreading direction than perpendic-

ular to it (Hess, 1964; Raitt et al., 1969; Keen and

Barrett, 1971). In young ocean lithosphere

Rayleigh wave fast directions are also parallel

to plate motion direction (Forsyth, 1975;

Nishimura and Forsyth, 1989; Montagner and

Tanimoto, 1991; Laske and Masters, 1998).

However, in older sea floor, Nishimura and

Forsyth (1989) found that the effect weakens,

possibly due to over-printing of different direc-

tions of absolute plate motion. Nishimura and

Forsyth analysed the spatial and depth depend-

ence of anisotropy of the Pacific Ocean floor,

finding it to be confined to the upper 200 km.

Thus, the anisotropy occurs mainly in the man-

tle lithosphere, but extends into the underlying

asthenosphere.

Birefringent effects on SKS waves are used to

determine azimuthal anisotropy. Because the

SKS wave is generated by a conversion at the

CMB of a core-travelling P-wave, the polarization

of the emerging S is SV. When the S-wave

encounters azimuthally anisotropic material it

splits into fast and slow components that arrive

at the surface out of phase, making the motion

elliptical. S-wave polarizations are termed radial

when parallel to the great circle between source

and receiver, and transverse if normal to it.

Knowing that the initial polarization is radial, it

is possible to reconstruct the incident waveform

to determine the fast direction and the phase

delay. The splitting process effectively differenti-

ates the waveform such that the transverse com-

ponent is the time derivative of the incident

radial component. To see this, consider a nearly

vertically incident split shear wave. Let the radial

component of the polarization be f(t) and suppose

the fast direction makes an angle  with the radial

component, the slow direction an angle of  þp/2

and that the travel time difference is t.After

splitting, the fast component is f(t þt/2) cos 

and the slow component is f (t t/2) sin .

Resolving these into the transverse direction (i.e.

at p/2 to the radial direction), one obtains

transverse ¼ f ðt þ t=2Þf ðt  t=2Þ½1=2 sin 2

ð1=2Þt sin 2

df ðtÞ

; for t small:

(17:38)

This property that the transverse component is

908 out of phase with the radial component is

useful for recognizing split energy in the pres-

ence of interfering phases, such as S, that nor-

mally have radial and transverse components in

phase.

Numerous studies of SKS splitting have been

published (e.g., Silver, 1996). Typically phase

delays are 1 to 2 s, corresponding to 2 to 4%

azimuthal anisotropy in the uppermost mantle

290 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

291

– [267–293] 13.3.2008 2:16PM

(200 km depth). Fast directions are often aligned

with finite extensions of this layer, but there are

many exceptions that require explanation.

Montagner et al. (2000) found that splitting pre-

dicted from surface wave anisotropy is in good

agreement with observations for regions under-

going large-scale coherent tectonics, such as the

western United States and Central Asia.

Seismic anisotropy in the upper mantle is

thought to be due mainly to oriented olivine

crystals. Since olivine crystals are orthorhombic,

a complete description requires nine independ-

ent elastic constants and three Euler angles to

define orientation. By combining different meas-

ures of anisotropy such as SKS splitting, azimu-

thal variation of surface wave dispersion, and

misalignment of wave motion relative to the

directions from which waves arrive, it is possible

to infer depth-averaged values of these constants

(e.g. Davis, 2003).

At depths greater than 220 km the mantle

appears to be less anisotropic, but is unlikely to

be perfectly isotropic (Boschi and Dziewonski,

2000; Panning and Romanowicz, 2006). The

alignment in the uppermost mantle is thought

to be caused by dislocation creep with the differ-

ent crystalline planes of olivine having different

effective viscosities and resulting in deformation

that depends on the orientations of individual

crystals. This causes an alignment of crystal axes

as strain progresses. At high homologous tem-

peratures (T/T

), the dominant deformation

mechanism is believed to be diffusion creep,

which destroys an existing fabric without gener-

ating a new one, and this is consistent with

weaker anisotropy of the asthenosphere. The

lower mantle is less anisotropic than the upper

mantle, probably because the minerals are less

anisotropic. There is some evidence of aniso-

tropic travel times for waves grazing the core–

mantle boundary, which could be explained as a

fabric in the D

layer.

The inner core is anisotropic. Compressional

waves travelling through it parallel to the rota-

tion axis have travel times 3 s to 4 s shorter

than waves travelling in the equatorial plane

(Poupinet et al., 1983). Explanations in terms of

axial elongation of the inner core were dis-

counted when it was shown that the splitting of

certain free-oscillation frequencies was explained

by an anisotropic inner core (Woodhouse et al.,

1986; Tromp, 1993). Later body wave analyses

have indicated lateral variations in the anisotropy

of the inner core (Creager, 1997). The anisotropy

is an important clue to the mechanism of inner

core formation by accretion primarily on its equa-

tor and steady deformation towards equilibrium

ellipticity (Yoshida et al., 1996). It is thought that

the inner core consists of "-iron, a hexagonally

close-packed phase with cylindrical symmetry,

and that anisotropy of the inner core is an expres-

sion of its crystalline alignment.

Inner core anisotropy is not perfectly aligned

with the rotation axis and is highly variable. Song

and Richards (1996) recognized the possibility of

seeing differential rotation of the inner core,

relative to the mantle, from slow variations of

travel times for seismic waves with inner core

paths. This has important implications for core

physics and the dynamo, and is discussed in

Section 24.6. The original report was followed by

widely different estimates of rotation rate as well

as refutations, but recent better controlled obser-

vations by Zhang et al. (2005), illustrated in

Fig. 17.16, leave little doubt that there is a real

effect. Interpretation depends on imprecisely

observed inner core structure. It should also be

noted that electromagnetic coupling of the inner

core to the complicated, irregular field of the

outer core allows the possibility that the inner

core rotation axis differs by a few hundredths

of a degree from that of the mantle. The observa-

tions may not see a simple differential rotation

about a common axis, but polar wander of the

inner core.

The misalignment of the axis of the inner

core anisotropy invites comparison with the mis-

alignment of the magnetic dipole axis. In both

cases we appeal to Curie’s (1894) principle of

symmetry, according to which no effect can

have lower symmetry than the combination of

its causes. Paterson and Weiss (1961) discussed

geological applications of this principle. In these

situations the principle must be applied statisti-

cally, that is we must consider the long-term

average alignment of the anisotropy axis to be

constrained by Curie’s principle and not the

instantaneous alignment, just as we average

17.9 SEISMIC ANISOTROPY 291

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

292

– [267–293] 13.3.2008 2:16PM

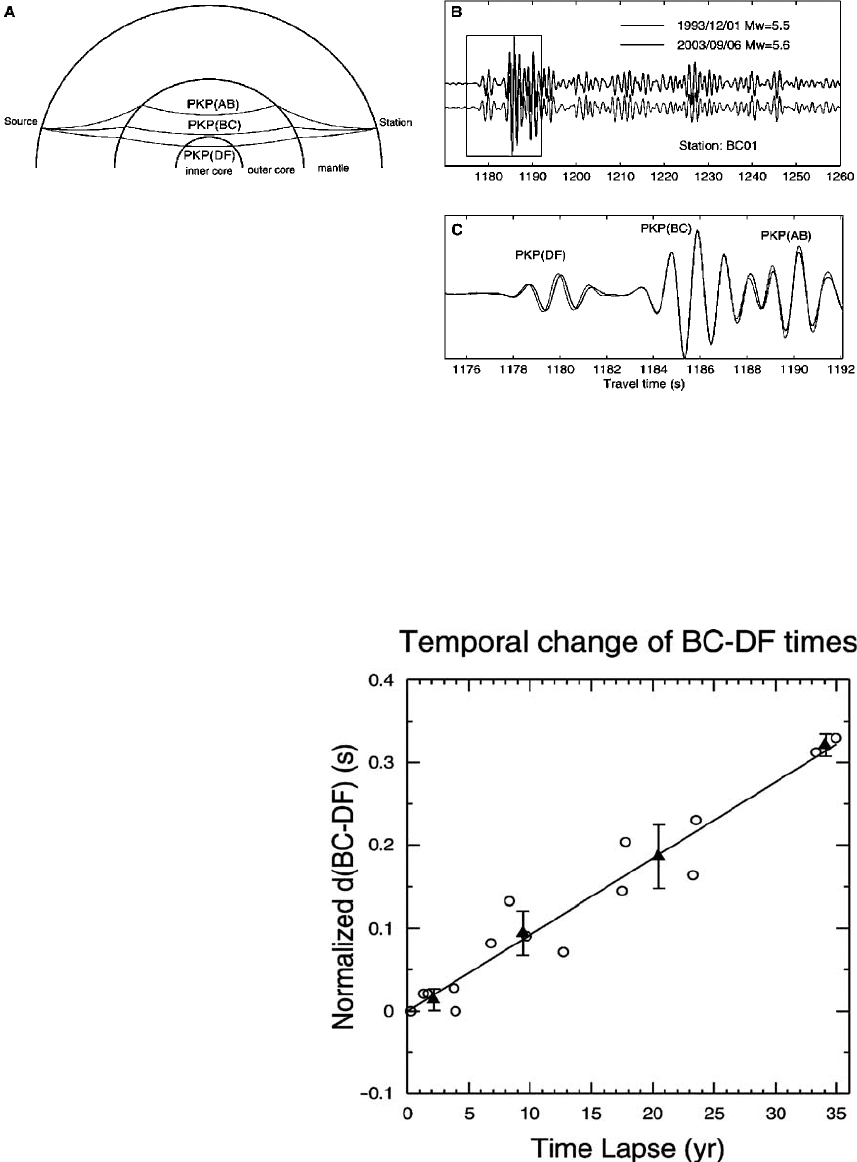
FI G U R E 17.16(a) Ray paths of PKP waves and an example of a waveform doublet used to detect a temporal

change of travel times through the inner core (Zhang et al., 2005). A doublet refers to a pair of earthquakes

separated in time, with highly correlated waveforms suggesting that they have nearly identical locations.

The phase change between waves that pass through the inner and outer cores increases with the time interval

between events. This has been taken as evidence that the inner core is rotating, relative to the mantle.

FI G U R E 17.16(b) Difference of BC–DF

times, d(BC–DF) (Fig. 17.16(a)) at station

COL (College, Alaska) as a function of the

time separation between the two events

of a doublet. (Zhang et al., 2005.)

292 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

293

– [267–293] 13.3.2008 2:16PM

the magnetic field over thousands of years to

demonstrate the axial dipole principle. We refer

to this principle in Sections 24.5 and 25.3. On a

similar time scale (controlled by core motions)

the inner core anisotropy must, by Curie’s princi-

ple, be aligned with the rotation axis. Two effects

must be expected from the electromagnetic cou-

pling to irregular motion in the outer core. The

material of the inner core may move relative to its

own rotation axis (polar wander of the inner core)

and the axis may be misaligned with that of the

mantle. By Curie’s principle, the second of these

effects would be averaged out over thousands of

years, but the first one would cause permanent

heterogeneity of grain alignment in the inner

core. It appears possible that seismic observations

may eventually clarify the details of present inner

core rotation.

17.9 SEISMIC ANISOTROPY 293

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

294

– [294–313] 13.3.2008 11:43AM

Finite strain and high-pressure equations

of state

18.1 Preamble

An equation of state is a relationship between

volume, V, pressure, P, and temperature, T,ofa

specified mass of material. If density, , is used

instead of V then specification of mass is

unnecessary, and in some treatments V is spe-

cific volume, 1/, but in this text V is the volume

of an arbitrary mass, m. Another alternative is

molar volume, but moles can be inconvenient

units for materials with non-integral propor-

tions of different elements. The simplest and

most familiar equation of state is the ideal gas

equation for n moles of gas, PV ¼nRT, where

R ¼N

k ¼8.314 47 J mol

1

is the gas constant

and is related to Boltzmann’s constant, k ¼

1.380 65 10

23

1

by Avogadro’s number,

¼6.022 14 10

mol

1

. It is an example of a

complete equation of state, by which is meant

one representing V as a function of both P and T,

not that it gives all of the properties. In dealing

with condensed matter (solids and liquids) it is

generally convenient to consider the P and T

effects separately. Compression at constant T is

described by the isothermal bulk modulus or

incompressibility, K

¼V(@P /@V)

. This is a

parameter of elasticity theory (Chapter 10),

which is restricted to small strains, that is, for

volume compression, P/K

¼DV/V 1. We refer

to elasticity theory as infinitesimal strain theory,

in which K

is treated as constant. For stronger

compressions we need a finite strain theory, in

which K

varies with P, sometimes referred to as

an isothermal equation of state. For a complete

equation of state it must be supplemented by

information about thermal expansion.

In the Earth, bulk modulus varies by a factor

exceeding 10 (for core material, relative to zero

pressure), making the necessity for a finite strain

theory obvious. Unfortunately there is no

agreed, general theory, but only rival ideas, all

of which must be recognized as empirical. Even

the definition of strain itself is problematic. Most

geophysical discussions have followed the ideas

of Birch (1952), who pioneered the interpreta-

tion of seismological observations of the deep

Earth in terms of a theory that was developed

from the classical elasticity study of Love (1927).

Birch’s theory is most simply presented in terms

of interatomic potentials, although its original

development was quite different. It works rea-

sonably well for minerals if used to estimate

density as a function of pressure, but if deriva-

tives (dK/dP,d

K/dP

) are required, as in the cal-

culation of thermal properties (Section 19.3) or

for extrapolation outside the range of fitted data,

then it is not satisfactory and the use of what we

call derivative equations is necessary. But the

search for further improvements continues and

thermodynamic arguments are central to this

search.

A finite strain theory makes a particular

assumption about the variation in temperature,

most commonly T ¼constant or even T ¼0, but

other alternatives are possible. For geophysical

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

295

– [294–313] 13.3.2008 11:43AM

purposes it is often more convenient to use an

adiabatic finite strain equation, so that no ther-

mal correction is needed to represent V(P)orP(V)

within the large regions of the Earth where the

temperature gradient is believed to be close to

adiabatic. It uses directly the seismologically

observed bulk modulus, which is not K

but K

representing adiabatic compression,

¼Vð@P=@VÞ

¼ K

ð1 þ TÞ; (18:1)

where

 ¼ K

=C

¼ K

=C

(18:2)

is the Gr ¨uneisen parameter, a subject of

Section 19.3. In the Earth K

exceeds K

by 5% to

10%. Another possibility is an equation represent-

ing compression on the melting curve, with mod-

ulus K

, which is referred to in Section 19.4.

The thermal properties required to add an

arbitrary temperature variation are not independ-

ent of the elastic properties described by a finite

strain theory. They are controlled by the same

atomic forces. The Gr

uneisen parameter is the

essential theoretical link because it can be repre-

sented in terms of elastic moduli and their pres-

sure derivatives (Section 19.3). This means that

such calculations require derivatives of the finite

strain equations on which they are based and care

is required in selecting a theory for which the

derivatives meet thermodynamic criteria.

Most finite strain equations are relationships

for P(V) and cannot be inverted to give analytical

expressions for V(P). Partly for this reason it is

often preferable to add thermal effects by con-

sidering the application of heat at constant V

rather than constant P. The increase in P with T

at constant V is termed thermal pressure, being

the pressure that prevents thermal expansion.

We have a thermodynamic identity (Appendix E)

ð@P=@TÞ

¼ K

; (18:3)

so that

K

dT ¼ 

C

dT; (18:4)

integrated at constant V. It is convenient to the

application of Eq. (18.4) that, for insulators at

high temperatures, the product ( K

), like ( C

)

in Eq. (18.4), is only slightly dependent on T (at

constant V). For metals, including the Earth’s

core, an electron heat capacity proportional to

T must be added.

Finite strain equations do not carry through

phase transitions. Different phases of a material

have different physical properties and the

parameters of an equation of state are specific

to a particular phase or crystal structure. Mineral

phase transitions in the mantle are marked by

discontinuities in properties such as K

or K

and

 as well as . However, some mineral phase

transitions (those in Table 2.4b) are not sharp

but smeared over ranges in pressure, so that

seismological estimates of parameters such as

dK/dP lose their normal meanings over these

ranges and equations of state can be applied

only very cautiously. They are fully effective

only when applied to those parts of the Earth

that are uniform in mineral structure as well as

composition, the outer core and most of the

lower mantle.

The changes in properties such as K

that

occur at phase transitions can be attributed to

the changes in atomic coordination. Thus, it is

interesting to note that at the inner core boun-

dary (ICB), between solid and liquid iron

alloys, the change in properties is very slight.

Most of the density difference is due to a differ-

ence in the abundance of solutes (Section 2.8),

which are nevertheless dilute enough to have

little effect on bulk modulus. The very slight

change in K

with melting is characteristic of

metals that melt with little change in atomic

coordination, as described by the dislocation

theory of melting (Section 19.4) and expected at

pressures sufficient to ensure that both solid and

liquid are close-packed.

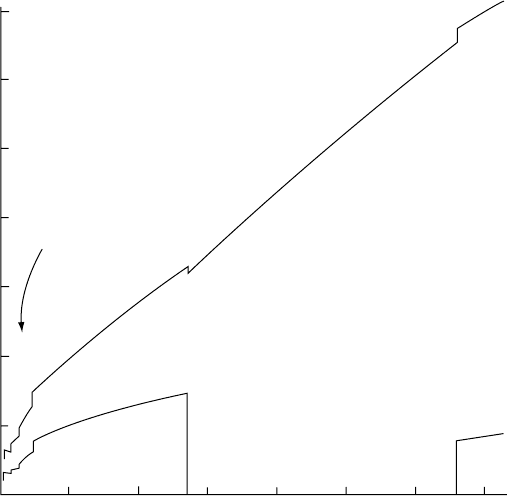
Appendix F gives selected details of the Earth

model PREM. This is a parameterized model in

the sense that density and the seismic wave

speeds, V

and V

are fitted to polynomials in

radius over different ranges, the parameters

being the polynomial coefficients. While this is

mathematically convenient and represents the

variations of  and K

with P (Fig. 18.1) adequately

for some purposes, it is of limited use for equa-

tion of state studies because the derivatives,

18 . 1 P R EA M B LE 295

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C18.3D

–

296

– [294–313] 13.3.2008 11:43AM

¼(@K

/@P)

and K

¼(@

/@P

)

, are incompat-

ible with any plausible equation of state. They

show trends that are consequences of the model

parameterization and do not follow the neces-

sary monotonic pressure variations. This can be

handled by fitting the data to an equation of

state, but then, of course, the chosen equation

imposes its own functional form and so deter-

mines details of the inferred properties. In this

circumstance information additional to the fit-

ted data is required to ensure that the equation

gives physically real behaviour for properties

that depend on derivatives of the equation. Fits

of lower mantle and core data to a derivative

equation are listed in Appendix F for comparison

with the PREM tabulation on which they are

based.

As discussed in Section 17.5, in a homogene-

ous, adiabatic layer the variation in density with

pressure is given by d/dP ¼/K

¼1/, which is

obtained directly from seismic velocities. This is

a semi-independent check on the P() variation

of an Earth model and so provides a test for

homogeneity. In layers where Earth models

clearly indicate homogeneity, the outer core

and most of the lower mantle, there is, therefore,

a redundancy in the information that is very

useful to equation of state studies. Instead of

fitting just a P– equation, we can differentiate

it to obtain a K– equation and, by taking the

ratio, we have a P/K vs  equation that can be

fitted. Since both P and K are listed in Earth

models, this eliminates the unknown K

from

an initial data fit, making the fit correspondingly

more certain. For this reason, as well as the sur-

ety of the pressure scale, over the pressure

ranges of the outer core and lower mantle,

there is a strong advantage to the use of Earth

model data for testing finite strain equations.

18.2 High-pressure experiments

and their interpretation

Laboratory simulation of deep Earth conditions

of pressure and temperature allows comparison

of measured properties of candidate terrestrial

materials with seismological data, providing

(10

Pa)

Pressure, P (10

Pa)

Rigidity,

Lower mantle

Transition

zone

Incompressibility, K

Inner

core

Outer

core

0.5 1.00 1.5 2.0 2.5

3.0

3.5

FI G U R E 18.1 Variations of the

elastic moduli, K and , with

pressure, P, for the PREM Earth

model.

296 FINITE STRAIN AND HIGH-PRESSURE EQUATIONS OF STATE