Справочник по безопасности дорожного движения

Подождите немного. Документ загружается.

безопасности дорожного движения возрас-тает, когда возрастает количество

происшествий и в особенности количество погибших. Когда эти цифры понижаются,

уменьшается и интерес к безопасности дорожного движения.

Теория о приспособлении поведения и условиях такого приспособления

Попытка Wilde сформулировать общую теорию для объяснения происшествий не удалась.

Более ог-раниченной теорией является теория о приспособле-нии поведения или

компенсации риска. Эта теория исходит из того, что участники дорожного движения в

большей или меньшей степени приспосабливают поведение относительно риска и

мероприятия по по-вышению безопасности дорожного движения, но не обязательно таким

образом, что риски или мероприятия, вызывающие приспособление поведения, будут

полностью компенсированы и тем самым не будут влиять на количество происшествий, -

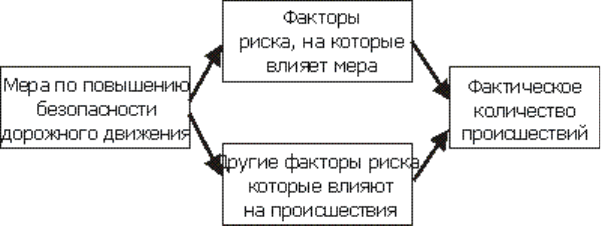
подобное утверждает Wilde. Логика этой теории представлена на рис. G.4.4.

Рис. G.4.4. Логика теории о приспособлении поведения (компенсации риска)

Предполагается, что каждая мера по повышению безопасности дорожного движения, как

считается, влияет на происшествия, влияя на один или несколько факторов риска, которые

увеличивают количество происшествий или ухудшают степень тяжести ранений (факторы

риска, на которые, как считают, влияет мера). Помимо этих факторов, мероприятие по

повышению безопасности дорожного движения может иметь непредвиденные влияния на

один или несколько других факторов риска, которые влияют на происшествия или степень

тяжести ранения. Если на эти факторы риска оказывается влияние в неблагоприятном

направлении, то это может полностью или частично перевесить благоприятное влияние

факторов риска, на которые, как считают, влияет мероприятие. Такие компенсирующие

изменения в других факторах риска, на которые в основном, как считают, влияет

мероприятие по повышению безопасности дорожного движения, называются

компенсацией риска. Схема, на которой строится рис. G.4.4, разработана Evans (1985,

1991).

Конкретизируем схему примером. Как считают, освещение дороги влияет на

происшествия, облегчая обнаружение других участников дорожного движения и

предметов на дороге в темноте. Расстояние обнаружения в темноте является фактором

риска, на который, как считают, влияет освещение дороги. Влияние освещенности дороги

на происшествие, которое влияло бы на расстояние обнаружения без изменения поведения

участников дорожного движения, называется инженерным эффектом мероприятия.

Инженерный эффект на рис. G.4.4. показан верхней стрелкой. Рассмотрим, как освещение

дороги приводит к тому, что участники дорожного движения ездят быстрее и снижают

внимательность. Такие изменения поведения не являются преднамеренными и могут

привести к тому, что освещение дороги будет иметь меньшее влияние на происшествия,

чем имела бы это мероприятие. Изменения в поведении можно назвать эффектом

поведения мероприятия и обозначить нижней стрелкой на рис. G.4.4. Чистый эффект

мероприятия определяется и инженерным эффектом, и эффектом поведения, и

направлением силы этих эффектов.

Многие исследователи приспособления поведения в дорожном движении намеревались

осветить вопрос, почему приспособление поведения встречается в одних случаях и не

встречается в других, и лучше описать формы приспособления поведения. Формой

приспособления поведения, которая вероятно является важной, но которую трудно

исследовать, является измененное внимание у участников дорожного движения. Низкий

уровень внимательности не всегда легко определить. Она не обязательно приводит,

например, к изменению скорости.

В стратегической институтской программе Институт экономики транспорта исследовал

условия приспособления поведения и формы такого поведения. Эта программа

исследовала приспособление водителей автомобилей при освещении дороги, при

использовании тормозов с антиблокировочными устройствами (тормоза ABS) и надувных

подушках безопасности. Кроме того, в более общем плане рассматривались условия

приспособления поведения. Предполагается, что условия для приспособления поведения

должны появиться, в частности, в следующих случаях (Bjоrnskau, 1994B):

1. Эффективность мероприятия

Мероприятие, приводящее к ощутимым улучшениям, которые, как считают участники

дорожного движения, снижают риск ДТП, более подвержена компенсации риска

(приспособлению поведения), чем мероприятие, не приводящее к видимым улучшениям.

Пример: разметка проезжей части дороги предполагается более подверженной

приспособлению поведения, чем отклоняющаяся колонка рулевого управления.

2. Снижает ли мероприятие количество происшествий и/или ранений или нет

Мера, сокращающая риск происшествий, более подвержена компенсации риска, чем мера,

снижающая степень тяжести ранений при происшествиях. Пример: ABS-тормоза более

подвержены компенсации риска, чем надувные подушки безопасности.

3. Если участники дорожного движения заранее компенсировали факторы риска, на

которые мера влияет или не влияет

Если участники дорожного движения уже приспособили поведение к фактору риска, на

который мероприятие не влияет, то мера более подвержена компенсации риска, чем если

бы такое приспособление не имело места. Пример: периодический контроль, как следует

предположить, больше подвержен приспособлению поведения, чем освещение дороги,

поскольку, как кажется, участники дорожного движения компенсируют технические

неисправности и неполадки, так что риск происшествий не увеличивается, но они не

приспосабливают поведение относительно темноты таким образом, чтобы увеличение

риска в темноте уменьшилось.

4. Величина инженерного эффекта

Чем больше инженерный эффект, тем более вероятным является приспособление

поведения. Пример: Более вероятно, что улучшение главных фар автомобиля

(применяемые для освещения при движении) приведет к приспособлению поведения при

езде в темное время суток, чем при езде при дневном свете.

5. Возможность достижения увеличения выгоды

Мероприятие может быть подвержено изменению поведения, если только можно

изменить поведение таким образом, что участники дорожного движения будут

испытывать пользу или удобства. Пример: трудно представить, что приспособление

поведения к шлагбауму на железнодорожном переезде увеличит выгоду участника

дорожного движения. Езда зигзагами между шлагбаумами, которая всегда, чрезвычайно

опасна и, кроме того, это может привести к повреждениям автомобиля. Большинство вряд

ли испытает при этом какую-либо выгоду или удобство. Снижение внимания, когда

запаздывает реагирование, также не является преимуществом и ведет лишь к неприятно

резкому торможению для того, чтобы остановиться перед шлагбаумом.

В программе Института экономики транспорта исследовался ряд этих предположений. В

частности, было найдено, что участники дорожного движения приспосабливают

поведение относительно освещенности дороги, увеличивая скорость в темное время суток

и сокращая внимательность (Bjоrnskau и Fosser, 1996). Далее было установлено, что на

поведение не влияют надувные подушки безопасности, но что водители автомобилей,

оборудованных тормозами ABS, держат более короткую дистанцию до впереди едущего

автомобиля, чем водители автомобилей, не оборудованных тормозами ABS (Fosser,

Sagberg og Sаtermo, 1996).

Может ли приспособление поведения объяснить недостаточное влияние ряда

мероприятий по повышению безопасности дорожного движения на происшествия?

Среди мероприятий по повышению безопасности дорожного движения, которые

описываются в данном Справочнике, есть мероприятия, которые, согласно имеющимся

исследованиям сокращают количество происшествий, и есть мероприятия, которые не

обеспечивают этого. К последней группе мероприятий относятся, например, пешеходные

и велосипедные дорожки, общее улучшение асфальтобетонного покрытия дороги,

осветление дорожных покрытий и основательное обучение водителей. Может ли

приспособление среди участников дорожного движения объяснить, почему эти и другие

мероприятия не приводят к уменьшению количества происшествий?

Ответом на этот вопрос в большинстве случаев будет "да", но во многих случаях с

определенной оговоркой. Да, можно всегда считать, что приспособление поведения

объясняет недостаточное влияние мероприятия на количество происшествий. Но очень

часто такое приспособление поведения недостаточно обосновано. Одним из немногих

примеров исследования, в котором четко установлено наступление приспособления

поведения, является исследование Амундсена (Amundsen, 1983) о светлых дорожных

покрытиях. Такие дорожные покрытия привели к увеличению скорости, в особенности в

темное время суток.

К сожалению, такой результат является редкостью. Никто, например, не показал, что

недостаточное сокращение количества происшествий в местах, где есть разметка,

объясняется приспособлением поведения участников дорожного движения. Нельзя

исключить этого, но нам неизвестно, является ли это объяснением того, что нельзя

доказать какого-либо сокращения количества происшествий. Приспособление поведения

не обязательно должно привести к тому, что мера теряет все свое влияние на количество

происшествий. Например, дорожное освещение сокращает количество происшествий с

травматизмом в темное время суток приблизительно на 30%. Это большое влияние.

Возможно поэтому следует считать, что эта мера подвержена приспособлению поведения.

На рис. G.4.5 представлены результаты исследования Института экономики транспорта о

приспособлении скорости водителями на участке дороги, где было установлено дорожное

освещение.

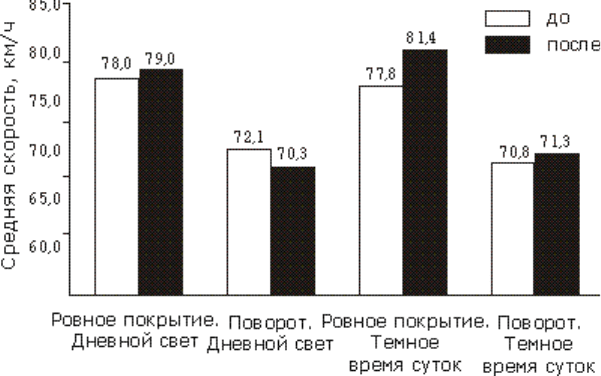
Рис. G.4.5. Изменение средней скорости при устройстве на дороге освещения.

Источник: Bjоrnskau и Fosser, 1996

На рис. G.4.5 представлены средняя скорость в км/ч на дороге с ровным покрытием и на

кривых, при дневном свете и в темное время суток, до и после устройства освещения.

Скорость возросла в темное время суток, особенно на ровной дороге. Если

проанализировать увеличение скорости от периода "до" до периода "после" при дневном

свете в качестве контрольной группы, то чистое увеличение скорости в темное время

суток можно считать равным приблизительно 3% на ровной дороге и на кривых. Такое

увеличение скорости, рассматривая изолированно, увеличит количество происшествий с

травматизмом приблизительно на 6%. Кроме того, исследование показало, что водители

автомобилей были менее внимательны на освещенной дороге, чем на неосвещенной.

Увеличение расстояния обнаружения определенных предметов в темное время суток,

измеренное в контролируемых условиях, можно применять как меру инженерного

эффекта дорожного освещения. Согласно Ketvirtis (1977), расстояние обнаружения

увеличивается с 50-75 м при правильно установленном ближнем свете автомобиля в

качестве единственного источника света до приблизительно 250 м, когда дорога имеет

освещение такого качества, которое требуется на государственных дорогах в Норвегии

(сила света 1-2 свечи на м2). Если за исходную точку взять скорость 78 км/ч, время

реакции водителя 1 с и коэффициент сцепления 0,8, длина тормозного пути составит

приблизительно 52 м. Это дает увеличение запаса безопасности 75 52 = 23 м до

устройства освещения, до 250 52 = 198 м после установки дорожного освещения. Другими

словами, инженерный эффект соответствует потенциальному сокращению количества

происшествий в темное время суток не менее, чем на 80%. Фактическое сокращение

количества происшествий составляет приблизительно 30%. Это указывает на то, что

освещение дорог подвержено значительному приспособлению поведения, которое

способствует сокращению, но не исключению влияния мероприятия на происшествия.

Однако не всегда можно считать, что приспособление поведения означает влияние

мероприятия на происшествия. Во-первых, инженерный эффект многих мероприятий

неизвестен или его трудно рассчитать. Во-вторых, наступление приспособления

поведения во многих случаях мало исследовано. В-третьих, неизвестно, в том числе, когда

речь идет об освещении, какая форма приспособления поведения имеет наибольшее

значение. Увеличение скорости или уменьшение внимания? Единственно, что получит

подтверждение результатами исследований, это в лучшем случае общее влияние всех

форм приспособления поведения, а не частичное.

4.4. Уверенность и неуверенность участников дорожного движения многосторонняя

проблема

Что такое уверенность?

Под уверенностью понимается чувство человека безопасности, т.е. каким образом они

субъективно испытывают риск происшествия в дорожном движении. Насколько люди

верят в риск происшествий и насколько неприятны чувства испытанного риска

происшествий? Ответ на этот составной вопрос является выражением уверенности людей.

Другими словами, уверенность имеет два измерения: 1) испытание людьми опасности

дорожного движения и 2) чувство людьми неприятности или страха, связанных с

опасностями дорожного движения.

Неуверенность в дорожном движении в Норвегии

Насколько уверенно большинство людей при движении по дорогам в Норвегии? Об этом

известно немного, а имеющиеся исследования по этому вопросу частично довольно

устарели. Schiddborg (1979) задал ряду водителей автомобилей и пешеходов прямой

вопрос о том, как они оценивают сложность и опасность дорожного движения

сегодняшнего дня. Характеристика "опасное" была дана 13% водителей, 19% пешеходов,

имевших водительские права, и 24% пешеходов, не имевших водительских

удостоверений.

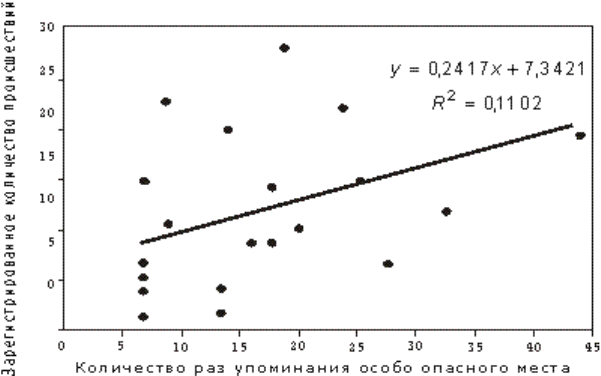
Рис. G.4.7. Взаимосвязь между количеством раз упоминания места как особо опасного и

количеством происшествий на этом месте в Хаугесунне, Норвегия. Источник: Hvoslef,

1980

Hvoslef (1980) опросил участников движения в Хаугесунне, задав им вопрос, чувствуют

ли они себя неуверенными в дорожном движении. 45% ответили "да", 23% ответили, что

иногда они чувствуют себя неуверенно, 30% ответили, что они не чувствуют себя

неуверенными, и 2% затруднились с ответом. Из тех, кто ответил "да" на вопрос об

неуверенности были 54% женщин и 35% мужчины. Hvoslef попросил также участников

дорожного движения назвать особо опасные места в Хаугесунне. На рис. G.4.7

представлена взаимосвязь между количеством раз упоминания места и количеством

зарегистрированных происшествий (сумма происшествий с травматизмом и

происшествий с материальным ущербом) на этом месте (всего 21 место). Количество раз,

называвшихся как особо опасные, изменялось в пределах от 7 до 42. Количество

происшествий на упоминавшихся местах изменялось в пределах от 1 до 29.

На рис. G.4.7 показано, что существует лишь слабая взаимосвязь между частотой

упоминания особо опасного места и количеством происшествий на этом месте. Другими

словами, места, упоминавшиеся участниками дорожного движения как особо опасные, не

обязательно являются местами, где происходит большинство происшествий.

Johansson и Naeslund (1986) провели подобное исследование в Упсале. Для четырех

различных групп водителей они установили корреляционные коэффициенты в пределах

от 0,02 до 0,08 между субъективными оценками опасности в определенных местах и

фактическим количеством происшествий, т.е. практически никакой взаимосвязи вообще.

Vaa (1991) анализировал взаимосвязь между риском ранений водителей в норвежских

областях и их испытанной степенью неуверенности во время ежегодных опросов

участников дорожного движения об их взгляде на политику содержания дорог

государственного дорожного управления. Использовались результаты, полученные в 19

областях. Взаимосвязь между испытанной неуверенностью и фактическим риском

составила - 0,04, т.е. практически не было никакой взаимосвязи. Vaa указывает, что

имеется основание сомневаться в ценности этого результата вследствие проблем

измерения неуверенности и вследствие того, что расчет взаимосвязи между риском и

неуверенностью делался с областями, а не с водителями.

Большинство людей воспринимают риск по ряду свойств источника риска (Brun, 1991,

1995). Если специалисты рассматривают риск как высокий или низкий, исходя из чисто

статистического уровня риска, то большинство людей используют также другие аспекты в

своих оценках риска. К ним относятся добровольность риска, степень личного контроля

риска, возможность катастрофы при происшествиях и насколько известен или привычен

риск. Риск ДТП большинство людей оценивают как частично добровольный риск с

относительно высокой вероятностью гибели.

Важной стороной неуверенности в дорожном движении является неуверенность изза

других. Kоltzow (1986) предложил понятие "заботливый страх" для того, чтобы описать

страх, который многие матери испытывают за своих детей, когда те играют на дорогах

или возле дорог с автомобильным движением. Понятие "заботливый страх" охватывает

также чувство физического бессилия, которое многие матери испытывают к участнику

дорожного движения; они переживают, что не могут что-либо сделать, чтобы повысить

безопасность детей, кроме как ограничить их свободу играть на улице. Неуверенность в

дорожном движении следует считать проблемой, если она ограничивает жизненные

потребности или приводит к тому, что люди отменяют нужные для них поездки;

например, не позволяют детям играть на улице без присмотра или ходить в магазин за

покупками. С другой стороны, фальшивая уверенность в дорожном движении также

представляет проблему. Если люди недооценивают опасности в дорожном движении и

проявляют неосторожность, это приводит к дорожно-транспортным происшествиям.

Неправильные представления риска в различных местах также представляют проблему.

Происшествия не обязательно происходят в тех местах, где люди считают езду самой

опасной.

Фальшивая уверенность и обоснованная неуверенность в отдельных случаях могут быть

взаимосвязаны. Неправильное представление водителя автомобиля о том, что езда по

дорогам в жилой застройке связана с низким риском (фальшивая уверенность), может

способствовать настолько неосторожной езде, что матери будут неуверенными за своих

детей.

Поиск "острых ощущений" и риск в дорожном движении

Люди сильно отличаются по своему отношению к риску. Крайними

противоположностями, возможно, являются матери, заботящиеся о безопасности своих

детей, с одной стороны, и рискованные молодые люди, которые выискивают

напряженность и любят смелые поступки, с другой стороны.

Вопрос о том, способствуют ли водители, ищущие острые ощущения, многим ДТП, в

последние годы обсуждался достаточно широко. Понятие поиск напряженности (острых

ощущений) ввел Zuckerman (1979, 1991). Любители острых ощущений - это люди,

которые имеют особо сильную потребность испытывать напряженность и которые

испытывают радость в осуществлении контроля в опасных ситуациях. Поэтому любители

острых ощущений ищут опасные ситуации или создают их сами и до предела напрягают

свои способности в таких ситуациях. Zuckerman разработал несколько тестов, которые

можно применять для идентификации искателей острых ощущений.

При опросе 300 молодых людей Moe и Jenens (1990) установили, что 15-20% из них, в

основном подростки, могут считаться искателями острых ощущений, исходя из

результатов теста Zuckerman. Молодые люди выполнили практическую езду на дороге.

Испытания показали, что искатели острых ощущений ехали наиболее быстро и

рискованно. Одновременно эта группа имела наилучшие навыки вождения.

Jonah (1996) обобщает 31 исследование о взаимосвязи между поиском острых ощущений

и особенностями вождения и приходит к выводу, что большинство этих исследований

свидетельствует о том, что искатели острых ощущений ездят менее осторожно по

сравнению с другими водителями. Среди мероприятий осторожности, применявшихся в

этих исследованиях, являются скорость, алкогольное воздействие и количество

нарушений правил дорожного движения.

В этих исследованиях не говорится о доле происшествий, которые можно отнести на

искателей острых ощущений.

4.5. Происшествия и величина риска как показатели безопасности дорожного

движения

Различные определения безопасности дорожного движения

Как упоминалось в п. 3 о происшествиях и рисках в дорожном движении, существуют три

способа определения безопасности дорожного движения, исходя из количества

происшествий.

1. Безопасность дорожного движения - это ожидаемое количество происшествий и

ранений

Под ожидаемым количеством происшествий или ожидаемым количеством ранений

понимается среднее количество происшествий или травмированных человек на единицу

времени в конечном итоге при неизменной интенсивности движения и неизменном

соотношении рисков.

2. Безопасность дорожного движения - это риск здоровью населения в дорожном

движении

Под риском здоровью населения в дорожном движении понимается количество раненых

или погибших на 100000 жителей в год.

3. Безопасность дорожного движения - это риск ранений участников дорожного

движения на пройденный километр

Безопасность дорожного движения можно также определить как количество раненых или

погибших на чел-км, пройденный в дорожном движении.

Ни одно из этих определений не является правильнее другого. Выбор определения

зависит от того, какую проблему хотят осветить. Все три определения связаны с рядом

проблем их толкования. Некоторые из этих проблем рассматриваются в этом разделе.

Проблемы толкования количества происшествий

Если определять безопасность дорожного движения как ожидаемое количество

происшествий, то естественно применять зарегистрированное количество происшествий

как показатель ожидаемого количества происшествий. Существуют две основные

проблемы относительно количества происшествий, которые предусматривают то, что

зарегистрированное количество происшествий в определенном месте в определенный

период не обязательно являются надежным показателем ожидаемого количества

происшествий. Этими двумя проблемами являются случайное изменение количества

происшествий и недостаточная регистрация происшествий. Проблемы, связанные с

недостаточной регистрацией, рассматриваются в п. 3. Здесь же рассматривается вопрос о

том, что понимается под случайным изменением количества происшествий.

Важно установить различие между систематическим и случайным изменением

происшествий (Elvik, 1988). Для объяснения разницы между систематическим и

случайным изменением количества происшествий был построен рис. G.4.8,

показывающий предполагаемые происшествия на перекрестке за восемь лет.

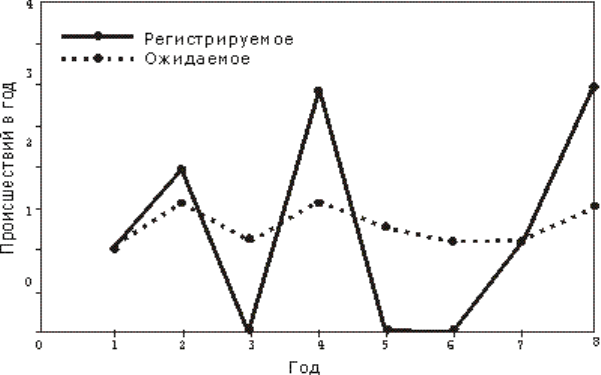
Рис. G.4.8. Ежегодно регистрируемое и ежегодное ожидаемое среднее количество

происшествий на перекрестке за восемь лет

На рис. G.4.8 темные точки представляют зарегистрированное количеством происшествий

на перекрестке в год. В первый год зарегистрировали 1 происшествие, второй год - 2,

третий год - 0 и т.д. Светлые точки - текущее среднее значение ежегодных

зарегистрированных количеств происшествий. В первый год оно равнялось

зарегистрированному количеству происшествий в этот год. Второй год - среднее значение

двух первых лет, т.е. (1 + 2)/2 = 1,5. Третий год - среднее значение трех первых лет, т.е. (1

+ 2 + 0)/3 = 1,0. Четвертый год - среднее значение первых четырех лет и т.д.

Видимо, что зарегистрированное количество происшествий в определенный год не

обязательно будет представительным для типичного или среднего количества

происшествий на перекрестке за известный период. Среднее ежегодное количество

происшествий в течение всего периода находится в пределах от 1,0 до 1,5. Напротив,

ежегодное зарегистрированное количество происшествий изменяется от 0 до 3. Можно

также видеть, что по мере накопления зарегистрированных количеств происшествий за

несколько лет среднее значение этих количеств за год будет более стабильным и меньше

подверженным влиянию зарегистрированному количеству происшествий за отдельный

год. Можно видеть, например, что 3 происшествия, случившиеся в четвертый год, дали

среднее ежегодное количество происшествий от 1,0 до 1,5. Напротив, три происшествия,

случившиеся на восьмой год, лишь увеличили среднее ежегодное количество

происшествий с 1,0 до 1,25.

Если предположить, что собраны данные о количестве происшествий для того же самого

перекрестка за очень большой период, например за этот период в целом почти не

повлияет зарегистрированное количество происшествий за определенный год. Среднее

количество, которое произойдет, как ожидается в конечном итоге при неизменной

интенсивности движения и неизменном соотношении рисков. Однако в течение такого

длительного периода, конечно, невозможно предвидеть, что на перекрестке будет

неизменная интенсивность движения или чтото не изменится. Поэтому на практике

невозможно применять развитие происшествий за 50 или 100 лет для того, чтобы сделать

оценку ожидаемому количеству происшествий на перекрестке, поскольку ожидаемое

количество происшествий не будет постоянным в течение такого длительного периода. То

же самое относится и к расчету ожидаемого количества происшествий для водителей

автомобилей. В реальных условиях продолжительность работы водителя не может быть

50 лет.

Поэтому настоящая величина количества происшествий на определенную единицу,

например перекресток, или водителя автомобиля, является всегда неизвестной.

Ожидаемое количество происшествий нельзя наблюдать непосредственно; его

необходимо рассчитывать. Наиболее часто применяемым методом расчета ожидаемого

количества происшествий является изучение большого количества единиц (перекресток,

участки дороги, водители, транспортные средства и т.д.), которые изменяются

относительно свойств, которые, как считают, влияют на количество происшествий.

Попытаемся объяснить систематическое изменение количества происшествий.

Мы говорим, что это систематическое изменение количества происшествий, когда какие-

либо единицы (перекресток, водители, автомобили, дороги) имеют более высокое или

низкое ожидаемое количество происшествий, чем другие единицы такого же рода.

Напротив, случайным изменением количества происшествий является изменение

зарегистрированного количества происшествий из года в год (или в более короткие

периоды) вокруг стабильного среднего значения ожидаемого количества происшествий.

Предположим, что рис. G.4.8 относится к 100 перекресткам. Тогда получили бы

систематическое изменение количества происшествий между перекрестками, если среднее

количество происшествий, например на 10 перекрестках с наибольшим движением,

находилось бы на уровне 5 в год, а на 10 перекрестках с наименьшим движением - на

уровне 0,1 в год. Два ряда факторов создают систематическое изменение количества

происшествий: интенсивность движения (экспонирование) и факторы риска (факторы,

которые влияют на вероятность происшествия при данной интенсивности движения).

Из-за случайного изменения количества происшествий, каждое изменение в

зарегистрированном количестве происшествий не означает, что изменяется также

ожидаемое количество происшествий. Например, сокращение числа погибших в год с 280

до 250 можно отнести за счет случайного изменения. Наоборот, сокращение раненых с

10000 до 9500 настолько велико, что оно не может быть отнесено исключительно за счет

случайностей.

Как "правило большого пальца" случайное изменение количества происшествий можно

приравнять квадратному корню из количества. Это означает, что случайное изменение

количества происшествий, рассчитанных в процентах от количества происшествий, будет