Современные проблемы машиностроения
Подождите немного. Документ загружается.


V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
71
Литература
1. Беляев А.Е. Прогрессивные зубчатые передачи: Сб. научн. Тр. Новоуральского го-
сударственного технологического ин-та. – Новоуральск: 2003. – 151 с.
2. А.с. 439653 СССР, Кл.F16H1/24. Зубчатая роликовая передача. С.В. Старухин, 1974.
3. А.с. 1446390 СССР, Кл. F16H1/24 . З убча тая роликовая передача. М. Л. Ерихов,
С.Г. Костенко, П.В. Ольштынский, В.М. Горох ов, 1988.
4. А.с. 1753100 СССР, Кл. F16H1/2 4. План етарный редуктор и способ его сборки.
М.Л. Ерихов, С.Г. Костенко, В.Т. Фонотов, 1992.
5. Патент 2191302 РФ, Кл. F16H1/24. С.Г. Костенко, В.Я. Герасимов, А.П. Третьяков,
В.А. Вотинов, 2002.
ОБОБЩЕННЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ
КОНТАКТНОГО ВЗАИМОДЕЙСТВИЯ РЕЗЬБОВЫХ СОЕДИНЕНИЙ
Н.В. Котенева, к.т.н., доц.
Алтайский государственный технический университет им. И.И. Ползунова,
656038, Россия, г. Барнаул, пр. Ленина, 46, тел. (385-2)-367-608
Е-mail: kot178@yandex.ru
При расчетах на жесткость узлов точных приборов и прецизионных металлорежущих
станков, различных деталей машин контактные перемещения имеют большое значение.
В большинстве и сследовани й контактная жесткость и зучалась при статическом на-
гружении. Однако на практике, как правило, стыки сопрягаемых деталей машин подвергают-
ся динамическому воздействию, как в нормальном или касательном направлении, так и од-
новременно из меняющихся касательной и нормальной нагрузок. К таким стыкам относятся
сопрягаемые поверхности резьбовых соединений, соединений с натягом, клиновые соедине-
ния и т. п. Применим закономерности упр угопластического контакта в условиях динамиче-
ского нагружения для определения параметров жесткости резьбовых соединений. Излагае-
мое ниже решение получено при следующих условиях:
- общая деформация деталей соединения является чисто упругой;
- местная деформация в зонах фактического контакта сопряженных п оверхностей яв-
ляется в общем случае упругопластической;
- плотность распределения выступов достаточно велика, а вершины выступов различ-
ных уровней статически равномерно распределены по контакт ирующим поверхностям;
- витки резьбы, благодаря малому углу подъема, имеют кольцевую форму, поэтому
можно считать стыковые поверхности резьбового соединения пл оскими;
- взаимное влияние выступов отсутствует;
- шероховатая поверхность образована одним из характерных для деталей соединения
видов механической обработки: точением, шлифованием, растачиванием;
- волнистостью поверхности гайки и сопрягаемой детали пренебрегаем:
- твердость одного из взаимодействующих тел (либо гайка, либо соединяемая деталь)
выше;
- поверхность более твердого тела имеет сферическую модель микронеровности.
Резьбовые соединени я относятся к наиболее распространенным в машин остроении
видам разъемных соединений.
Нагрузки, действующие в резьбовом соеди нении, подразделяются на технологические
и силы трения, которые взаимосвязаны. К технологическим силам относит ся усилие затяжки,
которое выбирается из условия обеспечения необходимой плотности стыка в зависимости от
приложенных к стыку внешних сил.

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
72
В течение эксплуатации усилие затяжки может самопроизвольно снижаться. Основ-
ными п ричинами, вызывающими его ослаблени е, являются: объемные пластические дефор-
мации в соедин ении, самопроизвольное увеличение пластических микроконтактных дефор-
маций на торце гайки (винта) и в витках резьбы и самоотвинчивание гаек в условиях вибра-
ционных нагрузок.
С учетом условий герметичности и плотности стыка усилие затяжки
1FkF
зз
, (1)
где
з
k
– коэффициент запаса, обеспечивающий плотность стыка;
F
– внешняя технологи-
ческая нагрузка;
– коэффициент основной нагрузки.
Коэффициент
з
k
в зависимости от условий работы и конструкционных особенностей
стыка при постоянных нагрузках
225,1
з
k
, при переменных нагрузках
45,2
з
k
.
Если на затянутый стык действует отрывающая сила
F
, т о часть ее
F
воспринима-
ется болтом, а часть
1F
разгружает стык и сопрягаемые детали под болтами [ 1].
После раскрытия стыка внешняя нагрузка полн ость ю передается на болт. Такое со-
стояние соединения опасно для п рочн ости болта и, как правило, недопустимо на практике с
точки зрения разгерметизации стыка. Поэтому усилие затяжки следует назначать таким, что-
бы при заданной внешней силе
F
стык оставался плотным, т. е. минимальное усилие затяж-
ки соединения определяется внешней нагрузкой и его конструкцией.
Величина
зависит от соотношения податливостей болта
б
и деталей со стыком
д
:
)(
бд
б
, (2)
Для коротких болтов и шпилек
dl
б
6
податливость определяется по формуле
бгр
бб
б
б
АЕ
l
.
, (3)
где
б
l
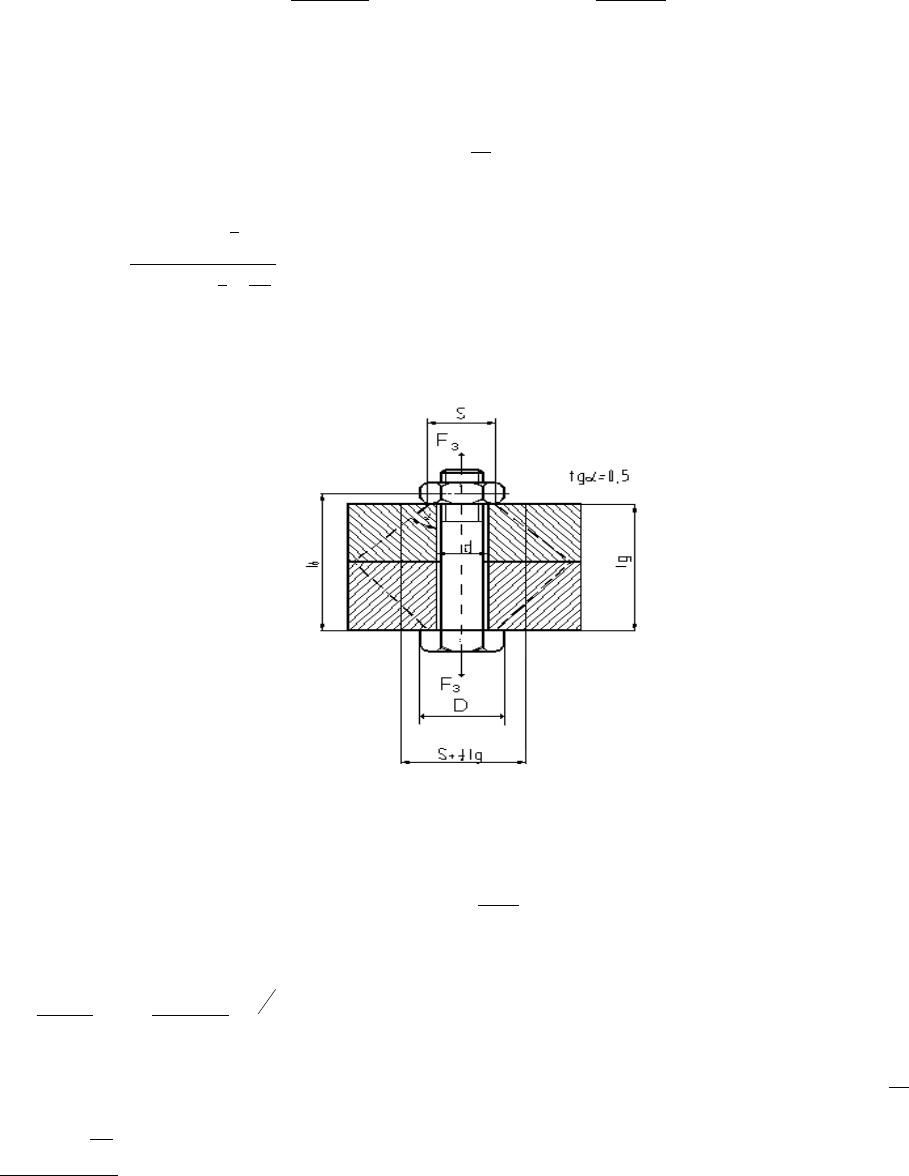
– расчетная длина болта (рис. 1);
б
А
– площадь поперечного сечения болта;
б
Е
– мо-
дуль упругости материала болта;
р
– податливость резьбы [1];
бг.
– податливость головки
болта [1].
Податливость соединяемых деталей может быть определена по формуле:
дд
д
д
АЕ
, (4)
где
д
– суммарная толщина соединяемых деталей;
д
Е
– модуль упругости материала дета-
лей;
д
А
– площадь условного цилиндра.
Площадь
д
А
является условной, предполагают, что усилия от головки болта и гайки
передаются деталям по конусам (рис.1), образующие которых наклонены к оси болта под уг-
лом = arctg 0.5, а диаметры меньших оснований конусов равны размеру
S
под ключ голов-
ки болта или гайки. Для упрощения расчетов эти деформируемые конусы заменяются ци-
линдрами, диаметры которых равны полусумме диаметров оснований конусов [1]. При сде-
ланном допущении
2
2
4
1
4
dlSA
дд
, где
S
– размер гайки под ключ;
d
– наружный
диаметр болта.
В работе [2] показано, что гибк ость отдельных элементов резьбового соединения с
учетом контактных деформаций может быть определена по формулам
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
73
k
АЕ
l
бгр
бб
б
б
.
;
k
АЕ
дд
д
д
, (5)
где
k
– контактная податливость резьбового соединения в нормальном направлении
Для определения величины
k
в условиях статик и с учетом упругопластических де-
формаций можно воспользоваться формулой
F
h
k
, (6)
где
F
– нормальное усилие;
h
– статическое упругопластическое сближение, определяемое
по формуле
1
11
1
max
ya
kHbA
FR
h
,где
a
A
– номинальная площадь контакта;
,b
– параметры
кривой опорной шероховатой поверхности;
H
– предельная твердость;
xam
R
– наибольшая
высота неровностей профиля;
y
k
– коэффициент, зависящий от
.
Рис.1. Схема контактирования торца гайки с сопрягаемой деталью
В условиях вибрац ионного воздействия контактную п одатливость можно рассчитать
по формуле
F
tx
k
, (7)
где
tx
динамическое сближение, определяемое по формуле
1
1
1
2
0max
1
2
2
1
h
vx
;
0
v
– начальная скорость нагружения, которая задается
одиночным ударным импульсом с последующим затуханием процесса;
m
a
;
max
1
R
kAHb
a
ya
;
m
– масса тела;
F
– нормальное усилие, являющееся в случае динамиче-
ского нагружения нормально поджатого контакта в каждый момент времени суммой нор-
мальной статической составляющей и динамической силы, изменяющейся во времени.
Предложенный метод расчета контактной жесткости резьбового соединения позволя-
ет учесть влияние физик о-механических свойств материалов деталей, их геометрических

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
74
размеров, параметров микрогеометрии сопрягаемых поверхностей, а также условий нагру-
жения.
Литература
1. Биргер И.А., Иосилевич Г. Б. Резьбовые соединения. М.: Машиностроение, 1973. –256 с.
2. Котенева Н.В. Динамическая контактная жесткость и прочность резьбовых соеди-
нений: Дисс. канд. техн. наук. – Барнаул: 1999. – 165 с.
РАЗРАБОТКА ВЫСОКОЭКОНОМИЧНОГО КОМПОЗИЦИОННОГО МАТЕРИАЛА
ДЛЯ МАЛОНАГРУЖЕННЫХ УЗЛОВ ТРЕНИЯ
Н.Б. Краснова
Южно-Российский Государственный технический университет
346428 Ростовская обл., г. Новочеркасск, ул. Просвещения, 132,
тел. (86352) 5-54-12. Моб.8-904-3476672
E-mail: Krasnova_NB@mail.ru
Для решения проблемы использования недорогих материалов с целью управления ан-
тифрикционными свойствами в узлах трения машин был проведен ряд исследований, основ-
ной целью которых являлась разработка композита на основе наиболее дешевого полимера, с
доступными и н едороги ми наполнителями и пластификаторами, который может быть ис-
пользован в малонагруженных узлах трения машин.
Основой антифрикционного композита является полипропилен, в качестве напол-
нителя были выбраны ценосферы Новочеркасской ГРЭС и порошок железа, а в качестве пла-
стификатора – стеариновая кислота. Эти ингредиенты являются легкодоступными и имеют
сравнительно низкую стоимость.
Предварительные исследования механических свойств показали незначительное
уменьшение прочности и ударной вязкости ценосферонаполненного полипропилена по срав-
нению с чистым полипропиленом. Наблюдалось также, что с введением в состав композита
порошка железа и ценосфер улучшились антифрикционные свойства: уменьшился коэффи-
циент трения и интенсивность износа. Результаты экспериментов также показали, что при
нанесении на дорожку трения стеариновой кислоты и графита снижается коэффициент тре-
ния до величин, соответствующих антифрикционным материалам, причем в значительно
большей степени у стеариновой кислоты.
Для изготовления экспериментальных образцов композита был и спользован метод
прямого горячего прессования, так как коэффициент трения полимерных образцов, изготов-
ленных этим методом ниже, чем коэффициент трения образцов аналогичного состава, изго-
товленных на термопластавтомате.
Для определения оптимального количественного состава антифрикционной полимер-
ной композиции использовался метод планирования эксперимента Бокса-Уилсона. На основе
экспериментальных данных было построено уравнение регрессии, в качестве параметра опти-
мизации принимался коэффициент трения. Из этого уравнения были получены зависимости
коэффициента трения композиционных материалов от содержания наполнителей и выбран о п-
тимальный состав композита: ценосферы – 10,9%; стеариновая кислота – 9 %; железо – 8 %;
полипропилен – 72,1 % по массе, названный ППСЦЖ. На материал данного состава с коэф-
фициентом трения f
тр
=0,08 при нагрузке 2 – 3 МПа был получен патент РФ.
Исследовалась микроструктура композита до опыта и после в области дорожки тре-
ния, что позволило сделать выводы о равномерном распределении наполнителя в полимер-
ной матрице и о том, что введение железного порошка не привело к различиям в структуре
материала. Кроме того, наблюдались изменения структуры композита по нормали к п оверх-

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
75
ности трения, особенно сильн о с приближением к поверх ности. Из микрофотографий также
видно, что в поверхностном слое трения при катастрофическом износе скапливаются цено-
сферы и порошок желез а, обладающие большей жесткостью, чем полипропилен, что приво-
дит к увеличению коэффициента трения и износа образцов.
С помощью термогравиметрического анализа была проведена оценка термостабиль-
ности образцов в процессе трения. В результате получены сведения о характере процессов,
происходящих между основным полимером и наполнителем при трении, и сделан вывод, что
полипропилен и стеариновая кислота образуют временные связи, причем более прочные у
композиционного материала, полученного при температуре 190
0
С, т.е. стеариновая кислота
пластифицирует п олипропилен.
Оказалось, что введение железного п орошка в антифрикционный композит уменьша-
ет температуру в зоне трения и температуру контртела, которая практически не меняется во
время работы, т. е. железный порошок увеличивает теплопроводность композита, что поло-
жительно влияет на работоспособность полученного материала.
Из определенных эксплуатационные и экономических характеристик разработанного
антифрикционного композита (ППСЦЖ), можно заключить, что он отвечает скоростным и
нагрузочным параметрам, параметрам трения а также экономически выгоден для примене-
ния в разли чн ых узлах т рения, в том числе для сухарей рычага копира, применяемых в круг-
лоткацких станках типа.
На заводе ОАО «Каменскволокно» (г. Каменск-Шахтинск, Ростовская обл.) были про-
ведены промышленные испытания, по результатам которых было дано заключение о воз-
можности применения экспериментального антифрикционного материала для сухарика ры-
чага ремизной стойки кр углоткацкого станка, а также возможности использования для дру-
гих деталей, работающих в сходных режимах трения.
Таким образом, создан новый дешевый антифрикционный композит, названный
ППСЦЖ, с оптимальным содержанием наполнителя, имеющий приемлемые физико-
механические характеристики и оптимальные характеристики трения и износа, рекомендо-
ванный к применению в узлах трения сельскохозяйственных машин и текстильной промыш-
ленности.
О ВОЗМОЖНОСТИ НАПРАВЛЕННОГО ВКЛЮЧЕНИЯ РАБОЧИХ ТЕЛ
В МЕХАНИЗМЕ СВОБОДНОГО ХОДА
С.А. Леонов, аспирант, В.Н. Филимонов, к.т.н., доцент
Владимирский государственный университет,
600000, г. Владимир, ул. Горького, 87, тел. (4922) 47 99 28
E-mail: anargo@ya.ru
Механизмы свободного хода широко используются в различных отраслях машино-
строения. Приводы стартеров, гидротрансформаторы, импульсные вариаторы машин раз-
личного назначения, пружинно-навивальные автоматы, приводы топок, подъемно-
транспортные машин ы, велосипеды, ручной инструмент – примеры областей их применения.
Широкое распространение механизмов свободного хода в машиностроении обусловлено их
специфическими свойствами. Они передают крутящий момент в силовой цепи в одном на-
правлении и рассоединяют силовую цепь в другом.
Известно много конструкций механизмов свободного хода [1]. Их разделяют на три
класса: фрикционные, нефрикционные и комбинированные. Фрикционные мех анизмы пере-
дают крутящий момент с помощью сил трения. Наиболее распространенным представителем
этого класса механизмов являются роликовые механизмы. Крутящий момент в них передает-
ся с помощью роликов, заклинивающихся межд у наружной и внутренней обоймами при по-

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
76
вороте их друг относительно друга в одном направлении и расклинивающихся в противопо-
ложном. Роликовые механизмы в России используют, например, в приводах стартеров авто-
мобильные компании ГАЗ и ВАЗ. Основной недостаток фрикционных схем заключается в
использовании сил трения. Согласно известному закону механики нормальная сила равна:
тр
F
N
f
.
Коэффициент трения f стали по стали при наличии смазки составляет несколько со-
тых, и нормальная сила, п о крайней мере, на порядок превышает силу трения. Таким обра-
зом, сопутствующие нормальные силы значительно превышают силы трения, непосредст-
венно участвующие в передаче крутящего мо мента. Это ведет к значительному увеличению
контактных напряжений между роликами и обоймами и к снижению долговечности фрикци-
онных механизмов свободного хода.
Указанный недостаток устраняется в нефрикционных мех анизмах , передающих кру-
тящий момент с помо щью нормальных сил. Классический представитель нефрикционных
механизмов – храповой механизм, содержащий храповик, обойму, в которой крепятся оси
рабочих тел (собачек) и сами рабочие тела. Передача крутящего момента происходит по-
средством упора собачек в зубья храповика, при котором используются нормальные силы.
Если в хр аповом мех анизме свободного хода используются жесткие собачки, то вследствие
погрешностей из готовления деталей механизма будет включаться и передавать крутящий
момент только одна собачка. Ук азанный недостаток устраняется введени ем упругих собачек
– изогнутых упругих пластин. Именно эта конструкция рассматривается в данной работе.
В механизме свободного хода с упругими пластинами имеет место сл учайный харак-
тер вклю чени я криволинейных пластин при заклинивании. Вполне вероятно включение не-
скольких пластин с одной сторон ы храповика, что будет означать неравномерную (односто-
роннюю) нагрузку на храповик и обойму, и соответственно на подшипники вала храповика и
обоймы. Возможно такое расположение криволинейных пластин, когда поворот храповика
относительно обоймы при заклинивании будет близок к углу, соответствующему одному ша-
гу храповика (расстоянию между дв умя соседними вершинами зубьев). Эт о приведет к уве-
личению ударной нагрузки в момент включения механизма.
Возможность направленного включения рабочих тел в храповом механизме с упруги-
ми пластинами достигается за счет того, что упругие криволинейные пластины разбиты на
два равных по к оличеству пластин пакета, смещенных один относительно другого. Меха-
низм содержит храповик 1, обойму 2, в которой крепятся оси упругих криволинейных пла-
стин 4,5, поджимаемых пружинами 3 к храповику (см. рис. 1).
Первый пакет включает
/2n
первых по порядку п ластин, расположенных справа от
осевой линии, второй –
/2n
следующих пластин (слева от осевой линии). В каждом из паке-
тов концы любых двух соседних криволинейных пластин 4 и 5 смещены один относительно
другого на величину
/2
S
S
n
, где S – шаг храповика, n – количество пластин.
Если, например, первая пластина 5 первого пакета находится во впадине своего зуба,
то вторая пластина 4 первого пакета смещена от впадины своего зуба на величину
/2
S
h
n
,
следующая пластина смещена н а величину 2h и т.д. Благодаря такому равномерному распре-
делению пластин в пакетах свободный ход при заклинивании сводится к минимуму и не пре-
вышает угла поворота х раповика, соответствующего
/hr
, где r – радиус храпови ка. Это
обеспечивает минимальные ударные нагрузки при заклинивании механизма.
В свою очередь, расположение пакетов друг относительно друга таково, что конец
первой пластины 6 второго пакета отстоит от впадины своего зуба на величину
1
h
/2
S
n

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
77
(рис. 1), в то время как конец первой пластины 5 первого пакета находится во впадине своего
зуба. Ан алоги чн ым оказывается смещение вторых пластин обоих пакетов друг относительно
друга и т.д.
Рис. 1. Храповой механизм свободного хода
Процесс заклинивания механизма при заданном расположении пластин в пакетах и па-
кетов друг относительно друга будет происходить следующим образом. Допустим, первой
включилась первая пластина 5 первого пакета. При дальнейшем повороте обоймы 2 против
часосвой стрелки, следующей включится первая пластина второго пакета, находящаяся с про-
тивоположной стороны храповика, так как ее конец расположен ближе к впадине своего зуба
(
1
h
h
), чем у оставшихся пластин. Затем включается вторая пластина первого пакета и т.д.
Тем самым резко снижается односторонняя нагрузка на храповик, обойму и подшипники.
Таким образом, предлагаемая конструкция механизма свободного хода позволяет до-
биться направленного характера включения упругих пластин.
Литература
1. Леонов А.И. Микрохраповые механизмы свободного хода. – М. Машиностроение,
1982. – 220 с.
МОДЕЛЬ ДЛЯ ОЦЕНКИ ДЛИНЫ КРАЕВОГО ЭФФЕКТА
В СЛОИСТОЙ СТРУКТУРЕ
А.Н. Литвинов, к.т.н., проф.
Пензенский государственный университет,
440026, г. Пенза, ул. Красная, 40, тел.: (841-2)-56-35-39
E-mail: lma-79@mail.ru
Задачи о действии внешних нагрузок на упругое полупространство имеют большое
практическое значение и относятся к числу фундаментальных, позволяющих на их основе
решать более сложные задачи. Особое значение имеет задача о действии сосредоточенной
силы на слоистое полупространство, решение которой позволяет исследовать напряженно-
деформированное состояние (НДС), определить наиболее нагруженные зоны конструкции и
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
78
оценить длины краевых эффектов, что позволяет, используя метод суперпозиций, решать за-
дачи о действии на гетерогенную конструкцию системы вн ешних сил. Это позволяет решать
также, контактные задачи для контактирующих тел различной конфигурации и исследовать
НДС в зоне контакта слоистых структур.
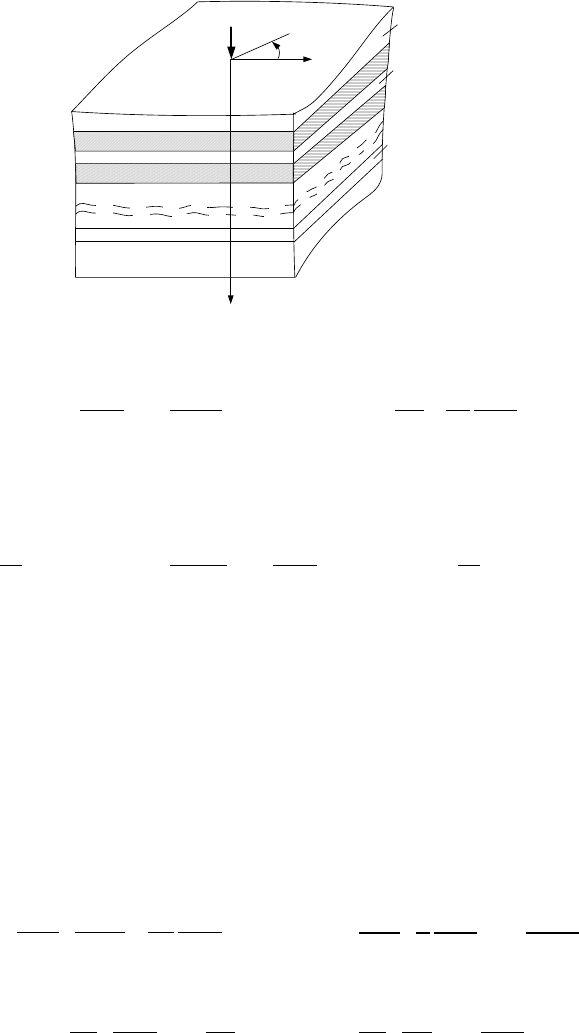
Рассмотрим общую модель, когда сосредоточенная сила
P
действует на слоистое по-
лупространство, состоящее из чередующихся жестких и трансверсально мягких слоев, кото-
рые на рисунке 1 заштрихованы. Слой, на который действует нагрузка, считаем нулевым
(k=0). Структура имеет любое количество слоев n. Задача рассматривается в цилиндрической
системе координат
rz
. В силу осевой симметрии компоненты тензоров напряжений и де-
формаций, а также вертикальные
k
W
и радиальные
k
U
перемещения жестких слоев зависят
только от радиальной
r
и осевой z координат.
z
k
k=1
k=0
0
P
θ
r
Рис. 1. Элемент конструкции
Радиальная и окружная деформации в жестких слоях определяются выражениями:
2
2
k
kk
rk
dU d W
z
dr dr
;
k
k k k
U z dW
r r dr
, (1)
где
k
z
– нормальная координата, отсчитываемая от срединной поверхности k-го жесткого
слоя до произвольной точки этого слоя, в которой вычисляется деформация.
Компоненты тензора деформаций мягких слоев определяются соотношениями [1]:
[]
1
1
1
k
kk
rz k k k k
k
dW dW
U U ñ ñ
s dr dr
;
[]
1
1
k
z k k
k
WW
s
, (2)
Здесь
[]k
rz
,
[]k
z
– деформ ация сдвига и трансверсальная деформация k-го мягкого слоя:
0,5
k k k
c h s
;
1
0,5
k k k
c h s
– расстояния от срединной поверхности k-го мягкого слоя
до k-го и (k+1)-го жестких слоев;
k
h
и
k
s
– толщины жесткого и мягкого слоев.
Жесткие слои гетерогенной структуры работают на растяжение (сжатие) и изгиб по-
этому радиальные
k
r
и окружные
k
напряжения в них определяют как
, ,0
k k k
rrиr
;
, ,0
k k k
и
, (3)
где
,
k
r и
и
,
k
è
– ради альные и окружные изгибные н апряжения вычислются в соответствии с
обобщенным законом Гука:
2
,
22
6
k
k k k k
r и
k
D W dW
h r r dr
;
2
,
22
6
1
k
k k k
ик
k
D dW d W
h r dr dr
. (4)
Мембранные напряжения в жестких слоях определяются выражениями:
,0
k
k k k
rk
k
A dU U
h dr r
;
,0
k
k k k
k
k
A U dU
h r dr
. (5)
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
79
Касательные
,
k
rz
и т рансверсальные
k
z
напряжения в мягких слоях определяются
выражениями
1
,1
k
kk
r z k k k k k
rr
dW dW
B U U сс
dd
;
1
k
z k k k
c W W
. (6)
Здесь:
3
2
12 1-
kk
k
k
Eh
D
;
1-
kk
k
k
Eh
A
;
k
k
k
G
B
s
;
k
z
k
k
E
C
s
;
,
kk
E
– модуль упругости и
коэффициент Пуассона для материала k-го жесткого слоя;
k
G
и
k
z
E
модуль сдвига и транс-
версальный модуль для материала k-го мягкого слоя.
Уравнения равновесия гетерогенной системы получим, используя принцип Лагранжа.
Рассмотрим частный случай, когда гетерогенная структура является регулярной, т.е. выпол-
няются условия:
k
EE
;
k
hh
;
k
GG
;
k
ss
;
k
;
ì
k
;
k
AA
;
k
DD
;
k
BB
;
k
CC
;
k
zz
EE
;
0,5
о k k
c с с h s
.
В эт ом случае математическая модель, описывающая НДС слоистой структуры, явля-
ется системой дифференциально-разностных уравнений равновесия в перемещениях:
– для верхнего (нагруженного) слоя (при k=0)
00
1
0 1 0 0
2
0 1 0 0 1 0 1 0
0;
;
2
î
U dW
dW
A U B U U C
r dr dr
P
D W C W W BC U U ñ W W r
r
(7)
– для остальных слоев (k = 1, 2, …):
1 -1
1 -1 0
22
1 -1
1 -1 1 -1
2 0;
2
2 0.
k k k
k k k k
k k k k
о k k о k k k
U dW dW
A U B U U U C
r d dr
D W C W W W
Bc U U с W W W
(8)
Здесь
и
– оператор Лапласа и оператор градиента;
r
– дельта функция в ци-
линдрической системе координат.
Решение уравнений (7), (8) должно удовлетворять условиям ограниченности дефор-
маций и напряжений при
k
, а перемещения
k
U
и
k
W
должны стремиться к нулю при
r
в соответствии с решением задачи Буссинеска для упругого полупространства [2].
Решение системы уравнений (7) и щется методом интегральных преобразований Фурье-
Бесселя, а уравнения (8) после применения к ним преобразования Фурье-Бесселя играют
роль граничных условий.
Окончательно выражения для перемещений в жестких слоях имеют вид:
2
2
2
11
1
0
2
2
1 j 0
1
0
1 exp ;
2
1 exp .
2
j
k j j j
j
j
k j j
j
Pc t
U r a sh k J rt dt
Dg
Pc t
W r a f k J rt dt
Dg
(9)
Напряжения в жестких слоях определяются выражениями:
23
2
()
, 1 1
2
1
0
3
( 1) exp( ) ( )
kj
r и o j j j
j
ct
a f k z rt dt
hg
;
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
80
23
2
()
, 1 2
2
1
0
3
( 1) exp( ) ( )
kj
и o j j j
j
ct
a f k z rt dt
hg
; (10)
3
2
()
, 2 1 1
1
0
2
( 1) ( ) exp( ) ( )
kj
r o o j j j
j
ct
a sh k z rt dt
hg
;
3
2
()
, 2 1 2
1
0
2
( ) exp( ) ( )
k
o o j j j
j
ct
a sh k z rt dt
hg
; при
0, 1, 2...k
Напряжения в транверсально мягких слоях определяются выражениями (6) с учетом
(9). Здесь введены следующие обозначения:
2
о
P
c
– эталонное напряжение;
0
0,5( )c c h S
;
1 exp( )
jj
a
;
31
aa
;
44
12
[ (1 exp( ))] [1 exp( )]
j j j j
b f t t
;
1 2 2 1
g ab a b
;
2
2 [1 ( )]
jj
f t ch
п ри
1,2j
;
1,2....;k
22
(1 )Gc
Ehs
;
42
1
3
12 (1 )
z
Ec
Eh s
;
42
2
3
3 (1 )Gc
Eh s
;
t cp
– безразмерный параметр преобразования Фу-
рье-Бесселя;
r
r
c
– безразмерный радиус;
0
()J rt
,
1
()J rt
– функции Бесселя нулевого и пер-
вого порядка соответственно от действительного аргумента;
p
– параметр преобразования
Фурье-Бесселя;
1 0 1
1
( ) ( ) ( )z rt J rt J rt
rt
;
2 0 1
1
( ) ( ) ( )z rt J rt J rt
rt
.
Характеристические показатели
1
и
2
являются решениями уравнения:
2 2 6
2 4 4
22
1 1 1
2 1 1 0
4 4 2 2 4
t t t
ch t ch t
(11)
Решения, соответствующие характеристическим показателям с положительной дейст-
вительной частью, исключаются из рассмотрения в соответствии с условиями ограниченно-
сти напряжений и перемещений при
z
, что соответствует
k
.
В качестве примера рассмотрим рег улярную гетерогенн ую систему со следующими
характеристиками:
0,01GE
;
0,25
ì
;
hs
;
2,5
ì
EG
. Результаты вычислений без-
размерных напряжений в жестких
()k
r
;
()k
и в трансверсально-мягких слоях
[]k
z
и
[]k
rz
при-
ведены на рисунке 2. Цифры у кривых указывают номер слоя, для которого выполнен расчет
безразмерных напряжений:
()
()
0
k
k
r
r
;
()
()
0
k
k
;
[]
[]
0
k
k
z
z
;
[]
[]
0
k
k
rz
rz
.
Представленные чи сленные результаты показывают распределение соответствующих
напряжений по радиусу
/0,5( ) 2 /( )r r h s r h s
и номеру слоя
k
. Напряжения
()k
r
и
()k
в нулевом слое имеют особенность в точке приложения силы, что является следствием
идеализации расчетной схемы относительно представления внешнего воздействия в виде со-
средоточенной силы. В реальных конструкциях внешняя нагрузка распределена по конт акт-
ной площадке, имеющей малую площадь
.F
Для сохранения осевой симметрии задачи мож-
но считать, что сила
P
равномерно распределена по круговой площадке, имеющей радиус
/,RF
что в принятых обозначениях соответствует безразмерном у радиусу
2 / /( ).R F h s
При
rR
значения этих напряжений практически совпадают с расчет-
ными напряжениями, которые убывают при удалении от точки приложения силы.
