Современные проблемы машиностроения
Подождите немного. Документ загружается.


V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
91
2
1
, , ( ) [1, , ]
k
s
A S I k
k
A
m m m x y y dA
,
где
k
A
– площадь поперечного сечения
k
-го слоя.
В системе уравнений (3) учтено слагаемое
Nv
, отражающее влиян ие продольных сил
в гибком стержне на поп еречные перемещения, в общем случае движения приводящее к не-
обходимости применения численных процедур нелинейного расчета. В дальнейшем при от-
сутствии волновых эффектов вдоль оси стержня будет выполняться линеаризация путем за-
мены полной продольной силы
( , )N x t
ее статической составляющей
()
st
Nx
.
Принимая для напряжения в
k
-м слое закон
()
( , , ) ( , , ) ( , , )
k
x k x k k x
x y t E x y t E x y t
,
1,...,ks
,
получим физическую систему для слоистого стержня
00
00
,
.
A S A S
S I S I
D D B B N
D D B B M
(4)
с обобщенными жесткостными и вязкостными характеристиками
2
1
, , ( ) [1, , ]
k
s
A S I k
k
A
D D D x E y y dA
,
2
1
, , ( ) [1, , ]
k
s
A S I k k
k
A
B B B x E y y dA
.
Объединив (3), (4) с учетом (1), имеем разрешающую систему двух дифференциаль-
ных равенств относительно искомых перемещений
0
( , )u x t
,
0
( , )v x t
. Выполнив переобозна-
чение
0
uu
,
0
vv
, запишем ее в виде
()
( , ),
( ) ( )
( ) ( ) ( , ) ( , ).
A S A S xx x xx x
A S x
I S I S st yy yy x
x A I S z y
D u D v B u B v u v c u c v
m u m v q x t
D v D u B v B u N v v c v u v
c u c v m v m v m u m x t q x t
(5)
Искомые функции должны удовлетворять начальным
( ,0) ( ,0) 0u x v x
,
( ,0) ( ,0) 0u x v x
(6)
и граничным условиям. Последние при наличии жестких связей на концах стержня записы-
ваются как
(0, ) (0, ) (0, ) 0u t v t v t
,
( , ) ( , ) ( , ) 0u l t v l t v l t
, (7)
а для деформируемых – в виде
00
00
00
(0, ) (0, ) (0, ),
(0, ) (0, ) (0, ),
(0, ) (0, ) (0, )
xx
yy
N t D u t C u t
Q t D v t C v t
M t D v t C v t
( , ) ( , ) ( , ),
( , ) ( , ) ( , ),
( , ) ( , ) ( , )
xl xl
yl yl
ll
N l t D u l t C u l t
Q l t D v l t C v l t
M l t D v l t C v l t
(8)
где
x
D
,
y
D
,
D
– жесткости, а
x
C
,
y
C
,
C
– вязкости продольной, поп еречной и угловой
концевых связей. На основе выражений (7), (8) могут быть записаны граничные условия для
других случаев закрепления стержня.
2. Решение системы уравнений (5) представим в виде разложений
1
( , ) ( ) ( )
u
j
uj uj
j
u x t T t x
,
1
( , ) ( ) ( )
v
j
vj vj
j
v x t T t x
(9)
по заданным координатным базисам
()
uj
x
,
()
vj
x
, удовлетворяющим граничным условиям
(8) с амплитудами, зависящими от времени:
()
uj
Tt
,
1,...,
u
jj
,
()
vj
Tt
,
1,...,
v
jj
. (10)

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
92
Подставив перемещения (9) в (5), полученную невязку первого уравнения продольных
колебаний ортогонализируем в интервале
[0, ]xl
к функциям базиса
uj
, а второго уравне-
ния – поперечных колебаний – к
vj
1
0
( , , ) ( ) 0
l
uj
L u v x x dx
, (
1,...,
u
jj
),
2
0
( , , ) ( ) 0
l
vj
L u v x x dx
, (
1,...,
v
jj
).
В результате для функций (10) получим систему
uv
jj
уравнений. Представим их в
форме двух матричных равенств
22
( ) ( ) ( )
00
()
uv
dd
t
dt dt
A T B T G
,
1,2
, (11)
относительно векторных функций
ò
1
( ) [ ( )... ( )]
u
u u uj
t T t T tT
,
ò
1
( ) [ ( )... ( )]
v
v v vj
t T t T tT
.
Компоненты 12-и матриц
()
A
,
()
B
и двух векторов
()
G
определяются выраже-
ниями
(1,0)
0
[( ) ]
l
ij ui A uj xx uj
a D dx
,
(1,1)
0
[( ) ]
l
ij ui A uj xx uj
a B c dx
, (
, 1,...,
u
i j j
),
(1,2)
0
l
ij ui A uj
a m dx
,
(1)
0
( ) ( , )
l
i ui x
g t q x t dx
, (
, 1,...,
u
i j j
),
(1,0)
0
[( ) ]
l
ij ui S vj x vj
b D dx
,
(1,1)
0
[( ) ]
l
ij ui S vj x vj
b B c dx
, (
1,...,
u
ij
,
1,...,
v
jj
),
(1,2)
0
l
ij ui S vj
b m dx
, (
1,...,
u
ij
,
1,...,
v
jj
),
(2,0)
0
[( ) ( ) ]
l
ij vi x uj S uj
a D dx
,
(2,1)
0
[( ) ( ) ]
l
ij vi x uj S uj
a c B dx
, (
1,.,
v
ij
,
1,.,
u
jj
),
(2,2)
0
()
l
ij vi S uj
a m dx
,
(2)
0
( ) [ ( , ) ( , )]
l
i vi y z
g t q x t m x t dx
, (
1,...,
v
ij
,
1,...,
u
jj
),
(2,0)
0
[( ) ( ) ]
l
ij vi I vj st vj yy vj vj
b D N dx
, (
, 1,...,
v
i j j
),
(2,1)
0
[( ) ( ) ]
l
ij vi I vj yy vj vj
b B c c dx
,
(2,2)
0
[ ( ) ]
l
ij vi A vj I vj
b m m dx
, (
, 1,...,
v
i j j
).
Представим нагрузки в виде произведения
( , ) ( ) ( )q x t q x f t
,
[ , , ]
x y z
q q q m
, (12)
координатного профиля нагрузки
()qx
и безразмерной функции времени
()ft
, записанной в
форме ряда Фурье
0
0
1
( ) cos sin
2
k
qk q qk q
k
a
f t a k t b k t
, (13)
0
2
( )cos
qk q
a q t k t dt
,
0
2
( )sin
qk q
b q t k t dt
,

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
93
где
q
,
2/
q
– частота и период заданной динамической нагр узки
()qt
. Каждая из на-
грузок
x
q
,
y
q
,
z
m
(12) может быть введена со своей специфической функцией (13).
Учитывая (12), (13) для векторов
()
G
(
1,2
), в правой части (11) получим
0
( ) ( )
0
( ) cos sin
k
qk q qk q
k
t a k t b k t
GG
, (14)
(1)
0
()
l
i ui x
g q x dx
, (
1,...,
u
ij
),
(2)
0
[ ( ) ( )]
l
i vi y z
g q x m x dx
, (
1,...,
v
ij
).
3. В соответствии с (14) частное решение системы уравнений (11) зададим в форме
0
( ) ( )
0
( ) cos sin
k
uu
u q q
kk
k
t k t k t
T C S
,
0
( ) ( )
0
( ) cos sin
k
vv
v q q
kk
k
t k t k t
T C S
(15)
Подстановка (14), (15) в (11) для
k
-й гармоники дает систему четырех уравнений
( 0) 2 2 ( 2) ( ) ( 1) ( )
( 0) 2 2 ( 2) ( ) ( 1) ( ) ( )
( 1) ( ) ( 0) 2 2 ( 2) ( )
( 1) ( ) ( 0) 2 2 ( 2) ( ) ( )
[]
[ ] ,
[]
[ ] .
i i u i u
qq
kk
i i v i v i
q q qk
kk
i u i i u
qq
kk
i v i i v i
q q qk
kk
kk
k k a
kk
k k b
A A C A S
B B C B S G
A C A A S
B C B B S G
,
1,2i
относительно векторов
()u
k
C
,
()u
k
S
,
()v
k
C
,
()v
k
S
, определяющих векторные функции (15).
4. Решение однородной системы, соответствующей (11), будем искать в виде
( ) exp( )
uu
ttTK
,
( ) exp( )
vv
ttTK
, (16)
где
u
K
и
v
K
– числовые векторы, содержащие по
u
j
и
v
j
элементов соответственно.
Подстановка (16) в (11) дает систему уравнений для векторов
u
K
и
v
K
11
22
0
( ) ( )
0
( ) ( )
u
v
K
AB
K
AB
(17)
( 0) ( 1) 2 ( 2)i i i
i
A A A A
,
( 0) ( 1) 2 ( 2)i i i
i
B B B B
,
1,2i
.
с характеристическим уравнением степени
2r
(
uv
r j j
) относительно
11
22
( ) ( )
det 0
( ) ( )
AB
AB
. (18)
Выделив среди
12
22r k k
корней уравнения (18)
1
k
действительн ых различных и
2
k
пары комплексно-сопряженных корней, общее решение однородной системы (11) запи-
шем в виде
1 1 2
1
1
11
()
exp( ) exp( )[ (Re cos Im sin )
()
(Re sin Im cos )],
k k k
u
ui ui ui
i i i i i i
v
i i k
vi vi vi
ui ui
i k i i
vi vi
t
c t t c t t
t
c t t
T
K K K
T
K K K
KK
KK
(19)
с собственными векторами
()
ui i
K
,
()
vi i
K
, при
i
удовлетворяющими (17). Основная
частота собственных колебаний определяется значением
min
корней второй группы.

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
94
В частном случае стержня с симметричной относительно отсчетной поверхности
0y
слоистой структурой имеем
0
S S S
D B m
. Если дополнительно для характеристик
основания положить
0
xx
c
, то получим матрицы
(1,0) (1,1) (1,2)
0 B B B
,
(2,0) (2,1) (2,2)
0 A A A
,
что приводит к распадению системы (11) на два независимых матричных равенства
2
(1, )
0
0
u
d
dt
AT
,
2
(2, )
0
0
v
d
dt
BT
,
описывающих свободные продольные и поперечные колебания. Раздельные решения их
()
u
tT
,
()
v
tT
п олучаются из (19), каждое со своим частотным спектром
1,
,...,
u
u u j
и
1,
,...,
v
v v j
соответственно.
5. Суммируя решения, полученные на основе разложений (9), а именно: частное, со-
стоящее из (9), (15) и общее однородной системы (9), (16), (19), получаем общее решение не-
однородной системы (11). Удовлетворив его начальным условиям (6) имеем функции пере-
мещений в начально-краевой задаче динамики продольно-поперечных колебаний слоисто-
неоднородного стержня.
6. Рассмотренная постановка, основанная на уравнениях движения в форме (3), позво-
ляет для выявления критических состояний стержня применить динамический критерий ус-
тойчивости, а именно – приравнять нулю минимальный корень характеристического уравне-
ния (18)
min cr
( ) 0N
. Тогда уравнение (18) примет вид
(10) (10)
(20) (20)
det 0
()
cr
N
AB
AB
. (20)
Раскрывая определитель (20) клеточной матрицы с квадратными блоками
(10)
A
,
(20)
B
,
в случае
(10)
det[ ] 0A
получим
1
(20) (20) (10) (10)
det ( ) 0
cr
N
B A A B
. (21)
Если в матрице
(20)
B
продольную силу представить через координатную функцию и
параметр, как
(0)
( ) ( )N x N n x
, то критическое значение последнего на основе (21) может
быть найдено из выражения
1
(20) (0) (20) (10) (10)
cr
0
det 0
N
N
B B A A B
.
(2,0)
0,
0
[( ) ( ) ]
l
vi I vj yy vj vj
ij
b D dx
,
,
0
()
l
N ij vi vj
b n x dx
, (
, 1,...,
v
i j j
).
В случае симметричной слоистой структуры при использовании базиса
v
, состояще-
го из одной функции, критический параметр продольной силы определяется формулой
1 1 1 1
(0)
0
cr
11
0
[( ) ( ) ]
()
l
v I v yy v v
l
vv
D dx
N
n x dx
. (22)

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
95
Если дополнительно положить постоянство поперечного сечения стержня и отсутст-
вие взаимодействия с основанием, то, задав базисную функцию
1
10
sin( )
v
v xl
для шар-
нирно закрепленного стержня при
( ) 1nx
, из (22) получим
2
(0)
2
I
cr
D
N
l
,
что обобщает формулу Эйлера на случай слоисто-неоднородных стержней.
ПРЕДОХРАНИТЕЛЬНЫЕ ЭНЕРГОСБЕРЕГАЮЩИЕ ГИДРОДИНАМИЧЕСКИЕ
И МЕХАНИЧЕСКИЕМУФТЫ КАК СРЕДСТВО ПОВЫШЕНИЯ НАДЕЖНОСТИ
И ДОЛГОВЕЧНОСТИ МАШИН
А.В. Мурин, к.т.н., доц., В.А. Осипов, к.т.н., доц.
Томский политехнический университет,
634050, г. Томск, пр. Ленина, 30, тел. (3882)-564-655
Уменьшение динамических нагрузок в машинах, как известно, увеличивает срок их
службы и является актуальной задачей и в настоящее время [1]. Экономические проблемы
нашего времени требуют использования энергосберегающих устройств. В достаточно пол-
ной мере таким требованиям отвечают приводы машин, снабженные блокируемыми предо-
хранительными гидродинамическими или инерционными механическими муфтами. Муфты
первого типа используют при положительных температ урах окружающей среды; вторые мо-
гут быть применены и при достаточно низких отрицательных.
Основные цели применения предохранительных муфт:
Плавное ускорение систем с большими массами;
Возможность применения недорогих асинхронных электродвигателей с коротко-
замкнутым ротором;
Разгруженный пуск и разгон электродвигателя;
Ограничение крутящего момента при пуске;
Эффективное демпфирование ударных нагрузок и колебаний;
Защита от перегрузки привода и машины;
Выравнивание нагрузки на элементы привода в многодвигательных машинах (с по-
мощью неблокируемых предохранительных гидромуфт).
Однако гидродинамическим муфтам, наряд у с достоинствами, обеспечившим им дос-
таточно широкое применение в различных машинах, свойственен недостаток в виде замет-
ных потерь энергии на установившемся режиме работы (вследствие скольжения), вызываю-
щий к т ому же необходимость охлаждения рабочей жидкости и уменьшающей продолжи-
тельность ее использования; скольжение уменьшает также долговечность подшипников и
уплотнений муфты.
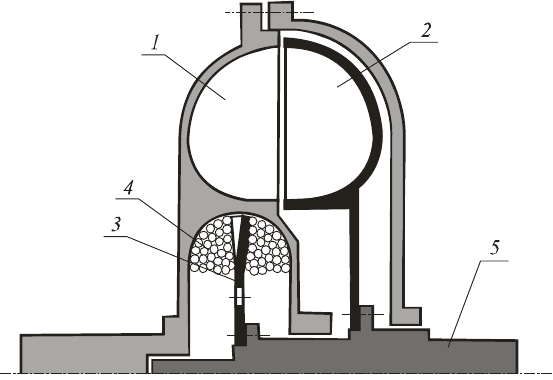
На кафедре теоретической и прикладной механики ТПУ разработаны конструкции
гидродинамической предохранительной блокируемой муфты (рис. 1) [2] и предохранитель-
ной инерционной муфты (ПИМ) (рис. 2) [5], лишенных отмеченных выше недостатков. Кро-
ме того ПИМ может работать и при низких (до -35 и ниже) температурах, без изменения ее
характеристик, так как ее рабочий заполнитель не содержит рабочей жидкости. Для обеспе-
чения гидромуфте защитных свойств на всех режимах , ее блокирующий механизм был вы-
полнен в виде центробежной муфты, состоящей из гофрированного диска 3, помещенного в
тороидальную камеру с гладкой поверхностью, заполненную сыпучим рабочим телом 4.
При разгоне насосного колеса 1 (рис. 1) и особенно после достижения им частоты
вращения близкой к номинальной, под действием в основном только гидравлического мо-
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
96
мента, передаваемого турбинном у колесу 2, последнее также начинает вращаться (после то-
го, как приложенный к нему момент станет превышать момент сил сопротивления). По мере
увеличения частоты вращения турбинного колеса, жестко соединенный с ним гофрирован-
ный диск 3 начинает постепенно сообщать (за счет сил трения и воздействия гофров, стенок
его отверстий) окружную скорость сыпучему материалу, что при водит к плавному увеличе-
нию центробежной силы, действующей на его частицы и прижимающей их к стенкам полос-
ти блокирующего механизма и гофрированному диску 3, и, в итоге к плавному возрастанию
момента, п ередаваемого блоки рующим устройством. При скорости турбинного колеса 2
близкой к номинальной, момент, передаваемый в процессе разгона блокирующим устройст-
вом, становится равным расчетному моменту и происходит блокирование гидромуфты. С
этого мгновения момент от ведущего звена м уфты 1 к его ведомому звену 5 передается толь-
ко за счет сил трения между гл адкими стенками к амеры и сыпучим материалом 4 с зажатым
в нем гофрированным диском 3, и муфта работает без скольжения.
При недоп устимых перегрузках происходит проскальзывание сыпучего материала 4
совместно с зажатым в нем гофрированным диском 3 отн осительно стенок полости, частота
вращения гофрированного ди ска 3, а вместе с ним и окружная скорость сыпучего материала
4, уменьшается, что, ес тественно, уменьшает центробежные силы, действующие на частицы
сыпучего материала и приводит к существенному уменьшению момента, передаваемого бло-
кирующим устройством. При этом, особенно при повышенных скольжениях, от насосного
колеса муфты на турбинное передается в основном только гидравлический момент.
Рис. 1. Предохранительная блокируемая гидромуфта: 1 – насосное колесо; 2 – турбинное колесо;
3 – гофрированный диск; 4 – металлические шарики; 5 – ведомый вал
При резком стопорении турбинного колеса дополнительная динамическая нагрузка от
массы сыпучего материала практически не передается на гофрированный диск 3, вследствие
возможности проскальзывания этого материала относительно названного диска и вследствие
проскальзывания частичек материала относительно др уг друга (кривые а на рис 4.
Исследования статических характеристик разработанной авторами [2-5], рис. 3,а пре-
дохранительной блокируемой гидромуфты (ПБГМ) подтвердило правильность принятых
решений, заложенных в ее конструкцию, позволило установить рациональную конструкцию
элементов блокирующего механизма (БМ). Это показали и экспериментальные исследования
ее свойств на переходных режимах работы.
Для исследования динамических характеристик была использована ПБГМ с вариан-
том БМ (рис.1): одноторовый (однодисковый) с ведущей камерой и гофрированным диском;
диски имели по 8 отверстий диаметром 7 мм и 8 гофров, высота которых не превышала диа-
метр шариков сыпучего материала.
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
97
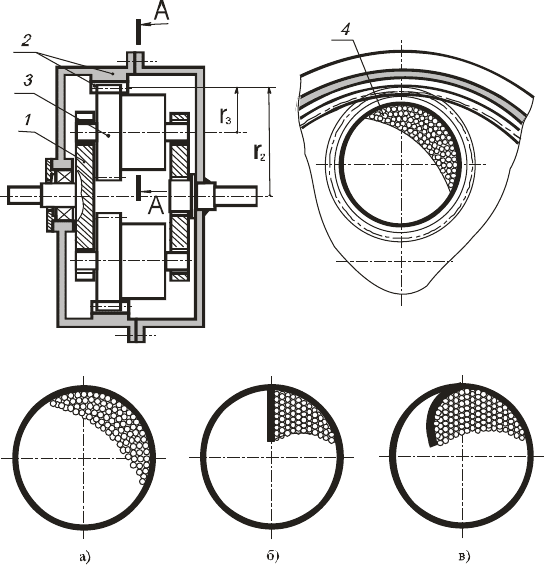
Рис. 2. Предохранительная инерционная муфта (ПИМ):
а) ПИМ с гладкими цилиндрическими барабанами;
б) ПИМ с цилиндрическими барабанами с радиальной перегородкой;
в) ПИМ с цилиндричес кими барабанами с криволинейной перегородкой
1 – водило; 2 – зубчатый венец (ведомое звено); 3 – барабаны-сателлиты; 4 –сыпучий дисбаланс
На рис. 4 представлены динамические характеристики при пуске (1) и торможении (2)
предохранительной блокируемой гидромуфты (кривые а)и и нерционных муфт с вариантами
барабанов-сателлитов (кривые б, в, г).
На основании проведенных исследований установлено, что ПБГМ обладает всеми
свойствами защитных гидромуфт, работает на установившемся режиме без скольжения, что
является ее преимуществом перед последней, а момент, передаваемый ею в стоповом режи-
ме превышает аналогичную величину момента гидромуфты не более чем на 4-5%.
Для ПИМ (рис. 2) установлено, что они обладают плавным пуском (рис.4, б, в, г), пре-
дохранительными свойствами в период экстренного торможения и кроме того демпфирую-
щими свойствами на установившемся режиме работы.
Конструкция водила 1 и набор сменных сателлитов-барабанов 3 позволял менять ве-
личину с = r
2
/r
3
в п ределах 2,074-2,24 (Здесь r
2
и r
3
делительные окружности колес 2 и 3). Ве-
домое колесо в виде венца выполнено заодно с корпусом муфты 2.
Получение внешних статических характеристик осуществлялось медленным заторма-
живанием. Динамические характеристики при пуске были получены при пуске привода под
предварительно установленной на тормозной электрогенератор нагрузкой , равной 75 Нм.
Исследование вли яния отношения с на величину М
пред.
при различных наполнениях
барабанов сыпучим дисбалансом показало, что величина предельн ого момента, передаваемо-
го ПИМ, прямо пропорционально величине этого соотношения (с). Так, например, увеличе-
ние с с 2,074 до 2,24 при заполнении барабана массой дисбаланса равной 0,5 кг увеличило
момент с 126 Нм до 132 Нм.
Анализ результатов исследований внешних статических характеристик показал, что
ПИМ в установившемся режиме работает без скольжения (n
1
=n
2
) (рис. 4-1, б, в, г).
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
98
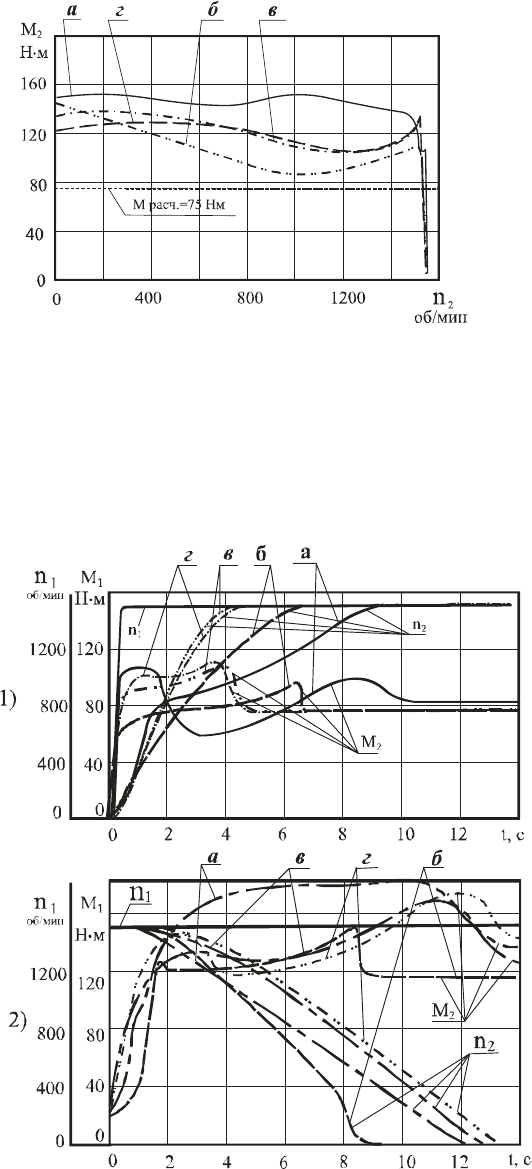
Рис. 3. Внешние статические характеристики:
а) блокируемой гидромуфты (рис. 1.)
при заполнении 0,9 и БМ 2,2 кг чугунной
дроби диаметром 2-4 мм;
б) ПИМ с цилиндрическими барабанами
заполнение чугунной дробью по 250 грамм
в каждый барабан; в) ПИМ с цилиндрически-
ми барабанами и радиальной перегородкой
заполнение чугунной дробью по 200 грамм в
каждый барабан; г) ПИМ с цилиндрическими
барабанами и криволинейной перегородкой
заполнение чугунной дробью
по 200 грамм в каждый барабан
При работе муфты со скольжением на участке n
2
примерно до 800 об/мин (рис. 3, б, в, г)
наблюдается уменьш ение передаваемого момента (про вал характеристики на в еличину
5-15%, после чего наблюдается увеличение момента. Величина ст опового момента (при
n
2
=0), к ак правило, превышает предельный момент муфты соответствующей «рабочему уча-
стку» ее характеристики на 5-13%.
Увеличение (до 15%) предельного момента, передаваемого ПИМ возможно введением
радиальных перегородок (прямых и криволинейных) (рис. 3, б, в, г).
Рис. 4. Динамические характеристики
(1-при пуске; 2- при торможении);
кривые: а) блокируемой гидромуфты
(рис. 1.) при заполнении 0,9 и БМ 2,2 кг
чугунной дроби диаметром 2-4 мм;
б) ПИМ с цилиндрическими барабанами
заполнение чугунной дробью
по 250 грамм в каждый барабан;
в) ПИМ с цилиндрическими барабанами
и радиальной перегородкой
заполнение чугунной дробью по 200
грамм в каждый барабан;
г) ПИМ с цилиндрическими барабанами
и криволинейной перегородкой
заполнение чугунной дробью
по 200 грамм в каждый барабан
Анализ внешних динамических характеристик ПИМ (рис.4-1,2 кривые б, в, г) показал,
что муфта облегчает пуск двигателя (кривая n
1
на рис. 4-1). Время разгона выходного вала
муфты n
2
составляет от 4 до 7 и более секунд, что позволяет плавно разогнать ведомую часть
привода. Пусковой момент при этом не превышает величину расчетн ого момента более, чем
на 60-70%, а отношение максимального динамического момента к расчетному моменту (рис. 4-2) не

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
99
превышает 2-2,26. То есть, ПИМ по своим характеристикам аналогична гидромуфт ам при
несколько больших осевых размерах и примерно одинаковых радиальных размерах.
Исследованные предохранительные муфты могут являются объектом исследования
при организации НИРС п ри изучении курса механики и равнозначной заменой редукторам
при выполнении курсового проекта.
Литература
1. А.В. Крутик (Машиностроитель, №6/2001)
2. Мурин А.В., Осипов В.А. Гидродинамическая предохранительная блокируемая
муфта. Патент РФ N 1075027, 1995. Кл. F 16 D 39 /00.
3. Мурин А.В., Сериков Б.А., Осипов В.А. Усовершенствованная предохранительная
гидромуфта с отнесенной рабочей полостью для п риводов подъемно-транспортн ых машин. –
Вестник машиностроения, 1979. – №4. – С. 18-22.
4. Осипов В.А. Основы выбора параметров предохранительных блокируемых гидро-
муфт и предохранительных инерционных муфт для приводов машин. Диссертация на соис-
кание ученой степени канд. техн. наук. – Томск, 1987.
5. А.с. 1038651 СССР. МКИ
4
F16D 43/20. Инерционная предохранительная муфта /
А.В. Мурин, В.А. Осипов (СССР). №3458747/25-27; Заявлено 31.03.82; Опубликовано
30.08.83, Бюл. №32. – 4 с. : ил.
МЕТОДИКА ОПРЕДЕЛЕНИЯ ФАКТИЧЕСКОЙ ПЛОЩАДИ КОНТАКТА
ДЕФОРМИРУЮЩЕГО РОЛИКА И ЗАГОТОВКИ
ПРИ ПОВЕРХНОСТНОМ ПЛАСТИЧЕСКОМ ДЕФОРМИРОВАНИИ
Я. Н. Отений, д.т.н., проф., А. Э. Вирт, к.т.н., А. М. Лаврентьев.
Камышинский технологический институт (филиал)
Волгоградского государственного технического университета
403874, Волгоградская область, г. Камышин, ул. Ленина, 6-А
Email: 100roj@mail.ru
К настоящему времени накоплен значительный теоретический и экспериментальный
материал, в котором рассматривается влияние конструктивных параметров деформирующего
элемента и технологических факторов на производительность и к ачество обработанной по-
верхности. В результате этого установлено, что качество п оверхностей деталей зависит от
большого количества технологических факторов обработки, конструктивных параметров де-
формирующих элементов, размеров деталей и вида обрабатываемых поверхностей. Основ-
ными факт орами и параметрами обработки, определяющими формирование поверхностного
слоя, являются: п одача, число проходов, форма и размеры деформирующих элементов, раз-
меры обрабатываемой детали, углы установки деформирующих элементов относительно об-
рабатываемой детали (угол внедрения и угол самозатягивания), усилие деформирования, ис-
ходная шероховатость, механические характеристики материала (пределы упругости и вре-
менного сопротивления) и некоторые другие величины.
Применительно к ППД деформирующими элементами обкатыванием и раскатывани-
ем при обработке цилиндрических деталей и плоскостей для описания взаимосвязи между
величинами, определяющими условия обработки и показателями качества, можно написать
следующую общую систему уравнений:
у
i
=f(P
у
, P
z
, s
о
, r
n
, r
пр
, R
d
, r
m
, r
р
, h
m
, h
р
, α, ω, ζ
Т
, ζ
в
, V
пр
, HB, R
исх
, θ
k
)
(1)
где: у
i
– один из показателей качества поверхностного слоя (параметры шероховатости, сте-
пень, гл убина упрочнения, величина остаточных напряжений); P
y
, P
z
– радиальная и каса-

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
100
тельная нагрузка, действующие на деформирующий элемента, s
o
– подача на оборот детали
или ин струмента; r
n
– начальный радиус деформирующего элемента (радиус, соответствую-
щий началу контактной зоны); r
пр
– профильный радиус деформирующего элемента (закруг-
ление ролика на начальном участке контакта); R
d
– радиус детали (радиус вала или отвер-
стия); r
m
, r
p
– максимальный радиус деформирующего элемента и изменение радиуса де-
формирующего ролика п о его длине; h
m
– максимальная глубина внед рения ролика в обраба-
тываемую деталь; h
р
– изменение глубины внедрения деформирующего элемен та по линии
максимального нагружения; α – задний угол между деформирующим элементом и обрабаты-
ваемой поверхностью(угол внедрения); ω – угол самозатягивания; ζ
Т
, ζ
в
– предел текучести и
предел временного сопротивления обрабатываемого материала; V
пр
– скорость проскальзы-
вания между контактными поверхностями деформирующего элемента и обрабатываемой де-
талью; НВ – твердость обрабатываемой детали; R
исх
– исходная шероховатость обрабаты-
ваемой поверхности;. θ
k
– контактная температура.
Конструктивные параметры деформирующих элементов (диаметр, длина, форма бо-
ковой поверхности, профильный радиус и др.) и технологические факторы (усилие деформи-
рования, угол самозатяги вания, угол внедрения) определяют геометрические параметры кон-
тактной зоны, а через параметры контакта (его форма, размеры в продольном и окружном
направлении), исходные свойства материала заготовки (предел текучести, предел временного
сопротивления, твердость) влияют на физико-механические явления в зоне контакта (напря-
жения, деформации, проскальзывание, температуру в очаге деформации).
В свою очередь, ч ерез физико-механические п роцессы в очаге деформации оконча-
тельно формируется качество поверхностного слоя.
В подтверждение вышесказанного дальнейшее развити е процесса ППД, как показы-
вают исследования, осуществляется в следующих направлениях:
• исследование воздействия инструмента или рабочего тела на обрабатываемую по-
верхность, изучение очага деформирования и анализ распределения в нем сил и напряжений;
• исследование т емпературных полей в очаге деформирования и их влиян ие на каче-
ство поверхностного слоя;
• исследование условий создания остаточных напряжений и глубины упрочненного
слоя;
• исследование микрогеометрии упрочненного слоя;
• изучение связей между параметрами обработки, показателями качества поверхности
и эксплуатационными свойствами деталей, разработка математических зависимостей, позво-
ляющих рассчитывать технологические параметры обработки с применением ЭВМ;
• разработка теоретических основ классификации методов ППД.
• разработка методики определения рациональных параметров инструмента.
Таким образом, для обоснованного назначения оптимальных режимов обработки и
конструктивных параметров деформирующих элементов необходимо раскрытие взаимосвязи
между перечисленными в формуле 1 величинами.
Теоретические исследования процесса поверхностного пластического деформирова-
ния, как правило, осуществляются на основе разработки и анализа математических моделей
геометрических параметров контакта и напряженно-деформированного состояния в очаге
деформации. В этой области различными авторами получен ряд зависимостей для определе-
ния площади контакта:
tg
iiri
RR
RR
F
y
pд
pд
к
4
25,0
4
5,05,0
[1]; (2)
