Smith G.T. Cutting Tool Technology: Industrial Handbook

Подождите немного. Документ загружается.

Figure 214. Graphical relationship of high speed machining of metals – according to Salomon’s machining trials. [Source:

Salomon, circa 1920’s–30’s]

Machining and Monitoring Strategies 433

did not indicate how such ballistic speeds might be in-

corporated into a production application, also, an ana-

lytical model of this high-rate cutting phenomenon

was not developed.

In the 1960’s and early 1970’s some consolidation

of important machining data occurred, with notable

work on UHSM cutting mechanisms, etc., that oc-

curred in various countries being led principally by

the USA in work from: Coldwell and Quackenbush

(1962), plus Recht (1964); Okushima et al. (1966) and

Tanaka et al. (1967) in Japan; Fenton and Oxley (1967)

in the United Kingdom; and Arndt (1972) in Australia.

However, although there was a general increase global

research activity during this period, it was somewhat

disparate and mainly of a fundamental, rather than ap-

plied nature.

e third period of HSM development was insti-

gated in the mid-to-late 1970’s by the United States

Navy, in conjunction with the Lockheed Missiles and

Space Company, Inc., who contracted a series of ma-

chinability studies on marine propellers

. Here, the

Lockheed group headed-up by King, were mainly

concerned with the feasibility of utilising HSM in a

production environment, primarily for aerospace alu-

minium alloys, then later, working on nickel-alumin-

ium-bronze. King’s team at Lockheed, demonstrated

that it was economically feasible to introduce ‘high-

speed-machining’ procedures into the production en-

vironment, thereby realising the signicant improve-

ments in productivity with this HSM application. Such

applied research work, promoted signicant activity

and interest in this HSM eld and, it soon became

clear that attention needed to be focussed for all of the

subsequent small and diverse research programmes.

3 ‘Marine propeller manufacture’ , whether from a wrought-

solid material, or nishing-o a casting, is probably the most

dicult and complex multi-axes milling operation that can

be undertaken – due to the fact that the propeller surfaces

to be machined are continuously changing their geometry as

they are essentially parabolically-curved. Invariably, the part

geometry is typied by say, the NACA/NASA Standard 16-021

‘aerofoil cross-sectional prole’ , which for high-performance

propellers are exacerbated by normally having both consider-

able rake and skew to each blade – creating an exceedingly

complex geometry and llet where the boss and blades inter-

sect*.

* See: Smith and Booth (1993) paper – in the references,

which goes some way to explain the propeller manufacturing

subject, and for more detailed multi-axes machining and for

subsequent machined propeller measurement information.

Finally, in these formative years of experimental

work into HSM, the fourth period of development be-

gan in 1979, when the USAF awarded a contract to the

General Electric Company, in this instance, to provide

a scientic basis for faster metal removal via HSM and

Laser-assisted machining

. A further contract by the

USAF in 1980, was also awarded to ‘General Electric’–

the group also being headed by Flom (1980). With this

new HSM contract, also being granted to Flom’s group,

with the objective to evaluate the production implica-

tions of the previous contract. Both of these contracts

being supported by a consortium of industrial com-

panies and selected universities in the USA – initiat-

ing the fourth HSM period of development. At around

this time (i.e. in the late 1970’s), the introduction of

computer numerical control (CNC) systems occurred

and as a result, they were immediately being tted to

a new range of machine tools, signicantly enhanc-

ing both their usability and programming capabilities,

acting as a catalyst in the development of HSM strate-

gies. As these CNC controllers became more sophis-

ticated and processing speeds substantially increased,

this meant that the potential for HSM could now be

fully realised. In recent years, HSM machine tools are

just about everywhere in machine shops around the

world, where ever there is a need for highly produc-

tive part production with very fast cycle times. Obvi-

ously, on HSM machines as the spindle speeds have

increased in association with both tool and their re-

spective workpiece materials (i.e. see Fig. 215), this has

meant that there are now considerable design implica-

tions on these machine tools, these topics will now be

succinctly discussed.

9.1.1 HSM Machine Tool Design

Considerations

Prior to a discussion concerning machine tool design

factors that must be addressed, before to fully-imple-

menting this HSM technology, one might ask the

question: ‘Why do we need to rotate cutters at such high

spindle speeds?’ ere are a number of advantages that

can accrue from adopting such a progressive produc-

4 USAF contract to the General Electric Company in 1979, was:

F 33615-79-C-5119 – for a feasibility study into the fast metal

removal operations by HSM and Laser-assisted machining.

434 Chapter 9

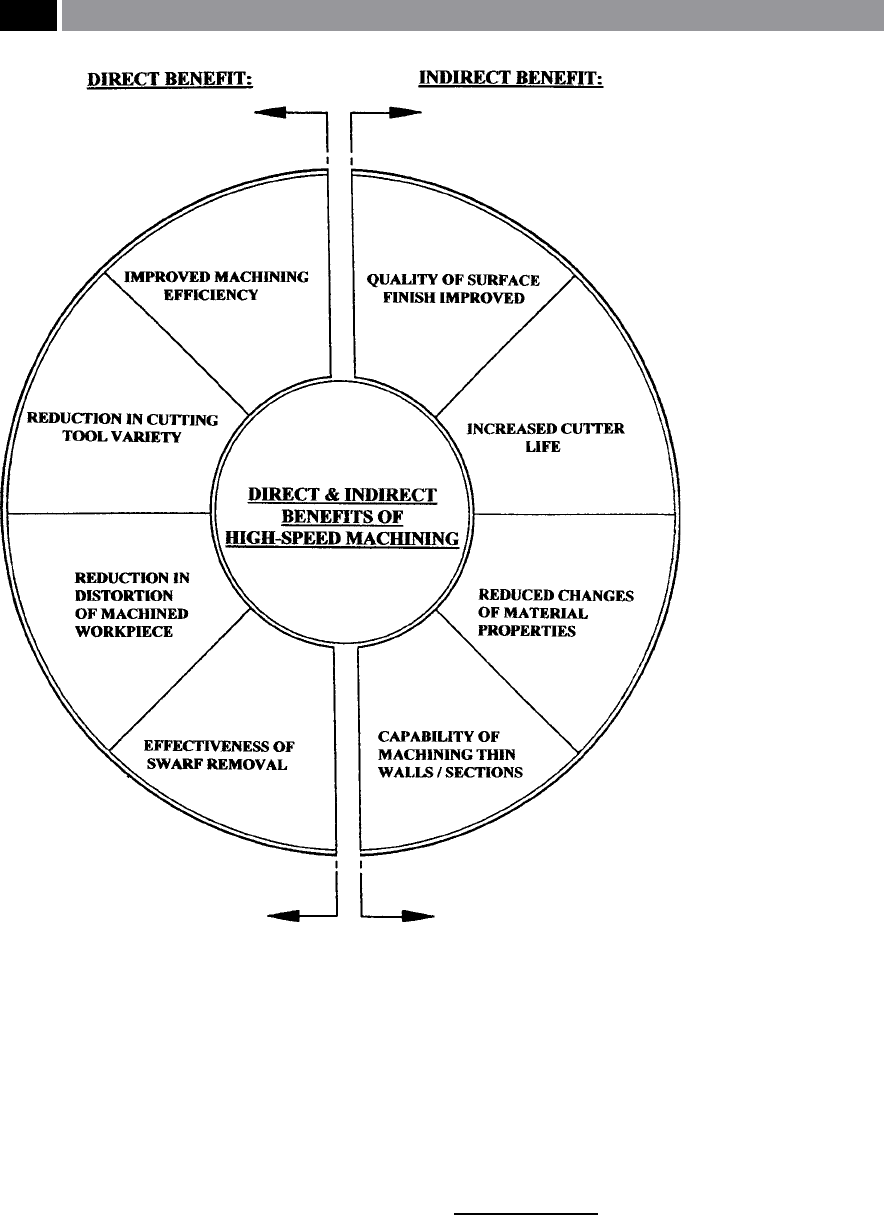
tion machining strategy (i.e. see Fig. 216) and, they

can be succinctly summarised as follows:

•

Direct benets

–

improved machining eciency,

–

reduction in cutting tool varieties,

–

reduction in distortion of workpiece,

–

eectiveness of swarf removal.

•

Indirect benets

–

quality of nish improved,

–

increased cutter life,

–

reduced changes in material properties,

–

capability of machining thin walls/sections.

ese production improvements are by no means all

that occur, as invariably, due to the superior machined

surface texture, the nal part surface may not need

to be deburred – a signicant real saving on complex

component geometries. Moreover, by employing an

HSM strategy, more simple xturing can be utilised, as

the actual tool forces are signicantly lessened.

It is an established fact that with higher rotational

cutter speeds the resulting cutting forces and tool

push-o are considerably reduced. In order to benet

from these improved cutting practices, the machine

tool’s axes must have both faster acceleration and de-

celeration – see Fig. 221, more will be mentioned con-

cerning these important dynamic aspects of a machine

tool’s operational performance shortly. Many of today’s

conventional and HSM machine tools, are based upon

a modular design concepts (Fig. 217a). is modular

design philosophy, allows the machine tool builder

the opportunity to standardise certain features over

a range of machine tools. Such practice benets the

manufacturer and consumer alike, by reducing design

Figure 215. The chronological development of cutting tool material introductions, which had an inuence on high-speed cut-

ting trends. [Courtesy of Yamazaki Mazak Corporation]

Machining and Monitoring Strategies 435

and development costs, while minimising the custom-

er’s purchasing costs, yet still allowing more attention

to be given to the detailed design of each ‘module’ in

the machine. So, an identical column, or table may be

common to a variety of machines and this trend can

oen be seen across a whole product range of ma-

chine tools. Not only are the major castings, or large

fabrications manufactured by employing modular

concepts, but this design philosophy also allows any

other smaller components to be standardised and t-

ted accordingly. Such as: the recirculating ballscrews;

servo-motors; linear scales – if tted; etc.; plus other

standardised items to be built into the constructed

machine tool ranges.

In order to minimise ‘

stick-slip’

in the slideway mo-

tions on heavy moving cast and fabricated members –

5 ‘Stick-slip’ or ‘Stiction’ , is the jerky-motion between sliding

members due to the formation and destruction of junctions

[due to localised pressure-eects]. (Kalpakjian, 1984)

Figure 216. Diagram illustrating the main benets to be gained from adopting a high-speed ma-

chining strategy. [Source: Smith, CNC Machining Technology, 1993]

436 Chapter 9

thereby giving faster response to CNC commands, ‘Ty-

choways’ (i.e see Fig. 217b), or similar mechanical aids

are usually strategically situated at set positions along

each hardened way of the machine tool’s orthogonal

axes (i.e normally at the ‘

Airy-points’

6 ‘Airy-points’ , are associated with any ‘elastic body’ that is

subject to load, where will undergo elastic deformation. e

magnitude of this deformation depends upon the extent of

the: load; contact area; plus the mechanical properties of the

contacting materials. Hence, if the prospective body is not

correctly supported, it will be subject to elastic deformation

– under its own weight. is problem was considered in 1856

by Sir G.B. Airy (Astronomer Royal) – who was interested in

minimising the elastic deections that arose when attempt-

ing to support and reduce the sagging in long focal length

refracting telescopes. Airy showed that by positioning these

two supports at prescribed distances, they could minimise

any potential error – when equated to the overall length of the

‘elastic member’ (i.e. in the length of the telescope). He found

that two conditions occur, one being for ‘line-standards’ – to

bring the ends square for measurement and calibration, and

secondly, relating to machine tools and many metrological

applications, where the ‘Points of minimum deection’ were

more appropriate, as follows:

Distance between each support = 0.554L

Using conventional recirculating ballsrews (Fig.

217c) for HSM applications is possible up to 100 m

min

–1

– in certain applications. Aer these linear velo-

cities have been reached and it is necessary to reverse

the axis direction, this can create ‘ballscrew wind-up’

problems. is ballscrew twisting, is despite the fact

that the ballscrew is very sti of the order >2,000

N µ

–1

, so if greater kinematic and dynamic perfor-

mance is required, then it might be necessary to utilise

linear-motor drives. A tabulated table for suitable

comparisons of the various types of motional drive

systems available today, is presented in Table 14.

It has been widely-reported that either a high-qual-

ity lead-, or ball-screw having rotary encoders, will

have a unidirectional repeatability to within 6-to-

Where: L = overall length of the ‘elastic member’. (Galyer and

Shotbolt et al., 1990)

Example: If a machine tool’s structural moving member is

1,000 mm in length and it is situated on a much longer ‘bed-

way’ , then the ‘Tychoways’ should (ideally) be symmerically-

positioned (i.e. xed to the moving member) at a distance of

554 mm apart – in order to obtain the minimum of elastic dis-

tortion as it moves backward and forward along the hardened

bedway.

Table 14. Comparison of dierent drive systems for machine tools

CONTRIBUTIONS: Leadscrew: Ballscrew: Belt-drives: Linear motor:

Noise Quiet Noisy Quiet Moderate

Back-driving Self-locking Easyback-drive

Backlash Increases with wear Constant Increases with belt wear Negligible

Repeatability ±

0.005 mm ±0.005 mm ±0.004 mm Best (<2 µm)

Duty Cycle Max. 60% Max. 100%

Eciency Bronze bushing 40% 90% 90% 90 to 95%

Life Short: high friction Longer Longer Longest

Shock-loads Higher Lower Low Highest

Smoothness Smooth: low speeds Smooth at all speeds Smoothest

Speeds Low High Higher Highest

Cost ££-Lowest £££-Moderate ££££-Highest

[Source: Johnson, 2001]

Machining and Monitoring Strategies 437

Figure 217. Typical ‘modular design’ and construction of machining centres, with ‘ballscrews’ and ‘tychoways’. [Courtesy of Cin-

cinnati Machines]

438 Chapter 9

7 µm. However, if linear encoders are tted this mini-

mises any potential ‘ballscrew wind-up’ , although the

problem of an ‘

Abbé -error’

is still present.

Yet another source of machine tool-induced prob-

lems are more specically termed ‘

uncertainties’

while ‘

hysteresis’

can also contribute to the overall ‘er-

ror budget’. us, hysteresis may result when the same

position has been commanded by the CNC controller,

7 ‘Abbés Principle’ – was derived by Professor Ernest Abbé in

1890 (i.e. having studied and graduating from the University

of Jena) and is still valid today. e Abbé principle simply

states that: ‘e line of measurement and the measuring plane

should be coincident’. An example of this ‘Abbé Law’ well-

known to engineers the world over, shows that a conventional

micrometer calliper ‘virtually-obeys’ the ‘Abbé principle (i.e.

there is a small ‘cosine error’ present – which can usually be

ignored), whereas, the Vernier calliper has a much larger o-

set between the xed and moving jaws – where the compo-

nent being measured is situated, to that of the beam – where

the scale’s reading for this measurement is taken. Ideally, both

measurement and reading should be lined-up, without an o-

set. [Sources: Busch, 1989; Whitehouse et al., 2002]

8 ‘Uncertainty of machine tool positioning’ – the question oen

asked in calibration-related tasks, is: ‘What is measurement

uncertainty?’ Uncertainty of measurement refers to the doubt

that exists about any measurement; there occurs a margin of

doubt for every measurement. is expression of measure-

ment uncertainty raises other questions: ‘How large is the mar-

gin?’ and ‘ How bad the doubt?’ Hence, in order to quantify

uncertainty two numbers are required: (i) being the width of

the margin – its interval, (ii) plusits condence level.

NB 

is latter value states how sure one is that the actual

value occurs within this margin.For example:On a CNC ma-

chine tool, the command may be to move the X-axis slide-

way 1000 mm plus, or minus 0.05 mm at the 95% condence

level. is uncertainty could be expressed, as follows: X-axis

slideway motion = 1000 mm ± 0.05 mm, at a level of con-

dence of 95%. In reality, what this statement is implying to

either the programmer, or calibration engineer is that they are

95% sure that the actual X-axis position now will lie between:

999.95 mm and 1000.05 mm. Many factors can contribute to

the overall ‘error budget’ as it is sometimes known, but this is

beyond the scope of the present discussion – see references for

further information. (Smith, 2002)

9 ‘Hysteresis’ ,

can be dened as: ‘e dierence in the indicated

value for any particular input when that input is approached in

an increasing input direction, versus when approached in a de-

creasing input direction.’ (Figliola and Beasley, et al. 2000)For

example:Hysteresis usually arises because of strain energy

stored in the system [i.e. in this case, within the machine

tool], by slack bearings, gears, ballscrews, etc. (Collett and

Hope, 1979)

but from opposite directions, causing the motion sys-

tem to creep by an amount larger than the backlash

alone (i.e. the hysteresis). is eect is the result of un-

seen working clearances and compounded by the ma-

chine’s elastic deformations, although by pre-loading

the ballscrews it will minimise some of these eects.

In HSM machining applications, all ballscrew and

indeed any screw-driven systems have some additional

limitations, such as its ‘critical speed’ of rotation. At the

critical speed, a ballscrew starts to resonate

at its rst

natural frequency (i.e termed ‘whipping’). Hence, the

critical speed is proportional to the ballscrew’s diam-

eter and is inversely proportional to the distance be-

tween the screw’s supports – squared. For a very long

and slender screw-driven machine tool application

with wide supports, here, most recirculating ballscrews

ould have a critical speed of approximately 2,500 rev

min

–1

. It should also be said, that for many ballscrews

assemblies they can be rotated at higher rotational

peeds than the 2,500 rev min

–1

previously mentioned,

before they reach their critical speed, but for very fast

accelerations and decelerations, then they become in-

creasing challenged. In fact, on some HSM machine

tool congurations, multi-start ballscrews have been

employed to increase linear response, but here the

‘critical speed’ will probably be lessened – due to re-

duced inherent ballscrew stiness. Even ‘matched’ twin

ballscrews have been tted to HSM machine tools – to

minimise any potential ‘yawing motions’ at high lin-

ear speed by the moving member along the machine’s

bedway. ese ballscrew limitations are probably why

linear-motional drives are becoming a realistic alter-

native, but they are only tted at present, to high capi-

tal cost HSM machine tools.

One of the bi-products of HSM’s greater stock re-

moval rates, is the excess volume of hot swarf which

must be speedily and eciently removed from the vi-

cinity of the machine – which is more readily achieved

for horizontal machine tool congurations. er-

mal eects in general on any machine tool become a

problem, particularly as many milling spindles utilise

direct-drives, with the motor being mounted in-situ

with the spindle. Here, the spindle motor creates heat,

the thermal eects of which can be analysed by either

10 ‘Resonant frequency’ , can be dened as: ‘e frequency at

which the magnitude ratio reaches a maximum value greater

than unity.’ (Figliola and Beasley et al., 2000)

Machining and Monitoring Strategies 439

a three-, or ve-probe spindle analyser, as depicted in

Fig. 218 along with a typical case-study for a spindle’s

thermal dri graph. Not only can such spindle analysis

equipment determine a spindle’s thermal growth, it can

also detect: thermal distortion; spindle error; machine

resonance; vibration; plus repeatability. In the case-

study graphically-depicted in Fig. 218b, the variation

in the machine tool’s temperature is the major cause

of positioning error. is thermal dri graph oers-up

a number of signicant questions that need to be ad-

dressed, such as: ‘How long does it take for the machine

tool to stabilise?’; ‘How much Z-axis growth does the

machine produce at full spindle speed?’; ‘How far has

the machine’s displacement become, because of distor-

tion in the machine tool structure?’. Spindle analysers

are able to operate at rotational speeds varying from

to 120,000 rev min

–1

, making them an ideal tool for

condition monitoring diagnostics on machine tool’s

equipped with HSM spindles for subsequent analyses.

In Appendix 15, a trouble-shooting guide has been

produced to high-light: problems; causes; tests; etc.;

that can be obtained from analyses by employing ma-

chine tool spindle analysers.

In Fig. 219, the polar plots illustrated show how the

spindle analyser has the ability to evaluate both a new

and rebuilt machine tool spindle’s condition. In the

spindle error indicated on the polar plot depicted in

Fig. 219a, it illustrates here, that a very badly rebuilt

spindle is simply not acceptable in this state. is poor

spindle performance, is in the main, largely the result

f signicant radial variability (i.e. total error: 12 µm

@ 4,005 rev min

–1

), which would severely compro-

mise any cutting tool’s machining performance. Con-

versely, in Fig. 219b, a well-worn spindle assembly is

hown prior to rebuild, having a total error of 4.6 µm

@ 1,702 rev min

–1

, aer its ‘correct’ rebuilding (Fig.

219c), the total error has been drastically reduced to

total error of 1.9 µm @ 1,700 rev min

–1

. Visually, the

dierences between these two polar plots is quite as-

tounding, in that both the asynchronous and average

errors present have virtually disappeared in the latter

case, making it ‘as-new’ and, ready to perform signi-

cant machining service. It is well-known fact by ma-

chinists familiar with their older and heavily-utilised

machine tools, that certain machine spindles will run

smoother and produce better machined roundness on

orkpieces if they are run at the so-called ‘sweet-spot’ ,

equally, the quality of the parts produced will be af-

fected if the spindle is run at its ‘sour-spot’. By utilis-

ing a spindle analyser, signicant information can be

gleaned from such rotational analyses, allowing speed

ranges to be selected which would currently optimise

the present status of the spindle’s condition, prior to

its potential rebuild – when called for at a due date in

the future.

For most machine tools today that are involved in

HSM activities, in general the spindle cartridges are

of three distinct design congurations – which inci-

dentally do not normally include ball bearing spindle

types

, such as:

•

Magnetic ‘active’ spindles (Fig. 220a) – typically

might have a cartridge with a speed range from:

,000 to 40,000 rev min

–1

, delivering 40 kW con-

tinuous power, peaking at over 50 kW . Such ‘active’

magnetic spindles can maintain 1 µm maximum

run-out, by digital control of the series of speci-

cally-orientated magnetic currents – being initi-

ated by radial and axial sensors, that continuously

monitor the spindle’s rotational axis position 10,000

times second

–1

NB F

urther renements to the spindle occur, with

these temperature-controlled milling spindle car-

tridges maintaining dynamic balance, regardless of

the milling cutting loads imposed, this latter fac-

tor being an important criterion when attempting

to reduce cutting tool vibrational eects. However,

these ‘active’ spindles are not cheap to purchase and

run, with another negative eect being that they are

normally rated for only several thousand hours op-

erational running time. Such cartridges come with

a variety of rotational speed ranges and spindle

power outputs.

•

Pneumatic spindles – have been available for many

years, with aerostatic bearings equalising the forces

exerted while cutting and remaining centralised

within the spindle’s housing, yet still achieving dy-

namic rotational balance,

11 ‘Ball bearing spindle designs’ , are not normally specied for

HSM operations, because at around 20,000 rev min

–1

– this be-

ing ‘mechanically-set’ as the upper rotational velocity of such

spindles. So, due to these high rotational speed eects and of

the combination of centrifugal forces, it means that at approx-

imately 80 m sec-1 rotational speed, the balls will lose contact

with the journal walls. As a result of this loss-of-contact the

hardened balls and raceways will rapidly wear out (i.e. the re-

sults of so-called: ‘Brinelling’ in the raceways, creating both

poor circumferential wear patterns, delaminations and associ-

ated frictional eects – leading to major debilitating spindle

roundness modications.) (Smith et al., 1992)

440 Chapter 9

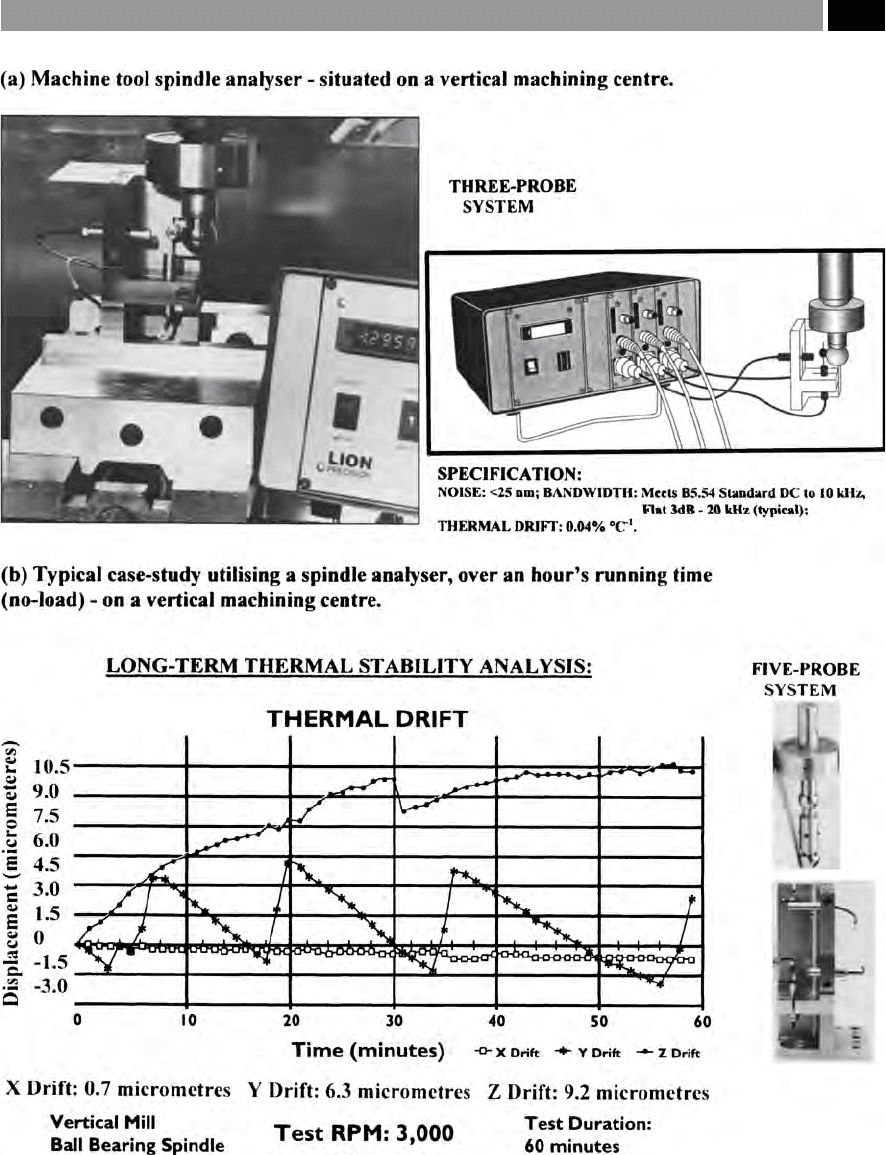
Figure 218. Machine tool spindle analysis system. [Courtesy of Lion Precision].

Machining and Monitoring Strategies 441

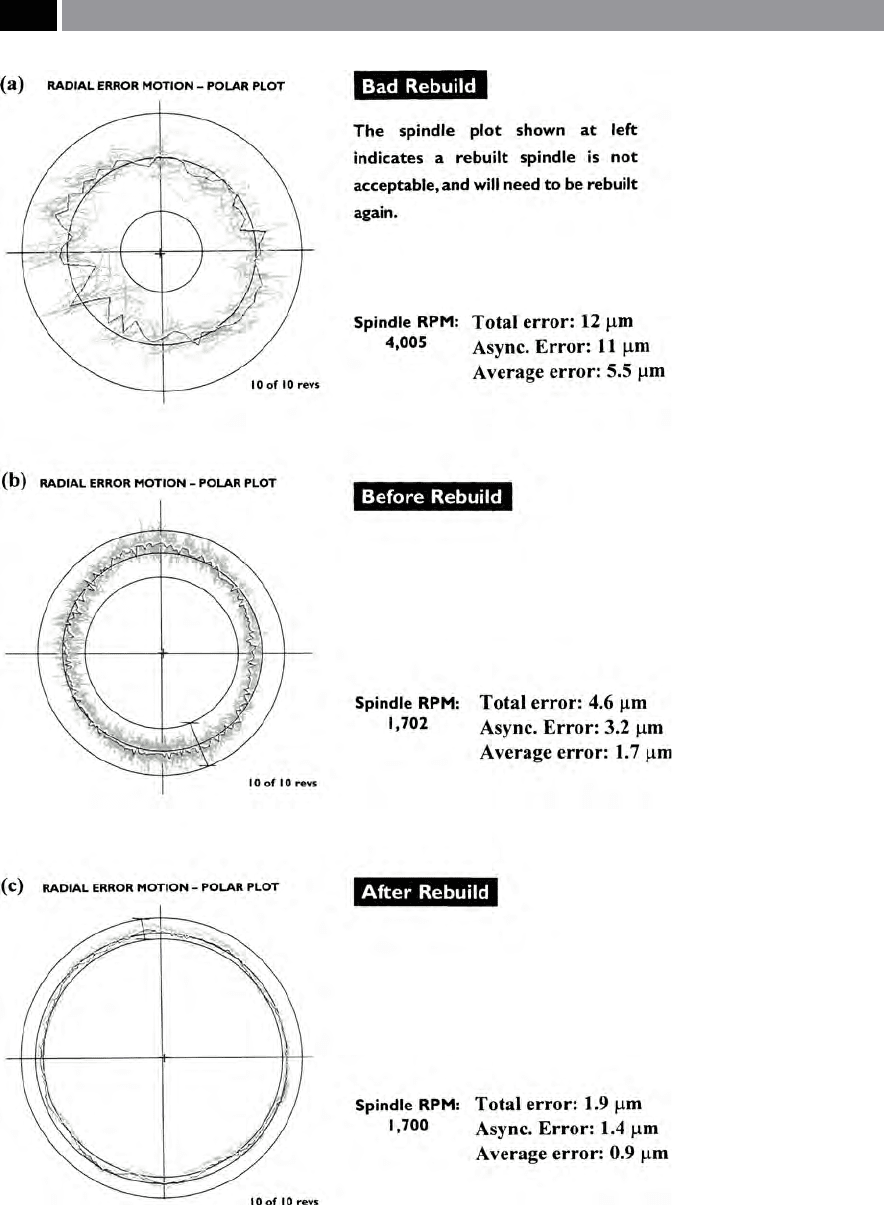
Figure 219. Machine tool spindle error plots, illustrating spindle condition. [Courtesy of Lion

Precision]

442 Chapter 9