Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

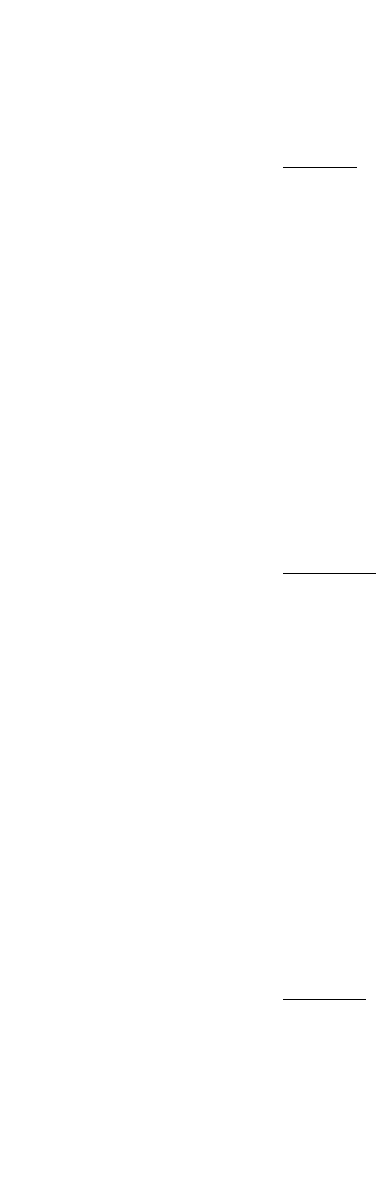
288 Chapter 9

Er c

−

()

which can be rewritten as

Er c Er c

xxy

() [() ]=+ −

To ﬁ nish the proof, let z be a portfolio that has zero covariance with y.

Then the preceding logic shows that c = E(r

). This result proves the

claim.

proposition 4 If in addition to the N risky assets, there exists a risk-free

asset with return r

, then the standard security market line holds:

Er r Er r

xfxMf

() [( ) ]=+ −

where

Cov ,()

Proof If there exists a risk-free security, then the tangent line from this

security to the efﬁ cient frontier dominates all other feasible portfolios.

Call the point of tangency on the efﬁ cient frontier M; then the result

follows.

Note It is important to repeat again that the terminology “market

portfolio” refers in this case to the “market portfolio relative to the

sample set of N assets.”

proposition 5 Suppose that there exists a portfolio y such that for any

portfolio x the following relation holds:

Er c Er c

xxy

() [() ]=+ −

where

Cov ,()

Then the portfolio y is on the envelope.

289 Calculating Efﬁ cient Portfolios When There Are No Short-Sale Restrictions

Proof Substituting in for the deﬁ nition of b

it follows that for any

portfolio x the following relation holds:

xSy xR c

yR c

−

Let x be the vector composed solely of the ﬁ rst risky asset: x = {1, 0, . . . ,

0}. Then the preceding equation becomes

yR c

Er c

−

=−

()

which we write

Say Er c

=−()

where S

is the ﬁ rst row of the variance-covariance matrix S. Note that

yR c

−

is a constant whose value is independent of the vector x. If

we let x be a vector composed solely of the ith risky asset, we get

Say E r c

=−()

This result proves that the vector z = ay solves the system Sz = R − c; by

Proposition 1, therefore, the normalization of z is on the envelope. But

this normalization is simply the vector y.

Calculating the Variance-Covariance Matrix

10.1 Overview

In order to calculate efﬁ cient portfolios, we must be able to compute the

variance-covariance matrix from return data for stocks. In this chapter

we discuss this computation, showing how to do the calculations in Excel.

The most obvious calculation is the sample variance-covariance matrix:

This is the matrix computed directly from the historic returns. We illus-

trate several methods for calculating the sample variance-covariance

matrix, including a direct calculation in the spreadsheet using the excess

return matrix and an implementation of this method with Visual Basic

for Applications (VBA).

While the sample variance-covariance matrix may appear to be an

obvious choice, a large literature recognizes that it may not be the best

estimate of variances and covariances. Disappointment with the sample

variance-covariance matrix stems both from its often unrealistic param-

eters and from its inability to predict. These issues are discussed brieﬂ y

in sections 10.5 and 10.6. As an alternative to the sample matrix, sections

10.9 and 10.10 discuss “shrinkage” methods for improving the estimate

of the variance-covariance matrix.

Before starting this chapter, you may want to peruse Chapter 34, which

discusses array functions. These are Excel functions whose arguments are

vectors and matrices; their implementation is slightly different from stan-

dard Excel functions. This chapter makes heavy use of the array functions

Transpose( ) and MMult( ) as well as some other “homegrown” array

functions.

10.2 Computing the Sample Variance-Covariance Matrix

Suppose we have return data for N assets over M periods. Writing the

return of asset i in period t as r

, we write the mean return of asset i as

iit

N==

∑

, ,...,

Then the covariance of the return of asset i and asset j is calculated as

1. We return to the issue of prediction in Chapter 13, which discusses the Black-Litterman

model of portfolio optimization.

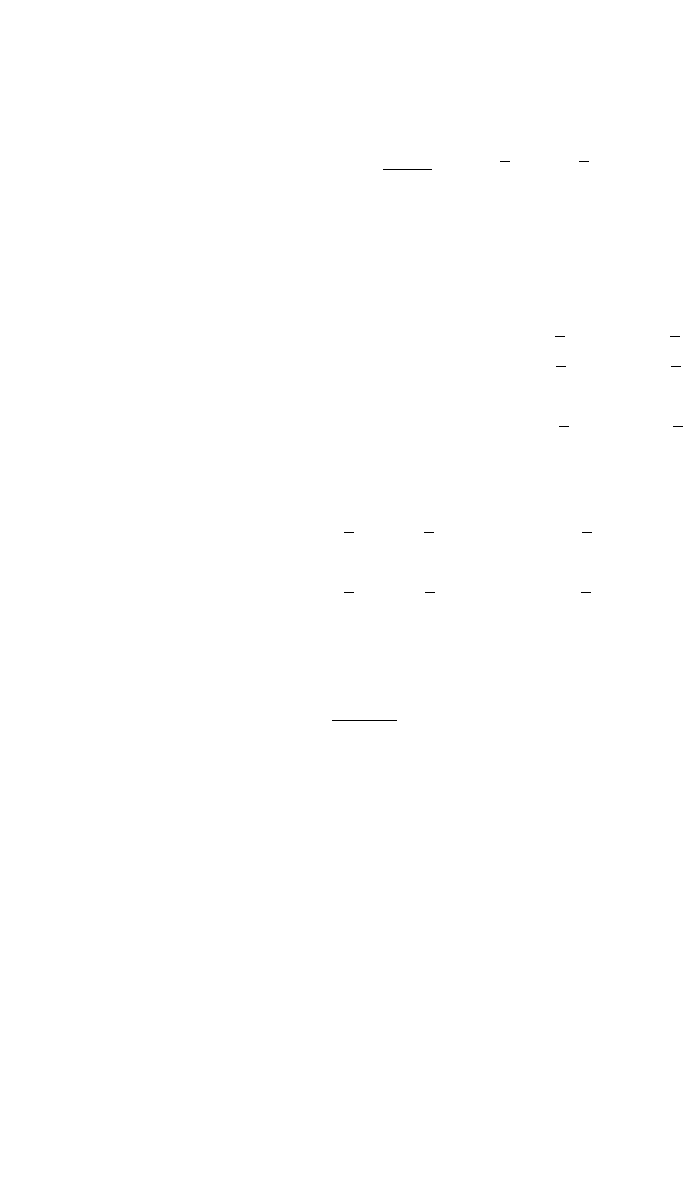
292 Chapter 10

ij it i jt j

rr rr ij N=

()

−

()

∗−

()

∑

Cov , , , ,...,

The matrix of these covariances (which includes, of course, the variances

when i = j) is the sample variance-covariance matrix. Our problem is to

calculate these covariances efﬁ ciently. Deﬁ ne the excess return matrix

to be

rr r r

−−

Matrix of excess returns

11 1 1

12 1 2





−−−

⎡

⎣

⎢

⎤

⎦

⎥

rrr

NM N1



Columns of matrix A subtract the mean asset return from the individual

asset returns. The transpose of this matrix is

rr rr r r

rrrr r r

NNNN NMN

−− −

⎡

⎣

⎢

⎤

⎦

⎥

11 1 12 1 1 1



 



Multiplying A

times A and dividing through by M − 1 gives the sample

variance-covariance matrix:

[]

∗

−

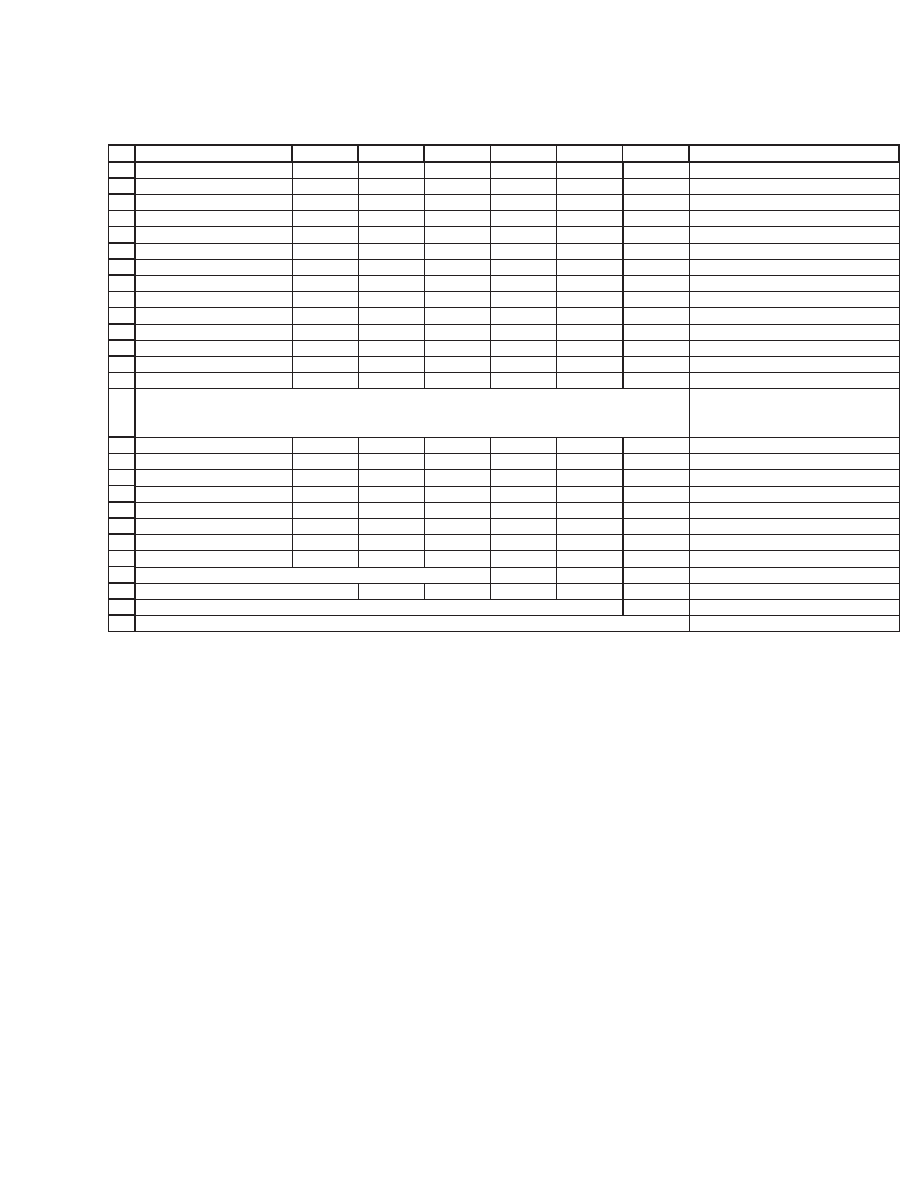
To consider the computational aspects, we use M = 11 years of annual

return data for N = 6 stocks. The following spreadsheet shows the price

data (adjusted for dividends) and the computed returns:

293 Calculating the Variance-Covariance Matrix

We illustrate the matrix method of computing the variance-covariance

matrix with our numerical example. Subtracting the mean return of each

asset from its annual return, we create the matrix of excess returns (rows

42–52 in the following spreadsheet). In rows 55–61 we compute the

sample variance-covariance matrix.

ABCDEFG H

Price data

Date GE MSFT JNJ K B

AIBM

4-Jan-93 2.36 2.68 6.78 20.37 2.34 11.79

3-Jan-94 4.15 2.64 7.20 18.47 4.21 14.62

3-Jan-95 4.98 3.68 10.91 19.90 4.20 15.53

2-Jan-96 8.80 5.73 19.43 29.03 8.09 20.41

2-Jan-97 13.51 12.64 24.44 27.59 13.93 30.78

2-Jan-98 21.64 18.49 29.15 38.01 20.19 31.60

4-Jan-99 30.57 43.37 38.04 34.14 23.47 30.94

3-Jan-00 40.51 48.51 39.36 20.93 36.27 39.24

2-Jan-01 42.42 30.26 43.80 23.52 48.13 48.78

2-Jan-02 34.82 31.58 55.19 28.70 41.39 51.05

2-Jan-03 22.25 23.52 52.15 32.00 32.81 59.63

2-Jan-04 31.86 28.16 51.49 37.36 48.86 81.95

Shares outstanding 10.56 10.86 2.97 0.41 0.84 0.79

Market value 336.44 305.82 152.93 15.44 41.01 65.13 <-- =G15*G17

Percentage of portfolio 36.70% 33.36% 16.68% 1.68% 4.47% 7.10% <-- =G18/SUM($B$18:$K$18)

Return data

Date GE MSFT JNJ K B

AIBM

3-Jan-94 56.44% -1.50% 6.01% -9.79% 58.73% 21.51% <-- =LN(G5/G4)

3-Jan-95 18.23% 33.21% 41.56% 7.46% -0.24% 6.04% <-- =LN(G6/G5)

2-Jan-96 56.93% 44.28% 57.71% 37.76% 65.55% 27.33%

2-Jan-97 42.87% 79.12% 22.94% -5.09% 54.34% 41.08%

2-Jan-98 47.11% 38.04% 17.62% 32.04% 37.11% 2.63%

4-Jan-99 34.55% 85.25% 26.62% -10.74% 15.05% -2.11%

3-Jan-00 28.15% 11.20% 3.41% -48.93% 43.53% 23.76%

2-Jan-01 4.61% -47.19% 10.69% 11.67% 28.29% 21.76%

2-Jan-02 -19.74% 4.27% 23.11% 19.90% -15.09% 4.55%

2-Jan-03 -44.78% -29.47% -5.67% 10.88% -23.23% 15.54%

2-Jan-04 35.90% 18.01% -1.27% 15.49% 39.82% 31.80%

Average 23.66% 21.38% 18.43% 5.51% 27.63% 17.63% <-- =AVERAGE(G23:G33)

Standard deviation 32.17% 40.71% 18.97% 23.86% 29.93% 13.56% <-- =STDEV(G23:G33)

Variance 0.1035 0.1657 0.0360 0.0570 0.0896 0.0184 <-- =VAR(G23:G33)

ANNUAL STOCK PRICE AND RETURN DATA FOR SIX STOCKS

General Electric (GE), Microsoft (MSFT), Johnson & Johnson (JNJ), Kellogg (K), Boeing (BA), IBM

294 Chapter 10

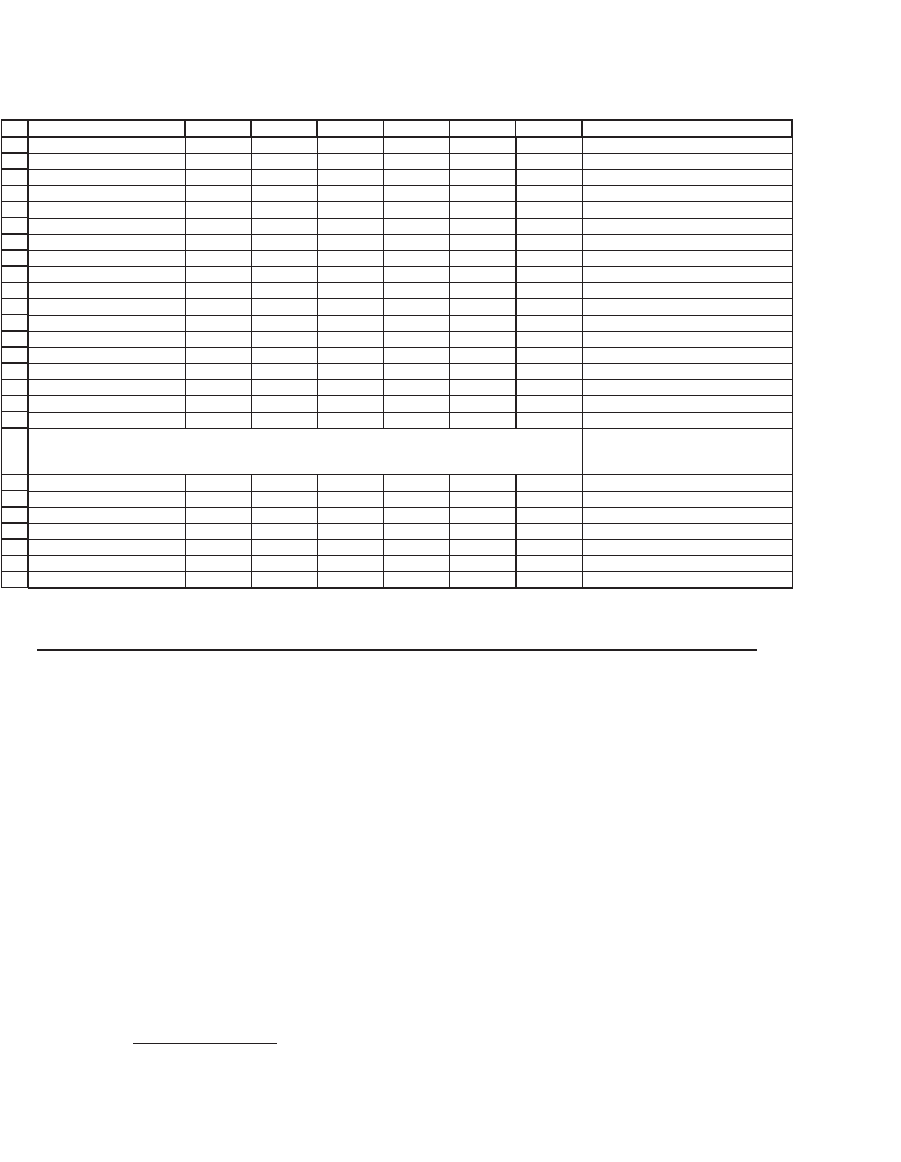
10.2.1 A Slightly More Efﬁ cient Alternative Method

As you might expect, there are alternative methods for computing the

variance-covariance matrix. The method illustrated here skips the com-

putation of the excess return matrix and does the calculation directly

inside the formula of cells B71:G76. It does so by using the array formula

= MMULT(TRANSPOSE(B23:G33-B35:G35),B23:G33-B35:G35)/10.

By writing B23:G33-B35 we directly subtract the means from each return

to create the vector of excess returns:

ABCDEFG H

Excess returns

Date GE MSFT JNJ K B

AIBM

3-Jan-94 32.78% -22.89% -12.42% -15.31% 31.11% 3.89% <-- =G23-G$35

3-Jan-95 -5.43% 11.83% 23.13% 1.94% -27.86% -11.59% <-- =G24-G$35

2-Jan-96 33.27% 22.90% 39.28% 32.25% 37.93% 9.70%

2-Jan-97 19.21% 57.73% 4.51% -10.60% 26.72% 23.46%

2-Jan-98 23.45% 16.65% -0.81% 26.53% 9.49% -15.00%

4-Jan-99 10.89% 63.87% 8.19% -16.25% -12.57% -19.74%

3-Jan-00 4.49% -10.18% -15.02% -54.44% 15.90% 6.14%

2-Jan-01 -19.05% -68.58% -7.74% 6.15% 0.67% 4.14%

2-Jan-02 -43.40% -17.11% 4.68% 14.39% -42.71% -13.08%

2-Jan-03 -68.45% -50.85% -24.10% 5.37% -50.86% -2.09%

2-Jan-04 12.24% -3.38% -19.70% 9.97% 12.20% 14.17%

GE MSFT JNJ K B

AIBM

0.1035 0.0758 0.0222 -0.0043 0.0857 0.0123

MSFT

0.0758 0.1657 0.0412 -0.0052 0.0379 -0.0022

JNJ 0.0222 0.0412 0.0360 0.0181 0.0101 -0.0039

-0.0043 -0.0052 0.0181 0.0570 -0.0076 -0.0046

A 0.0857 0.0379 0.0101 -0.0076 0.0896 0.0248

IBM

0.0123 -0.0022 -0.0039 -0.0046 0.0248 0.0184

Note: To put the array formula into cells B56:G61:

1. Mark the whole area B56:G61

2. Type <-- {=MMULT(TRANSPOSE(B42:G52),B42:G52)/10} into one of the cells.

3. When finished typing, hit [Ctrl]+[Shift]+[Enter] to put in the formula as an array formula.

Uses the array formula {<-- {=MMULT(TRANSPOSE(B42:G52),B42:G52)/10}} to compute

the sample var-cov matrix

295 Calculating the Variance-Covariance Matrix

10.3 Should We Divide by M or by M - 1? Excel versus Statistics?

In the foregoing calculations we divided by M − 1 instead of M in order

to get the unbiased estimate of the variances and covariances. But

perhaps this choice hardly matters. We quote from a major text: “There

is a long story about why the denominator is M − 1 instead of M. If you

have never heard that story, you may consult any good statistics text.

Here we will be content to note that the M − 1 should be changed to M

if you are ever in the situation of measuring the variance of a distribution

whose mean is known a priori rather than being estimated from the data.

(We might also comment that if the difference between M and M − 1

ever matters to you, then you are probably up to no good anyway—e.g.,

trying to substantiate a questionable hypothesis with marginal data.)”

ABCDEFG H

Return data

Date GE MSFT JNJ K B

AIBM

3-Jan-94 56.44% -1.50% 6.01% -9.79% 58.73% 21.51% <-- =LN(G5/G4)

3-Jan-95 18.23% 33.21% 41.56% 7.46% -0.24% 6.04% <-- =LN(G6/G5)

2-Jan-96 56.93% 44.28% 57.71% 37.76% 65.55% 27.33%

2-Jan-97 42.87% 79.12% 22.94% -5.09% 54.34% 41.08%

2-Jan-98 47.11% 38.04% 17.62% 32.04% 37.11% 2.63%

4-Jan-99 34.55% 85.25% 26.62% -10.74% 15.05% -2.11%

3-Jan-00 28.15% 11.20% 3.41% -48.93% 43.53% 23.76%

2-Jan-01 4.61% -47.19% 10.69% 11.67% 28.29% 21.76%

2-Jan-02 -19.74% 4.27% 23.11% 19.90% -15.09% 4.55%

2-Jan-03 -44.78% -29.47% -5.67% 10.88% -23.23% 15.54%

2-Jan-04 35.90% 18.01% -1.27% 15.49% 39.82% 31.80%

Average 23.66% 21.38% 18.43% 5.51% 27.63% 17.63% <-- =AVERAGE(G23:G33)

Standard deviation 32.17% 40.71% 18.97% 23.86% 29.93% 13.56% <-- =STDEV(G23:G33)

Variance 0.1035 0.1657 0.0360 0.0570 0.0896 0.0184 <-- =VAR(G23:G33)

GE MSFT JNJ K B

AIBM

0.1035 0.0758 0.0222 -0.0043 0.0857 0.0123

MSFT

0.0758 0.1657 0.0412 -0.0052 0.0379 -0.0022

JNJ 0.0222 0.0412 0.0360 0.0181 0.0101 -0.0039

K -0.0043 -0.0052 0.0181 0.0570 -0.0076 -0.0046

0.0857 0.0379 0.0101 -0.0076 0.0896 0.0248

IBM

0.0123 -0.0022 -0.0039 -0.0046 0.0248 0.0184

Uses the array formula {<-- {=MMULT(TRANSPOSE(B23:G33-B35:G35),B23:G33-

B35:G35)/10}} to compute the sample var-cov matrix

2. Numerical Recipes: The Art of Scientiﬁ c Computing by William H. Press, Brian P.

Flannery, Saul A. Teukolsky, and William T. Vetterling (Cambridge University Press,

1986). Slightly adapted from p. 456.

296 Chapter 10

Excel itself is somewhat confused on this issue of dividing by M or by

M − 1. In the following spreadsheet we show several ways of computing

the means, variances, standard deviations, and covariances:

ABCDEFG H

Date GE MSFT JNJ K B

AIBM

3-Jan-94 56.44% -1.50% 6.01% -9.79% 58.73% 21.51%

3-Jan-95 18.23% 33.21% 41.56% 7.46% -0.24% 6.04%

2-Jan-96 56.93% 44.28% 57.71% 37.76% 65.55% 27.33%

2-Jan-97 42.87% 79.12% 22.94% -5.09% 54.34% 41.08%

2-Jan-98 47.11% 38.04% 17.62% 32.04% 37.11% 2.63%

4-Jan-99 34.55% 85.25% 26.62% -10.74% 15.05% -2.11%

3-Jan-00 28.15% 11.20% 3.41% -48.93% 43.53% 23.76%

2-Jan-01 4.61% -47.19% 10.69% 11.67% 28.29% 21.76%

2-Jan-02 -19.74% 4.27% 23.11% 19.90% -15.09% 4.55%

2-Jan-03 -44.78% -29.47% -5.67% 10.88% -23.23% 15.54%

2-Jan-04 35.90% 18.01% -1.27% 15.49% 39.82% 31.80%

Mean GE MSFT JNJ K B

AIBM

23.66% 21.38% 18.43% 5.51% 27.63% 17.63% <-- =AVERAGE(G3:G13)

23.66% 21.38% 18.43% 5.51% 27.63% 17.63% <-- =SUM(G3:G13)/COUNT(G3:G13)

Variance GE MSFT JNJ K BA IBM

0.0941 0.1507 0.0327 0.0518 0.0814 0.0167 <-- =COVAR(G3:G13,G3:G13)

0.0941 0.1507 0.0327 0.0518 0.0814 0.0167 <-- =VARP(G3:G13)

0.1035 0.1657 0.0360 0.0570 0.0896 0.0184 <-- =VAR(G3:G13)

Standard

deviation

GE MSFT JNJ K BA IBM

0.3067 0.3882 0.1808 0.2275 0.2854 0.1293 <-- =SQRT(G20)

0.3067 0.3882 0.1808 0.2275 0.2854 0.1293 <-- =STDEVP(G3:G13)

0.3217 0.4071 0.1897 0.2386 0.2993 0.1356 <-- =STDEV(G3:G13)

Covariance(GE,MSFT)

0.0690 <-- =COVAR(B3:B13,C3:C13)

0.0690 <-- {=MMULT(TRANSPOSE(B3:B13-B16),C3:C13-C16)/11}

0.0758 <-- {=MMULT(TRANSPOSE(B3:B13-B16),C3:C13-C16)/10}

0.0758 <-- =COVAR(B3:B13,C3:C13)*11/10

SOME CONFUSION ABOUT M VERSUS M - 1 IN EXCEL?

Excel distinguishes between the population variance (Varp, which

divides by M) and the sample variance (Var, which divides by M − 1) and

distinguishes between the population and sample standard deviation

(Stdevp and Stdev, respectively). However, Excel does not make the

same distinction for its covariance function Covar. As you can see in cell

B30, Covar divides by M, in the same way that Varp divides by M. If you

want to create a corresponding covariance function that divides by M − 1,

you either have to multiply Covar by

M −1

as in cell B33 or you have to

use the array function =MMULT(TRANSPOSE(B3:B13-B16),C3:C13-

C16)/10 as in cell B32. If Excel were completely logical, it would have two

297 Calculating the Variance-Covariance Matrix

functions: Covarp, which divides by M (corresponding to Varp or Stdevp),

and Covar, which divides by M − 1 (corresponding to Var or Stdev).

Confused? Don’t worry! As the quote that starts this section indicates,

perhaps it doesn’t matter very much.

10.4 Alternative Methods for Computing the Sample Variance-Covariance

Matrix

In this section we brieﬂ y discuss two alternatives to the techniques

described in the previous section. The ﬁ rst alternative is a VBA array

function that directly computes the sample variance-covariance matrix,

and the second alternative makes use of Excel’s Offset function.

10.4.1 A VBA Function to Compute the Variance-Covariance Matrix

Our ﬁ rst alternative uses a VBA function.

3,4

Function VarCovar(rng As Range) As Variant

Dim i As Integer

Dim j As Integer

Dim numCols As Integer

numCols = rng.Columns.Count

numRows = rng.Rows.Count

Dim matrix() As Double

ReDim matrix(numCols - 1, numCols - 1)

For i = 1 To numCols

For j = 1 To numCols

matrix(i - 1, j - 1) = Application.

WorksheetFunction.Covar(rng.Columns(i), rng.Columns(j)) _

* numRows / (numRows - 1)

Next j

Next i

VarCovar = matrix

End Function

3. This section, which can be skipped on ﬁ rst reading, requires some knowledge of Excel’s

programming language Visual Basic for Applications (VBA), which is discussed in

Chapters 37–43.

4. I thank Amir Kirsh for developing this function.