Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

298 Chapter 10

This function is an array function (meaning that it has to be applied

using Ctrl-Shift-Enter). Here’s an example:

ABCDEFG H

Return data

Date GE MSFT JNJ K B

AIBM

3-Jan-94 56.44% -1.50% 6.01% -9.79% 58.73% 21.51% <-- =LN(G5/G4)

3-Jan-95 18.23% 33.21% 41.56% 7.46% -0.24% 6.04% <-- =LN(G6/G5)

2-Jan-96 56.93% 44.28% 57.71% 37.76% 65.55% 27.33%

2-Jan-97 42.87% 79.12% 22.94% -5.09% 54.34% 41.08%

2-Jan-98 47.11% 38.04% 17.62% 32.04% 37.11% 2.63%

4-Jan-99 34.55% 85.25% 26.62% -10.74% 15.05% -2.11%

3-Jan-00 28.15% 11.20% 3.41% -48.93% 43.53% 23.76%

2-Jan-01 4.61% -47.19% 10.69% 11.67% 28.29% 21.76%

2-Jan-02 -19.74% 4.27% 23.11% 19.90% -15.09% 4.55%

2-Jan-03 -44.78% -29.47% -5.67% 10.88% -23.23% 15.54%

2-Jan-04 35.90% 18.01% -1.27% 15.49% 39.82% 31.80%

GE MSFT JNJ K B

AIBM

0.1035 0.0758 0.0222 -0.0043 0.0857 0.0123

MSFT 0.0758 0.1657 0.0412 -0.0052 0.0379 -0.0022

JNJ 0.0222 0.0412 0.0360 0.0181 0.0101 -0.0039

-0.0043 -0.0052 0.0181 0.0570 -0.0076 -0.0046

0.0857 0.0379 0.0101 -0.0076 0.0896 0.0248

IBM

0.0123 -0.0022 -0.0039 -0.0046 0.0248 0.0184

USING A VBA FUNCTION TO COMPUTE THE COVARIANCE MATRIX

General Electric (GE), Microsoft (MSFT), Johnson & Johnson (JNJ), Kellogg (K), Boeing (BA), IBM

Uses the homemade array formula {=varcovar(B23:G33)} to compute the sample varcov

matrix

VarCovar uses the Excel Covar function to compute the entries of the

variance-covariance matrix. Because Covar divides by M, whereas we

want to divide through by M − 1, the line

Application.WorksheetFunction.Covar(rng.

Columns(i), rng.Columns(j)) _

* numRows / (numRows - 1)

adjusts by multiplying by

M − 1

10.4.2 The Variance-Covariance Matrix Using Excel’s Offset Function

Another way to calculate the variance-covariance function uses Excel’s

Offset function.

Offset takes a bit of getting used to: This function allows

5. Shay Zafrir, an MBA student at Tel-Aviv University, suggested using this function to

deﬁ ne the var-cov matrix.

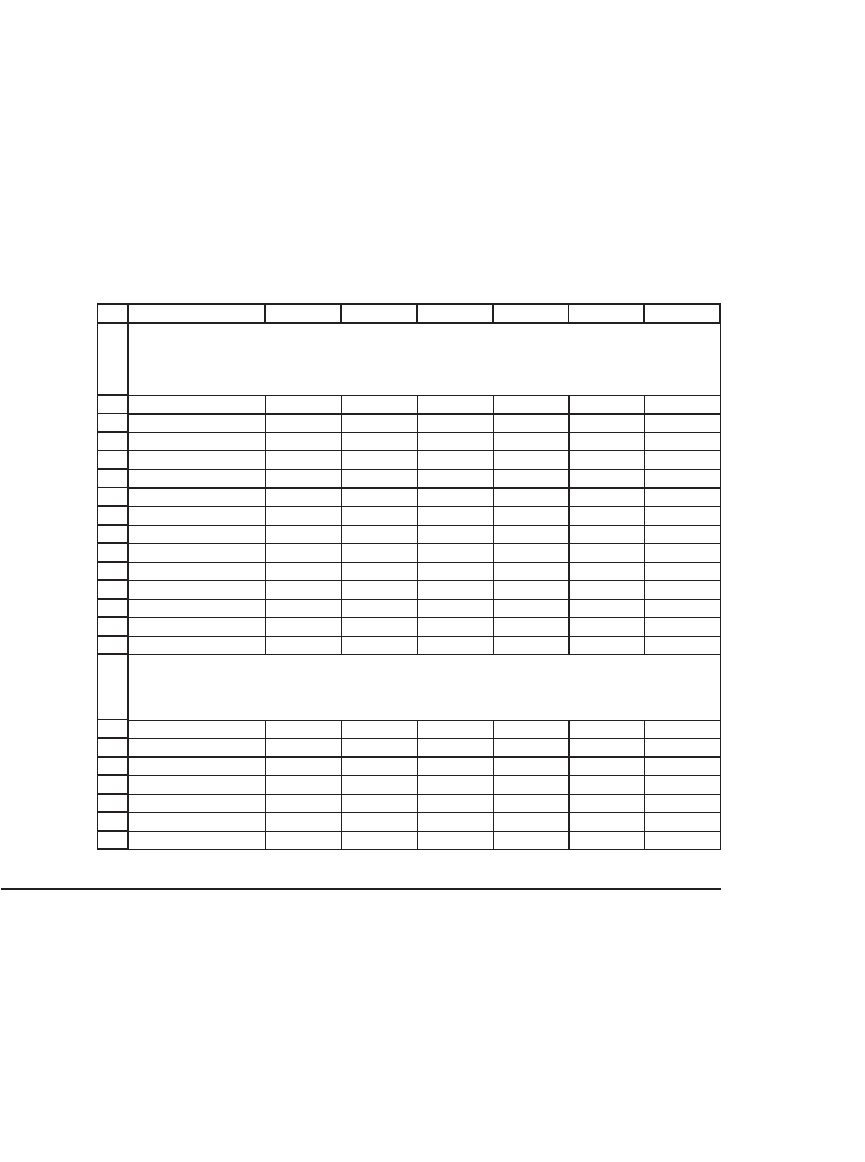
299 Calculating the Variance-Covariance Matrix

you to deﬁ ne a block of cells relative to some initial cell. Thus, for

example, Offset(initial cells, rows, columns) refers to a block of cells of

the same size as the initial cells, but rows and columns over from the

initial cells. The technique is illustrated in the following spreadsheet.

Note that the borders 0, 1, 2, 3, 4, 5 have been added to the variance-

covariance matrix in the lower half of the spreadsheet:

ABCDEF

Return data

Date GE MSFT JNJ K B

A IBM

3-Jan-94 56.44% -1.50% 6.01% -9.79% 58.73% 21.51%

3-Jan-95 18.23% 33.21% 41.56% 7.46% -0.24% 6.04%

2-Jan-96 56.93% 44.28% 57.71% 37.76% 65.55% 27.33%

2-Jan-97 42.87% 79.12% 22.94% -5.09% 54.34% 41.08%

2-Jan-98 47.11% 38.04% 17.62% 32.04% 37.11% 2.63%

4-Jan-99 34.55% 85.25% 26.62% -10.74% 15.05% -2.11%

3-Jan-00 28.15% 11.20% 3.41% -48.93% 43.53% 23.76%

2-Jan-01 4.61% -47.19% 10.69% 11.67% 28.29% 21.76%

2-Jan-02 -19.74% 4.27% 23.11% 19.90% -15.09% 4.55%

2-Jan-03 -44.78% -29.47% -5.67% 10.88% -23.23% 15.54%

2-Jan-04 35.90% 18.01% -1.27% 15.49% 39.82% 31.80%

012345

0.1035 0.0758 0.0222 -0.0043 0.0857 0.0123

0.0758 0.1657 0.0412 -0.0052 0.0379 -0.0022

0.0222 0.0412 0.0360 0.0181 0.0101 -0.0039

-0.0043 -0.0052 0.0181 0.0570 -0.0076 -0.0046

0.0857 0.0379 0.0101 -0.0076 0.0896 0.0248

0.0123 -0.0022 -0.0039 -0.0046 0.0248 0.0184

USING OFFSET AND COVAR TO CREATE THE

VARIANCE-COVARIANCE MATRIX

Sample var-cov matrix, uses the formula

=COVAR(OFFSET($B$4:$B$14,0,B$17),OFFSET($B$4:$B$14,0,$A18))*11/10 to

compute the sample var-cov matrix. This formula is copied in each cell.

10.5 Computing the Global Minimum Variance Portfolio

The two most prominent uses of the variance-covariance matrix are to

ﬁ nd the global minimum variance portfolio (GMVP) and to ﬁ nd efﬁ cient

portfolios. Both uses illustrate the problematics of working with sample

data and provide us with the introduction needed for sections 10.7–10.10,

which discuss alternatives to the sample variance-covariance matrix. In

this section we discuss the GMVP.

300 Chapter 10

Suppose there are N assets having a variance-covariance matrix S. The

GMVP is the portfolio x = {x

, x

, . . . , x

} that has the lowest variance

from among all feasible portfolios. The minimum variance portfolio is

deﬁ ned by

xxx x

GMVP GMVP GMVP GMVP N

⋅

⋅⋅

−

{ ... } {

,, ,

, , , , where

1111 1,, ,

N-dimensional

... }

↑



This formula is due to Merton.

The particular fascination of the minimum variance portfolio is that it

is the only portfolio on the efﬁ cient frontier whose computation does

not require the asset expected returns. The mean m

GMVP

and the variance

GMVP

of the minimum variance portfolio are given by

μσ

GMVP GMVP GMVP GMVP GMVP

xEr xSx=⋅ =⋅⋅(),

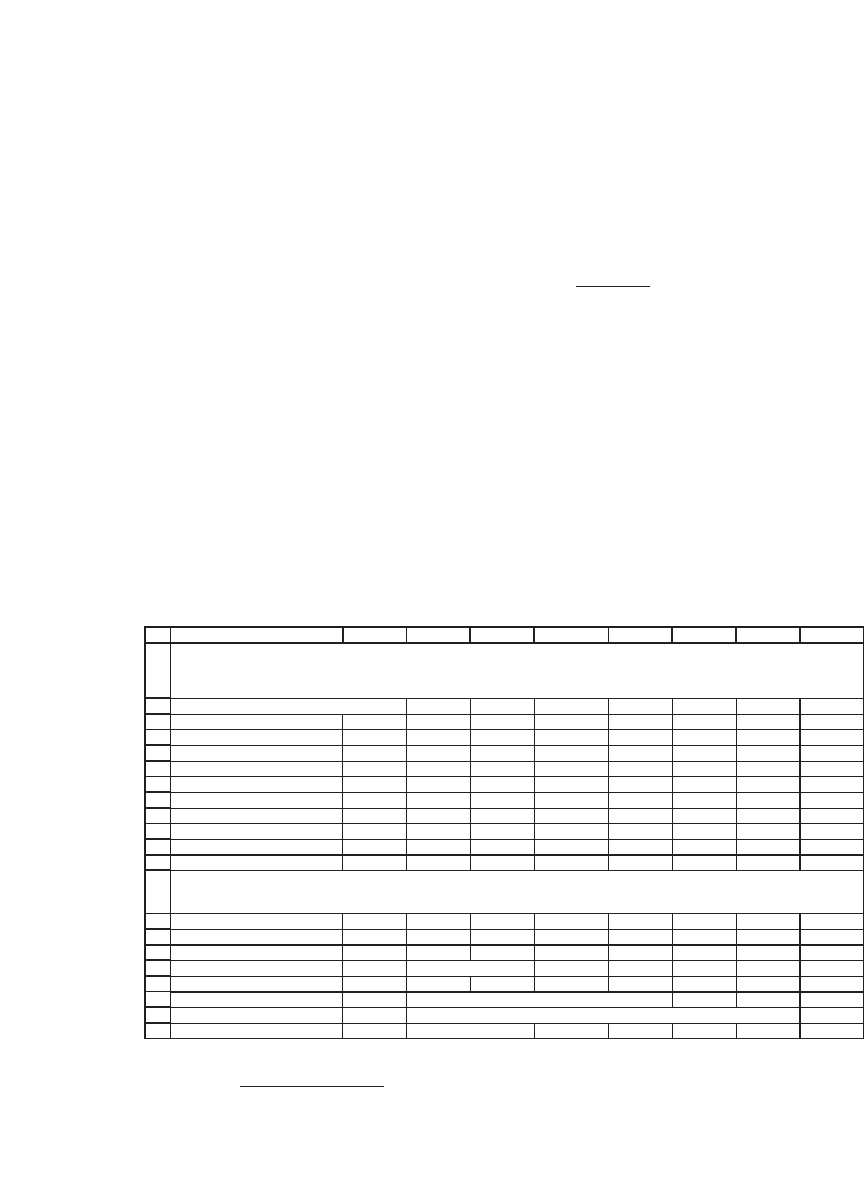
Here’s an implementation of these formulas for our particular

example:

ABCDEFGH

Sample variance-covariance matrix

GE MSFT JNJ K B

A IBM One

GE 0.1035 0.0758 0.0222 -0.0043 0.0857 0.0123 1

MSFT

0.0758 0.1657 0.0412 -0.0052 0.0379 -0.0022 1

JNJ

0.0222 0.0412 0.0360 0.0181 0.0101 -0.0039 1

-0.0043 -0.0052 0.0181 0.0570 -0.0076 -0.0046 1

0.0857 0.0379 0.0101 -0.0076 0.0896 0.0248 1

IBM

0.0123 -0.0022 -0.0039 -0.0046 0.0248 0.0184 1

Mean

23.66% 21.38% 18.43% 5.51% 27.63% 17.63%

GE MSFT JNJ K B

A IBM

0.6105 -0.1034 0.2074 0.0539 -0.7704 1.0019

Sum

1.0000 <-- =SUM(B15:G15)

GMVP mean

0.1273 <-- =SUMPRODUCT(B11:G11,B15:G15)

GMVP variance

0.0060 <-- {=MMULT(MMULT(B15:G15,B4:G9),TRANSPOSE(B15:G15))}

GMVP standard deviation

0.0773 <-- =SQRT(B20)

The global minimum variance portfolio (GMVP) is computed below with the formula

{=MMULT(TRANSPOSE(I4:I9),MINVERSE(B4:G9))/MMULT(MMULT(TRANSPOSE(I4:I9),MINVERSE(B4:G9)),I4:I9)}

COMPUTING THE GLOBAL MINIMUM VARIANCE PORTFOLIO USING THE

SAMPLE VARIANCE-COVARIANCE MATRIX

6. Robert C. Merton 1973. “An Analytical Derivation of the Efﬁ cient Portfolio Frontier,”

Journal of Financial and Quantitative Analysis 7, pp. 1851–1872.

301 Calculating the Variance-Covariance Matrix

Note that the GMVP for our six stocks has two short positions (BA

and MSFT) and that it has a very large positive position in GE and IBM.

This is a potentially objectionable feature of computing the GMVP with

the sample variance-covariance matrix: It is not credible that an investor

seeking minimum variance would put 61 percent of his portfolio in GE

and 100 percent of his portfolio in IBM, ﬁ nancing these positions with a

short of 77 percent in BA and 10 percent in MSFT. The noncredible

portfolios produced by the sample variance-covariance matrix have led

to a variety of techniques for alternative methods of computing this

matrix, which are discussed in sections 10.7–10.9. But before turning to

this topic, we consider the computation of the efﬁ cient portfolio.

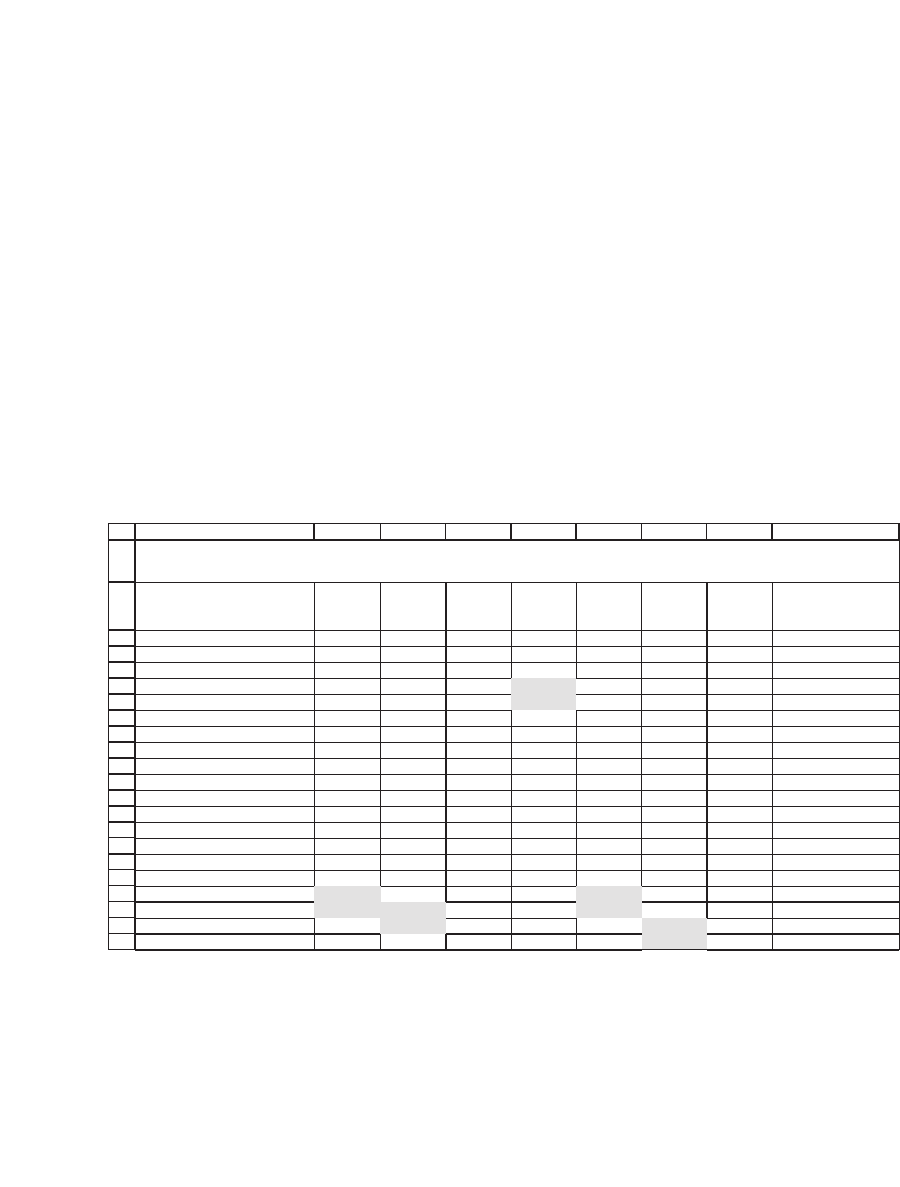
10.6 Computing an Efﬁ cient Portfolio

Following our discussion in Chapter 9, we can compute an efﬁ cient port-

folio by solving the equation:

Efﬁ cient portfolio =

SEr c

−

[() ]

[() ]Sum{ }

where S is the variance-covariance matrix, E(r) is the vector of expected

returns, and c is a constant. In the next spreadsheet we assume the E(r)

is the vector of historic asset means, and we set c = 2 percent. The efﬁ cient

portfolio is given in row 14.

ABCDEFGHI

GE MSFT JNJ K BA IBM Means

GE 0.1035 0.0758 0.0222 -0.0043 0.0857 0.0123 23.66%

MSFT

0.0758 0.1657 0.0412 -0.0052 0.0379 -0.0022 21.38%

JNJ 0.0222 0.0412 0.0360 0.0181 0.0101 -0.0039 18.43%

K -0.0043 -0.0052 0.0181 0.0570 -0.0076 -0.0046 5.51%

0.0857 0.0379 0.0101 -0.0076 0.0896 0.0248 27.63%

IBM 0.0123 -0.0022 -0.0039 -0.0046 0.0248 0.0184 17.63%

Risk-free rate 2%

GE MSFT JNJ K B

AIBM

Efficient portfolio 26.37% -6.05% 36.98% -4.81% -33.87% 81.39%

Market value ($billion) 336.44 305.82 152.93 15.44 41.01 16.98

Market proportions 38.73% 35.21% 17.61% 1.78% 4.72% 1.96% <-- =G16/SUM($B$16:$K$16)

COMPUTING AN EFFICIENT PORTFOLIO

The efficient portfolio is computed by the array formula {=TRANSPOSE(MMULT(MINVERSE(B3:G8),I3:I8-

B10)/SUM(MMULT(MINVERSE(B3:G8),I3:I8-B10)))} . The cells below use TRANSPOSE( ) to make this a row vector.

302 Chapter 10

Row 16 of the spreadsheet shows the market values of the individual

stocks on the last date of the data (beginning of January 2004). Row 17

computes the proportions of a portfolio that is composed of the market

weights of each asset. The difference between these market weights and

the efﬁ cient-portfolio weights is striking.

The spreadsheet shows two additional problems associated with using

the sample variance-covariance matrix for portfolio optimization.

The ﬁ rst problem is that the optimal portfolio exhibits a number of

very signiﬁ cant short-sale positions and some equally unrealistically

large long positions. Running a Data Table that calculates the envelope

portfolios for various values of c shows that the whole efﬁ cient frontier

contains portfolios with very large short and long positions. The high-

lights that follow indicate changes of sign that occur when c changes.

Only JNJ has positive weights on the whole envelope of stocks.

ABCDEFGHI

GE MSFT JNJ K BA IBM

Largest

long

position

Smallest position

-10% 44.68% -8.31% 28.41% 0.57% -56.66% 91.32% 91.32% -56.66%

-9% 43.92% -8.22% 28.76% 0.35% -55.72% 90.91% 90.91% -55.72%

-8% 43.10% -8.12% 29.15% 0.11% -54.69% 90.46% 90.46% -54.69%

-7% 42.19% -8.01% 29.57% -0.16% -53.56% 89.97% 89.97% -53.56%

-6% 41.18% -7.88% 30.04% -0.46% -52.31% 89.42% 89.42% -52.31%

-5% 40.06% -7.74% 30.57% -0.79% -50.91% 88.81% 88.81% -50.91%

-4% 38.80% -7.59% 31.16% -1.15% -49.35% 88.13% 88.13% -49.35%

-3% 37.39% -7.41% 31.82% -1.57% -47.59% 87.37% 87.37% -47.59%

-2% 35.78% -7.21% 32.57% -2.04% -45.59% 86.50% 86.50% -45.59%

-1% 33.94% -6.98% 33.43% -2.58% -43.30% 85.50% 85.50% -43.30%

0% 31.81% -6.72% 34.43% -3.21% -40.65% 84.34% 84.34% -40.65%

1% 29.32% -6.41% 35.59% -3.94% -37.55% 82.99% 82.99% -37.55%

2% 26.37% -6.05% 36.98% -4.81% -33.87% 81.39% 81.39% -33.87%

3% 22.80% -5.61% 38.65% -5.86% -29.44% 79.46% 79.46% -29.44%

4% 18.42% -5.06% 40.70% -7.15% -23.99% 77.08% 77.08% -23.99%

5% 12.91% -4.38% 43.28% -8.77% -17.13% 74.10% 74.10% -17.13%

7% -3.89% -2.30% 51.14% -13.71% 3.77% 64.99% 64.99% -13.71%

9% -38.68% 2.00% 67.42% -23.94% 47.07% 46.13% 67.42% -38.68%

11% -153.79% 16.25% 121.30% -57.80% 190.31% -16.27% 190.31% -153.79%

Data table: Optimal portfolio for various c's: the table header (hidden) in row 22 refers to the

computation of the efficient portfolio in row 14

If we think that the portfolio proportions derived in this way are

unrealistic, then in terms of the optimization process, there must be

something wrong with either the variance-covariance matrix or the

vector of means (perhaps both). We will return to this topic both in

sections 10.7–10.10 of this chapter and in Chapter 13 on the Black-

Litterman model.

303 Calculating the Variance-Covariance Matrix

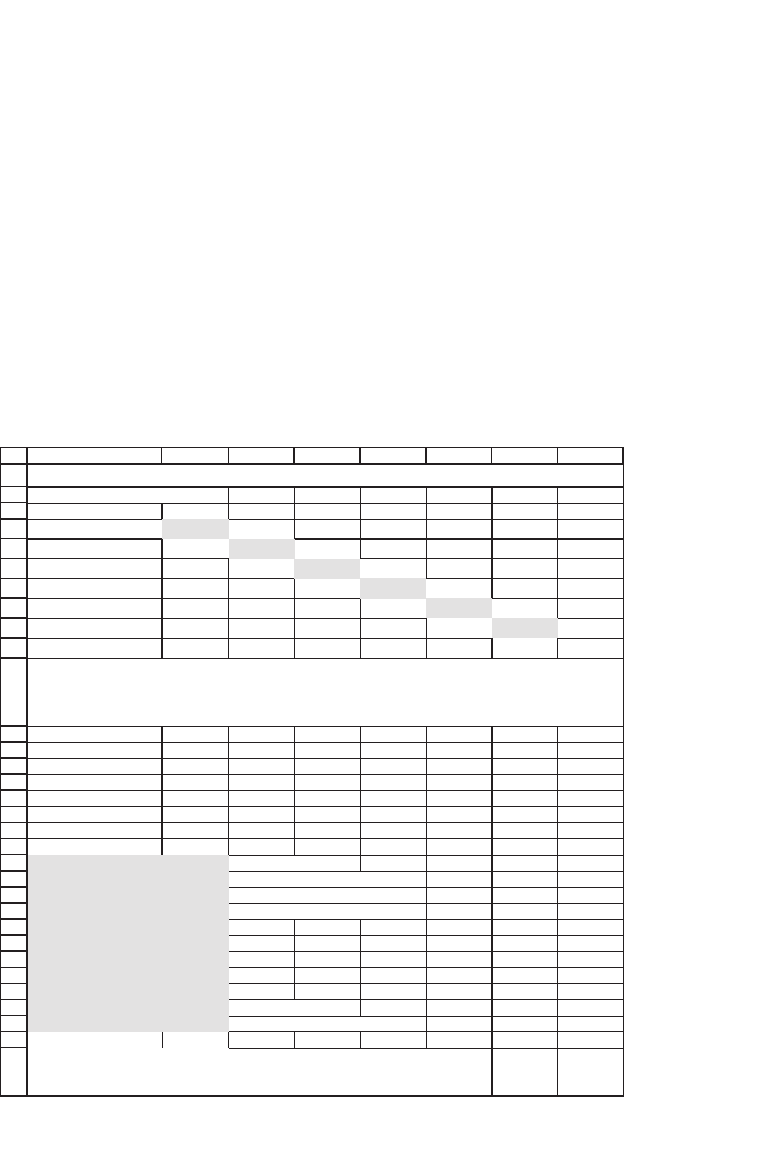
The second problem illustrated by this example relates to the implau-

sible correlations implied by the sample variance-covariance matrix.

In the next spreadsheet we show the matrix of correlations. For the

period surveyed, the largest correlation (between General Electric and

Boeing) is 0.89; examining the matrix shows that there are a number of

other very large and implausible correlations: There are six correlation

coefﬁ cients larger than 0.5. This is hard to believe! The smallest correla-

tion (between Boeing and Kellogg), −0.10, is perhaps also a problem—

could it be that when the returns on Boeing go up, the sales of cereals

decrease?

ABCDEFG

Variance-covariance matrix

GE MSFT JNJ K BA IBM

0.1035

0.0758 0.0222 -0.0043 0.0857 0.1414

MSFT 0.0758

0.1657

0.0412 -0.0052 0.0379 0.1400

JNJ 0.0222 0.0412

0.0360

0.0181 0.0101 0.0455

K -0.0043 -0.0052 0.0181

0.0570

-0.0076 0.0122

BA 0.0857 0.0379 0.0101 -0.0076

0.0896

0.0856

IBM 0.1414 0.1400 0.0455 0.0122 0.0856

0.2993

GE MSFT JNJ K BA IBM

123456GE

1 0.5791 0.3632 -0.0560 0.8905 0.8035 MSFT

2 0.5340 -0.0532 0.3113 0.6288 JNJ

3 0.4002 0.1780 0.4386 K

4 -0.1067 0.0934 BA

5 0.5226 IBM

Largest correlation 0.8905 <-- =MAX(B14:G18)

2nd largest correlation 0.8035 <-- =LARGE(B14:G18,2)

3rd largest correlation 0.6288 <-- =LARGE(B14:G18,3)

4th largest correlation 0.5791 <-- =LARGE(B14:G18,4)

5th largest correlation 0.5340

6th largest correlation 0.5226

7th largest correlation 0.4386

8th largest correlation 0.4002

9th largest correlation 0.3632

Smallest correlation -0.1067 <-- =MIN(B14:G18)

Average correlation 0.3685 <-- =AVERAGE(C14:G18)

#NAME?

THE CORRELATION MATRIX

Number of

correlations greater

than 0.5 6

<-- =COUNTIF(B14:G18,">0.5")

304 Chapter 10

10.7 Alternatives to the Sample Variance-Covariance: The Single-Index Model

The sample variance-covariance matrix is easily computable from his-

torical data, but—as shown in the previous section—it has its problems.

In particular, the sample matrix makes it difﬁ cult to predict the GMVP,

and using it for portfolio optimization often leads to implausible asset

positions (both long and short). In this section and the next we consider

several alternatives to using the sample matrix. All these methods have

two common features:

•

They leave the variances alone—they compute them from the sample

variance.

•

They change the covariances (the off-diagonal) elements of the

variance-covariance matrix.

10.7.1 The Single-Index Model

The single-index model (SIM) began as an attempt to simplify some of

the computational complexities of calculating the variance-covariance

matrix.

The basic assumption of the SIM is that the returns of each asset

can be linearly regressed on a market index x:





iiixi

=+ +

αβ ε

where the correlation between e

and e

is zero. Given this assumption, it

is easy to establish the following two facts:

Er Er

iiix

ijx

()

≠

⎧

⎨

⎩



αβ

ββσ

when

Essentially the SIM assumes involves changes in the estimates of the

covariances, but not the sample variance. We illustrate the computation

of the SIM with our six-asset example, adding a seventh column for the

returns on the S&P 500. Regressing the returns of each asset on the

Standard & Poor’s 500 portfolio, we get the betas in row 20:

7. W. F. Sharpe 1963. “A Simpliﬁ ed Model for Portfolio Analysis,” Management Science 9,

pp. 277–293.

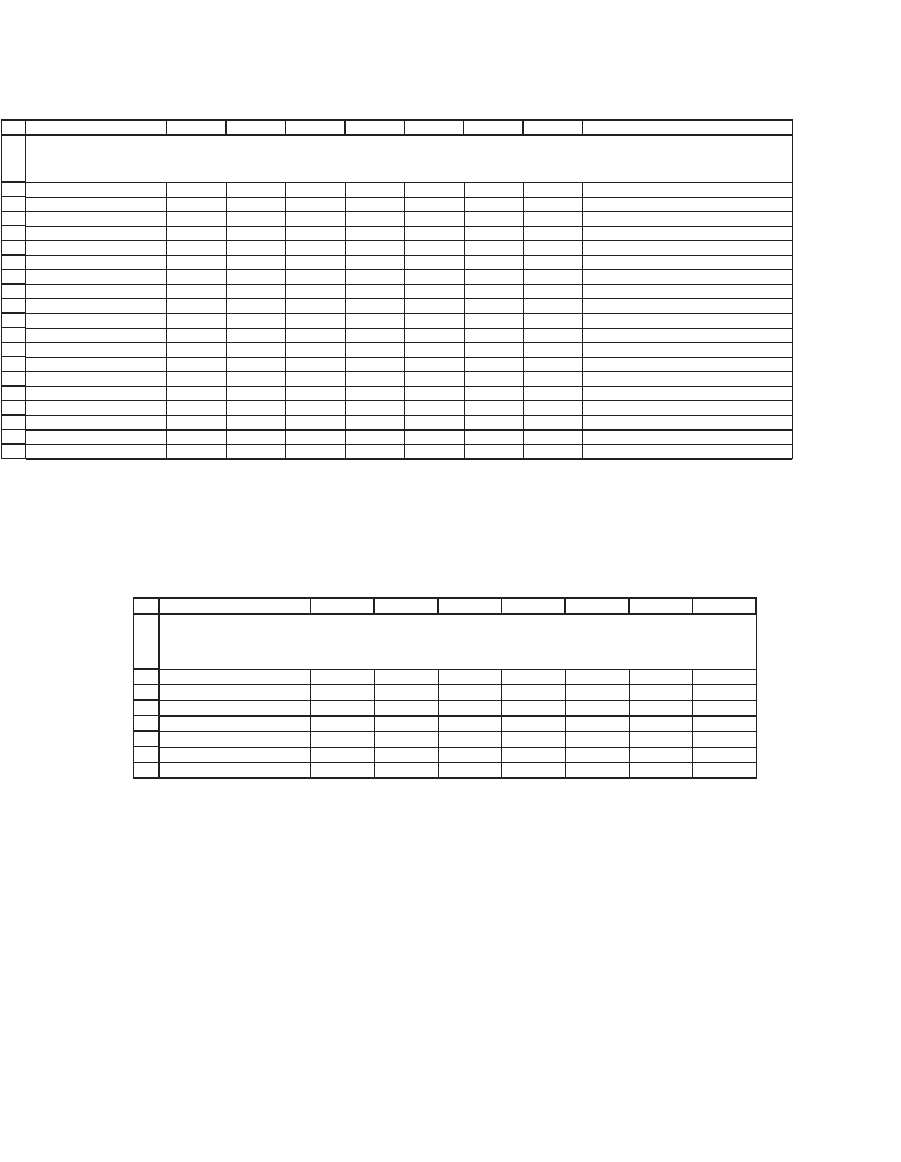
305 Calculating the Variance-Covariance Matrix

Using the wonders of Excel array functions (Chapter 35), we can

compute the SIM variance-covariance function:

IHGFEDCBA

Return data

Date GE MSFT JNJ K BAIBMSP500

3-Jan-94 56.44% -1.50% 6.01% -9.79% 58.73% 21.51% -2.35%

3-Jan-95 18.23% 33.21% 41.56% 7.46% -0.24% 6.04% 30.16%

2-Jan-96 56.93% 44.28% 57.71% 37.76% 65.55% 27.33% 21.19%

2-Jan-97 42.87% 79.12% 22.94% -5.09% 54.34% 41.08% 22.07%

2-Jan-98 47.11% 38.04% 17.62% 32.04% 37.11% 2.63% 26.65%

4-Jan-99 34.55% 85.25% 26.62% -10.74% 15.05% -2.11% 8.59%

3-Jan-00 28.15% 11.20% 3.41% -48.93% 43.53% 23.76% -2.06%

2-Jan-01 4.61% -47.19% 10.69% 11.67% 28.29% 21.76% -18.95%

2-Jan-02 -19.74% 4.27% 23.11% 19.90% -15.09% 4.55% -27.82%

2-Jan-03 -44.78% -29.47% -5.67% 10.88% -23.23% 15.54% 27.91%

2-Jan-04 35.90% 18.01% -1.27% 15.49% 39.82% 31.80% 4.34%

Average 23.66% 21.38% 18.43% 5.51% 27.63% 17.63% 8.16% <-- =AVERAGE(H4:H14)

Standard deviation 32.17% 40.71% 18.97% 23.86% 29.93% 13.56% 19.59% <-- =STDEV(H4:H14)

Variance 0.1035 0.1657 0.0360 0.0570 0.0896 0.0184 0.0384 <-- =VAR(H4:H14)

Beta 0.3411 0.9185 0.2598 0.2344 0.1046 0.0186 <-- =SLOPE(G4:G14,$H$4:$H$14)

ESTIMATING THE VARIANCE-COVARIANCE MATRIX USING

THE SINGLE-INDEX MODEL

ABCDEFG

GE MSFT JNJ K BA IBM

GE 0.1035 0.0120 0.0034 0.0031 0.0014 0.0002

MSFT

0.0120 0.1657 0.0092 0.0083 0.0037 0.0007

JNJ 0.0034 0.0092 0.0360 0.0023 0.0010 0.0002

K 0.0031 0.0083 0.0023 0.0570 0.0009 0.0002

0.0014 0.0037 0.0010 0.0009 0.0896 0.0001

IBM 0.0002 0.0007 0.0002 0.0002 0.0001 0.0184

The SIM var-cov matrix uses the array formula

{=IF(B24:G24=A25:A30,B18:G18,MMULT(TRANSPOSE(B20:G20),B20:G20)*H18)} to compute the

sample var-cov matrix

This array function needs to be picked apart:

•

It contains an If function, which as we know has three parts: If(condition,

answer if condition is true, answer if condition is false)

•

The condition B24:G24=A25:A30 asks if the “cross entries” in the row

B24:G24 (which contains the stock names as a row) are equal to the

entries in the column vector A25:A30. To see this condition with greater

clarity, we have inserted the formula If(B24:G24=A25:A30,1,0) into the

following spreadsheet. As you can see this step creates a spreadsheet

with 1 on the diagonal and zero elsewhere:

306 Chapter 10

•

The ﬁ rst If condition in our SIM variance-covariance matrix is IF(B24:

G24=A25:A30, B18:G18, ....). This says that if we are on the diagonal, we

should put in the asset’s return variance.

•

The second If condition says that if we are off-diagonal, we should

put in MMULT(TRANSPOSE(B20:G20),B20:G20)*H18). The formula

TRANSPOSE(B20:G20),B20:G20) creates a matrix of b

. The for-

mula multiplies this matrix by the variance of the S&P 500, given in

column H.

10.8 Alternatives to the Sample Variance-Covariance: Constant Correlation

The constant-correlation model of Elton and Gruber (1973) computes

the variance-covariance matrix by assuming that the variances of the

asset returns are the sample returns, but that the covariances are all

related by the same correlation coefﬁ cient, which is generally taken to

be the average correlation coefﬁ cient of the assets in question. Since

Cov(r

, r

) = s

= r

, this assumption means that in the constant-

correlation model

σσ

σρσσ

ii i

ij i j

=≠

⎧

⎨

⎩

when

Using our data for the 10 stocks, we can implement the constant-

correlation model. We ﬁ rst compute the correlations of all the stocks:

ABCDEFG

GE MSFT JNJ K B

AIBM

100000

MSFT

010000

JNJ

001000

000100

000010

IBM

000001

The SIM var-cov matrix uses the array formula

{=IF(B2:G2=A3:A8,1,0)} to compute the sample var-cov matrix

307 Calculating the Variance-Covariance Matrix

ABCDEFG H

Return data

Date GE MSFT JNJ K BA IBM

3-Jan-94 56.44% -1.50% 6.01% -9.79% 58.73% 21.51%

3-Jan-95 18.23% 33.21% 41.56% 7.46% -0.24% 6.04%

2-Jan-96 56.93% 44.28% 57.71% 37.76% 65.55% 27.33%

2-Jan-97 42.87% 79.12% 22.94% -5.09% 54.34% 41.08%

2-Jan-98 47.11% 38.04% 17.62% 32.04% 37.11% 2.63%

4-Jan-99 34.55% 85.25% 26.62% -10.74% 15.05% -2.11%

3-Jan-00 28.15% 11.20% 3.41% -48.93% 43.53% 23.76%

2-Jan-01 4.61% -47.19% 10.69% 11.67% 28.29% 21.76%

2-Jan-02 -19.74% 4.27% 23.11% 19.90% -15.09% 4.55%

2-Jan-03 -44.78% -29.47% -5.67% 10.88% -23.23% 15.54%

2-Jan-04 35.90% 18.01% -1.27% 15.49% 39.82% 31.80%

Average

23.66% 21.38% 18.43% 5.51% 27.63% 17.63% <-- =AVERAGE(G4:G14)

Standard deviation

32.17% 40.71% 18.97% 23.86% 29.93% 13.56% <-- =STDEV(G4:G14)

Variance

0.1035 0.1657 0.0360 0.0570 0.0896 0.0184 <-- =VAR(G4:G14)

Average correlation

0.1999 <-- =AVERAGE(B23:G28)-1/6

GE MSFT JNJ K BAIBM

GE 1.0000 0.5791 0.3632 -0.0560 0.8905 0.2819

MSFT

0.5791 1.0000 0.5340 -0.0532 0.3113 -0.0406

JNJ

0.3632 0.5340 1.0000 0.4002 0.1780 -0.1529

-0.0560 -0.0532 0.4002 1.0000 -0.1067 -0.1427

0.8905 0.3113 0.1780 -0.1067 1.0000 0.6116

IBM

0.2819 -0.0406 -0.1529 -0.1427 0.6116 1.0000

ESTIMATING THE VARIANCE-COVARIANCE MATRIX USING

THE CONSTANT-CORRELATION APPROACH

Uses the array formula {=MMULT(TRANSPOSE(B4:G14-B16:G16),B4:G14-

B16:G16)/10/MMULT(TRANSPOSE(B17:G17),B17:G17)} to compute the correlations

In the preceding spreadsheet we took our constant correlation to

be the average correlation of our sample of the six stocks (cell B19). Of

course this approach is open to variations: Suppose we feel that the

average correlation of stocks in the future will be about 0.3. Then we can

directly estimate the constant-correlation matrix from the return data.