Simon Benninga. Financial Modelling 3-rd edition
Подождите немного. Документ загружается.

248 Chapter 8
proportion in the portfolio; the covariance of each pair of assets appears
once, multiplied by twice the product of the individual assets’ propor-
tions. Another way of writing the variance is to use the notation
Var( ) , Cov( , )rrr
iii ijij
==
σσ
We may then write
Var( )rxx
Xi
ji
jij
=
∑∑
σ
The most economical representation of the portfolio variance uses
matrix notation. It is also the easiest representation to implement for
large portfolios in Excel. In this representation we call the matrix that
has s
ij
in the ith row and the jth column the variance-covariance
matrix:
S
N
N
N
NNN
=
σσσ σ
σσσ σ
σσσ σ
σσσ σ
11 12 13 1
21 22 23 2
31 32 33 3
123
...
...
...
NNN
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
.
Then the portfolio variance is given by Var(r
p
) = x
T
Sx.
If we have two portfolios x = [x
1
, x
2
, . . . , x
N
] and y = [y
1
, y
2
, . . . , y
N
], then
the covariance of the two portfolios is given by Cov(x, y) = xSy
T
= ySx
T
.
8.4.1 Portfolio Calculations Using Matrices—An Example
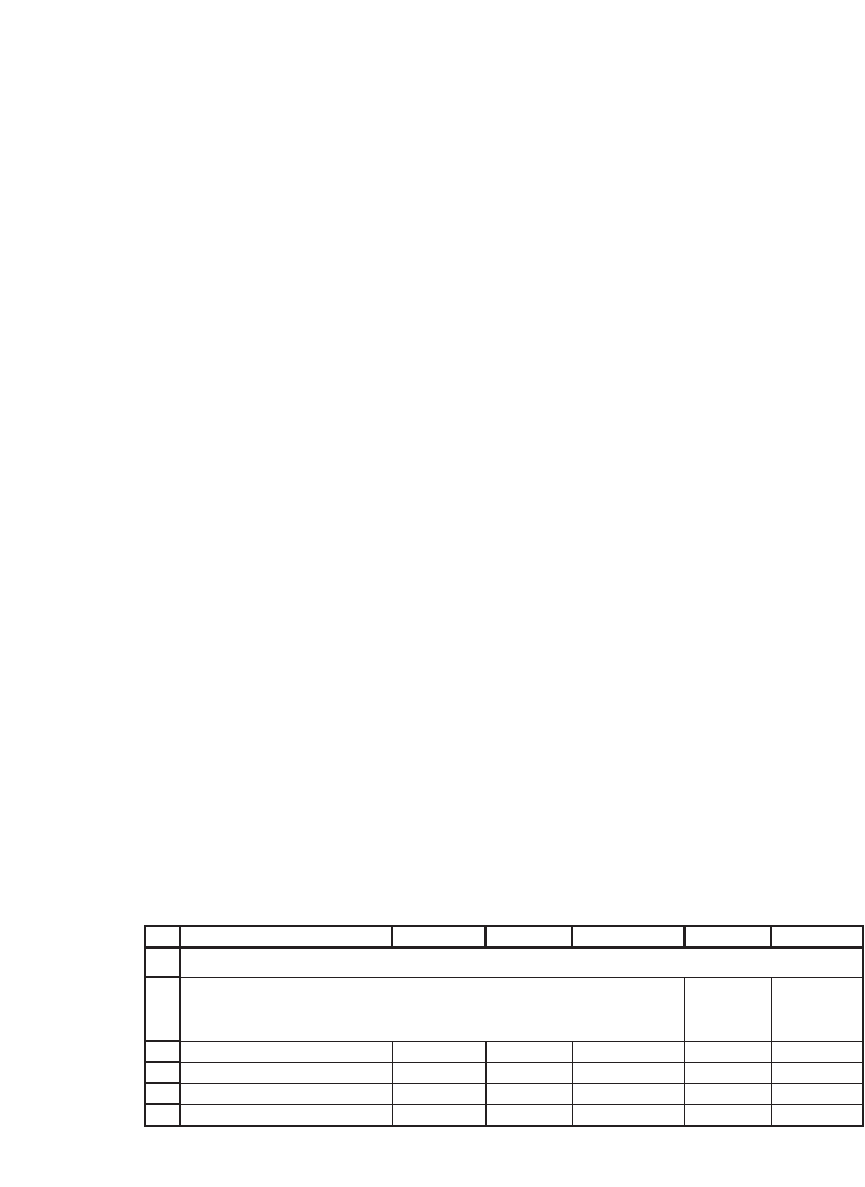
We implement the preceding formulas in a numerical example. Suppose
that there are four risky assets that have the following expected returns
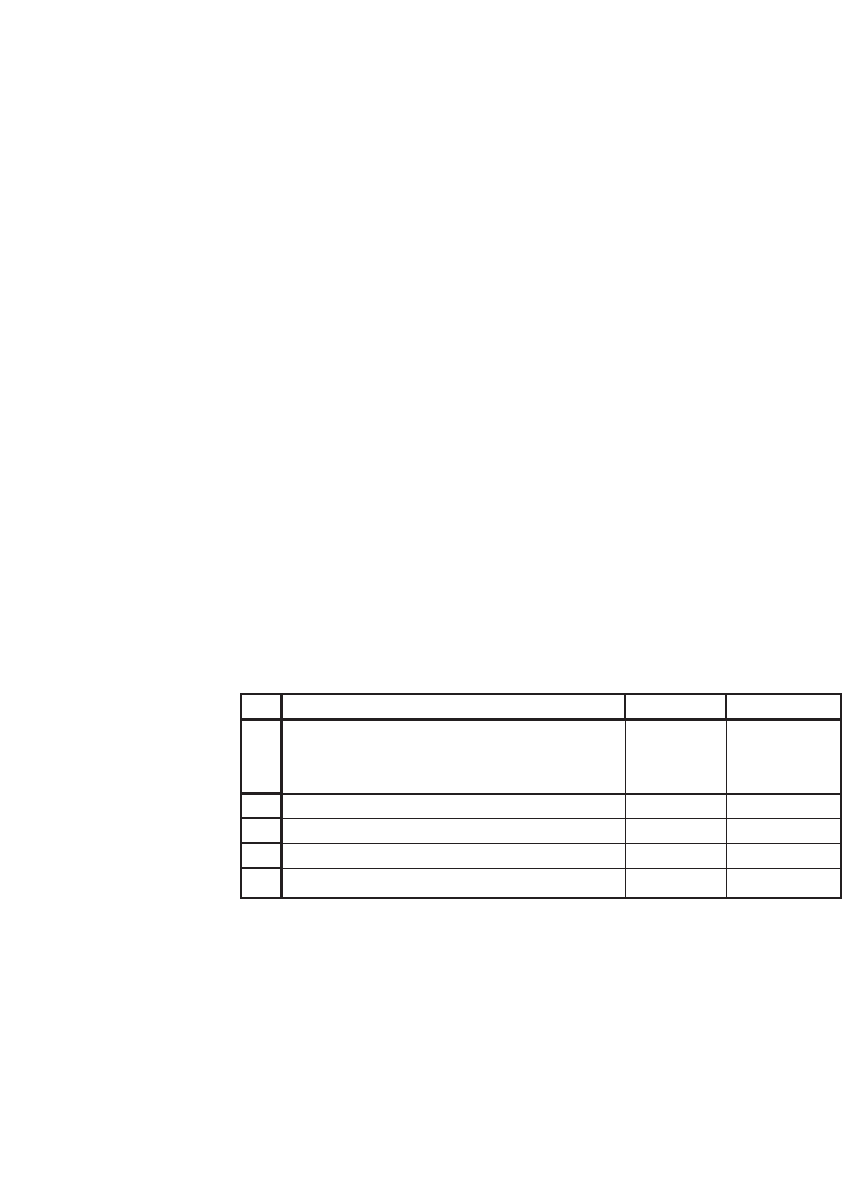
and variance-covariance matrix:
1
2
3
4
5
6
ABCDE
Mean
returns
E
F
(r)
0.10 0.01 0.03 0.05 6%
0.01 0.30 0.06 -0.04 8%
0.03 0.06 0.40 0.02 10%
0.05 -0.04 0.02 0.50 15%
Variance-covariance, S
A FOUR-ASSET PORTFOLIO PROBLEM
249 Portfolio Models—Introduction
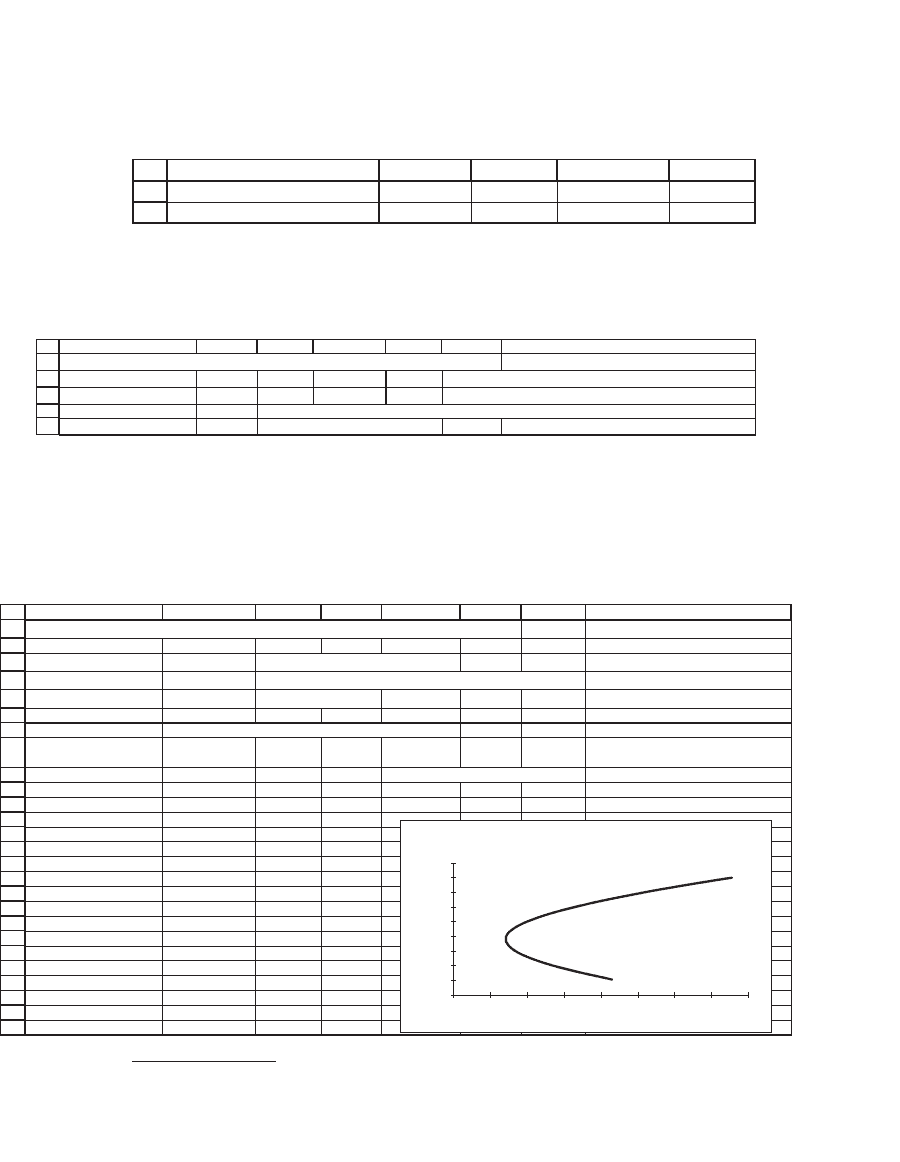
We consider two portfolios of risky assets:
8
9
ABCD
Portfolio x 0.2 0.3 0.4 0.1
Portfolio y 0.2 0.1 0.1 0.6
E
We calculate the means, variances, and covariance of the two portfolios.
We use the Excel array function Mmult for all the calculations and the
array function Transpose to make a row vector into a column vector.
3
11
12
13
14
15
ABCDEF G
Portfolio x and y statistics: Mean, variance, covariance, correlation
Mean, E(r
x
)
9.10%
Mean, E(r
y
)
12.00% <-- =MMULT(B9:E9,$F$3:$F$6)
Variance,
σ
x
2
0.1216
Variance,
σ
y
2
0.2034 <-- =MMULT(B9:E9,MMULT(A3:D6,TRANSPOSE(B9:E9)))
Covariance(x,y) 0.0714 <-- =MMULT(B8:E8,MMULT(A3:D6,TRANSPOSE(B9:E9)))
Correlation,
ρ
xy
0.4540 <-- =B14/SQRT(B13*E13)
We can now calculate the standard deviation and return of combina-
tions of portfolios x and y. Note that once we have calculated the means,
variances, and the covariance of the returns of the two portfolios, the
calculation of the mean and the variance of any portfolio is the same as
for the two-asset case.
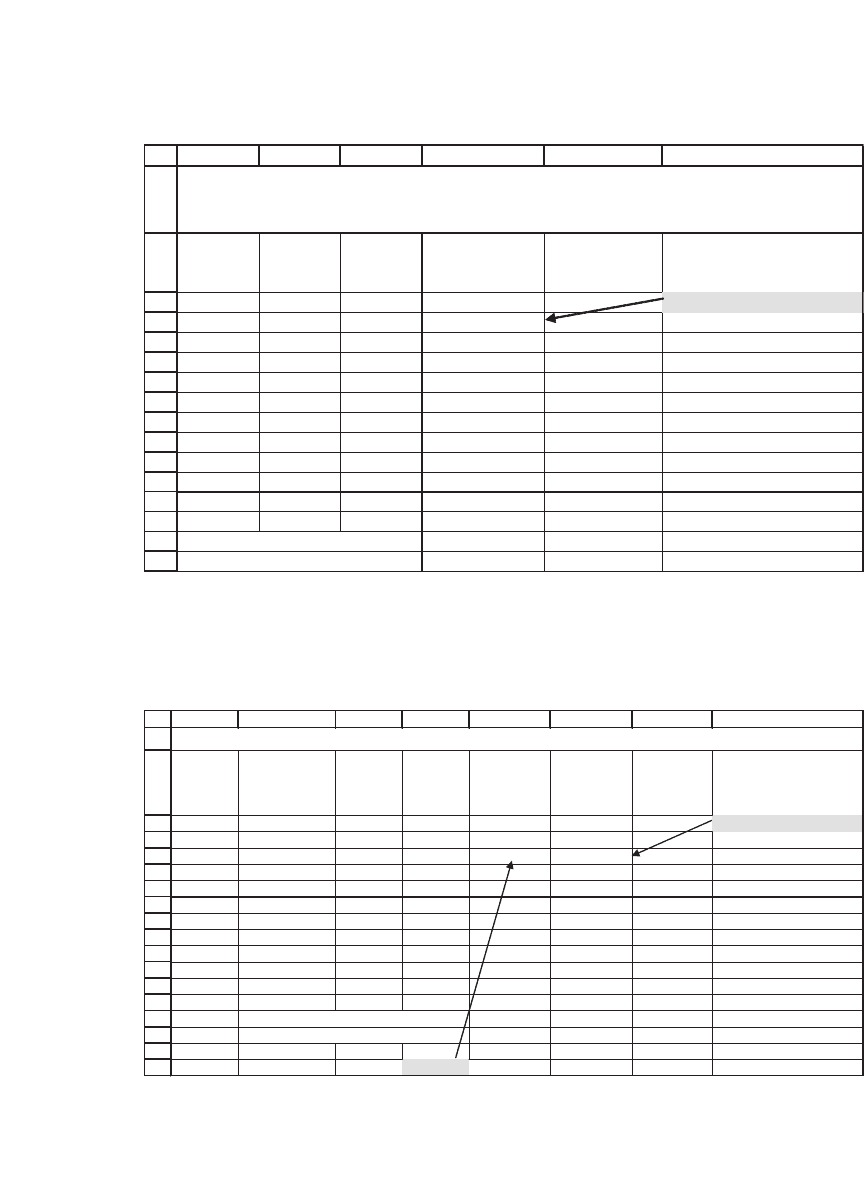
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
HGFEDCBA
Calculating returns of combinations of Portfolio X and Portfolio Y
Proportion of Portfolio X 0.3
Mean return, E(r
p
)
11.13% <-- =B26*C12+(1-B26)*F12
Variance of return, σ
p
2
14.06% <-- =B26^2*C13+(1-B26)^2*F13+2*B26*(1-B26)*C15
Stand. dev. of return, σ
p
37.50% <-- =SQRT(B28)
Table of returns (uses this example and Data|Table)
Proportion
of X
Stand. dev. Mean
37.50% 11.13% <-- Table header: =B29, =B27
0 45.10% 12.00%
0.1 42.29% 11.71%
0.2 39.74% 11.42%
0.3 37.50% 11.13%
0.4 35.63% 10.84%
0.5 34.20% 10.55%
0.6 33.26% 10.26%
0.7 32.84% 9.97%
0.8 32.99% 9.68%
0.9 33.67% 9.39%
1 34.87% 9.10%
1.1 36.53% 8.81%
1.2 38.60% 8.52%
Returns of Combinations of Portfolios X
and Y
8%
9%
9%
10%
10%
11%
11%
12%
12%
13%
30% 32% 34% 36% 38% 40% 42% 44% 46%
Standard deviation
Mean return
3. Remember that MMult and Transpose are array functions and must be entered by
pushing [Ctrl]+[Shift]+[Enter] simultaneously.

250 Chapter 8
8.5 Effi cient Portfolios
An effi cient portfolio is the portfolio of risky assets that gives the lowest
variance of return of all portfolios having the same expected return.
Alternatively, we may say that an effi cient portfolio has the highest
expected return of all portfolios having the same variance. Mathemati-
cally, we may defi ne an effi cient portfolio as follows: For a given return
m, an effi cient portfolio p = [x
1
, x
2
, . . . , x
N
] is one that solves
min ( )xx r
ijij p
ji
σ
=
∑∑
Var
subject to
xr E r
x
ii
i
p
i
i
==
=
∑
∑
μ
()
1
The effi cient frontier is the set of all effi cient portfolios. As shown by
Black (1972), the effi cient frontier is the set of all convex combinations
of any two effi cient portfolios. This statement means that if x = [x
1
, x
2
, . . . ,
x
N
] and y = [y
1
,
y
2
, . . . , y
N
] are effi cient portfolios and if a is a constant,
then the portfolio Z defi ned by
zax ay
ax a y
ax a y
ax a y
NN
=+− =
+−
+−
+−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
()
()
()
()
1
1
1
1
11
22
is also effi cient. Thus we can fi nd the whole effi cient frontier if we can
fi nd any two effi cient portfolios.
By this theorem, once we have found two effi cient portfolios x and y,
we know that any other effi cient portfolio is a convex combination of x
and y. If we denote the mean and variance of x and y by {E(r
x
), s
2
x
} and
{E(r
y
), s
2
y
}, and if z = ax + (1 − a)y, then
Er aEr aEr
aaaaxy
zx y
zx y
() ()( )()
() ()
=+−
=+− +−
1
121
222 22
σσ σ
Cov( , )
==+− +−aaaaxSy
xy
T22 2 2
121
σσ
() ()
251 Portfolio Models—Introduction
Further details of the calculation of effi cient portfolios are discussed in
Chapter 9.
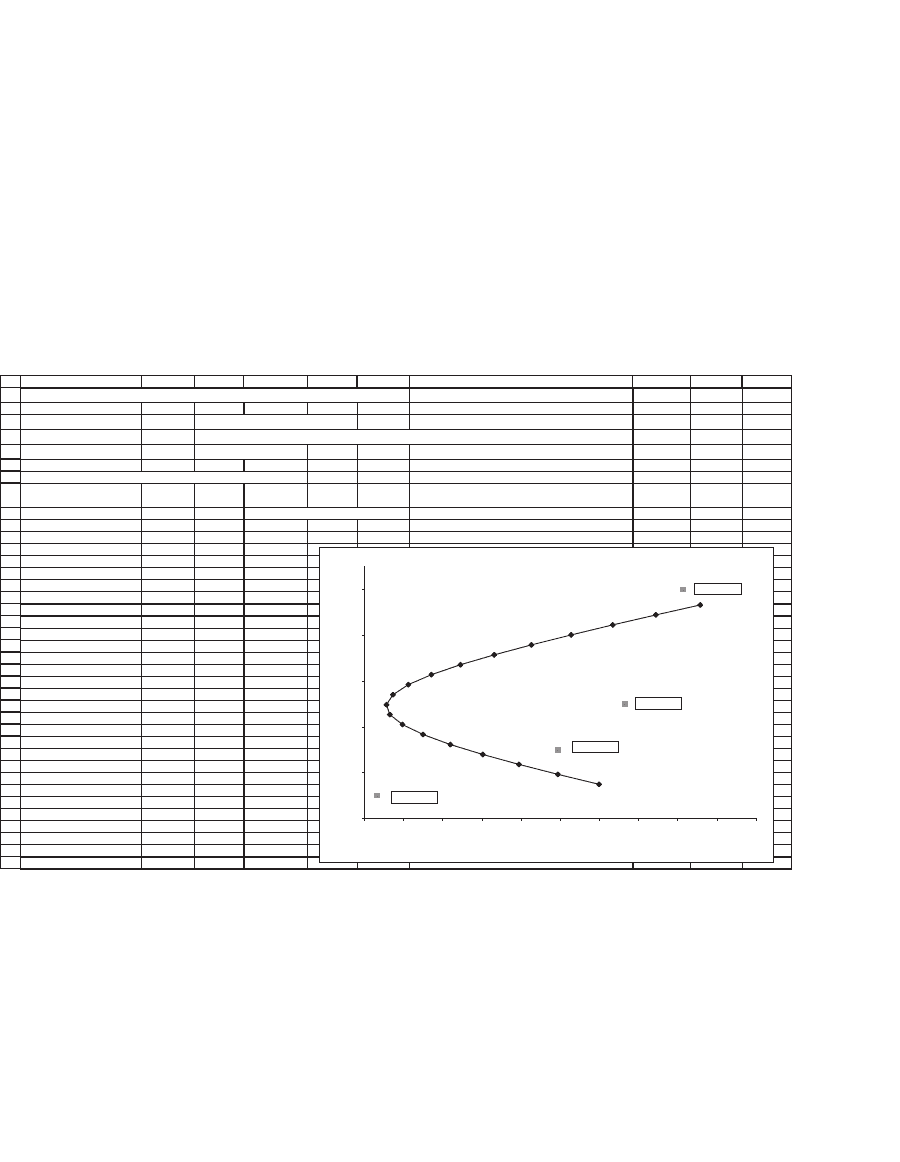
8.5.1 Showing That Portfolios x and y Are Not Effi cient
To show that effi ciency is a nontrivial concept, we show that the two
portfolios whose combinations are graphed in the previous section are
not effi cient. This fact is easy to see if we extend the data table to include
numbers for the individual stocks:
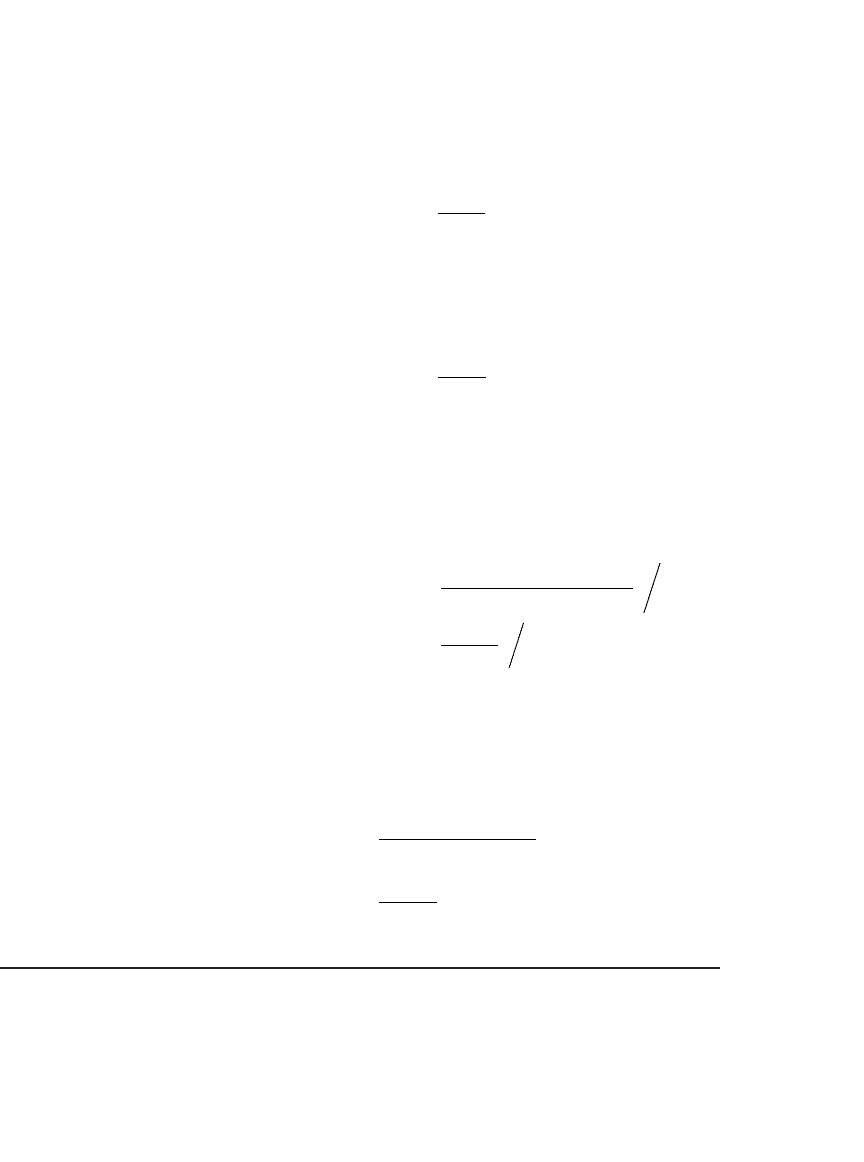
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
ABCDEF G HI
Calculating returns of combinations of Portfolio x and Portfolio y
Proportion of Portfolio x 0.3
Mean return, E(r
p
)
11.13% <-- =B18*B12+(1-B18)*E12
Variance of return,
σ
p
J
2
14.06% <-- =B18^2*B13+(1-B18)^2*E13+2*B18*(1-B18)*B14
Stand. dev. of return, σ
p
37.50% <-- =SQRT(B20)
Table of returns (uses this example and Data|Table)
Proportion
of X
Stand. dev. Mean
37.50% 11.13% <-- Table header: =B21,=B19
-0.80 72.88% 14.32%
-0.65 67.23% 13.89%
-0.50 61.72% 13.45%
-0.35 56.40% 13.02%
-0.20 51.33% 12.58%
-0.05 46.59% 12.15%
0.10 42.29% 11.71%
0.25 38.57% 11.28%
0.40 35.63% 10.84%
0.55 33.66% 10.41%
0.70 32.84% 9.97%
0.85 33.26% 9.54%
1.00 34.87% 9.10%
1.15 37.52% 8.67%
1.30 41.00% 8.23%
1.45 45.13% 7.80%
1.60 49.74% 7.36%
1.75 54.72% 6.93%
1.90 59.96% 6.49%
Stock A 31.62% 6.00%
Stock B 54.77% 8.00%
Stock C 63.25% 10.00%
Stock D 70.71% 15.00%
Portfolios x and y and the Four Stocks
5%
7%
9%
11%
13%
15%
30% 35% 40% 45% 50% 55% 60% 65% 70% 75% 80%
Standard deviation
Mean return
Stock A
Stock D
Stock C
Stock B
Were the two portfolios effi cient, then all of the individual stocks
would fall on or inside the graph of the combinations. In our case, two
of the stock returns (stock A and stock D) fall outside the frontier
created by combinations of portfolios x and y; thus x and y cannot be
effi cient portfolios. In Chapter 9 you will learn to compute effi cient
portfolios, and as you will see there, this task requires considerably more
computation.
252 Chapter 8
8.6 Conclusion
In this chapter we have reviewed the basic concepts and mathematics of
portfolios. In succeeding chapters we shall describe how to compute the
variance-covariance matrix from asset returns and how to calculate effi -
cient portfolios.
Exercises
1. The attached spreadsheet fm3_chapter08.xls includes price data for the Dow-Jones
30 Industrials from July 1997 through July 2007. Isolating the data for Alcoa (AA)
and Johnson & Johnson (JNJ), confi rm the following statistics about the returns of
these two stocks:
1
2
3
4
5
6
7
8
9
10
11
12
ABCDEF G
Monthly statistics AA JNJ
Average 0.68% 0.72% <
--
=AVERAGE(F16:F135)
Sigma 10.12% 5.84% <
--
=STDEVP(F16:F135)
Covariance 0.0002 <
--
=COVAR(C16:C135,F16:F135)
Correlation 0.0398 <
--
=CORREL(C16:C135,F16:F135)
0.0398 <
--
=C5/(C4*F4)
Annual statistics AA JNJ
Average 8.11% 8.61% <
--
=12*F3
Sigma 35.07% 20.24% <
--
=SQRT(12)*F4
ALCOA (AA) AND JOHNSON & JOHNSON (JNJ)
Return statistics, 1997-2007
2. Using the data from the previous exercise, compute the statistics for each of the
preceding two subperiods, July 1997–July 2002 and July 2002–July 2007.
3. Repeat exercise 2 for Merck (MRK) and Johnson & Johnson (JNJ). Merck had a
big crisis in 2003–2004 related to Vioxx (http://en.wikipedia.org/wiki/Vioxx). Is this
evident in the statistics?
4. Suppose that in July 1997 you bought and held through July 2007 a portfolio com-
posed of 50% Alcoa (AA) and 50% Johnson & Johnson (JNJ) stock.
a. Compute the average monthly return and standard deviation of returns for this
portfolio.
b. Vary the proportion of Alcoa from −1 to 1 and plot the portfolio average returns
as a function of the standard deviation.
5. Following are annual return statistics for two mutual funds from the Vanguard
family:

253 Portfolio Models—Introduction
Use Excel to graph the combinations of standard deviation of return (x-axis) and
expected return (y-axis) from varying the percentage of Index 500 Fund in the
portfolio from 0% to 100%.
6. Using the database of the DJ Industrials (for 1997–2007), compute for General
Electric (GE), Home Depot (HD), and Procter & Gamble (PG)
a. Average monthly returns
b. Covariances of the monthly returns
c. Monthly expected return and monthly standard deviation of a portfolio that is
equally invested in the three stocks
7. Suppose that X and Y are two random variables and that Y = X
2
. Let X have values
−5, −4, −2, 2, 4, 5 with equal probabilities. Show that the correlation coeffi cient
between X and Y is zero. Does this fact mean that X and Y are independent random
variables?
8. Consider two assets, A and B, that have the following means and variances:
Er Er
rr
AB
AB
() . () .
() . .
==
==
003 005
0 0025 0 0045
,
Var , Var( )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
AB
Source: http://www.vanguard.com
Year ended
31 December
Index 500
Fund
Windsor
Fund
1997 33.40% 22.00%
1996 23.00% 26.40%
1995 37.60% 30.10%
1994 1.30% -0.10%
1993 10.10% 19.40%
1992 7.60% 16.50%
1991 30.50% 28.60%
1990 -3.10% -15.50%
1989 31.70% 15.00%
1988 16.60% 28.70%
1987 5.30% 1.20%
1986 18.70% 20.30%
1985 31.80% 28.00%
1984 6.30% 19.50%
Vanguard's Windsor Fund and Index
500 Fund Returns
The Index 500 fund mimics the SP500 index; the
Windsor Fund is an "aggressive" growth fund
C
254 Chapter 8
Now consider three cases:
ρρρ
AB AB AB
=+ =− =110,,.
Graph the combinations of portfolio means and variances for each case. (Graphs
like these appear in virtually all elementary fi nance books. The standard deviation
usually appears on the x-axis and the portfolio mean return on the y-axis. In this
case, if you want to put all three graphs on the same set of axes, you will have to
reverse this arrangement or use a trick.)
9. Consider a three-asset world with the following parameters:
Mean returns
%
%
%
, Variance-covariance matrix=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
=
10
12
14
003 002 005
00204006
005 006 06
.. .
...
.. .
−
−
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
Suppose you have two portfolios with the following portfolio weights:
Portfolio
Portfolio
1030205
2050401
=
()
=
()
...
...
a. Calculate the mean and variance of each portfolio’s returns and the covariance
and correlation coeffi cient of the portfolios’ returns.
b. Create a graph of the means and variance of convex combinations of the
portfolios.
10. In the following spreadsheet, implement the correct formula for cell B12 so that the
portfolio gives the target return indicated in cell B10:
1
2
3
4
5
BA
Mean
return
Standard
deviation
of return
Stock 1 12% 35%
Stock 2 18% 50%
Covariance(r
1
,r
2
)
0.08350
C
11. Using the data in the previous exercise, fi nd two portfolios whose standard deviation
of returns is 45%. (There’s an analytical solution to this problem, but it can also be
solved by Solver.)

255 Portfolio Models—Introduction
Appendix 1: Adjusting for Dividends
When downloading data from Yahoo or other sources, the “adjusted
price” includes an adjustment for dividends. In this appendix we discuss
two ways of making this adjustment.
4
The fi rst, and simplest, method of
adjusting for dividends is to add them to the annual change in price. In
the following example, if you purchased GM stock at the 1986 year-end
price of $33 per share and held it for one year, you would, at the end of
the year, have made 0.57 percent.
Discretely compounded return, per1987
30 69 2 50
33 00
1 0 568=
+
−=
..
.
.ccent
The continuously compounded return is calculated by
Continuously compounded return, 1987
30 69 2 50
33 00
=
+
⎡
⎣
⎢
⎤
⎦
⎥
=
ln
..
.
00 567.percent
(The choice between discrete and continuous compounding is discussed
in appendix 2.)
4. It might be argued that since the free sources available on the Web make these adjust-
ments automatically, the details in this appendix are superfl uous. Nevertheless we think
they offer some interesting insights. (If you disagree, turn the page!)
256 Chapter 8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ABC D E F
Year
Share
price at
end year
Dividend
per share
Discretely
compounded
return
Continuously
compounded
return
1986 33.00 =(B4+C4)/B3-1
1987 30.69 2.50 0.57% 0.57%
1988 41.75 2.50 44.20% 36.60%
1989 42.25 3.00 8.38% 8.05% <-- =LN((C4+B4)/B3)
1990 34.38 3.00 -11.54% -12.26%
1991 28.88 1.60 -11.35% -12.04%
1992 32.25 1.40 16.54% 15.30%
1993 54.88 0.80 72.64% 54.60%
1994 42.13 0.80 -21.78% -24.56%
1995 52.88 1.10 28.13% 24.79%
1996 55.75 1.60 8.46% 8.12%
Arithmetic annual return
13.43% 9.92% <-- =AVERAGE(E4:E13)
Standard deviation of returns
27.15% 22.84% <-- =STDEVP(E4:E13)
GENERAL MOTORS (GM) STOCK
ADJUSTING FOR DIVIDENDS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
GH IJKLM N
Year
Effective
shares held at
beginning of
year
Share
price at
end year
Dividend
per share
Total
dividends
received
Number
of shares at
end of year
Value of
shares at
end of year
1986 33.00 33.000 =H5+K5/I5
1987 1.00 30.69 2.500 2.500 1.081 33.188
1988 1.08 41.75 2.500 2.704 1.146 47.855 <-- =L5*I5
1989 1.15 42.25 3.000 3.439 1.228 51.867
1990 1.23 34.38 3.000 3.683 1.335 45.882
1991 1.33 28.88 1.600 2.136 1.409 40.677
1992 1.41 32.25 1.400 1.972 1.470 47.403
1993 1.47 54.88 0.800 1.176 1.491 81.835
1994 1.49 42.13 0.800 1.193 1.520 64.014
1995 1.52 52.88 1.100 1.672 1.551 82.021
1996 1.55 55.75 1.600 2.482 1.596 88.963
Annualized continous return 9.92% <-- =LN(M13/M3)/10
Compound geometric return
10.43% <-- =(M13/M3)^(1/10)-1
=H5*J5
GM: REINVESTING THE DIVIDENDS IN SHARES
Dividend Reinvestment
Another way of calculating returns is to assume that the dividends are
reinvested in the stock:
Consider fi rst 1987: Since we purchased the share at the end of 1986,
we own one share at the end of 1987. If the 1987 dividend is turned into
257 Portfolio Models—Introduction
shares at the end of 1987 price, we can use it to buy 0.081 additional
shares:
New shares purchased at end of 1987
250
30 69
0 081==
.
.
.
Thus we start 1988 with 1.081 shares. Since the 1988 dividend per share
is $2.50, the total dividend received on the shares is 1.081 ∗ $2.50 = $2.704.
Reinvesting these dividends in shares gives
New shares purchased at end of 1988
2 704
41 75
0 065==
.
.
.
Thus, at the end of 1988, the holder of GM shares will have accumulated
1 + 0.081 + 0.065 = 1.146 shares.
As the spreadsheet fragment shows, this reinvestment of dividends will
produce a holding of 1.596 shares at the end of 1996, worth $88.963.
We can calculate the return on this investment in one of two ways:
Continuously compounded return
End- value
Beginning inves
= ln
1996
ttment
percent
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
=
10
88 963
33 00
10 9 92ln
.
.
.
Note that this continuously compounded return (the method preferred
in this book) is the same as that calculated in the fi rst spreadsheet frag-
ment in this appendix from the annual returns (cell E15).
An alternative is to calculate the geometric return:
Compound geometric return
End- value
Initial investment
=
⎡
⎣
⎢
⎤
1996
⎦⎦
⎥
−
=
⎡
⎣
⎢
⎤
⎦
⎥
−=
110
110
1
88 963
33 00
11043
/
/
.
.
.percent
Appendix 2: Continuously Compounded versus Geometric Returns
Using the continuously compounded return assumes that P
t
= P
t−1
e
r
t
, where
r
t
is the rate of return during the period (t − 1, t). Suppose that r
1
, r
2
, . . . , r
12
are the returns for 12 periods (a period could be a month or it could be a
year), then the price of the stock at the end of the 12 periods will be
