Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

•

Chapter 14 shows how to do an event study. An event study is an

attempt to determine whether a particular event in the capital market

or in the life of a company affected a company’s stock market perfor-

mance. The event-study methodology aims to separate company-speciﬁ c

events from market- and/or industry-speciﬁ c events, and has often been

used as evidence for or against market efﬁ ciency.

•

Finally, Chapter 15 is an introduction to value-at-risk (VaR) techniques

in a portfolio context.

238 Portfolio Models

Portfolio Models—Introduction

8.1 Overview

In this chapter we review the basic mechanics of portfolio calculations.

We start with a simple example of two assets, showing how to derive the

return distributions from historical price data. We then discuss the general

case of N assets; for this case it becomes convenient to use matrix nota-

tion and exploit Excel’s matrix-handling capabilities.

It is useful before going on to review some basic notation: Each

asset i (assets may be stocks, bonds, real estate, or whatever,

although our numerical examples will be largely conﬁ ned to stocks) is

characterized by several statistics: E(r

), the expected return on asset i;

Var(r

), the variance of asset i’s return; and Cov(r

, r

), the covariance of

asset i’s and asset j’s returns. Occasionally we will use m

to denote the

expected return on asset i. In addition, it will often be convenient to

write Cov(r

, r

) as s

and Var(r

) as s

(instead of s

, as usual). Since the

covariance of an asset’s returns with itself, Cov(r

, r

), is in fact the vari-

ance of the asset’s returns, this notation is not only economical but also

logical.

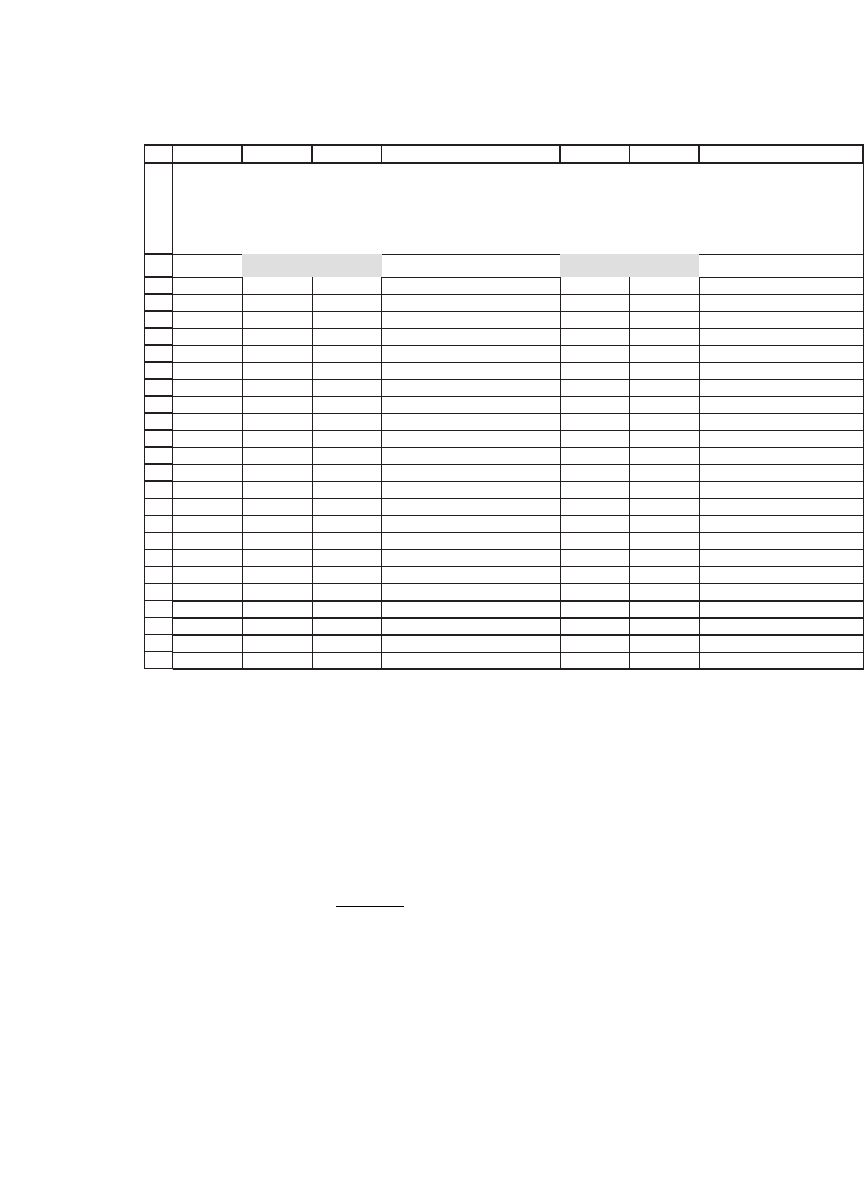
8.2 Computing Returns for Walmart and Target

In this section we compute the return statistics for two stocks:

Walmart (stock symbol WMT) and Target (TGT). We download the

price and dividend data for each stock from Yahoo (see Chapter 2,

appendix 2). With some slight massaging, we get the following

spreadsheet:

240 Chapter 8

These data give the closing price at the end of each month for each stock

and make an appropriate adjustment for dividends (see appendix 1 of

this chapter). First we calculate the monthly return for each stock. This

is the percentage return that would be earned by an investor who bought

the stock at the end of a particular month t − 1 and sold it at the end of

the following month. For Walmart’s stock in month t, the monthly return

WMT,t

is deﬁ ned as

WMT t

⎛

⎝

⎜

⎞

⎠

⎟

−

We note two things about this return calculation: First, we use the

continuously compounded return on the stock. An alternative would

have been to use the discrete return, P

WMT,t

WMT,t−1

− 1. Appendix 2 at

the end of this chapter discusses the reasons for our choice of the con-

tinuously compounded return. Second, the return data incorporate the

dividends into the prices, in a manner explained in appendix 1.

We now make a heroic assumption: We assume that the return data

for the 60 months represent the distribution of the returns for the coming

ABC D EF G

Date WMT TGT WMT TGT

5-Jul-01 26.07 37.40

1-Aug-01 22.00 33.53 -16.97% -10.92% <-- =LN(C5/C4)

4-Sep-01 20.07 30.73 -9.18% -8.72% <-- =LN(C6/C5)

1-Oct-01 20.02 30.15 -0.25% -1.91% <-- =LN(C7/C6)

1-Nov-01 23.35 36.38 15.39% 18.78%

3-Dec-01 24.79 39.79 5.98% 8.96%

2-Jan-02 23.03 43.04 -7.36% 7.85%

4-Feb-02 18.09 40.66 -24.14% -5.69%

1-Mar-02 19.17 41.85 5.80% 2.88%

1-Apr-02 20.25 42.36 5.48% 1.21%

1-May-02 22.79 40.29 11.82% -5.01%

3-Jun-02 20.52 37.03 -10.49% -8.44%

3-Oct-05 50.93 55.37 7.95% 6.97%

1-Nov-05 52.19 53.31 2.44% -3.79%

1-Dec-05 55.31 54.76 5.81% 2.68%

3-Jan-06 55.63 54.54 0.58% -0.40%

1-Feb-06 58.46 54.29 4.96% -0.46%

1-Mar-06 60.23 51.90 2.98% -4.50%

3-Apr-06 65.46 52.99 8.33% 2.08%

1-May-06 60.84 48.92 -7.32% -7.99%

1-Jun-06 67.51 48.87 10.40% -0.10%

3-Jul-06 67.65 49.17 0.21% 0.61%

Prices Returns

PRICE AND RETURN DATA FOR WALMART (WMT)

AND TARGET (TGT)

Yahoo adjusts prices for dividends

241 Portfolio Models—Introduction

month. We thus assume that the past gives us some information about

the way returns will behave in the future. This assumption allows us to

assume that the average of the historic data represents the expected

monthly return from each stock. It also allows us to assume that we may

learn from the historic data what is the variance of the future returns.

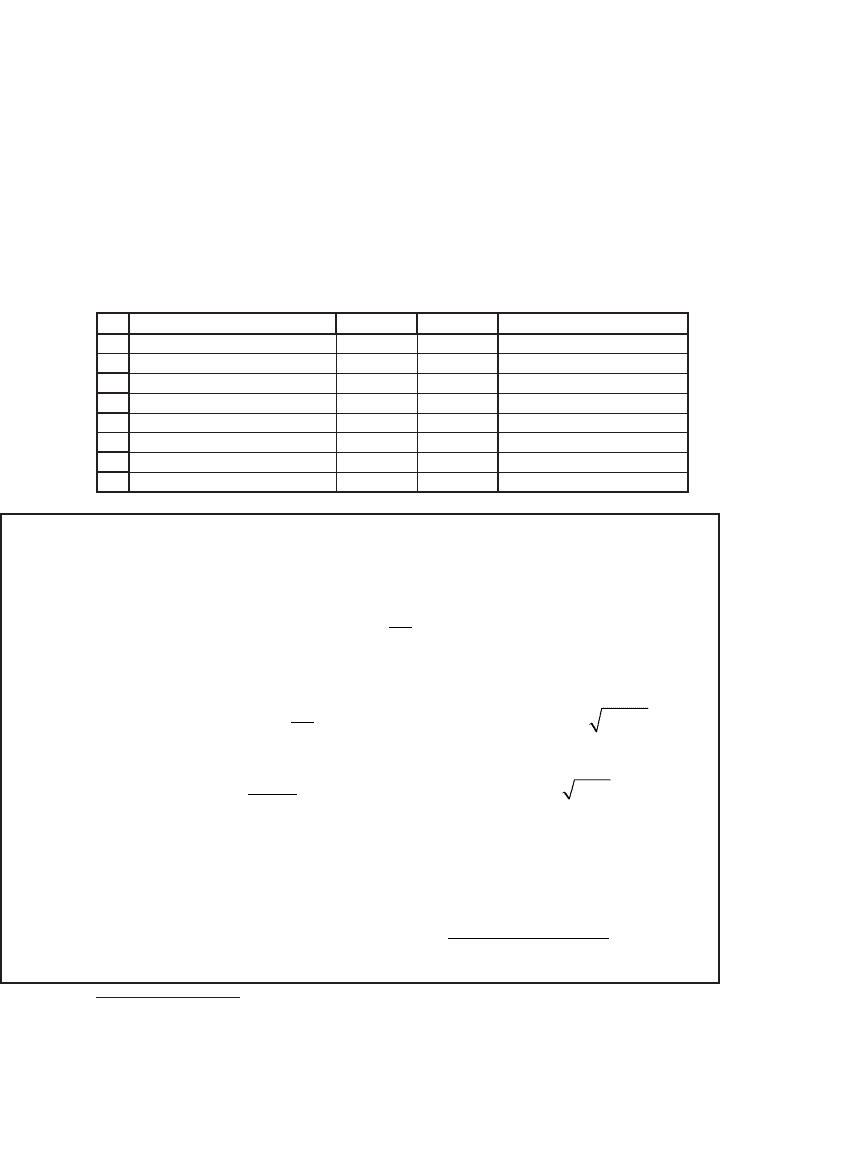
Using the Average, Varp, and Stdevp functions in Excel, we calculate the

statistics for the return distribution:

DEFG

WMT TGT

Monthly mean 1.59% 0.46% <-- =AVERAGE(F5:F64)

Monthly variance 0.0093 0.0052 <-- =VARP(F5:F64)

Monthly standard deviation 9.63% 7.19% <-- =STDEVP(F5:F64)

Annual mean 19.07% 5.47% <-- =12*F67

Annual variance 0.1114 0.0620 <-- =12*F68

Annual standard deviation 33.37% 24.90% <-- =SQRT(F72)

Excel and Statistics Note

Note that we have used Varp instead of Var and Stdevp instead of Stdev.

When the mean is deﬁ ned by

WMT WMT t

()=

∑

, then the deﬁ nitions of

these four functions are given by

Varp Stdevp V==−=

∑

Population variance

rEr

WMT t WMT

[()]; aarp

Var Stdev Var==

−

−=

∑

Sample variance

rEr

WMT t WMT

[()];

There are two reasons why we choose Varp instead of Var: The ﬁ rst reason

is that we implicitly assume that the historical data represent the distribution.

The second reason for choosing Varp is that our choice makes the Excel Slope

function consistent with the deﬁ nition of b,

it Mt

Covariance( , )

Variance( )

1. There’s another point of view on this issue. As stated by Press et al. in their splendid

book Numerical Recipes: “There is a long story about why the denominator is M − 1

instead of M. If you have never heard that story, you may consult any good statistics

text. . . . We might also comment that if the difference between M and M − 1 ever

matters to you, then you are up to no good anyway—e.g., trying to substantiate a

questionable hypothesis with marginal data” (Numerical Recipes, 1st edition, page 456,

slightly adapted).

242 Chapter 8

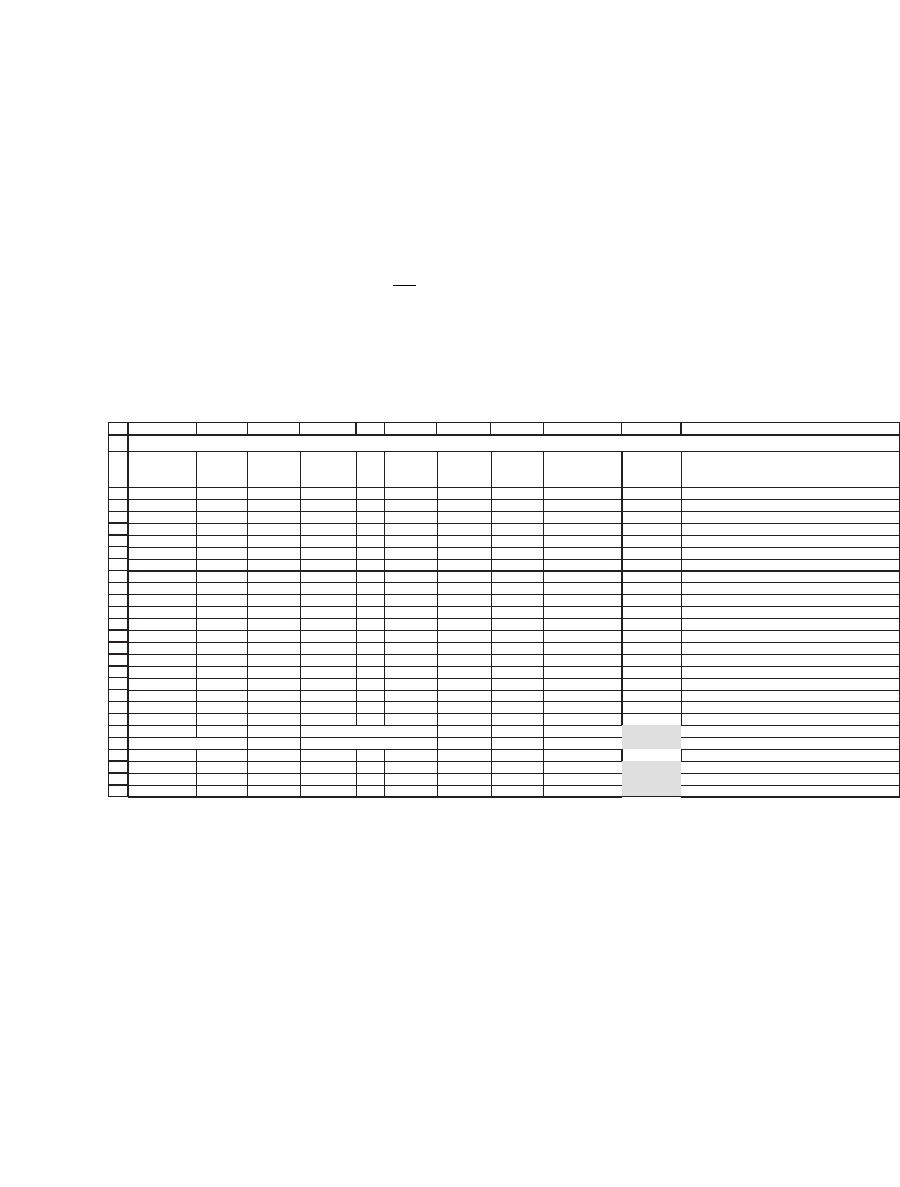
Next we want to calculate the covariance of the returns. The covariance

(and the correlation coefﬁ cient, which is derived from it) measures the

degree to which the returns on the two assets move together. The deﬁ ni-

tion is

Cov ,

()[()][()]rr

rErrEr

WMT TGT WMT t WMT WMT t WMT

=−⋅−

∑

where M is the number of points in the distribution (in our case, M =

60). This computation is easily set up in Excel:

ABCDEFGH I J K

Date WMT Return

Return

minus

mean

TGT Return

Return

minus

mean

Product

5-Jul-01 26.07 37.40

1-Aug-01 22.00 -16.97% -18.56% 33.53 -10.92% -11.38% <-- =G4-$G$65 0.0211 <-- =D4*H4

4-Sep-01 20.07 -9.18% -10.77% 30.73 -8.72% -9.18% 0.0099

1-Oct-01 20.02 -0.25% -1.84% 30.15 -1.91% -2.36% 0.0004

1-Nov-01 23.35 15.39% 13.80% 36.38 18.78% 18.33% 0.0253

3-Dec-01 24.79 5.98% 4.40% 39.79 8.96% 8.50% 0.0037

2-Jan-02 23.03 -7.36% -8.95% 43.04 7.85% 7.40% -0.0066

4-Feb-02 18.09 -24.14% -25.73% 40.66 -5.69% -6.14% 0.0158

1-Mar-02 19.17 5.80% 4.21% 41.85 2.88% 2.43% 0.0010

1-Apr-02 20.25 5.48% 3.89% 42.36 1.21% 0.76% 0.0003

1-Nov-05 52.19 2.44% 0.85% 53.31 -3.79% -4.25% -0.0004

1-Dec-05 55.31 5.81% 4.22% 54.76 2.68% 2.23% 0.0009

3-Jan-06 55.63 0.58% -1.01% 54.54 -0.40% -0.86% 0.0001

1-Feb-06 58.46 4.96% 3.37% 54.29 -0.46% -0.92% -0.0003

1-Mar-06 60.23 2.98% 1.39% 51.90 -4.50% -4.96% -0.0007

3-Apr-06 65.46 8.33% 6.74% 52.99 2.08% 1.62% 0.0011

1-May-06 60.84 -7.32% -8.91% 48.92 -7.99% -8.45% 0.0075

1-Jun-06 67.51 10.40% 8.81% 48.87 -0.10% -0.56% -0.0005

3-Jul-06 67.65 0.21% -1.38% 49.17 0.61% 0.16% 0.0000

Average 1.59% <-- =AVERAGE(C4:C63) 0.46% Covariance 0.0038 <-- =AVERAGE(J4:J63)

Standard deviation 9.63% <-- =STDEVP(D4:D63) 7.19% 0.0038 <-- =COVAR(D4:D63,H4:H63)

Correlation 0.5484 <-- =J65/(C66*G66)

0.5484 <-- =J65/(STDEVP(C4:C63)*STDEVP(G4:G63))

0.5484 <-- =CORREL(C4:C63,G4:G63)

COMPUTING THE COVARIANCE FOR WALMART (WMT) AND TARGET (TGT)

The column Product contains the multiple of the deviation from the

mean in each month, that is, the terms [r

WMT,t

− E(r

WMT

)] [r

TGM,t

− E(r

TGT

)],

for t = 1, . . . , 12. The covariance is Average(product) = 0.0038. While it

is worthwhile calculating the covariance this way at least once, there is

a shorter way, which is also illustrated: The Excel function Covar(SLE

returns,BBY returns) calculates the covariance directly. To calculate the

covariance using Covar there is no necessity to ﬁ nd the difference

between the returns and the means. Simply use Covar directly on the

columns, as illustrated in cell J66 of the spreadsheet.

The covariance is a hard number to interpret, since its size depends

on the units in which we measure the returns. (If we were to write the

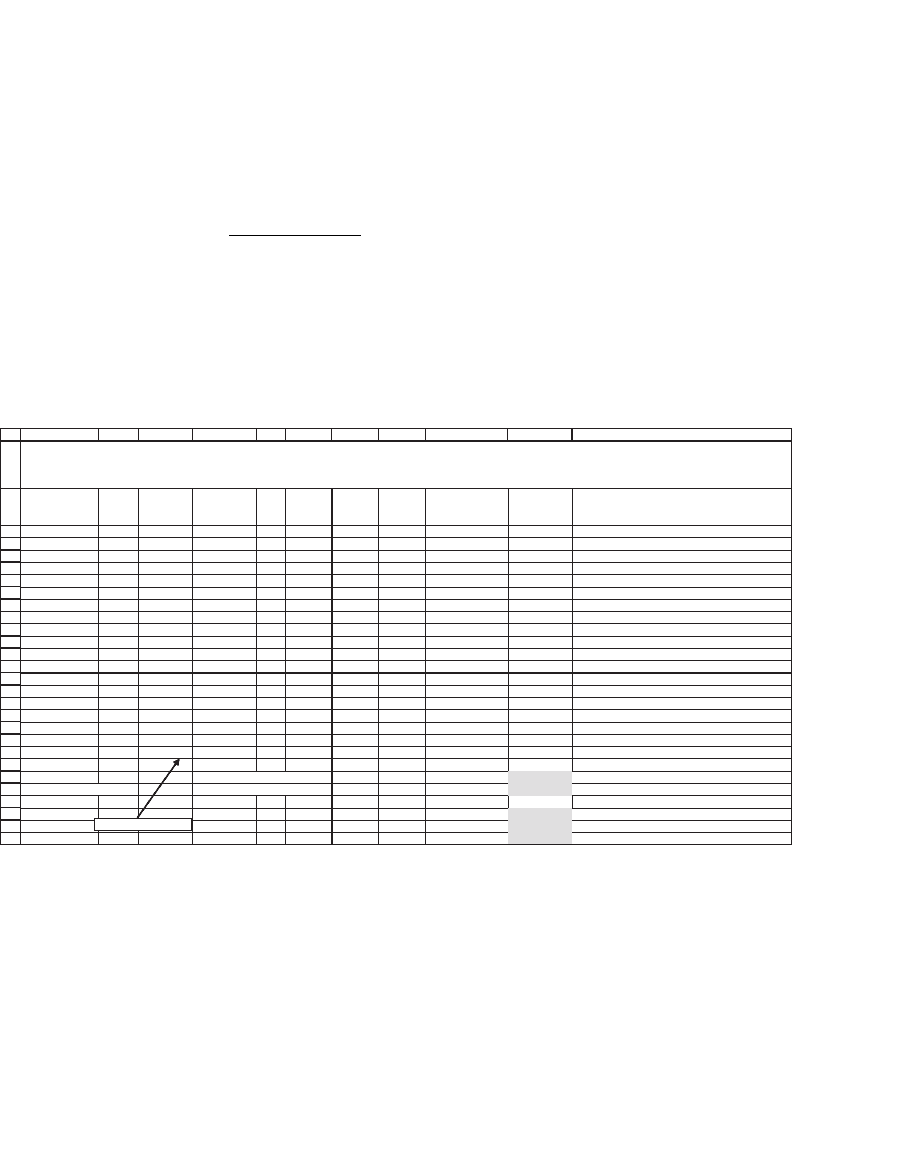
243 Portfolio Models—Introduction

returns in percentages—i.e., 4 instead of 0.04—then the covariance would

be 38, which is 10,000 times the number we just calculated.) We can also

calculate the correlation coefﬁ cient r

, which is deﬁ ned as

σσ

WMT TGT

Cov ,

()

The correlation coefﬁ cient is unit-free; calculating it for our example

gives r

WMT,TGT

= 0.4415. As illustrated in the preceding spreadsheet, the

correlation coefﬁ cient can be calculated directly in Excel using the func-

tion Correl(WMT returns,TGT returns) (cell J70).

ABCDEFGH I J K

Date WMT Return

Return

minus

mean

TGT Return

Return

minus

mean

Product

5-Jul-01 26.07 37.40

1-Aug-01 22.00 -16.97 -18.56 33.53 -10.92 -11.38 <-- =G4-$G$65 211.24 <-- =D4*H4

4-Sep-01 20.07 -9.18 -10.77 30.73 -8.72 -9.18 98.84

1-Oct-01 20.02 -0.25 -1.84 30.15 -1.91 -2.36 4.34

1-Nov-01 23.35 15.39 13.80 36.38 18.78 18.33 252.87

3-Dec-01 24.79 5.98 4.40 39.79 8.96 8.50 37.37

2-Jan-02 23.03 -7.36 -8.95 43.04 7.85 7.40 -66.22

4-Feb-02 18.09 -24.14 -25.73 40.66 -5.69 -6.14 158.12

1-Mar-02 19.17 5.80 4.21 41.85 2.88 2.43 10.22

1-Apr-02 20.25 5.48 3.89 42.36 1.21 0.76 2.94

1-Nov-05 52.19 2.44 0.85 53.31 -3.79 -4.25 -3.63

1-Dec-05 55.31 5.81 4.22 54.76 2.68 2.23 9.39

3-Jan-06 55.63 0.58 -1.01 54.54 -0.40 -0.86 0.87

1-Feb-06 58.46 4.96 3.37 54.29 -0.46 -0.92 -3.09

1-Mar-06 60.23 2.98 1.39 51.90 -4.50 -4.96 -6.91

3-Apr-06 65.46 8.33 6.74 52.99 2.08 1.62 10.93

1-May-06 60.84 -7.32 -8.91 48.92 -7.99 -8.45 75.26

1-Jun-06 67.51 10.40 8.81 48.87 -0.10 -0.56 -4.92

3-Jul-06 67.65 0.21 -1.38 49.17 0.61 0.16 -0.22

Average 1.59 <-- =AVERAGE(C4:C63) 0.46 Covariance 37.9731 <-- =AVERAGE(J4:J63)

Standard deviation 9.63 <-- =STDEVP(D4:D63) 7.19 37.9731 <-- =COVAR(D4:D63,H4:H63)

Correlation 0.5484 <-- =J65/(C66*G66)

0.5484 <-- =J65/(STDEVP(C4:C63)*STDEVP(G4:G63))

0.5484 <-- =CORREL(C4:C63,G4:G63)

COMPUTING THE COVARIANCE FOR WALMART (WMT) AND TARGET (TGT)

All percentages expressed as whole numbers: The covariance grows by a factor of 10,000, but the correlation is unchanged

=LN(B63/B62)*100

The correlation coefﬁ cient measures the degree of linear relation

between the returns of Stock A and Stock B. The following facts can be

proven about the correlation coefﬁ cient:

•

The correlation coefﬁ cient is always between +1 and −1: −1 ≤ r

≤ 1.

•

If the correlation coefﬁ cient is +1, then the returns on the two assets

are linearly related with a positive slope; that is, if r

= 1, then

rcdr d

At Bt

=+ >,where 0

244 Chapter 8

•

If the correlation coefﬁ cient is −1, then the returns on the two assets

are linearly related with a positive slope; that is, if r

= −1, then

rcdr d

At Bt

=+ <,where 0

•

If the return distributions are independent, then the correlation coef-

ﬁ cient will be zero. (The opposite is not true: If the correlation coefﬁ cient

is zero, this fact does not necessarily mean that the returns are indepen-

dent. See the exercises for an example.)

8.2.1 A Different View of the Correlation Coefﬁ cient

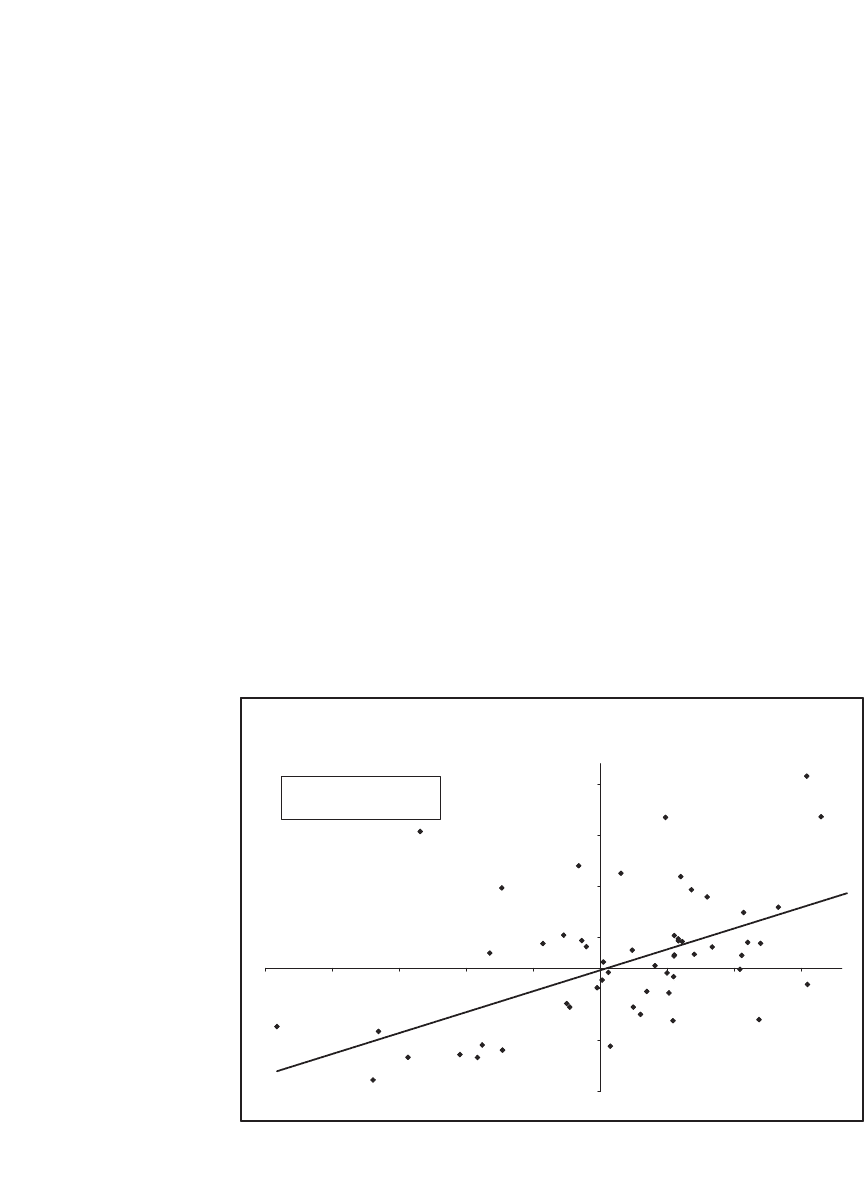
Another way to look at the correlation coefﬁ cient is to graph

the Walmart and Target returns on the same axes and then use the

Excel Trendline facility to regress the returns of TGT on those of

WMT. (The use of Excel’s Trendline function—used to calculate the

regression equation—is explained in Chapter 33.) You can conﬁ rm from

the previous calculations that the regression R

is the correlation

squared:

Graphing Walmart Returns (x-axis) and Target Returns (y-axis)

Is the Correlation

y = 0.4091x – 0.0019

= 0.3008

–12%

–7%

–2%

13%

18%

–25% –20% –15% –10% –5% 0% 5% 10% 15%

Walmart

Target

245 Portfolio Models—Introduction

8.3 Calculating Portfolio Means and Variances

In this section we show how to do the basic calculations for a portfolio’s

mean and variance. Suppose we form a portfolio invested equally in

WMT and TGT. What will be the mean and the variance of this portfolio?

It is worth doing the brute force calculations at least once in Excel.

ABCD E F G HI J

Proportion of WMT 0.5

Proportion of TGT 0.5 <-- =1-B2

WMT

return

TGT

return

Portfolio

return

1-Aug-01 -16.97% -10.92% -13.95% <-- =$B$2*B6+$B$3*C6 Asset returns WMT TGT

4-Sep-01 -9.18% -8.72% -8.95% <-- =$B$2*B7+$B$3*C7 Mean return 1.59% 0.46% <-- =AVERAGE(C6:C65)

1-Oct-01 -0.25% -1.91% -1.08% Variance 0.0093 0.0052 <-- =VARP(C6:C65)

1-Nov-01 15.39% 18.78% 17.08% Standard deviation 9.63% 7.19% <-- =SQRT(I8)

3-Dec-01 5.98% 8.96% 7.47% Covariance 0.0038 <-- =COVAR(B6:B65,C6:C65)

2-Jan-02 -7.36% 7.85% 0.24%

4-Feb-02 -24.14% -5.69% -14.92% Portfolio mean return

1-Mar-02 5.80% 2.88% 4.34% 1.02% <-- =AVERAGE(D6:D65)

1-Apr-02 5.48% 1.21% 3.35% 1.02% <-- =B2*H7+B3*I7

1-May-02 11.82% -5.01% 3.40% Portfolio return variance

3-Jun-02 -10.49% -8.44% -9.46% 0.0055 <-- =VARP(D6:D65)

1-Jul-02 -21.80% -13.33% -17.57% 0.0055 <-- =B2^2*H8+B3^2*I8+2*B2*B3*H10

1-Aug-02 -1.40% 2.71% 0.65%

3-Sep-02 -8.66% -14.73% -11.69% Portfolio return standard deviation 7.42% <-- =STDEVP(D6:D65)

1-Oct-02 18.82% 2.00% 10.41%

1-Nov-02 21.95% 14.57% 18.26%

2-Dec-02 -3.08% -14.78% -8.93%

2-Jan-03 -16.56% -6.17% -11.37%

3-Feb-03 2.36% 1.77% 2.06%

3-Mar-03 -1.07% 2.12% 0.53%

CALCULATING THE MEAN AND STANDARD DEVIATION OF A PORTFOLIO

The mean portfolio return is exactly the average of the mean returns

of the two assets:

Expected portfolio return == +

=⋅

Er Er Er

p WMT TGT

() . ( ) . ( )

05 05

051559 05 046 102%%%+⋅ =.. .

In general the mean return of the portfolio is the weighted average return

of the component stocks. If we denote by x the proportion invested in

WMT and 1 − x the proportion invested in stock TGT, then the expected

portfolio return is given by

Er xEr xEr

p WMT TGT

() ( )( )( )=+−1

However, the portfolio’s variance is not the average of the two variances

of the stocks! The formula for the variance is

Var Var Var Cov ,() ()() ()()( )rx r x r xx rr

p WMT TGT WMT TGT

=+−+−

121

Another way of writing this relation is as follows:

246 Chapter 8

σσ σ ρ σσ

p WMT TGT WMT TGT WMT TGT

xxxx

222 22

121=+−+−() ()

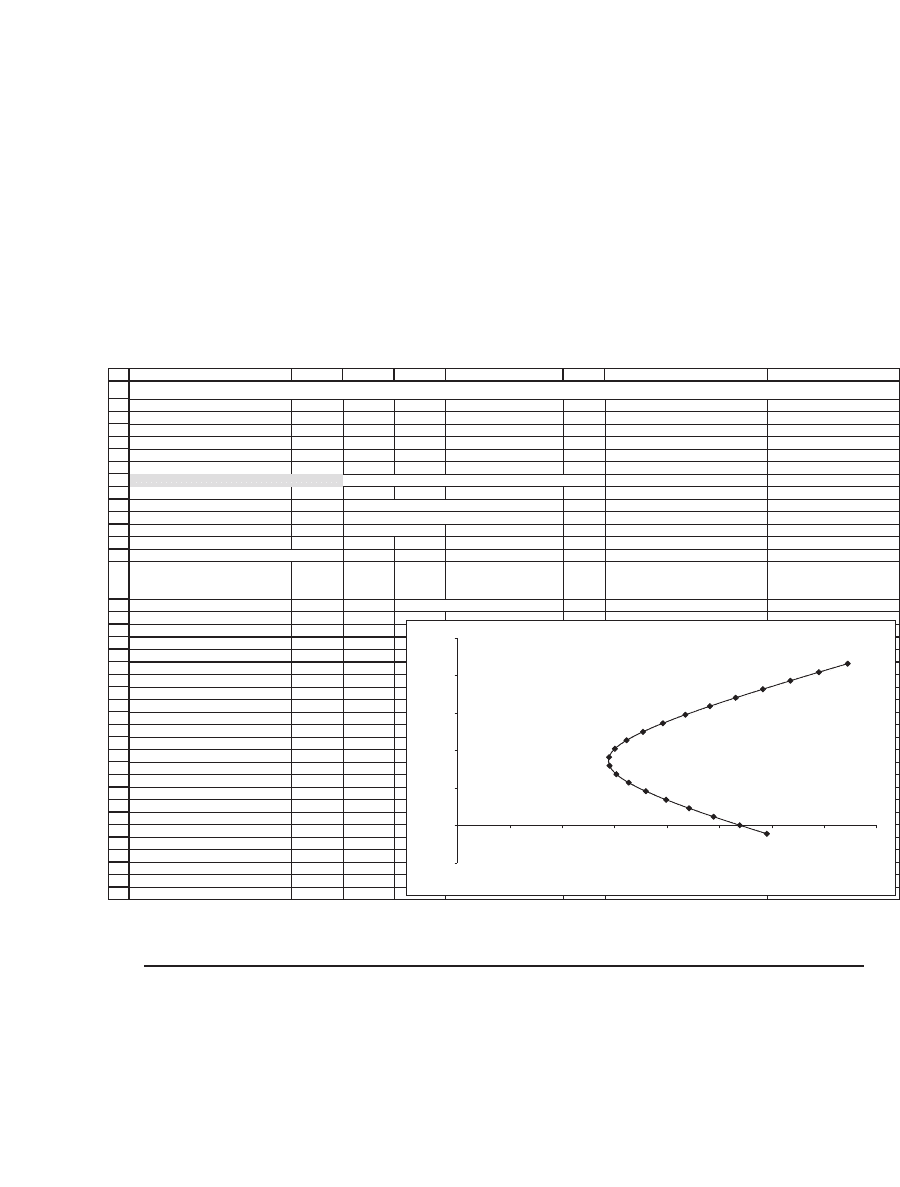
A frequently performed exercise is to plot the means and standard

deviations for various portfolio proportions x. To do this we build a table

using Excel’s Data|Table command (see Chapter 30); cells B16 and C16

contain the data table’s header, which refers to cells B12 and B10,

respectively.

ABC HGFED

Asset returns WMT TGT

Mean return 1.59% 0.46%

Variance 0.93% 0.52%

Standard deviation 9.63% 7.19%

Covariance 0.0038

Proportion of WMT 0.5 <-- In the data table below this is varied from -0.5 to 1.5

Portfolio mean return 1.02% <-- =B8*B3+(1-B8)*C3

Portfolio return variance 0.0036 <-- =B8^2*B4+(1-B8)^2*C4+2*B8*(1-B8)*B7

Portfolio return standard deviation 6.01% <-- =SQRT(B11)

Data table: Varying the proportion of WMT

Portfolio

standard

deviation

Porfolio

mean

return

Proportion of WMT 6.01% 1.02% <-- =B12,=B10, Table header

-0.5 11.81% -0.11%

-0.4 10.77% 0.00%

-0.3 9.78% 0.12%

-0.2 8.84% 0.23%

-0.1 7.96% 0.34%

0 7.19% 0.46%

0.1 6.54% 0.57%

0.2 6.06% 0.68%

0.3 5.80% 0.80%

0.4 5.78% 0.91%

0.5 6.01% 1.02%

0.6 6.46% 1.14%

0.7 7.08% 1.25%

0.8 7.84% 1.36%

0.9 8.70% 1.48%

1 9.63% 1.59%

1.1 10.62% 1.70%

1.2 11.65% 1.82%

1.3 12.71% 1.93%

1.4 13.79% 2.04%

1.5 14.89% 2.16%

CALCULATING THE MEAN AND STANDARD DEVIATION OF A PORTFOLIO

Portfolio Mean and Standard Deviation

Varying the Proportions of WMT and TGT

-0.5%

0.0%

0.5%

1.0%

1.5%

2.0%

2.5%

0% 2% 4% 6% 8% 10% 12% 14% 16%

Standard deviation

Mean return

8.4 Portfolio Mean and Variance—The General Case

In the previous sections we discussed the computation of a portfolio’s

mean, variance, and standard deviation for a portfolio that is composed

of only two assets. In this section we extend the discussion to portfolios

of more than two assets. For this case, matrix notation greatly simpliﬁ es

247 Portfolio Models—Introduction

the writing of the portfolio problem.

In the general case of N assets,

suppose that the proportion of asset i in the portfolio is denoted by x

We write the portfolio composition X and the vector of means E(r) as

column vectors:

⎡

⎣

⎢

⎤

⎦

⎥

⎡

⎣

⎢



()

⎢⎢

⎢

⎤

⎦

⎥

We may then write X

and E(r)

as the transpose of these two vectors:

xxx x

Er Er Er Er

[]

,, ,

,,,

...

() [ ( ) ( )... ( )]

The expected return of the portfolio whose proportions are given by

X is the weighted average of the expected returns of the individual

assets:

Er xEr

xii

() ()=

∑

which, in matrix notation, can be written as

Er xEr xEr Er x

pii

( ) () () ()===

∑

The portfolio’s variance is given by

Var Var( ) Cov( , )() ()rxr xxrr

Xii

ij i j

==+=

∑∑∑

111

This looks bad, but it is really a straightforward extension of the expres-

sion for the variance of a portfolio of two assets that we had before: Each

asset’s variance appears once, multiplied by the square of the asset’s

2. Chapter 31 gives an introduction to matrices sufﬁ cient to deal with all the problems

encountered in this book. Since Excel has excellent matrix-handling capabilities, it is

recommended that you study Chapter 31 before going on with the current chapter. The

Excel matrix functions MMult and MInverse used in portfolio problems are discussed

in this chapter.