Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)

Подождите немного. Документ загружается.

9.4 Genetische Evolutionsverfahren für mehrerer Zielgrößen 235

Dabei ist u eine Zufallszahl im Bereich u ∈ [0,1] und η

eine Zahl größer Null,

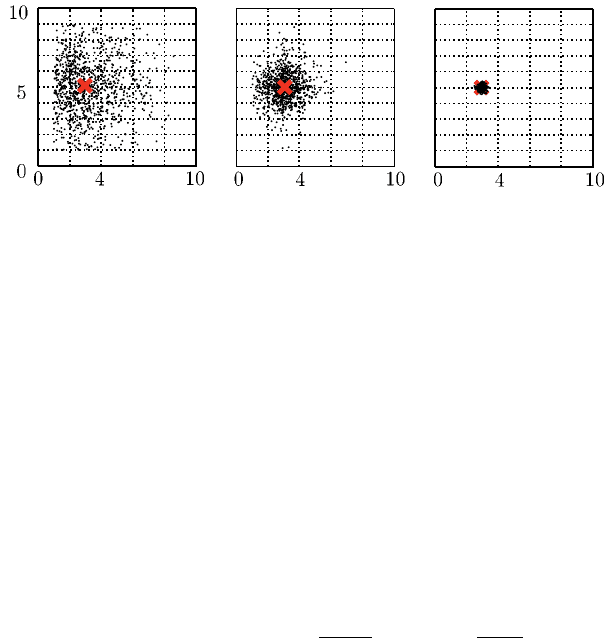
welche die Streubreite der Mutation beeinﬂusst. Abbildung 9.13 zeigt die Auswir-

kung von η

auf die Mutation zweier Faktoren (x

= 3,x

= 5) mit x

∈ [1,9].

Typische Werte für η

liegen im Bereich η

∈ [5,50].

Abb. 9.13 Polynom Mutation reeller Zahlen (x

= 3,x

= 5)

9.4.3 Randbedingungen

Die Integration von komplexen Randbedingungen für Faktoren und Zielgrößen ist

in den meisten genetischen Optimierungsverfahren einfach. Zur Verallgemeinerung

wird für jede Randbedingung g (x,z), welche eine Funktion der Faktoren und Ziel-

größen ist, eine Gleichung c(x, z) so formuliert, dass bei Verletzung der Randbedin-

gung ein negativer Funktionswert auftritt.

Randbedingung Gleichung

g(x,z) ≤ K ⇒ c(x,z) = [K −g (x,z)]w

g(x,z) ≥ K ⇒ c(x,z) = [g (x,z) −K]w

g(x,z) = K ⇒ c(x,z) =

g(x,z) −K

≤ g (x,z) ≤ K

⇒ c(x, z) =

−K

−



g(x,z) −



Dabei sind K Konstanten und w ≥ 0 optionale Gewichtungsfaktoren, die eine

Normierung der Randbedingungen und einen direkten Vergleich untereinander er-

möglichen.

Verletzt ein Testpunkt eine Randbedingung c(x,z) < 0, schließt dieses die Zu-

gehörigkeit zur Pareto Grenze aus. Werden zwei Individuen in einem Fitnesstest

verglichen, so gewinnt das Individuum, welches keine Randbedingungen verletzt

gegenüber ein Individuum, welches mindestens eine Randbedingung verletzt. Sol-

len oder können Randbedingungen im Fitnesstest nicht separat betrachtet werden,

da dieses im verwendeten Algorithmus nicht vorgesehen ist, so wird jede Zielgröße

bei Verletzung mindestens einer beliebigen Randbedingung durch den Maximalwert

der Zielgröße plus den Absolutbetrag der Summe aller verletzenden Randbedingun-

=10 η

= 100

236 9 Optimierung

gen ersetzt.

∗

= z

i,max



∑

min(0,c (x, z))



Verletzung → c(x , z) < 0 (9.13)

Dadurch wird sichergestellt, dass die Individuen mit Verletzung mindestens ei-

ner Randbedingung schlechtere Zielgrößenwerte aufweisen als die Individuen, die

keine Verletzung aufweisen. Dieses führt zu einer automatischen Bevorzugung der

Individuen ohne Verletzung.

9.4.4 Ausgewählte Verfahren (NSGA-II und ε-MOEA)

Die erfolgreichen und weit gefächerten Einsatzmöglichkeiten genetischer Optimie-

rungsverfahren haben dazu geführt, dass eine Vielzahl verschiedener Algorithmen

entwickelt wurden. Bekannte Verfahren sind unter Anderen: VEGA [162, 163], HL-

GA [101], MOGA [58, 57], NPGA [73], SPEA(2) [202, 203, 200, 201], NSGA-

II [30, 35, 129], PAES [89], PESA [24] und ε-MOEA [34].

Im Rahmen dieser Arbeit werden exemplarisch die Verfahren NSGA-II und ε-

MOEA kurz dargestellt wurden.

NSGA-II (Non-dominated Sorting Genetic Algorithm)

Das Verfahren NSGA-II ﬁndet sich in vielen kommerziellen und freien Optimie-

rungstools [30, 35, 129]. Der prinzipielle Ablauf dieses Verfahrens besteht aus den

folgenden Schritten:

1. Wähle n

zufällige Individuen, welche die Start-Generation G

bilden

2. Bestimme den Rang und die Crowding Distance (CD) für jedes der n

Ind.

3. Wähle geeignete Eltern E

aus der aktuellen Generation G

mittels Rang und CD

4. Berechne Kinder K

durch Kreuzung der Eltern und anschließender Mutation

5. Bestimme Rang und CD für alle Individuen (G

∪K

)

6. Erzeuge eine neue Generation G

i+1

mittels Rang und CD aus G

∪K

7. Weiter bei Schritt 3, wenn Abbruchbedingung der Optimierung nicht erfüllt ist

Im Initialisierungsschritt des NSGA-II werden n

zufällige Individuen ausge-

wählt, welche die erste Generation G

bilden. Zur Beurteilung und Vergleich der

einzelnen Individuen wird der Rang und die Crowding Distance (CD) jedes einzel-

nen Individuums bestimmt.

Zur Bestimmung des Rangs eines Individuums werden alle Individuen in Gren-

zen (Fronten) eingeteilt (Abbildung 9.14). Der Rang eins enthält dabei alle Indivi-

duen der aktuellen Pareto Grenze, also alle Individuen, die nicht von einem anderen

Individuum dominiert werden. In Rang zwei beﬁnden sich alle Individuen, die auf

der Pareto Grenze liegen, wenn alle Individuen des Rangs eins entfernt und somit

nicht berücksichtigt werden. Alle weiteren Ränge enthalten entsprechend die Indi-

viduen, welche auf der Pareto Grenze liegen, wenn alle Individuen der vorherigen

9.4 Genetische Evolutionsverfahren für mehrerer Zielgrößen 237

Ränge entfernt wurden. Da dieses grundsätzliche Bestimmungsverfahren viel Re-

chenzeit beansprucht, wurde von DEB et al. ein Sortierungsalgorithmus entwickelt,

welcher die benötigte Rechenzeit deutlich reduziert [35].

Abb. 9.14 Rang Zuordnung

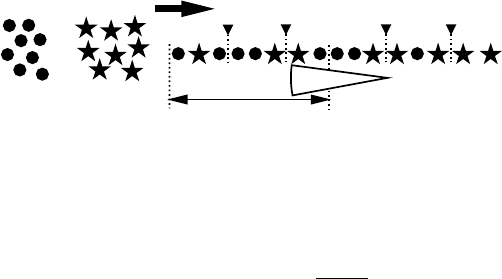
Die Crowding Distance (CD) beurteilt die Individuen eines Rangs untereinan-

der. Dabei ist die CD ein Maß für den Abstand eines Individuums zu seinen benach-

barten Individuen. Zur Bestimmung der CD werden die Individuen eines Rangs

separat für jede Zielgröße aufsteigend sortiert. Jedem Individuum, welches für eine

Zielgröße das kleinste oder größte (erste oder letzte) Element darstellt, wird der Wert

= ∞ zugewiesen. Alle anderen Individuen besitzen bei separater Betrachtung

jeder Zielgröße mindestens ein Individuum, welches einen kleineren oder größeren

Zielgrößenwert aufweist. Die CD eines Individuums ist die Summe der Abstände

zu den benachbarten Individuen für jede Zielgröße (Abbildung 9.15). Damit die

Zielgrößen untereinander vergleichbar sind, werden diese durch die aktuelle Spann-

breite der jeweiligen Zielgröße, welche durch die zwei Randpunkte der Zielgröße

deﬁniert sind, normiert.

∑

k=0

k,i+1

−z

k,i−1

k,max

−z

k,min

(9.14)

CD = ∞

1,i+1

1,i−1

2,i+1

1,min

= z

1,max

2,min

= z

2,i−1

2,max

1,i+1

−z

1,i−1

1,max

−z

1,min

2,i+1

−z

2,i−1

2,max

−z

2,min

Abb. 9.15 Crowding Distance

238 9 Optimierung

Zur Auswahl geeigneter Eltern werden jeweils zwei zufällige Individuen aus der

aktuellen Generation ausgewählt und deren Fitness verglichen, wobei das ﬁttere In-

dividuum als ein Elternteil ausgewählt wird. Die Fitness wird dabei durch den Rang

und die Crowding Distance beschrieben. Hat ein Individuum einen geringeren Rang,

so ist es aus einer Grenze, die näher an der gesuchten Pareto Grenze liegt und somit

zu bevorzugen. Weisen beide Individuen den gleichen Rang auf, so ist das Individu-

um zu bevorzugen, welches in einem Bereich mit weniger Individuen liegt. Zur Ver-

besserung der gleichmäßigen Verteilung von Individuen auf der betrachteten Grenze

wird im nächsten Optimierungsschritt eher in diesem Bereich ein neues Individuum

benötigt. Das Individuum mit größerer Crowding Distance ist somit zu bevorzugen.

Randpunkte werden durch die Zuweisung CD = ∞ automatisch inneren Individuen

vorgezogen. Weisen zwei Individuen den gleichen Rang und CD auf, so wird ein

zufälliges der beiden Individuen als Elternteil gewählt. Ein Individuum i ist einem

Individuum j somit vorzuziehen, wenn:

Rang

< Rang

oder [Rang

= Rang

und CD

> CD

] (9.15)

Aus zwei Eltern werden im nächsten Schritt durch Kreuzung (Kapitel 9.4.1) und

Mutation (Kapitel 9.4.2) zwei neue Individuen (Kinder) berechnet. Die Auswahl

von Eltern und Erzeugung von Kindern wird solange vorgesetzt bis eine vorgegebe-

ne Anzahl von neuen Individuen ermittelt wurde (zum Beispiel n

neue Individuen).

Zur Erzeugung der neuen Generation G

i+1

werden die Individuen der vorherge-

henden Generation G

und alle neu erzeugten Individuen (Kinder) zusammen be-

trachtet und sortiert (Rang und CD). Die besten n

Individuen nach Gleichung 9.15

bilden anschließend die neue Generation G

i+1

(Abbildung 9.16).

Kinder

sortiert (Rang + CD)

i+1

Abb. 9.16 Erzeugung einer neuen Generation (NSGA-II)

Beispiel

Zur Veranschaulichung des dargestellten Verfahrens wird das folgende Testproblem

mit zwei Zielgrößen und drei Faktoren betrachtet [30].

(x) =

∑

i=1

−10e

−0.2

i+1

(x) =

∑

i=1

0.8

+ 5 sin





−5 ≤ x

≤ 5

(9.16)

Eine Monte-Carlo-Simulation (Kapitel 7.3.1) mit 1000 Individuen zeigt eine

deutliche Streuung im Zielgrößenraum und lässt die ungefähre Position der gesuch-

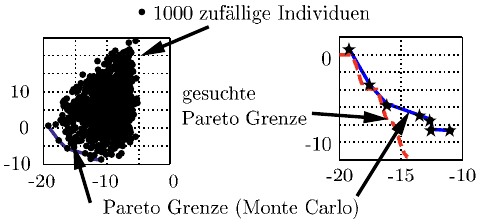
9.4 Genetische Evolutionsverfahren für mehrerer Zielgrößen 239

ten Pareto Grenze erkennen (Abbildung 9.17). Nur wenige Individuen liegen da-

bei auf oder in der Nähe der gefundenen Pareto Grenze. Weiterhin zeigt sich, dass

in der durchgeführten Monte-Carlo-Simulation die gefundenen Lösungen für klei-

ne z

deutlich von der idealen Pareto Grenze abweichen. Eine reine Monte-Carlo-

Simulation ist somit zur Bestimmung der Pareto Grenze nicht zielführend.

Abb. 9.17 Testproblem, Monte-Carlo

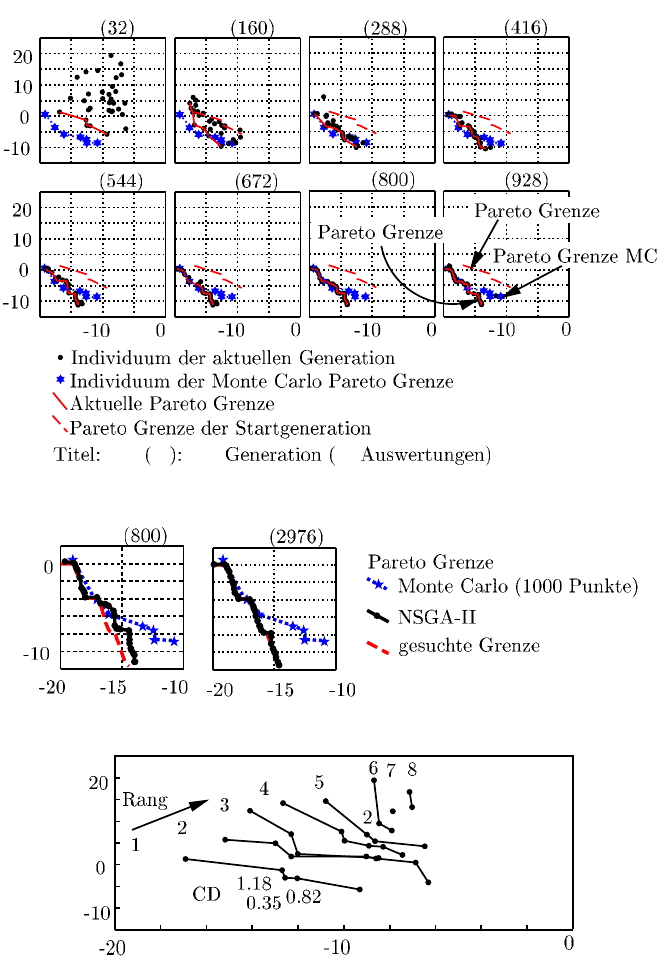
Abbildung 9.18 zeigt hingegen den Verlauf der NSGA-II Optimierung bei einer

gewählten Populationsgröße von n

= 32. Ausgehend von der im gesamten Ziel-

raum verteilten Startpopulation G

entwickelt sich die Population schnell in Rich-

tung der gesuchten Pareto Grenze. Bereits in der achten Generation G

und somit

nach 288 Auswertungen der Testfunktion wird eine ähnliche Güte der Pareto Gren-

ze erreicht wie nach 1000 Auswertungen für die Monte-Carlo-Simulation. Nach

800 Auswertungen G

ist die gefundene Pareto Grenze bereits deutlich näher an

der idealen und gesuchten Grenze als nach der Monte-Carlo-Simulation (1000 Aus-

wertungen). Nach 3000 Auswertungen und 92 Generationen liegen alle Individuen

gleichmäßig verteilt an der gesuchten Pareto Grenze (Abbildung 9.19). Die Konver-

genzgeschwindigkeit der Optimierung hängt neben der Komplexität des betrachte-

ten System ebenfalls von der Wahl der Optimierungsparameter (Populationsgröße,

Kreuzungswahrscheinlichkeit, ···) ab.

Zur Veranschaulichung der Crowding Distance (CD) ist in Abbildung 9.20 die

erste Generation der durchgeführten NSGA-II Optimierung mit Rang und einigen

CDs dargestellt. Alle äußeren Punkte jedes Rangs sind große Zahlen (∞) zugewie-

sen. Im ersten Rang (aktuelle Pareto Grenze) weist der mittlere Datenpunkt die ge-

ringste CD auf, so dass alle anderen Datenpunkte des Rangs im direkten Vergleich

dem mittleren Datenpunkt vorzuziehen sind.

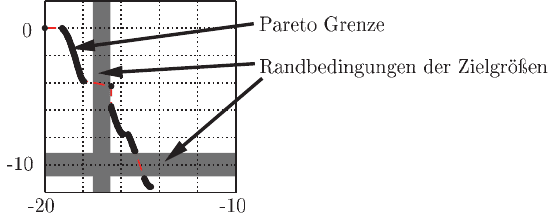
Werden zusätzlich folgende Randbedingungen der Optimierungsaufgabe hinzu-

gefügt, so wird die in Abbildung 9.21 dargestellten Pareto Grenze durch das NSGA-

II Verfahren ermittelt.

≤ −17.5

≥ −16.5



→ g (z

) = −0.5+

−17.0 −z

≤ −11.0

≥ −9.0



→ g (z

) = −1.0+

−10.0 −z

(9.17)

240 9 Optimierung

Gn m n

Abb. 9.18 Optimierungsverlauf (NSGA-II)

Abb. 9.19 Pareto Grenze (NSGA-II)

∞

Abb. 9.20 Rang und CD der ersten Generation G

des Testproblems

9.4 Genetische Evolutionsverfahren für mehrerer Zielgrößen 241

Abb. 9.21 Pareto Grenze mit Randbedingungen für beide Zielgrößen (Testproblem)

ε-MOEA

Neben Verfahren wie NSGA-II, die mit einer einzelnen Gruppe von Individuen ar-

beiten, welche während des Optimierungsprozesses kontinuierlich verbessert wer-

den, existieren ebenfalls Verfahren wie zum Beispiel das ε-MOEA [34], die zwei

separate Gruppen von Individuen zur Optimierung einsetzen. Neben der Populati-

onsgruppe welche Individuen der aktuellen Generation beinhaltet, enthält die zweite

Gruppe nur Individuen der aktuellen Pareto Grenze und wird als Elite Gruppe be-

zeichnet. Die Elite Gruppe besitzt im Gegensatz zur Populationsgruppe keine vor-

gegebene Größe und kann je nach gefundenen Individuen anwachsen oder schrump-

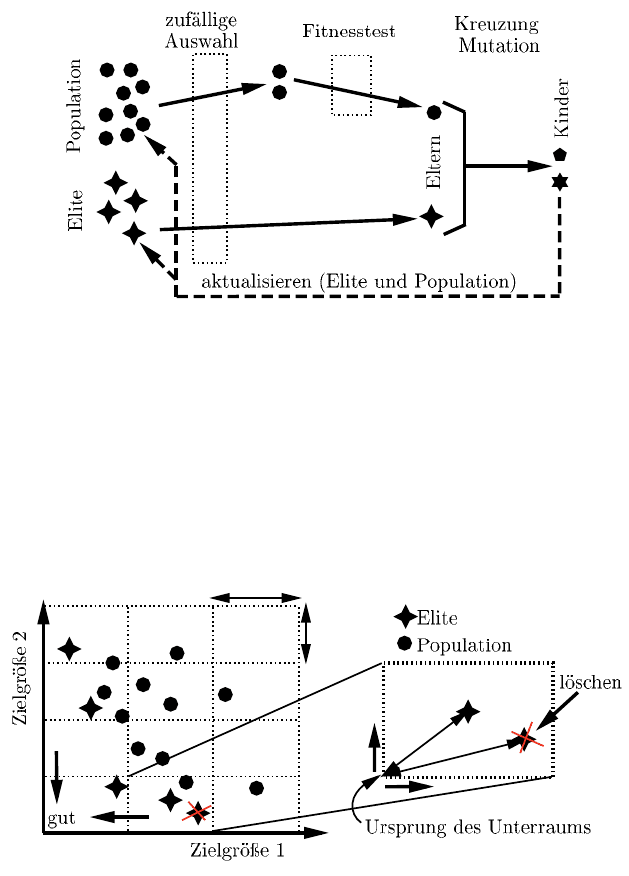
fen. Der grundlegende Optimierungsablauf von ε-MOEA ist in Abbildung 9.22

schematisch dargestellt. Zur Erzeugung zweier Eltern werden aus der Populations-

gruppe zwei zufällige Individuen ausgewählt und verglichen. Ist ein Individuum

ﬁtter (dominant) als das Andere wird dieses als erstes Elternteil gewählt. Sollte kein

Individuum dominant sein so wird ein zufälliges der beiden Individuen ausgewählt.

Als zweites Elternteil wird ein zufälliges Individuum der Elitegruppe gewählt, wo-

bei hier sichergestellt ist, dass es sich um ein besonders ﬁttes Individuum handelt,

da es auf der aktuellen Pareto Grenze liegt. Durch Kreuzung und Mutation wer-

den aus den Eltern neue Individuen (Kinder) berechnet und anschließend jeweils in

die Polpulations- und Elitegruppe einsortiert. Die Populationsgruppe enthält dabei

konstant die festgelegte Populationsgröße und die Elitegruppe alle Individuen der

aktuellen Pareto Grenze bei Berücksichtigung aller Individuen des gesamten Opti-

mierungsprozesses.

Werden als Faktoren reelle Zahlen eingesetzt, können grundsätzlich unendlich

viele Ergebnisse auf der Pareto Grenze gefunden werden. Während der Optimie-

rung würde dadurch die Individuenanzahl der Elitegruppe kontinuierlich ansteigen.

Eine uneingeschränkte Steigerung der Individuenanzahl würde jedoch den Optimie-

rungsprozess deutlich verlangsamen, da die gesamte Pareto Grenze und somit jeder

Punkt der Elitegruppe gleichzeitig optimiert werden muss. In der Praxis sind Lösun-

gen für ein Problem gesucht, die sich merklich voneinander unterscheiden, so dass

eine gezielte Auswahl der ’besten’ Pareto optimalen Lösung stattﬁnden kann, was

gegen eine uneingeschränkte Anzahl an Individuen in der Elite Gruppe spricht.

Der ε-MOEA Algorithmus verwendet zur Begrenzung der Elitegruppe eine Un-

terteilung des Zielgrößenraums in Schichten der Breite ε

, wie es in Abbildung 9.23

242 9 Optimierung

Abb. 9.22 ε-MOEA

dargestellt ist. In jedem durch diese Unterteilung gebildeten Unterraum darf nur

ein Individuum der Elitegruppe existieren. Sind mehrere Individuen in einem Un-

terraum vorhanden, so wird nur das Individuum in die Elitegruppe übernommen,

welches den geringsten Abstand zum Ursprung des Unterraums aufweist (Abbil-

dung 9.23, rechts). Dieses zusätzliche Gütekriterium wird eingeführt, da alle Indivi-

duen aus der Elitegruppe auf der Pareto Grenze liegen und somit über die Dominanz

keine Entscheidung getroffen werden kann welches Individuum zu bevorzugen ist.

Abb. 9.23 ε-MOEA Gitter

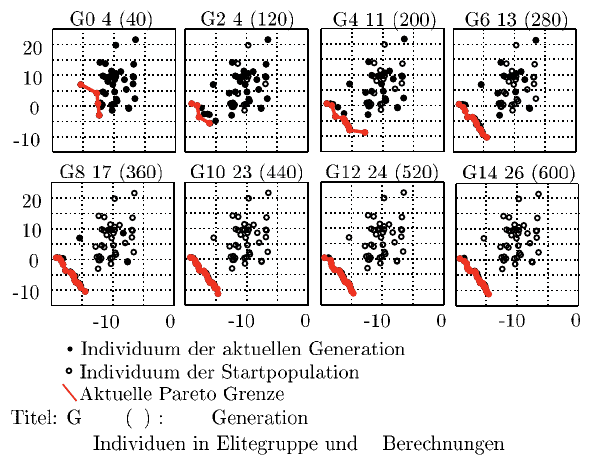
Abbildungen 9.24 und 9.25 zeigen den Optimierungsverlauf der Optimierungs-

aufgabe aus Gleichung 9.16. Beginnend mit einer weit streuenden Startpopulation

werden schnell Individuen in der Nähe der wahren Pareto Grenze ermittelt. Bereits

in Generation 6 (nach 280 Auswertungen der Funktion) wird die Pareto Grenze gut

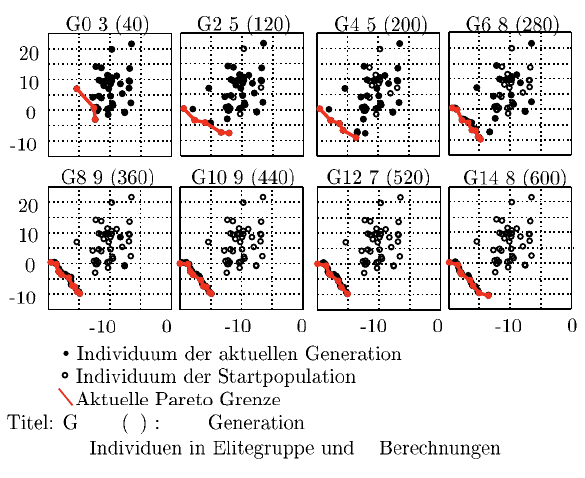
abgebildet. Die Vergrößerung der Schichtweite von ε = 0.1 auf ε = 0.5 weist ei-

ne deutliche Reduktion der Individuenanzahl der Elitegruppe auf, wobei eine gute

Gleichverteilung bei beiden Einstellungen erzielt wird.

< a

9.5 Zusammenfassung 243

Bei steigender Anzahl der betrachteten Zielgrößen weist ε-MOEA schnell große

Elitegruppen auf, so dass die geschickte Wahl der ε Werte an Bedeutung zunimmt.

Abhilfe können hier zusätzliche Randbedingungen für die Zielgrößen (Maximal-

werte) schaffen, die sich zum Beispiel automatisch an die aktuell gefundenen Be-

reiche der Zielgrößen anpassen und somit bei steigender Anzahl von Individuen in

der Elitegruppe den Zielgrößenbereich weiter einschränken.

Abb. 9.24 ε-MOEA: Beispiel mit ε = 0.1

9.5 Zusammenfassung

Typische Optimierungsaufgaben technischer Systeme weisen mehrere Zielgrößen



,···,z



auf, die gleichzeitig verbessert werden müssen, sich jedoch teilwei-

se widersprechen. Das optimierte System wird daher ein optimierter Kompromiss

zwischen allen betrachteten Zielgrößen sein.

Klassische Optimierungsalgorithmen (z.B. Gradientenverfahren, genetische Op-

timierung, ···) sind in der Lage lediglich eine Zielgröße zu betrachten, so dass

durch eine mathematische Kombination der Zielgrößen eine übergeordnete Ziel-

größe z

∗

= f



,···,z



erzeugt wird, welche anstelle der einzelnen Zielgrößen

optimiert wird. Der durchzuführende Kompromiss zwischen den einzelnen Zielgrö-

ßen wird dabei bereits vor der eigentlichen Optimierung durch die gewählte über-

geordneten Zielgröße festgelegt. Das Ergebnis der Optimierung ist genau die eine

m n k m

1,2

= 0.1

n k

244 9 Optimierung

Abb. 9.25 ε-MOEA: Beispiel mit ε = 0.5

Lösung, welche die übergeordnete Zielgröße bei gegebenen Startwert und Optimie-

rungsalgorithmus optimiert.

In der Praxis ist jedoch meistens vor der Optimierung nicht bekannt wie die ein-

zelnen Zielgrößen am geschicktesten kombiniert werden und welche Kompromisse

zwischen den Zielgrößen eingegangen werden sollen oder können. Sinnvoll ist des-

halb eine gleichzeitige Betrachtung jeder einzelnen Zielgröße und Ermittlung von

’optimalen’ Lösungen bei denen eine beliebige Zielgröße nur verbessert werden

kann, wenn mindestens eine der andere Zielgrößen verschlechtert wird. Diese Lö-

sungen stellen die Menge der Kompromisslösungen dar, welche bei Betrachtung

aller Zielgrößen gefunden werden können. Sie werden Pareto optimale Lösungen

genannt und bilden die Pareto Grenze. Mit diesen Lösungen ist es dem Anwender

im Anschluss an den Optimierungsprozess möglich einen sinnvollen Kompromiss

zwischen den Zielgrößen zu ermitteln, da er alle Kompromisse zwischen den Ziel-

größen plus den zugehörigen Faktoreinstellungen (Fertigungsaufwand, Kosten, ···)

kennt.

Zur Bestimmung der Pareto optimalen Lösungen beziehungsweise der Pareto

Grenze haben sich genetische Optimierungsalgorithmen für mehrere Zielgrößen be-

währt. Sie besitzen nur eine geringe Wahrscheinlichkeit in lokale Optima zu verhar-

ren, können mit komplexen, nichtlinearen und nichtstetigen Funktionszusammen-

hängen arbeiten, sind ﬂexibel an unterschiedlichste Problemstellungen anpassbar

und nicht deﬁnierte Faktorbereiche sind unproblematisch. In der Praxis zeigt sich,

dass bereits die heute vorhandenen Algorithmen für fast alle Anwendungen aus-

1,2

= 0.5

m n k m

n k