Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)
Подождите немного. Документ загружается.

Kapitel 9
Optimierung
9.1 Einleitung
Neben Analysen zur Bestimmung von Zusammenhänge zwischen kontrollierba-
ren Eingangsvariablen (Faktoren) und Ausgangsgrößen (Qualitätsmerkmale) eines
technischen Systems ist meist eine Optimierung von Systemeigenschaften durch-
zuführen. Dabei sind Faktoreinstellungen gesucht, welche ausgewählte Zielgrößen
(Qualitätsmerkmale) z
1
,···,z
n
z
für den angestrebten Systemeinsatz optimieren. Die
Zielgrößen sollen dabei einen vorgegebenen Wert annehmen beziehungsweise mi-
nimiert oder maximiert werden. Optimierungsziele werden zur Vereinfachung der
angewendeten Algorithmen in Minimierungsaufgabe umgewandelt. .
Optimierungsziel Minimierung
min[z(x)] ⇒ min[z (x)]
max[z(x)] ⇒ min[−z (x)]
z(x) = c ⇒ min
|
c −z (x)
|
(9.1)
Bei der Betrachtung mehrerer Zielgrößen ist es nur in den wenigsten Fällen mög-
lich eine Faktorkombination zu finden, die alle Zielgrößen gleichzeitig minimiert
(optimiert), so dass nach einem optimalen Kompromiss zwischen allen Zielgrößen
(und den dazugehörigen Faktoreinstellungen) gesucht wird. Abbildung 9.1 zeigt da-
zu ein fiktives Beispiel mit zwei Zielgrößen und zwei ausgewählten Faktoren. Ge-
sucht ist ein Computersystem, welches eine Simulationsaufgabe in einer möglichst
kurze Zeit berechnet und gleichzeitig wenig kostet. Dabei werden beide Zielgrößen
unter anderem durch die Anzahl der Prozessoren und die Rechengeschwindigkeit
jedes einzelnen Prozessors beeinflusst. Zwischen den betrachteten Zielgrößen muss
ein Kompromiss gefunden werden, wobei eventuell nicht nur die beiden Zielgrö-
ßen (Preis, Rechenzeit) sondern ebenfalls die dazugehörigen Faktoreinstellungen
zu berücksichtigen sind. So kann bei ähnlichen Eigenschaften für die Zielgrößen
(ähnlicher Preis und Rechengeschwindigkeit) zum Beispiel ein Einzelrechner einem
Rechencluster vorgezogen werden.
K. Siebertz et al., Statistische Versuchsplanung, VDI-Buch, 225
DOI 10.1007/978-3-642-05493-8_9, © Springer-Verlag Berlin Heidelberg 2010

226 9 Optimierung
Abb. 9.1 Optimierung mehrerer Zielgrößen
Im ersten Schritt des Optimierungsprozesses sind Lösungen gesucht, die auf oder
in der Nähe der Pareto Grenze liegen. Die Pareto Grenze wird dabei durch Pareto
optimale Ergebnisse definiert. Ein Pareto optimales Ergebnis zeichnet sich dadurch
aus, dass keine Zielgröße verbessert (verringert) werden kann ohne eine andere Ziel-
größe zu verschlechtern. Somit sind alle Ergebnisse auf der Pareto Grenze als ’op-
timal’ anzusehen. Sind genügend Punkte auf der Pareto Grenze bestimmt worden
wird im zweiten Schritt ein akzeptabler Kompromiss zwischen den Zielgrößen mit
optionaler Berücksichtigung der Faktoreinstellungen gewählt.
9.2 Dominanz
Zur Bestimmung, ob ein Datenpunkt x
0
mit den dazugehörigen Zielgrößen zur ge-
suchten Pareto Grenze gehört, wird überprüft, ob der Datenpunkt im Zielgrößen-
raum von anderen Punkten dominiert wird beziehungsweise welche Datenpunkte
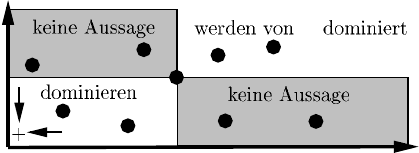
von ihm dominiert werden. Dabei dominiert ein Punkt a einen Punkt b, wenn er in
mindestens einer Zielgröße besser und in allen anderen mindestens gleichwertig ist
(Abbildung 9.2). Im Gegensatz dazu wird ein Punkt a von einem Punkt b dominiert
wenn er in mindestens einer Zielgröße schlechter und in allen anderen Zielgrößen
gleichwertig oder schlechter ist.
Abb. 9.2 Dominanz von Datenpunkten im Zielgrößenraum
Wird nur ein Individuum (Datenpunkt) I
i
betrachtet, existiert ein eindeutiger Be-
reich im Zielgrößenraum, welcher durch das Individuum I
i
dominiert wird und ein
x
1
x
2
z
1
z
2
z
(
x
)
z
1
z
2
→
→
→
→
→
→
→
→
→
→ · · ·
9.3 Reduktion auf eine Zielgröße 227
zweiter welcher Individuen enthält, welche das Individuum I
i
dominieren (Abbil-
dung 9.3). In allen anderen Bereichen kann keine Aussage über die Dominanz des
Individuums I
i
getroffen werden, da einige Zielgrößen besser und andere schlechter
sind als die der Individuen dieser Bereiche.
Abb. 9.3 Dominanz eines Individuums I
i
9.3 Reduktion auf eine Zielgröße
Eine auch heute noch weit verbreitete Methode verschiedene Zielgrößen gleichzei-
tig zu optimieren ist die Zusammenfassung in eine übergeordnete Zielgröße z
∗
.
z
∗
= g
z
1
,···,z
n
z
(9.2)
Die Schwierigkeit dabei ist eine sinnvolle Kombination
g
z
1
,···,z
n
z
der einzel-
nen Zielgrößen vor der Optimierung zu bestimmen. Dazu ist bereits vor der eigentli-
chen Optimierung ein umfangreiches Wissen über die Abhängigkeiten der einzelnen
Zielgrößen und Faktoren notwendig.
Gewichtete Summe
Eine beliebte und einfache Kombination der Zielgrößen ist die gewichtete Summe
bei der jede Zielgröße mit einem vorher festgelegtem Gewicht w
k
multipliziert wird.
z
∗
=
n
z
∑
k=1
w
k
z
k
mit
n
z
∑
k=1
w
k
= 1 (9.3)
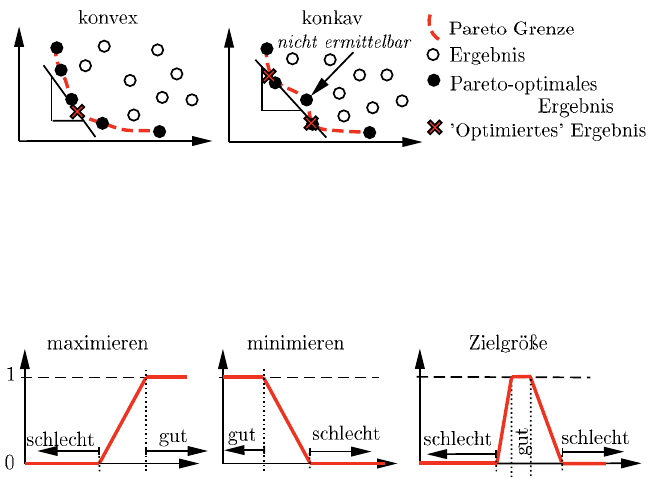
Das optimierte Ergebnis hängt dabei direkt von dem Verhältnis der einzelnen
Gewichte zueinander ab (Abbildung 9.4). Ist die Pareto Grenze konvex, so kann
grundsätzlich jeder Punkt der Grenze durch eine geeignete Kombination der Ge-
wichte ermittelt werden. Bei konkaven Pareto Grenzen sind jedoch eventuell wich-
tige Bereiche nicht ermittelbar.
Gewichtetes Produkt
Ein weiteres Kombinationsverfahren der Zielgrößen ist das Produkt normierter und
gewichteter Größen (siehe Kapitel 5.2.1). Dazu werden die Zielgrößen z
1
,···,z
n
z
im
ersten Schritt auf den Bereich [0, 1] normiert. Die Abbildung 9.5 zeigt eine typische
I
i
z
1
z
2
I
i
I
i
228 9 Optimierung
Abb. 9.4 Optimierung durch gewichtete Summe
Normierungen, wobei der normierte Funktionswert z
norm
= 1 für ein ideales und
z
norm
= 0 für ein unzureichendes Ergebnis steht.
Abb. 9.5 Normierung von Zielgrößen
Neben den dargestellten linearen Normierungsfunktionen werden häufig auch
sigmoidale (s-förmige) Funktionen verwendet, wie sie in Gleichung 8.41 (Kapi-
tel 8.8) als Aktivierungsfunktion für künstliche Neuronale Netzwerke eingesetzt
werden. Die übergeordnete Zielgröße z
∗
ist das (negative) Produkt der normierten
Zielgrößen.
z
∗
= −
n
z
∏
k=1
z
norm,k
(9.4)
Nimmt die übergeordnete Zielgröße den Wert z
∗
= 0 an, ist mindestens eine der
Zielgrößen z
norm,k
= 0 im nicht akzeptierten Bereich. Ein Wert von z
∗
= −1 bedeutet
hingegen, dass alle normierten Zielgrößen im optimalen Bereich liegen.
Werden alle Zielgrößen in eine übergeordnete Zielgröße kombiniert, so kann die-
se mit klassischen Minimierungsverfahren optimiert werden. Dabei kommen meist
Gradientenverfahren [146] aber auch Verfahren wie simulated annealing (Kapi-
tel 7.4) oder genetische Optimierung (Kapitel 9.4) zum Einsatz. Bei der Anwendung
eines Gradientenverfahrens ist zu beachten, dass diese bei Löchern im Faktorraum
häufig Probleme aufweisen, so dass genetische Algorithmen hier Vorteile bieten
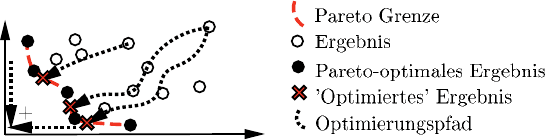
können. Abbildung 9.6 zeigt schematisch den Optimierungsfortschritt bei Verwen-
dung von zwei verschiedenen Startpunkten eines Gradientenverfahrens beziehungs-
weise bei Kombination der Zielgrößen zu unterschiedlichen übergeordneten Ziel-
größen.
z
1
z
2
z
1
z
2
w
2
w
1
w
2
w
1
z
z
norm
z z
9.3 Reduktion auf eine Zielgröße 229
Abb. 9.6 Optimierung mittels einer übergeordneten Zielgröße
Je nach Startpunkt oder Kombination der Zielgrößen werden andere oder auch
gleiche Lösungen auf der Pareto Grenze gefunden. Bei Verwendung klassischer
Verfahren wird lediglich ein Ergebnis ermittelt, welches zum großen Teil von dem
vorher definierten Zusammenhang der Zielgrößen abhängt. Das ermittelte Ergebnis
wird in den folgenden Entwicklungsschritten als ’optimales’ Ergebnis verwendet.
Neben dem ’optimierten’ Ergebnis befinden sich jedoch verschiedene Ergebnisse
mit nahezu identischen oder ebenfalls akzeptablen Zielwertkombinationen. Diese
alternativen Lösungen, die dem Anwender nicht zur Verfügung stehen, können je-
doch entscheidende Vorteile gegenüber der gefundenen Lösung aufweisen. Dieses
können beispielsweise vorteilhafte Faktorkombinationen sein, die eine einfachere
Fertigung ermöglichen oder eine robustere Lösung darstellen. Weitere Ergebnisse
auf der Pareto Grenze sind nur durch eine erneute Optimierung mit neuen Zielgrö-
ßenkombinationen oder neuem Startpunkt ermittelbar. Der benötigte Rechenauf-
wand für die Optimierung wird dadurch vervielfacht und das grundsätzliche Pro-
blem der richtigen Wahl der Gewichte und Kombinationsfunktion ist nicht gelöst,
so dass das gefundene Ergebnis bei jeder Optimierung in gewissen Grenzen zufällig
ist.
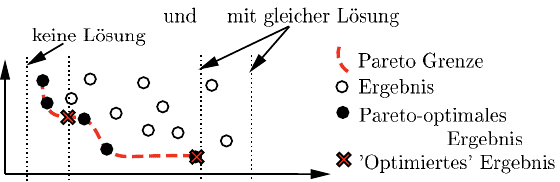
ε-Constraint
Eine Alternative zur Kombination der Zielgrößen zu einer übergeordneten Zielgröße
z
∗
bietet die ε-Constraint-Methode [
116]. Dabei wird lediglich eine der Zielgrößen
z
a
∈
z
1
,···,z
n
z
optimiert. Alle anderen Zielgrößen werden als Nebenbedingung
mit festzulegenden Maximalwerten ε definiert (Abbildung 9.7):
z
b
≤ ε
b
b = 1, ···,n
z
b 6= a (9.5)
Existiert eine Lösung für die Minimierungsaufgabe von z
a
so ist diese Lösung
eine Lösung der Pareto Grenze. Durch die Optimierung der einzelnen Zielgrößen
in Kombination mit unterschiedlichen Maximalwerten ε für die übrigen Zielgrößen
können grundsätzlich alle Punkte der Pareto Grenze ermittelt werden.
z
1
z
2
z
∗
1
z
∗
1
z
∗
2
Start
1
Start
2
230 9 Optimierung
Abb. 9.7 ε-Constraint-Methode
9.4 Genetische Evolutionsverfahren für mehrerer Zielgrößen
In der Praxis ist es im Gegensatz zu den im Vorfeld dargestellten Optimierungsver-
fahren mit einer übergeordneten Zielgröße vorteilhaft, alle Zielgrößen parallel zu
betrachten und die komplette Pareto Grenze zu bestimmen. Die ermittelten Pare-
to optimalen Lösungen sollen dabei möglichst gleichmäßig auf der Pareto Grenze
verteilt sein (siehe Abbildung 9.4). Zur Ermittlung der Lösungen haben sich geneti-
sche Optimierungsverfahren für mehrere Zielgrößen bewährt und durchgesetzt. Sie
bieten die Möglichkeit alle Bereiche einer Pareto Grenze zu bestimmen, auch wenn
komplexe Zusammenhänge zwischen Faktoren und Zielgrößen oder unter Zielgrö-
ßen vorliegen. Weiterhin bereiten ihnen nicht definierte Bereiche im Faktorraum
(Löcher) keine Schwierigkeiten und Randbedingungen für Faktoren und Zielgrö-
ßen lassen sich leicht in die Optimierungsalgorithmen integrieren. Bei steigender
Anzahl der Zielgrößen steigt der Rechenaufwand zur Bestimmung der Pareto Gren-
ze schnell an, so dass typischerweise Metamodelle (Kapitel 8) mit kurzer Rechen-
zeit und hoher Genauigkeit anstelle von komplexen Simulationsmodellen eingesetzt
werden.
In der Literatur finden sich verschiedenste genetische Optimierungsverfahren,
die mehr oder weniger die biologische Evolution nachahmen. So werden Merkma-
le von einer zur nächsten Generation vererbt mit anderen gekreuzt oder zufällig
mutiert. In folgenden Generationen ’überleben’ hauptsächlich die Individuen (Fak-
toreinstellungen), die fitte (gute) Eigenschaften in den Zielgrößen aufweisen. Abbil-
dung 9.8 zeigt den verallgemeinerten Ablauf einer genetischen Optimierung. Basie-
rend auf einer vorhandenen Gruppe von Individuen mit unterschiedlichen Faktorein-
stellungen (i
te
Genaration) werden durch ein zu bestimmendes Verfahren verschie-
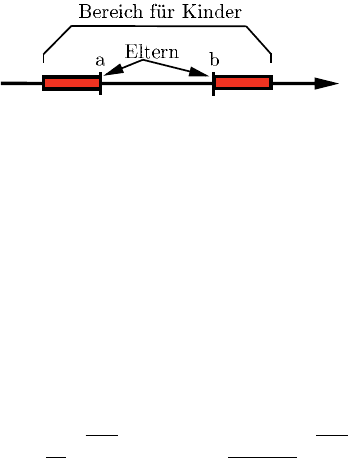
dene Individuen ausgewählt und als Eltern deklariert. Durch Kreuzung der verschie-
denen Eltern entstehen sogenannte Kinder, wobei die Eigenschaften (Faktoreinstel-
lungen) direkt von den Eltern und der Art der Kreuzung abhängen. Im Anschluss an
die Kreuzung findet mit geringer Wahrscheinlichkeit eine Mutation der einzelnen
Eigenschaften (Faktoreinstellungen) statt. Dazu werden die Faktoreinstellungen un-
abhängig von den Eltern verändert, wodurch gewährleistet wird, dass während des
Optimierungsprozesses beliebige Faktoreinstellungen erzeugt werden können, die
nicht aus der Elterngeneration erzeugbar sind. Dadurch wird gewährleistet, dass das
z
1
z
2
ǫ
1
ǫ
2
ǫ
3
ǫ
4
ǫ
1
ǫ
3
ǫ
4

9.4 Genetische Evolutionsverfahren für mehrerer Zielgrößen 231
Optimierungsverfahren nicht in einem lokalen Minimum stecken bleibt und mit ei-
ner voreingestellten Wahrscheinlichkeit alle Bereiche des Faktorraums geprüft wer-
den. Sind die Faktoreinstellungen der Kinder festgelegt, werden die dazugehörigen
Zielgrößen bestimmt und im nächsten Schritt die neue Generation G
i+1
ermittelt.
Dazu werden durch ein zu bestimmendes Verfahren die fittesten (besten) Individuen
aus den Kindern und der vorgehenden i
ten
Generation gewählt. In einem iterativen
Prozess werden diese vier Schritte solange wiederholt bis eine maximale Iterations-
anzahl erreicht wurde oder keine signifikante Verbesserung der gefundenen Pareto
Grenze mehr erzielt wird.
Abb. 9.8 Genetisches Evolutionsverfahren
Binäre Kodierung
Traditionell werden in Computer gestützten genetischen Optimierungsverfahren die
Faktoreinstellungen binär kodiert. Seien x
u
und x
o
die untere und obere Grenze eines
Faktors x
u
≤x ≤x
o
und n
b
die Anzahl der verwendeten Bits
b
0
,···,b
n
b
−1
zur Dar-
stellung des Faktors x. Bei gegebener Binärdarstellung wird die Faktoreinstellung
für x durch folgende Gleichung berechnet:
x = x
u
+
n
b
−1
∑
k=0
2
k
b
k
x
o
−x
u
2
n
b
−1
(9.6)
Zur Veranschaulichung wird ein Rohrdurchmesser d mit zwei Bits kodiert (2
2
=
4 Stufen), wobei x
u
= 6 und x
o
= 9 sind (Tabelle 9.1). Der binäre Wert
0
10
0
(b
1
= 1 b
0
= 0) repräsentiert damit die Faktoreinstellung:
x = 6 +
2
0
0 + 2
1
1
9 −6
2
2
−1
= 6 + 2
3
3
= 8 (9.7)
Wird eine minimale Auflösung ∆
min
eines Faktors x für eine Optimierung benö-
tigt, so muss die Anzahl n
b
so gewählt werden, dass folgende Ungleichung erfüllt
ist.
2
n
b
≥
x
o
−x
u
∆
min
(9.8)
i
i + 1
i + 1
Eltern Kinder
i

232 9 Optimierung
b
1
b
0
x
0 0 6
0 1 7
1 0 8
1 1 9
Tabelle 9.1 Binäre Kodierung
Die binäre Kodierung der Faktoren begrenzt im Vergleich zur Verwendung des
reellen Zahlenraums die möglichen Faktorstufen und somit auch die erzeugbaren
Datenpunkte, was eine schnelle Konvergenz der Optimierung günstig beeinflussen
kann. Eine Einschränkung der Lösungen durch die binäre Kodierung ist jedoch in
vielen Fällen nicht erwünscht, so dass verschiedene Verfahren entwickelt wurden,
die neben der binären Kodierung ebenfalls einen sinnvollen Einsatz reeller Zahlen
in genetischen Optimierungsverfahren ermöglicht.
9.4.1 Kreuzung
Die Kreuzung jedes Faktors x zweier Eltern a und b wird in der genetischen Opti-
mierung mit einer vorgegebenen Wahrscheinlichkeit p
K
durchgeführt, wobei typi-
sche Werte im Bereich p
K
∈ [0.6,1.0] liegen.
Binäre Kodierung
Die Kreuzung zweier binär kodierter Variablen (Faktoren) mit zwei Schnittpunkten
ist beispielhaft in Abbildung 9.9 dargestellt. Im ersten Schritt des Kreuzungsalgo-
rithmus werden zufällig zwei Schnittpunkte in der binären Darstellung ausgewählt.
Anschließend werden die Kinder durch einfaches Vertauschen der Bits zwischen
den zwei Schnittpunkten ermittelt. Durch die Kreuzung werden zwei Kinder er-
zeugt, die ähnliche Faktorwerte aufweisen wie deren Eltern. In der Literatur finden
sich ähnliche Verfahren mit nur einem Schnittpunkt, bei dem alle Bits auf einer Seite
des Schnittpunkts vertauscht werden oder Verfahren bei denen für jedes Bit einzeln
mit einer vorgegeben Wahrscheinlichkeit entschieden wird, ob das Bit vertauscht
wird.
Abb. 9.9 Kreuzung (binär)
Reelle Faktoren
Zur Kreuzung reeller Zahlen sind verschiedene Algorithmen entwickelt worden
KinderEltern
9.4 Genetische Evolutionsverfahren für mehrerer Zielgrößen 233
(Fuzzy Recombination [187], BLX [42], SBX [31, 33, 7], vSBX [7, 8], PCX [32],
XLM [179], PNX [8], PBX [102], UNDX [133]).
Das einfache BLX (Blend Crossover) erzeugt Kinder aus zwei Eltern a und b
durch die zufällige Wahl einer reellen Zahl aus einem Bereich, der wie folgt definiert
ist (Abbildung 9.10):
[min(a,b) −α
|
a −b
|
,max(a, b) + α
|
a −b
|
] (9.9)
Bei steigendem α wird somit ein größerer Bereich durch die Kinder abgedeckt.
Ein typischer Wert für α liegt bei α = 0.5.
Abb. 9.10 Kreuzung durch BLX
Der vSBX Algorithmus ist eine Verbesserung des SBX (Simulated Binary Cros-
sover) und verwendet zur Bestimmung der Faktoreinstellung k eines Kindes zwei
unterschiedliche Gleichungen k
1,2
, wobei vor der Kreuzung eine der beiden Glei-
chungen mit gleicher Wahrscheinlichkeit ausgewählt wird:
k
1
=
0.5[(1+ β
1
)a + (1 −β
1
)b]
0.5[(3−β
2
)a −(1 −β
2
)b]
0 < u ≤0.5
0.5 < u ≤ 1
k
2
=
0.5[(1−β
1
)a + (1 + β
1
)b]
0.5[−(1 −β
2
)a + (3 −β
2
)b]
0 < u ≤0.5
0.5 < u ≤ 1
(9.10)
β
1
=
1
2u
1
η
K
+1
β
2
=
1
2(1 −u)
1
η
K
+1
(9.11)
Die Zufallsvariable u ∈ [0,1] ist dabei für jede Variable (Faktor) und Kreuzung
neu zu bestimmen. Der im Vorfeld festzulegende und meist konstante Parameter η
K
bestimmt die Streuung der Kinder um die Eltern. Abbildung 9.11 zeigt beispielhaft
den Einfluss von η
K
auf die Kreuzung zweier Eltern, welche durch zwei Faktoren
(x
1
,x
2
) definiert sind. Die Erhöhung von η
K
führt zu einer Verringerung der Streu-
ung. Typische Werte für η liegen zwischen 5 und 20.
9.4.2 Mutation
Die Mutation ändert zufällig Faktorstufen im Faktorraum, wodurch die Erzeugung
von Datenpunkten (Kinder) ermöglicht wird, die nicht durch eine Kreuzung der
x
α |a − b|
α |a − b|
|a − b|
234 9 Optimierung
Abb. 9.11 Kreuzung reeller Zahlen (1,1) und (3,5) durch vSBX
ausgewählten Eltern erzielt werden können. Dadurch wird dem Optimierungsver-
fahren ermöglicht sich selbständig aus lokalen Minima zu befreien, da in regelmä-
ßigen Abständen zufällige Bereiche des Faktorraums und die dazugehörigen Ziel-
größen geprüft werden. Die festzulegende Wahrscheinlichkeit der Mutation ist mit
p
M
= 0···0.5 deutlich geringer als die Wahrscheinlichkeit der Kreuzung (Kapi-
tel 9.4.1).
Binäre Kodierung
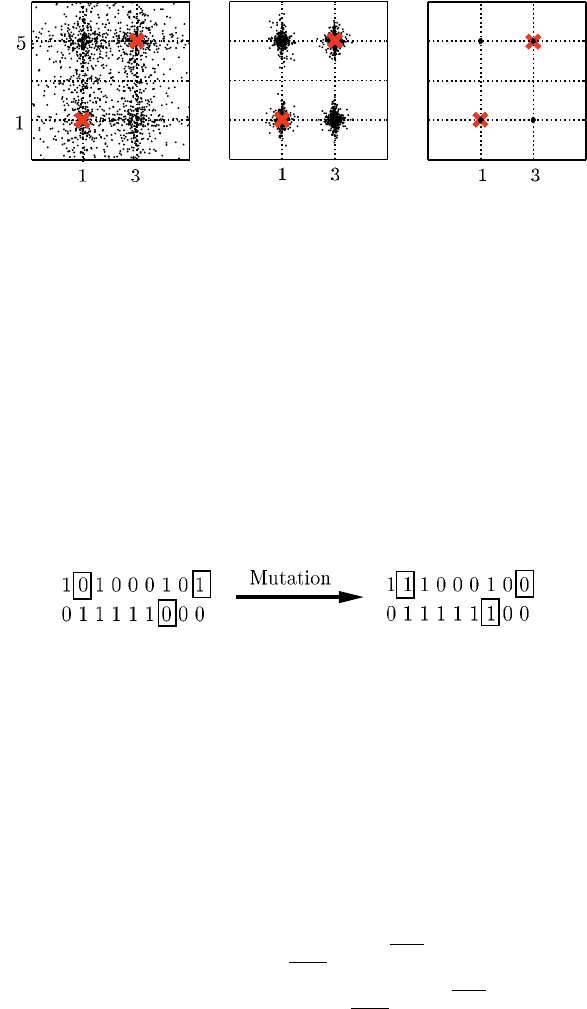
Die Mutation eines binär kodierten Faktors wird durch eine zufällige Änderung ein-
zelner Bits erzeugt (Abbildung 9.12), wobei jedes einzelne Bit mit der vorgegebenen
Wahrscheinlichkeit p
M
vertauscht wird.
Abb. 9.12 Mutation (binär)
Reelle Faktoren
Die Mutation eines reellen Faktors kann grundsätzlich durch die Wahl eines zufäl-
ligen Wertes aus dem Definitionsbereich erreicht werden, wobei sich jedoch zeigt,
dass eine Streuung um den aktuellen Faktorwert sich positiv auf den Optimierungs-
prozess auswirkt. Typische Verfahren sind dabei non-uniform-, Normverteilung und
Polynom Mutation [147]. Bei gegebener unterer und oberer Grenze des zu mutie-
renden Faktors x
u
≤ x ≤ x
o
wird die Polynom Mutation durch folgende Gleichung
berechnet.
x
M
= x + β (x
o
−x
u
)
mit β =
2u + [1 −2u]
h
1 −
x−x
u
x
o
−x
u
i
η
M+1
1
η
M+1
−1 u ≤ 0.5
1 −
2[1 −u] + 2 [u −0.5]
h
1 −
x
o
−x
x
o
−x
u
i
η
M+1
1
η
M+1
u > 0.5
(9.12)
x
1
x
2
x
1
x
1
η
K
= 1
η
K
= 10
η
K
= 100
Kinder
nachher
Kinder
vorher
