Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)
Подождите немного. Документ загружается.

8.8 Künstliche Neuronale Netzwerke 215
Versteckte Ebenen Anzahl Gewichten
b
0 n
y
n
f
+ 1
1 n
vE1
n
f
+ 1
+ n
y
(n
vE1
+ 1)
2 n
vE1
n
f
+ 1
+ n
vE2
(n
vE1
+ 1) + n
y
(n
vE2
+ 1)
n
f
: Anzahl Neuronen der Eingangsebene [Faktoren]
n
vE1/2
: Anzahl Neuronen der vesteckten Ebene 1 bzw. 2
n
y
: Anzahl Neuronen der Ausgangsebene [Ausgangsvariablen]
(8.53)
Ende des Trainings
Das Training eines Künstlichen Neuronalen Netzwerks wird abgebrochen, wenn
mindestens eine der folgenden Kriterien erreicht wird:
1. der Approximationsfehler der Trainingsdaten einen vorgegeben Grenzwert un-
terschreitet,
2. der Approximationsfehler von ausgewählten Testdaten, die nicht in den Traings-
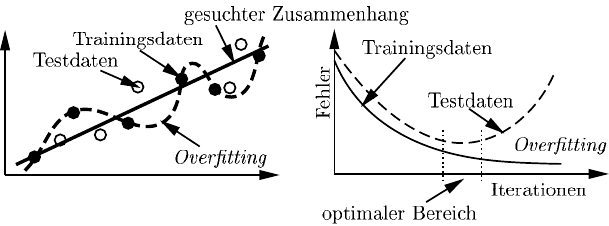
daten enthalten sind, deutlich ansteigt, welches ein Zeichen für Overfitting an
die gegebenen Trainingsdaten ist (Abbildung 8.16). Die verwendeten Testdaten
sollten dabei genauso wie die Trainingsdaten gleichmäßig über den gesamten
Faktorraum verteilt sein, so dass die Qualität des Netzwerks im gesamten Fak-
torraum geprüft wird.
3. eine vorher festgelegte maximale Anzahl an Trainingsschritten überschritten
wird
Abb. 8.16 Approximationsfehler und Overfitting
Neben den hier dargestellten Feedforward Netzwerken existieren deutlich kom-
plexere Strukturen, in denen beispielsweise die Aktivierung eines Neurons nicht
nur von den Neuronen der vorhergehenden Ebene, sondern auch anderen Ebenen
abhängt. Grundsätzlich können mit Künstlichen Neuronalen Netzwerken komplexe
Zusammenhänge gut abgebildet werden, wobei bereits einfache Feedforward Netz-
werke mit einer oder zwei versteckten Ebenen in fast allen Anwendungsfällen aus-
reichend sind. Die optimale Wahl der Netzwerkstruktur (z.B. Anzahl Neuronen pro
Ebene) ist im Vorfeld häufig schwierig und führt in der Praxis dazu, dass verschiede-
x
y, ˆy
216 8 Metamodelle
ne Netzwerke erzeugt werden und durch ein zu definierendes Beurteilungskriterium
das vorteilhafteste für die aktuelle Aufgabe gewählt wird.
Abbildung 8.17 zeigt die Approximation der Beispielfunktion aus Gleichung 8.17
bei Verwendung verschiedener Netzwerke mit einer versteckten Ebene und unter-
schiedlicher Neuronenzahl. Bereits zwei Neuronen in der versteckten Ebene genü-
gen, um den gesuchten Zusammenhang ausreichend genau zu approximieren (Ab-
bildung 8.17 [Mitte,oben] und 8.18). Durch die Verwendung von einem Neuron
wird hingegen lediglich ein globaler Trend abgebildet und die Wahl von fünf Neu-
ronen erhöht die Qualität der Approximation nur geringfügig. Die Gefahr des Over-
fittings steigt bei fünf Neuronen an, da mehr Gewichte als Datenpunkte zum Trai-
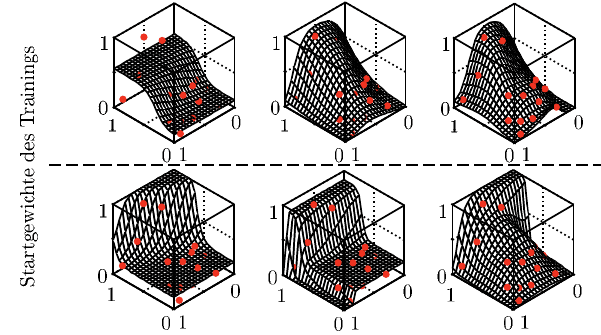
ning vorhanden sind. Die untere Zeile in Abbildung 8.17 zeigt die Approximation
der jeweils gleichen Netzstrukturen, wenn zum Training andere Startwerte für die
Gewichte als in der ersten Zeile verwendet werden. In dem dargestellten Beispiel
wird dadurch ein deutlich anderer Zusammenhang zwischen Ein- und Ausgangsva-
riablen ermittelt. Die Summe der Approximationsfehler der gegebenen Trainings-
punkte ist nahezu identisch zu den Modellen aus der ersten Zeile. Dieses zeigt, dass
mit Künstlichen Neuronalen Netzwerken einerseits komplexe Zusammenhänge dar-
gestellt werden können, auf der anderen Seite es aber ebenfalls notwendig ist, das
ermittelte Metamodell auf seine Allgemeingültigkeit zu prüfen. Dieses wird in den
meisten Fällen durch die Prüfung der Approximationsgenauigkeit an bekannte Da-
tenpunkte (Testpunkte), welche nicht zum Training des Netzes verwendet wurden,
durchgeführt. Grundsätzlich ist eine Prüfung des Metamodells nach seiner Erstel-
lung nicht nur für Künstliche Neuronale Netzwerke notwendig, sondern für alle
dargestellten Metamodelle durchzuführen, die sich automatisch an komplexe Zu-
sammenhänge anpassen können.
Abb. 8.17 Künstliche Neuronale Netzwerke: Beispiele
ˆy
x
2
ˆy
x
2
x
1
ˆy
x
2
ˆy
x
2
ˆy
x
2
ˆy
x
2
n
vE1
= 1
n
vE1
= 2
n
vE1
= 5
V arianteb
x
1
x
1
x
1
x
1
x
1
V ariantea

8.9 Qualität von Metamodellen 217
Abb. 8.18 KNN mit zwei Neuronen in einer versteckten Ebene
8.9 Qualität von Metamodellen
Die hohe Flexibilität und Anpassungsfähigkeit vieler Verfahren zur Erstellung von
Metamodellen ermöglicht eine gute Approximation von unbekannten und komple-
xen Zusammenhängen zwischen Ein- und Ausgangsvariablen eines zu analysieren-
den Systems. Es besteht jedoch die Gefahr, ein Metamodell zu erzeugen, welches
sich zwar gut an die gegebenen Datenpunkte anpasst, dessen Vorhersagegenauig-
keit für neue Faktorkombinationen jedoch gering ist. Dieses kann durch falsch ge-
wählte Parameter (Abbildung 8.19,Θ = 100), eine falsche Interpretation des Zu-
sammenhangs basierend auf den gegeben Daten (Abbildung 8.17, Zeile 2) oder ein
Overfitting an die gegebenen Daten (Abbildung 8.16) auftreten. Daher ist ein nie-
mals zu vernachlässigender Kernpunkt bei der Verwendung von Metamodellen die
Überprüfung beziehungsweise Abschätzung der Qualität des Metamodells für die
Approximation von unbekannten Faktorkombinationen.
Eine typische Beurteilungsgröße ist dazu der mittlere quadratische Approxima-
tionsfehler (MSE:mean squared error):
MSE =
1
n
r
n
r
∑
i=1
(y
i
− ˆy
i
)
2
(8.54)
In einigen Anwendungen wird anstelle des MSE der Mittelwert der absoluten
Differenz (|y
i
− ˆy
i
|) verwendet. Zur Stabilisierung des Ergebnisses ist ebenfalls der
Einsatz des Medians anstelle des Mittelwerts möglich.
Eine Betrachtung des Approximationsfehlers beziehungsweise der Residuen
(y
i
− ˆy
i
) an den Datenpunkten D
e
, welche zur Erzeugung des Metamodells ver-
wendet wurden, wie es bei einfachen linearen Regressionsmodellen aus physikali-
schen Experimenten bekannt ist, reicht bei komplexen Metamodellen basierend auf
Computer-Simulationen nicht aus. So verläuft beispielsweise ein Metamodell auf
Basis des Kriging-Ansatzes immer genau durch die zum Training verwendeten Da-
tenpunkte (Abbildung 8.4), was eine sinnvolle Beurteilung des Metamodells durch
die Residuen dieser Datenpunkte ausschließt. Entsprechendes gilt bei Overfitting an
die gegebenen Trainingsdaten.
x
2
ˆy
x
1
218 8 Metamodelle
Testdaten
Eine der einfachsten Möglichkeiten zur Beurteilung eines Metamodells ist die Er-
mittlung der Residuen oder des mittleren quadratischen Approximationsfehlers an
zusätzlichen Datenpunkte D
t
, welche nicht zur Erzeugung des Metamodells ver-
wendet wurden. Sind die Residuen an diesen Datenpunkten in der gleichen Grö-
ßenordnung wie die Residuen der Datenpunkte D
e
und gleichzeitig in einer für
die durchzuführenden Analysen akzeptablen Größe, so wird davon ausgegangen,
dass das Metamodell den grundsätzlichen Zusammenhang zwischen Ein- und Aus-
gangsvariablen richtig abbildet und die Approximationsgenauigkeit ausreichend ist.
Bei der Wahl der Testpunkte D
t
ist darauf zu achten, dass der gesamte Faktorraum
gleichmäßig und vollständig abgedeckt wird, da die Modellqualität für den gesam-
ten Faktorraum gewährleistet sein muss, um im Weiteren vertrauenswürdige Unter-
suchungen durchzuführen.
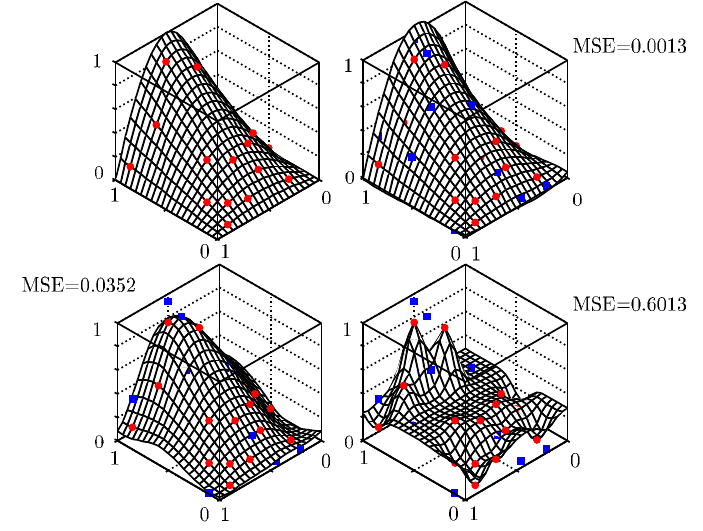
Der MSE von 10 zufällig gewählten Faktorkombinationen für die drei Kriging-
Modelle aus Abbildung 8.4 zeigen bereits deutlich, dass im dargestellten Beispiel
die Wahl von Θ = 0.01 das sinnvollste Metamodell erzeugt (Abbildung 8.19).
ˆy
x
2
x
1
θ = 10
ˆy
x
2
x
1
θ = 100
ˆy
x
2
x
1
θ = 0.01
x
1
x
2
y
Abb. 8.19 Testdaten zur Überprüfung eines Metamodells
Grundsätzlich muss der Anwender bei einer begrenzten Anzahl an Datenpunkten
entscheiden, wie viele Datenpunkte für die Erzeugung des Metamodells verwendet
werden sollen und wie viele zur Kontrolle der Qualität.
8.9 Qualität von Metamodellen 219
Kreuzvalidierung
Werden zur Analyse komplexe Simulationsmodelle mit langen Rechenzeiten ver-
wendet, so ist es häufig notwendig, alle Datenpunkte zur Erzeugung des Metamo-
dells zu verwenden, da ansonsten die vorhandene Komplexität der Zusammenhänge
nicht abgebildet werden kann. In diesen Fällen wird die Kreuzvalidierung (cross
validation) zur Prüfung der Modellqualität eingesetzt. Dabei werden drei Verfahren
der Kreuzvalidierung unterschieden.
Die zufällige Untergruppen-Validierung unterteilt die vorhandenen Datenpunkte
in eine Trainings- und eine Testgruppe, wobei die Testsgruppe meist kleiner ist als
die Gruppe der Trainingsdaten. Das Metamodell wird nur mit den Trainingsdaten
erzeugt und die Qualität des Metamodells mit den Daten der Testgruppe gemessen
(zum Beispiel mit MSE). Dieses wird mehrmals mit unterschiedlichen (zufälligen)
Aufteilungen der Daten wiederholt und der Mittelwert aller MSE gebildet, welcher
dann als Gütekriterium verwendet wird. Problematisch kann sich hierbei auswir-
ken, dass die Aufteilung zufällig durchgeführt wird. So können einige Datenpunkte
niemals und andere mehrmals zur Testgruppe gehören, was den Datenpunkten un-
terschiedliche Bedeutung in der Modellerzeugung beziehungsweise Kontrolle zu-
kommen lässt.
Aus diesem Grund wird in den meisten Fällen die k-fold Kreuzvalidierung ver-
wendet. Dabei werden die gegebenen Datenpunkte in k gleichgroße Untergruppen
K
1
,···,K
k
unterteilt. Eine Untergruppe wird dann zum Test der Qualität und die
restlichen k −1 Untergruppen zur Erzeugung des Metamodells verwendet. Dieses
wird für jede der k Gruppen durchgeführt und anschließend der Mittelwert aller
k Qualitätswert gebildet. Typischerweise wird k = 10 gewählt. Der Vorteil dieser
Methode ist, dass jeder Punkt genau einmal als Testpunkt und k −1 mal zur Erzeu-
gung des Metamodells verwendet wird und somit jeder Datenpunkt gleichberechtigt
eingesetzt wird. Eine sinnvolle Erweiterung der k-fold Kreuzvalidierung ist die Er-
zeugung der Untergruppen, so dass jede der k Gruppen annähernd den gleichen
Mittelwert aufweist. Dieses kann zwar nicht garantieren, dass die k Untergruppen
gleichmäßig verteilt sind, jedoch steigt die Wahrscheinlichkeit deutlich an.
Wird jeder einzelne Datenpunkt als Gruppe betrachtet (k = n
r
), so wird von
Leave-One-Out Kreuzvalidierung gesprochen (siehe auch DFFITS Kapitel 3.4.3.1).
Hierbei handelt es sich um einen Sonderfall der k-fold Kreuzvalidierung, so dass das
grundsätzliche Berechnungsverfahren sich nicht unterscheidet. In der Praxis wird
die Leave-One-Out Kreuzvalidierung bei steigender Anzahl der gegebenen Daten-
punkte sehr rechenintensiv, so dass dieser Sonderfall hauptsächlich bei geringen
Datenmengen angewendet wird.
Auch wenn die Kreuzvalidierung bei einem Vergleich verschiedener Metamo-
dellansätze oder Parameter nicht garantieren kann, dass das Metamodell mit dem
kleinsten mittleren MSE das für die Anwendung beste Modell darstellt, hat es sich
in vielen Bereichen als sinnvolles Kriterium etabliert.
220 8 Metamodelle
8.10 Faktorwahl
In der Praxis treten meist eine Vielzahl von Faktoren (Parameter) auf, die während
der Analyse eines technischen Systems berücksichtigt werden können. Die Beur-
teilung, ob ein Faktor für das gesuchte Metamodell notwendig oder vernachlässig-
bar ist, ist vor der eigentlichen Analyse oft schwierig. Die Berücksichtigung aller
Faktoren mit dazugehörigen Interaktionen und nachträglicher Auswahl durch eine
Sensitivitätsanalyse (Kapitel 10) ist dabei meist zu rechen- und zeitaufwendig.
In verschiedenen Anwendungen ist es somit sinnvoll, bereits während der Er-
stellung des Metamodells eine Auswahl der verwendeten Faktoren zu ermöglichen.
Wird beispielsweise ein einfaches lineares Regresionsmodell (Kapitel 8.2 und 8.3)
der folgenden Form verwendet, so können verschiedenste Faktoren
x
j
,x
2
j
,···
be-
rücksichtigt werden.
ˆy
i
= b
0
+ b
1
x
i1
+ b
2
x
i2
+ ···+ b
n
f
x
i n
f
(8.55)
Zur Abbildung komplexer Zusammenhänge werden meist viele Terme verwen-
det, was zu einem überangepassten (overfitting) Metamodell führt welches auch un-
wichtige Faktoren mitberücksichtigt. Eine schnelle und sinnvolle Sensitivitäts- oder
weiterführende Analyse ist mit diesen Metamodellen nur schwer möglich.
Klassische Verfahren
Zur Bestimmung signifikanter Faktoren existieren verschiedene Verfahren, die ein
’gutes’ aber nicht unbedingt das für die Aufgabe ’beste’ Metamodell erzeugen.
Bei der Vorwärts-Selektion (forward selection) wird mit einem einfachen Basis-
modell M
0
gestartet. Dieses Modell enthält dabei nur eine Konstante (ˆy = b
0
). Sind
bereits Faktoren bekannt, die in jedem Fall für das Metamodell signifikant sind,
werden diese ebenfalls dem Basismodell zugefügt. In einem iterativen Prozess wird
anschließend in jedem Schritt das Metamodell mit einem Faktor erweitert. Dazu
wird in jedem Schritt dem aktuellen Metamodell jede der noch verfügbaren Fak-
toren und Faktorkombinationen einzeln hinzugefügt und jeweils die Verbesserung
der Modellgüte des Metamodells bestimmt. Der Faktor, welcher die Modellgüte am
stärksten verbessert, wird anschließend dem Metamodell hinzugefügt. Im folgenden
Iterationsschritt ist dann das erweiterte Metamodell als Basismodell zu verwenden.
Die Erweiterung des Metamodells endet, wenn eine vorgegebenes Güte des Meta-
modells erreicht wurde oder keine signifikante Verbesserung mehr erzielt werden
kann.
Die Rückwärts-Selektion (backward selection) geht im Gegensatz zur Vorwärts-
Selektion von einem Metamodell aus, welches alle zur Verfügung stehenden Fak-
toren enthält. In einer Iteration wird in jedem Schritt der Faktor gesucht, welcher
die Modellgüte am wenigsten verschlechtert. Dieser Faktor wird aus dem Modell
entfernt.
Der Begriff Schrittweise-Regression (stepwise regression) bezeichnet eine Kom-
bination der Vorwärts- und Rückwärts-Selektion, wobei nach jedem zugefügten
Faktor geprüft wird, ob ein beliebiger Faktor aus dem Metamodell wieder entfernt
werden kann [41].
8.10 Faktorwahl 221
Existiert nur eine geringe Anzahl von möglichen Faktoren und Faktorkombina-
tionen, werden in seltenen Fällen alle möglichen Metamodelle (Faktorkombinatio-
nen) erzeugt und anschließend das Modell mit der besten Güte gewählt. Der Re-
chenaufwand steigt jedoch bei diesem Verfahren (all subsets) schnell mit steigender
Faktoranzahl an [61].
Gütekriterien
Zur Beurteilung der Modellgüte werden in der Praxis verschiedene Kriterien vorge-
schlagen [1, 165, 104].
adjusted R
2
adjR
2
= 1 −
n
r
−1
n
r
−n
f
−1
1 −R
2
Aikaike
0
s Informationskriterium AIC = n
r
log
SSE
n
r
+ 2
n
f
+ 1
Bayessches Informationskriterium BIC = n
r
log
SSE
n
r
+ log (n
r
)
n
f
+ 1
PRESS ˆ= Leave −One −Out Kreuzvalidierung
Mallows C
p
C
p
=
SSE
ˆ
σ
2
+ 2
n
f
+ 1
−n
r
ˆ
σ
2
aus Gesamtmodell( alle Faktoren) gesch
¨
atzt
Der Einsatz des BIC-Kriteriums führt dabei im Vergleich zum AIC-Kriterium typi-
scherweise zu weniger Faktoren im optimierten Modell. Neben diesen hauptsächlich
eingesetzten Gütekriterien existieren viele erweiterte Kriterien wie CIC, DIC, EIC,
MAIC3, CAIC, ABIC [
151, 173, 78, 18, 150]
Die dargestellten Verfahren sind relativ instabil, so dass sich bei kleinen Ände-
rungen in den vorhandenen Daten teilweise deutlich andere Metamodelle ergeben.
Ridge Regression
Zur Ermittlung des gesuchten Metamodells wird daher alternativ die Summe der
Fehlerquadrate minimiert, wobei eine zusätzliche Straffunktion für die Regressi-
onskoeffizienten zur Regulierung des Modells verwendet wird [
71, 117, 37].
min
b
"
n
r
∑
i=1
(y
i
− ˆy
i
)
2
+ λ
n
f
∑
j=0
b
2
j
#
(8.56)
Bei steigendem λ sinken die Absolutwerte der einzelnen Regressionskoeffizi-
enten, wobei Koeffizienten für unsignifikante Faktoren schnell gegen Null streben
und somit eine Variablenselektion stattfindet. Die erzeugten Metamodelle werden
bei steigendem λ einfacher, wodurch die Varianz des Metamodells sinkt jedoch der
Approximationsfehler für die einzelnen Datenpunkte steigt. Durch eine Kreuzvali-
dierung werden die erzeugten Metamodelle typischerweise beurteilt, wodurch das
geeignetste λ (Metamodell) gewählt wird. Damit die Straffunktion unabhängig von
den Dimensionen der einzelnen Faktoren ist, werden die Daten auf eine einheitliche
Varianz von eins normiert. Dieses Verfahren ist in der Literatur als Ridge Regression
bekannt und die gesuchten Regressionskoeffizienten können in Abhängigkeit von λ
direkt wie folgt bestimmt werden [192]:
ˆ
b
λ
= (X
0
X + λ I)X
0
Y
ˆ
Y = X
ˆ
b
λ
(8.57)
222 8 Metamodelle
I ist dabei die quadraitsche Einheitsmatrix der Größe n
f
+ 1.
LASSO
Im sogenannten LASSO Verfahren wird anstelle der quadratischen Straffunktion
die Summe der Absolutwerte verwendet λ
n
f
∑
j=0
b
j
[182, 183]. Diese Straffunktion
drückt unsignifikante Faktoren deutlich stärker gegen Null, wobei die Regressions-
koeffizienten im Gegensatz zur Ridge-Regression wirklich zu Null werden, so dass
eine eindeutige Faktorselektion ermöglicht wird. Neben der Ridge Regression und
LASSO existieren in der Literatur weitere Ansätze für Straffunktionen und weiter-
entwickelte Verfahren [60, 40, 67].
Da die meisten Metamodelle in folgende allgemeine Form umgewandelt werden
können, sind die dargestellten Ansätze auch bei anderen Modelltypen als lineare
Regressionmodelle grundsätzlich einsetzbar [50].
ˆy
i
=
n
k
∑
k=0
F
k
(x
i
)b
k
(8.58)
Dabei sind F
k
beliebige Basisfunktionen, die jeweils von mehreren Faktoren abhän-
gen können.
8.11 Zusammenfassung
Zur Analyse und Optimierung technischer Systeme werden in der Praxis immer
häufiger komplexe Simulationsmodelle eingesetzt. Obwohl die zur Verfügung ste-
hende Rechenleistung kontinuierlich ansteigt, ist die benötigte Rechenzeit einer der
kritischsten Punkte im Entwicklungs- und Analyseprozess. Parallel zur Rechenka-
pazität steigt nämlich die Komplexität der Simulationsmodelle zur Erhöhung der Si-
mulationsqualität und die zu berücksichtigenden Faktoren ebenfalls stetig an. Eine
direkte Analyse mit einem komplexen Simulationsmodell ist dadurch in den meis-
ten Fällen aus zeitlicher Sicht nicht sinnvoll. Daher werden Metamodelle gesucht,
welche den zur Analyse benötigten Zusammenhang zwischen Eingangsvariablen
(Faktoren) x und der zu untersuchenden Ausgangsvariablen y mit ausreichender
Genauigkeit und minimaler Rechenzeit abbilden. Die dazu erzeugten Metamodelle
benötigen zur Approximation eines Ergebnisses wenige Millisekunden, wobei das
komplexe Simulationsmodell Stunden oder Tage rechnet.
Metamodelle werden grundsätzlich auf Basis von bekannten Datenpunkten auf-
gebaut welche durch Messungen oder Simulationen ermittelt wurden. Dabei kann
es sich um bereits vorhandene Daten oder speziell für die Projektaufgabe ermittel-
te Daten handeln. Werden neue Daten erzeugt, ist es sinnvoll speziell für diesen
Zweck ausgelegte Testfelder wie Latin Hypercubes oder gleichverteilte Testfelder,
wie sie in Kapitel 7 beschrieben sind, zu verwenden. Sie liefern bei einer gegebenen
Anzahl von bestimmbaren Datenpunkten die größte Menge an Informationen über
die gesuchten Zusammenhänge. Grundsätzlich gilt, dass eine Erhöhung der Daten-
8.11 Zusammenfassung 223
punkteanzahl und somit der Informationsmenge zu einem genaueren Metamodell
führt.
Basierend auf den vorhandenen Datenpunkten wird ein Metamodell erzeugt, wel-
ches komplexe Zusammenhänge abbildet und dazu die vorhandenen Informationen
der Datenpunkte optimal ausnutzt. Dabei ist eine automatische Anpassung des Me-
tamodells an die gegebenen Datenpunkte ohne Vorgabe eines Zusammenhangs zwi-
schen Ein- und Ausgangsvariablen, wie es bei einer einfachen linearen Regression
notwendig ist. Wäre eine Vorgabe des Zusammenhangs bereits vor der eigentlichen
Analyse erforderlich und nicht korrekt vom Anwender definiert, so kann kein Me-
tamodell erzeugt werden, welches die wahren Zusammenhänge optimal abbildet.
Grundsätzlich wird bei Metamodellen zwischen lokalen und globalen Verfah-
ren unterschieden. Lokale Verfahren wie das Kriging approximieren den gesuchten
Funktionswert y an einer unbekannten Faktorkombination x
0
durch Datenpunkte in
einer vorher definierten Umgebung um x
0
. Globale Verfahren wie Künstliche Neu-
ronale Netzwerke bilden hingegen ein Metamodell, welches auf allen Datenpunkten
basiert.
Vor der Erzeugung eines Metamodells muss entschieden werden, ob die Appro-
ximation des Modells wie beim Kriging genau durch die bekannten Datenpunk-
te verlaufen soll oder ob die Approximation eines mittlerer Verlaufs sinnvoller ist.
Bei vorhandenen Streuungen in den Datenpunkten ist der mittlere Verlauf des Zu-
sammenhangs für eine Analyse vorzuziehen. Auch bei Verwendung von Computer-
Simulationen bei denen keine direkte zufällige Streuung auftritt, kann durch kleine
Änderungen der Faktoreinstellungen das Ergebnis deutlich schwanken, da das Si-
mulationsmodell zum Beispiel am Ende des Simulationslauf noch nicht vollständig
eingeschwungen ist. Auch in diesen Fällen ist die Vorhersage des mittleren Verlaufs
der Ausgangsvariablen oft sinnvoller.
Neben der Wahl der zu verwendenden Faktoren und der Wahl aussagekräftiger
Variablen zur Beurteilung des betrachteten Systems sowie die Wahl des Modelltyps
ist die Überprüfung der erzeugten Metamodelle einer der wichtigsten Schritte in der
Erzeugung von Metamodellen. Die Vernachlässigung der Qualitätsprüfung ist einer
der häufigsten Fehler für den missglückten Einsatz von Metamodellen in der Praxis.
Eine Prüfung der Metamodelle kann durch die Beurteilung der Approximations-
genauigkeit von zusätzlichen Datenpunkten erfolgen, die nicht zur Erzeugung des
Metamodells verwendet wurden oder durch Verfahren wie die Kreuzvalidierung,
welche zur Erzeugung des Metamodells Datenpunkte auslassen, um diese anschlie-
ßend zur Überprüfung zu verwenden.
Grundsätzlich sind bei allen Metamodellen Extrapolationen außerhalb der abge-
sicherten Datenpunkte, welche zur Erzeugung des Metamodells verwendet wurden,
zu vermeiden oder nur mit Vorsicht und weiteren Kontrollen zu verwenden.
SIMPSON et al. vergleicht verschiedene Metamodelle und gibt folgende grund-
sätzlichen Empfehlungen [170]. Metamodelle auf Basis von Polynomen wurden
ursprünglich für Daten mit zufälligen Fehlern (physikalische Experimente) entwi-
ckelt. Durch ihre einfache Implementierung finden sie jedoch auch bei Computer-
Experimenten häufig Anwendung. Sie sollten lediglich zur Analyse bei wenigen
Faktoren und einfachen Zusammenhängen eingesetzt werden. Zur Verbesserung der
224 8 Metamodelle
Metamodelle können bei geringer Faktoranzahl ebenfalls Splines eingesetzt wer-
den. Treten keine oder unwesentliche zufällige Streuungen in den Daten auf (de-
terministisch) wird bei stark nichtlinearen Zusammenhängen und einer Faktoran-
zahl n
f
< 50 Kriging empfohlen. Werden viele Faktoren, betrachtet sind Künstliche
Neuronale Netzwerke vorteilhaft. Das optimale Verfahren zur Erstellung des Meta-
modells hängt von vielen Randbedingungen ab, so dass alle Empfehlungen lediglich
als Hinweise gedeutet werden können. Bei korrekter Anwendung bieten jedoch alle
Metamodellansätze ausreichend gute Ergebnisse, wobei ein Vergleich verschiedener
Ansätze während einer Analyse zur zusätzlichen Absicherung sinnvoll ist.
