Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)
Подождите немного. Документ загружается.

sehr klein gewählt, so erhalten lediglich die Messdaten in der lokalen Umgebung
des gesuchten Punkts x
0
ein deutliches Gewicht für die Approximation des gesuch-
ten Funktionswerts. Das erzeugte Metamodell ist in diesen Fällen meist zu stark an
die gegebenen Messdaten angepasst (overfitting). Die Approximation der bekannten
Messdaten ist dann zwar sehr genau jedoch können hohe Abweichungen bei Fak-
torkombinationen auftreten, die nicht zur Erstellung des Metamodells verwendet
wurden. Große Werte für h führen auf der anderen Seite zu einer starken Glättung
des Funktionszusammenhangs, so dass die Vorhersage des Funktionswerts immer
weiter auf den globalen Mittelwert ¯y zuläuft.
Ein grundsätzliches Problem tritt an den Rändern des Faktorraums auf, bei denen
die gegebenen Datenpunkte zur Approximation nicht mehr symmetrisch um den ge-
suchten Punkt x
0
verteilt sind. Wird beispielsweise eine eindimensionale Funktion
f betrachtet, die am Rand des Faktorraums kontinuierlich fallend ist, so stehen zur
Approximation lediglich Datenpunkte mit Funktionswerten größer als y
0
zur Verfü-
gung. Die Vorhersage ˆy
0
wird dadurch größer sein als der wahre Funktionswert y
0
.
Typischerweise steigt der Fehler zum Rand hin an (Abbildung 8.8).
8.7 Kernel- und Lokale Polynom-Regression 205
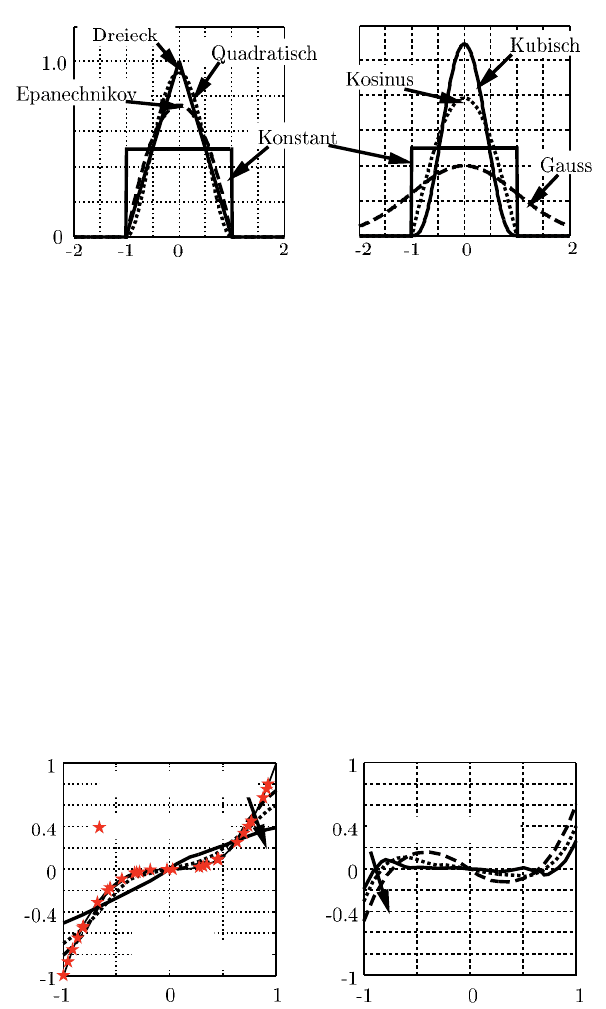
K (u)
u
u
Abb. 8.7 Kernel-Funktionen
h = 0.25, 0.5, 1.0
h = 0.25, 0.5, 1.0
y
x
x
y − ˆy
Datenpunkt
y = x
3
K (x) = 1 − |x|
Abb. 8.8 Kernel-Regression, Beispiel: y = x
3

206 8 Metamodelle
Die Kernel-Regression wird sinnvoll eingesetzt, wenn eine hohe Anzahl von Da-
tenpunkten vorliegen, welche mit einer zu glättenden Messstreuung überlagert sind.
Eine Anhäufung von Datenpunkten in bestimmten Regionen des Faktorraums (Clus-
terung) führt automatisch zu einer stärkeren Gewichtung dieser Regionen, so dass
eine gute Gleichverteilung der Datenpunkte vorliegen sollte.
Zur Erhöhung der Approximationsgenauigkeit kann an der Stelle x
0
nicht nur ein
gewichteter Mittelwert bestimmt, sondern ebenfalls ein Polynom mit dem Grad d 6=
0 angepasst werden (Lokale Polynom-Regression) [23, 65], wodurch besonders die
Fehler an den Rändern des Faktorbereichs verringert werden. Im eindimensionalen
Fall (1 Faktor) ist dadurch eine Funktion der folgenden Form gesucht:
ˆy (x
0
) = β
0
(x
0
) + β
1
(x
0
)x
0
+ β
2
(x
0
)x
2
0
+ ···+ β
d
(x
0
)x
d
0
= β
0
(x
0
) +
d
∑
k=1
β
k
(x
0
)x
k
0
(8.32)
Die gesuchten β
k
(x
0
) werden mittels der gewichteten Methode der kleinsten Feh-
lerquadrate ermittelt, bei der das Minimum der folgenden Gleichung bestimmt wird:
min
β
n
r
∑
i=1
K
x
i
−x
0
h
y
i
−
"
β
0
+
d
∑
k=1
β
k
x
k
i
#!
2
(8.33)
Gelöst wird diese Minimierungsaufgabe durch die Gleichung:
ˆy (x
0
) = X
0
X
0
B(x
0
)X
−1
X
0
B(x
0
)Y (8.34)
mit X =
1 x
1
x
2
1
··· x
d
1
1 x
2
x
2
1
··· x
d
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1 x
n
r
x
2
n
r
··· x
d
n
r
X
0
=
1,x
0
,x
2
0
,···,x
d
0
B = diag(β
0,1
,β
0,2
,β
0,n
r
)
Y = (1, y
1
,y
2
,···,y
n
r
)
0
(8.35)
Abbildung 8.9 zeigt deutlich die erreichbare Verbesserung des Metamodells bei
Verwendung einer lokalen Polynom-Regression mit dem Grad d = 2. In der Praxis
zeigt sich, dass Polynome des Grads d ≤ 2 meistens für eine gute Approximation
im Randbereich ausreichen.
Bei mehreren Faktoren (n
f
> 1) wird überwiegend ein linearer Ansatz mit d = 1
eingesetzt.
min
β
n
r
∑
i=1
K(x
i
−x
0
)
n
f
∏
j=1
h
j
y
i
−
"
β
0
+
n
f
∑
j=1
β
j
x
i j
#!
2
mit K (x
i
−x
0
) = K
x
i1
−x
01
h
1
,
x
i2
−x
02
h
2
,···,
x
in
f
−x
0n
f
h
n
f
(8.36)
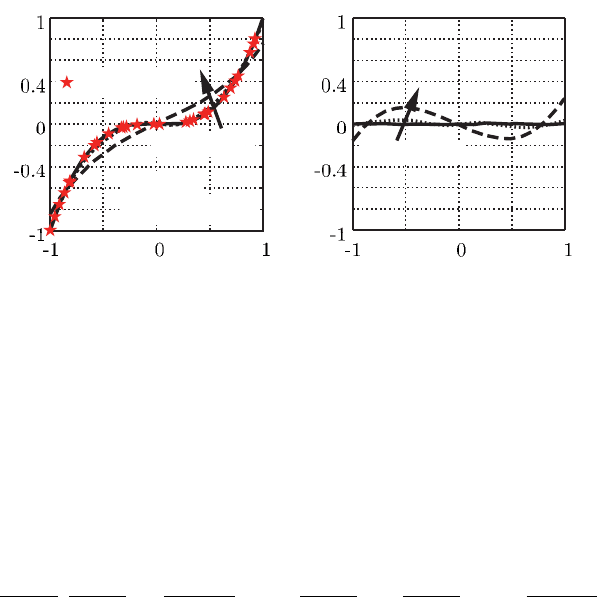
8.7 Kernel- und Lokale Polynom-Regression 207
Abb. 8.9 Lokale Polynom-Regression (Polynom Grad 2)
Für jeden Faktor kann dabei eine unterschiedliche Bandbreite h
j
gewählt werden,
was den Aufwand zur optimalen Wahl der Bandbreiten erschwert. Die mehrdimen-
sionale Kernel-Funktion muss ebenfalls die folgende Grundvoraussetzung erfüllen.
Z
K (u) du = 1 (8.37)
Die einfachste Form zur Erzeugung einer mehrdimensionalen Kernel-Funktion ist
die Multiplikation eindimensionaler Kernel-Funktionen, die für jede Dimension
(Faktor) separat berechnet werden.
K
x
i1
−x
01
h
1
,
x
i2
−x
02
h
2
,···,
x
in
f
−x
0n
f
h
n
f
!
= K
x
i1
−x
01
h
1
K
x
i2
−x
02
h
2
···K
x
in
f
−x
0n
f
h
n
f
!
(8.38)
Zur Approximation von y an der Stelle x
0
wird ebenfalls Gleichung 8.34 einge-
setzt, wobei die folgenden Definitionen gelten:
X =
1 x
11
x
12
··· x
1n
f
1 x
21
x
22
··· x
2n
f
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1 x
n
r
1
x
n
r
2
··· x
n
r
n
f
X
0
=
1,x
01
,x
02
,···,x
0n
f
B = diag(K (x
1
−x
0
),K (x
2
−x
0
),···,K (x
n
r
−x
0
))
(8.39)
Abbildung 8.10 zeigt die Approximation des zwei-dimimensionalen Beispiels
aus Gleichung 8.17 bei Verwendung unterschiedlicher Bandbreiten h = const. Durch
eine steigende Bandbreite nähert sich das Metamodell immer weiter der einfachen
linearen Regression, was zu deutlich höheren Approximationsfehlern führt. Kleine-
re Bandbreiten liefern genauere Vorhersagen im inneren Bereich, weisen aber bei
Extrapolation in diesem Beispiel deutliche Fehler auf.
y
y − ˆy
x
x
h = 0.5, 1, 2
Datenpunkt
y = x
3
K (x) = 1 − |x|
h = 0.5, 1, 2
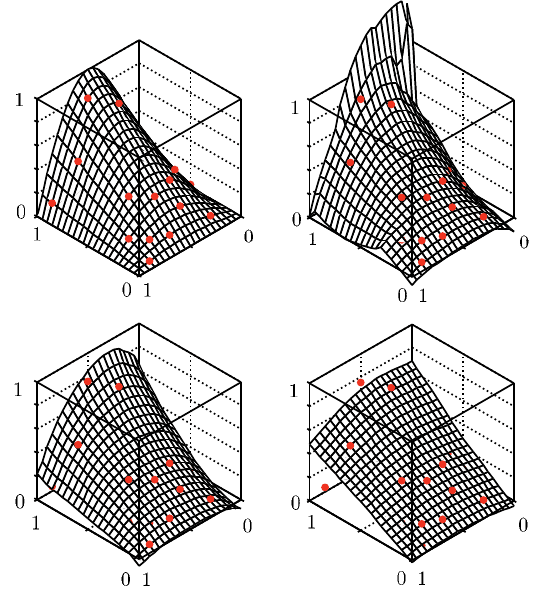
208 8 Metamodelle
Abb. 8.10 Lokale Polynom-Regression: Beispiel
Soll zur Verbesserung der Approximationsgenauigkeit ein komplexeres Poly-
nom eingesetzt werden, so fließt dieses in die Bestimmung von X und X
0
ein
X
0
=
1,x
01
,x
02
,x
2
01
,x
2
02
.
In verschiedenen Literaturstellen wird die Wahl der Bandbreite bei einem oder
mehreren Faktoren diskutiert [106, 83, 158, 188, 39, 85].
Eine interessante Anwendung der lokalen Polynom-Regression bietet die Kom-
bination mit einem Kriging (Kapitel 8.5) Verfahren. Dabei wird der globale Trend
des zu approximierenden Zusammenhangs durch die lokale Polynom-Regression
modelliert und durch ein Kriging Modell die verbleibende Abweichung zwischen
dem globalen Trend und den bekannten Datenpunkten [174].
8.8 Künstliche Neuronale Netzwerke
Künstliche Neuronale Netzwerke (KNN) sind Metamodelle die durch das biologi-
sche Nervensystem inspiriert wurden. Die Hauptelemente eines KNNs bilden soge-
y
x
2
x
1
h = 0.6
ˆy
x
2
x
1
ˆy
x
2
x
1
ˆy
x
2
x
1
h = 0.8
h = 1.5
8.8 Künstliche Neuronale Netzwerke 209
nannte Neuronen, welche durch Informationsaustausch untereinander verschiedene
Aufgaben (zum Beispiel Approximation eines Funktionswerts y an einer unbekann-
ten Faktorkombination x
0
) lösen können. KNNs werden dabei durch Beispieldaten
(bekannte Versuchsdaten) trainiert. Trainieren bedeutet in diesem Zusammenhang,
entsprechend den biologischen Vorgängen im Gehirn, die Anpassung der Verbin-
dungen beziehungsweise des Informationsaustauschs zwischen den einzelnen Neu-
ronen.
Die ersten Künstlichen Neuronalen Netzwerke wurden bereits 1943 von dem
Neurophysiologen WARREN MCCULLOCH und dem Logiker WALTER PITS vorge-
stellt. Bedeutsame Weiterentwicklungen und Einsatzmöglichkeiten sind jedoch erst
zwischen 1970 und 1980 erzielt worden. In Kombination mit modernen Computer-
Systemen bieten KNNs eine gegen Störgrößen und einzelne Fehler in den Daten
robuste Methode zur Erzeugung von Metamodellen [109].
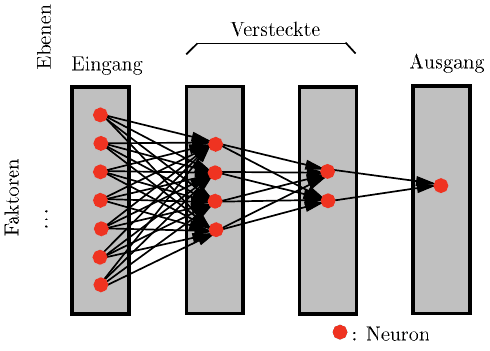
Neben anderen Netzwerktypen wird das einfache Feedforward Netzwerk in vie-
len Fällen zur Erzeugung von Metamodellen eingesetzt. Abbildung 8.11 zeigt eine
schematische Darstellung dieses Grundtyps, bei dem die Neuronen (Punkte) in un-
terschiedlichen Ebenen aufgeteilt werden. Die erste Ebene (Eingangs Ebene) erhält
die verschiedenen Faktoreinstellungen (x
1
,···,x
n
f
) des untersuchten Systems als
Eingangssignal. Auf der gegenüberliegenden Seite befindet sich die Ausgangsebene
in der sich die gesuchte Approximation ˆy wiederfindet. Das Künstliche Neuronale
Netzwerk kann dabei eine oder auch gleichzeitig mehrere Ausgangsvariablen ap-
proximieren. In den meisten Fällen ist es sinnvoll für jede zu untersuchende Aus-
gangsvariable y ein eigenes KNN zu verwenden, da dieses nur dadurch speziell an
die zu untersuchende Ausgangsvariable angepasst werden kann. Zwischen Ein- und
Ausgangsebene können sich eine oder mehrere versteckte Ebenen befinden, wobei
in den meisten praktischen Fällen nicht mehr als zwei versteckte Ebenen benötigt
werden.
Abb. 8.11 Feedforward Netzwerk
1
2
x
1
x
2
x
n
f
x
3
ˆy
210 8 Metamodelle
Aktivierung eines Neurons
Die Hauptinformation jedes einzelnen Neurons ist seine Aktivierung, welche durch
eine reelle Zahl a = [0,1] repräsentiert wird. Die Aktivierung in einem einfachen
Feedforward Netzwerk hängt dabei nur von der Aktivierung der Neuronen aus der
vorhergehenden Ebene ab.
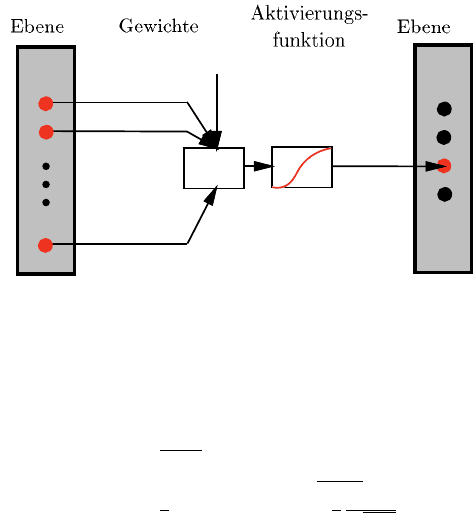
Abbildung 8.12 zeigt schematisch die Berechnungsmethode zur Ermittlung der
Aktivierung eines Neurons aus Ebene k + 1 in Abhängigkeit aller Neuronen aus
Ebene k und einer Konstanten b
k0
. Im ersten Schritt wird dazu jedem Neuron aus
Ebene k ein Gewicht b
k
zugeordnet und die Summe aller gewichteten Aktivierungen
und der Konstante b
k0
gebildet.
S
k+1
= b
k0
+ a
k1
b
k1
+ a
k2
b
k2
+ ···+ a
kn
e
b
kn
e
(8.40)
Die Aktivierung des Neurons aus Ebene k +1 wird im zweiten Schritt durch eine
im Voraus definierte Aktivierungsfunktion a (S) bestimmt.
Abb. 8.12 Aktivierung eines Neurons
Der größte Teil aller Anwendungen verwendet dazu eine sigmoidale (s-förmige)
Aktivierungsfunktion, wie sie in Abbildung 8.13 und Gleichung 8.41 dargestellt
sind.
a(S) =
1
1+e
−S
, a
0
(S) = a (S) [1 −a (S)]
a(S) = tanh(S) , a
0
(S) =
sinh(S)
cosh(S)
a(S) =
2
π
acos(S) , a
0
(S) =
2
π
1
√
1−S
2
(8.41)
Allen Aktivierungsfunktionen ist gemein, dass ihre theoretischen Extremwerte
niemals erreicht werden. Die genaue Form der Aktivierungsfunktion hat einen ge-
ringen Einfluss auf die Qualität des erzeugten Künstlichen Neuralen Netzwerks.
Eine Auswirkung weist die Wahl jedoch auf die Geschwindigkeit des Trainingspro-
zesses auf. Durch die einfache Berechnung der Ableitung der ersten dargestellten
Aktivierungsfunktion (logistische Funktion) wird diese in der Praxis häufig den an-
deren Funktionen vorgezogen. Aktivierungen von a ≥0.9 werden dabei meistens als
k
k + 1
b
k0
b
k1
b
k2
b
kn
e
P
S
a (S)
a

8.8 Künstliche Neuronale Netzwerke 211
Abb. 8.13 Aktivierungsfunktionen
komplett aktiviert und a ≤ 0.1 als nichtaktiviert interpretiert, so dass hauptsächlich
der Funktionsbereich [0.1,0.9] verwendet wird. Durch die flache Form der sigmoi-
dalen Funktionen bei großen Absolutwerten wird der Einfluss von Extremwerten
(zum Beispiel Ausreißer) in den Daten deutlich gedämpft.
Normierung von Daten
Daten aus physikalischen Experimenten können durch die Verwendung des Mittel-
werts µ, der Standardabweichung σ und einem gewählten Z-Wert mit folgenden
Gleichungen normiert beziehungsweise zurückkonvertiert werden:
normieren n
j
=
r
σ
x
j
+
0.1 −r
h
µ
σ
+ x
∗
j,min
i
R
¨
ucktransformation x
j
=
σ
r
n
j
+
µ + σ
h
x
∗
j,min
−
0.1
r
i
mit r =
0.8
x
∗
j,max
−x
∗
j,min
und x
∗
j,min / max
= µ ∓Zσ
(8.42)
Sollen hingegen gleichverteilte Daten auf den Bereich [0.1, 0.9] normiert wer-
den, wird folgende Umrechnung verwendet, wobei x
j,min / max
der wahre minimale
beziehungsweise maximale Wert der Variablen x
j
darstellt:
normieren n
j
=
x
j
−x
j,min
x
j,max
−x
j,min
0.8 + 0.1
R
¨
ucktransformation x
j
=
n
j
−0.1
0.8
x
j,max
−x
j,min
+ x
j,min
(8.43)
Training (Fehlerrückführung)
Zur Bestimmung der verschiedenen Gewichte b wird das Künstliche Neurale Netz-
werk mit bekannten Daten trainiert. Dazu wird beispielsweise die Fehlerrückfüh-
rung (Backpropagation) eingesetzt, welche mittels eines Gradientenverfahrens den
quadratischen Fehler der Approximation y − ˆy minimiert. Im allgemeinen Fall kann
ein neuronales Netzwerk n
a
≥1 Ausgangsvariablen ( ˆy
1
,···, ˆy
n
a
) aufweisen, so dass
der quadratischen Fehler für eine gegebene Faktoreinstellung die Summe aller ein-
zelnen Fehlerterme ist:
E
i
=
1
2
n
a
∑
l=1
[y
l
− ˆy
l
]
2
=
1
n
a
n
a
∑
l=1
[y
l
−a (S
l
)]
2
(8.44)
a (S)
a (S)
S
S
tanh (S)
2
π
acos (S)
1
1+e
−S
212 8 Metamodelle
S
l
steht in diesem Zusammenhang für die gewichtete Summe, welche in die Akti-
vierungsfunktion a zur Berechnung der l
ten
Ausgangsvariable eingesetzt wird.
Werden n
r
bekannte Datensätze zum Training des Künstlichen Neuralen Netz-
werks eingesetzt, so berechnet sich der gesamte Fehler durch:
E =
1
n
r
n
r
∑
i=1
E
i
(8.45)
Bei gegebenen aktuellen Werten der Gewichte b wird im ersten Schritt des Trai-
ningsverfahrens der Gradient des Fehlers E in Abhängigkeit der Gewichte
∂ E
∂ b
be-
stimmt. Dazu wird der Einfluss der Gewichte auf den Fehler ausgehend von der
letzten Ebene (Ausgangsebene) rückwärts bis zur ersten Ebene (Eingangsebene)
berechnet, wodurch auch der Name des Verfahrens (Fehlerrückführung) entstanden
ist.
Die partielle Ableitung des Fehlers E für jedes Gewicht b
kl
zwischen einem
Ausgangs-Neuron l und einem Neuron k aus der vorherigen Ebene mit der mo-
mentanen Aktivierung a
k
lässt sich berechnen durch:
∂ E
∂ b
lk
= −a
k
a
0
(S
l
)[y
k
− ˆy
k
] = −a
k
δ
l
(8.46)
Im Gegensatz zur Ausgangsebene, in der die Zielwerte y
k
bekannt sind, existieren
für alle anderen Ebenen keine direkten Zielwerte, wodurch die partiellen Ableitun-
gen in Abhängigkeit der δ
m
und b
ml
Werte der folgenden Ebene berechnet werden
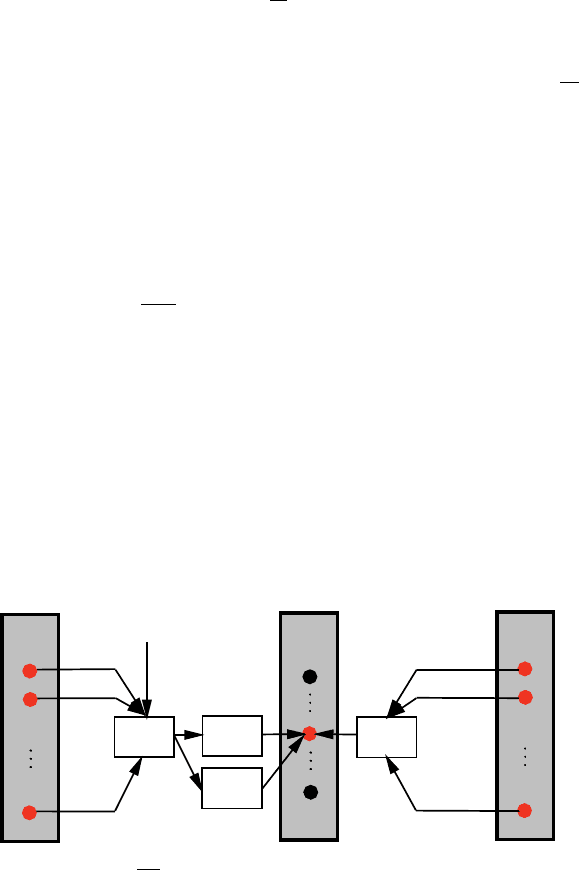
müssen (Abbildung 8.14).
δ
l
= a
0
(S
l
)
∑
m
δ
m
b
∗
ml
mit b
∗
: Gewichte der folgenden Ebene
(8.47)
Abb. 8.14 Berchnung von
∂ E
∂ b
lk
P
b
l1
b
l2
b
l0
S
l
a (S
l
)
1
2
1
l
a
′
(S
l
)
1
2
P
δ
2
b
∗
2l
δ
1
b
∗
1l
Ebene
n
Ebene
n−1
Ebene
n+1

8.8 Künstliche Neuronale Netzwerke 213
Durch die Gleichungen 8.46 und 8.47 können somit die Gradienten des Fehlers
E in Abhängigkeit jedes Gewichts b bei Betrachtung eines bekannten Datensatzes
bestimmt werden. Bei der Berücksichtigung von n
r
Datensätzen wird der Gradient
jedes Gewichts b durch die Summe der einzelnen Gradienten berechnet:
∂ E
∂ b
lk
∑
=
n
r
∑
i=1
∂ E
∂ b
lk
i
(8.48)
Nachdem durch die Bestimmung der Gradienten ein Richtungsvektor B
g
zur Mi-
nimierung von E bestimmt wurde, wird die Länge s entlang dieses Vektors gesucht,
die ausgehend von den momentanen Gewichten B
0
den Fehler E minimiert.
min
s
E (B
0
+ sB
g
) (8.49)
Neben anderen Verfahren wird hierzu das Konjugierte-Gradienten-Verfahren ein-
gesetzt [109, 146, 19].
In einem iterativen Prozess wird das Training solange fortgesetzt, bis ein Ab-
bruchkriterium erreicht wird (zum Beispiel Unterschreiten einer maximalen Fehler-
grenze oder Überschreiten einer maximalen Anzahl an Iterationen). Aus mathemati-
scher Sicht ist die Minimierung des Fehlers komplex, da meist viele lokale Minima
und Bereiche mit sehr flachen Gradienten existieren.
One-of-N Kodierung
Zur Erhöhung der Vorhersagequalität von Künstlichen Neuronalen Netzwerken ist
es gerade bei komplexen Zusammenhängen sinnvoll den Faktorraum in überlappen-
de Unterbereiche aufzuteilen. Dieses wird beispielsweise durch die One-Of-N Ko-
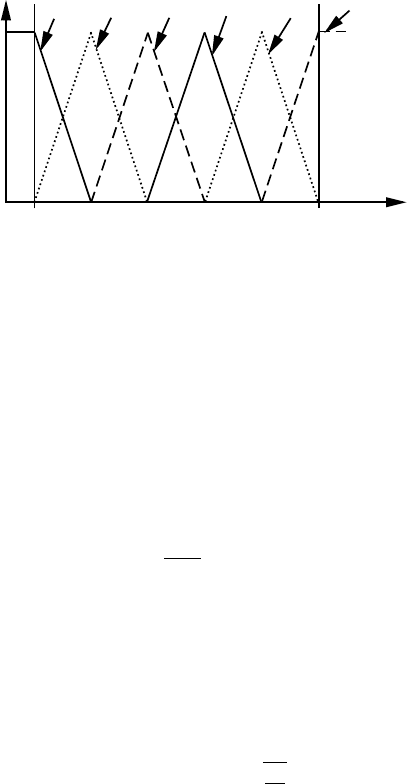
dierung erreicht, welche aus der Fuzzy-Technologie bekannt ist (Abbildung 8.15).
Eine Eingangsvariable (Faktor) x
j
wird dazu durch N Variablen x
j
0
,···,x
j
N−1
er-
setzt, wodurch das Neuron der Eingangsebene für die Variable x
j
durch N neue
Neuronen (Eingangsvariablen) substituiert wird. Die einzustellenden Werte für die
N Variablen x
j
0
,···,x
j
N−1
werden wie folgt in Abhängigkeit von der Originalvaria-
blen x
j
berechnet (Abbildung 8.15).
x
jl
= max
0,
d
x
j
−
min
(
x
j
)
+ld
x
j
−x
j
d
x
j
!
l = 0,···, N −1
mit d
x
j
=
max
(
x
j
)
−min
(
x
j
)
N−1
(8.50)
Durch die Aufteilung werden für unterschiedliche Bereiche des Faktors x
j
unter-
schiedliche Neuronen und somit unterschiedliche Bereiche des Künstlichen Neuro-
nalen Netzwerks aktiviert. Mit der zusätzlichen Erhöhung der Gewichteanzahl kann
meist ein besseres Netzwerk trainiert werden, als wenn die Erhöhung der Anzahl
lediglich durch mehr Neuronen in den versteckten Ebene erzielt wird.
Wahl der Schichten
In der Praxis tritt die Schwierigkeit auf, eine sinnvolle Wahl für die Anzahl der
Schichten und Neuronen sowie die Iterationsanzahl des Trainingsprozesses zu fin-
den. In nahezu allen Fällen ist eine versteckte Ebene zur Abbildung auch kom-
214 8 Metamodelle
x
j
x
j0
x
j3
x
j2
x
j1
x
j5
x
j4
0
1
x
j0
, · · · , x
j5
N = 6
min (x
j
)
max (x
j
)
Abb. 8.15 One-of-N Kodierung mit N=6
plexer Zusammenhänge ausreichend. Eine zweite versteckte Ebene ist nur bei sehr
komplexen oder nicht-kontinuierlichen Zusammenhängen notwendig (zum Bei-
spiel Sägezahn-Funktion). In allen anderen Anwendungen wird die Genauigkeit
des Künstlichen Neuronalen Netzweks durch eine zweite versteckte Ebene zwar
geringfügig verbessert, jedoch nimmt die Trainingsgeschwindigkeit des Netzwerks
deutlich ab.
Für die Wahl der Neuronenanzahl existieren lediglich Faustformeln. Bei der Ver-
wendung von einer versteckten Ebene kann als erster Startpunkt die folgende An-
zahl an Neuronen gewählt werden [109]:
n
vE1
=
√
n
y
n
f
mit n
y
< n
f
(8.51)
Bei sehr komplexen Zusammenhängen können mehr Neuronen und bei einfa-
chen Zusammenhängen weniger Neuronen sinnvoll sein. Um ein Overfitting des
Netzwerks zu verhindern, sollte mit kleiner Anzahl von Neuronen gestartet und in
einem iterativen Prozess sukzessive erhöht werden. Für die Verwendung von zwei
versteckten Ebenen existiert die folgende Faustformel zur Berechnung der Anzahl
der Neuronen [109]:
n
vE1=n
y
r
2
n
vE2=n
y
r
mit r =
3
r
n
f
n
y
und n
y
< n
f
(8.52)
Bei der Wahl der Neuronen ist zu beachten, dass die Anzahl der zu bestimmen-
den Gewichte b schnell mit steigender Anzahl der Neuronen wächst und dadurch
ebenfalls die Anzahl der benötigten Trainingsdaten n
r
> n
b
.
