Shani G. Radiation Dosimetry: Instrumentation and Methods
Подождите немного. Документ загружается.

280 Radiation Dosimetry: Instrumentation and Methods
dose is uniform within the solution, except for the region
within the beta range to the edge of the container. The
equation for the equilibrium dose rate at a point within
the solution is given by
, (4.53)
where C is the specific activity of the solution in mCi/g and
is the average energy of the emitted beta particle in MeV.
The problem of TLD response dependence on the
finite size of the TLD, for both external and internal beta
irradiations, can then be summarized in Figure 4.78. where
the TLD is irradiated by a beam of beta (
) particles.
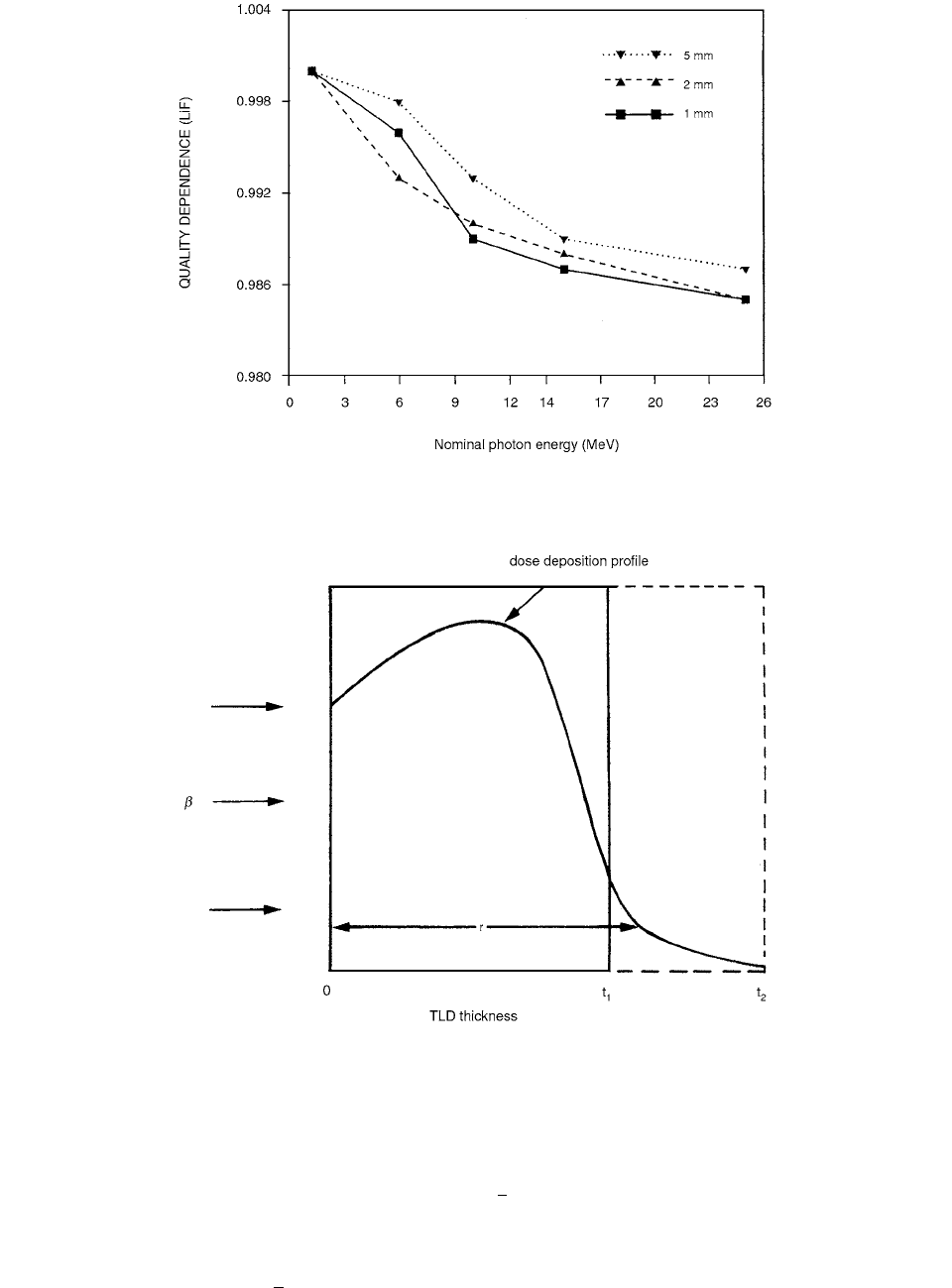
FIGURE 4.77 The quality dependence of LiF TLDs evaluated according to the Burlin cavity expression for an LiF disc of 3.61-mm
diameter and different thicknesses in megavoltage photon beams. (From Reference [53]. With permission.)
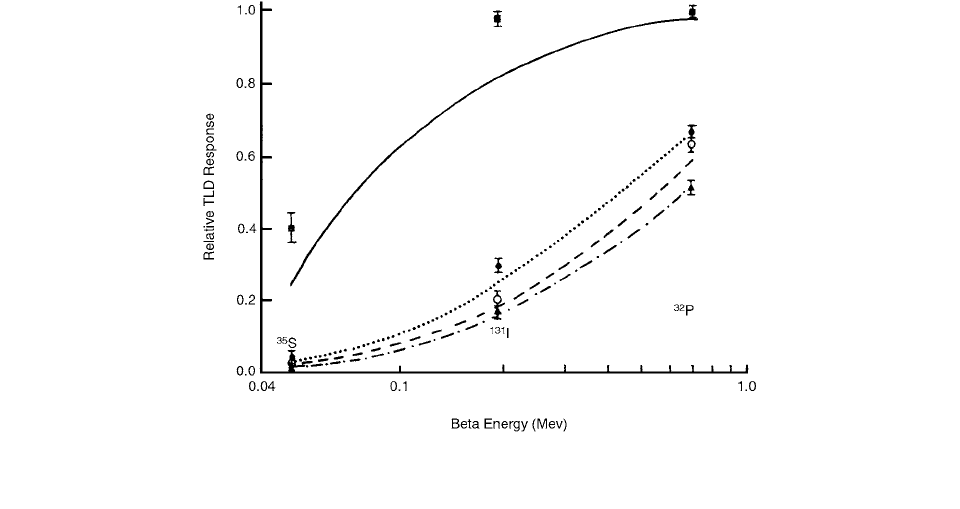
FIGURE 4.78 If the beta range r is large compared to the TLD thickness, as in t
1
, then energy is absorbed across the TLD. If the
thickness is considerably larger, as in
t
2
, then only a fraction of the TLD is involved in energy absorption. Dosimeters of thicknesses
t
1
and t
2
will give roughly the same total amount of light. The average dose hence determined will be lower for the thick dosimeter.
(From Reference [58]. With permission.)
Dose rate 2140
CE cGyh
E
Ch-04.fm Page 280 Friday, November 10, 2000 12:01 PM
Thermoluminescent Dosimetry 281
For a TLD immersed in a radioactive solution for a
specified time, if E
tot
represents the total energy absorbed
within the region R occupied by the TLD in the absence
of the TLD E
self
denotes the energy absorbed within the
region R due to radiation sources within region R, and E
surr
is the energy absorbed within R due to radiation sources
outside region R, then
(4.54)
When the region
R is occupied by the TLD, E
self
is
then absent. The energy absorbed in the TLD is just E
surr.
Since E
tot
is the energy absorbed by the TLD when cali-
brated in an external beam to receive the same equilibrium
dose as in the radioactive solution, the relative TLD
response, (S
u
/S
0
) is then given by
(4.55)
where
S
0
is the TLD response in an external photon beam
radiation and S
u
is the decreased response in-solution irra-
diation, so that the decrease in relative TLD response is
[1 (S
u
/S
0
)] or (S
0
S
u
)/S
0
. This equation indicates that
when E
self
is large, the fraction of energy contributed to the
region from the radioactivity displaced is large, and hence
the decrease in relative response is large, and vice versa.
When the range of beta is comparable to R, the fraction
of energy absorbed depends strongly on the size and geom-
etry of the region, and a more detailed analysis is required.
For internal geometry dosimetry, the objective is to
determine dose at a point in a medium. Restricting this
consideration to a point in a solution with uniformly
distributed radioactivity, the dose delivered to this point
can be determined by two separate methods. In the first
method, referred to here as the “direct calibration”
method, Equation (4.53) is used to establish a calibration
curve of light output vs. dose for a TLD immersed in a
radioactive solution and, hence, determine an unknown
dose. In the second method, to be referred to as “the
displacement model” method, the
60
Co calibration curve
for the TLD is used. To obtain the same dose, this cali-
bration curve requires a larger light output (LO) than in
the first approach. Hence, the LO from the immersed
TLD in the unknown solution is corrected upward for
the calculated decreased relative response, E
surr
/E
tot
; i.e.,
LO is divided by the ratio E
surr
/E
tot
to obtain the corrected
LO and then the dose. Thus, there are two independent meth-
ods of determining the dose, with the displacement model
giving a confirmation of the measured dose as well as pro-
viding a basic understanding of the decreased response. The
results of measurements and the calculations using the dis-
placement model are summarized in Figure 4.79.
An analytical Monte Carlo simulation code has been
used by Karaiskos et al. [59] to perform dosimetry calcu-
lations around an
192
Ir high-dose-rate brachytherapy source
utilized in the widely used microSelectron afterloaded sys-
tem. Measurements of anisotropy functions using LiF TLD-
100 rods have been performed in a polystyrene phantom to
support the Monte Carlo calculations.
The active source consisted of a 0.60 mm in diameter
by 3.5 mm long cylinder of pure iridium metal, within which
the radioactive material was uniformly distributed. It was
encapsulated in stainless steel and welded to a steel cable.
E
tot
E
self
E
Surr
S
u
S
o
-----
E
Surr
E
tot
----------
1
E
self
E
tot
---------
FIGURE 4.79 Comparison of relative TLD response between direct calibration (symbols) and displacement model (lines): rod–(),(---);
chip–(
), (._._._); disc–().(
…
); ultrathin disc–(), (—). (From Reference [53]. With permission.)
Ch-04.fm Page 281 Friday, November 10, 2000 12:01 PM

282 Radiation Dosimetry: Instrumentation and Methods
The capsule is 5 mm long and 1.1 mm in overall diameter
and its distal end is a steel cap with a 0.55-mm radius. The
dose calculation formalism proposed by AAPM Task Group
43 has been followed. Dose rate (r,
), in medi-um at point
(r,
), where r is the distance in cm from the active source
center and
is the polar angle relative to the longitudinal
axis of the source, is expressed as:
(4.56)
where
S
k
is the source air-kerma strength in units of U (1 U
l
Gym
2
h
1
1 cGy cm
2
h
-1
). is the dose rate constant
defined as the dose rate in the medium per unit source
strength at radial distance r
0
1 cm along the transverse
axis, and
0
/2, so that
(4.57)
G(r,
) is the geometry function in units of cm
2
which
accounts for the variation of relative dose due only to the
spatial distribution of activity within the source, ignoring
photon absorption and scattering in the source structure.
At distances greater than approximately 2–3 times the
active source dimension (i.e., for the given source greater
than approximately 1 cm), the geometry function is well-
approximated (within 1%) by the inverse-square law used
in point-source approximation. g(r) is the dimensionless
radial dose function which accounts for photon attenuation
and scattering in the medium and encapsulation along the
transverse axis (
0
/2) and is by definition unity at r
0
1 cm, i.e., g(1) 1, so that
(4.58)
F(r,
) is the dimensionless dose anisotropy function
which accounts for photon attenuation and scattering at
any polar angle
, relative to that for
0
/2, and is by
definition unity at
0
/2; i.e., F(r,
/2) 1, so that
(4.59)
An equivalent dose calculation formalism in terms
of the tissue attenuation factor,
T(r), is also used in
many computer-assisted brachytherapy treatment-planning
systems:
(4.60)
In this expression the product g(r) of Equation (4.56)
has been replaced by the product fT(r). The factor f is
the air kerma in air to water kerma in air conversion
factor, which is equal to the ratio of mean mass energy
absorption coefficients for water and air. This ratio is
almost constant and has a value of 1.11 for energies
between 150 keV and 4 MeV. Thus, f is also equal to 1.11
for the
192
Ir primary energy range. The factor T(r) is well-
approximated by the ratio of water kerma in water to
water kerma in air and accounts for the combined atten-
uation and scattering in water. It is noted that for the given
source, the formalism of Equation (4.60) is valid at radial
distances greater than approximately 1 cm, where, as
mentioned above, the geometry factor G(r,
) is well-
approximated by the inverse-square law.
TLDs were placed in small cylindrical TLD polysty-
rene receptors (3 mm in diameter and 6 mm long) having
a cylindrical hole of 1-mm diameter in their centers to
accommodate the dosimeters. A 30
30 1.1-cm
3
slab
of polystyrene, prepared in a milling machine with an
accuracy of 0.1 mm, was constructed to accommodate
TLD receptors and a plastic catheter (2-mm outer diame-
ter), inside which the source was driven. This slab was
sandwiched between other identical polystyrene slabs to
build a 30 30 30-cm
3
phantom which approximates
the water spherical phantom of 30-cm diameter used in
MC calculations. [59]
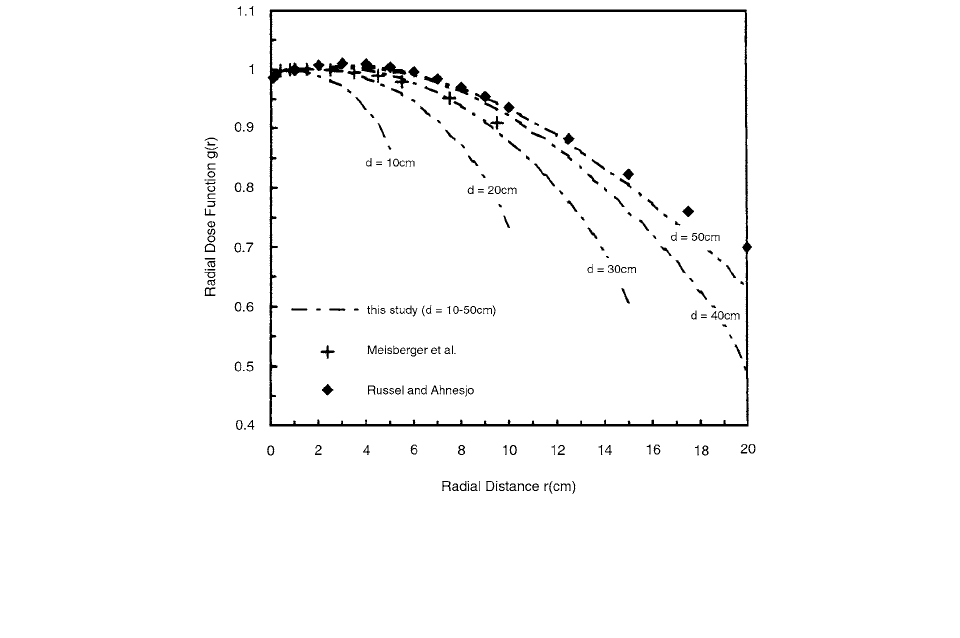
In Figure 4.80, radial dose functions calculated for
spherical water phantoms of different diameters (d
10–50 cm) are presented. The figure demonstrates that
phantom dimensions significantly affect the radial func-
tions at radial distances near phantom edges, where devi-
ations of up to 25% are observed. This effect is due to the
reduction of scatter contribution to overall dose at the
edges of the phantom and should be taken into account in
the case of estimating the dose near the body edges.
Using the MC code and the CSDA electron ranges
proposed by ICRU Report 37, the average starting energy
of the electrons generated in the TLD material was found
to be less than 100 keV over the whole range of measure-
ment distances and angles, and the corresponding
R was
less than 0.006 cm, thus giving the value of factor d less
than 0.02. As a result of this, the TLD material behaves
like a large cavity in
192
Ir
-rays, and the LiF TLD
response can be calculated using the simplified equation:
(4.61)
where
E
i
is the energy of the ith photon in the point of
measurement, (
en
/
)E
i,LiF
is the mass energy absorption
D
˙
D
˙
r
,() S
k
Gr,
()
Gr
0
,
0
()
---------------------
Fr,
()gr()
D
&
r
0
,
0
()S
k
gr()
D
˙
r,
0
()Gr
0
,
0
()
D
˙
r
0
,
0
()Gr,
0
()
-----------------------------------------
Fr
,()
D
˙
r,
()Gr,
0
()
D
˙
r,
0
()Gr,
()
------------------------------------
D
˙
r
,() S
k
f
1
r
2
----
Tr()Fr
,()
D
LiF TLD
D
water
--------------------
en
-------
water
LiF
E
i
en
-------
E
i,LiF
i
E
i
en
-------
E
i, water
i
Ch-04.fm Page 282 Friday, November 10, 2000 12:01 PM
Thermoluminescent Dosimetry 283
coefficient of LiF at energy E
i
and (
en
/
)E
i,water
is the mass
energy absorption coefficient of water at this energy E
i
.
VI. MISCELLANEOUS TLD
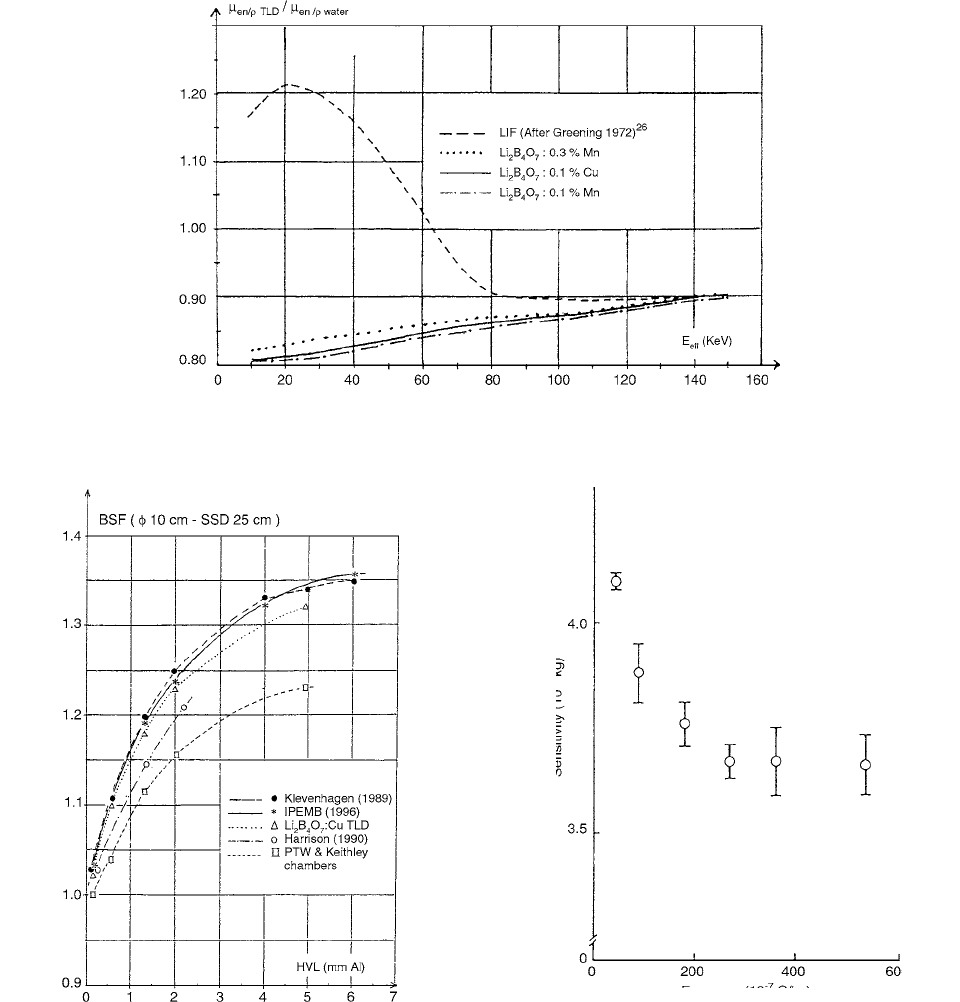
Backscatter factors (BSF) for low-energy x-rays derived
from Monte Carlo calculations have been recommended
in the UK code of practice for kilovoltage dosimetry pub-
lished by IPEMB. [60] Coudin and Marinello [61] have
measured backscatter factors (BSF) using lithium borate
doped with copper (0.1% per mass of copper) in the form
of powder (average density 1.30 g cm
3
, grain size varying
from 74
m to 175
m) spread out in thin layers either
directly on the surface of the medium or on a mylar sheet
for experiments in air. Li
2
B
4
O
7
:0.1% Cu
17
was chosen
among different common TL materials due to its relatively
flat energy response (Figure 4.81), its high sensitivity per
unit volume, its dose-rate independent response, its water
equivalence in this energy range, and the fact that its intrin-
sic response is not influenced by the direction of the beam.
According to the recommendations of the various pro-
tocols, the absorbed dose at the surface of a water phantom
for low-energy x-rays can be determined from measurement
of primary beam kerma and BSF. This quantity is defined
as a ratio of water kermas at the phantom surface and free
in air in the absence of the phantom. Within the range of
10 to 100 kV, as charged-particle equilibrium is always
achieved and
bremsstrahlung radiation is negligible, there
is little distinction between kerma and dose. Consequently,
(4.62)
where R
det
is the reading of the detector (lithium borate or
ion chamber) with and without phantom , and
is the ratio of mass energy absorption coeffi-
cients of the detector medium to water for photon energy
fluence spectra at the phantom surface or in air.
TL measurements have been performed using a very
thin layer of 0.4 mm (about three times the average grain
size), which is sufficient to ensure the electronic build-up
while minimizing the primary photon attenuation.
BSF obtained using Li
2
B
4
O
7
:0.1% Cu are very close
(within 1.7%) to the data calculated by Monte Carlo meth-
ods, being slightly lower in general.
Figure 4.82 shows experimental results obtained with
both the ion chambers and those measured by Klevenhagen
with a specially designed flat ion chamber. There is a very
good agreement between Klevenhagen’s results and the
IPEMB data. However, large discrepancies are pointed out
with the flat ion chambers used. This is probably due to
their different characteristics.
Calibration of Mg
2
SiO
4
(Tb)(MSO) thermolumines-
cent dosimeters for use in determining diagnostic x-ray
FIGURE 4.80 Radial dose functions, g(r), as a function of radial distance, r, calculated by our code with the
192
Ir microSelectron
HDR source centered at a spherical water phantom of different diameters (
d 10–50 cm). Experimental data of Meisberger et al.
performed using a different
l92
Ir source design centered at a 25 25 30-cm
3
water phantom, and Monte Carlo calculations of
Russel and Ahnesjo performed using the
l92
Ir microSelectron HDR source centered at an unbounded water phantom, have also been
plotted for comparison. (From Reference [59]. With permission.)
BSF
R
det
ph
en
det
w
()
surf
R
det
air
en
det
w
()
air
------------------------------------------------
R
det
ph
R
det
air
en
r
/
det
w
()
Ch-04.fm Page 283 Friday, November 10, 2000 12:01 PM
284 Radiation Dosimetry: Instrumentation and Methods
doses was performed by Kato et al. [62] The results
shown in Figure 4.83 demonstrate that the detector sen-
sitivities depend on their exposure in the low-dose
region. The sensitivity at 5.16 l0
6
C/kg (20 mR) was
about 10% greater than that at 2.58 l0
5
C/kg ( 100
mR). For doses greater than 2.58 l0
5
C/kg (100 mR),
it was quite uniform, within 1%.
For the x-ray exposures, the tube voltage was altered in
20-kVp increments through a range from 40 to 140 kVp.
Exposure times were adjusted so that the exposures were
about 2.58
10
5
C/kg (100 mR). Other experimental fac-
tors were the same as for the experiment described above.
FIGURE 4.81 Ratio of mass energy absorption coefficient for the TL materials to the mass energy absorption coefficient of water
as a function of photon energy. The borate curves have been calculated from Hubbells’ data. (From Reference [62]. With permission.)
FIGURE 4.82 BSF measured by different authors with different
types of detectors compared to the IPEMB’s data. (From Refer-
ence [61]. With permission.)
FIGURE 4.83 Sensitivity of the thermoluminescent dosimeters
to various exposures. Sensitivity: response of TLD per 1 C/kg
exposure; unit of TLD reading is nC. The Mg
2
SiO
4
(Tb) detectors
on a styrofoam block were exposed to x-rays using various expo-
sure times under the following conditions: tube voltage, 100 kVp;
filter, 2.5 mm Al; and field size, 20
20 cm
2
. Error bars indicate
the standard deviations. (From Reference [62]. With permission.)
Ch-04.fm Page 284 Friday, November 10, 2000 12:01 PM

Thermoluminescent Dosimetry 285
The results obtained are shown in Figure 4.84. The
sensitivity of the MSO detectors used decreased linearly
with increasing tube voltage from 60 to 140 kVp. The
MSO detector, Mg
2
SiO
4
(Tb) phosphor, is more sensitive
than are other phosphors, such as LiF and CaSO
4
(Tm).
The sensitivity of the MSO detectors depended on their
orientation to the central beam. Figure 4.85 shows the
sensitivity of the MSO detector.
Experimental evidence has been obtained confirming
the significance of deep traps for thermal quenching of
luminescence in
-A1
2
O
3
. [63] The effect of deep traps
on thermoluminescence (TL) parameters of the dosimetric
peak was first detected in dosimetric
-A1
2
O
3
powder and
pellets. The presence of deep traps in nominally pure
anion-defective crystals of corundum was suggested by
indirect evidence. Specifically, the competitive role of
deep traps in trapping of carriers was associated with a
change in the dosimetric sensitivity when the crystal was
exposed to a high-dose irradiation. The state of deep traps
affects basic features of the main TL peak at 450 K in
anion-defective corundum.
Figure 4.86 illustrates glow curves for anion-defective
-Al
2
O
3
crystals excited at 460 K (curve 1), 620 K (curve 2),
and 720 K (curve 3) under UV radiation. The data suggest
an important regularity which underlies the proposed
model: the occupancy of deep traps increases with the
excitation temperature.
Aluminum oxide dosimeters have been shown to
exhibit radioluminescence linearly with dose and dose rate
to very high values, with minimal visible coloration. [64]
Small Czochralski-grown crystals were prepared from
high-purity aluminium oxide and chemically pure silicon
dioxide. A heating rate of 10°C s
1
was used. Al
2
O
3
:Si
has been shown to exhibit a useful log-linear response
from 0.1 kGy to at least 10 kGy. In addition, a peak sum
ratio method, effectively obviating many calibration prob-
lems, has been demonstrated for determining absorbed
dose in this dose range. Above 10 Gy, the response is
nonlinear, becoming saturated at about 30 Gy.
Figure 4.87 shows the thermoluminescence glow curve
for 0.2% silicon doping after exposure at an absorbed dose
FIGURE 4.84 Sensitivity of the thermoluminescent dosimeters
to tube voltages. Sensitivity: response of TLD per 1 C/kg expo-
sure; unit of TLD reading is nC. Exposures were adjusted to
approximately 2.58
10
5
C/kg (100 mR). The conditions of
exposure, excluding total exposures and tube voltage, were the
same as those of Figure 4.83. Error bars indicate the standard
deviations. (From Reference [62]. With permission.)
FIGURE 4.85 Sensitivity of the thermoluminescent dosimeters
(TLD) in air and on a Rando phantom. Sensitivity: response of
TLD per 1 C/kg exposure; unit of TLD reading is nC. The
Mg
2
SiO
4
( MSO) detectors were exposed to 100-kVp x-rays on
a styrofoam block and on a Rando phantom. On the Rando phan-
tom, thermoluminescent sensitivity was determined for 100-kVp
x-rays parallel with and perpendicular to the central axis of the
cylindrical MSO detectors. Error bars indicate the standard errors
estimated from the variation of the TLD sensitivities and the
reproducibility of the Shonka-Wyckoff chamber. (From Refer-
ence [62]. With permission.)
Ch-04.fm Page 285 Friday, November 10, 2000 12:01 PM
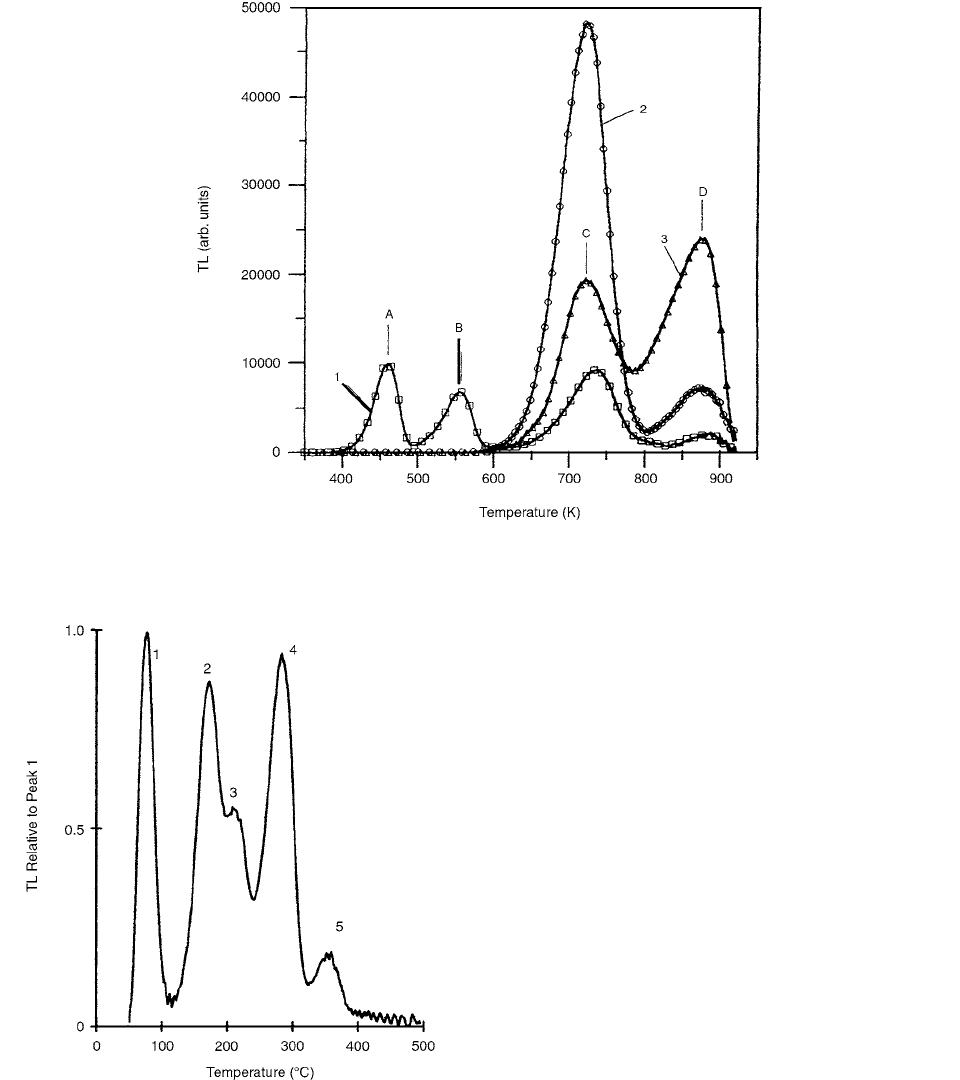
286 Radiation Dosimetry: Instrumentation and Methods
of 100 Gy. Five glow peaks are obvious and well-separated.
While the first, appearing at a temperature of approximately
90°C, fades quickly at room temperature, the remaining
four are sufficiently stable for use in dosimetry. Figure 4.88
shows the changing shape of the glow curve as absorbed
dose increases. Peak 1 is not shown since the time starting
from exposure was large with respect to its lifetime. Peak
2 increases in amplitude, peak 3 decreases somewhat, peak
4 decreases dramatically, and, while it is not obvious from
the scale of this graph, peak 5 increases. No peak was found
to have an amplitude linear with dose. The integral of peak
5 was found to increase nearly linearly with the logarithm
of dose, up to a value of 10 kGy.
To characterize the thermoluminescence (TL) of Bra-
zilian topaz, Al
2
SiO
4
(F,OH)
2
, TL emission spectra of as-
received samples and gamma-irradiated samples (with 100
Gy, 1 kGy, and 10
6
Gy) submitted or not submitted to a
previous annealing procedure were presented by Yukihara
et al. [65] All the samples show a broad emission band
between 300 and 600 nm for all the glow peaks between
50 and 400°C. In some gamma-irradiated samples, a nar-
row emission band between 200 and 350 nm was also
observed.
Studies were performed using pieces of two large
crystals: No. 1, a colorless topaz of unknown origin, and
No. 2, a light blue topaz from Marambaia (Minas Gerais,
Brazil). From these large crystals, smaller pieces of 3
3 1 mm
3
(20–60 mg) were obtained. Other topazes were
also used for comparison.
Figure 4.89 shows typical emission spectra of unan-
nealed samples of four topazes. Except for topaz 1, the
spectra are very broad and similar, ranging from 300 to
560 nm.
FIGURE 4.86 Glow curves of anion-defective -Al
2
O
3
crystals excited by UV radiation at the heating rate of 2 K s
1
. The excitation
temperatures were 460 K (1), 620 K (2), and 720 K (3). (From Reference [63]. With permission.)
FIGURE 4.87 Glow curve for 0.2% silicon doping of aluminium
oxide. The glow curve was measured immediately after a 100-Gy
exposure in 1 min. (From Reference [64]. With permission.)
Ch-04.fm Page 286 Friday, November 10, 2000 12:01 PM
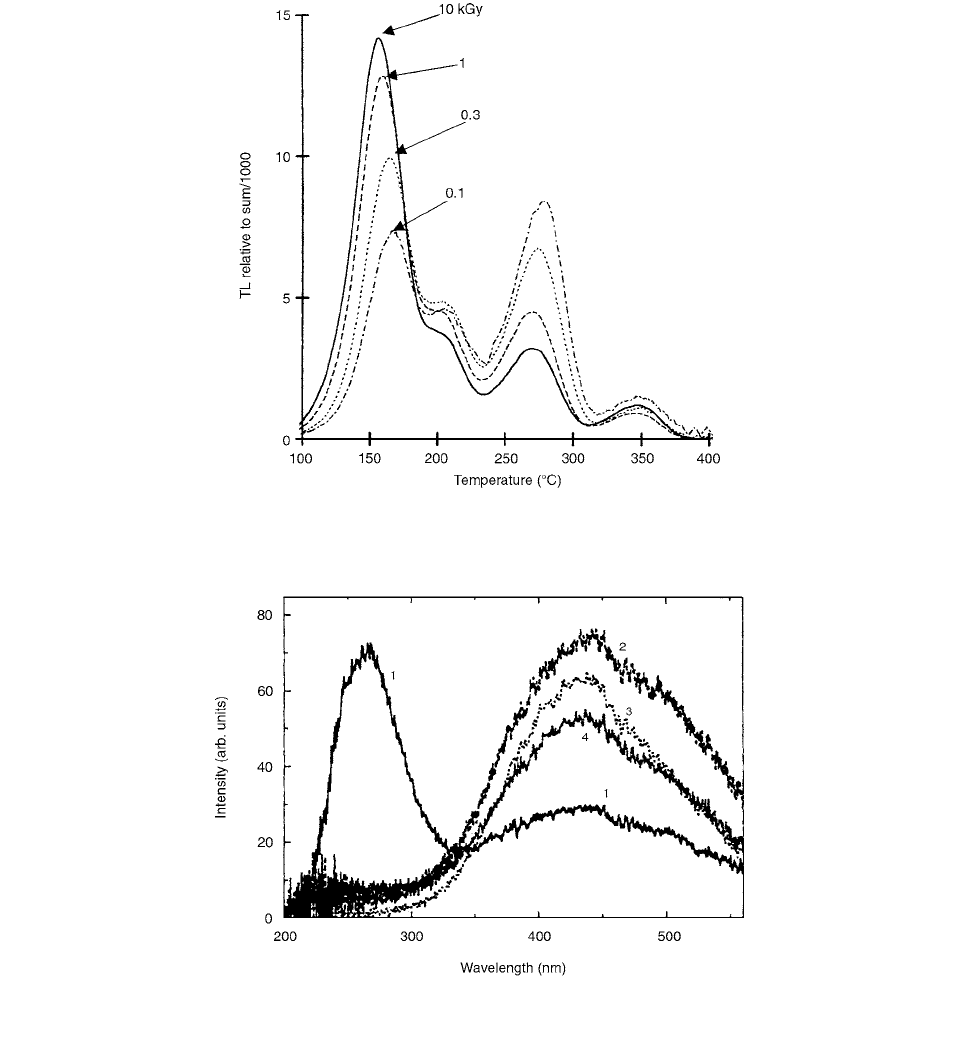
Thermoluminescent Dosimetry 287
LET dependence of Al
2
O
3
:C and CaF:Mn (TL)
dosimeters was investigated by Osvay and Ranogajec-
Komor [66], using glow-curve analysis to determine the
efficiencies of TL light production for alpha particle and
neutron irradiation relative to gamma exposure. No high-
temperature peak or significant change of glow-curve
shape was found after irradiation by high LET (alpha and
neutron) radiation. Gamma sensitivity of Al
2
O
3
:C com-
pared to CaF:Mn was 6:1. However, the relative TL effi-
ciency for alpha particle irradiation of Al
2
O
3
:C was a
factor of 10 lower than that of CaF
2
Mn. Neutron sensitiv-
ity was found to be similar for the two materials.
Figure 4.90 shows the glow curve of Al
2
O
3
:C and
CaF
2
:Mn after 1 mGy gamma irradiation. The glow peak
of aluminium oxide is at approximately 180°C and of
calcium fluoride, it is at 240°C.
Dosimeters were irradiated with alpha particles for 5,
10, 20, 40, and 60 min (3, 6, 12, 24, and 36 mGy). The
standard deviation of TL measurements for alpha particles
was about 12%. The dose-response curves for the Al
2
O
3
:C
FIGURE 4.88 Change in shape of the glow curve for silicon-doped aluminum oxide with increasing dose. Each glow-curve shape
is normalized to the integral for that curve. (From Reference [64]. With permission.)
FIGURE 4.89 TL emission spectra of unannealed samples irradiated with 10
3
Gy (No. 2) and 10
6
Gy (Nos. 1, 3, and 4), averaged
in the range 10–300°C. (From Reference [65]. With permission.)
Ch-04.fm Page 287 Friday, November 10, 2000 12:01 PM
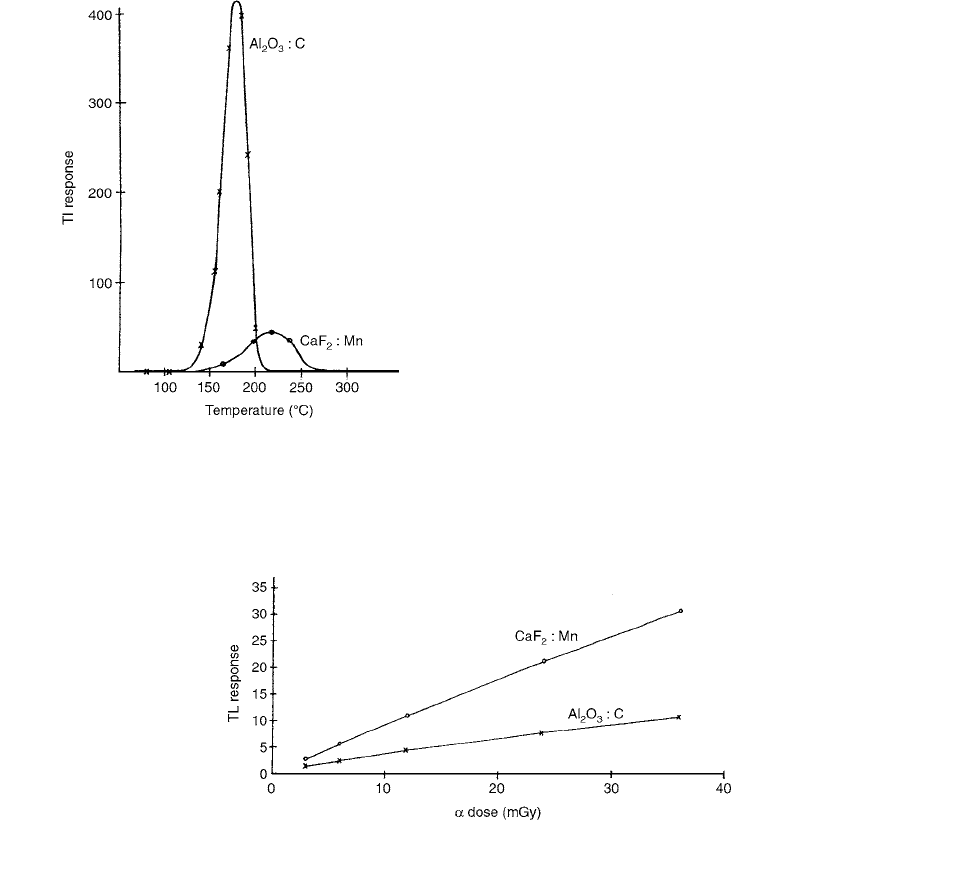
288 Radiation Dosimetry: Instrumentation and Methods
and CaF
2
:Mn dosimeters are shown in Figure 4.91. The
TL light outputs measured under the peaks of dosimeters
irradiated with alpha particles are linear in the dose range
investigated.
The glow curves of dosimeters after 3-mGy alpha
irradiation can be seen in Figure 4.92. The sensitivity of
CaF
2
:Mn to 5-MeV alpha particles is a factor of 3 higher
than compared to Al
2
O
3
:C. The peak induced by high LET
alpha radiation is split into two components in the dose
range investigated.
Figure 4.93 represents the TL output of aluminum
oxide to low LET (curve A: 1-mGy gamma) and to high
LET (curve B: 1-mSv neutron) radiation. The thermal
neutron sensitivity was found to be similar (about 0.04 as
compared to gamma irradiation) for both materials.
The thermostimulated luminescence (TSL) of pow-
dered synthetic CaSO
4
crystals was studied by Gerome
et al. [67] with various types of doping rare earth (RE
3+
)
impurities: Dy
3
, Tm
3
, Ho
3
, Er
3
or Gd
3
. Defects in
anionic groups (SO
x
types) were shown to be
responsible for the UV lattice emission and the trapping
centers, while the RE
3
ions are just radiative emission
centers.
The origin of this UV emission is generally tentatively
explained either (a) by an undesired contamination from
radiative impurities, such as Tm
3
that has a group of three
near-UV lines in the considered spectral range; however,
a fine spectral analysis allows one to dismiss such a
hypothesis when possible, because these UV emissions
are often too weak for good resolution to be possible; or
(b) by an emission of the CaSO
4
lattice. Similar emissions
have been observed in other undoped sulphates (CaSO
4
,
BaSO
4
, SrSO
4
, PbSO
4
, etc).
CaSO
4
samples were obtained by a synthesis method.
Samples were prepared by dissolving CaSO
4
2H
2
O in sul-
phuric acid and vacuum-evaporating the excess acid around
300°C. The oxide (Dy
2
O
3
, Tm
2
O
3
,…) was added for dop-
ing. Crystals of undoped and doped calcium sulphate were
washed, annealed at 750°C for about 2 h, and sieved to
36–50
m. Figure 4.94 shows the TSL of CaSO
4
undoped
or doped with the various RE
3
registered through a 340-
nm filter, after x irradiation at room temperature.
Figure 4.95 shows the TSL curves of CaSO
4
:RE
3+
for
the main emission line of each RE
3
.
Two new thermoluminescent (TL) phosphors
BaSO
4
:Eu,P and BaSO
4
:Eu,Na were prepared by Shinde
et al. [68] by three different methods, recrystallization, co-
precipitation, and sintering at high temperature. The phos-
phors exhibit variations in the thermoluminescent charac-
teristics and also in their electron spin resonance (ESR)
spectra. Both phosphors show changes in their glow-curve
shape and TL sensitivity with the method of preparation
and with the concentration of co-dopant (sodium/phos-
phorus). Maximum TL sensitivity (
5 times that of
CaSO
4
:Dy) was obtained in the case of BaSO
4
:Eu,Na (0.7,
2.5 mol%), prepared by sintering in air at 900°C.
FIGURE 4.90 TL glow curve of gamma-irradiated dosimeters
(1 mGy gamma). (From Reference [66]. With permission.)
SO
4
2
FIGURE 4.91 TL responses as a function of alpha exposure. (From Reference [66]. With permission.)
Ch-04.fm Page 288 Friday, November 10, 2000 12:01 PM

Thermoluminescent Dosimetry 289
Figures 4.96, 4.97, and 4.98 show the TL glow curves
of BaSO
4
:Eu (0.5 mol%), BaSO
4
:Eu,P (0.5, 0.2 mol%),
and BaSO
4
:Eu,Na (0.5,0.2 mol %) prepared by three
methods: recrystallization (R), co-precipitation (P), and
sintering (S). It can be seen from Figure 4.96 that the basic
structure of the glow curves of BaSO
4
:Eu (P) and
BaSO
4
:Eu (S) is similar to that of (Figure 4.98)
BaSO
4
:Eu,Na (P) and BaSO
4
:Eu,Na (S), respectively. The
peak heights are found to change with sodium co-doping.
The glow curves of BaSO
4
:Eu (P) and BaSO
4
:Eu,Na (P)
consist of three glow peaks at about 165, 215, and 270°C,
respectively. BaSO
4
:Eu (S) and BaSO
4
:Eu,Na (S) show a
single broad peak at a relatively high temperature of about
265°C. The glow curve of BaSO
4
:Eu (R) shows only one
peak, at about 170°C, whereas the glow curve of
BaSO
4
:Eu,Na (R) is composed of a main peak at about
165°C and a small peak at 215°C. Figure 4-97 shows the
TL glow curves of BaSO
4
:Eu,P, prepared by three different
methods. In this case also, the glow curves are found to
change with the method of preparation. This indicates that
the glow peak structure is altered when different methods
of preparation are used.
Thermoluminescence investigation of Sr
3
(PO
4
):Eu
2
,
a commercially available x-ray phosphor, was reported
by Otvos. [69] Its TL emission spectrum is dominated by
a single emission band centered at 420 nm, which is
characteristic of Eu
2
. The glow curve of the Eu
2
band
has two well-separated peaks. Sr
3
(PO
4
): Eu
2
seems to
be the best choice for studying thermoluminescence (TL)
kinetics and the relation between radioluminescence (RL)
and TL.
In Figure 4.99, a TL glow curve can be seen measured
in parallel in both emission bands. The irradiation was
performed at room temperature (RT) by an
90
Sr beta
source. The heating rate was l°C s
1
. The glow curve was
measured in the two emission regions simultaneously. The
figure clearly shows that the blue and red emission bands
have completely different glow peak structures. This indi-
cates that not only the luminescence centers responsible
for the different emission bands are different, but the
charge traps and consequently the charge transfer mech-
anisms involved are different, as well.
The perovskite-like KMgF
3
shows, when properly
doped, thermoluminescence (TL) characteristics that
make this phosphor a good candidate for ionizing radiation
dosimetry. [70] With KMgF
3
:Yb single crystals, the TL
emission shows a sharp peak at 410 nm. This is very
advantageous for the instrumentation of TLD analysis. A
glow curve is shown in Figure 4.100.
Natural thermoluminescence (TLN) as well as
gamma- and beta-induced thermoluminescence (TLI)
were studied by Barcena et al. [71] in a set of micas
FIGURE 4.92 TL glow curves of alpha-irradiated dosimeters.
(From Reference [66]. With permission.)
FIGURE 4.93 TL glow curves of Al
2
O
3
:C dosimeter irradiated
by gamma dose of 1 mGy (curve A) and thermal neutron dose
of 1 mSv (curve B). (From Reference [66]. With permission.)
Ch-04.fm Page 289 Friday, November 10, 2000 12:01 PM
