Shani G. Radiation Dosimetry: Instrumentation and Methods

Подождите немного. Документ загружается.

270 Radiation Dosimetry: Instrumentation and Methods

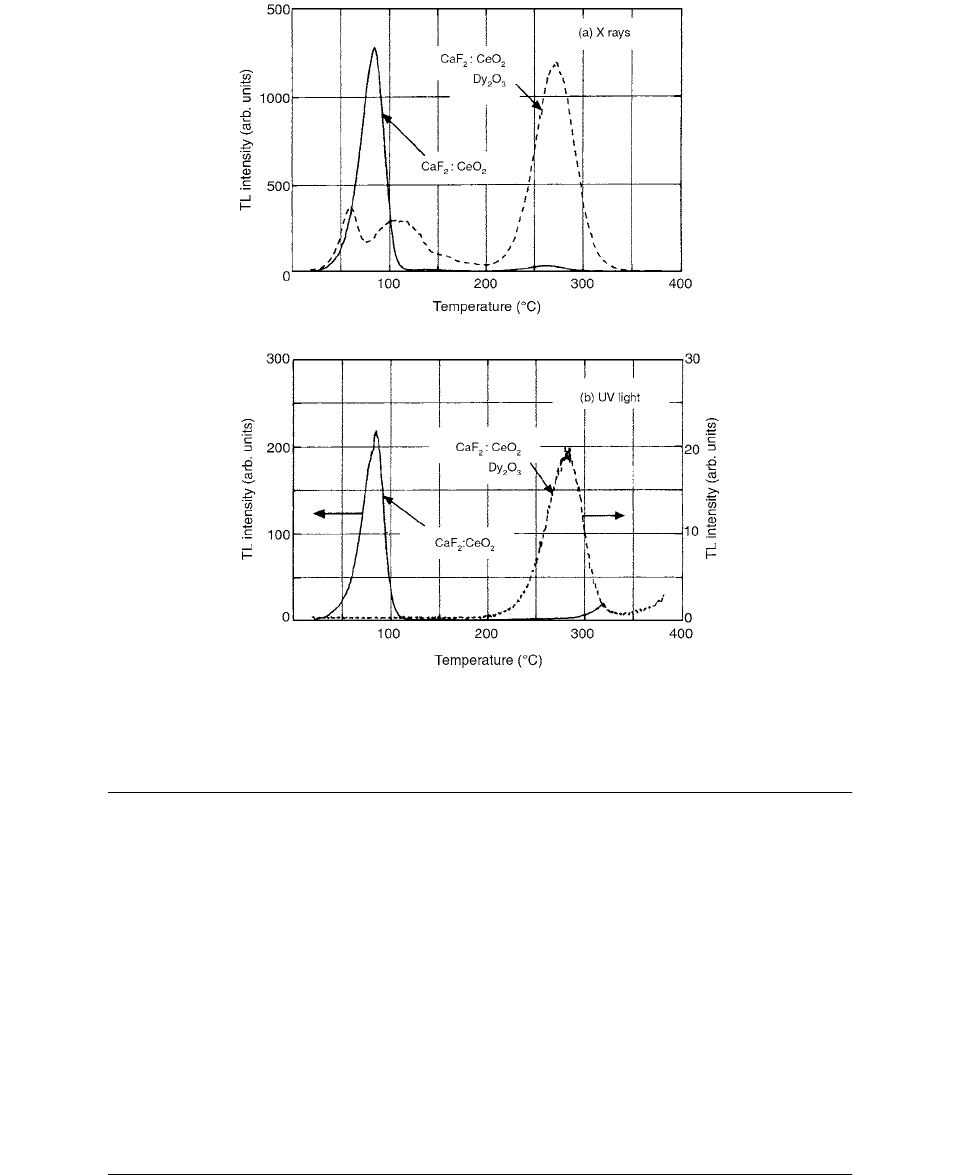
The TL emission spectra for both x and UV irradiation

show a broad band with a peak around 380 nm which is

believed to be caused by Ce

coupled with O

2

centers, but

no emission bands at 2.64 eV (470 nm) or 2.18 eV (570 nm)

have been observed for S-2. From the solid curves of Figure

4.64a and b, it is found that the glow peak of 2 is highly

sensitive for UV irradiation as compared to S-1, but the peak

temperature is too low to use it for practical purposes. [43]

FIGURE 4.64 TL glow curves of S-2 (solid curves) and S-3 (dashed curves): (a) after x irradiation of 25 Gy, (b) after UV irradiation

of 1.2 J. (From Reference [43]. With permission.)

TABLE 4.4

Density and Atomic Number of the Materials used in the Determination of the Quality

Dependence of TL Materials

Effective Atomic

TL Material Number Density (g cm

–3

)

Water 7.50 1.00

LiF 8.27 2.64

LiF:Mg:Ti (TLD-100) 8.27 2.64

LiF:Mg (0.18%):Cu (0.0024%):P(2.3%) 8.67 2.64

7.31 2.44

CaF

16.87 3.18

CaF

:Mn (3%) 17.12 3.18

CaSO

15.6 2.96

Source: From Reference [44]. With permission.

Ch-04.fm Page 270 Friday, November 10, 2000 12:01 PM

Thermoluminescent Dosimetry 271

V. THEORETICAL ASPECTS AND MONTE

CARLO CALCULATIONS OF TL DOSIMETRY

A Monte Carlo simulation of the quality dependence of

different TL materials was performed by Mobit et al. [44]

in the form of discs 3.61 mm in diameter and 0.9 mm

thick, in radiotherapy photon beams relative to



-rays.

The TL materials were CaF

, CaSO

, LiF and Li

It was found that there was a signiﬁcant difference in the

quality dependence factor derived from Monte Carlo simu-

lations between Lif and LiF:Mg:Cu:P but not between CaF

and CaF

:Mn. The quality dependence factors for Li

varied from 0.990  0.008 (1 sd) for 25-MV x-rays to

0.940  0.009 (1 sd) for 5-kV x-rays relative to

-rays. For CaF

the quality dependence factor varied from

0.927  0.008 (1 sd) for 25 MV x-rays to 10.561  0.008

(1sd) for 50-kV x-rays. For LiF TLD, there was no sig-

niﬁcant dependence on the ﬁeld size or depth of irradiation

in the kilovoltage energy range.

Table 4.4 lists the TLD materials simulated, with their

effective atomic numbers and densities.

The quality dependence factor, , is deﬁned as

(4.39)

where is the average absorbed dose in the TL mate-

rial and is the average absorbed dose in water of the

same volume placed at the same point in the uniform water

phantom. The assumption used in deriving Equation (4.39)

is that the light output is directly proportional to the

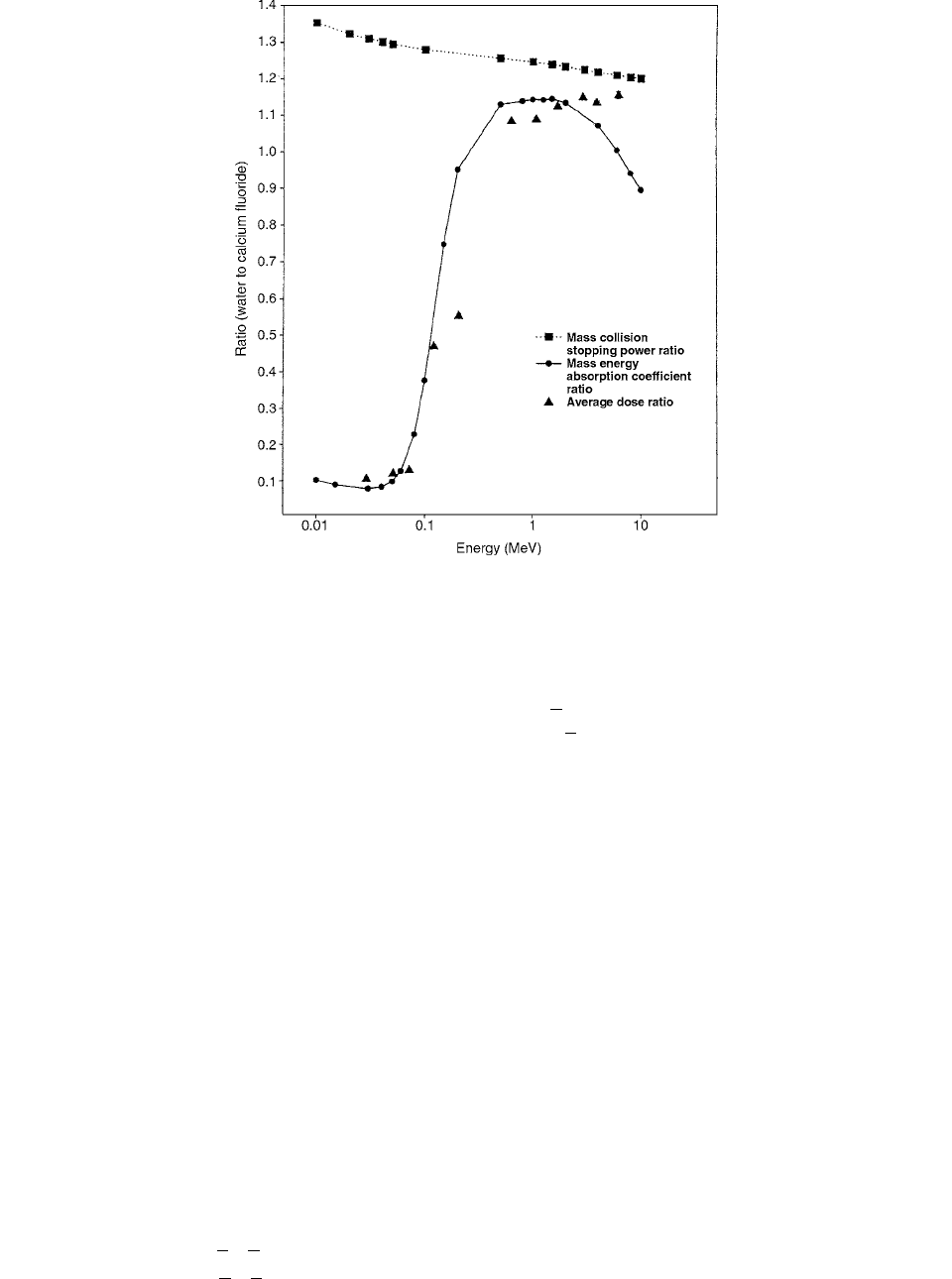
absorbed dose in the TL material. Figure 4.65 shows the

mass energy–absorption coefﬁcient ratio, the mass colli-

sion stopping power ratio, and the Monte Carlo calculated

average dose ratio of water to CaF

from 50-kV to 25-MV

x-rays. All these ratios are plotted against the mean energy

on the phantom surface.

Figure 4.66 shows the average dose ratio of water to

LiF obtained by Monte Carlo simulations of kilovoltage

and megavoltage photon beams. The mass energy–

absorption coefﬁcient ratio and the mass collision stopping

power ratio of water to LiF are also shown. The quality

dependence factor for LiF TLD in kV x-rays relative to



-rays ranges from 1.36  0.01 for 50-kV x-rays to 1.03 

0.01 for 300-kV x-rays.

Monte Carlo simulations with the EGS4 code system

have been performed by Mobit et al. [45] to determine

the quality dependence of diamond TLDs in photon

beams ranging from 25-kV to 25-MV x-rays and also in

megavoltage electron beams. It has been shown that dia-

mond TLDs in the form of discs of thickness 0.3 mm and

FIGURE 4.65 Calcium ﬂuoride TLD discs, 0.9 mm thick, in MV and kV x-ray beams: comparison of the Monte Carlo derived

average dose ratio, water to CaF

, with the mass collision stopping power and mass energy–absorption coefﬁcient ratios, as a function

of the mean photon energy. (From Reference [44]. With permission.)

D

TLD

()

D

TLD

()

------------------------------



TLD

Ch-04.fm Page 271 Friday, November 10, 2000 12:01 PM

272 Radiation Dosimetry: Instrumentation and Methods

diameter 5.64 mm show no signiﬁcant dependence on the

incident energy in clinical electron beams when irradiated

close to d

max

, but require an energy correction factor of

1.050  0.008 compared with diamond TLDs irradiated



-rays. The correction factor increases with depth

of irradiation and this effect is greater for thicker detec-

tors. The Monte Carlo predicted sensitivity in x-ray beams

is constant within 2.5% over the energy range 250 kV to

25 MV. However, the sensitivity decreases by about 60%

for 25 kV x-rays compared with



-rays.

Stones with controlled amounts of selected impurities

can be used with considerable success as detectors of

ionizing radiation of all types. Selected stones can be used

as thermoluminescent dosimeters (TLDs) or radiation

dosimeters in dc mode.

Figure 4.67 shows the comparison between the aver-

age dose ratio of water to diamond and the mass energy

–absorption coefﬁcient ratio of water to carbon. The two

curves are very similar, but in the kilovoltage energy range

the dose ratio of water to diamond curve is slightly lower

than that for the mass energy–absorption coefﬁcient ratio

curve. This could be due to perturbation effects of dia-

mond detectors in kilovoltage photon beams or an effec-

tive point of measurement effect, as the dose is averaged

over a greater effective volume for the diamond detector

(about 3.5 equivalent thicknesses since the density of dia-

mond is 3.5 times greater than that of water).

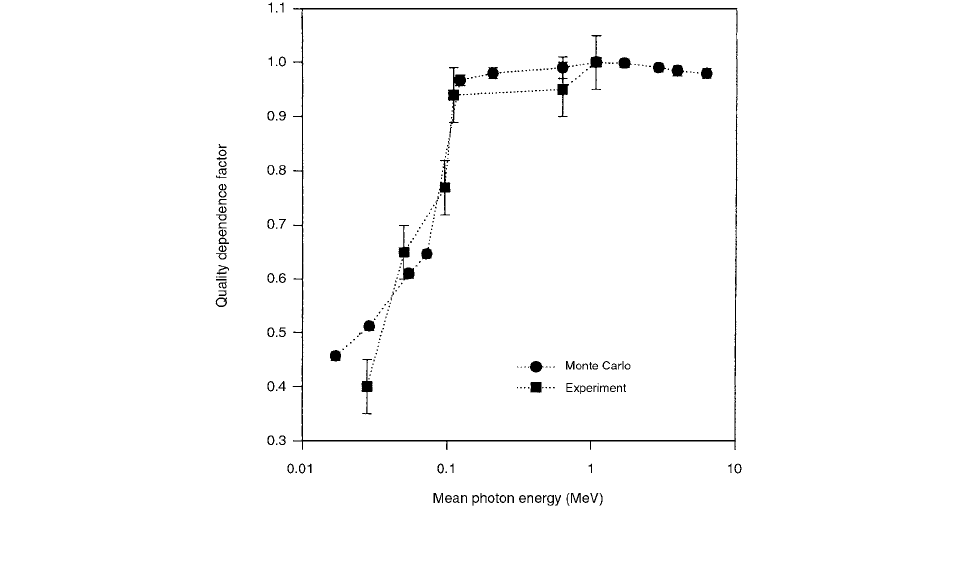
Figure 4.68 shows a comparison between experimen-

tal measurements of Nam et al. [46] and Mobit et al. [45]

FIGURE 4.66 Lithium ﬂuoride TLD discs, 0.9 mm thick, in MV

and kV x-ray beams: comparison of the Monte Carlo derived aver-

age dose ratio, water to LiF, with the mass collision stopping power

and mass energy–absorption coefﬁcient ratios, as a function of the

mean photon energy. (From Reference [44]. With permission.)

FIGURE 4.67 A comparison of the Monte Carlo derived average dose ratio with the mass collision stopping power ratios and the

mass energy–absorption coefﬁcient ratios for water to diamond (carbon). (From Reference [45]. With permission.)

Ch-04.fm Page 272 Friday, November 10, 2000 12:01 PM

Thermoluminescent Dosimetry 273

Monte Carlo simulations in photon beams ranging from

25-kV to 25-MV x-rays. The comparisons have been made

for TLDs irradiated at the surface of a phantom. In the

megavoltage energy range where the dosimeters were irra-

diated inside a phantom, the difference between Monte Carlo

simulation and measurement is less than 1.0%, while in the

kilovoltage energy range there is a disagreement of up to

10%. The experimental determination for kilovoltage x-ray

beams by Nam et al. was in air and not in a phantom, and

this alone can account for a difference of more than 10%.

LET effects are not accounted for by the Monte Carlo

simulations. There is also an uncertainty in the energy

spectra between experiments and Monte Carlo simula-

tions, and this can be signiﬁcant, especially for low-energy

kV x-rays. Diamond TLDs calibrated in



-rays require

a correction factor of 1.047  0.008 to correct for the

under-response of diamond TLDs in electron beams com-

pared to



-rays.

The response of TL dosimeters irradiated with electron

beams in a water-equivalent phantom depends not only on

the dose but also on the electron energy and dosimeter

volume. For a constant electron dose, the TLD response

falls with decreasing energy and increasing TL dosimeter

volume. [47]

Holt et al. [48] derived a semi-empirical relationship

which, similar to the Burlin approach, incorporates the

ﬁnite size of the dosimeter but succeeds in predicting the

TLD sensitivity variations with electron energy quite well.

They express the dose, D

, in the medium as a function

of the dose, D

, in the cavity through the standard rela-

tionship

(4.40)

where



and



are electron ﬂuences and S

and S

, are

mass stopping powers in the medium m and cavity c,

respectively. Holt et al. then made an assumption that the

cavity causes a perturbation of the energy spectrum, i.e.,







. The ratio







was deﬁned as the cavity per-

turbation factor K

and approximated by the following

expression:

(4.41)

where signiﬁes the ratio of mass stopping powers

S

and f represents the fraction of the electron energy

entering the cavity and absorbed in the cavity. Similar

to Burlin theory, relates the electron spectrum build-

ing to its maximum value in the cavity, while (1

 f)

represents the decay in the cavity of the electron spec-

trum which was generated in the medium. In Equation

(4.41) K

is the dose correction factor for the TLD

response to electrons relative to

Co gamma-rays. Thus,

l/K

represents the calculated relative TLD response as

FIGURE 4.68 A comparison of the Monte Carlo derived quality dependence factor of diamond TLDs with experiment as a function

of photon quality (kV x-rays). (From Reference [45]. With permission.)

-------



------

-----





------

-------

[]

1

1 f()

Ch-04.fm Page 273 Friday, November 10, 2000 12:01 PM

274 Radiation Dosimetry: Instrumentation and Methods

follows:

(4.42)

where the electron dose to the medium D

(E) is related

to the

Co gamma-ray dose D

(



) through Bragg-Gray

cavity theory and



is the thermoluminescence calibra-

tion factor relating the TL signal Q to the dose. The

stopping power ratios and differ by less than

0.5% over the range of electron energies used in our

experiment. Thus, is assumed equal to 1in

Equation (4.42)

Figure 4.69 shows the measured relative responses for

the 0.4- and 1.0-mm-thick TL dosimeters irradiated at the

depth of dose maximum (d

max

) in the polystyrene phantom,

with electrons in the energy range between 0.68–20.9 MeV.

The 0.68-MeV points were obtained by irradiating the TL

dosimeters on the polystyrene phantom surface with the

Sr-Y ophthalmic applicator; all other points were obtained

by irradiations with a linac. The relative responses of the

TL dosimeters are normalized to the response per unit

dose, measured with

Co gamma-rays. The relative TLD

responses are plotted as a function of the mean electron

energy at d

max

phantom. The TLD response per unit dose

depends strongly on electron energy and thickness of TL

dosimeters.

The CEPXS/ONEDANT code package [49] was used

by Deogracias et al. [50] to produce a library of depth-dose

proﬁles for monoenergetic electrons in various materials

for energies ranging from 500 keV to 5 MeV in 10-keV

increments. The various materials for which depth-dose

functions were derived include lithium ﬂuoride (LiF), alu-

minum oxide (Al

), beryllium oxide (BeO), calcium

sulfate (CaSO

), calcium ﬂuoride (CaF

), lithium boron

oxide (LiBO), soft tissue, lens of the eye, adipose, muscle,

skin, glass, and water. Material data sets were ﬁt to ﬁve

polynomials, each covering a different range of electron

energies, using a least-squares method.

The ﬁfth-order polynomials were of the form:

In the polynomial expression, D(x,E) is the depth dose, x

represents the depth in centimeters, E is the energy in keV,

and a – r are the polynomial coefﬁcients.

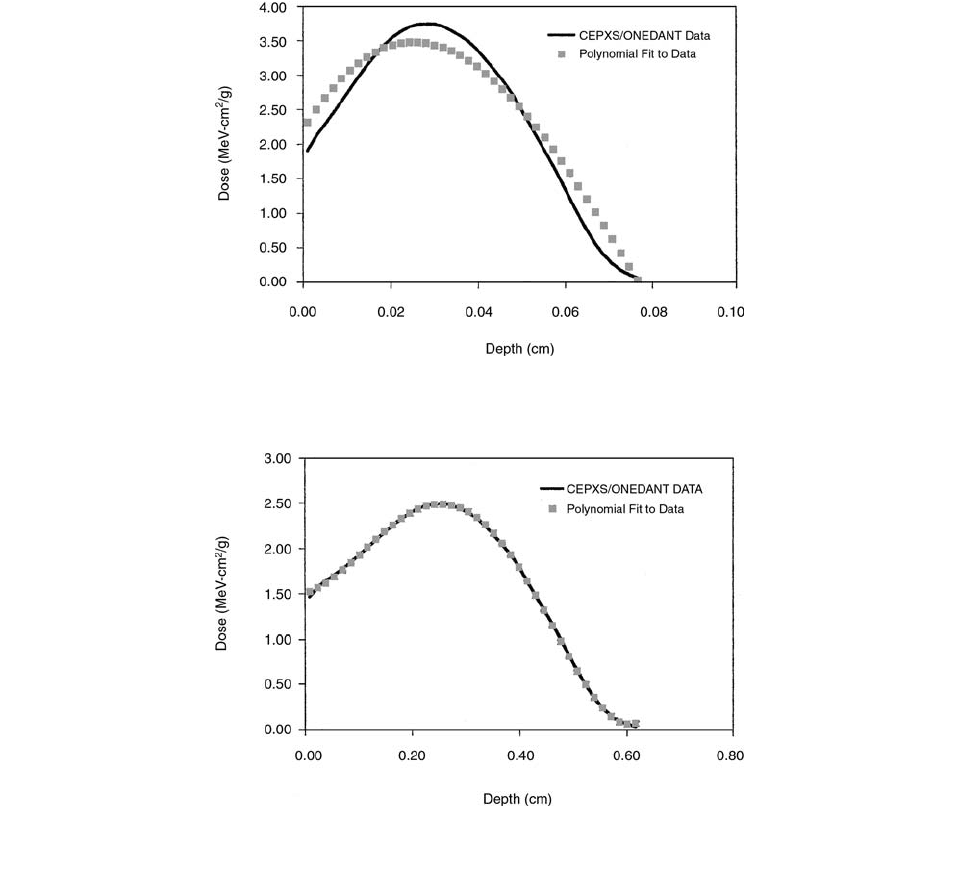
Figure 4.70 shows the comparison between the simu-

lated data and the polynomial ﬁt for an energy of 500-keV.

The polynomial ﬁt for the 500-keV energy does not

correlate as well as the ﬁts for the higher energies. This

is due to the extreme increase in the dose-to-depth ratio

in the lower energies, which the polynomial equation cannot

adequately compensate. The 500-keV ﬁt is the worst-case

ﬁt for the entire energy range in all materials. Figure 4.71

shows the comparison at an energy of 2700 keV.

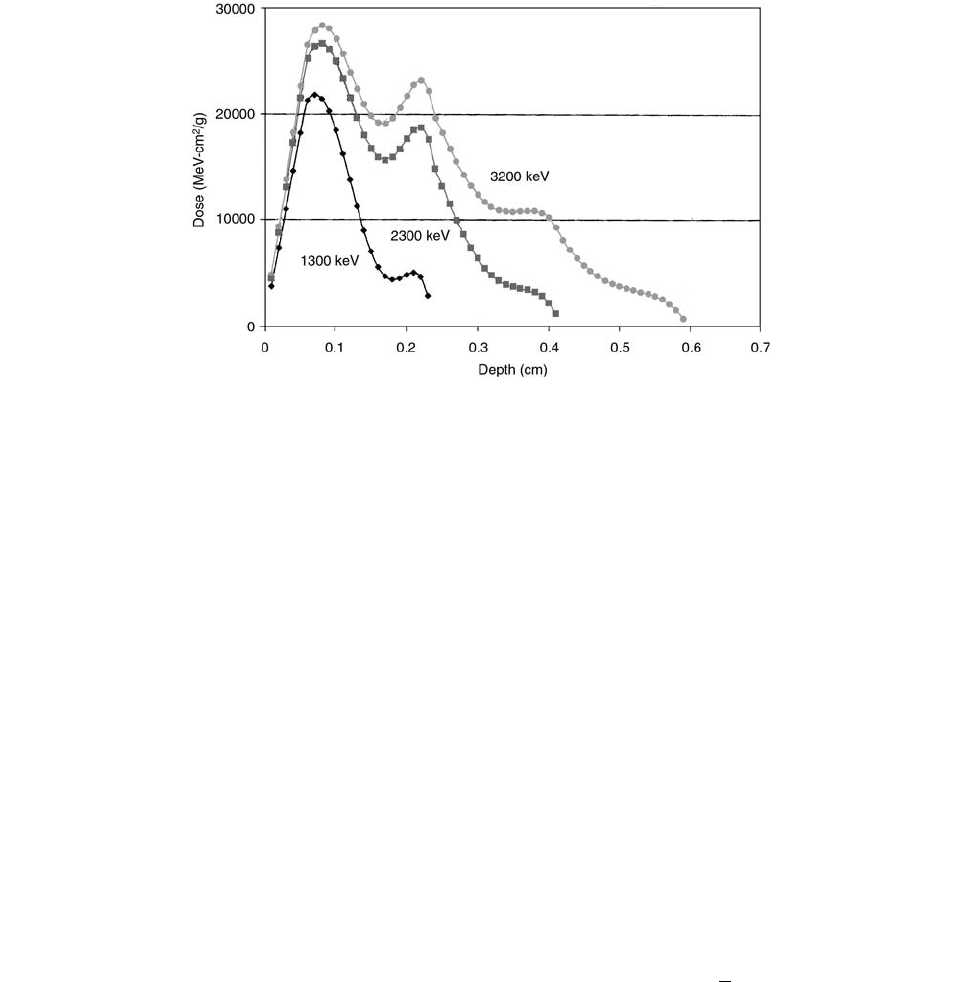
Figure 4.72 is an example of the depth-dose curve

generated from a beta particle spectrum. The energy range

for all the spectrums begins at 500 keV, and the endpoint

energy of the spectrum is varied from 1300 to 3200 keV.

FIGURE 4.69 Relative response of the 0.4- and 1.0-mm thick TLD normalized to the response per unit dose in a

Co beam. (From

Reference [41]. With permission.)

------

E()

----------------

E()



()

---------------

E()



E()



()

---------------

E()



()

---------------









E()



()

---------------





E()





()

-------------------

E()



()

---------------



E() S

()

E()S

()

DxE,()ax

Ecx

 ex

E

 fx

E

 jx

kxE

lxE

mxE nx oE



 pE

qE r (4.43)

Ch-04.fm Page 274 Friday, November 10, 2000 12:01 PM

Thermoluminescent Dosimetry 275

The shape of the curve is based on a complex interaction

between the beta spectrum, polynomial dose equation, and

the energy range of the spectrum. The increase in energy

range produces an increase in dose for all depths up to

the range of the highest-energy beta particle.

Thermoluminescent dosimetry is a relative method; that

is, it is necessary to initially calibrate the detector in a

known radiation ﬁeld, usually a

Co source. In most prac-

tical situations, the gamma spectra are different from those

of primary

Co gamma rays, because of scattering in irra-

diated media, and it is important to know the effect of the

gamma spectrum on the dosimeter response.

The energy dependence of the response of various

TL detectors for

Co gammas degraded in water was

investigated by Miljanic and Ranogajec-Komor. [51]

They irradiated several types of thermoluminescent

dosimeters (LiF:Mg,Ti; Al

:Mg,Y; and CaF

:Mn) at

different depths in a water phantom placed at a distance

of 2.5 m from a panoramic

Co source. Detectors were

encapsulated in Plexiglas holders with a wall thickness

of 0.5 cm. Reference dosimetry was carried out using a

Fricke dosimeter and an ionization chamber.

For

Co photons, TL detectors are “intermediate”-

size detectors. In this intermediate size range, the absorbed

dose in the medium is calculated according to the Burlin

general cavity theory, which includes cavities of all sizes.

The mean absorbed dose in the detector (D

) in rela-

tion to the absorbed dose at a speciﬁed point in the sur-

rounding medium (D

) is given by

(4.44)

where s

d,n

and (





)

d,m

are, respectively, the ratios of mass

collision stopping powers and mass energy absorption

FIGURE 4.70 Depth-dose curve ﬁt comparison between the polynomial dose equation and the CEPXS/ONEDANT data for 500-keV

electrons in LiF. (From Reference [50]. With permission.)

FIGURE 4.71 Depth-dose curve ﬁt comparison between the polynomial dose equation and the CEPXS/ONEDANT data for 2700-keV

electrons in LiF. (From Reference [50]. With permission.)

D

d,n

1 d()



()

d,m

d

Ch-04.fm Page 275 Friday, November 10, 2000 12:01 PM

276 Radiation Dosimetry: Instrumentation and Methods

coefﬁcients of the detector and the medium, and d is a

weighting factor which takes into account the size of the

detector. It is given by

(4.45)

where



is the effective mass attenuation coefﬁcient for

electrons and g is the average path length through the

detector. Burlin originally used the following expression

for

where V is the volume and S is the total surface area.

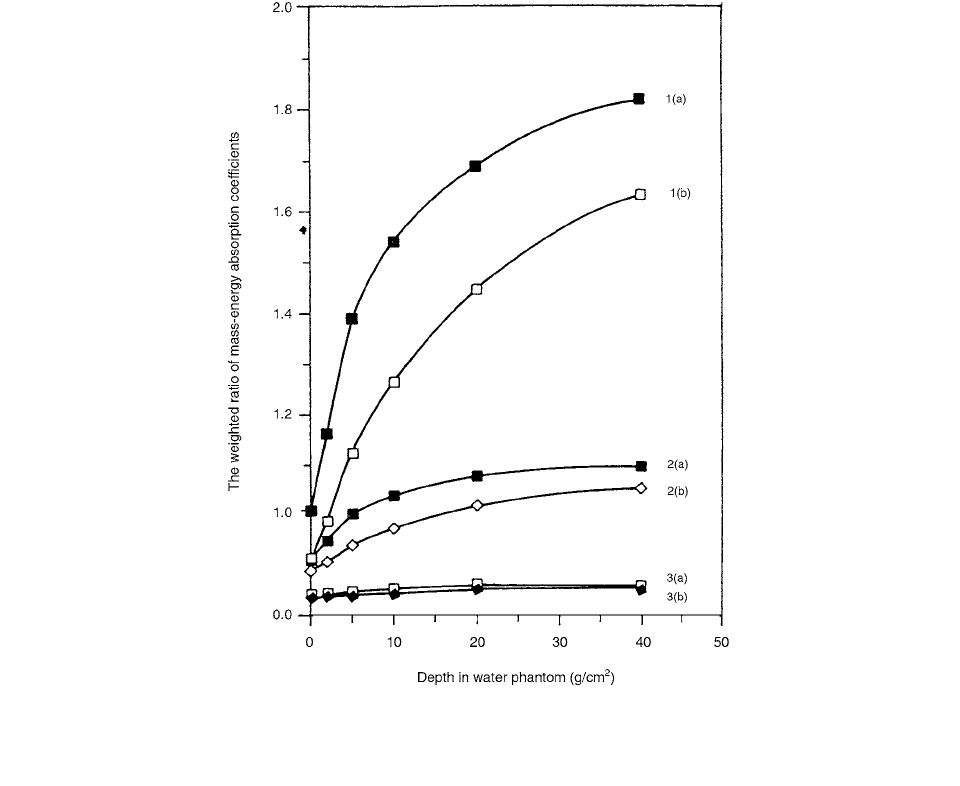
The ratios of mass energy absorption coefﬁcients for

different TLDs and water, weighted over energy spectra

given by Seltzer [52], for scattered components and for

the whole spectrum are shown in Figure 4.73

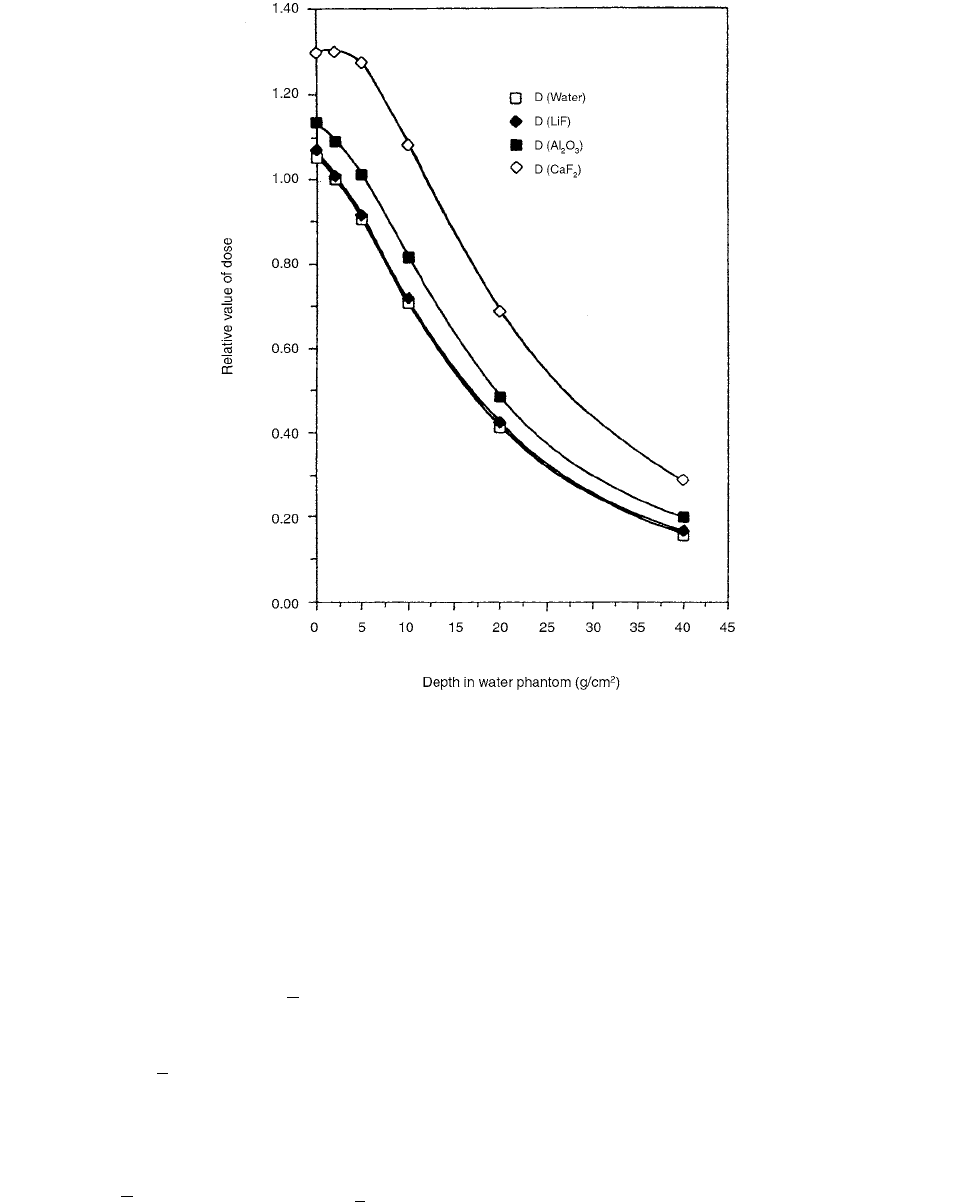
The experimental results of dose distribution measure-

ments with different TL dosimeters are shown in Figure 4.74.

Doses in water from the results of the Fricke dosimeter

were calculated.

EGS4 Monte Carlo simulations have been performed

by Mobit et al. [53] to examine general cavity theory for a

number of TLD cavity materials irradiated in megavoltage

photon and electron beams. The TLD materials were LiF,

, CaF

, and CaSO

irradiated in Perspex, water, Al,

Cu, and Pb phantoms. For megavoltage photon beams, this

has been done by determining the dose component (1

 d)

resulting from photon interactions in the cavity compared

with the dose component resulting from photon interactions

in the phantom material (d) by Monte Carlo simulations

and analytical techniques. The results indicate that the Burlin

exponential attenuation technique can overestimate the dose

contribution from photon interactions in a 1-mm thick LiF

cavity by up to 100%, compared with the Monte Carlo

results for LiF TLDs irradiated in a water or Perspex phan-

tom. However, there is agreement to within 1% in the quality

dependence factor, determined from Burlin’s cavity theory,

Monte Carlo simulations, and experimental measurements

for LiF and Li

TLDs irradiated in a Perspex or a water

phantom. The agreement is within 3% for CaF

TLDs.

However, there is disagreement between Monte Carlo sim-

ulations and Burlin’s theory of 6 and 12% for LiF TLDs

irradiated in copper and lead phantoms, respectively. The

adaptation of Burlin’s photon cavity theory and other mod-

iﬁcations to his photon general cavity theory for electrons

have been shown to be seriously ﬂawed. [53]

Mobit et al. presented cavity theory in the following

way. When a detector is placed in a medium exposed to

ionizing radiation in order to measure dose, it forms a

cavity in that medium. The cavity is generally of different

atomic number and density to the medium. Cavity theory

gives the relation between the dose absorbed in a medium

med

) and the average absorbed dose in the cavity decay.

(4.46)

where f

med,cav

is a factor that varies with energy, radiation

type, medium, size, and composition of the cavity. For a

cavity that is small compared with the range of the electrons

incident on it in a photon beam, the Bragg-Gray relation

applies and f

med,cav

is given by the average mass collision

stopping power ratio of the medium to the cavity (s

med,cav

generally evaluated according to Spencer and Attix. For a

cavity that is large compared with the electrons incident on

it, f

med,cav

is given by the ratio of the average mass energy

absorption coefﬁcient of the medium to the cavity material.

The Burlin cavity theory equation (4.44) requires a

value to be provided for d which represents the proportion

FIGURE 4.72 Depth-dose curves generated from normalized and scaled Y-90 beta particle spectrum source for varying energy ranges

in LiF. (From Reference [50]. With permission.)

d 1 e



g

()



g

4 VS()

med

cav

med,cav



Ch-04.fm Page 276 Friday, November 10, 2000 12:01 PM

Thermoluminescent Dosimetry 277

of the dose in the cavity that is due to secondary electrons

generated in the medium. This can be calculated directly

using the Monte Carlo method, and the values can be com-

pared to the theoretical predictions. Burlin proposed that d

could be estimated by assuming that electrons incident on

the cavity are exponentially attenuated, so that d is given by

(4.47)

where g is the path length of electrons entering the cavity

and



is the effective mass attenuation coefﬁcient of elec-

tron ﬂuence penetrating the cavity. In order to be able to

compare the Monte Carlo calculations of d with the Burlin

theory, values of



and g are required. Values for g range

from 4V/S, where V is the volume of the cavity and S is

its surface area, to 1.539t for a TLD chip, where t is the

thickness of the chip. For a cylinder 6 mm long and 1 mm

in diameter, the predicted value of g would thus range

from 0.92 to 1.54 mm, although the latter would be an

overestimate for a cylinder. Values of



for LiF in a

beam vary from 8.5 cm

1

[54] through 13.4 cm

1

[55]

to 15.9 cm

1

[56]. The value of



from Chan and Burlin

is based on the expression

(4.48)

where R

CSDA

is the continuous slowing down approxima-

tion of electron range. The value of Paliwal and Almond

is derived from

(4.49)

where

max

is the maximum calculated energy of the sec-

ondary electrons, which for



-rays is 1.04 MeV.

Further discussion can be found in Horowitz. [57]

The quality dependence factor is deﬁned as [53]

(4.50)

FIGURE 4.73 The weighted ratios of mass energy absorption coefﬁcients for different TLDs and water at different depths in a water

phantom (evaluated from Seltzer [52]); curves 1, 2, and 3 are for CaF

, Al

and LiF, respectively, (a) only for the scattered

component of the spectra and (b) for the whole spectra. (From Reference [51]. With permission.)



x







1

----------------------

1 e



g

()



--------------------------





CSDA



0.01



LiF

14E

max

1.09



TL X()D

med

X()[]TL Co()D

med

Co()

Ch-04.fm Page 277 Friday, November 10, 2000 12:01 PM

278 Radiation Dosimetry: Instrumentation and Methods

where TL(X)/D

med

(X) is the light output (TL) per unit dose

in a medium for the beam quality X of interest. TL(Co)/

med

(Co) is the light output per unit dose in the same

medium for



-rays. In calculating the value of

using either the Monte Carlo method or cavity theory

method, the assumption is made that

TL(X) is directly

proportional to the absorbed dose in the TL material.

Assuming that

TL(X) is directly proportional to the

average absorbed dose in the TLD , the dose to the

medium in an x-ray beam is obtained from

(4.51)

for TLDs calibrated in



-rays.

The Burlin factor ( f

w,LiF

) is given by

(4.52)

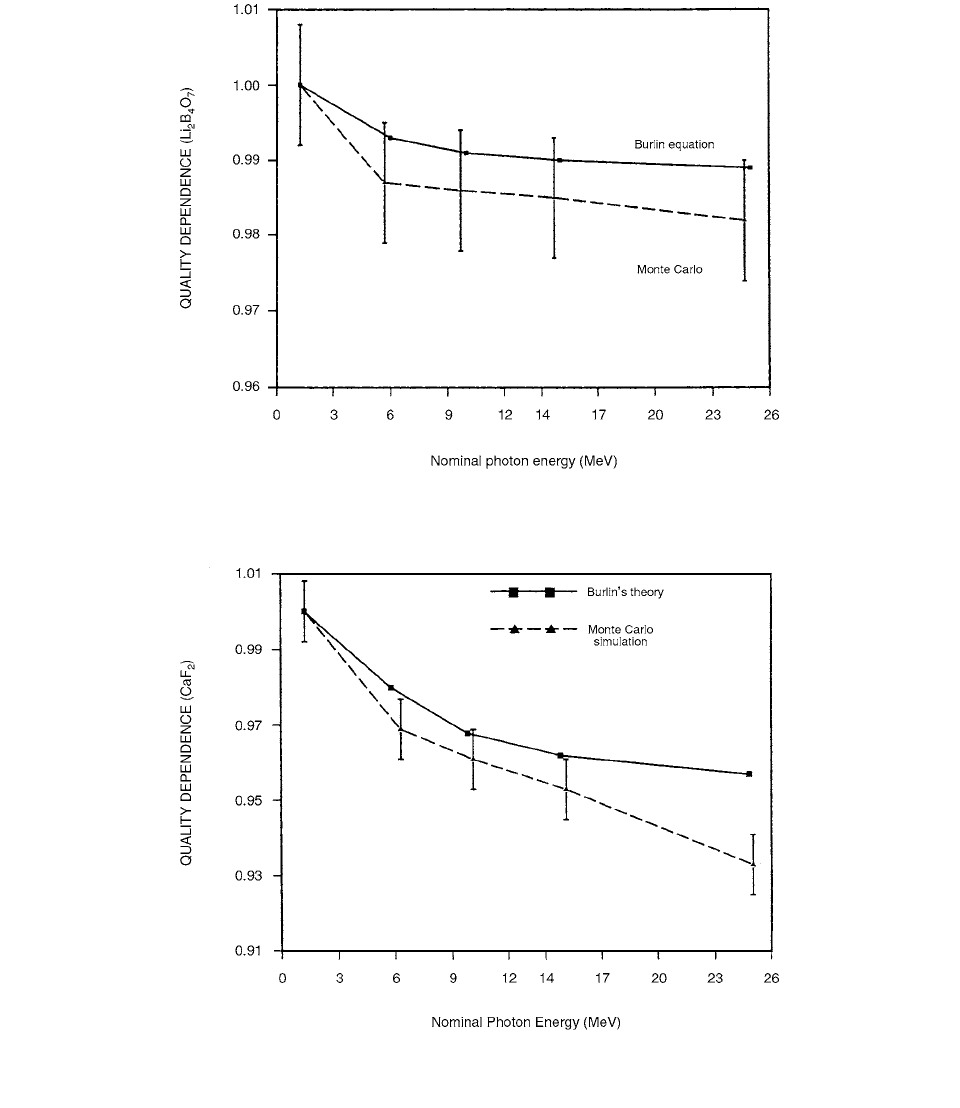
The Burlin general cavity equation was evaluated for

calcium ﬂuoride (CaF

) and lithium borate (Li

) discs

of thickness 0.9 mm and diameter 3.61 mm. The results

of the calculations are displayed in Figures 4.75 and 4.76

for Li

and CaF

respectively.

For lithium borate, the Burlin general theory gives a lower

estimate of the deviation from unity of the quality dependence

factor by a maximum of 1% compared with the Monte Carlo

calculated results. For CaF

the maximum difference is 3%

for 25-MV x-rays. This difference may be attributable to the

cavity perturbation effects of CaF

in photon beams. Cavity

perturbation effects are larger for CaF

than either Li

or LiF. This means that the secondary electrons produced

from photon interactions in the medium are perturbed more

by the CaF

than either the LiF or the Li

cavities.

Despite this, the agreement between Burlin cavity theory and

Monte Carlo simulation for both LiF and CaF

is still within

3% for the entire energy range studied. [53]

Figure 4.77 shows that the quality dependence of LiF

TLDs in megavoltage photon beams does not depend sig-

niﬁcantly on the size of the LiF TLD materials, at least

for the LiF TLD sizes simulated.

A model was developed by Woo and Chen [58] to

enable dose determination for thermoluminescent

FIGURE 4.74 Results of dose distribution measurements with different types of TL dosimeters as a function of depth in water

phantom. Dose to water was evaluated from the measurements using the Fricke dosimeter. (From Reference [51]. With permission.)

TLD

()

med

X() D

TLD

TL Co()D

med

CO()[]F



w,LiF

D

LiF

w,LiF

1 d()







()

w,LiF

[]

Ch-04.fm Page 278 Friday, November 10, 2000 12:01 PM

Thermoluminescent Dosimetry 279

dosimeters immersed in a radioactive solution such as used

in radioimmunotherapy. For low-energy beta emitters used

in such therapy, the size of the dosimeter results in a much

lower light output than when irradiated with an external

Co beam to the same dose as delivered to the medium.

The model takes the size of the dosimeter into account and

hence allows calculation of the dose in the actual medium.

The dose determined is the dose averaged over the

volume of the TLD. If the dose distribution is not uniform

across the TLD, as in the case of low-energy electrons

whose range is comparable to the TLD thickness, it would

be more useful to relate the total light output to the

integrated dose or total energy absorbed by the dosimeter.

For low-energy beta radiation with range comparable to

the TLD size, the dose so determined will be lower than

the dose to the medium, due to the displacement effect.

In the case of beta sources, the calculation is based

on the fact that all the beta energy is absorbed and the

FIGURE 4.75 A comparison of the quality dependence factor derived from Monte Carlo simulation and from the Burlin cavity equation

for a 3.61-mm diameter and 0.9-mm thick disc of Li

in megavoltage photon beams. (From Reference [53]. With permission.)

FIGURE 4.76 A comparison of the quality dependence factor derived from Monte Carlo simulation and the Burlin cavity equation

for a 3.61-mm diameter and 0.9-mm thick disc of CaF

in megavoltage photon beams. (From Reference [53]. With permission.)

Ch-04.fm Page 279 Friday, November 10, 2000 12:01 PM