Shani G. Radiation Dosimetry: Instrumentation and Methods

Подождите немного. Документ загружается.

180 Radiation Dosimetry: Instrumentation and Methods

The results show that the C

factors for converting the

in-phantom air-kerma-calibrated chamber reading, to the

absorbed dose to water, are nearly constant for incident

electron energy between 4 and 11 MeV, for prototype

chambers with 0.018 mm thick copper layers, and between

4 and 15 MeV for chambers with 0.035 mm thick copper

layers. The C

factors are proportional to the product of

water/air stopping-power ratio and perturbation factor.

When the designated chamber is irradiated by an electron

beam at a depth d in a water phantom the absorbed dose

to water is

(3.192)

The variation of , with energy for a particular elec-

tron chamber, depends on both the electron ﬂuence–per-

turbation correction factor and the stopping power ratio

for the phantom material to air, . The conversion

factor can be written as

(3.193)

where is a correction factor for a secondary-standard

NE2561 chamber to account for the lack of air equivalence

of the chamber wall, electrode, and build-up cap, and

is a correction factor for the effect of absorption and

scattering in the chamber wall, electrode, and build-up

cap at the calibration of the chamber irradiated in air by

Co beam or a 2-MV x-ray beam. g is the fraction of

the energy of the charged particles lost to bremsstrahlung.

The perturbation factor, , corrects for the effect of

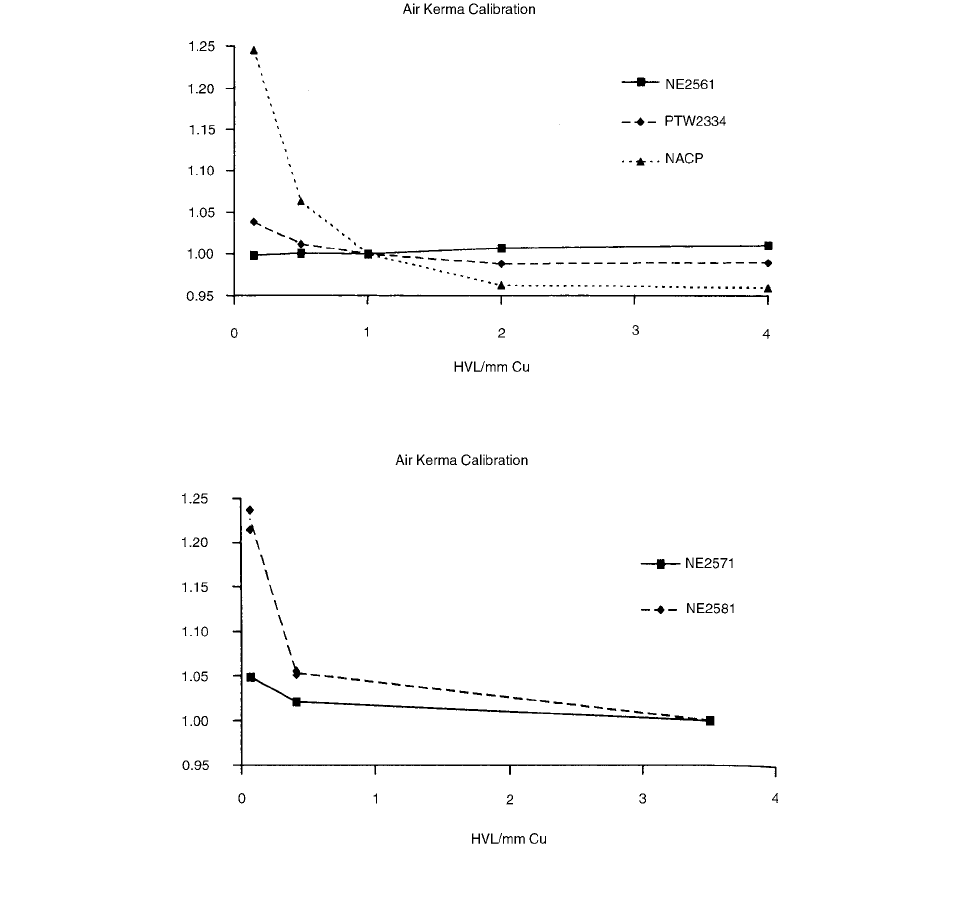
FIGURE 3.87 The variation of the chamber calibration factor with beam quality. (From Reference [92]. With permission.)

FIGURE 3.88 The variation of the chamber calibration factor with beam quality. (From Reference [92]. With permission.)

 N

med,air

att

1 g()k

{}P

cal

()S

water,air



att

cal

Ch-03.fm(part 2) Page 180 Friday, November 10, 2000 11:59 AM

Ionization Chamber Dosimetry 181

non-medium-equivalent wall material and central elec-

trode and for the deviation of the effective point of mea-

surement of the chamber from the chamber center during

the intercomparison of a secondary-standard NE2561

chamber and an electron chamber.

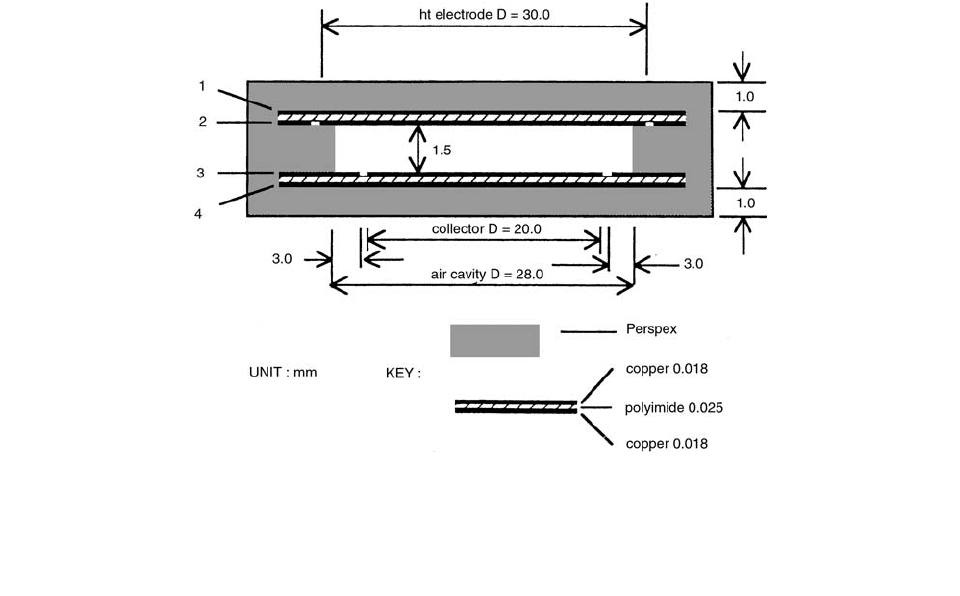
The geometrical details of the NPL chambers are shown

in Figure 3.89.

The conversion factor for a particular electron cham-

ber varies with both the electron ﬂuence–perturbation correc-

tion factor and the stopping power ratio for water to air,

. Relative values of C

are shown in Figure 3.90.

X. LIQUID DIELECTRIC IONIZATION

CHAMBERS

Ionization chambers ﬁlled with a dielectric liquid instead

of a gas have many basic advantages. The sensitive volume

of a liquid-ionization chamber (LIC) can be made much

smaller than that of a gas-ionization chamber and still

provide the same ionization current. A high spatial reso-

lution, not possible with a gas chamber, can thereby be

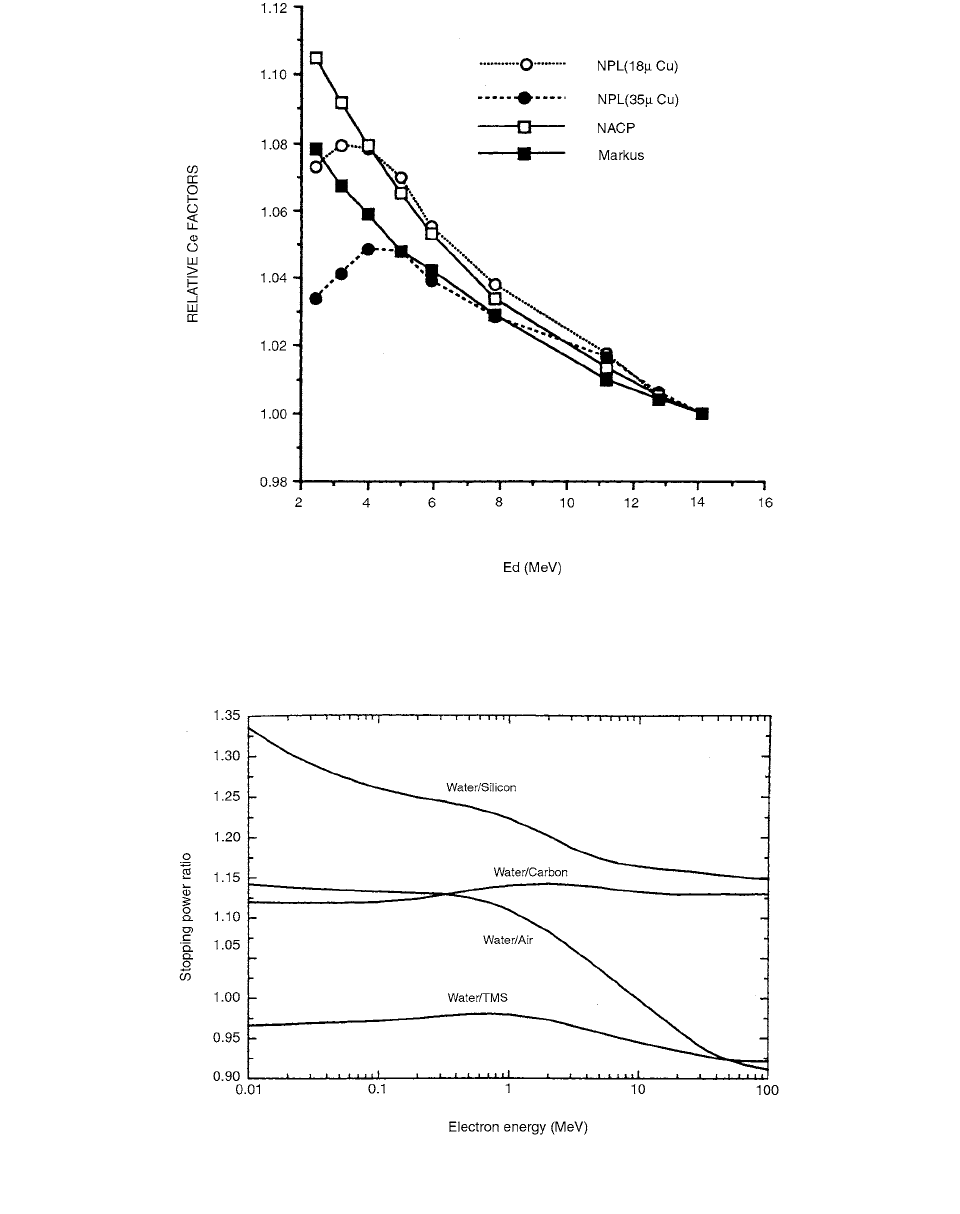
achieved. The stopping power ratio for the dielectric liquid

to water varies by only a few percent in the range 1–50

MeV, compared to about 20 percent for air to water in the

same energy range (Figure 3.91).

Two dielectric liquids, isooctane and tetramethylsilane

(TMS), have been tested by Wickman and Nystrom [94]

as sensitive media in parallel-plate ionization chambers.

The ionization chambers use graphite electrodes and have

a high spatial resolution due to a coin-shaped ionization

volume of 2 mm

(diameter 3 mm, height 0.3 mm). The

detectors show a calibration stability within l% over

several years. In neither of the liquids did general recom-

bination exceed 2% in pulsed radiation ﬁelds and dose

rates up to 7 Gy min

1

The mobility of ions is reported to be extremely high.

The collision stopping power ratio to water is found to be

almost constant (within about 0.2%) in the electron

energy range of 0.01–50 MeV, while isooctane has a mod-

erate variation of 2% (Figure 3.92).

The leakage current is a rough measure of the amount

of impurities in a dielectric liquid. Obviously, there are

some initial chemical exchanges due to liquid and chamber

wall interactions, as a new ionization chamber has to be

rinsed several times by emptying and ﬁlling it with fresh

liquid during the ﬁrst weeks before a low and stable resid-

ual current is established. A typical residual current at room

temperature that can be achieved at a polarization potential

of 900 V (3.0 MV m

1

) is about 5  10

14

A in isooctane,

as well as in TMS. This current corresponds to a resistivity

of about 3

 10

m. The resistivity reported for highly

puriﬁed hydrocarbon liquids is 3 to 30 times higher. The

residual current is temperature-dependent, as well as ﬁeld

strength–dependent. The leakage current is slightly

increased directly after the polarization voltage has been

connected but stabilizes within a few minutes. When a

FIGURE 3.89 A cross-sectional view of the NPL plane-parallel chamber with 0.018-mm-thick copper layers. The thickness of each

copper layer (1,2,3, or 4) is 0.018 mm and the thickness of the polymide layer is 0.025 mm. The diameter of the collecting electrode

is 20 mm and the width of the guard ring is 3 mm. The diameter of the air cavity is 28 mm and the thickness is 1.5 mm. The thickness

of the front and back Perspex wall is 1 mm. For a 0.035-mm-thick copper-layered version, the geometry is exactly the same, except

that the copper layers are 0.035 mm thick. (From Reference [93]. With permission.)

water, air

Ch-03.fm(part 2) Page 181 Friday, November 10, 2000 11:59 AM

182 Radiation Dosimetry: Instrumentation and Methods

FIGURE 3.90 Relative factors for the plane-parallel chambers used by Ma et al. The values normalized to the values for

. (From Reference [93]. With permission.)

FIGURE 3.91 Stopping power ratio to water of the dielectric liquid TMS and other materials commonly used as sensitive media

for dosimeters. (From reference [99]. With permission.)

14.4 MeV

Ch-03.fm(part 2) Page 182 Friday, November 10, 2000 11:59 AM

Ionization Chamber Dosimetry 183

chamber has been rinsed and a low current has been estab-

lished, this will typically remain stable for years and

appears to be unaffected by normal use of the chamber.

A residual current of 5  A corresponds to a dose

rate from ionization radiation of 0.2 mGy min

1

isooctane and 0.13 mGy min

1

in TMS for the type of

chamber used in this investigation.

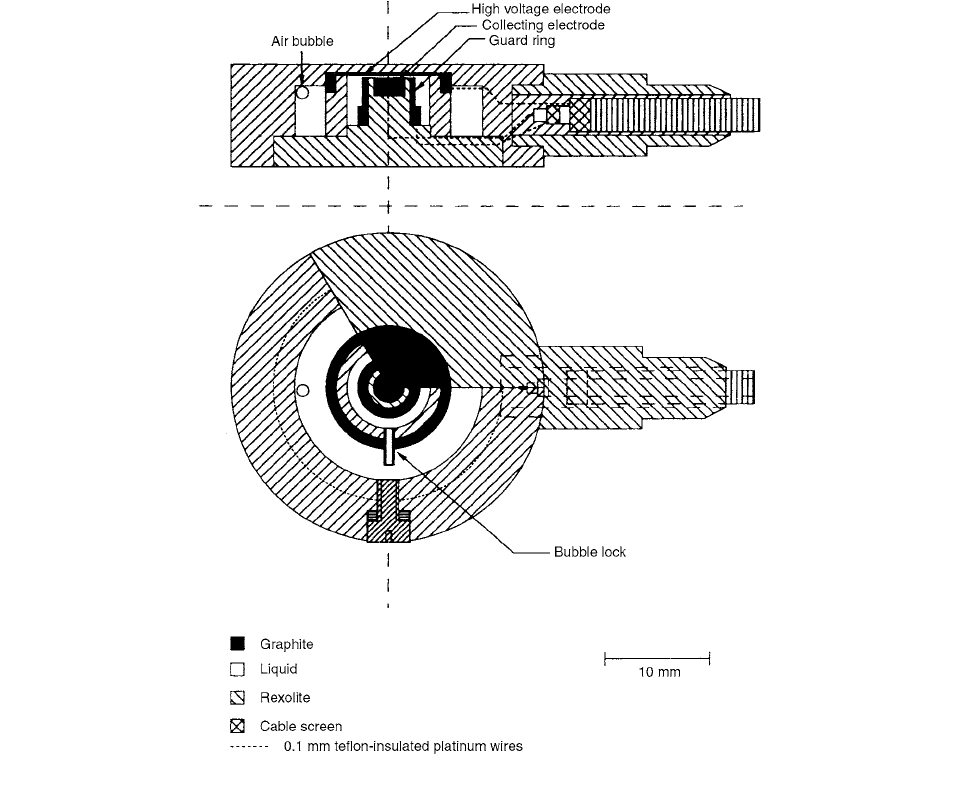
The basic chamber design is illustrated in Figure 3.93.

Strong emphasis during the development of the chamber

has been placed on the creation of a small, robust, versa-

tile, and easy-to-handle detector with a stable response

that can be used as simply as any gas-ionization chamber

for routine calibration and measurements in radiation ther-

apy ﬁelds. The chamber is watertight and can be used with

the same liquid for years.

The electrodes are made of thin discs of pure graphite.

In the earlier chamber designs, thin layers of evaporated

beryllium were used. The reason for the exchange was that

beryllium reacts with the liquid in a way not yet understood,

causing a slow and constant drop in the detector sensitivity.

No signiﬁcant change in calibration stability has been found

when graphite discs are used as electrodes.

An air bubble has been introduced in order to com-

pensate for the approximately four times greater volume

change with temperature in the liquid compared to the

chamber body materials. The liquid container has been

divided into two compartments; the air bubble is placed

in the outer part, and a “bubble lock” between the two

compartments is introduced in order to prevent air from

coming between the electrodes.

The distances between the ions formed in the track

of an ionizing particle are much shorter than in the gas.

The ion recombination in the liquid is much more pro-

nounced and must often be corrected for. In the track

of a highly energetic particle, liquid ions are formed in

clusters containing one or a few ion pairs, and there is

a signiﬁcant initial recombination of the ions in their

original clusters. The amount of ions liberated per 100

eV of absorbed energy at zero external electric ﬁeld is

commonly deﬁned as . The intra-cluster recombina-

tion is affected by the temperature and by the external

electric ﬁeld. The value at room temperature varies

from approximately 0.1 to 1 for the various dielectric

liquids. For “impurity-free” 2, 2, 4-trimethylpentane

(isooctane) and TMS, is 0.33 and 0.74, respectively.

[94]

The free-ion yield, , is a measure of the probability

that the electrons formed by the ionization radiation have

sufﬁcient energy to escape from the electric ﬁeld of the

parent positive ions.

In the measurements of the collection efﬁciency, the

absorbed dose in water was simultaneously monitored by

a small plane-parallel air-ionization chamber with a well-

known and small general recombination that was cor-

rected for. The results are presented in Figures 3.94. It is

seen from the ﬁgures that the general recombination in

isooctane is noticeably dependent on the pulse repetition

rate when the polarizing voltage is 500 V. This effect

decreases when the voltage is increased to 900 V and

is, at that voltage, almost negligible for pulse rates under

100 pulses per second. This pulse rate effect depends on

the fact that the transport time of some of the ions is longer

than the pulse interval; this means that new ions are

injected by the following pulse before these slow-motion

FIGURE 3.92 Mass collision stopping power ratios, water to isooctane (—) and TMS (- -), normalized to 1.00 at the electron energy

T  1 MeV. (From Reference [94]. With permission.)

14

Ch-03.fm(part 2) Page 183 Friday, November 10, 2000 11:59 AM

184 Radiation Dosimetry: Instrumentation and Methods

ions have been cleared from the liquid. This then causes

an increased recombination when the pulse repetition rate

increases. The ion transport in the chamber has been stud-

ied by the use of a DC-ampliﬁer with high sensitivity and

a fairly good response time.

Chemical decomposition of the liquid by radiation-

induced bond ﬁssions and an uncontrolled recombination

of the fragments to form other molecules than the original

compound can affect the calibration.

One kg of 224-trimethylpentane contains 5.3 

molecules, and the absorbed energy of 1 J creates 3.2 

affected molecules. From these ﬁgures, the relative

number of affected molecules per Gy of absorbed dose in

the liquid is (3.2  ) (5.3  ), or 6  %.

Most hydrocarbons have their G-values within a factor of

three of that of isooctane. The dependence of G

ﬁ

on the

ﬁeld strength is shown in Figure 3.95.

The absorbed dose to liquid, , at a ﬁeld strength

E is given by

(3.194)

The absorbed dose to water can then be calculated from

(3.195)

where is the absorbed dose to water, is the

absorbed dose to liquid, is the free-ion yield per

absorbed energy at ﬁeld strength E, is the correction

factor for general recombination, is the mass of

active liquid volume, and , is the collected charge in

liquid. The factor f accounts for different cavity-theory

effects in the conversion from dose in the liquid layer of

the chamber to dose in water. In electron beams,

, where is the Spencer-Attix stopping

power ratio of water to liquid with a cut-off energy cor-

responding to the energy of electrons with a range cor-

responding to the average distance across the liquid layer,

i.e., 0.02 g cm

2

. corrects for any electron ﬂuence

change due to the Rexolite-graphite wall and should be

close to 1, as the materials are thin and are very nearly

“water equivalent.”

FIGURE 3.93 Cross-sectional views of the chambers used. (From Reference [94]. With permission.)

6

liq

sat

liq

E()[]

liq

f

liq

E()

sat

liq

Wliq,

 S

Wliq,

Ch-03.fm(part 2) Page 184 Friday, November 10, 2000 11:59 AM

Ionization Chamber Dosimetry 185

In photon beams the factor f is dependent on the

energy and on the physical dimensions of the cavity and

wall. At very low energies, the major contribution to the

energy deposition in the liquid is from electrons released

by photon interactions in the liquid. In this case the factor

f can be approximated by

(3.196)

At high energies, on the other hand, where the liquid

layer and walls are thin compared with the secondary elec-

tron ranges, only a small fraction of the electrons in the

liquid is generated in the liquid or in the wall. In this case

the sensitive volume behaves like a Bragg-Gray cavity:

(3.197)

In the megavoltage range, however, none of these sit-

uations is approximated very accurately. Burlin and Chan

(94a) suggested a weighting factor, d, related to cavity

size for the intermediate situation in which the cavity

behaves neither as a Bragg-Gray cavity nor as a large

cavity:

(3.198)

FIGURE 3.94 Collection efﬁciency with pulse dose at pulse radiation (pulse length ~3



s) and different pulse repetition

frequency and polarization voltages. (From Reference [94]. With permission.)

sat

---







()

liq



---

liq



---

liq

1( d )







()

liq



Ch-03.fm(part 2) Page 185 Friday, November 10, 2000 11:59 AM

186 Radiation Dosimetry: Instrumentation and Methods

Here d is the fraction of the electrons in the liquid gener-

ated by photon interactions outside the liquid.

The ﬁrst term of Equation (3.198) then becomes

(3.199)

where



is the fraction of the outside-cavity electrons

generated in the wall. The fact that the liquid-ionization

chamber in the present work has a front wall consisting

of two materials, graphite and Rexolite, demands a further

split of Expression (3.199):

(3.200)

Here



is the fraction of the wall-generated electrons

originating from the graphite and (1 



) is the fraction

of those generated in the Rexolite. An approximate expres-

sion for the f-factor would thus be [94]

(3.201)

The general collection efﬁciency has been measured

by Johansson and Wickman [95] in liquid isooctane

) and tetramethylsilane (Si(CH

)

) as the sensitive

media in a parallel-plate ionization chamber, with an elec-

trode distance of 1 mm, intended for photon and electron

dosimetry applications. The measurements were made at

potential differences of 50, 100, 200, and 500 V. Measure-

ments were performed for each liquid and electric ﬁeld

strength, with the decay rate of

99m

Tc used as the dose-

rate reference. The maximum dose rate was about 150

mGy min

1

in each experiment.

If the general collection efﬁciency, deﬁned as the ratio

of the ionization current to the saturation current, is

denoted by f, the ionization current–polarizing voltage

relation derived by Mie [96] can be expressed as

(3.202)

where and are the mobilities of the ions;



is the

recombination rate constant; e is the electronic charge; d

is the distance between the collecting electrodes; q is the

amount of charge liberated by the radiation and escaping

initial recombination per unit volume and time in the

medium; U is the polarizing voltage of the ionization cham-

ber;



is the permittivity of the medium in the chamber;

and



is the permittivity of free space. The recombination

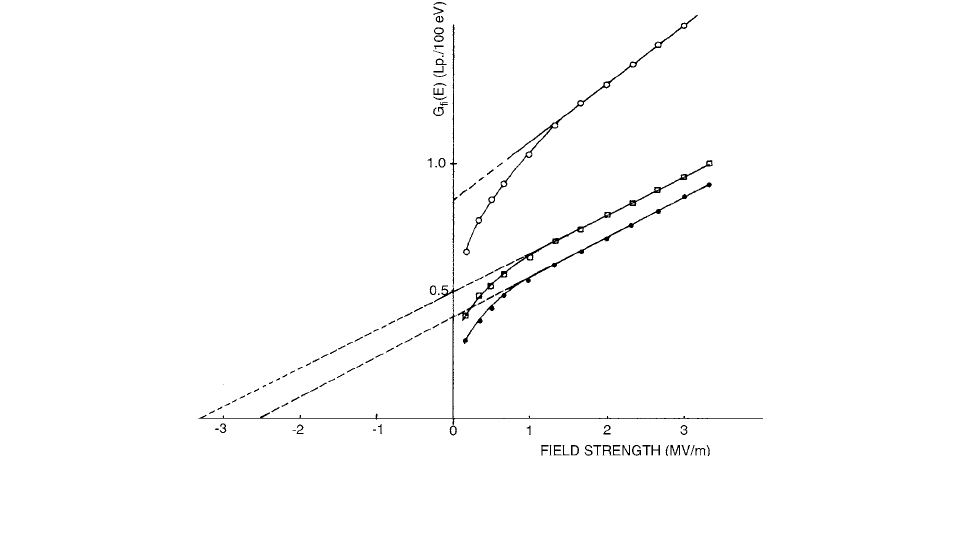
FIGURE 3.95 The amount of free-ion pairs per 100 eV of absorbed energy at different ﬁeld strengths in TMS () and isooctane

(

) irradiated with

Co photons. Isooctane irradiated with 190-kV x-rays (). (From Reference [94]. With permission.)





()

wall

liq



()S

liq

[]







()

liq



()







()

rex

liq

[]

1 a()s

liq

}

---







()

liq



()







()

rex

liq

[]



()s

liq

}





()10[]1 f(){}



------------------------------------------------------------------------------------------





---

--------





-------------





12/





()





-------------------------



Ch-03.fm(part 2) Page 186 Friday, November 10, 2000 11:59 AM

Ionization Chamber Dosimetry 187

rate constant and the ion mobilities are speciﬁc constants

of the sensitive medium.

If the ionization chamber contains air at normal pres-

sure and temperature with a



value of 3.56, the factor

in the square brackets in Equation (3.202) can be ignored

for . The equation for the general collection

efﬁciency is then reduced to

(3.203)

When using an ionization chamber with a dielectric liquid

instead of a gas as the sensitive medium, the ion-produc-

tion density is increased by a factor of about 300. The

ionization current never achieves saturation with respect

to the initial recombination. The characteristic relation

between the ionization current from an irradiated dielec-

tric liquid and the electric ﬁeld strength is shown in Figure

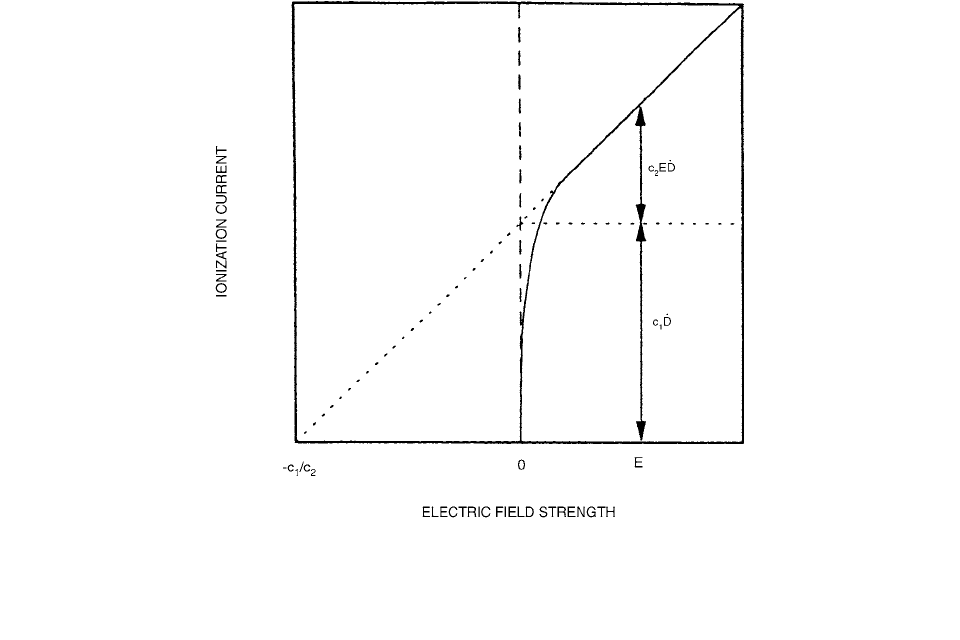
3.96. The ionization current can be described as the sum

of two components. The ﬁrst term consists of the product

, and the second term is the product , where

and are constants characteristic of the liquid, E is the

electric ﬁeld strength, and is the dose rate.

The ions can escape initial recombination by diffusion

or by the combined effect of diffusion and the inﬂuence

of the external electric ﬁeld. Under constant irradiation

conditions and with negligible general recombination, the

ionization current will increase linearly with electric ﬁeld

strength. In Figure 3.96, the constants and represent

the fractions of the ionization current that escape initial

recombination due to diffusion and due to the external

electric ﬁeld, respectively.

The body of the parallel-plate liquid-ionization cham-

ber used by Johansson and Wickman for the experiments

was made of Rexolite

, a styrene copolymer with a density

of 1.05 g cm

1

, and the electrodes were made of pure

graphite. The chamber had cylindrical symmetry without

any guard. It was irradiated towards the plane frontal side

during the experiments. The thickness of the chamber wall

in the irradiation direction was 1 mm, consisting of

0.7 mm Rexolite

and 0.3 mm graphite. The sensitive

volume had a diameter of 3 mm and thickness of 1 mm,

and was ﬁlled through a hole with diameter of 0.3 mm in

the center of the second electrode. The total sensitive

volume of the chamber was 7.07  10

9

. The dielectric

liquids used were isooctane (C

; Merck, isooctane

analysis grade 99.5%) and tetramethylsilane (TMS;

Si(CH

)

; Merck, NMR calibration grade 99.7%). The

liquids were used without any further puriﬁcation.

The relative dose-rate distribution in the liquid layer

at the irradiation geometry was calculated by the function

(3.204)

FIGURE 3.96 The characteristic relation of the ionization current from a dielectric liquid and the electric ﬁeld strength in a liquid-

ionization chamber. The ionization current is the sum of the two components , where is the fraction of ions that

escape initial recombination due to diffusion, is the fraction of ions that escape initial recombination due to the external electric

ﬁeld strength,

E is the electric ﬁeld strength, and is the dose rate. (Fom Reference [95]. With permission.)



0.7 f 1





----------------







y

-------



h()

y

-------



h





d









Ch-03.fm(part 2) Page 187 Friday, November 10, 2000 11:59 AM

188 Radiation Dosimetry: Instrumentation and Methods

where  is the relative photon ﬂuence,



the linear atten-

uation coefﬁcient of the different materials, t is the thick-

ness of the different materials, is the linear attenuation

coefﬁcient, and h is the thickness of the

99m

Tc solution.

For the theoretical general collection efﬁciency, a

mean q value for the sensitive volume was used. This mean

value was calculated as

(3.205)

where is the mean value of the amount of charge liber-

ated per unit volume and time in the liquid by the radiation

and escaping initial recombination, is an experimentally

determined correction factor, is the theoretical ioniza-

tion current in the absence of general recombination, and

is the liquid volume in the ionization chamber. The

general collection efﬁciency derived by Mie, Equation

(3.202), also contains the parameter



. For two ions of

opposite sign at a separation distance R and approaching

each other with a velocity, the recombination rate constant



is given by

(3.206)

where , the Onsager escape distance [56], is the sepa-

ration distance at which the Coulombic potential energy

is equal to the diffusion kinetic energy of the ions and D

is the sum of the diffusion coefﬁcients of the ions. For

dielectric media with a low permittivity, the ratio is

large and the recombination rate constant can be approx-

imated by the equation (Debye 1942)

(3.207)

This approximation of the recombination rate constant

leads to a



value of 1 for dielectric liquids. [95]

m (in Equation 3.202) is a constant purely dependent

on the recombination rate constant and the mobilities of

the ions in the medium. From the experimental results,

the speciﬁc m values for isooctane and tetramethylsilane

were empirically determined by an iterative method, using

the values for the electrode distance and the polarizing

voltages and by assuming . Measured values of

m, k, k

, and



are given in Table 3.32.

From the deﬁnition of the m value (Equation (3.202))

and the approximation of the recombination rate constant

(Equation (3.206)), a relation between the mobilities of

the ions of different signs can be derived as

(3.208)

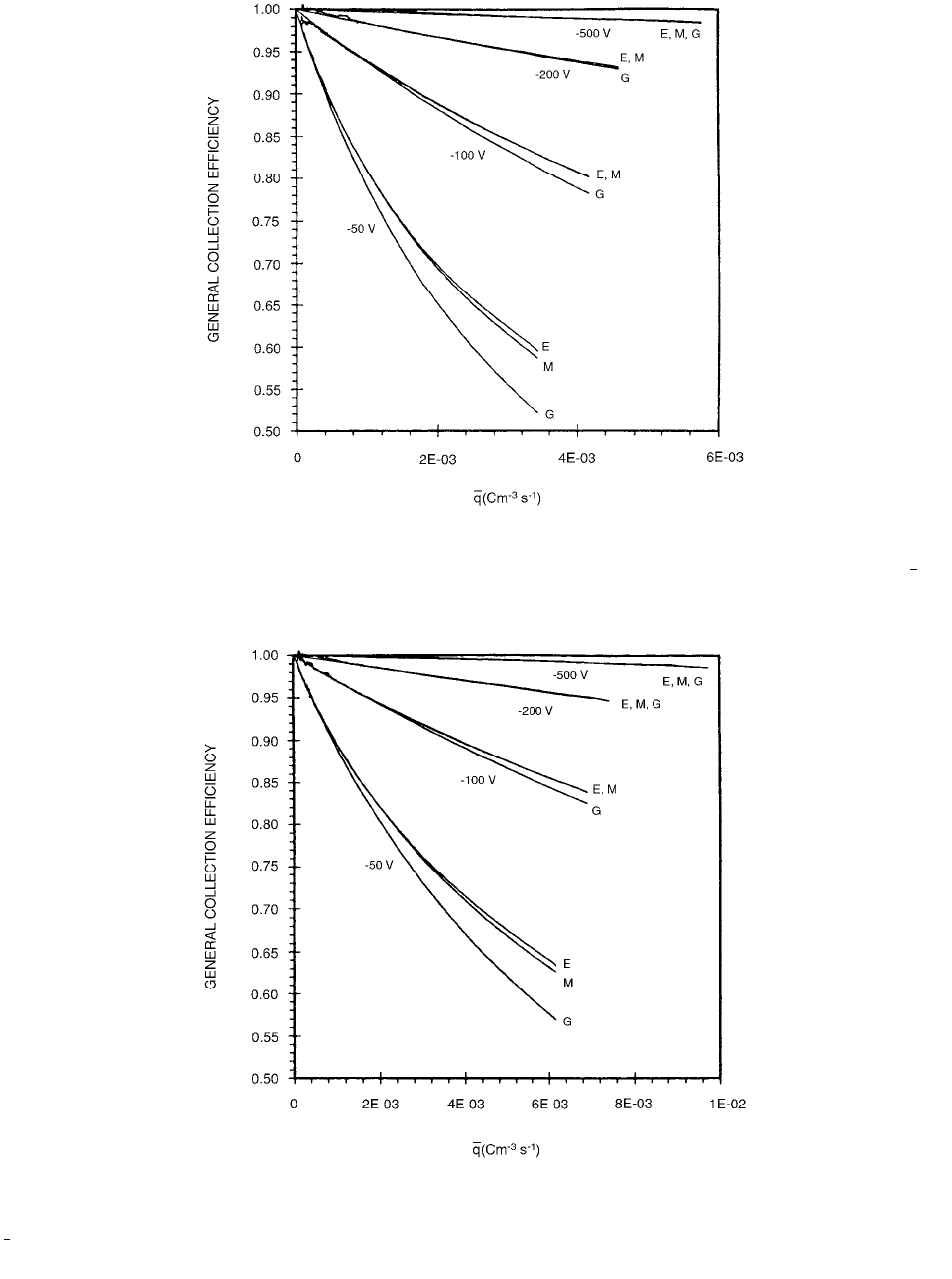
The experimentally determined general collection efﬁ-

ciencies are well described by the theoretical general collec-

tion efﬁciency equation derived by Mie (Figures 3.97 and

3.98). However, probably as a result of the approximate

space charge correction, the theoretical expression shows a

lower general collection efﬁciency for all of the experiments.

The maximum deviation is less than 1% of the saturation

current at a general collection efﬁciency of 60%. For general

collection efﬁciencies down to 90%, the simpliﬁed equation

proposed by Greening [95a] can also be used, showing a

deviation from the experimental general collection efﬁciency

of less than 1% of the saturation current. [95]

Two new liquid-ionization chamber designs, consist-

ing of cylindrical and plane-parallel conﬁgurations, were

presented by Wickman et al. [97] They are designed to be

suitable for high-precision measurements of absorbed

dose to water at dose rates and photon energies typical for

LDR intermediate photon energy brachytherapy sources.

The chambers have a sensitive liquid–layer thickness of

1 mm and sensitive volumes of 7 mm

(plane-parallel) and

20 mm

(cylindrical). The liquids used as sensitive media

in the chambers are either isooctane (C

), tetramethyl-

silane (Si(CH

)

) or mixtures of these two liquids in the

approximate proportions 2 to 1.

TABLE 3.32

Experimentally Determined m Values and the Corresponding Mobilities of

the Ions (k

, k

) and the Recombination Rate Constants (



) for Isooctane

and Tetramethylsilane

m (s

I/2

–1/2

V m

–1/2

) k

–1

) k

–1

)



–1

)

Isooctane 2.0  10

2.9  10

–8

2.9  10

–8

5.4  10

–16

Tetramethylsilane 1.4  10

5.3  10

–8

9.0  10

–8

1.4  10

–15

Source: From Reference [95]. With permission.



theor

liquid

-------------



theor

liquid





()



-------------------------



---------

----







----







expexp

1



R



()



-------------------------



1



1k

()

----------------------------------------



Ch-03.fm(part 2) Page 188 Friday, November 10, 2000 11:59 AM

Ionization Chamber Dosimetry 189

FIGURE 3.97 Experimental (E) and theoretical (Mie (M); Greening (G)) general collection efﬁciency in the parallel-plate liquid-

ionization chamber, ﬁlled with isooctane and operated at the polarizing voltages 50, 100, 200, and 500 V, as a function of , the

mean value of the amount of charge liberated by irradiation and escaping initial recombination. (From Reference [95]. With

permission.)

FIGURE 3.98 Experimental (E) and theoretical (Mie (M); Greening (G)) general collection efﬁciency in the parallel-plate liquid-

ionization chamber, ﬁlled with tetramethylsilane and operated at the polarizing voltages 50, 100, 200, and 500 V, as a function of

the mean value of the amount of charge liberated by irradiation and escaping initial recombination (From Reference [95]. With

permission.

Ch-03.fm(part 2) Page 189 Friday, November 10, 2000 11:59 AM