Seuront L. Fractals and Multifractals in Ecology and Aquatic Science

Подождите немного. Документ загружается.

124 Fractals and Multifractals in Ecology and Aquatic Science

4.2.3 sc a l E d wi n d o w E d va r i a n c E an a l y s i s

4.2.3.1 theory

Scaled windowed variance (SWV) analyses, also referred to as roughness-length analyses, are

applicable only to fBm signals. Those methods are based on dividing a temporal signal x( t ) into

nonoverlapping windows of size t and computing the standard deviation, SD(i), in each of these

windows as:

SD ixtx

() [()]

−













∑

(4.36)

(t)w

(t)

0 400 800 1200

1600 2000

–10

–20

0 400 800 1200

1600 2000

–10

–30

–20

0 400 800

Time

1200

1600 2000

–10

–30

–20

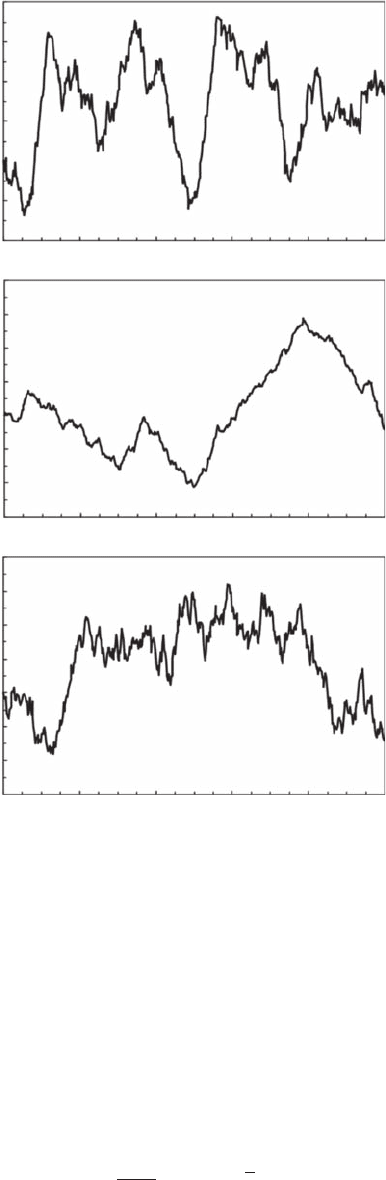
Figure 4.17 Behavior sequence random walks w

( t ) obtained for (A) the New Holland honeyeater and (B)

the red wattlebird, and (C) for the New Holland honeyeater in the presence of red wattlebird.

2782.indb 124 9/11/09 12:09:12 PM

Self-Afﬁne Fractals 125

where

is the average within each interval. The average standard deviation, SD(t), for each win-

dow size t is further expressed as:

SD i

() ()

∑

(4.37)

where n is the number of nonoverlapping windows of size t. This procedure is iterated for all pos-

sible window sizes. For a fractal signal x( t ), SD(t) scale with t as:

SD(t) ∝ t

(4.38)

where H is the Hurst exponent described above. The subsequent fractal dimension D

SWV

is derived

from Equation (4.9) as:

SWV

= 2 − H (4.39)

Initially introduced by Mandelbrot (1985), this method applies no correction to the trends present

within a given window and potentially leads to bias in H estimates (Schmittbuhl et al. 1995; Turcott

and Teich 1995). Trends in the signal seen within a given window can, however, be corrected either

by subtracting a linearly estimated trend (that is, line-detrended scaled windowed variance analy-

sis, ldSWV) or the values of a line bridging the rst and last values of the signal (bridge-detrended

scaled windowed variance analysis [bdSWV]) (Cannon et al. 1997). Note that line detrending and

bridge detrending are conceptually similar to the detrending procedure used in detrended uctua-

tion analysis (Section 4.2.2) and illustrated in Figure 4.12.

4.2.3.2 case study: temporal distribution of the calanoid copepod Temora Longicornis

4.2.3.2.1 The Study Organism

Copepods are the largest and most diversied group of crustaceans, they are the most numerous

metazoans (that is, multicelled organisms) in the aquatic communities, and they are considered

the most plentiful group on Earth, outnumbering even the insects, which include more species but

fewer individuals. As an example, considering a mean density of just one copepod per liter of the

overall volume of the open ocean (that is, 1347 × 10

) would suggest a total world population

in the order of 1.35 × 10

(Boxshall 1998). They include over 14,000 species, 2,300 genera, and 210

families, a surely underestimated number. Their habitat ranges from freshwater to hypersaline con-

ditions, from subterranean caves to water collected in bromeliad leaves or leaf litter on the ground,

from streams, rivers, and lakes to the sediment layer in the open ocean, from the highest mountains

to the deepest ocean trenches, and from the cold polar ice–water interface to the hot active hydro-

thermal vents. Copepods may be free-living, symbiotic, internal, or external parasites on almost

every phylum of animals in water. The usual length of adults is 1 to 2 mm, but adults of some spe-

cies may be as small as 0.2 mm and others may be as large as 10 mm. Copepods are the dominant

forms of the marine plankton that constitute the secondary producers in the marine environments.

As such, they constitute a fundamental step in the oceanic food chain, linking microscopic algal

cells to juvenile shes and whales, and play a pivotal role in the functioning of marine systems and

biogeochemical cycles (Roemich and McGowan 1995).

More specically, the calanoid copepod Temora longicornis (Figure 4.18A) is a very abundant

and nearly ubiquitous species in coastal waters. It is also of great ecological signicance in many

areas as it represents 35 to 70% of the total copepod population in the Southern Bight of the North

Sea (Daan 1989) and in the eastern English Channel (Seuront 2005c); in Long Island Sound (USA),

it is able to remove up to 49% of the daily primary production (Dam and Peterson 1993).

2782.indb 125 9/11/09 12:09:14 PM

126 Fractals and Multifractals in Ecology and Aquatic Science

4.2.3.2.2 Experimental Procedures and Data Analysis

Sampling was conducted in the coastal waters of the eastern English Channel (see Figure 4.8) for 66

hours. Water was continuously sampled from a depth of 10 m through a weighted seawater intake

and directly brought through a 200-mm mesh plankton net using a Flight pump with a 300 l-min

–1

2.4

Time (h)

2.2

2.0

1.8

0.90.5 1.3 1.7 2.1 2.5

2000

1500

1000

500

Abundance (ind m

–3

)

0 20 30 5040 7060

Log τ

Log s (τ)

Figure 4.18 The calanoid copepod Temora longicornis (A), a high-frequency time series of the abundance

of adult male and female T. longicornis sampled in the inshore waters of the eastern English Channel (B), and

the related log-log plot of S(t) vs. t (Equation 4.38) resulting from the scaled windowed variance analysis.

2782.indb 126 9/11/09 12:09:17 PM

Self-Afﬁne Fractals 127

output, connected to a 10-cm-diameter plastic tubing. Every 3 minutes, ltered organisms were

collected and immediately preserved in a 10% formaldehyde solution. This resulted in a total of

1321 samples. Adult males and females from each sample were subsequently enumerated under

a dissecting microscope. The resulting time series (Figure 4.18B) exhibits signicant semidiurnal

tidal cycle (that is, 12.5 hours) but was also characterized by very violent and erratic uctuations.

A previous power spectrum analysis showed a very strong scaling behavior over more than two

decades, with b = 1.42 (Seuront and Lagadeuc 2001), thus suggesting that the temporal distribution

of T. longicornis belongs to the family of fractional Brownian motions. After detrending, the scal-

ing properties of the time series shown in Figure 4.18B were investigated using Equation (4.38) and

the fractal dimension derived from Equation (4.39).

4.2.3.2.3 Results and Discussion

The log-log plot of s(t) versus t shows a unique scaling regime over the whole range of available

scales (Figure 4.18C), with H = 0.37, thus D

SWV

= 1.64. The presence of a unique scaling regime

suggests that the same process, or similar processes, is responsible for the scaling structure of the

abundance of T. longicornis for time scales ranging from 6 minutes to 66 hours. Using Taylor’s

hypothesis of frozen turbulence, the related spatial scales range between 92 m and 120 km. Note

that applying rescaled range (R/S) analysis (see Section 4.2.6) to the same data set returned a very

similar value for the Hurst exponent; that is, H = 0.34, thus D

= 1.66. In contrast, the Hurst expo-

nent derived from power spectrum analysis led to a signicantly lower value for H, H = 0.21 (that

is, D

FFT

= 1.79). This is in agreement with previous studies that showed the potential differences

in the H values returned by R/S analysis (Section 4.2.6), power spectrum analysis (Section 4.2.1),

roughness-length analysis (Section 4.2.3), variogram analysis (Section 4.2.8), and wavelet analysis

(Section 4.2.8); see, for example, Mulligan (2004) for a review. This issue is addressed hereafter in

Section 4.2.10.

4.2.3.2.4 Ecological Interpretation

The fractal dimensions obtained for the temporal distribution of Temora longicornis, bounded

between 1.76 and 1.79, are higher than those expected for passive scalar advected by three-dimen-

sional turbulence (see Section 4.2.1). Those fractal dimensions are also lower than those found

for phytoplankton distribution from in situ time series of in vivo uorescence

([..];D ∈−161167

Seuront et al. 1996a, 1996b, 1999) and from satellite images of sea-surface chlorophyll patterns

([..];D ∈−098169

Denman and Abbott 1988, 1994; Smith et al. 1988). This can be related to the

differences existing between phytoplankton and zooplankton in terms of size and motility, suggest-

ing that copepod behaviors such as diel migration, phototaxis, rheotaxis, social behaviors, and pre-

dation pressure—behaviors relevant at the space and time scales of the present study—induce larger

fractal dimensions (that is, a atter power spectrum and weaker scale dependence) in comparison

with phytoplankton. This is consistent with numerical experiments based on simple predator–prey

formulations considered in a turbulent frame that demonstrated that the interactions between diel

vertical migration and turbulent shear could lead to a atter zooplankton power spectrum (Steele

and Henderson 1992). Similar conclusions were reached by Powell and Okubo (1994) from their

study of interacting plankton populations in two-dimensional turbulence. In addition, the fractal

dimension estimated here from the distribution of T. longicornis is very similar to that estimated for

the oceanic copepod Neocalanus cristatus abundance transects from the subarctic Pacic,

D =180.

(Tsuda 1995), over a similar range of scales (that is, between tens of meters and over 100 kilome-

ters), suggesting that the distribution of zooplankton species could be very similar independent of

their surrounding environments. This is also consistent with the white spectra ( b = 0) found for

total zooplankton density in the St. Laurence estuary (Currie and Roff 2006), leading to fractal

dimension

D → 2.

2782.indb 127 9/11/09 12:09:20 PM

128 Fractals and Multifractals in Ecology and Aquatic Science

4.2.4 si g n a l su m m a T i o n co n v E r s i o n mE T h o d

The signal summation conversion (SSC) method is used to rene the analysis of signals for which

b (power spectrum analysis; see Section 4.2.1 and Figure 4.5) or a (detrended uctuation analysis;

see Section 4.2.2 and Figure 4.13) are near 1. This method is then used to rene fractal analysis

near the fGn/fBm boundary. Taking the cumulative sum of a signal x( t ) converts an fGn to an fBm

signal or an fBm to a summed fBm signal. Corrected scaled windowed variance analyses—that is,

line-detrended scaled windowed variance analysis (ldSWV) or bridge-detrended scaled windowed

variance analysis (bdSWV)—are then applied to the cumulate series to estimate the Hurst exponent

′

H .

When

01<

′

≤H

the signal is an fGn with

HH=

′

In contrast, when

′

H ,

the signal is a frac-

tional Brownian motion with

HH=

′

−1.

4.2.5 di s p E r s i o n an a l y s i s

The dispersion analysis, originally introduced using relative dispersion of spatial data

(Bassingthwaighte 1988), was later extended to the temporal domain (Bassingthwaighte and

Raymond 1995). It is very similar to the original scaled windowed variance method but uses the

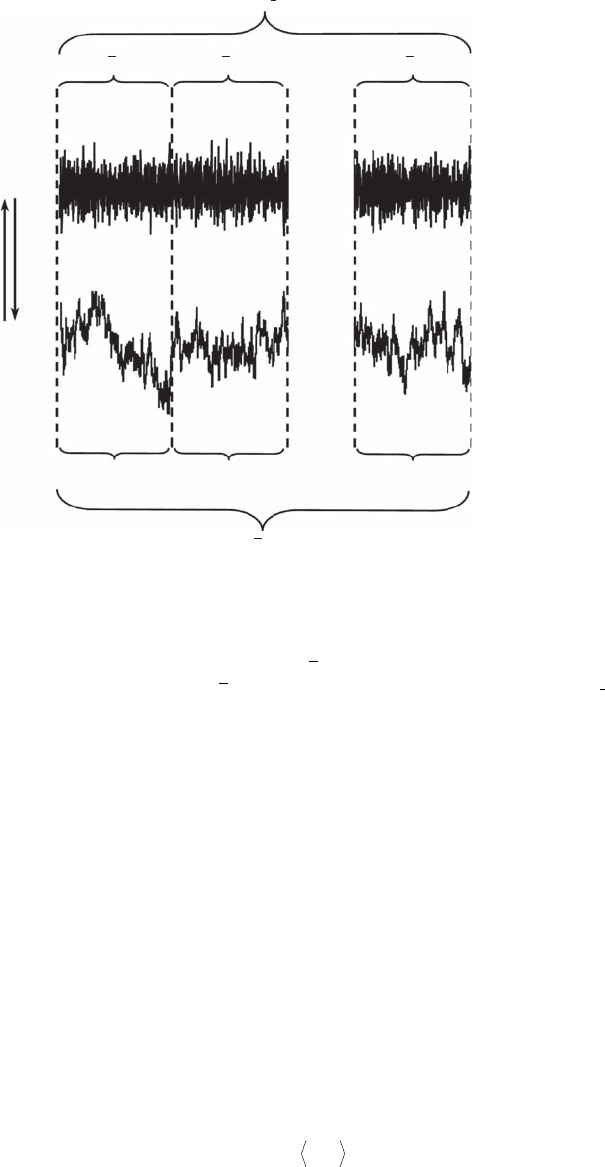
standard deviation of the windows means (Figure 4.19). Specically, a temporal signal x( t ) is divided

into nonoverlapping windows of size t. The mean

of each window is computed as:

xxt

∑

()

(4.40)

The standard deviation of the local means is subsequently estimated as:

() []

−













∑

(4.41)

where n is the number of nonoverlapping windows of size t and

the average of the n

values.

This procedure is iterated for all possible window sizes, and for a fractal signal,

()

is related

to t following the power-law form:

()

ττ



−1

(4.42)

where H is the Hurst exponent. The dispersion analysis is applicable to fGn signals or to differenti-

ated fBm signals.

4.2.6 rE s c a l E d ra n g E an a l y s i s a n d T h E hu r s T di m E n s i o n , D

4.2.6.1 theory

Historically, the rescaled range (R/S) analysis is the rst method developed for assessing H. R/S

analysis was initiated by Hurst (1951) and Hurst et al. (1965) to describe the long-term depen-

dence of water levels in river and reservoirs. Specically, R/S analysis was developed to con-

front the question of how high the Aswan Dam had to be built so that it would contain the

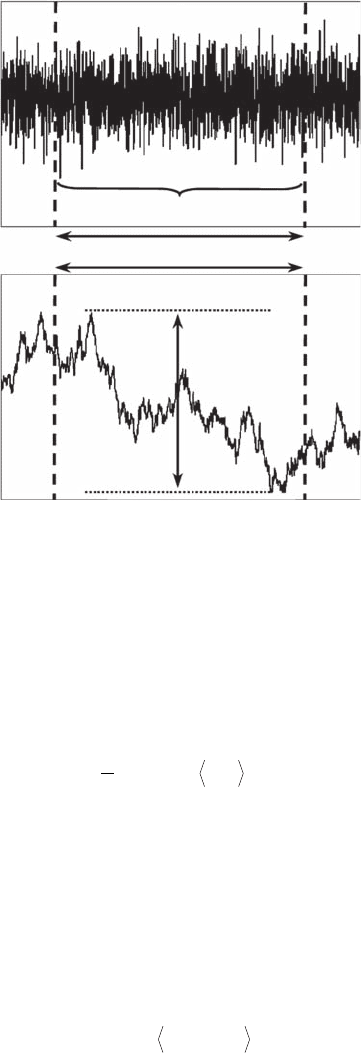
greatly varying levels of the Nile within a given temporal window of size t (Figure 4.20). The

rationale used to develop this method lies behind the three criteria of an ideal reservoir: (1) the

outow is uniform, (2) the water level is the same at the beginning and at the end of the obser-

vation window, and (3) the reservoir never overows. Looking at retrospective records of water

levels, x( t ), Hurst (1951) estimated the time series of the increase in water volume in the dam

as the summed difference of inow and outow, y( t ). The range R of y( t ), R = y

max

( t ) − y

min

( t ),

then denes how high the dam should be built. Finally, dividing the range by the standard devia-

tion of outow uctuations, S(t), Hurst (1951) found that the ratio R/S(t) showed a power-law

2782.indb 128 9/11/09 12:09:27 PM

Self-Afﬁne Fractals 129

relationship with the size of the observation window t as

/(),

ττ



where H is the so-called

Hurst exponent. This relation provides a sensitive method for revealing long-run correlations in

random processes. It comes directly from the above and Figure 4.20 that R/S analysis was theo-

retically developed to work on fGn signals (or differentiated fBm signals) but provides irrelevant

results for fBm signals.

R/S analysis can, however, more generally be applied to any regularly sampled temporal signal.

Consider a discrete time series x( t ) and the interval, or window, of length t. Within this window,

one can dene two quantities: R(t), the range taken by the values of x( t ) in the interval t, and S(t),

the standard deviation of the values of x( t ) within the window. R(t) is measured with respect to a

trend in the window, where the trend is estimated as the line connecting the rst and the last points

within the window. R(t) is thus expressed by the following:

RXtXt

() max(,)min(,)

τττ

=−

≤≤

(4.43)

where X(t, t) is the variable dened as

Xt xt xt

(, )(() () )

=−

. The mean over the time lag t is

substracted to remove a trend in the window when the expectation of x( t ) is not zero. R(t) is then the

Diﬀerenciation

Dispersion Analysis (Disp)

Scaled Windowed Variance Analysis (SWV)

Integration

fBm

fGn

Figure 4.19 Principles of the scaled windowed variance (SWV) and dispersional (Disp) methods. SWV

and Disp both use local statistical measures to derive the Hurst exponent H from fractional Brownian motion

(fBm) and fractional Gaussian noise (fGn) signals, respectively. For a given interval size, these local statistical

measures are the standard deviation SD

for SWV and the mean

for Disp, and the related scale-dependent

measures are the mean of local standard deviation

()x

and the standard deviation of local means

().SD

(See Equations 4.37, 4.38, 4.41, and 4.42.)

2782.indb 129 9/11/09 12:09:34 PM

130 Fractals and Multifractals in Ecology and Aquatic Science

self-adjusted range. S(t) is dened as:

Sxtxt

() () ()

=−

(

)













∑

(4.44)

A reliable measurement of S(t) requires data with a constant sampling interval, because the expected

difference between successive values of x( t ) is a function of the distance separating them. Here, S(t)

is used to standardize the range R(t) to allow comparisons of different data sets; if S(t) is not used,

the range R(t) can be calculated on data sets that have a nonconstant sampling interval. A discus-

sion of the importance of the division by the standard deviation S(t) to obtain a statistical quantity

of extreme robustness can be found in Mandelbrot and Wallis (1969).

The R/S statistics is subsequently dened as follows:

RS RS/()()/ ()

τττ

(4.45)

where R/S(t) is the self-rescaled self-adjusted range. The basis of the method is that, because of self-

afnity, one expects the range taken by the values of x( t ) in a window of length t to be proportional

to the window length to a power equal to the so-called Hurst exponent H following:

R/S(t) = kt

(4.46)

Water Level

fGnfBm

Cumulative Diﬀerence of Inﬂow

and Outﬂow

Figure 4.20 Principle of the rescaled range method. The standard deviation (SD) of a fractional Gaussian

noise (fGn) and the range R of the corresponding fractional Brownian motion (fBm) are estimated over a

window of size t. The Hurst exponent H is subsequently estimated as the slope of the power-law relationship

between the ratio between R and SD and the scale of observation t; see Equation (4.46).

2782.indb 130 9/11/09 12:09:38 PM

Self-Afﬁne Fractals 131

where k is a constant. In particular, Feller (1971) proved that the asymptotic behavior for any inde-

pendent random process with nite variance is given by:

R/S(t) = kt

1/2

(4.47)

and are most of the time referred to as “Brownian” processes.

However, many (if not most) processes in nature are not independent random processes but show

signicant long-term correlations. In this case, the asymptotic scaling law is modied and R/S(t) is

asymptotically given by a power law, t

. The corresponding exponent H is referred to as the Hurst

exponent, and can be conveniently used to characterize the long-range dependence of a random

variable. A persistent behavior (that is, an increase in the value of the random variable is expected

to be followed by another increase) is characterized by 0.5 < H < 1. An antipersistent behavior (that

is, an increase in the value of the random variable is expected to be followed by a decrease) is char-

acterized by 0 < H < 0.5. Many data on natural phenomena that show persistent behavior can be

found in the literature, including uctuations of argon concentration (Bejar et al. 1995), Rhine and

Nile ush (Mandelbrot and Wallis 1969), and genome organization (Almirantis and Provata 1999).

To contrast with the aforementioned Brownian processes, Mandelbrot (1983) introduced the concept

of “fractional Brownian motion” to describe random processes characterized by Hurst exponents

H such as H ≠ 0.5.

In practice, for a given window length t, one subdivides the input series in a number of inter-

vals of length t, measures R(t) and S(t) in each interval, and calculates R/S(t) as the average ratio

RS()/(),

ττ

as in Equation (4.45). This process is iterated for a number of window lengths, and the

logarithms of R/S(t) are plotted vs. the logarithm of t. If the trace is self-afne, this plot follows a

straight line whose slope equals the Hurst exponent H. The fractal dimension of the trace can then

be calculated following:

= 2 − H (4.48)

where H is the Hurst exponent and D

the Hurst fractal dimension.

Finally, although the R/S analysis described above has been illustrated in the framework of a

temporal random process x( t ), one must note that it can be equivalently applied to any random pro-

cess, recorded in time or in space.

4.2.6.2 example: r/s analysis and river Flushing rates

R/S analysis was illustrated using the daily ushing rate of the Seine River (France) from 1993 to

2001 (Figure 4.21A). The resulting log-log plot of R/S(t) vs. t does not follow a straight line over

the whole range of available t, but instead two scaling regions are separated by a clear break for

t = 63 days (Figure 4.21B). The related Hurst exponents are H = 0.67 and H = 0.43 for t < 63 and

t > 63 days, respectively. These exponents reect the presence of both persistence and antipersis-

tence in the Seine water-ow statistics. The corresponding Hurst fractal dimensions are D

= 1.33

and D

= 1.57. This observation clearly diverges from the water-ow statistics of the Rhine (1808–

1966), which is characterized by its Brownian properties (H ≈ 0.55 and D

= 1.45), and also from

the water-level statistics of the Nile (622 to 1469), which show a high degree of persistence, and

H ≈ 0.51 (D

= 1.09) (Mandelbrot and Wallis 1969).

4.2.7 au T o c o r r E l a T i o n an a l y s i s

Autocorrelation (AC) functions are widely used in time-series analysis to describe to what extent the

value of a given event, x( t ), of a time series depends on its past values h lag apart, that is, x(t − h); see,

for example, Legendre and Legendre (2003). Autocorrelation functions have, however, rarely been

directly used to estimate the Hurst exponent H and the related fractal dimension.

2782.indb 131 9/11/09 12:09:40 PM

132 Fractals and Multifractals in Ecology and Aquatic Science

The h-lagged autocorrelation coefcient, r(h), denes how strongly the local value of the signal

x( t ) depends on the one h lag before, that is, x(t − h). The h-lagged autocorrelation coefcient is

bounded between −1 and 1. Specically, a positive correlation indicates that the trends of deviation

of x( t ) and x(t − h) relative to the mean of the signal are in the same direction. In contrast, negative

values of r(h) reveal opposite trends of deviation of x( t ) and x(t − h) relative to the mean of the signal,

that is, anticorrelation. The autocorrelation coefcient, r(h), for lags h (h = 0, 1, . . . , n) is dened as:

xt xxth x

−−

−−−













−

∑

(())(( )) (xxt x

() )−













∑

(4.49)

Using the classical denition of the correlation coefcient (see Feller 1968), van Beek et al. (1989)

derived that in the special case h = 1 the nearest-neighbor correlation between values of an fGn

signal was expressible directly by the correlation coefcient r:

r = 2

− 1 (4.50)

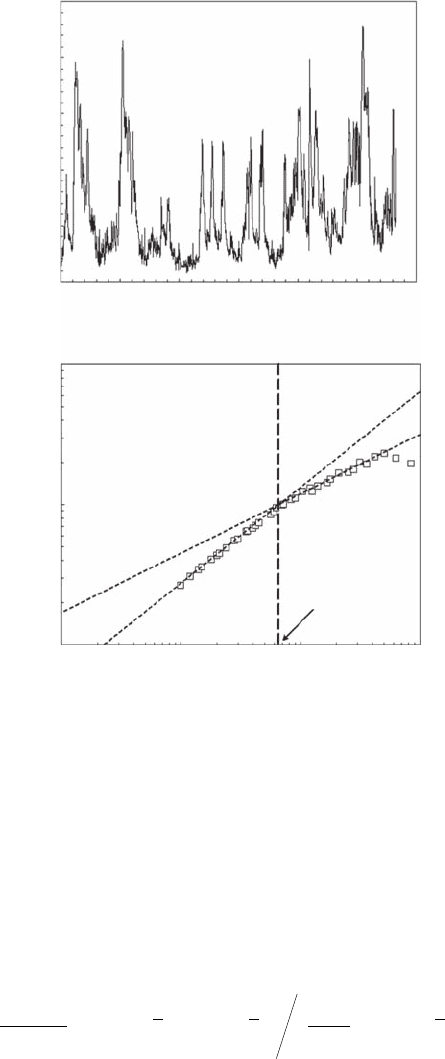
2500

2000

1500

1000

500

0 500

R/S (τ)

Flushing Rate (m

)

100

110 100 1000

1000

Time (days)

H = 0.67, r

= 0.99

H = 0.43,

= 0.99

= 63 days

1500 2000 2500 3000

Figure 4.21 The Hurst dimension, illustrated using a time series of daily ushing rate of the Seine River

(France) from 1993 to 2001 (A) that clearly show two scaling regimes (B), with D

= 1.33 and D

= 1.57 for

scales lower and higher than 63 days, respectively.

2782.indb 132 9/11/09 12:09:43 PM

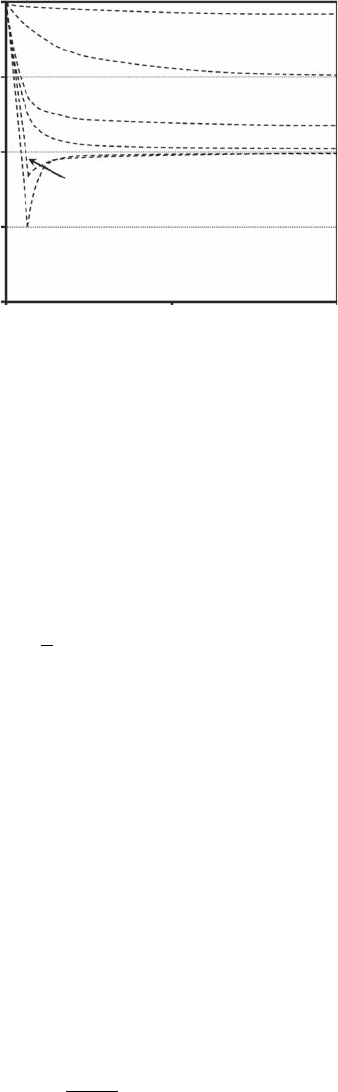
Self-Afﬁne Fractals 133

where the exponent r relates to the Hurst coefcient of the fBm signal whose increments yield

the fGn signal in question as r = 2 H

fGn

− 1. Equation (4.50) has further been extended to correla-

tion between nonadjacent neighbors through the autocorrelation function of an fGn signal with

0 ≤ H ≤ 1 (Bassingthwaighte and Beyer 1991) as:

rh hh

HH H

=+−+−

12 1

22 2

(| |||||)

(4.51)

The closer H is to 1, the slower r(h) decays (Figure 4.22), that is, the longer the memory of the

process. More generally, long-memory correlation (or long-term dependence) is for 0.5 < H < 1,

H = 0.5 when there is no correlation in the fGn signal, and when H = 0.5 the fGn signal shows

anticorrelation. Note that Equation (4.51) is applicable to fGn or differenced fBm signals for both

discrete and continuous values of h (Bassingthwaighte and Beyer 1991).

4.2.8 sE m i v a r i o g r a m an a l y s i s

4.2.8.1 theory

Semivariogram (SV) analysis is based on geostatistics and regionalized variables (RV) theory

(Matheron 1971; Journel and Huijbregts 1978), and is applicable to stationary signals. RVs are con-

tinuous variables whose variations are too complex to be described by traditional mathematical

functions (Phillips 1985). Patterns of variation in RVs can then be expressed by their semivariance

g(h) dened as:

()

[()( )]

()

xt xt h

=−+

∑

(4.52)

where x(t + h) is the value of the dependent variable x( t ) at a point separated from point t by distance,

or lag h, and N(h) is the number of pairs of data points separated by the lag h. The semivariogram is

the plot of g (h) as a function of h. The semivariance has, under certain conditions (see, for example,

1.0

0.5

0.0

–0.5

r (h)

–1.0

H = 0.60

H = 0.80

H = 0.90

H = 0.99

H = 0.40

H = 0.01

Figure 4.22 The autocorrelation function r(h) of simulated fractional Gaussian noise (fGn) signals with

different Hurst exponents H shown as a function of the lag, h. The correlation is trivially maximum at r( 0) = 1,

and the closer H is to 1, the slower n decays (that is, the longer the memory of the process). Long-term depen-

dence (or long-memory correlation) occurs for 0.5 < H < 1, H = 0.5 when there is no correlation, and when

H < 0.5 the fGn signal shows anticorrelation.

2782.indb 133 9/11/09 12:09:49 PM