Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.

MOMENTS
OF INERTIA
OF COMPOSITE
AREAS
191
Second
Method.
The
moment
of inertia
of the
T-section
may
also be
determined
as follows
:
First
find
the
moment of inertia of the
T-section
with
respect
to
the axis
XiXi
by
subtracting
the moments of
inertia
of the
parts
a
4
and
a
5
from
the
moment
of
inertia of
the
rectangular
area ABCD
and
then
find
J
x
for
the
T-section
by
use of the
parallel
axis
theorem.
Thus,
the
moment
of
inertia,
I
x
,
of
the T-section with
respect
to
the
XiX\
axis
is,
and
221.
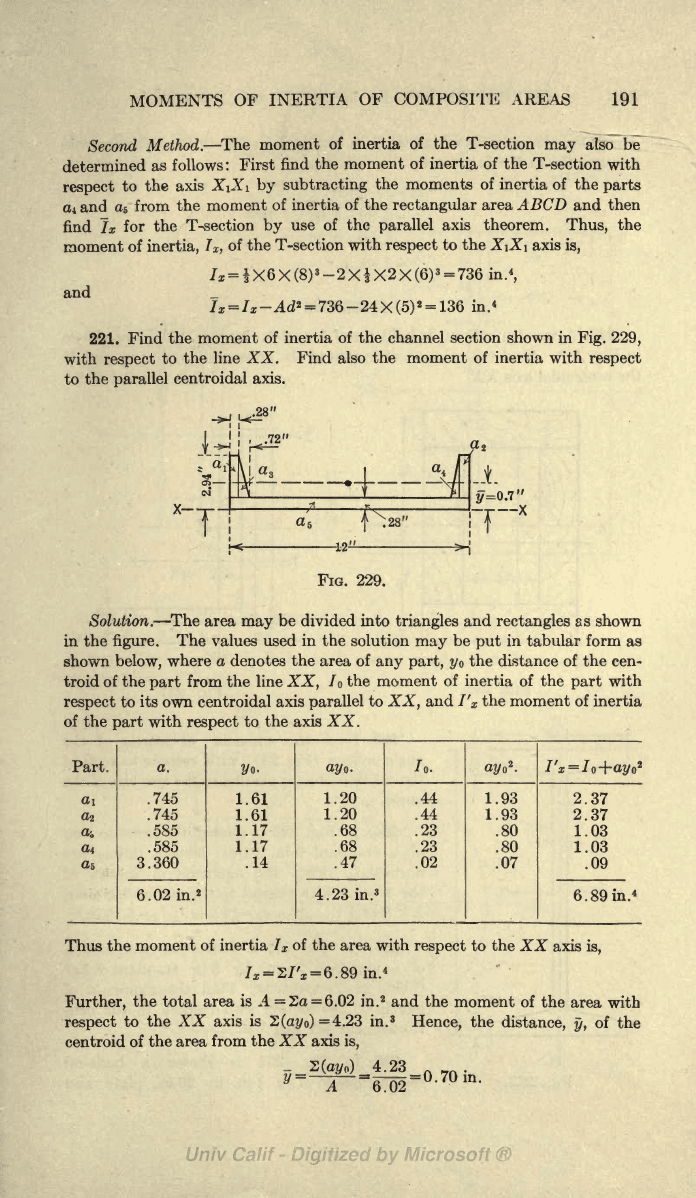
Find
the
moment
of inertia of the channel section shown in
Fig.
229,
with
respect
to
the
line
XX.
Find also
the moment of
inertia with
respect
to
the
parallel
centroidal axis.
V3Mfi
4
J
<N
I Q
Y
X
FIG. 229.
Solution.
The
area
may
be divided
into
triangles
and
rectangles
as
shown
in the
figure.
The values used
in the
solution
may
be
put
in tabular form as
shown
below,
where
a denotes
the
area of
any part, yo
the distance of
the
cen-
troid
of the
part
from the line
XX,
I
the
moment of inertia of the
part
with
respect
to its
own centroidal
axis
parallel
to
XX,
and
I'
x
the
moment of inertia
of the
part
with
respect
to
the
axis XX.
Part.
192
SECOND MOMENT. MOMENT OF
INERTIA
Therefore,
the
moment
of
inertia with
respect
to
a line
through
the
centroid
and
parallel
to XX
is
given by
the
equation,
=
6.89-6.02X(.70)2
=
6.89-2.95
=
3.94
in.
4
PROBLEMS
222.
A
wooden
column
is built
up
of four
2-in.
by
8-in.
planks
as shown
in
Fig.
230.
Find
the moment
of
inertia
of the cross-section with
respect
to
the
centroidal axis XX.
Ans.
7^
=
981
in.
4
x--
-H?
id?
-J
T
x
FIG.
230.
FIG. 231.
223.
Find the moment of
inertia of the
angle
section
(Fig.
231)
with
respect
to
each of
the
centroidal axes
parallel
to
the
two
legs
of the
angle.
224. In
Fig.
232 is
shown
the
cross-sor tion
of a standard
9-in.
21-lb. I-beam
(fillets
are
neglected).
Find the moments of
inertia of
the
section with
respect
to the
centroidal
axes,
XX
and
YY.
Ans.
I
x
=
84.9
in.
4
;
7^
=
5.16
in.
4
225. In
Fig.
233 is
shown
the
cross-section
of
a standard
3$
-in.
by
5-in.
standard Z-bar
(fillets
are
neglected).
Find the moments of
inertia of
the
section with
respect
to the
cen-
troidal
axes
XX
and YY.
T~
|Y
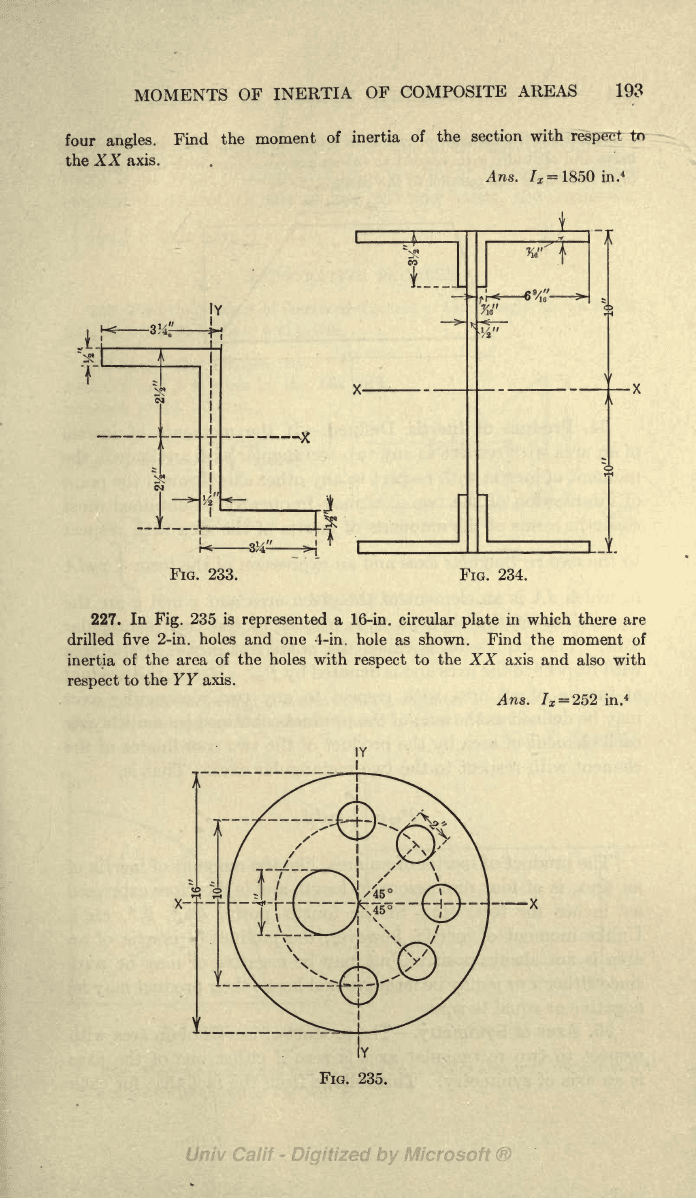
226. In
Fig.
234 is shown
a
built-up
FIG.
232.
section
made
of
a
|-in.
by
20-in.
plate
and
MOMENTS
OF
INERTIA
OF
COMPOSITE
AREAS
193
four
angles.
Find
the
moment
of
inertia
of the
section with
respert
tn
the
XX axis.
Ans.
7^=1850
in.
4
*
*r

194
SECOND
MOMENT. MOMENT OF
INERTIA
228.
Find the
moment of
inertia of a
trapezoid
(Fig.
236),
in
terms of
its
bases
and
altitude,
with
respect
to
(a)
an
axis
coinciding
with its
larger base;
(6)
a centroidal
axis
parallel
to the
bases.
FIG. 236.
94. Product
of
Inertia
Defined.
If
the
moments of inertia
of
an area with
respect
to
any
two
rectangular
axes
are
known,
the
moment
of inertia with
respect
to
any
other
axis
through
the
point
of
intersection
of the
two axes
may
frequently
be
obtained
most
easily
in terms of the moments
of
inertia of the area
with
respect
to the two
rectangular
axes and
an
expression
of
the form
I
xydA
in
which
dA
is an element of the
given
area
and
x and
y
are
the
coordinates
of the
element with
respect
to the two
rectangular
axes.
This
expression
is
called the
product
of
inertia of the area
with
respect
to
the axes and
is
denoted
by
P
xy
.
Hence,
the
product
of
inertia
of
an area with
respect
to
any
two
rectangular
axes
may
be defined
as the sum of the
products
obtained
by
multiplying
each element
of
area
by
the
product
of
the
two coordinates of
the
element
with
respect
to
the
two
rectangular
axes. That
is,
P
xv
=
(xydA.
The
product
of
inertia
of
an
area,
like the
moment
of inertia of
an
area,
is of
four
dimensions
in
length
and is therefore
expressed
as
inches
(or
feet,
etc.)
to the fourth
power (in.
4
,
ft.
4
,
etc.).
Unlike
moment of
inertia,
however,
the
product
of inertia
of
an
area
is not
always
positive,
but
may
be
negative
or
may
be
zero,
since
either
x or
y
may
be
negative
and hence
their
product may
be
negative
or
equal
to
zero.
95.
Axes of
Symmetry.
The
product
of
inertia of
an
area
with
respect
to
two
rectangular
axes is zero if either
one of the axes
is
an
axis of
symmetry.
This
follows
from
the
fact
that for
each

AXES
OF SYMMETRY
195
product
xydA
for
an element
on
one side of the axis
of
symmetry
there
is
an
equal
product
of
opposite sign
for the
corresponding
element
on
the other side of
the
axis
and
hence,
the
expression
xydA equals
zero.
ILLUSTRATIVE PROBLEM
229. Find the
product
of
inertia of the area of
the
triangle,
shown
in
Fig.
237,
with
respect
to the
x-
and
?/-axes.
Solution.
The
relation be-
tween
x and
y
is
given
by
the
equation
y
=
%x.
Hence,
r
rs
en*
=
xydA
=
xydxdy
J
Jo Jo
90
X
FIG.
237.
PROBLEMS
230. Find the
product
of
inertia of the
area of a
rectangle, having
a
base b
and an altitude
h,
with
respect
to
two
adjacent
sides.
.4ns.
P
=
231. Find the
product
of inertia of
the
quadrant
of a circular
area,
shown
in
Fig.
238,
with
respect
to
the
x-
and
t/-axes,
in terms
of its radius
r.
Ans.
P
w
=
|r
4
.
FIG. 238.
FIG.
239.
232. Find the
product
of
inertia of the
rectangular
area with
respect
to the
x-
and
7/-axes
as
shown
in
Fig.
239.

196
SECOND
MOMENT.
MOMENT
OF
INERTIA
i-T
FIG.
240.
233.
Find
the
product
of
inertia
of
the
triangular
area
with
respect
to
the
x-
and
?/-axes
as
shown in
Fig.
240.
Ans.
P
XV
=
192
in.
4
234.
Find
the
product
of
inertia,
with
respect
to
the
coordinate
axes,
of the
area
bounded
by
the
parabola
y
z
ax,
the
line x
=
6,
and
the
x-axis.
Ans.
Pxv
=
r,ab
z
.
96. Parallel Axis
Theorem
for
Products of
Inertia.
When
the
product
of inertia
of an
area is
known
for
any pair
of
rectangular
axes
passing
through
the
centroid
of the
area,
the
product
of
inertia
of
the
area
with
respect
to
any parallel
set
of axes
may
be
determined
without
in-
tegrating. Thus,
in
Fig.
241,
X'X' and
Y'Y'
are
axes
which
pass
through
the
centroid, C,
of the
area;
XX and YY
are
parallel
axes
passing
through
the
point
0.
x
The coordinates
of C
with
respect
to XX and
YY
are
denoted
by
x
and
y.
If
the
product
of inertia of
the area
with
respect
to
XX
and YY
be
denoted
by
P
xy
and the
product
of inertia
with
respect
to
X'X'
and
Y'Y'
be denoted
by
P
iy
,
then,
by
definition,
x'
p
IG 241
=
|
x'y'dA+xy
\dA+y
Cx'dA+x
\y'dA.
Since
each of the
last two
integrals
is
the
first moment
of
the
area with
respect
to a
centroidal
axis,
each
integral
is
equal
to
zero.
The
equation
then
becomes,
P
xv
=P
xv
+Axy.
PARALLEL
AXIS
THEOREM
FOR PRODUCTS OF
INERTIA
197
That
is,
the
product
of
inertia
of any
area with
respect
to
any
pair
of
rectangular
axes
in its
plane
is
equal
to
the
product
of
inertia
of
the
area with
respect
to
a
pair
of parallel
centroidal axes
plus
the
product
of
the
area and the
coordinates
of
the centroid
of
the
area
with
respect
to
the
given
pair of
axes.
ILLUSTRATIVE
PROBLEM
235.
Find the
product
of
inertia of
the
area
shown
in
Fig.
242
with
respect
to the x-
and
z/-axes.
Solution.
The
area
may
be
divided
into
rectangles
a\
and
a
2
as shown.
Using
the
formula
Pxy
=
Pxy-\-A.xy
we
have,
for the
area
a\,
P
xv
=
0+12X1X3
=
36 in.
4
,
and
for
area
a
2
,
Hence,
for
the entire
area,
FIG.
242.
PROBLEMS
236.
Find the
product
of inertia
of the
area
shown in
Fig.
243
with
respect
to
the x-
and
?/-axes.
-6
FIG. 243.
FIG.
244.
237.
Locate
the centroid of
the
angle
section
shown
in
Fig.
244
and
deter-
mine the
product
of
inertia with
respect
to
centroidal axes
parallel
to
the
two
legs
of the
angle.
Ans.
P=
18.3
in.
4

198
SECOND
MOMENT.
MOMENT OF
INERTIA
97.
Moments of
Inertia
with
Respect
to
Inclined
Axes.
The
moments
of inertia of
an area with
respect
to
different
lines
(in
the
plane
of the
area)
which
pass through
a
given
point
are in
general
unequal.
The determination of the
moment of
inertia
of
an
area
by
the
method
of
Y
integration
i s
compara-
tively
simple
for
certain
lines but
rather
difficult
for
other lines.
Equations
(1)
and
(2)
below make
it
possible
to determine
the
moment of
inertia
with
respect
to
any
line
passing
through
a
given point
in
the
area
in
terms
of
the
moments
of
inertia and
product
of
inertia of
the
area
with
respect
to
two
rectangular
axes
passing
through
the
point.
The
equations
may
be
derived as
follows:
The
moment
of
inertia of the
area
shown
in
Fig.
245
with
respect
to OX'
is
expressed
by
the
equation,
l
x
,=
|
y
/2
dA
=
I
(y
cos
6
x sin
6)
2
dA
=
cos
2
e
I
y
2
dA+sin
2
I x
2
dA-2
sin 6
cos 6 I
xydA
FIG.
245
=
I
X
cos
2
d+I
y
sin
2
6 2P
xv
sin d cos
In
a similar manner
the
following
equation
may
be
derived,
Iy
=
I
x
sin
2
cos
2
d
+
2P
xy
sin
6
cos d.
(D
(2)
Thus,
from
these
equations,
the moment
of inertia of an
area
with
respect
to an axis
inclined at an
angle
8 with
one
of a
given pair
of
rectangular
axes
may
be
found,
without
integrating,
if the
moments of inertia
and
the
product
of
inertia
of
the
area
with
respect
to
the
given rectangular
axes are known.
By
adding equations
(1)
and
(2)
the
following important equa-
tion is
obtained,
(3)

PRINCIPAL
AXES 199
That
is,
the
sum
of the
moments
of
inertia of
an area
with
respect
to all
pairs
of
rectangular
axes,
having
a
common
point
of
intersec-
tion,
is constant.
It should
be noted
also that each side
of
equation
(3)
is
equal
to the
polar
moment
of inertia
of
the
area with
respect
to
an axis
passing
through
the
point
(Art. 89).
Axes
for
Which
the
Product
of
Inertia is Zero.
It
may
be
shown
that
through
any point
in
an area there is one
set of
rect-
angular
axes
for
which the
product
of
inertia
is zero.
Thus from
Fig.
245.
PX'V'
=
fx'y'dA
=(%
cos
6+y
sin
0)(y
cos z
sin
6)dA
=
(cos
2
0-sin
2
d^jxydA+cos
sin
0f(y
2
-x
2
)dA
=P
XV
cos
20+%(I
x
-I
y
)
sin
20
Hence
P
x
y
=
when
tan
20
=
=
y
.
iy
LX
98.
Principal
Axes. In
the
analysis
of
many engineering
problems
the moment of inertia
of an area
must be found
with
respect
to a certain axis called a
principal
axis. A
principal
axis
of
inertia
of
an
area,
for a
given point
in the
area,
is
an axis about
which
the
moment of inertia of the
area
is
either
greater
or
less
than
for
any
other axis
passing through
the
given
point.
It
can
be
proved
that
through any
point
in an
area two
rectangular
axes
can be
drawn
for
which
the moments of
inertia of
the area are
greater
and
less, respectively,
than for
any
other
axes
through
the
point.
There
are then two
principal
axes of
inertia of an
area for
any
point
in
the
area.
Further,
it can be
shown
that axes for
which the
product
of inertia is
zero are
principal
axes.
And,
since
the
product
of
inertia of an
area
is
zero for
symmetrical
axes,
it
follows that axes
of
symmetry
are
principal
axes.
The
above
statements
may
be demonstrated as
follows:
The
direction
of the
principal
axes
may
be
determined
from
equation
(1)
of
Art. 97 which
may
be
written
in
the
form,
r l+cos20
,
.
l-cos20
I*
=
I
x ~
\-I
v
~
Pxu
sin 20
200
SECOND
MOMENT.
MOMENT
OF
INERTIA
The
value
of 6 which will
make
/*>
have a
maximum or
a
minimum
value
may
be found
by
equating
the first
derivative of
I&
with
respect
to 6 to
zero.
Thus,
=
=
sin
26(I
y
-I
I
)-2Pxv
cos 20
=
0,
au
whence,
tan
26
=
2P
XV
I
*-I*
From this
equation
two values
of
20
are
obtained
which differ
by
180,
the
corresponding
values
of 6
differing
by
90. For
one
value
of the
value
of
I?
will
be a
maximum and for the
other,
a min-
imum. If P
xy
=
(which
will
always
be
the case if either
the
x- or
?/-axis
is an axis of
symmetry)
the value of
is
zero,
and
hence axes
of
symmetry
are
principal
axes.
ILLUSTRATIVE
PROBLEM
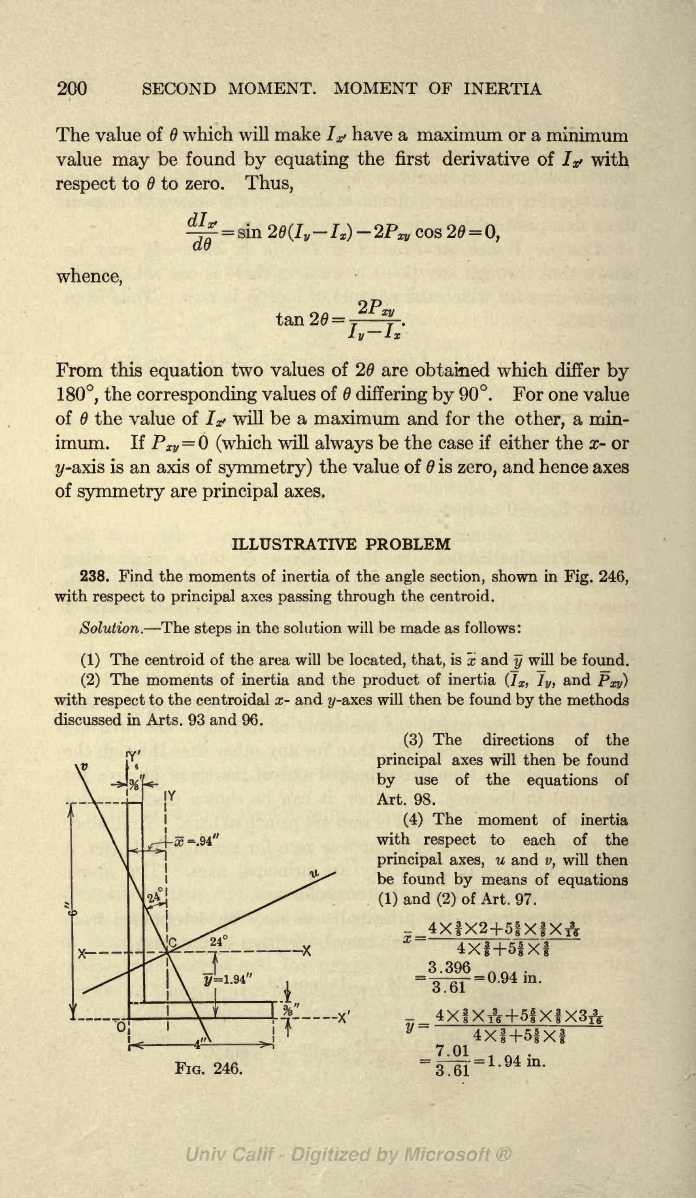
238.
Find the moments of
inertia
of
the
angle
section,
shown
in
Fig.
246,
with
respect
to
principal
axes
passing
through
the
centroid.
Solution.
The
steps
in the solution will be made as
follows:
(1)
The centroid of
the
area will
be
located,
that,
is
x
and
y
will be
found.
(2)
The moments of inertia and
the
product
of
inertia
(Ix
,
Iy,
and
Pxy)
with
respect
to the centroidal
x-
and
?/-axes
will
then be found
by
the
methods
discussed
in
Arts. 93
and
96.
(3)
The
directions
of
the
principal
axes
will
then
be found
by
use of
the
equations
of
Art.
98.
(4)
The
moment of
inertia
with
respect
to
each
of
the
principal
axes,
u
and
v,
will then
be
found
by
means of
equations
(1)
and
(2)
of Art.
97.
: _4X|X2+5|X|XA
4Xf+5fXi
3.396
=
3.61
'0.94 in.
FIG. 246.
7.01
3.61
4Xf+5fXf
=
1.94 in.
