Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


POLAR
MOMENT OF
INERTIA
181
axis
(or
direction of
the
axis)
about which
the moment of
inertia
is
taken
will be denoted
by
subscripts.
Thus,
the
moments of
inertia
of the area
A
(Fig.
216)
with
respect
to the
x-
and
7/-axes
are
expressed
as follows:
and
-f:
x
2
dA.
Units
and
Sign.
Since
the moment
of inertia
of an
area
is the sum
of
a
number
of terms
each
of which is
the
product
of an area and
the
square
of a
distance,
the
F
IG-
216.
moment
of
inertia of an area
is
expressed
as
a
length
to
the
fourth
power.
If,
then,
the inch
(or
foot)
be taken
as the unit
of
length,
the
moment of
inertia
will
be
expressed
as inches
(or
feet)
to the
fourth
power (written
in.
4
or
ft.
4
). Further,
the
sign
of
each of
the
products
x
2
dA is
always positive
since
x
2
is
always positive,
whether x
is
positive
or
negative,
and
dA
is
essentially
positive.
Therefore the
moment
of
inertia,
or second
moment,
of an area
is
always positive.
In
this
respect
it
differs
from
the
first moment
of
an
area,
which
may
be
positive,
negative,
or
zero, depending
on
the
position
of the
moment
axis.
89. Polar
Moment
of Inertia.
The
moment
of
inertia of an
area
with
respect
to a line
perpendicular
to the
plane
of
the
area is called
the
polar
moment
of
iner-
tia
of
the
area
and,
as
noted
in
Art.
88,
will
be
denoted
by
/.
Thus the
polar
moment
of
inertia,
with
respect
to the
z-axis,
of
an
area
in
the
^-plane
(Fig.
217)
may
be
ex-
FIG.
217.
pressed
as
follows:

182
SECOND
MOMENT. MOMENT
OF INERTIA
,.-/**
(x
2
+y
2
)dA
Therefore,
=
Jx
2
dA+
\y
2
dA.
Hence
the
following proposition may
be stated :
The
polar
moment
of
inertia
of
an
area
with
respect
to
any
axis
is
equal
to the sum
of
the
moments
of
inertia
of
the area
with
respect
to
any
two
rectangular
axes
in
the
plane of
the area
which
intersect
on the
given,
polar
axis.
90. Radius
of
Gyration.
Since
the
moment of inertia
of
an
area
I.
Radius
or
Lryration.
Since tne
moment 01 inertia
01
an
f I x
2
dA
or
I r
2
dA, etc.,
)
is four dimensions
of
length,
it
may
be
expressed
as the
product
of the total
area, A,
and
the
square
of a
distance,
k.
Thus,
I
x
=j'y
2
dA=Ak
x
2
,
or
J
z
=
Cr
2
dA=Ak
2
.
The distance
k
is called
the
radius of
gyration
of
the
area
with
respect
to
the
given axis,
the
subscript
denoting
the
axis
with
respect
to which the moment of
inertia is taken.
The
radius of
gyration
of
an area with
respect
to
a
line, then,
may
be defined
as
a distance such
that,
if
the area
were conceived to be
concentrated
at
this distance from the
given line,
the
moment of inertia
would
be the same
as the
moment of inertia of the actual or
distributed
area with
respect
to the same
line.
From
the
equation
I
v
=
I
x
2
dA=Ak
v
2
,
it will be
noted that
k
v
2
,
the
square
of
the radius
of
gyration
with
respect
to
the
?/-axis,
is
the mean of the
squares
of the
distances,
from
the
2/-axis,
of the
equal
elements of area into
which the
given
area
may

PARALLEL
AXIS THEOREM FOR
AREAS
183
be
divided,
and
that
it
is not the
square
of the
mean
of
these dis-
tances.
The
mean
distance
(x)
of the elements
of
area from the
?/-axis
is the
centroidal distance
as
discussed
in the
preceding chap-
ter.
Hence
Ax
2
does
not
represent
the
moment of
inertia of an
area with
respect
to the
?/-axis.
91.
Parallel
Axis
Theorem
for Areas.
If the moment
of
inertia
of an
area with
respect
to a
centroidal axis
in
the
plane
of
the
area
is
known,
the
moment
of inertia with
respect
to
any
parallel
axis
in
the
plane may
be
determined,
without
integrating, by
means
of
a
proposition
which
may
be
established as
follows:
In
Fig.
218
let
Y
Y
be
any
axis
through
the
centroid, C,
of
an
area
and let
Y'Y'
be
any
axis
parallel
to
YY
and
at a distance
d therefrom.
Further,
let the moment of inertia
of
the
area with
respect
to the axis YY
be denoted
by
7
and
the
moment of inertia with
respect
to
Y'Y'
by
/.
By
definition
then,
/=
\(x+d)
2
dA
=
Jx
2
dA+2d
\xdA-\-d
2
CdA.
I=l+Ad
2
since
j
Therefore,
Hence the
following
proposition
may
be stated:
The
moment
of
inertia
of
an area with
respect
to
any
axis in the
plane
of
the area is
equal
to
the
moment
of
inertia
of
the area
with
respect
to a
parallel
centroidal
axis
plus
the
product
of
the
area and
the
square
of
the
distance
between
the two
axes. This
proposition
is
called the
parallel
axis
theorem.
A
corresponding
relation
exists
between the radii
of
gyration
of
the
area with
respect
to
two
parallel
axes,
one of which
passes

184
SECOND
MOMENT.
MOMENT OF
INERTIA
through
the
centroid of
the
area.
For,
by replacing
/
by
Ak
2
and
7
by
Ak
2
the
above
equation
becomes,
=
Ak
2
+Ad
2
.
Whence,
where
k
denotes
the
radius
of
gyration
of
the
area with
respect
to
any
axis
in
the
plane
of
the
area and
Tt
denotes
the
radius of
gyra-
tion of
the area with
respect
to
a
parallel
centroidal axis.
Similarly,
for
polar
moments of
inertia
and
radii
of
gyration,
it
can
be shown
that,
J
=
J+Ad
2
,
and,
where
J
and
k
denote the
polar
moment of
inertia and
radius of
gyration,
respectively,
of the
area with
respect
to
the
centroidal
axis
and
J
and k
denote
the
polar
moment of
inertia and
radius of
gyration,
respectively,
of the
area with
respect
to an
axis
parallel
to the centroidal
axis and at a
distance
d
therefrom.
92. Moments of Inertia
by
Integration.
In
determining
the
moment of inertia of
a
plane
area with
respect
to a
line,
it
is
pos-
sible to select the element of
area
in
various
ways
and to
express
the area of the element in terms of
either cartesian
or
polar
coor-
dinates.
Further,
the
integral
may
be either
a
single
or
double
integral,
depending
on
the
way
in which
the
element of
area is
selected;
the
limits
of
integration
are
determined,
of
course,
from
the
boundary
curve of the area. In
any case,
however,
the
elementary
area must be taken so that
:
(1)
All
points
in the element are
equally
distant
from
the axis
with
respect
to which the moment of
inertia
is to
be
found,
other-
wise the distance x in
the
expression
x
2
dA
would be
indefinite.
Or,
so
that,
(2)
The
moment of inertia of
the
element,
with
respect
to the
axis
about which the moment of inertia of the
whol6 area is
to be
found,
is
known,
the moment of
inertia of
the area then
being
found
by
summing
up
the
moments
of
inertia
of
the
elements.
Or,
so
that,
(3)
The centroid
of the
element
is
known
and also the
moment
of
inertia of the element
with
respect
to an
axis
which
passes

MOMENTS
OF
INERTIA
BY INTEGRATION
185
through
the centroid
of
the
element
and
is
parallel
to the
given
axis;
the
moment of
inertia
of
the
element
may
then be
expressed
by
means
of
the
parallel
axis
theorem.
The
moments
of
inertia
of some
of
the
simple
areas will
now be
found
in the
following
illustrative
problems.
ILLUSTRATIVE
PROBLEMS
208. Determine
the
moment
of
inertia of a
rectangle,
in terms of
its base
b
and
altitude
h,
with
respect
to
(a)
a
centroidal axis
parallel
to the
base;
(6)
an axis
coinciding
with
the
base.
Solution.
(a)
Centroidal
Axis.
The element of area will be selected in
accordance
with
rule
(1) above,
as
indicated
in
Fig.
219. The moment of
inertia
of the
rectangular
area
with
respect
to the
centroidal
axis, then,
is,
<|N
FIG. 219.
FIG.
220.
(6)
Axis
Coinciding
with the
Base.
First
Method. The
element
of
area
will
be
selected
as
indicated
in
Fig.
220.
The
moment of
inertia of the
rect-
angle
with
respect
to
the
base,
then, is,
h
=

186
SECOND
MOMENT.
MOMENT OF
INERTIA
Second
Method.
Since the moment of inertia
of the
rectangle
with
respect
to a centroidal axis
is
-^bh
3
,
the moment of inertia
with
respect
to the
base
may
be found
from
the
parallel
axis theorem
(Art.
91)
.
Thus,
209.
Determine
the
moment of
inertia
of
a
triangle,
in
terms of its
base
b
and
altitude
h,
with
respect
to
(a)
an axis
coinciding
with its
base; (6)
a
centroidal
axis
parallel
to
the
base.
Solution.
(a)
Axis
Coinciding
with
the
Base. The
elementary
area
will
be selected
as
shown
in
Fig.
221. The
moment of
inertia of
the
area
of the
triangle
with
respect
to
the
base, then, is,
Cy
2
dA
=
C
y
2
xdy.
But,
from
similar
triangles,
Hence,
hy
h
'
Therefore,
-y)dy
x
_/__
__
+
j___
FIG.
221.
FIG.
222
(b)
Centroidal
Axis
Parallel to
the Base.
The
centroidal axis
parallel
to
the base
(axis XX)
is shown
in
Fig.
222
(see
Prob.
173).
Using
the
parallel

MOMENTS OF INERTIA BY INTEGRATION
187
axis
thoerem,
the
moment of inertia of the
triangular
area
with
respect
to the
centroidal axis
is,
210. Determine the moment
of inertia of the area of a
circle,
in terms of
its radius
r,
with
respect
to an axis
coinciding
with the
diameter;
(a)
using
cartesian
coordinates;
(ft)
using
polar
coordinates.
Solution.
(a)
Cartesian Coordinates. The
element of
area will
be
selected as shown
in
Fig.
223.
The
moment of
inertia
of the
circular
area
with
respect
to
the
diameter,
then,
is,
FIG. 223.
FIG. 224.
(6)
Polar
Coordinates. The
element of
area
will be
selected
as
shown
in
Fig.
224.
Hence,
C
T
C
2ir
I
(P
sin
0)*
pdpde
Jo Jo

188
SECOND
MOMENT.
MOMENT OF
INERTIA
3
sin
2
6
dpdd
4
suv
4
211.
Determine
the
polar
moment
of inertia
of
the
area of a
circle of
radius
r
with
respect
to
a centroidal
axis
:
(a)
by integration
;
(6)
by
use of
the
theorem
of Art. 89.
Solution.
(a)
By Integration.
By
selecting
the
element
of
area
as
indicated in
Fig. 225,
the
polar
moment of
inertia of
the
circular area
is,
.Jp%U
=
I
p*2irpdp
FIG.
225.
4*
(6) By
Use
of
Theorem
of
Art.
89.
Snce
I
and
I
y
are each
equal
to
\-n-r
4
(Prob.
210),
the
polar
moment of
inertia
of
the
area
of
the
circle
is,
212.
Find
the
moment
of
inertia,
with
respect
to the
re-axis,
of
the
area
bounded
by
the
parabola
y*=2x,
and
the line a:
=
8 in.
Solution.
First
Method.
The element
of area will
be
selected
in
accord-
ance
with
rule
(1)
of Art. 92 as
indicated
in
Fig.
226.
The
moment of
inertia
of
the
given
area with
respect
to the
z-axis,
then,
is,
l
x
=
y*dA
-
x)dy
=
2
-
dy
lOJo
136.5 in.<
MOMENTS
OF INERTIA BY
INTEGRATION
189
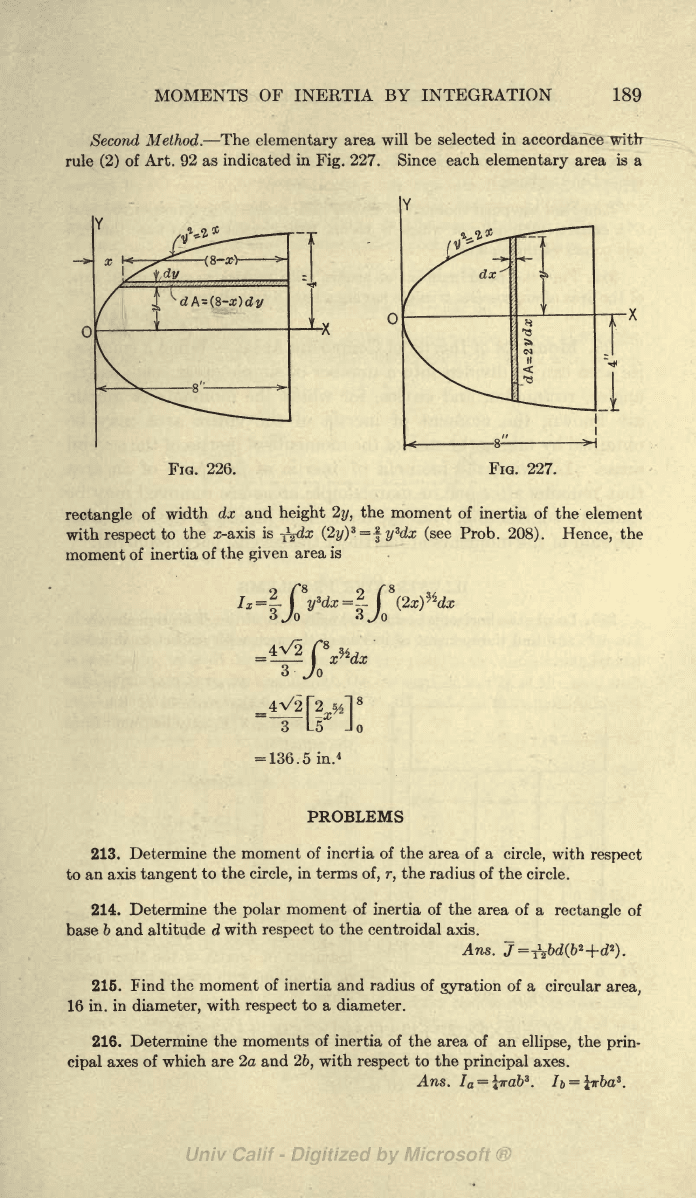
Second
Method.
The
elementary
area
will
be selected
in
accordance
witrr
rule
(2)
of Art.
92
as
indicated
in
Fig.
227. Since
each
elementary
area
is
a
FIG. 226.
FIG.
227.
rectangle
of width
dx and
height
2y,
the
moment of
inertia
of the
element
with
respect
to
the
x-axis
is
-^^dx
(2,y)
3
=^y
3
dx
(see
Prob.
208).
Hence,
the
moment
of
inertia
of the
given
area
is
!*-=
=
4
-^
C>dx
3
Jo
3 L5
Jo
136. 5
in.
4
PROBLEMS
213.
Determine
the moment
of
inertia of the
area
of
a
circle,
with
respect
to
an axis
tangent
to the
circle,
in
terms
of,
r,
the radius of
the
circle.
214.
Determine
the
polar
moment of
inertia of the
area
of
a
rectangle
of
base
b
and
altitude
d
with
respect
to the
centroidal
axis.
Ans.
j=
215.
Find the
moment of inertia and
radius of
gyration
of
a
circular
area,
16
in.
in
diameter,
with
respect
to a
diameter.
216.
Determine
the moments
of
inertia of the
area
of
an
ellipse,
the
prin-
cipal
axes of
which
are
2a
and
26,
with
respect
to the
principal
axes.
Ans.
I
a

190 SECOND
MOMENT.
MOMENT OF INERTIA
217. The base of
a
triangle
is
8
in. and
its
altitude
is 10 in.
Find
the
moment of inertia and radius of
gyration
of the area of
the
triangle
with
respect
to the
base.
218. Find the
polar
moment of inertia and radius of
gyration
of the
area
of
a
square,
each
side of
which
is
15
in.,
with
respect
to
an axis
through
one
corner of
the
square.
219.
Find
the
polar
moment of
inertia,
with
respect
to a
centroidal
axis,
of
the area
of an isosceles
triangle
having
a base
b
and altitude
h.
Ans.
J=
93. Moments
of
Inertia of
Composite
Areas.
When
a
compos-
ite
area
can
be divided into a number of
simple areas,
such as tri-
angles,
rectangles,
and
circles,
for
which the moments of inertia
are
known,
the moment of inertia of
the
entire
area
may
be
obtained
by taking
the sum of the moments of
inertia of the several
areas.
Likewise,
the moment
of
inertia of the
part
of an area
that remains after
one or more
simple
areas are removed
may
be
found
by
subtracting,
from
the moment of inertia of the total
area,
the sum
of the moments of inertia of the
several
parts
removed.
ILLUSTRATIVE
PROBLEMS
220. Locate
the horizontal centroidal
axis, XX,
of
the T-section
shown
in
Fig.
228 and find the
moment
of inertia of the
area
with
respect
to
this cen-
troidal axis.
K
_
(
-
*-\
Solution. First Method.
The dis-
tance,
y,
of
the centroid
of the area
from the axis
XiXi
may
be found
from
the
equation,
IB
X-i
-i
Thus,
FIG. 228.
12+12
=
5
in.
The
moment
of inertia
with
respect
to
the
XX
axis
is the sum
of the
moments
of inertia
of
the
three
parts
a\, 02,
and
as,
with
respect
to that axis.
Thus,
=
4+48
+
.
67+83.
33
=
136 in.
4
