Seely F.B. Analytical Mechanics for Engineers

Подождите немного. Документ загружается.

PRINCIPAL

AXES

201

/*=-AXfX(5f)

+5iXtX(U)

TVX4X(t)

+4XtX(lf)

5.57+3.30+0.02+4.59

13.

in.

0.02+1.19+2.00+1.69

=4.

in.

To determine

xv,

the

value of

P^y

will

first

be found and then the

value of

xy may

found

means of the

formula

Art. 96.

Thus,

1.26+0.56

1.82

in.

Using

the formula

Art. 96 we have

1.82-3.61X(-0.94)X(-1.94)

-4.76 in.

The

directions of

the

principal

axes are

found

from

the

formula of Art.

98,

Thus,

/. 20

48 or

228,

and

24 or

114.

From the

formula of

Art.

97,

the moment of inertia

with

respect

the

axis

making

angle

24 with

(denoted

is,

13.48

cos

24+4.90

sin

-2( -4.76)

sin 24

cos

11.23+0.81+3.53

15.59

in.

Using

114 and

denoting

the

corresponding

axis

by v,

have,

13.48

cos

114

+4.90

sin

114

-2(

-4.76)

sin

114

cos

114

202 SECOND MOMENT.

MOMENT

INERTIA

2.23+4.08-3.53

2.78 in.

Hence,

the

principal

moments

inertia are

15.59 in.

and

2.78

in.

The

corresponding

radii of

gyration

are

2.08 in. and

0.88 in.

PROBLEMS

239. In

the

Z-section

shown

Fig.

247,

Find the

principal

moments of

inertia.

25.32

in.

and

9.11

in.

Ans.

31.2 in.

;

3.20

in.

240. Show

that

the

moment of

inertia of

the

area of

square

is constant

for all axes

the

plane

the

area

which

pass

through

the center.

'30

FIG.

247.

FIG.

248.

241.

Fig.

248

represents

the

cross-section

a standard

10-in. 25-lb.

I-beam.

7a;

122.1 in.

6.89 in.

and A

=7.37 in.

Find the moment

inertia and radius of

gyration

the section with

respect

to a line

making

angle

30 with

the z-axis.

Ans.

93.3

in.

99. Moments of Inertia of Areas

Graphical

and

Approximate

Methods.

It is

sometimes

necessary

to determine

the

moment

of inertia of

an area

having

bounding

curve

which

cannot

defined

mathematical

equation.

The

moment

of inertia

such

an area

may

determined

graphical

method

approximate

method.

MOMENTS

INERTIA

OF AREAS

203

Graphical

Method. Let

the area within

the outer

curve

Fig.

249

be denoted

and

let

the line with

respect

to which the

mo-

ment

of inertia

A is to be

determined

be denoted

XX.

Draw

any line,

such

X'X',

parallel

and

the

distance

h from

XX.

Draw

any

chord,

such

BB,

and

project

the

points B,B

X'X'

thereby

obtaining

the

points

C,C.

Connect

the

points

C,(7

any point,

lines

intersecting

BB at

points

D,D.

Project

the

points D,D,

X'X'

thereby

obtaining

the

points

E,E.

Connect the

points

E,E,

lines

cutting

the

line

BB in

points

F,F.

This

construction

may

repeated

for

number

of chords

parallel

BB,

thus

obtaining

a number

points

similar

F,F.

All

such

points

may

connected

smooth

curve,

the area

within which

will

denoted

A'.

The

moment

of inertia

of A

with

respect

the

axis XX is

given

the

product

the

area of

and h

(A'h

This

fact

may

proved

follows:

Denoting

by x',

and

have,

from

the

similar

triangles

PFF

and

PEE,

and,

from

the similar

triangles

PDD

and

PCC,

U* T*

(1)

(2)

204

SECOND

MOMENT. MOMENT

INERTIA

From

(1)

and

(2),

the

following

equation

obtained,

The moment of inertia of the

area A

with

respect

XX,

then,

given

the

equation,

C C C

dA=

xdy

x"dy

A'.

The area

may

obtained

means

of a

planimeter

approximate

methods.

Approximate

Method.

Although

the

method

described

above is

importance,

the amount of work

involved in

any

numerical

prob-

lem is considerable.

approximate

method will

now be

described

which

can

easily

applied

any

area.

For

convenience,

how-

ever,

simple

area will

be selected so

that

the

approximate

value

of the moment of inertia

determined

this

method

may

compared

with the exact value.

Thus,

let the

moment

of inertia

the

area of a

rectangle,

with

respect

to an axis

coinciding

with

its

base,

be found. The

area

may

divided

into

any

convenient

number of

equal

narrow

strips parallel

the

base,

as shown in

Fig.

250.

(The

narrower

the

strips

the

closely

will

the

result

agree

with

the exact

result.)

Let the

area be

divided

into

ten

such

strips

each

0.2 in.

FIG. 250.

width.

The

moment of

inertia

the

rectangle

equal

to the sum of the moments

inertia of

the

strips.

The

moment

inertia

any

particular strip

with

respect

to the

base

of the

rectangle

where

the distance

the centroid

the

particular

strip

from

the

base.

The first

term is small and

may

omitted

without

serious

error. The

moment

inertia of each

strip

then

approx-

MOMENT

OF INERTIA

MASS

DEFINED

205

imately

equal

to the

product

of the area of

the

strip

and the

square

the

distance

of its centroid from

the base.

Hence,

the

moment

of inertia

of the

rectangle

is,

|X13.3

15.96

in.

According

Art. 92 the exact value

is,

MOMENTS

INERTIA OF BODIES

100. Moment

Inertia

of Mass Defined.

the

analysis

the

motion of a

body,

the

body

frequently

regarded

system

particles

and

expressions

are

frequently

met in the

analysis

which involve the mass of a

particle

and its

distance from

line or

plane.

The

product

the

mass

of a

particle

and

the first

power

of its

distance

from a line or

plane

is called

the first moment

the

particle

as discussed in Art. 79 while

the

product

the

mass of the

particle

and

the

square

its distance

from

the

line

plane

is called the second moment of the

mass of the

particle

or more

frequently

the moment

inertia

the

mass

of the

particle

(or

briefly

the moment of inertia of the

particle)

with

respect

the

line or

plane.

The moment of inertia of a

system

particles

(mass-system

body)

with

respect

a line

plane

is the

sum

of the

moments of inertia of the

particles

with

respect

the

given

line

plane. Thus,

if the masses of

the

particles

of a

system

are denoted

by mi, m^,

m^,

. . . and the

distances

of the

particles

from a

given

line are denoted

by r\,

7-2

. .

the

moment of

inertia of the

system may

expressed

follows

-\-m2T2

-\-m3T3

. .

the

mass

system

constitutes a

continuous

body

the

summation

the

above

equation

may

replaced

definite

integral,

and

the

expression

for

the

moment of inertia of the

body

then

becomes,

dM,

206

SECOND

MOMENT. MOMENT OF

INERTIA

where

represents

an element of

mass of the

body

and r

the

distance of

the

element from the

given

line or

plane.

The

limits

of the

integral must,

course,

so chosen that

each

element of

mass

of the

body

is included in the

integration.

Therefore,

the

moment

of inertia

of a

body

with

respect

to a line

plane

may

defined as the sum

of the

products

obtained

multiplying

each

elementary

mass of

the

body by

the

square

of its

distance

from

the

given

line or

plane.

The moment of

inertia of

the

mass

of a

body

(or

briefly

the

moment

inertia of a

body)

has

physical

significance,

since common

experience

teaches

that if a

body

free to rotate about an

axis,

the farther from the axis

the mate-

rial

placed,

that

is,

the

greater

the

moment of

inertia of

the

body

becomes,

the

greater

is the moment of the

forces

required

give

the

body

prescribed

rotation in a

specified

time.

Thus,

if a rod

is free to rotate

about a

vertical

axis and

carries two

spheres

which

may

moved

along

the

rod, experience

shows

that

the

farther

from the axis the

spheres

are

placed

the

greater

is the

torque required

produce

a definite rotation

in a

given

time.

Units. No

special

one-term name has been

given

the unit

moment of

inertia of

body, hence,

the units of mass arid

the

unit

length

used are

specified.

Thus,

if the

mass

of a

body

expressed

pounds

and the dimensions of the

body

are

expressed

feet,

the moment of inertia of

the

body

expressed

pound-

foot

units

(written

lb.-ft.

).'

engineering problems, however,

the

pound

generally

used as the

unit

force,

which

case mass

equal

to force divided

acceleration

will

be dis-

cussed

Arts. 139

and

141,

and the unit of mass

is,

therefore,

derived

unit

being expressed

terms

the

units of force

(pound),

length

(foot) ,

and time

(second)

Thus,

the dimensional

equation

for

mass

~=~T

~j~-

And since the unit

of moment of

inertia

involves

the units of

mass and of

length

squared,,

then

engineering

problems

the

unit of moment of inertia is

also

derived

unit,

the dimensions of

which

are

j^-XL

that

is,

Ib.-sec

-ft.

The

name

geepound

slug

is sometimes

used

for

the

engineer's

unit

mass,

the first because the

unit

of mass is

the

mass of a

body

that

weighs g (32.2 approximately)

pounds,

and

the second because

mass

is a

measure

the

sluggishness (inertia)

RADIUS

GYRATION

207

the

body.

Thus the

moment

of inertia of

body

is some-

times

expressed

geepound-foot

slug-foot

units

(geepound-

ft.

slug-ft.

important,

however,

keep

in mind

that

the unit of moment

inertia is

derived

unit,

being expressed

in terms of the fundamental

units

force,

length,

and time.

101. Radius of

Gyration.

frequently

convenient to

express

the moment

of inertia of

body

terms

factors,

one of

which

is the mass of the whole

body.

Since

each

term

the

expression

for

moment of inertia as denned

above is one dimension

in mass and

two dimensions

length,

the moment of

inertia of

body

may

expressed

as the

product

of the

mass, M,

the

whole

body

and

the

square

of a

length.

This

length

defined as the

radius

gyration

of the

body

and

will

be denoted

Thus,

the moment

inertia, 7,

of a

body

with

respect

to a

given

line

plane

may

expressed by

the

product

and

hence,

or k

The radius of

gyration

body

with

respect

any axis,

then,

may

regarded

as the distance from the axis

which the mass

may

conceived

to be concentrated and have the

same

moment of

inertia with

respect

the axis

as does the actual

(or distributed)

mass.

Viewed

differently,

the radius of

gyration

body

with

respect

to an axis is a distance

such

that the

square

of this distance is

the

mean of the

squares

the

distances

from the axis of the

(equal)

elements of

mass

into

which the

given body

may

be divided

(not

the

square

of the mean of the

distances)

102. Parallel Axis Theorem for Masses. If

the

moment

inertia

of a

body

with

respect

to an

axis

passing through

its

cen-

troid

(center

gravity

mass-center)

known,

the

moment of

inertia

of the

body

with

respect

any parallel

axis

may

found,

without

integrating, by

use

the

following

proposition.

The moment

inertia

body

with

respect

any

axis

equal

the

moment

inertia

the

body

with

respect

to a

parallel

axis

through

the

mass-center

the

body plus

the

product

the

mass

the

body

and the

square of

the distance

between the two

axes.

This

proposition may

stated

equational

form as

follows:

208

SECOND

MOMENT.

MOMENT

INERTIA

where

denotes the

moment of

inertia

the

body

with

respect

axis

through

the

mass-center and I

denotes the

moment

inertia

with

respect

to a

parallel

axis which

distance d

from

the

axis

through

the

mass-center.

Proof.

Let

Fig.

251

represent

the

cross-section

of a

body

con-

taining

the

mass-center,

Further,

let the

moment of

inertia

of the

body

with

respect

to an

axis

through

and

perpendicular

this section

be denoted

and

let

the

moment of

inertia with

respect

to a

parallel

axis

through

The

expression

for

then,

is,

FIG.

251.

the

point

denoted

C\(x+d)

]dM

C(x

)dM+d

CdM+2d

(xdM.

Therefore,

I=I+Md

since

This theorem is

frequently

called

the

parallel

axis

theorem

for

masses.

similar

relation

may

found between the radii of

gyration

with

respect

to the two axes.

Thus,

if the

radii

gyra-

tion

with

respect

to the two

parallel

axes be

denoted

k and

the

above

equation may

written,

+Md

Hence,

103. Moments

of Inertia with

Respect

Two

Perpendicular

Planes.

The determination

the

moment

of inertia

body

MOMENTS OF INERTIA OF

SIMPLE

SOLIDS

209

with

respect

a line is

frequently simplified

by making

use

of the

following

theorem : The

sum

the

moments

inertia

body

with

respect

to two

perpendicular

planes

equal

the

moment

inertia

the

body

with

respect

the line

intersection

the two

planes.

Proof.

If the moment of

inertia of the

body (Fig.

252)

with

respect

xy-

and

x^-planes

denoted

and

respectively,

the

expressions

for

the moments

inertia

are,

and

dM.

By adding

these two

equations

the

resulting equation

is,

FIG.

252.

104. Moments of

Inertia of

Simple

Solids

Integration.

determining

the

moment

inertia of a

body

with

respect

axis

the method of

integration,

the

mass of the

body may

divided

into elements in

various

ways,

and either

cartesian

polar

coordinates

may

used,

leading

to a

single,

double,

triple

integration, depending

on the

way

the element

chosen.

The

elements of mass

should

always

selected, however,

that,

(1)

All

points

in the element are

equally

distant

from

the

axis

(or

plane)

with

respect

to which

the

moment

inertia

to be

found,

otherwise

the distance

from

the axis

to the

element

would

be indefinite.

Or,

that,

(2)

The moment

of inertia of

the

element with

respect

to the

axis

about which

the

moment of

inertia of the

body

found is

known;

the

moment

inertia of the

body

is then

found

summing up

the

moments

inertia

of the

elements.

Or,

that,

(3)

The mass-center

the

element is

known and

the

moment

of inertia of the element

with

respect

an axis

through

its

mass-

center

and

parallel

to the

given

axis

known,

which

case,

the

moment of inertia of

the

element

may

expressed

use of the

parallel

axis

theorem

(Art.

102).

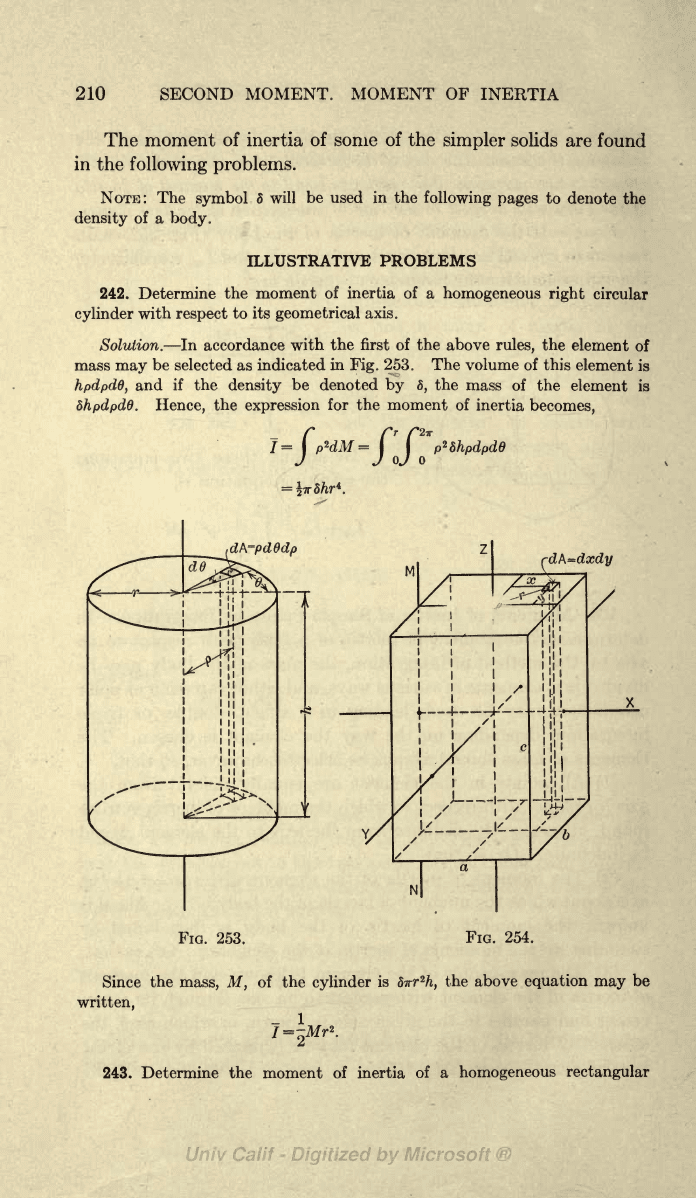
210 SECOND

MOMENT.

MOMENT

INERTIA

The moment

inertia

of some of the

simpler

solids

are

found

the

following problems.

NOTE:

The

symbol

5 will

be used in the

following

pages

denote

the

density

of a

body.

ILLUSTRATIVE

PROBLEMS

242. Determine

the moment of inertia

homogeneous

right

circular

cylinder

with

respect

to its

geometrical

axis.

Solution.

accordance

with

the first of the

above

rules,

the

element

mass

may

be selected

indicated

Fig.

253. The volume of this

element

hpdpdd,

and

if the

density

be denoted

the

mass of

the

element is

Shpdpdd.

Hence,

the

expression

for the moment

inertia

becomes,

=/'

=/X

fr5hr*.

FIG.

253.

FIG.

254.

Since

the

mass,

the

cylinder

dTrr

the

above

equation

may

written,

243. Determine the moment

of inertia

of a

homogeneous

rectangular