Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.

THEOREMS
OF
PAPPUS AND
GULDINUS 171
193.
Find the
distance
from the
larger
base of the centroid of
the
area-of
the
trapezoid
shown
in
Fig.
203.
Ans.
z/
o'~r^
j~-
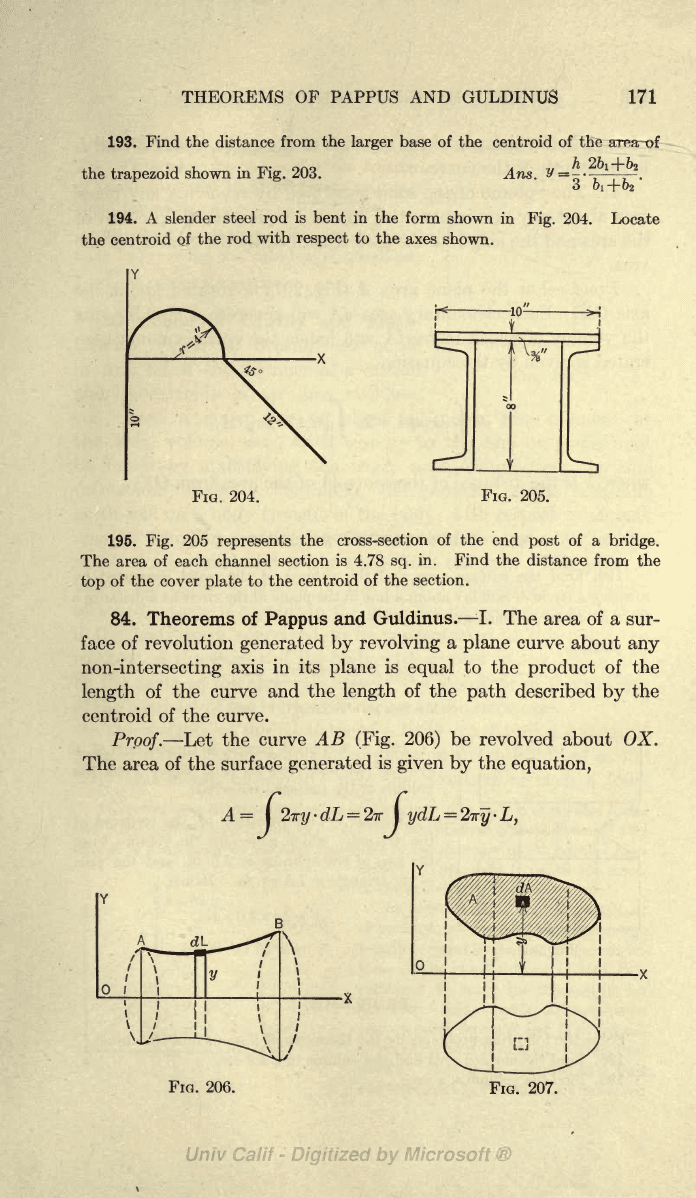
194.
A
slender
steel
rod is bent in the
form
shown in
Fig.
204. Locate
the
centroid
of
the
rod with
respect
to
the
axes
shown.
-10-
FIG. 204.
FIG.
205.
196.
Fig.
205
represents
the cross-section
of
the end
post
of a
bridge.
The
area
of
each channel
section
is
4.78
sq.
in.
Find
the
distance
from the
top
of the
cover
plate
to
the centroid
of
the
section.
84. Theorems
of
Pappus
and
Guldinus.
I.
The area of a
sur-
face of
revolution
generated by
revolving
a
plane
curve
about
any
non-intersecting
axis
in its
plane
is
equal
to the
product
of
the
length
of the
curve
and the
length
of
the
path
described
by
the
centroid of
the curve.
Proof.
Let
the
curve
AB
(Fig.
206)
be
revolved about OX.
The
area
of the
surface
generated
is
given
by
the
equation,
A=
(
2irydL
Y
/

172
FIRST MOMENTS
AND
CENTROIDS
where
y
is the distance of the
centroid
of
the curve
from OX
and
L
is the
length
of the curve.
II. The volume of
the
solid
generated
by
revolving
any plane
area about
any
non-intersecting
line
in its
plane
is the
product
of
the
area and
the
length
of the
path
described
by
the centroid
of
the
area.
Proof.
Let
the
plane
area
A
(Fig.
207)
be rotated about
the
axis
OX. Each
elementary
area
dA
will
generate
a circular
ring
the volume of which
is
2irydA
and hence the entire volume
gen-
erated is
given
by
the
equation,
=
j
27rydA
=
2-jr (
ydA
=
where
V is the
distance
of the centroid
of
the area from OX.
ILLUSTRATIVE
PROBLEMS
196. Find
the
surface
area and the
volume
of the solid
generated
by
rotating
a circle
of
radius
r
about a
line
in
the
plane
of the circle
at a distance a
from
its
center,
a
being greater
than r.
Solution:
A
=
2-71-a
X
2-n-r
=
4ir
2
ar,
FIG.
208.
197. A
V-shaped groove
is
turned out of
a
cylinder
as
indicated
by Fig.
208. Find
the
volume of
the
material
removed.
Solution.
The
distance
of the
centroid of
the
triangle,
which
generates
the
volume,
from
the
axis of
the
cylinder
is 2.5
in. and
the
area
of
the
triangle
is
1.5
sq.
in.
Hence,
K-2rX2.5Xl.fi
=
23.55
cu. in.
PROBLEMS
Solve
the
following problems
by
the theorems
of
Pappus
and
Guldinus
:
198.
Find
the
surface area and the
volume
of a
sphere.
199.
Find the
volume
of a
cone.

CENTER
OF GRAVITY
AND MASS-CENTER
173
200.
Find
the
^-coordinate
of
the
centroid
of
the
trapezoid
shown
in
209.
Determine
the volume
of
the frustum
of a cone
generated
by
revolving
the
trapezoid
about
the
z-axis.
201. Find the
volume
of
the
ellipsoid
gene-
rated
by
revolving
the
right
half of
the
ellipse,
r^
o
2
=
li
about
the w-axis.
FIG.
209.
85.
Center
of
Gravity
and
Mass-
Center.
Center
of
Gravity.
As
noted
in Art.
80,
if the distance
of a certain
point
(centroid)
in an
area, volume,
etc.,
from a
given
line or
plane
is
known,
the moment
of
the
area,
volume,
etc.,
with
respect
to
the
line or
plane
may
be
found
by
multiplying
the whole
area, volume,
etc.,
by
this
(centroidal)
distance.
Similarly,
the
moment of the resultant
earth-pull
on a
body
(weight
of
the
body)
with
respect
to an axis
may
be
found
by
multiplying
the
weight
of the
body
by
the dis-
tance
of a
certain
point
in the
body
from the
axis. This
point
is
called the center
of
gravity
of the
body.
The center of
gravity
of a
body,
then,
is a
point
in the
body
(or
its
extension)
such that
if the
body
were conceived
to
be
concentrated
at this
point
the
moment
of the
weight
of the
body
with
respect
to
any
axis
would
be
the
same as
the
algebraic
sum of
the moments
of
the
weights
of the
particles
of the
body
with
respect
to
the same axis.
The
weights
of
the
particles
of
a
body
constitute a
system
of
parallel
forces
having points
of
application
which
are fixed in
the
body
and
it can
be shown
1
that
the resultant of such
a force
1
CENTER
OF A SYSTEM
OF PARALLEL
FORCES.
//
a
system of
parallel forces
have
fixed points
of application
in a
rigid
body
the resultant
of
the
system
will
pass
through
a
fixed point
in
the
body regardless
of
the direction
of
the
parallel force
system.
This
point
is called
the center
of the
system
of
forces.
In
order to
show that the
resultant
of such
a
force
system
does
pass through
a definite
point
in
the
body
for all direc-
tions of
the
parallel
force
system,
it
is
sufficient to
prove
the
proposition
for
two such
forces.
In
Fig.
210
are shown
two
parallel
forces P
and
Q
which
act
at
points
A and B
of
a
rigid
body
(not
shown).
Let it
be
assumed first
that
the
forces act
in
the
direction indicated
P
>
174
FIRST MOMENTS
AND
CENTROIDS
system passes
through
a definite
point
in the
body regardless
of
the
way
in which
the
body may
be turned. Hence the
center of
gravity
of a
body
is a
definite
point
in the
body through
which the
weight
of the
body (earth-pull
on
the
body)
acts
regardless
of the
position
of the
body.
If,
then,
W
denotes the
weight
of
a
body
and
w
or dW
denotes
the
weight
of
any particle
of the
body
the coordinates of which
are
x, y,
and
z,
the coordinates
x,
y,
and
z
of the
center
of
gravity
of
the
body may
be
found from the
equations
:
Wx=2wx=
xdW,
=
j
Wz=2wz= I
zdW,
by
the
full
lines.
If
the
point
in
which
the
resultant of
P
and
Q
intersects the
line AB
be denoted
by
H
it can
be
shown
(Art. 24)
that
--
Let
it be
assumed
next that
the
action lines of
P
and
Q
are rotated
through
an
angle
90
6
as
indicated
by
the dotted
lines,
and that
the
action line
of
the
resultant of the two
forces in
this
position
intersects
the
line AB
in the
point
H'.
Let
BJ and
H'l
be drawn
perpendicular
to
the
action
lines
of
P
and
Q
and let the
point
where
the resultant
of
P
and
Q
intersects BJ be
denoted
by
K.
It
can
be
shown as
before
that,
JK
=
IH'
=
^^BJ
=
-^AB
sin
0.
Hence
in
the
triangle AIH',
sin
6
Since
AH=AH' it is evident that
H' coincides with
H,
and hence
the resultant
of P and
Q
passes through
a
definite
point
H
on
the line
AB
regardless
of the
direction of
the
two
parallel
forces.
It is obvious that
the
proof may
be extended to
any
number
of
forces,
for,
the resultant
of P and
Q, just found, may
be combined
with
a third
force, S,
which has
a fixed
point
of
application
C
(say)
in the
body,
and in the same
manner
it can be shown that the resultant of
these
two
forces
will
pass
through
a fixed
point
on
the line
HC and so on.
So far as
the relations
of the
forces to
the
body
are concerned
it is
obviously
immaterial whether
the
body
remains
fixed
and
the forces be rotated relative
to the
body
as
discussed
above,
or whether
the forces remain
fixed in
direction
and
the
body
be rotated. Hence the center of a
system
of
parallel
forces
which
have fixed directions and
which
have
fixed
points
of
application
in
a
rigid
body may
also
be defined
as
the
point
in
the
body through
which
the
resultant
of the forces will
pass
regardless
of the
way
in
which
the
body
is turned.

CENTER
OF GRAVITY
AND
MASS-CENTER
175
Mass-center.
As defined
in Art.
82,
the
centroid
of
the
mass
of a
body
is the
point
in the
body
(or
its
extension)
such
that
if
the
mass
were
conceived
to
be
concentrated at
this
point,
its
moment
with
respect
to
any
line or
plane
would
be
equal
to the
algebraic
sum
of the
moments
of the
masses of the
particles
of the
body
with
respect
to
the line or
plane.
In
discussions
(particularly
in
Kinetics)
in
which
the relation
between
mass
and
weight
are
involved,
the
term
mass-center
(or
center
of
mass)
is
frequently
used
instead of
centroid
of
mass.
It will
be shown
in
Part
III
(Kinetics)
that the
mass
of a
body
/
W\
is
proportional
to its
weight
(
M
=
) .
It can
be
shown, therefore,
\
y
/
that
the center
of mass of
a
body may,
for
all
practical
purposes,
be
regarded
as the same
point
as the
center of
gravity
of
the
body.
Thus the
^-coordinate
of the
mass-center
is
CxdM
CxgdW
~~M~
gW
'
Now,
if
g
be
regarded
as
constant
(and
for all
practical
purposes
it
may
be so
regarded),
the last term
in the
above
equation
becomes
CxdW
center of
gravity
of
the
body.
~
,
and this is the
expression
for the
x-coordinate of the
ILLUSTRATIVE
PROBLEM
202.
Gravel
is
piled
on
a floor so that the
pressure
on the
beams which
sup-
port
the floor increases
in
the direction
of
the
beams as
shown
in
Fig.
211.
The
intensity
of
pressure
varies from
zero at
the left end of
the
beam
to
a
maximum
ofp
w
=
800 Ib.
per
foot
at
the
right
end. What
is
the
weight
of
the
gravel
and how far
from
the
left
end
of
the
beam
does
the resultant
weight
act?
Solution. Let the
intensity
of
pres- FIG.
211.
sure
at
any
distance x from the left
end
of the
beam be
p
x
Ib.
per
foot.
This
pressure
may
be
assumed to be
constant

176 FIRST MOMENTS
AND
CENTROIDS
over a
length
dx
and
hence the
weight
of
gravel
over this
length
is dW
=
But
p
x
=Y'pm-
Therefore
the
total
pressure
on the
beam
(weight
of
gravel) is,
W-fpdx
=
r^
Jo
I
Hence,
the
total
pressure
of
the
gravel
(its
weight)
is the
same in
magnitude
as
it
would
be if the
gravel
were
spread
uniformly
to a
depth
equal
to
one-half
that
of the maximum
depth.
The
total
weight, however,
would then
act at
the center of
the
beam,
whereas,
according
to the
above distribution
it must
act
at a
distance
x
such
that,
-/
Wx=
dWx,
Therefore,
This
result
might
have been
obtained,
without
taking
the
above
detailed
steps,
from the
fact
that
the
gravel
may
be conceived
to be
concentrated
in
a
plane
(of
triangular shape),
the
position
of
the center of
gravity
of
the
gravel
then
being
the
same as
the centroid of
the
triangular
area
(Prob. 173).
PROBLEMS
203. Two
homogeneous
spheres
A
and
B,
connected
by
a
rod,
are
mounted
on
a
vertical axis as
shown
in
Fig.
212.
The
weights
of
the
spheres
are
20
lb. and
60
lb.,
respectively,
and the
weight
of the
rod
is 10
lb.
How far
^
rom
tae
ax
*s *s
tne center
f
gravity
of the
three
bodies?
Ans,
7.94
in.
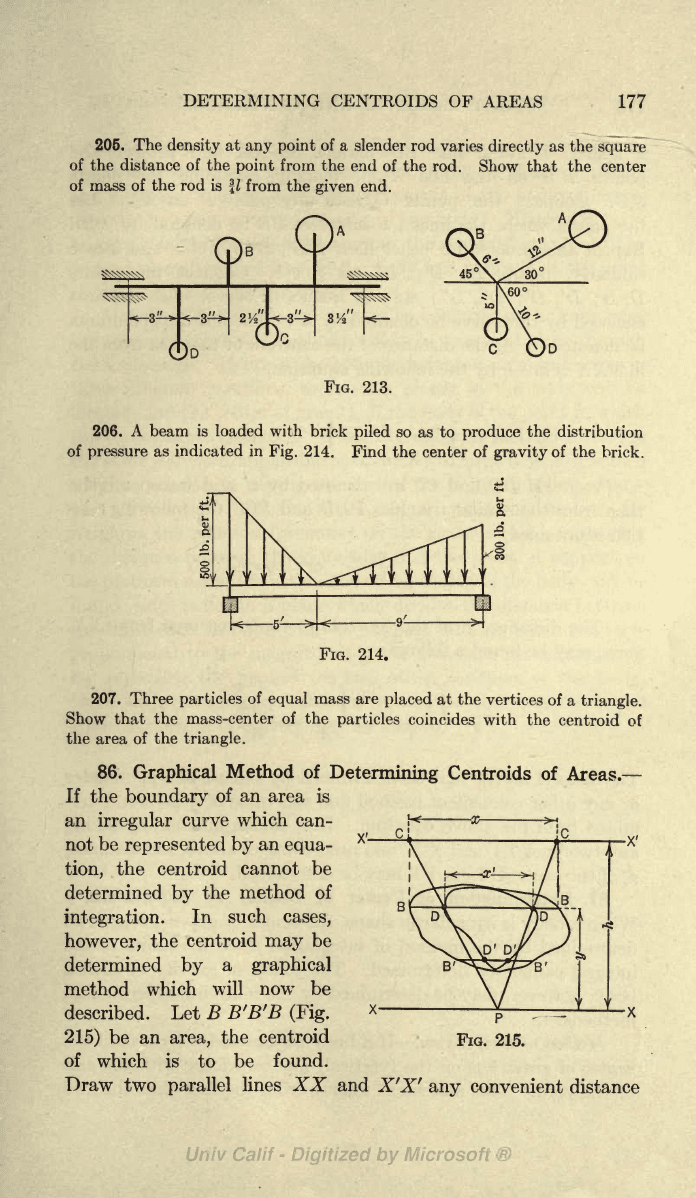
204. Four
bodies
A,
B,
C,
and
D
FIG. 212.
are carri e(j
by
a
rotating
shaft as
shown
in
Fig.
213.
The
weights
of
the
bodies are
20,
15, 10,
and 8
lb.,
respectively,
and
the
distances
of
their
centers of
gravity
from the
axis
of
the
shaft are
12,
6,
5,
and
10
in.,
respectively.
Find the center
of
gravity
of the
four
bodies when
in the
positions
shown.
DETERMINING
CENTROIDS OF
AREAS
177
205. The
density
at
any point
of a slender
rod
varies
directly
as the
square
of
the
distance
of
the
point
from the
end
of the
rod.
Show
that the center
of
mass of
the rod is
f
Z
from
the
given
end.
45
I
FIG.
213.
206.
A
beam is loaded with
brick
piled
so
as
to
produce
the
distribution
of
pressure
as indicated
in
Fig.
214. Find the center of
gravity
of the
brick.
\
m
FIG.
214.
207.
Three
particles
of
equal
mass
are
placed
at the
vertices
of
a
triangle.
Show that
the
mass-center
of the
particles
coincides
with the
centroid
of
the
area of
the
triangle.
86.
Graphical
Method
of
Determining
Centroids
of
Areas.
If the
boundary
of
an
area
is
an
irregular
curve which
can-
not
be
represented
by
an
equa-
tion,
the
centroid
cannot
be
determined
by
the
method
of
integration.
In
such
cases,
however,
the
centroid
may
be
determined
by
a
graphical
method
which
will
now be
described.
Let
B B'B'B
(Fig.
215)
be an
area,
the
centroid
of
which is to
be found.
Draw two
parallel
lines XX
and
X'X'
any
convenient distance

178
FIRST
MOMENTS
AND
CENTROIDS
h
apart.
Draw a line BB
parallel
to XX
and
project
the
points B,B
on the line
X'X',
thereby
obtaining
the
points
C,C.
Connect the
points C,C
to
any point
P
on
XX.
Let
the
points
where the lines CP
intersect
BB
be
denoted
by
D,D.
Repeat
this
process
for
other lines
B'B',
B"B",
etc.,
and
locate
similarly, points D',
D'; D",
D";
etc.
Connect
the
points
D, D;
D',
D';
D",
D"}
etc.,
by
a
smooth
curve.
Let
the
area
enclosed
by
this
curve be
denoted
by
A
1
'.
Then,
if
the
given
area
be denoted
by A,
the
distance of
the
centroid
of the
area
from
the
line
XX is
given
by
the
following
equation,
Proof.
If DD
and CC are
denoted
by
x
f
and x
respectively,
then from the similar
triangles
PDD
and
PCC
the
following
rela-
tion is
obtained,
x x' .
T
=
or
xy
=
hx
.
h
y
The
distance,
y,
of the
centroid of
the
given
area from
XX,
then,
may
be found a follows:
ly-xdy
hlx'dy
A
,
T.-J
j_
-I.A-
y ~i
f*
~i~*
The areas
A and
A'
maybe
determined
by
the
use
of a
planimeter
or
any
other convenient method and
the
value of
y
is
then
deter-
mined from the
above
equation.
In
a
similar
manner,
by
taking
any
two
lines
YY
and
Y'Y'
and
proceeding
as
above,
the
distance,
x,
of the
centroid from
YY
may
be
determined.
87.
Determination of Center
of
Gravity by
Experiment.
When
a
body
is
irregular
in
shape,
the
center of
gravity
cannot
be
determined
by
the method
of
integration
since the
limits
of the
integral
cannot be
determined. The
center
of
gravity
of
such
a
body,
however, may
be
determined
by
the
following experimental
methods.
Method
of
Suspension.
If
a
body
be
suspended
by
a
cord the
center of
gravity
is on the
(vertical)
line
coinciding
with
the axis
of the
cord.
This
statement follows
from the fact
that
the
two

DETERMINING
CENTER
OF GRAVITY
BY
EXPERIMENT
179
forces
which
hold
the
body
in
equilibrium (the
upward
tension in
the
cord
and the
downward
earth-pull)
must
be
equal,
opposite,
and
collinear,
and
the
earth-pull
or
weight
of the
body
of
course
acts
through
the
center of
gravity
of the
body.
Hence if
a
body
be
suspended
from
each of
two
points,
the center of
gravity
will
be
located
in each
of
two lines in the
body
and
hence is at
the
point
of intersection
of the
two lines.
Method
of
Balancing.
If
a
body
be balanced
on a
knife-edge
the
center of
gravity
of the
body
will
be in
a vertical
plane
through
the
knife-edge.
Hence if
the
body
be balanced
on a
knife-edge
in
three
different
positions,
three such
planes
in
the
body
will be
located,
and the
center of
gravity
of the
body
is
the
point
in
which
the
three
planes
intersect.
A
slightly
different method
involving
the same
principle,
applicable particularly
to
large
bodies of known
weights,
consists
in
resting
one
end
of the
body
on a line
of
sup-
port
(knife-edge)
and
the other
end on
platform
scales.
By
weighing
the
reaction
(pressure)
on the scales
and
by measuring
the
distance between
the
knife-edge
and the
point
of
support
on
the
platform
scales the action line
of
the
weight
of the
body
may
be
found,
since it
lies in a
plane
which divides the distance
between
the
knife-edge
and the
point
of
support
into
segments inversely
proportional
to the
magnitudes
of the
reactions at the
supports.
By
repeating
the
process
for two
other
positions
of the
body,
three
such
planes
may
be found as in
the above
method,
and
hence the
center of
gravity
may
be located.

CHAPTER VI
SECOND
MOMENT.
MOMENT OF
INERTIA
1.
MOMENTS OF
INERTIA OF
AREAS
88. Moment
of
Inertia
of an
Area Defined.
In
the
analysis
of
many engineering
problems as,
for
example,
in
determining
the
stresses
in
a
beam or
column, expressions
of the form I x
2
dA are
frequently
met,
in
which
dA
represents
an element of an area A
}
and
x is
the
distance
of the
element from
some axis
in,
or
perpen-
dicular
to,
the
plane
of the
area,
the
limits of
integration
being
such
that each
element
of
the
area is included in the
integration.
An
expression
of this
form
is called
the second moment of the
area
or the
moment
of
inertia
of
the
area with
respect
to the
given
axis. The
moment
of inertia of an area
with
respect
to an axis
in,
or
per-
pendicular
to,
the
plane
of
the area
may, then,
be denned as the
sum of the
products
obtained
by multiplying
each element of
the
area
by
the
square
of its distance from the
given
axis.
The term
moment of inertia is
somewhat
misleading,
since
inertia
is
a
property
of
physical bodies, only,
and hence
an area
does not
possess
inertia. For
this
reason the
term,
second
moment
of an
area,
is to be
preferred, particularly
when
contrasting
the
expressions
of
the
form
here
discussed
with
expressions
which were
defined as
first moments of areas in
Chapter
V. It
may
be
noted
that each
term x
2
dA
in
the
summation which
represents
the
moment of inertia of an area can be written in the form
x(xdA),
and
hence
represents
the moment of
the
moment of an
element of
area,
that
is,
the second
moment of the
element. The term
moment
of
inertia,
however,
is
very
widely
used,
due to
the fact
that the
expression
is of the same form as an
expression
to be dis-
cussed later
(Art. 100)
which
is
defined as the
moment of inertia
of a
body
and which
does have a
physical
significance.
The moment of
inertia
of an
area
with
respect
to an axis will
be
denoted
by
I for
an
axis
in the
plane
of
the area and
by
J
for
an axis
perpendicular
to
the
plane
of the
area.
The
particular
180
