Seely F.B. Analytical Mechanics for Engineers

Подождите немного. Документ загружается.

CONICAL

PIVOT

151

the

frictional

moment

for a

solid

flat

pivot and,

hence,

will

not

given

detail.

The

fFictional

moment

found

For

uniform

pressure,

For

uniform

wear,

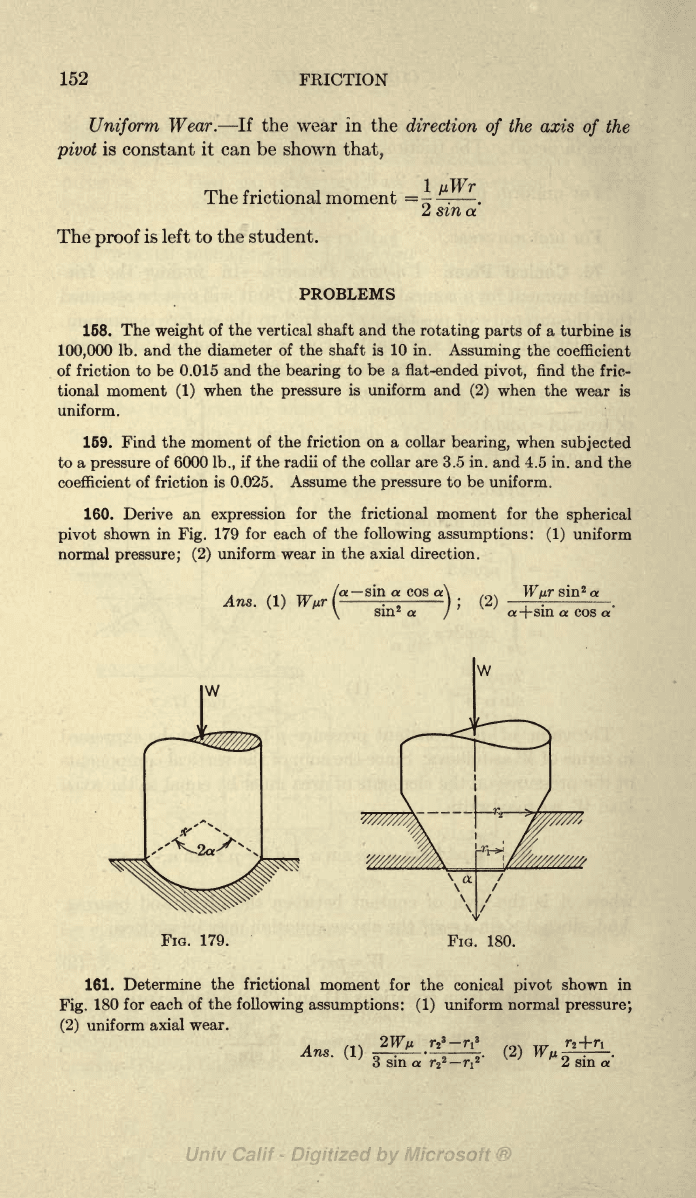
76. Conical

Pivot.

Uniform

Pressure. In

finding

the

fric-

tional

moment

for

a conical

pivot

(Fig.

178)

it will first

assumed

that the

intensity

pressure,

normal to the

surface is

constant.

The

frictional

force at

any

point

course is

horizontal.

Referring

Fig.

178,

find

the frictional moment as follows:

Frictional

force

an element

of area

fipdA

;

Moment

of this

force

Total

frictional

moment

sn a

2-n-fjip

r*_

sin a

(1)

FIG.

178.

The

value of

the constant

pressure

(1)

may

expressed

terms of W as

follows : Since the

sum

of the

vertical

components

the

pressures

the

elements of

area

must

equal

the axial

load

may write,

pdA

sin a

sin a I

dA=pA

sin

where

is the area

contact

between

the

pivot

and

bearing.

And,

since

Xsma

irr

the

above

equation

may

written,

(2)

By eliminating p

from

equations (1)

and

(2)

the final

expression

is,

Frictional

Moment

sin a

152

FRICTION

Uniform

Wear.

the wear

the

direction

the axis

the

pivot

is constant it can

be shown

that,

The

fictional moment

The

proof

is left to the student.

sin a

PROBLEMS

158.

The

weight

the vertical shaft and the

rotating

parts

turbine

100,000

Ib. and

the diameter of

the

shaft is

in.

Assuming

the

coefficient

of friction to be 0.015

and the

bearing

to be a

flat-ended

pivot,

find the

fric-

tional moment

(1)

when

the

pressure

is uniform

and

(2)

when the

wear is

uniform.

159. Find

the moment of the

friction on a collar

bearing,

when

subjected

to a

pressure

of 6000

Ib.,

if the radii

of the collar are

3.5 in. and

4.5 in. and

the

coefficient

friction

0.025.

Assume the

pressure

to be

uniform.

160.

Derive

expression

for the frictional moment for

the

spherical

pivot

shown

Fig.

179

for each

of the

following assumptions: (1)

uniform

normal

pressure;

(2)

uniform

wear

in the

axial

direction.

Ans.

(1)

Sin a cos a

sin

(2)

Wur

sin

a+sin

cos a'

FIG.

179.

FIG.

180.

161.

Determine

the frictional

moment for the conical

pivot

shown in

Fig.

180 for

each

of the

following

assumptions:

(1)

uniform normal

pressure;

(2)

uniform axial

wear.

Ans.

(1)

3 sin

sin

ROLLING RESISTANCE

153

77.

Rolling

Resistance.

rigid

wheel

roller

which

car-

ries

a vertical

load rests on

rigid

horizontal

surface,

horizontal

force,

however

small,

will cause

the wheel

or roller to

roll

on the

surface.

If a wheel rolls over

yielding

surface,

however,

resistance

to the motion is

encountered

due to the fact that the

surface

immediately

front of

the

wheel

being

deformed.

Fig.

181

shown

wheel

carrying

vertical load

Let

be a

horizontal

force which

causes

the

center

the

wheel

move with

constant

velocity.

Since

the surface

which

the

wheel

rolls

deforms

under

the

wheel,

the

pressure

between

the

wheel and the

surface

dis-

tributed

over the

area

of con-

tact. The

resultant

pressure

reaction

of the

surface on the

wheel,

then, passes through

some

point,

the area of contact

shown

in the

figure.

Since

the

velocity

of the wheel

constant,

the three

forces

acting

it are

equilibrium

and

hence

the

reaction, R,

of the

surface on

the wheel

must

pass through 0,

the

center of the

wheel.

Taking

moments

about

have,

Since

the

depression

usually

small,

OA is

approximately equal

the

radius of the wheel.

using

this

approximation

and

denoting

the value

of P is

found

be,

The

force

P is

equal

to the horizontal

component

of the

reaction

and

is called

the

rolling

friction

rolling

resistance;

the distance a

sometimes

called

the

coefficient

of rolling

resistance.

However,

since

a is a linear

quantity

and

not a

pure

number

it is

not a true

coefficient.

The value of

generally expressed

in inches.

The

laws

rolling

resistance are not

well

known,

and

there

need

further

investigation

on the

subject.

It was

assumed

Coulomb

hat

the

coefficient of

rolling

resistance is

independent

the

radius

154

FRICTION

of the wheel. Tests

by Dupuit

indicate

that the

coefficient

varies

as the

square

root of

the diameter.

Whether

the

conclusion

the

latter

is correct or

not,

seems reasonable

assume

that

the

value of

the

coefficient

depends

on the

diameter of

the

wheel.

The

values of

the coefficient of

rolling

resistance

given

various

investigators

are not

agreement

and

should

used

with

caution.

COEFFICIENTS

ROLLING

RESISTANCE

(Due

Coulomb

and

Goodman}

(inches)

Lignum

vitse

on oak

0.0195

Elm

oak

0327

Steel

steel.. 007 to

0.015

Steel

wood

06 to

.10

Steel

on macadam

road

.20

Steel

on soft

ground

3.0 to

5 .

Pneumatic

tires

good

road . 02

to . 022

Pneumatic

tires

mud

road 04

to .06

Solid

rubber tire

good

road 04

Solid

rubber tire

mud

road

09 to .11

The

resistance

due

rolling may

regarded

equivalent

couple.

In order

to show that

this

statement is

true,

con-

sider

the wheel

represented

Fig.

182.

flexible cord

passing

over

the wheel

carries

at its ends

weights

and

TF+w.

Assume

just

great

enough

cause the

wheel to

move

with

constant

velocity.

Since the

wheel

is in

equilibrium

under the

action of the

two

vertical

forces,

and

W-\-w,

and

the

reaction,

of the surface

it is evident

that the latter force

must

ver-

tical.

The reaction

may

replaced

equal

parallel

force

through

and

couple

having

a moment

equal

to Ra.

Since

the

force, R, through

also

passes through

the

center of the

wheel

it will

not

effect

the

rotation.

Therefore

the

rolling

resist-

ance

equivalent

the

couple

Ra.

The moment

wr, then,

which

causes

the

wheel

roll

equal

to Ra.

FIG.

182.

BELT FRICTION

155

For

moving heavy

weights,

such as

machines, houses,

etc.,

two

rollers

are

frequently

used as shown

Fig.

183.

If the

coefficient

rolling

resistance

the same at the

top

and

bottom

of the rollers it can

be shown

that the

force

required

to overcome

friction is

given

the

expression,

() O

'3%%%%^^

FIG.

183.

PROBLEMS

162.

The

rolling

resistance

for the

wheels

of a

freight

car is

Ib.

per

ton.

the diameter

of the

car wheels

is 33

in.,

what is the coefficient of

rolling

resistance?

Ans. 025

in.

163.

oak

beam

which

carries

a load of

5000 Ib. rests on

elm

rollers

the

diameters of which are

6 in.

The

rollers rest

a horizontal oak track. What

horizontal force is

required

to move the load

the

weight

of the beam is

neglected?

164.

What is

the

rolling

resistance

wagon

wheel

on a

macadam

road

if the diameter

of the

wheel

is 4 ft. 6 in.?

Assume the

coefficient of

rolling

resistance to

0.2 in.

Ans.

14.8 Ib.

per

ton.

78.

Belt Friction. Belt friction is

important

the

trans-

mission

power

belt

and

rope

drives and

resisting

large

loads

means of band

brakes,

capstans,

etc.

belt,

rope,

steel

band

passes

over

smooth

cylinder

pulley

the tensions

the

belt, rope,

or band

on the

two sides of

the

pulley

are

equal.

If the

cylinder

pulley

rough,

however,

the tensions will

not,

general,

equal.

In the

present

article

the

relation between

the tensions

in the

belt, etc.,

the

two sides of a

rough

pulley,

when

the belt is about

slip,

will be

determined. It

is evident

that

the

greater

tension must be

just

large

enough

to overcome

the

smaller

tension

in addition

to the

friction

between

the

belt and

the

pulley.

Fig.

184

(a)

represented

a belt on a

pulley,

the

angle

contact

being

and

the

belt

tensions

being

and

T%.

Let

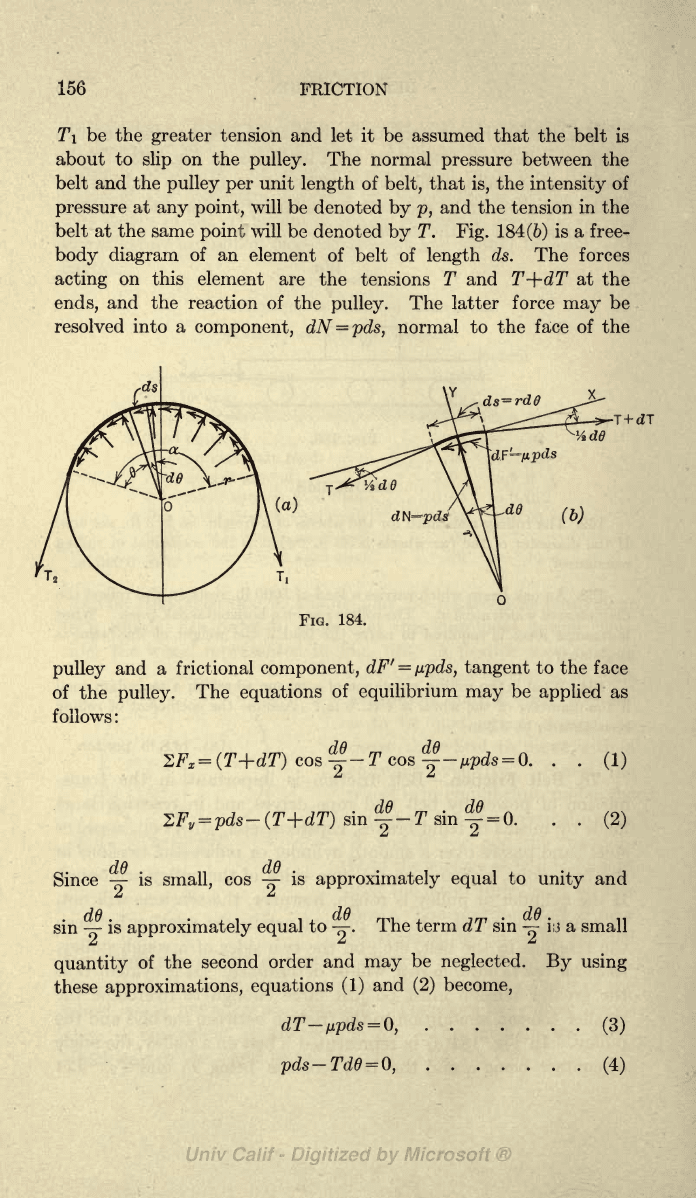
156

FRICTION

be the

greater

tension

and let it be assumed that

the belt

about to

slip

on the

pulley.

The normal

pressure

between

the

belt and the

pulley per

unit

length

belt,

that

is,

the

intensity

pressure

any point,

will

denoted

by p,

and

the

tension

the

belt at the same

point

will be

denoted

Fig.

184(6)

is a free-

body diagram

element

belt of

length

ds. The forces

acting

on this

element are

the tensions

T and

T-\-dT

the

ends,

and

the reaction of

the

pulley.

The latter force

may

resolved into a

component,

pds,

normal

to the

face

the

FIG.

184.

pulley

and a

frictional

component,

upds,

tangent

the

face

the

pulley.

The

equations

equilibrium may

applied

follows :

(1)

pds-(T+dT)

sin

-T sin

(2)

Since

-jr-

small,

cos

-^-

approximately equal

unity

and

sin

approximately

equal

-^r.

The term

sin

iu a small

quantity

the

second

order

and

may

neglected.

using

these

approximations,

equations

(1)

and

(2)

become,

pds-TdB

(3)

(4)

BELT

FRICTION

157

Eliminating pds

from

equations (3)

and

(4)

have,

(5)

integrating

equation

(5)

the relation

between

and

may

found as follows

That

is,

T~2

or.

(6)

where

the

base of

natural

logarithms

and a is

measured

radians.

should be

noted

that in

the

derivation

equation

(6)

the belt

assumed to be

perfectly

flexible.

ILLUSTRATIVE PROBLEM

165.

the

band

brake

shown in

Fig.

185 the force

100

lb.,

the

angle

contact, a,

is 270

(|TT

radians),

and

the coefficient

friction, ju,

for

the band

and

the brake

wheel

0.2.

the

brake wheel

rotates

in a

counter-clockwise

direction

find

the

tensions

in the band and the

frictional

moment

developed.

FIG.

185.

Solution.

Since

the

operating

lever

ACB is in

equilibrium

the

equation

may

applied,

from

which the band

pull

that

is,

the tension

found.

Thus,

13001b.

158

FRICTION

Since

is now

known,

the

tension

may

be found from the belt-friction

formula.

Thus,

1300X(2.718)-

log

1300+0.3*-

log

2.718

3.114

.942X.434

3.522.

33301b.

Frictional

moment

-TJX

2030X10

20,300

Ib.-in.

PROBLEMS

166.

body weighing

2000

Ib.

suspended by

means

rope

wound

turns around

a drum.

If the

coefficient

friction is

0.3

what

force

must

exerted at

the

other

end

the

rope

to hold the

body?

167.

boat is

brought

rest

means

of a

rope

which

wound around

capstan.

If a force of 4000 Ib.

exerted

the

boat

and

pull

of 100

Ib.

is exerted on

the

other

end

of the

rope,

find the

number of turns

the

rope

makes around

the

capstan, assuming

the value of

0.25.

Ans.

2.36

turns.

168.

body

weighing

500

Ib. is raised

means

of a

rope

which

passes

over

a round

beam,

the

angle

contact

being

180.

If the

coefficient of friction

0.4,

what

the

least

force

which will

raise the

body?

What is

the

least

force

which will

hold the

body?

FIG.

186.

169.

rope

wound twice

around a

post.

pull

of 50 Ib. at

one end

the

rope

will

just

support

a force of 6000 Ib. at the other

end,

what

the

coefficient

friction?

170. A

body having

weight,

ton

suspended by

means

wire

rope

which

passes

over

two

fixed

drums,

shown

Fig.

186.

If the

coefficient

of friction

for

the

rope

and

drums is

0.3,

what

force,

will

required

(a)

to hold

the

body; (6)

to start the

body upwards?

Ans.

(a)

4881b,

BELT FRICTION

159

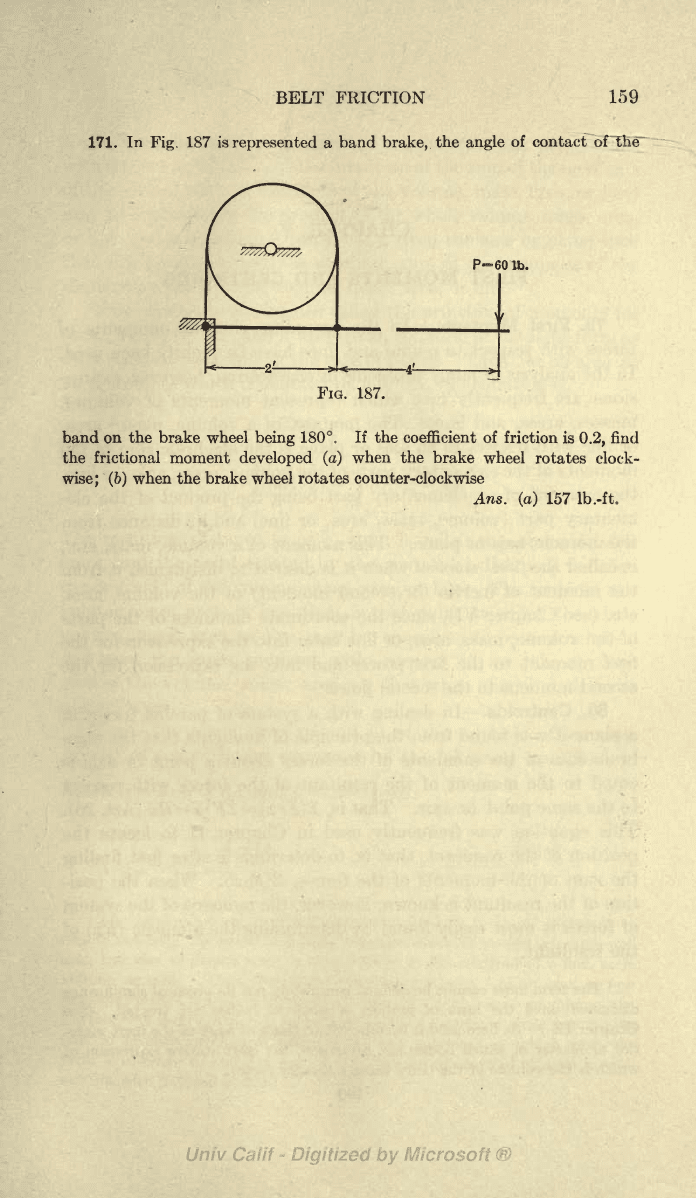
171.

Fig.

187 is

represented

a band

brake,

the

angle

of contact ofHie~

P-601b.

FIG. 187.

band on

the brake

wheel

being

180.

the coefficient of

friction

0.2,

find

the frictional moment

developed

(a)

when

the

brake

wheel

rotates clock-

wise; (b)

when

the brake

wheel

rotates

counter-clockwise

Ans.

(a)

157

Ib.-ft.

CHAPTER

FIRST MOMENTS

AND

CENTROIDS

79.

First

Moments. In

the

preceding

chapters

moments

forces with

respect

points

and lines

have

frequently

been used.

In the

analysis

many

problems

engineering, however, expres-

sions are

frequently

met which

represent

moments of

volumes,

masses, areas,

and

lines.

The moment of

volume, mass,

area,

or line with

respect

axis or

plane

is the

algebraic

sum of the

moments of the

elementary parts

the

volume, mass, area,

line,

the

moment

elementary part

being

the

product

the ele-

mentary part

(volume,

mass, area,

line)

and

its distance from

the moment axis or

plane.

This

moment of a

volume, mass, etc.,

is called the

first

moment when it is

desired to

distinguish

from

the moment of inertia

(or

second

moment)

of the

volume,

area,

etc.

(see

Chapter VI),

since the

coordinate

distances

the

parts

the

volume, mass, area,

line

enter into

the

expression

for

the

first moment

to the

first

power

and into

the

expression

for the

second moment to the second

power.

80. Centroids.

dealing

with a

system

parallel

forces

plane

it was found from the

principle

moments that the

alge-

braic sum of the moments

the forces

about a

point

or axis

equal

to the moment of the resultant of the forces

with

respect

to the same

point

or axis. That

is,

2(F-x)

2F-x

(Art.

26).

This

equation

was

frequently

used in

Chapter

to locate

the

position

of the

resultant,

that

is,

to determine

after first

finding

the sum of the moments of the

forces,

2(F-x).

When

the

posi-

tion of the resultant is

known, however,

the

moment of

the

system

forces is most

easily

found

determining

the moment

(Rx)

the

resultant.

The

term

mass

cannot

be denned

completely

nor

its

physical

significance

discussed

until the

laws

motion

physical

bodies are

treated.

(See

Chapter

IX.)

here used it is sufficient to think of mass as

the

inert

mate-

rial

or matter of which

bodies

are

composed,

the

quantitative

expression

which

the

volume

of the

body

times a

density

factor.

160