Seely F.B. Analytical Mechanics for Engineers

Подождите немного. Документ загружается.

CENTROIDS

161

a similar

way

the

moment

of a

volume, mass,

area,

or line

with

respect

axis or

plane

(made up

of the sum of the

moments

the

several

parts

elements

of the

volume, mass, area,

line)

may

expressed

as the

product

of the whole

volume,

mass, area,

line,

and

distance,

(or

etc.),

from the

axis

plane

such

that

this

product equals

the

algebraic

sum of the moments of

the

elementary

parts

of the

volume, mass, area,

or line.

This

relation

is sometimes called the

principle

of moments

for

areas, volumes,

etc.,

and

leads to

equation

of the same form

does

the

same

principle

in the case of forces.

Thus,

for an

area

an element of

which

denoted

dA,

the

equation is,

/<<"*>-/<

The

resulting

distance

etc.),

called the

centroidal

dis-

tance,

and

the

point

located

the centroidal

distances is

called

the

centroid

the

volume, mass, area,

or line.

The centroid of a

volume,

mass,

area,

line,

then,

is that

point

at which the whole

volume,

mass, area,

line

may

conceived to be concentrated

and have the same moment

with

respect

to an axis or

plane

as has the

volume,

mass,

area,

or line

when distributed

in its

natural

way.

Hence the

coordinates

and

the centroid of an

area,

}

and of a

line, L,

are

expressed

the

following

equations,

which

2a= I dA

and

2l=

dL.

The

term

center

of gravity

sometimes

used in

technical literature to

denote not

only

the

point

in a

body

through

which the

resultant

earth-pull

acts,

but also to

denote

what

here

denned

the

centroid of a

line, area,

volume,

or mass.

Thus,

the

phrase

center

gravity

of an

area,

or vol-

ume, etc.,

used instead of the

phrase

centroid

the

area,

volume,

etc.

Further,

the

term

centroid

sometimes

used in

restricted sense as

applying

only

geometrical

figures

(lines,

areas,

and

volumes),

which

case,

the

term

mass-center

or center

mass is

used

instead of

centroid of mass

con-

nection

with

physical

bodies.

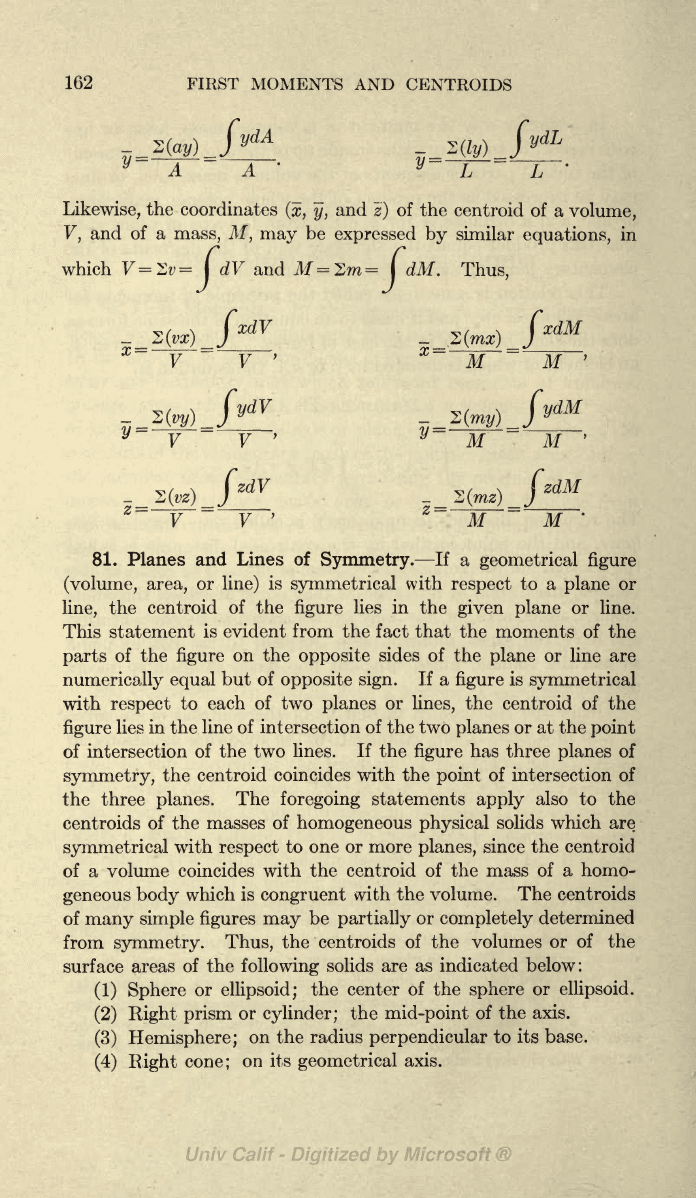
162

FIRST

MOMENTS AND

CENTROIDS

= =

A A

Likewise,

the

coordinates

(x,

and

the

centroid of a

volume,

and of

mass, M,

may

expressed

similar

equations,

which V=2v=

and

M=2m

dM.

Thus,

V MM

81. Planes

and Lines of

Symmetry.

If a

geometrical figure

(volume,

area,

line)

symmetrical

with

respect

to a

plane

line,

the centroid

of the

figure

lies

the

given plane

line.

This

statement

is evident from the fact that

the moments of the

parts

the

figure

on the

opposite

sides of the

plane

or line are

numerically

equal

but of

opposite sign.

If a

figure

symmetrical

with

respect

each of two

planes

lines,

the centroid of the

figure

lies in the line of

intersection of the

two

planes

the

point

intersection of

the two

lines.

the

figure

has three

planes

symmetry,

the centroid

coincides

with

the

point

of intersection of

the three

planes.

The

foregoing

statements

apply

also to the

centroids

of the masses

homogeneous

physical

solids which

are

symmetrical

with

respect

to one or more

planes,

since the

centroid

volume

coincides

with the centroid of the mass

of a homo-

geneous

body

which

congruent

with

the volume. The centroids

many

simple figures may

partially

completely

determined

from

symmetry.

Thus,

the centroids

of the

volumes

the

surface

areas

of the

following

solids are

indicated

below:

(1)

Sphere

ellipsoid;

the center of the

sphere

ellipsoid.

(2) Right

prism

cylinder;

the

mid-point

the axis.

(3) Hemisphere;

the radius

perpendicular

its

base.

(4)

Right

cone;

on its

geometrical

axis.

CENTROIDS

INTEGRATION

163

And

the

centroids

the

following

areas,

and of

their

bounding

lines,

are as

indicated below:

(5)

Circle

ellipse;

the center

of the

circle or

ellipse.

(6)

Isosceles

triangle;

on the

median

bisecting

the

angle

between

the

equal

sides.

(7)

Semicircle;

on the radius

perpendicular

to the

base.

82. Centroids

by Integration.

determining

the centroid of

volume, mass,

area,

or line

the

method of

integration,

from the

equations

of Art.

(Vx=

xdV,

Ax= I

xdA,

etc.),

it is

possible

to select

the

element

volume, area, etc.,

in various

ways

and

express

the element

in terms

of either

cartesian

polar

coordi-

nates.

The

resulting

integral

may

be a

single,

double,

or a

triple

integral,

depending

on the

way

the element

selected. The

integral,

course,

is a

definite

integral,

the limits of

integration

depending

on the

boundary

curve or surface of the

figure

body.

any

case

the

element of

volume, mass,

area,

or line

must be

taken

that,

1. All

points

of the

element are the

same

distance from

the line

plane

about which moments are

taken;

otherwise,

the distance

from the

line or

plane

to the

element will be

indefinite.

Or,

that,

The centroid

the

element is

known,

which

case

the

moment of the

element about

the moment axis or

plane

is the

product

of the element

and the

distance of its

centroid from the

axis

plane.

The

centroids of

some

of the common

figures

(lines,

areas,

and

volumes)

will be found

the

following

illustrative

problems.

ILLUSTRATIVE

PROBLEMS

Find, by

the

method of

integration,

the

centroids

of the

following figures

with

respect

to the axes

indicated.

172.

Arc

of a Circle.

The

radius

which

bisects

the arc

will

taken

as the x-axis

(Fig.

188).

By symmetry

the

centroid

lies on

this

axis.

Hence

y=Q.

r denotes

the radius

the

arc and

the subtended

angle,

then,

terms of

polar

coordinates,

the ele-

ment

arc, dL,

and

its distance

x from

the

7/-axis

are dL

rd6

and

x=r

cos

Thus,

the

element of arc is

selected in

accordance

with

the first

of the

above

rules

and

may

be found as follows: FIG. 188.

164

FIRST

MOMENTS AND

CENTROIDS

\xdL

-XT-

J-a

cos 6-rde

COS

sin a.

Therefore,

__2r

sin

_2r

sin

sin a

2ra

~^~~'

If the arc

is a

semicircle,

that

is,

if a

radians,

then,

. That

is,

the distance of the

centroid of a

semicircular arc

from

the center of the

circle

slightly

less than

two-thirds

of the radius of

the

circle.

173. Area

of a

Triangle.

In accordance with

the first

the

above

rules

the

elements

area will

be taken as

strips

parallel

to the base of

the

triangle (Fig.

189)

Since

each

element is bisected

the median

drawn from

the

vertex

opposite

the

base,

the

centroid of

each

element,

and

hence

the

entire

area,

lies on

this

median.

If x denotes the

width

of the

strip,

the area

the

strip

is dA

xdy.

Thus,

xydy.

From similar

triangles,

the relation

between

x and

is,

Hence,

/ i

A 11' 1

Therefore,

The

centroid of a

triangular

area,

then,

at a

distance of one-third of the altitude

from

the

FIG. 189.

base.

174.

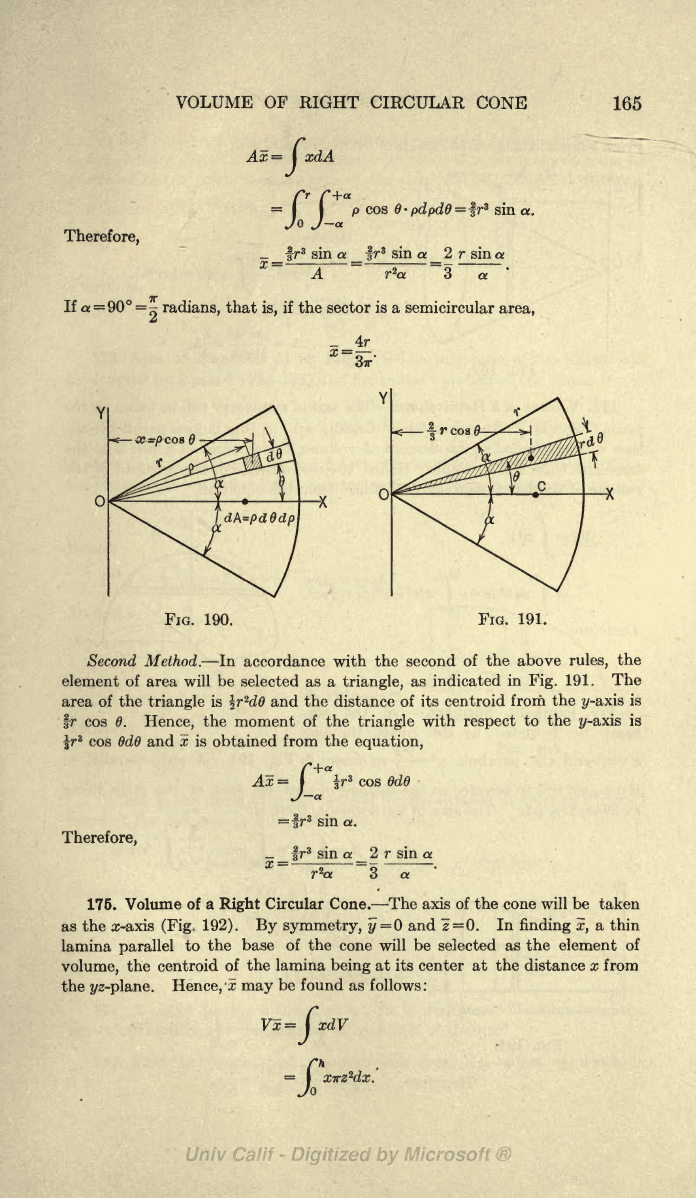
Sector

Circle.

First Method.

The element

of area will be

selected in

accordance with the

first of the above rules as

indicated

Fig.

190.

Since the area

symmetrical

with

respect

the

z-axis,

the centroid lies on

this axis and hence

0. The

value

may

then be found from

the

equa-

tion,

VOLUME

RIGHT

CIRCULAR

CONE

165

Ax= xdA

Therefore,

cos

6-pdpdd

sin

sin a

r*a

If a;

radians,

that

is,

the

sector

semicircular

area,

FIG. 190.

FIG. 191.

Second Method.

accordance with

the second

the above

rules,

the

element

of area

will

selected

as a

triangle,

indicated

Fig.

191.

The

area of

the

triangle

and the distance of its

centroid

from the

i/-axis

cos

Hence,

the moment of the

triangle

with

respect

the

?/-axis

cos ede

and

obtained

from the

equation,

/*+

cos

6dd

J-<*

sin

Therefore,

__|r

sin

a_2

sin

~3~oT~'

175.

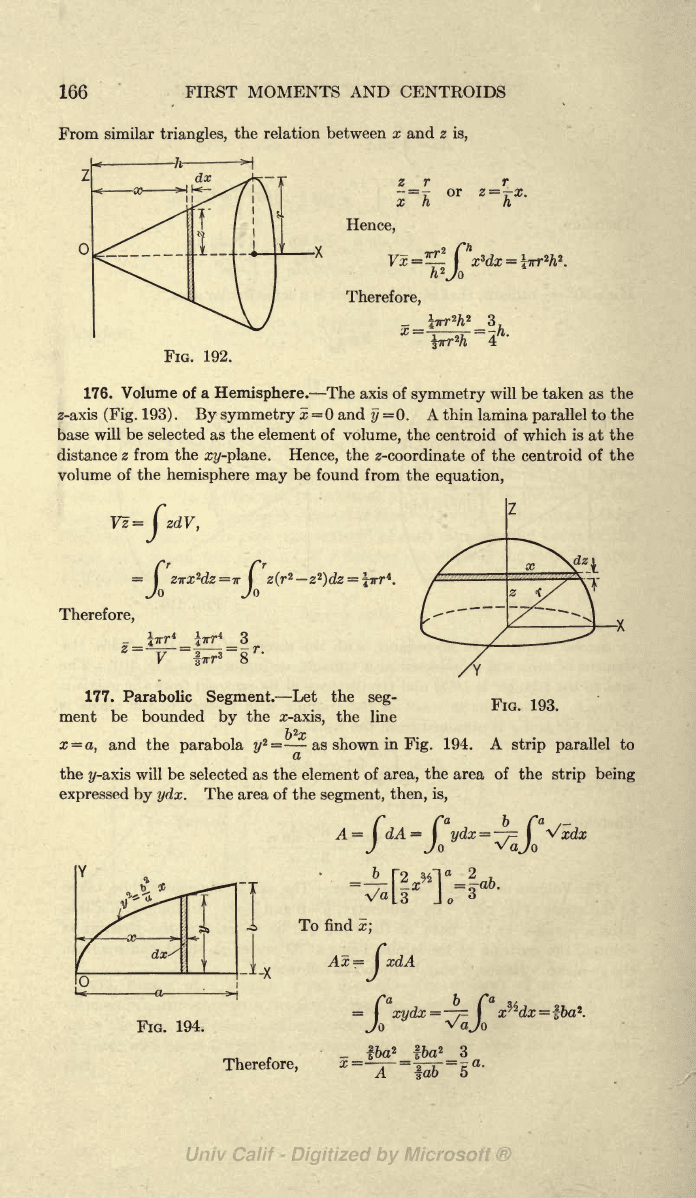
Volume

of a

Right

Circular

Cone.

The

axis

of the

cone

will be taken

the z-axis

(Fig.

192).

symmetry,

i/=0

and

0=0.

finding x,

thin

lamina

parallel

the

base of the

cone will be

selected as the

element

volume,

the

centroid

the

lamina

being

at its center at the distance x from

the

?/z-plane.

Hence,

-x

may

be found

follows:

Vx=

CxdV

-f

"Jo

166

FIRST MOMENTS

AND

CENTROIDS

From

similar

triangles,

the

relation

between

and

is,

r r

-=r

or z

x h

Hence,

.=!

h*Jo

Vx=^

Therefore,

FIG. 192.

176.

Volume of a

Hemisphere.

The

axis of

symmetry

will be taken as

the

z-axis

(Fig.

193).

By symmetry

and

0. A thin

lamina

parallel

the

base will

be selected

the

element of

volume,

the

centroid of

which

the

distance

z from

the

xy-pl&ue.

Hence,

the

z-coordinate of

the

centroid

the

volume

the

hemisphere

may

found from

the

equation,

zdV,

zirx

dzTr I

z(r

Therefore,

z=-

FIG. 193.

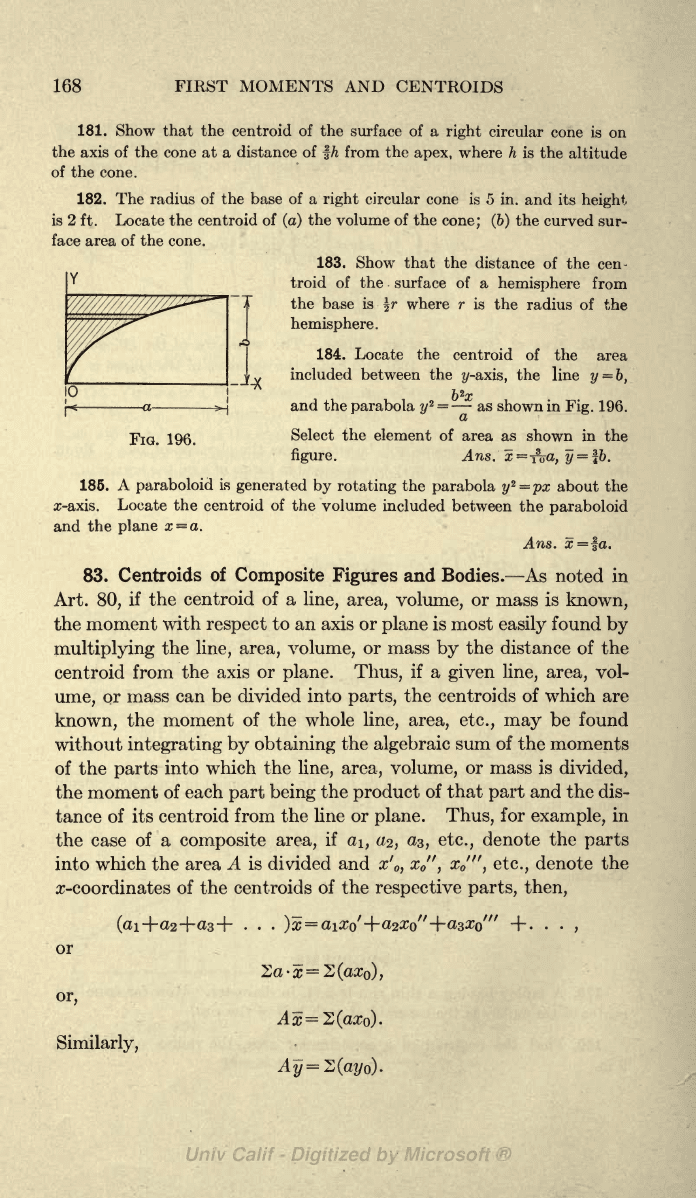
177. Parabolic

Segment.

Let the

seg-

ment be bounded

the

x-axis,

the

line

and the

parabola

as shown

Fig.

194. A

strip

parallel

the

?/-axis

will

selected as the element

area,

the

area

the

strip

being

expressed

ydx.

The area of the

segment,

then,

is,

CdA=

ydx

-^=

("Vxdx

Vajo

To find

Ax=

CxdA

FIG.

194.

Therefore,

-_|6a

fba

AREA OF

QUADRANT

ELLIPSE

167

find

</,

the

same

elementary strip

will

selected,

but

since

each

point

of the element is not

the

same distance

from

the

z-axis,

its

moment

must be

expressed

the

product

of the area of

the

strip

and its

centroidal

distance,

from the

x-axis.

Thus,

Therefore,

-K

|ab

178. Area

Quadrant

of an

Ellipse.

The

semi-axes

of the

ellipse

will

be denoted

and

(Fig.

195)

and hence the

equation

of the

ellipse

strip parallel

to the

y-axis

will be selected

as the

element of

area.

From

the

equation

the

ellipse

y may

expressed

terms

of x

the

equation,

Hence,

FIG.

195.

\irab

To find

the same

strip

will

be used

for

the

element of

area,

its

centroid

being

at the distance

from the

z-axis.

Thus,

Therefore,

Fto-ite-*

(\a*-

2oJo

PROBLEMS

179.

pulley

having

thin rim

ft.

diameter. How far

from

the

center

of the

pulley

the centroid

of each

half of the

rim?

180.

Find the

centroid

semicircular

area,

the

radius

which

in,

168

FIRST

MOMENTS

AND

CENTROIDS

181.

Show that the centroid of the

surface of a

right

circular

cone

the axis of the

cone at a

distance of

|/i

from the

apex,

where

the

altitude

of the

cone.

182.

The

radius

of the base

right

circular

cone is 5

in.

and its

height

ft. Locate

the centroid

(a)

the

volume of the

cone;

(6)

the

curved sur-

face

area

of the cone.

183.

Show that the

distance of

the

cen

troid of the

surface of a

hemisphere

from

the

base

where

is the

radius of

the

hemisphere.

184.

Locate

the

centroid

of the

area

included between the

y-axis,

the

line

and

the

parabola

shown

Fig.

196.

FIG. 196.

Select the

element

of area as

shown

in the

figure.

Ans.

x=Tua,y

%b.

186.

paraboloid

generated

rotating

the

parabola

y*=px

about the

x-axis.

Locate the

centroid

the

volume

included between

the

paraboloid

and

the

plane

Ans.

x=|a.

83.

Centroids

Composite

Figures

and Bodies.

noted

Art.

80,

the

centroid

line,

area, volume,

or mass

known,

the

moment with

respect

to an axis or

plane

most

easily

found

multiplying

the

line,

area, volume,

or mass

the

distance of the

centroid

from the

axis or

plane.

Thus,

given

line,

area,

vol-

ume,

mass

can be

divided

into

parts,

the centroids of which are

known,

the

moment of the whole

line, area, etc., may

be found

without

integrating by

obtaining

the

algebraic

sum of the

moments

of the

parts

into which

the

line,

area,

volume,

or mass is

divided,

the

moment

each

part

being

the

product

of that

part

and the dis-

tance of its

centroid

from the line

plane.

Thus,

for

example,

the case

of a

composite

area,

a\,

0,2, as, etc.,

denote the

parts

into which

the area

A is divided and

etc.,

denote the

^-coordinates of the

centroids of the

respective

parts,

then,

(0,1+0,2+0,3

aixo

xo"+0,3X0"

. .

or,

Similarly,

CENTROIDS OF COMPOSITE

FIGURES 169

From

similar

equations

the

centroid of a

composite

line,

volume,

mass

may

be found.

Thus,

Ly=2(ly

ILLUSTRATIVE

PROBLEMS

186. Locate

the

centroid

of the T-section

shown

Fig.

197.

Solution.

axes

selected as indicated

is evident from

symmetry

that

z=0.

dividing

the

given

area

into

areas

and a

and

by taking

moments about

the bottom

edge

the

area,

may

be found

as follows:

in.

__12X1+12X5

^"^

6X2+6X2

FIG.

197.

FIG. 198.

187.

Locate

the

centroid of

the

volume of the

cone and

hemisphere

shown

Fig.

198,

the

values of r

and h

being

in. and 18

in.

respectively.

Solution.

The

axis

symmetry

will

be taken

the

?/-axis.

From

sym-

metry

then

By taking

the x-axis

through

the

apex

of the

cone

as shown

the

equation

H(vyo)

becomes,

That

is,

Therefore,

h+2r

X(18)

+2X6Xl8+|X(6)

18-1-2X6

16.2

in.

170

FIRST MOMENTS

AND

CENTROIDS

PROBLEMS

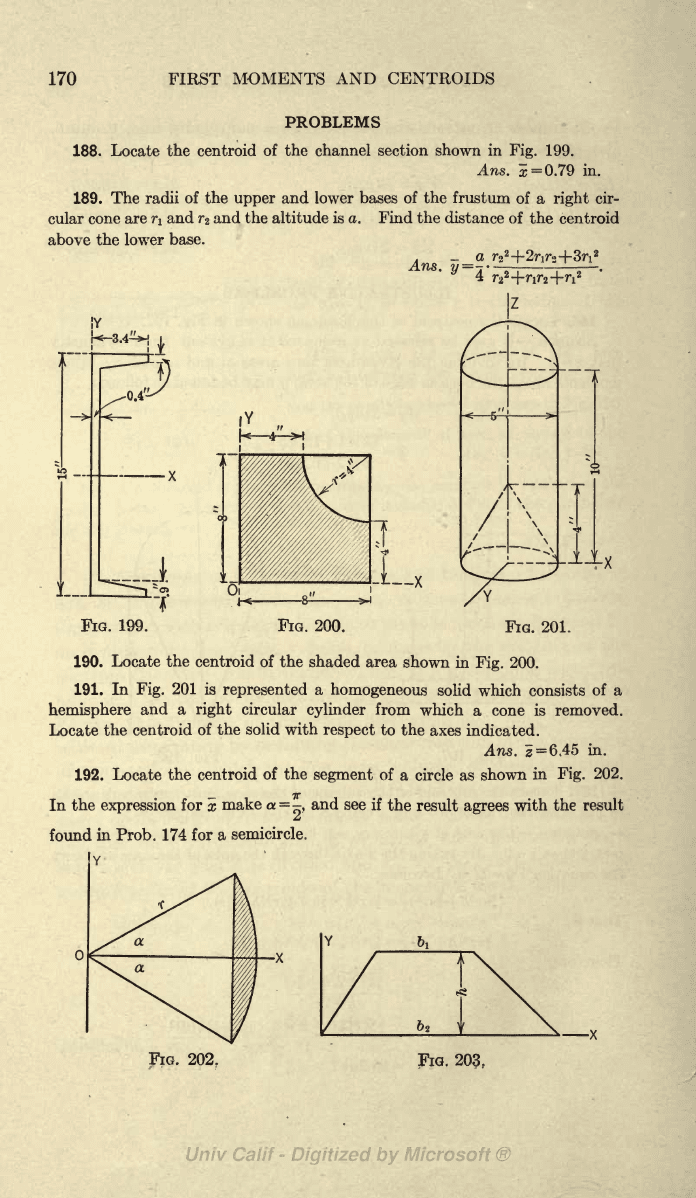
188. Locate

the centroid

of the channel section

shown in

Fig.

199.

Ans.

5=0.79

in.

189. The

radii

the

upper

and lower

bases of

the

frustum

right

cir-

cular

cone

are

and

and the

altitude is a. Find

the

distance of

the

centroid

above

the lower

base.

+2rir

+3r

FIG.

199.

FIG.

200.

FIG. 201.

190.

Locate

the

centroid

the

shaded

area

shown in

Fig.

200.

191. In

Fig.

201 is

represented

homogeneous

solid

which consists

of a

hemisphere

and a

right

circular

cylinder

from

which

a cone

is removed.

Locate

the

centroid

of the

solid

with

respect

the

axes

indicated.

Ans.

6,45

in.

192. Locate

the

centroid

of the

segment

a circle as

shown

Fig.

202.

In the

expression

for

make

=-,

and

see if

the result

agrees

with

the

result

found

in Prob.

174

for

semicircle.

FIG.

202.

FIG.

203,