Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


MOMENTS
OF INERTIA
OF SIMPLE
SOLIDS 211
parallelepiped
with
respect
to
(a)
a
central
axis
parallel
to an
edge;
(b)
a
median
line of one face.
Solution,
(a)
Central
Axis
Parallel to an
Edge.
Let the
lengths
of
the
edges
be denoted
by a,
6,
and
c,
and
let the
z-axis,
parallel
to
the
edge
c,
be the
central axis about which
the moment of inertia is
to
be
found,
as
shown
in
Fig.
254.
The
parallelepiped
may
be
divided into
elementary
volumes as
indicated,
the
mass of
each- element
being dcdxdy.
The
moment of inertia
with
respect
to
the
z-axis, then,
is,
-f:i\
dc(x
z
+y
2
)dxdy
a*b
.
ab*
i2
+
i2
In
a similar
way
it
can
be
shown that the
moments of
inertia
with
respect
to
central axes
parallel
to
the
edges
a and
6
are
and
Thus,
the moment of
inertia of a
homogeneous
rectangular prism
with
respect
to a central
axis
parallel
to
any
one of
the
three
edges
is
expressed
in
terms
of the mass and
the
lengths
of the other
two
edges.
(6)
A Median Line
of
One
Face.
In
order
to
determine the
moment of
inertia
with
respect
to a median line of
one face
the
formula of
Art.
102
may
be
used.
Thus,
if
the line MN
(Fig.
254)
be
taken
as
the
axis,
the
moment of
inertia
with
respect
to MN is
]O
\&
244. Determine
the
moment
of
inertia of
a
homogeneous sphere
with
respect
to a
diameter.

212
SECOND
MOMENT. MOMENT OF
INERTIA
Solution. The
cross-section of the
sphere
in the
xy-pl&ne
is
shown
in
Fig.
'255.
In
accordance with the second rule
above,
the element of
volume
may
be taken
as a
thin
circular
lamina
included
between two
planes
parallel
to
the
2-plane,
as shown in
cross-section.
This
element,
then,
may
be
regarded
as
a
circular
cylinder
of radius x
and altitude
dy.
The
mass of
the
elemental
cylinder
is
fax*dy
and
its
moment of inertia with
respect
to the
?/-axis
is
%dirx*dy
(Prob.
242).
Hence,
the
moment of inertia
of the entire
sphere
with
respect
to
the
y-axis
is,
7
=
x*dy
245.
Determine the moment
of
inertia
of
a
homogeneous
right
circular
cone
about
its
geometrical
FIG. 255.
Solution.
A
cross-section
of the
cone in
the
xy-p\&ne
is
shown
in
Fig.
256,
the
y-axis
being
taken
as
the
geometric
axis.
In
accordance with
the second
rule
above,
the element
of
volume
is
taken as
a
circular lamina included
between
two
planes
parallel
to
the
base,
the
height
of
the
lamina
being
dy.
The mass
of this elemental
cylinder
is dirx
2
dy
and its moment of
inertia
with
respect
to
the
?/-axis
is
%5irx
4
dy.
The
moment of
inertia
of
the cone with
respect
to
the
?/-axis, then, is,
f.
I
v
=
^87r
I
x*dy.
Jo
The
relation
between
x
and
y
may
be
found
from similar
triangles. Thus,
h
=
h-y
r
x
That
is,
Hence,
r
=
57r^f
(h-yYdy
FIG.
256.
MOMENTS
OF INERTIA
OF
SIMPLE
SOLIDS
213
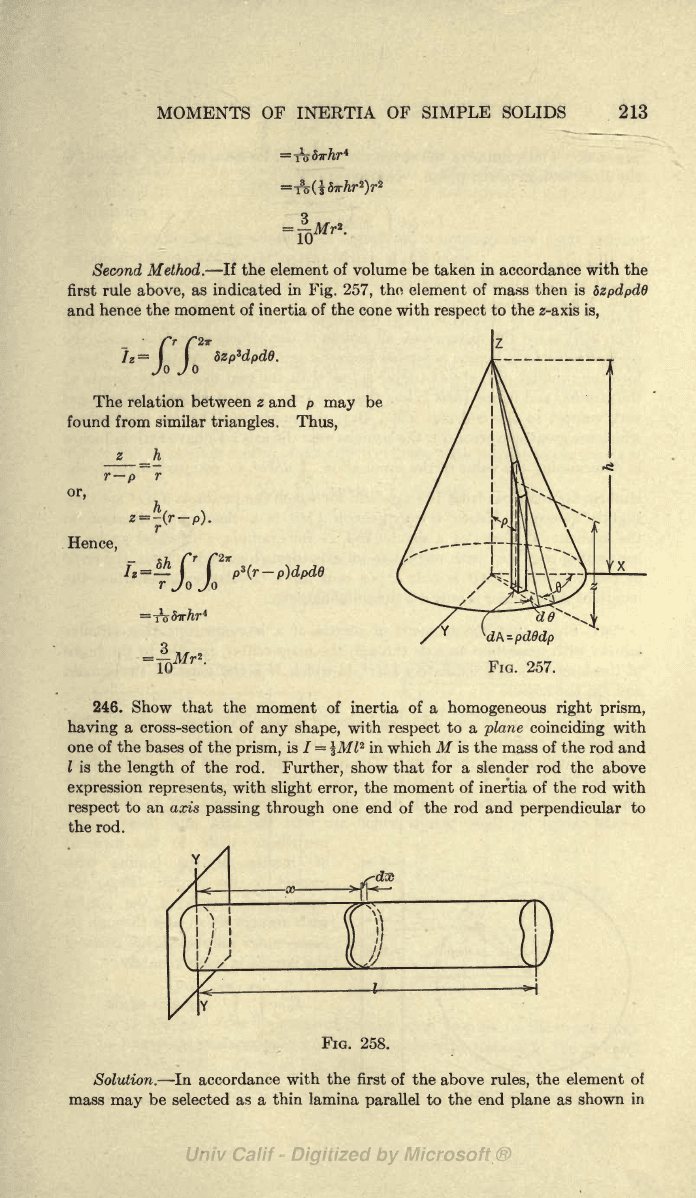
Second
Method.
If the element of volume be
taken
in
accordance
with the
first
rule
above,
as indicated
in
Fig.
257,
the element of
mass
then is
dzpdpdd
and
hence
the moment of
inertia
of the
cone
with
respect
to
the z-axis
is,
dzp
3
dpd6.
The relation
between
z and
p
may
be
found from similar
triangles.
Thus,
r-p
r
or,
Hence,
=
**
C
T
r*p3(r-
r
Jo Jo
fa**'
FIG. 257.
246.
Show
that the
moment
of
inertia
of a
homogeneous
right
prism,
having
a cross-section
of
any
shape,
with
respect
to a
plane coinciding
with
one of the bases
of
the
prism,
is
/
=
\M
I
2
in
which
M is the
mass
of the
rod and
I
is the
length
of the
rod.
Further,
show
that for a
slender
rod the
above
expression
represents,
with
slight error,
the moment of inertia of the rod
with
respect
to
an
axis
passing
through
one end of the rod
and
perpendicular
to
the
rod.
FIG.
258.
Solution.
-In
accordance
with the
first of the
above
rules,
the element
of
mass
may
be selected
as
a
thin
lamina
parallel
to the
end
plane
as
shown
in

214 SECOND MOMENT. MOMENT OF
INERTIA
Fig.
258.
The
volume of the element is
Adx and its
mass is
8Adx,
where A
is
the cross-section of the
prism.
Hence,
=
dA
I
Jo
x
2
dx
If
the moment of inertia
is taken with
respect
to
an end
axis
(Y
F),
then,
x
(Fig.
258)
is
not
the distance of all
points
in the
lamina from the
axis;
the
greater part
of the lamina
is
farther
from the
axis than the
distance
x. There-
fore
the
product
dM-x
2
=
(8Adx}x
2
is less
than the
real
moment of
inertia of
the
lamina,
and
hence
\Ml
2
is less than
the
true
moment of
inertia
of
the
rod
with
respect
to the end
axis
YY.
But,
the
products
dMx
2
for the
laminas
which are
greatly
in error
(for
the laminas
near
the
axis
YY}
have little
influence
in
determining
the value of the
summation,
I
dMx
2
,
in
comparison
with the
laminas far removed from
the
axis and
for
which
the
products
dMx
2
are
only
slightly
in
error.
Hence,
the
expression
\Ml-
is
a close
approximation
to
the
moment of inertia of a
slender
rod,
as for
example,
a
flywheel
spoke
or
connecting rod, etc.,
with
respect
to
an
axis
through
an end.
Thus,
the
error
in
the
expression
\Ml
2
is
only
1
per
cent for
a circular
cylinder
when the
length
of the
cylinder
is
only
4.3 times its
diameter.
247.
Show that
the
moment
of
inertia of a
homogeneous
thin
circular
lamina with
respect
to an axis
through
the
mass-center, parallel
to the
bases
of the
lamina,
is
approximately
|Afr
2
,
in
which
M is
the
mass of the
lamina
and
r
is
the
radius.
Solution. A
top
view and an
end
view
of the
lamina are shown in
Fig.
259.
The
element of volume
will
be taken as a
prism
of
altitude
t
and
cross-section
pdpde,
as indicated
in
the
figure.
The
mass of
the element
is
Stpdpde
.
Now
if
the thickness
t
is
relatively small,
all
points
in
any elementary
prism
are
approximately
at the same distance
(y
=
p
sin
6}
from the
re-axis
except
for those
prisms
which are near the
axis,
and
these
prisms
contribute little to
the
momen.t
of inertia
of the
lamina with
respect
to
the
z-axis.
Thus,
the
moment
of
inertia of the lamina
with
respect
to
an axis
through
its
mass-center
parallel
to the bases of
the
lamina
is
approximately,
sin
2
edpde
FIG. 259.
MOMENTS
OF INERTIA
OF
SIMPLE
SOLIDS
215
It
should
be
noted
that
the smaller
the
value
of t
becomes,
the
closer is
the
approximation.
The above
expression
is
also a close
approximation
to
the
moment
of inertia
of the lamina with
respect
to a diameter
of either
base of
the
lamina.
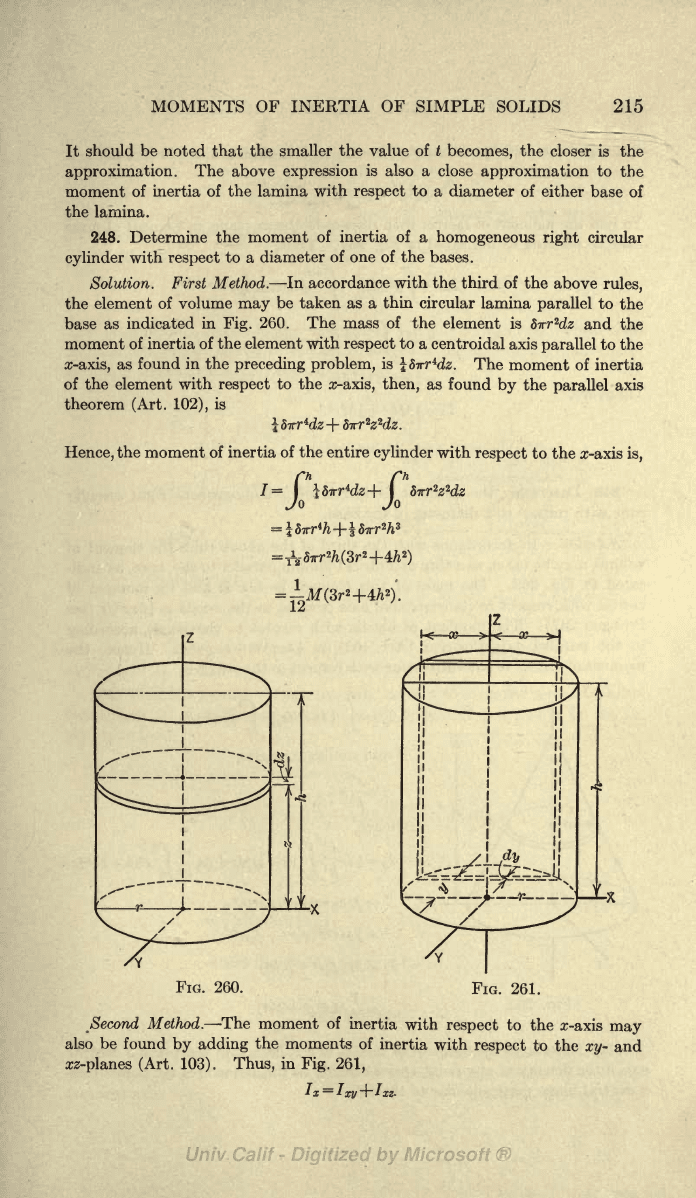
248. Determine the
moment
of inertia of
a
homogeneous
right
circular
cylinder
with
respect
to a
diameter
of one of the
bases.
Solution.
First Method.
In accordance with the
third of the
above
rules,
the
element of
volume
may
be taken as a
thin
circular
lamina
parallel
to
the
base
as indicated
in
Fig.
260.
The
mass
of
the
element is 8Trr
z
dz
and
the
moment
of inertia of
the element
with
respect
to a
centroidal
axis
parallel
to the
z-axis,
as found
in the
preceding
problem,
is
^8-rrr^dz.
The
moment of
inertia
of the
element
with
respect
to the
z-axis,
then,
as
found
by
the
parallel
axis
theorem
(Art. 102),
is
Hence,
the moment of inertia
of the entire
cylinder
with
respect
to the
z-axis
is,
-
P-l
4
C
H
~Jo
*
"
r Z
Jo
FIG.
260.
FIG.
261.
Second Method.
The
moment of
inertia
with
respect
to
the
x-axis
may
also be found
by
adding
the
moments of
inertia
with
respect
to
the
xy-
and
rrz-planes
(Art. 103). Thus,
in
Fig.
261,

216
SECOND
MOMENT. MOMENT OF INERTIA
From
Problem
246 the moment
of inertia with
respect
to
the end
(xy)
plane
is
To
find the moment
of
inertia with
respect
to the
zz-plane
an element of
mass
may
be
selected
as
indicated in
Fig.
261.
Thus,
=
Cy*dM
=
l
+r
y
r+r
=
26/i
j
y*V
r
*-
Therefore,
249. Determine
the moment of inertia of a
homogeneous
right
circular
cone
with
respect
to a diameter
of the base.
Solution.
In
accordance with
the third of the
above
rules the
element
of
volume
may
be
taken as a thin
cylindrical
lamina
parallel
to the
base,
as indi-
cated
in
Fig.
262.
The
mass
of this element is 5irx
2
dz
and its
moment of
inertia with
respect
to
its
centroidal
axis
parallel
to
the
x-axis
is
%8-jrx
4
dz
(see
Problem
247).
The moment of
inertia with
respect
to the
re-axis,
according
to the
parallel
axis theorem
(Art.
102),
is
^birx^dz-^-dirx^dz.
Hence,
the
moment
of inertia of the entire
cone with
respect
to the
z-axis
is,
*=
|
h
\fax*dz+
r
Jo
Jo
8-n-xWdz.
From
similar
triangles,
r
Hence,
r
2
C
h
-2
I
z
*(
h
~
h*jo
FIG.
262.
250.
Determine
the
moment
of inertia
of
a
sphere
with
respect
to a central
axis
if
the
density
at
any point
varies
directly
as
the
distance
of the
point
from
a central
plane
perpendicular
to
the axis.

N
MOMENTS
OF INERTIA
OF SIMPLE
SOLIDS
217
Solution.
The moment axis
will
be
taken
as
the
y-axis
of
coordinates
(Fig.
263).
The element of volume will
be
taken as a
thin
lamina
parallel
to
the
zz-plane.
The
density
at all
points
in this lamina is
proportional
to
y
and
hence
may
be>denoted
by
ky. Hence,
the
element of
mass is
kyirx
z
dy
and
the
mass of
the
sphere
is
M
The
moment
of inertia of
the
cylindrical
lamina is
\kyirx*dy
(Prob.
242)
and
the
moment
of
inertia
of the
entire
sphere
is
the
sum
of
the moments of
inertia of
the
elementary cylinders.
Thus,
-/.
yx*dy
FIG. 263.
251.
Find the
moment
of
inertia,
with
respect
to a central
axis,
of a
cast-
iron
sphere
10 in.
in
diameter. Assume
the
weight
of cast
iron to be 450
Ib.
per
cubic foot.
Solution.
The
mass of the
sphere
is,
450
M
4/5 \'
=
3*
(l2J
Ib.-sec.
2
32T2
r
=
.296 lb.-sec.
2
-ft.
(or
slug-ft.
2
).
PROBLEMS
252. Determine
the moment
of
inertia of a
homogeneous right
circular
cone about an
axis
through
the
center
of
gravity
perpendicular
to the
geo-
metrical
axis.
Ans.

218 SECOND
MOMENT.
MOMENT OF
INERTIA
253.
A
homogeneous
cylindrical
rod is
2
ft.
long
and the
radius
is
2
in.
If the
moment of
inertia
is
found
with
respect
to
a line
through
one
end
of
the
rod
perpendicular
to its axis
by
using
the
approximate
formula of
Problem
246,
what
is the
error
in the
result,
in
per
cent?
254. Determine the moment of
inertia of
a steel
cylinder
6
in.
in
diameter
and
12
in.
high,
about
its
geometric
axis.
Assume
the
weight
of
steel
to be
490 Ib.
per
cubic
foot.
255. Show that
the
moment of
inertia of
a
homogeneous
slender
rod
with
respect
to an axis
through
the
mid-point
of
the rod
and
perpendicular
to the
rod is
approximately
-
256.
Determine the
moment
of
inertia
of
a
homogeneous
ellipsoid,
the
principal
axes
of
which
are
2a,
26,
and
2c,
about the
axis
2a.
Ans.
/
257. Determine
the
moment
of
inertia of
a
homogeneous
elliptic
cylinder,
in
which
the
principal
axes of
the
cross-section
are 2a
and
26,
with
respect
to
(1)
the
geometrical axis,
and
(2)
an axis
through
the
center
of
gravity
coin-
cident
with
the axis 2a of the
cross-section.
Ans.
(1)
7
=
105. Moments of
Inertia of
Composite
Bodies.
If
a
body
can
be
divided into several
finite
parts,
the moment of
inertia
of
each
of
which
is
known,
the moment of
inertia
of
the
given
body
may
be
Obtained
by
adding
the moments of
inertia
of
the
several
parts.
In like manner
if
parts
of a
body
are
removed,
the
moment of
inertia
of the remainder
may
be
obtained
by
subtracting
from the
moment
of
inertia of the
original
body
the sum
of
the moments
of
inertia of the
parts
removed.
ILLUSTRATIVE
PROBLEMS
258. Determine the moment of
inertia of
a
homogeneous,
hollow,
circular
cylinder
with
respect
to its
geometric
axis,
in
terms
of its
mass
M
and its inner
and outer
radii,
r\
and
r
2
.
Solution.
Let
/
2
and M
2
denote the
moment of
inertia and the
mass
of
a
solid
cylinder
of radius
r
2
and let
7i
and
Mi
have
similar
meanings
for
the
cylinder
of
radius
n
which
is
removed.
Then,
MOMENTS
OF
INERTIA
OF COMPOSITE
BODIES
219
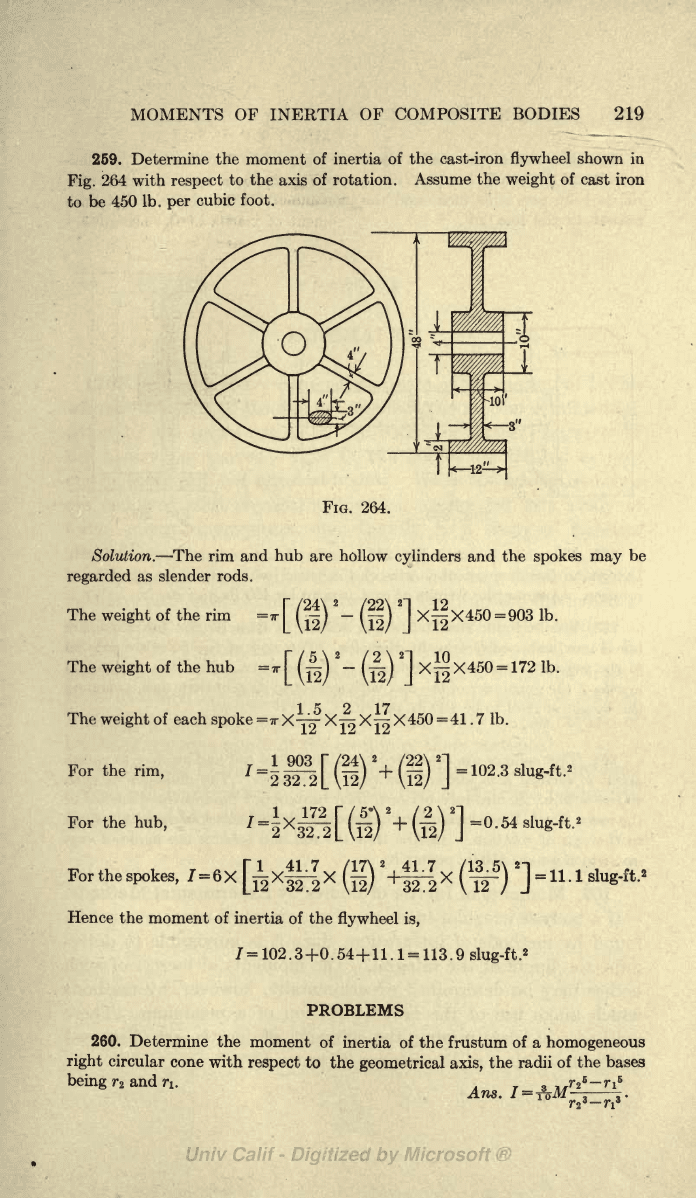
259. Determine the moment
of inertia of
the cast-iron
flywheel
shown
in
Fig.
264
with
respect
to the
axis of
rotation.
Assume the
weight
of
cast
iron
to
be 450
Ib.
per
cubic
foot.
FIG.
264.
Solution.
The rim
and
hub
are
hollow
cylinders
and
the
spokes may
be
regarded
as slender rods.
Ib.
Ib.
The
weight
of the rim
=
The
weight
of the
hub
=*
-
The
weight
of each
spoke
=7rX^X^
\i
i
41.7
Ib.
For
the
hub,
^*I|[
g)
*+
g)
]
=0.54
slug-ft.
,
7=6X xX X
-11.1
Hence
the
moment of
inertia of the
flywheel is,
7
=
102.
3+0.
54
+
11. 1
=
113. 9
slug-ft.
2
PROBLEMS
260.
Determine the
moment
of
inertia of
the frustum of a
homogeneous
right
circular
cone
with
respect
to the
geometrical
axis,
the radii of
the bases
being
r
2
and
n.
-
Ans.
/
220
SECOND
MOMENT.
MOMENT
OF
INERTIA
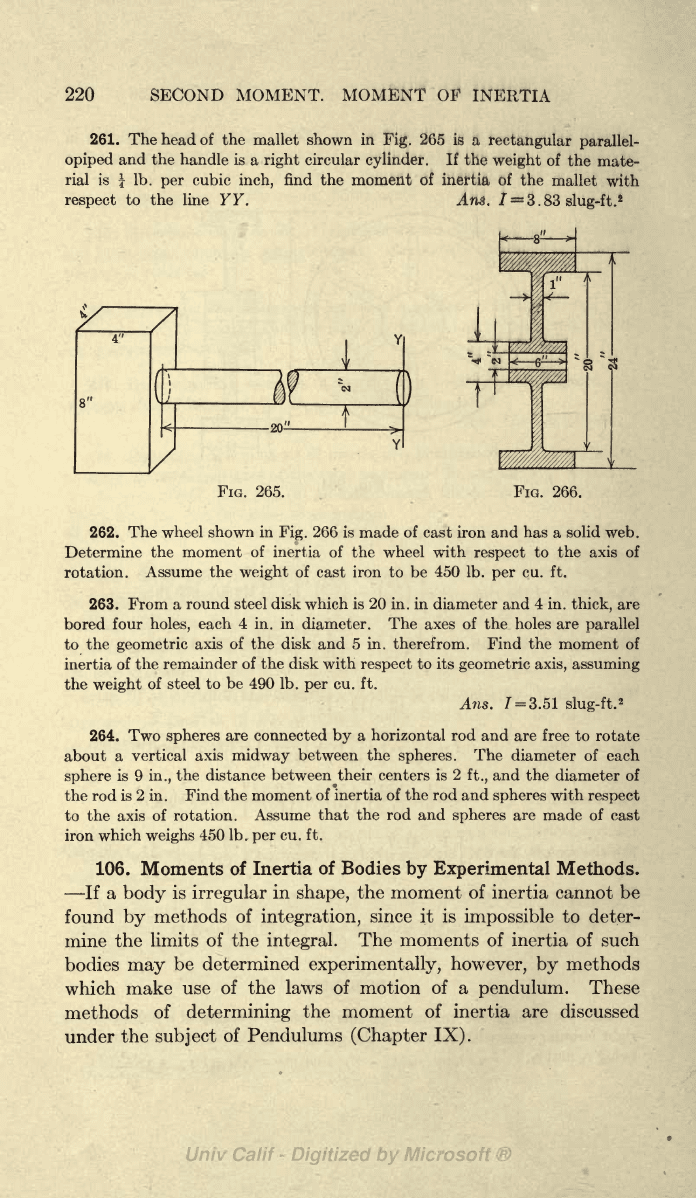
261. The
head of the mallet
shown
in
Fig.
265 is
a
rectangular
parallel-
epiped
and
the
handle is
a
right
circular
cylinder.
If
the
weight
of
the
mate-
rial is
Ib.
per
cubic
inch,
find the moment
of
inertia of the
mallet
with
respect
to the line
YY. Ans.
7
=
3.83
slug-it.
2
4"
-20-
,4
l"
_
I
FIG.
265. FIG. 266.
262.
The
wheel
shown
in
Fig.
266 is
made
of cast
iron and
has a solid
web.
Determine
the moment
of
inertia of the
wheel with
respect
to the axis of
rotation.
Assume the
weight
of cast iron to be
450
Ib.
per
cu. ft.
263.
From a
round steel disk
which is
20
in.
in
diameter and
4
in.
thick,
are
bored
four
holes,
each
4
in.
in
diameter.
The
axes
of the holes are
parallel
to
the
geometric
axis
of the disk
and
5
in. therefrom.
Find the moment
of
inertia of
the remainder
of the disk
with
respect
to its
geometric axis, assuming
the
weight
of steel
to be
490 Ib.
per
cu.
ft.
Ans.
7
=
3.51
slug-ft.
2
264.
Two
spheres
are connected
by
a horizontal
rod
and
are
free to
rotate
about
a
vertical axis
midway
between the
spheres.
The
diameter of each
sphere
is
9
in.,
the distance
between
their
centers is
2
ft.,
and the
diameter of
the rod is
2
in.
Find the moment
of inertia
of the rod
and
spheres
with
respect
to
the
axis
of rotation.
Assume that
the rod
and
spheres
are
made
of
cast
iron which
weighs
450 Ib.
per
cu. ft.
106. Moments
of Inertia
of
Bodies
by
Experimental
Methods.
If a
body
is
irregular
in
shape,
the moment of inertia cannot be
found
by
methods of
integration,
since it is
impossible
to
deter-
mine
the
limits of the
integral.
The moments of
inertia of such
bodies
may
be
determined
experimentally, however, by
methods
which
make
use
of the laws of motion
of a
pendulum.
These
methods
of
determining
the moment of inertia are discussed
under
the
subject
of Pendulums
(Chapter
IX).
