Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


SPEED-TIME GRAPH
And
the
total
acceleration
of P
is,
241
a
P
=
V(2.62)
2
+
(39
.4)
2
=
39.5
ft./sec.
2
.
The
acceleration
of
M, only,
is
shown in
Fig.
284.
PROBLEM
282.
A
train,
while
rounding
a curve of mile
radius, changes
its
speed
uniformly
from
20
mi./hr.
to
30
mi./hr.
in 20
sec.
What
is the
total accelera-
tion
of the train at
the
beginning
and
at the end
of the
20-sec.
period?
119.
Speed-time
Graph.
In
finding
the
total
acceleration
of a
point
from the
equation
a
=-j-
(in
rectilinear
motion),
or,
dt
dv
in
finding
the
tangential
acceleration
from the
equation
at
=
-r
(in
curvilinear
motion), by
the
calculus
method,
v
must be
expressed
algebraically
in terms
of
t.
The relation
between
v and t
may
some-
times be
shown
more
conveniently,
graphically,
by
plotting
a
speed-time
(v-t) graph
the coordinates of
any point
on
which
are
simultaneous
values
of
the
speed
and time
of the
moving
point
(similar
to the distance-time
graph
in
Art.
113).
One
such
graph
is shown
in
Fig.
285.
Since
the
slope
of the
speed-time
curve is
represented by
-7-,
the
slope
of the
v-t
graph
at
any
point repre-
sents,
to some
scale,
the acceleration
of
the
moving point
at
the
corresponding
instant.
It is
important
to
note
that
this
method
gives only
that acceleration
which
is
due to
the
change
in
the
magnitude
of the
velocity.
It is
applicable,
therefore,
only
to
the
total
acceleration
for
rectilinear motion or
to the
tangential
accel-
eration
for curvilinear
motion.
ILLUSTRATIVE
PROBLEM
283. In
Fig.
285
is
represented
the
speed-time
graph
for
a
point
which
moves on
a circular
path.
What is
the
magnitude
of
the
tan-
gential
acceleration
at
the
end of
15
sec.?
Solution.
at
at
the
end
of 15 sec.
=
slope
at
A
2X20
4X5
=
2
ft./sec.
2
100--
60--
20--
5
10 15
20
25
t,
sec.
FIG.
285.
242 MOTION OF
A PARTICLE
PROBLEMS
FOR
ARTICLES
118 AND
119
284. A train
running
on a
straight
track has a
speed
of 30 mi.
per
hr. when
passing
a certain
mile
post
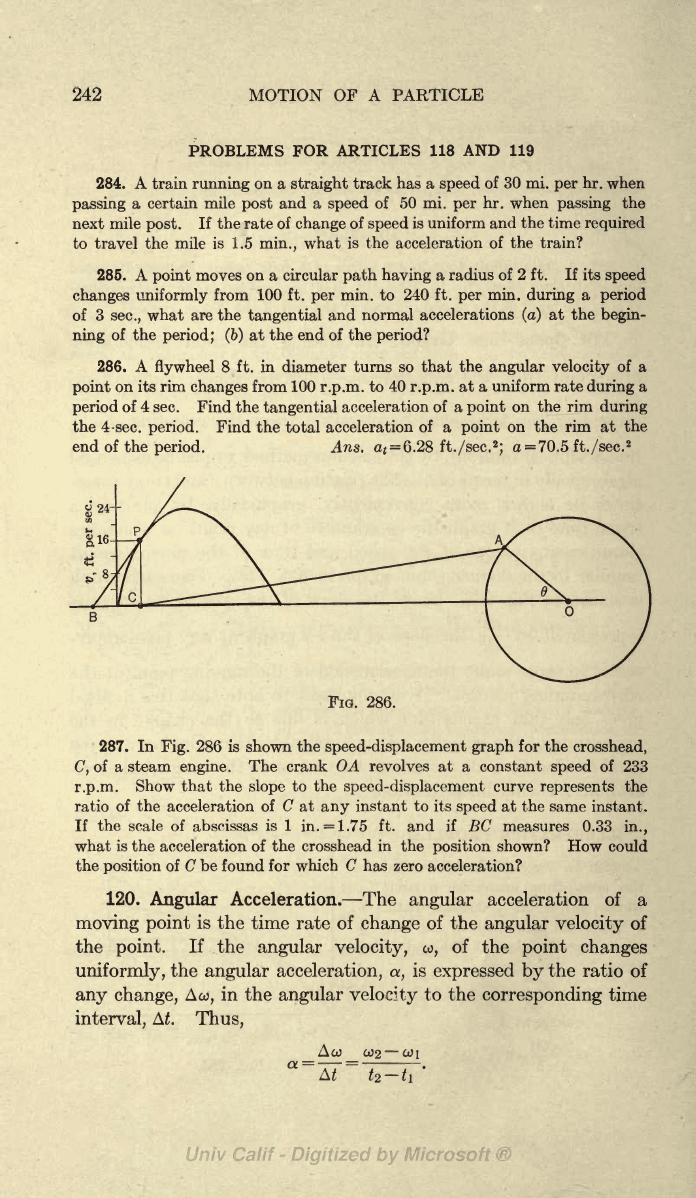
and a
speed
of 50 mi.
per
hr. when
passing
the
next
mile
post.
If the rate of
change
of
speed
is
uniform
and
the
time
required
to travel the mile is
1.5
min.,
what
is the acceleration
of the train?
285. A
point
moves on a circular
path having
a radius
of
2
ft.
If
its
speed
changes uniformly
from 100
ft.
per
min.
to 240 ft.
per
min.
during
a
period
of 3
sec.,
what
are the
tangential
and normal
accelerations
(a)
at the
begin-
ning
of the
period;
(6)
at the end of
the
period?
286. A
flywheel
8 ft.
in
diameter
turns so that
the
angular
velocity
of a
point
on
its
rim
changes
from
100
r.p.m.
to
40
r.p.m.
at a uniform rate
during
a
period
of
4
sec. Find
the
tangential
acceleration
of
a
point
on
the
rim
during
the 4
-sec.
period.
Find
the total acceleration
of
a
point
on the
rim
at
the
end
of the
period.
Ans.
a*
=
6.28
ft.
/sec,
2
;
a
=70.5
ft.
/sec.
2
FIG. 286.
287. In
Fig.
286 is
shown
the
speed-displacement graph
for
the
crosshead,
C,
of a steam
engine.
The crank
OA
revolves at a
constant
speed
of
233
r.p.m.
Show
that the
slope
to the
speed-displacement
curve
represents
the
ratio
of
the acceleration
of C
at
any
instant to its
speed
at the same
instant.
If
the
scale of abscissas
is 1
in.
=
1.75
ft.
and if BC measures
0.33
in.,
what
is the
acceleration of
the crosshead
in the
position
shown? How could
the
position
of C
be
found for which
C
has zero acceleration?
120.
Angular
Acceleration. The
angular
acceleration of a
moving point
is
the time
rate
of
change
of
the
angular
velocity
of
the
point.
If the
angular
velocity,
co,
of
the
point
changes
uniformly,
the
angular acceleration, a,
is
expressed by
the
ratio of
any
change,
Ao>,
in the
angular
velocity
to
the
corresponding
time
interval,
AZ.
Thus,

LINEAR AND
ANGULAR
ACCELERATIONS
_243
If
the
angular velocity
of
the
point
does
not
change
uniformly,
the
above
equation gives
only
the
average
acceleration
during
the
time
interval A. When
the
acceleration
varies
from
instant
to
instant its value at
any
instant
is the
average
acceleration
during
an
indefinitely
small time
interval
including
the
instant.
Or,
expressed
mathematically,
the instantaneous
angular
acceleration
is,
T
.
Aco
dco
a=
Limit
-T-.
=
-T*
And since
co
=
,
a
may
also
be
expressed
by
the
equation,
dt\dt)
dt
2
'
In
order to
find a
from the
above
equations,
w
and
must be
expressed
in
terms of
t.
The
unit of
angular
acceleration is
any
convenient unit of
angular velocity
per
unit
of
time;
such
as,
degree
per
second
per
second
(deg./sec.
2
),
revolution
per
minute
per
second
(rev./min./
sec.)
radian
per
second
per
second
(rad./sec.
2
),
etc.
PROBLEMS
288. What
is the
angular
acceleration of a
point
on
the
rim
of the
flywheel
having
the
motion described
in Problem
286?
289.
What
is
the
angular
acceleration of the
train
having
the
motion
described
in
Problem
282?
Ans.
a
=
0.000555
rad./sec.
2
290.
A
particle
moves
on a
circular
path
according
to
the
law
0=3t
2
+2t.
What
is
the
angular velocity
and the
angular
acceleration of the
particle
at
the end of 4
sec.?
121. Relation
between
Linear
and
Angular
Accelerations. In
many
problems
in kinematics it
is
con-
venient
to make
use of the
relation
between
the
linear
and
angular
ac-
celerations
of
a
point.
This
relation
may
be
found
as
follows:
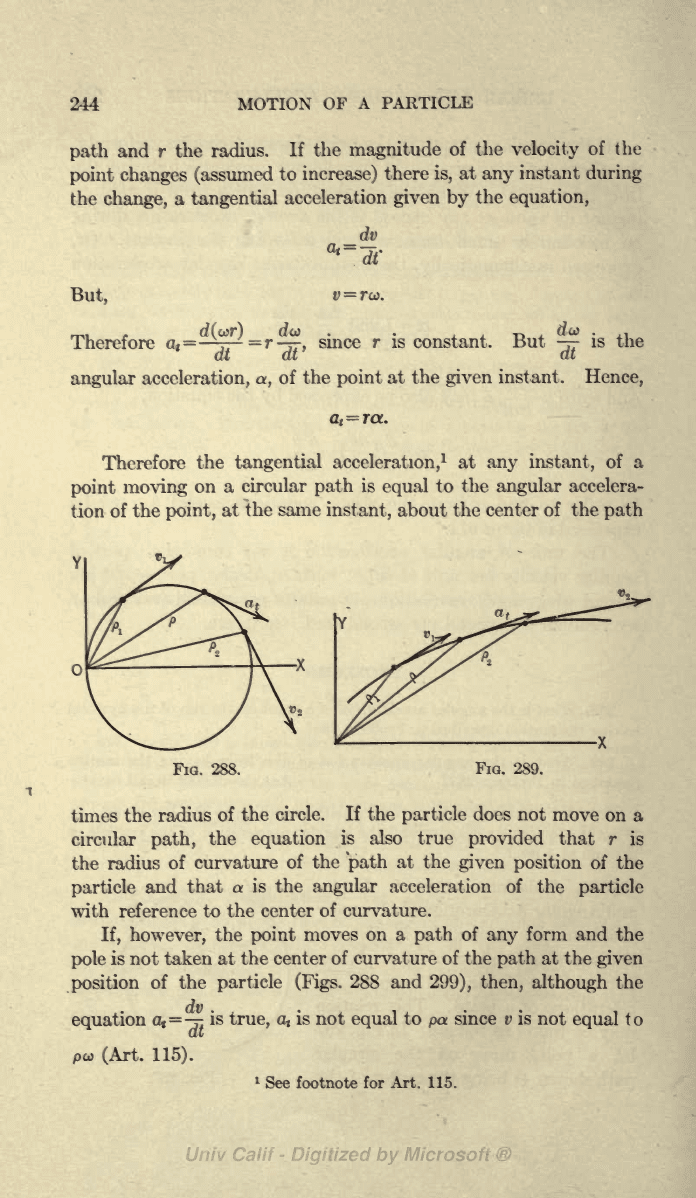
In
Fig.
287
let a
point
move
on
the
circular
path shown,
being
the center of
the
Fia.
287.
244
MOTION
OF
A PARTICLE
path
and
r the radius.
If the
magnitude
of the
velocity
of the
point changes
(assumed
to
increase)
there
is,
at
any
instant
during
the
change,
a
tangential
acceleration
given
by
the
equation,
dv
But,
=
ro>.
Therefore
a
t
=
, r-jr,
since
r
is
constant.
But
-
-
is the
at
at
at
angular
acceleration, a,
of the
point
at
the
given
instant.
Hence,
Therefore
the
tangential acceleration,
1
at
tmy
instant,
of a
point
moving
on
a
circular
path
is
equal
to
the
angular
accelera-
tion
of the
point,
at
the same
instant,
about
the
center of the
path
FIG.
288.
FIG. 289.
times
the
radius
of
the
circle.
If the
particle
does
not
move
on a
circular
path,
the
equation
is
also
true
provided
that
r
is
the
radius
of
curvature
of the
path
at the
given position
of
the
particle
and
that
a is
the
angular
acceleration
of
the
particle
with reference to
the center
of curvature.
If, however,
the
point
moves
on
a
path
of
any
form and the
pole
is not taken at
the center of curvature
of the
path
at
the
given
position
of the
particle (Figs.
288
and
299), then,
although
the
equation
0,=-^
is
true,
a,
is not
equal
to
pa
since v is
not
equal
to
P
o>
(Art.
115).
1
See footnote for
Art.
115.
AXIAL
COMPONENTS
OF
ACCELERATION
245
The normal
acceleration,
rco
2
,
of the
particle
(not
shown
in
the above
diagrams),
unlike
the
tangential
acceleration,
is
inde-
pendent
of the
angular
acceleration.
It
depends
on the
angular
velocity
at the
instant,
and
not on
the rate at which the
angular
velocity
is
changing
at the
instant.
F
IQ< 290.
PROBLEMS
291. As the drum
(Fig.
290)
turns,
the
weight
A is
wound
up
with decreas-
ing
speed.
If its
speed
decreases
20
ft.
/sec.
each
second,
what
is
the
angular
acceleration
of
a
point
on
the rim of the
drum?
292. A rod
3 ft.
long
is rotated
in
a
hori-
zontal
plane
about a vertical axis
through
one
end
of
the rod
so that the
angular
velocity
in-
creases
uniformly
from
10 to 40
r.p.m.
in 3 sec.
Find
the
tangential
acceleration
of
the
mid-point
of the
rod.
Ana.
0^
=
1.57
ft.
/sec.
2
122.
Axial
Components
of Accelera-
tion.
The
component,
in
a
given
direc-
tion,
of an
acceleration of a
point
is the
rate of
change,
in the
given
direction,
of
the
velocity
of the
point.
In
general,
the rate of
change,
in
the
given
direction,
of the
velocity
of the
point
is
due
partly
to
a
change
in
the
magnitude
and
partly
to
a
change
in
the
direction
of the
velocity.
It will
be
noted
that
the
tangential
and normal
ac-
celerations,
at
and
a,
which
are
dis-
cussed
in
the
preceding
articles are
components
of an
acceleration,
one
of
.which,
a
t
,
is the rate of
change
of
the
velocity
due to a
change
in
its
magnitude
only,
and
the
other, a,
is the rate
of
change
of the
velocity
due to
a
change
in
its
direction
only.
Thus,
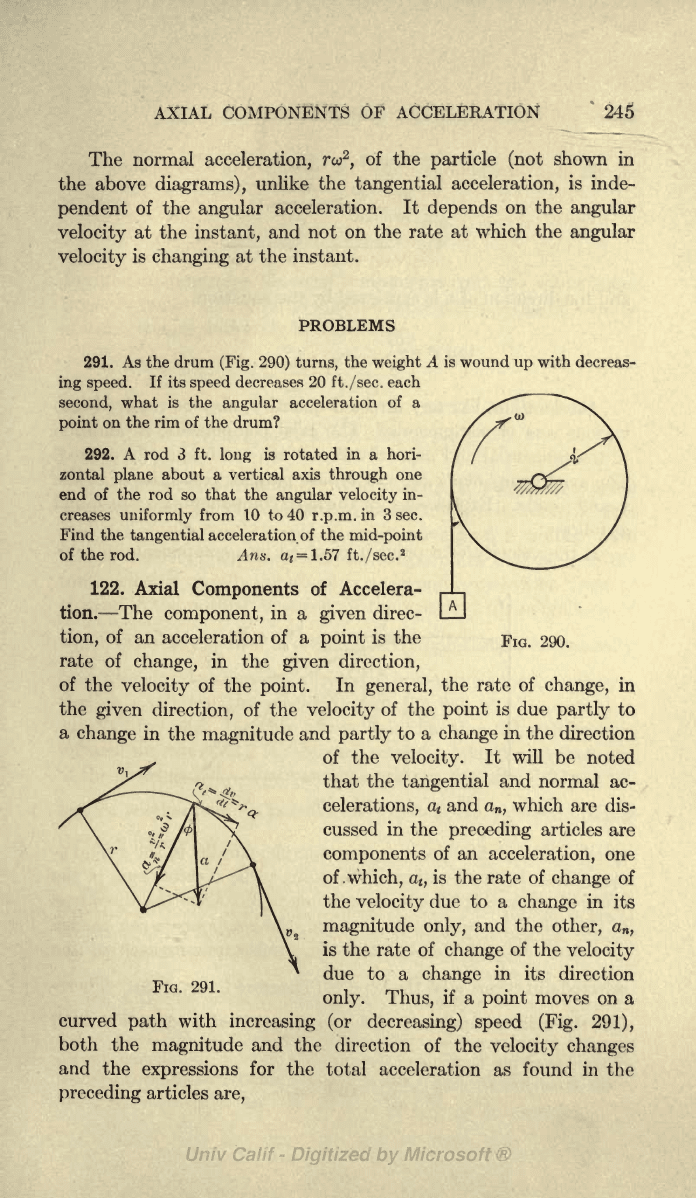
if a
point
moves on
a
curved
path
with
increasing
(or
decreasing)
speed (Fig. 291),
both
the
magnitude
and the
direction
of the
velocity
changes
and
the
expressions
for the
total
acceleration as
found
in the
preceding
articles
are,
FIG. 291.

246
MOTION
OF
A
PARTICLE
a
=
a
t
4>
a
n
dt
r
and the direction of
a
is
expressed
by
the
equation,
tan
<b=.
a
n
Acceleration,
like
any
directed
quantity, may
be
resolved
into
various
sets
of
components.
The axial
components,
in
addition
to
the
tangential
and
normal
components,
are
frequently
desired.
The axial
components
(a
x
and a
y)
are
parallel,
respectively,
to
the
x- and
?/-axes.
Expressions
for the
axial
components
may
be found
as follows:
If the
velocity
of a
point
is resolved
into
components
in
arbi-
FIG. 292.
trarily
selected
directions, as,
for
example,
parallel
to
the x-
and
y-
axes,
then
the
acceleration
of
the
point
is
the
(vector)
sum of the
rates of
change
in these
components.
But since the directions
of the
velocity components
are
fixed,
the
components
can
change
in
magnitude
only,
and
hence the
acceleration
in each of
the
selected
directions is
of
the
type
-j-
(Theorem
I,
Art.
118).
There-
fore the
axial
components
of
the
acceleration of a
point
(Fig.
292)
are,
dv
x
dv
v
a
x
=
-TT
and a
v
=
-
dt
dt

AXIAL
COMPONENTS
OF ACCELERATION 247
And since
v
x
=-
T
-
and
v***~j.
the
axial
components
may
also be
at
at
written,
d*x d
2
y
a
x
=
W2
and
a
v
=
-^
2
.
In order
to determine
the axial
components
from the above
equa-
tions,
v
x
(or
x)
and
v
v
(or
y)
must be
expressed
in
terms of
t,
unless
v
x
and
Vy
change
uniformly
in
which
case,
~
At" t
2
-t
l
'
and,
// /
_
AVy
_
V
yVy
It is
important
to
note that
the
velocity
of a
point
in
a
given
direction
may
be
zero without
making
the acceleration in
that
direction
zero. For
example,
a
point
moving
on
a
circular
path
has no
velocity
component
normal to the
path,
that
is,
v
t
is the
total
velocity
(t>
n
=
0)
but
there is a normal
acceleration
(rate
of
change,
in
the
normal
direction,
of the
velocity)
the
magnitude
of
v
2
which
as
already
shown,
is
.
Similarly,
a ball
thrown
horizontally
from
a
window
has no vertical
velocity
just
as it leaves the
window,
that
is,
v
y
=
0,
but the acceleration
of the ball at that instant is
Oy
=
32.2
ft./sec.
2
In
other
words,
v
y
is
changing through
its zero
value
at
the rate
of
32.2
ft.
/sec.
each second.
Likewise,
the
velocity
of
the
crosshead
of a steam
engine
is zero at
the end
of
the
stroke,
but
its
acceleration,
-r,
has
a
large
value as the
velocity
changes
through
its
zero
value.
PROBLEMS
293.
The total
acceleration
of a
point
on the rim
of a
pulley,
at
a
given
instant,
is
40
ft./sec.
2
in a direction
making
an
angle
of
20
with the
radius
to
the
point.
If the radius
of
the
pulley
is
18 in.
what
is the
angular
velocity
and the.
angular
acceleration
of the
point
at
the
given
instant?
Ans.
(o
=
5.01
rad./sec.;
a
=
9.
12
rad./sec.
2
294.
A
particle
moves
on the
path
xy
=
4,
according
to the
law,
x
=
2t
z
.
(a)
Find
the x-
and
^/-components
of
the
velocity
and
of
the
acceleration
at
the
end
of
2
sec.
(6)
Determine the
total
acceleration
by
combining
the
com-
ponents
graphically,
(c)
Find the
tangential
and
normal
components
graph-
ically
by
resolving
the total acceleration in
the
tangential
and
normal
direc-
tions.

248
MOTION
OF A
PARTICLE
123. Motion of a
Projectile.
The
equations
developed
in
the
preceding
article will here be used
in the
analysis
of
the
motion
of
a
projectile.
The actual motion
of a
projectile
is
influenced
by
a
number of
factors,
such as the rotation of the
projectile
due
to
the
rifling
of
the
barrel,
wind
velocity,
humidity,
etc.,
which
require
modifications in
the
results
found
from
the
assumed ideal
condi-
tions.
The
motion
of
a
projectile
moving
without rotation in
a
vacuum
will
here
be considered.
The motion
may
be
studied
by
treating
the
components
of
the
motion
in
the x-
and
^-directions
as
follows:
Let
a
projectile
be
given
an
initial
velocity
u
in a
direction
making
an
angle
6
with
the hori-
zontal and let
the
point
of
pro-
jection
be taken
as
the
origin
as
shown in
Fig.
293. The
accelera-
tion of the
projectile during
its
<
flight
is
constant
and is
directed
i-e
r
-J
vertically
downward. This
con-
FlQ 293
stant
acceleration,
denoted
by
gy
is
the
acceleration due
to
gravity,
since
the
projectile
is a
freely
falling
body,
that
is,
no forces
except
the
earth-pull (its
weight)
act
on it.
Hence,
-
=
or v
x
=u
x
=u
cos
0,
(1)
and,
v
v
a
v
=
v
v
=g
or
v
v
=
u
v
gt
=
u
sin 6
gt,
. .
(2)
I
considering
v
v
and
u
v
positive
when
directed
upward.
The
horizontal
distance,
x
}
traveled
in
any
time
interval t
is,
(3)
and the vertical
distance,
y,
traveled
in
any
time
interval
t is the
average
velocity
times the time interval.
Hence,
u
sin
6-\-(u
sin
6
gt)
.
,
//n
y
=
-
-2
-
-t
=
u
sin
d-t-^gt
2
. . .
(4)
Particular
values found from
the above
equations
are
of
special
importance,
namely,
the
range
on a horizontal
plane,
the
greatest
height,
and the
time
corresponding
to
each of
these
distances.

MOTION OF
A PROJECTILE
249
Time
of
Flight.
Since
y equals
zero when the
projectile
reaches
the
rr-axis,
the time of
flight,
t
T
,
is
given by
t in the
equation,
Therefore,
tr=
*^
....... ...
(5)
y
Range.
The
range,
r,
equals
the value of x in
equation
(3)
when
t
=
t
r
.
Therefore,
u
2
sin 26
r=
-
.
g
Time
to
Reach
Greatest
Height.
When
the
projectile
reaches
its
greatest height,
v
v
=
0.
Hence,
the
time,
t
h
,
required
for
the
pro-
jectile
to reach
its
greatest
height
is
given
by
t in
the
equation,
v
y
=
u
sin
0gt
=
0.
Therefore,
u
sin
Greatest
Height.
The
greatest height, h,
will be
given
by y
in
equation
(4)
when
t
has the
value
t
h
.
Hence,
1
(u
sin
0)
2
h
=
2
'
The
equation
of the
path
of the
projectile
(called
the
trajectory)
may
be obtained
by eliminating
t
from
equations
(3)
and
(4),
which
gives
the
following
equation
:
0-
2u
2
cos
2
6'
Hence the
trajectory
is a
portion
of a
parabola
with
its axis
vertical.
PROBLEMS
295. A bullet
is
projected upward
at an
angle
of 60
with
the
horizontal
with
a
velocity
of 2000
ft.
/sec.
Find the
range
and time of
flight.
Ans.
r
=
108,000
ft.
296. A
shot
is fired from
a
gun
on the
top
of a cliff
400 ft.
high,
with
a
velocity
of
768 ft.
/sec.,
the
angle
of
elevation of the
gun
being
30. Find
the
range
on a horizontal
plane through
the
base of the
cliff.
Ans.
r
=
5543
yd.

250
MOTION OF A PARTICLE
124.
Uniformly
Accelerated Rectilinear
Motion.
Many
examples
of
straight-line
motion
with constant
acceleration
occur
in
engineering
practice,
such
as
the motion
of a
freely falling
body
or
of
a train
leaving
a station under
the action
of
a
con-
stant
draw-bar
pull.
Further,
from the
preceding
article it will
be
noted
that
one of the
components
of a
curvilinear
motion
may
be
a
uniformly
accelerated rectilinear
motion.
The rela-
tions between
the
distance, time,
velocity,
and
acceleration,
for
uniformly
accelerated
rectilinear motion
may
be
deduced
as
follows
:
By definition,
At;
v
u
a=
AT
........
<
or,
v
=
u+at,
.......
(2)
in
which
u
and v are
the initial
and
final
velocities,
respectively,
corresponding
to the time
interval At or
simply
t.
Since
the
velocity
increases
or decreases
uniformly,
the
average
velocity
is x
and the
distance, s,
traveled in
time t
is,
u+u+at
~~~
(4)
By
eliminating
t from
equations
(2)
and
(4),
the
following
equa-
tion
is
obtained
:
v
2
=
u
2
+2as
........
(5)
Hence,
for
uniformly
accelerated,
rectilinear
motion,
the
fol-
lowing
equations express
the relations
between
the
distance,
time,
velocity,
and
acceleration,
v
=
u+at,
........
(6)
s=ut+at
2
,
.......
(7)
(8)
