Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.


PART
II
KINEMATICS
107. Introduction.
Kinematics treats of the
motion
of bodies
without
considering
the
manner
in
which
the motion is
influenced,
either
by
the
forces
acting
on
the
bodies
or
by
the character
of
the
bodies themselves.
That
is,
the bodies are treated as
geo-
metric solids
and
not
physical
bodies. When
the
geometric
solids
are
endowed with
physical
properties,
we are led
to
a
study
of
force, energy,
momentum, etc.,
that
is,
to a
study
of
Kinetics
(Part
III).
Kinematics
deals with
the
relation
between
distance,
time,
velocity,
and acceleration.
In
order to
build
up
the
fundamental
conceptions
which are
involved
in the
study
of the
motion
of
bodies,
the kinematics
of a
particle
(material point)
will
be
treated
first. A
particle
is
a
body,
or
part
of a
body,
the
dimen-
sions
of which
are
negligible
compared
with its
range
of motion.
Bodies are
made
up
of
particles,
and the
study
of the motion
of
bodies
is
largely
a
study
of
the
motion of their
particles.
In
treating
of
the
motion of bodies
(Chapter
VIII),
only rigid
bodies
will be
considered,
and the motion
of the
rigid
bodies
will
be
restricted
to
translation, rotation,
and
plane
motion.
221
CHAPTER VII
MOTION OF A PARTICLE
108.
Types
of Motion.
The motion
of a
particle
along
a
straight
line
path
is called rectilinear motion. The
motion of
a
particle
along
a
curved
path
is called
curvilinear
motion. If
the
moving particle
describes
equal
distances
in
equal periods
of
time,
however
small,
the motion is said
to
be
uniform.
If
unequal
dis-
tances are
described
by
the
moving point
in
equal
periods
of
time,
the
motion is said
to be
non-uniform
or variable.
Thus,
if
the crank
shaft of
a steam
engine
revolves at
a
constant
FIG.
267.
number of revolutions
per
minute,
the crosshead
of the
engine
has a
non-uniform rectilinear
motion,
the
crank
pin
has
a uniform
curvilinear
motion,
and
any
intermediate
point
on
the
connecting
rod has a
non-uniform,
curvilinear
motion.
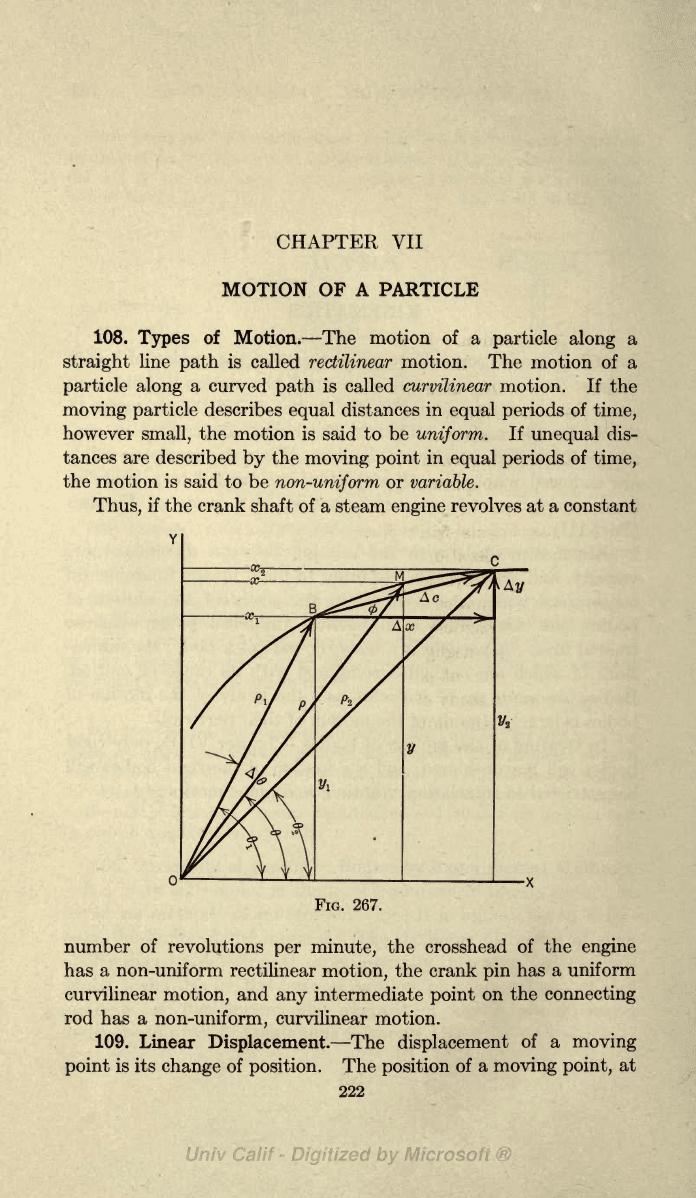
109.
Linear
Displacement.
The
displacement
of
a
moving
point
is
its
change
of
position.
The
position
of
a
moving point,
at
222

LINEAR
DISPLACEMENT
223
any
instant,
may
be
specified
in
a number
of
ways, as,
for
example,
by
stating
the
rectangular
coordinates
or the
polar
coordinates of
the
point.
Thus,
in
Fig.
267
the
position,
at
any instant,
of the
point
M
as it travels
along
the curve
from
B
to C
may
be
specified
by
the coordinates
(x, y)
or
by
(p, 0),
p
being
the
radius vector and
6 its direction
angle.
The
displacement
Ac of the
point
as it moves
from
the
position
(xi,
y\)
or
(pi,
0i)
to the
position (x2,
2/2)
or
(p2,
62)
is the
straight
line
BC,
that
is,
the
vector drawn from
B
to C.
This
displacement may
be
expressed
as the vector sum
1
of
its a;- and
^/-components.
Thus,
Ac
=
Az-B>
Ay,
in
which,
i
Ax
=
X2
xi
is the
displacement
in the
x-direction,
and
A?/
=
2/2
2/1
is the
displacement
in the
^/-direction.
The
magnitude
of Ac
may
be
expressed
algebraically
by
the
equation,
and
its direction with
the
x-axis
may
be
expressed
by
the
equation,
tan
(j>
=
~.
Ax
The
displacement
Ac
may
be
expressed
also as the
vector
dif-
ference
of the radius
vectors
to the
two
positions
of
the
moving
point.
Thus,
that
is,
Ac is the directed
distance which
must be
added to
pi
to
give
p
2
.
Or,
in other
words, p2
is
the
vector
sum of
pi
and
Ac.
1
The
symbol
-H
will
be used in this
and
succeeding
chapters,
when
dealing
with
vector
quantities,
to denote the
fact
that the
addition
of
the
quantities
is a
geometric
or
vector
addition.
Thus,
if R
is
the
resultant of
the forces
P
and
Q,
the
triangle
law
may
be
expressed
by
the
equation
R
=
P
+>
Q.
And,
if
u
and
w
are
components
of the
velocity
v,
this
fact
may
be
expressed
by
the
equation
v
=
u
4>
w.
Similarly,
the
symbol
>
will
be
used
to
denote vector
subtraction.
Thus,
t>
2
>
v\
denotes
the
geometric
or
vector
difference of
two
velocities
and
not
their
scalar
difference,
that
is,
the
difference
of their
magni-
tudes, only.

224
MOTION
OF
A
PARTICLE
Expressed algebraically, by
the law of
cosines,
the
magnitude
of
Ac
may
be
written,
Ac
=
pi
2
+p
2
2
2pip
2
cos
A0.
The
unit
of
displacement
is
any
convenient
unit of
length,
such as
the
inch, foot,
mile,
etc. It will be
noted,
however,
that
displacement
is a
directed distance
or
length,
that
is,
a
vector
quantity.
Displacements,
therefore,
may
be
combined and
resolved
according
to
the
parallelogram
(or
triangle)
law like forces
and other
vector
quantities.
It
is
important
to note that
by
one
of
the
above
equations
the
displacement
is
expressed
as the
vector
sum
of two
directed
distances,
whereas
by
the
other
equation
it is
expressed
as
the vector
difference
of two directed distances.
Fur-
ther,
one
vector
equation
is sufficient to
express
both the
magnitude
and
the
direction
of the
displacement,
whereas
two
algebraic
equa-
tions
are
required
for the same
purpose.
If the
displacement
of
the
particle
is
decreased
indefinitely,
the
point
C
(Fig.
267)
will
approach
the
point
B
and,
in
the
limit,
the
chord
Ac
becomes
coincident with the
tangent
to
the
path
at
B.
Therefore,
the
direction
of motion
of
the
particle
at
any
point
on
its
path
is
tangent
to the
path
at
that
point.
110.
Angular
Displacement.
The
angular
displacement
of a
moving
point
is the
change
in
the
angle
which the
radius
vector
to
the
point
makes
with some
fixed
reference line.
Thus,
in
Fig.
267,
the
angular
displacement,
Ad,
corresponding
to the
linear
displacement,
Ac,
is,
A0=0i
02-
The
unit
of
angular
displacement
may
be
any
convenient
angular
measure,
such
as the
degree, revolution,
radian,
etc.
It
is
important
to
note that
the
angular displacement
of a
point
depends
upon
the
reference
point
or
pole
about which
the
radius
vector
is
assumed
to revolve.
If the
point
moves on a
circular
arc,
the
radius
vector
is
usually
taken
as the
radius of the
circle
and
the
pole
is the
center of the circle.
LINEAR AND ANGULAR
DISPLACEMENTS
225
PROBLEMS
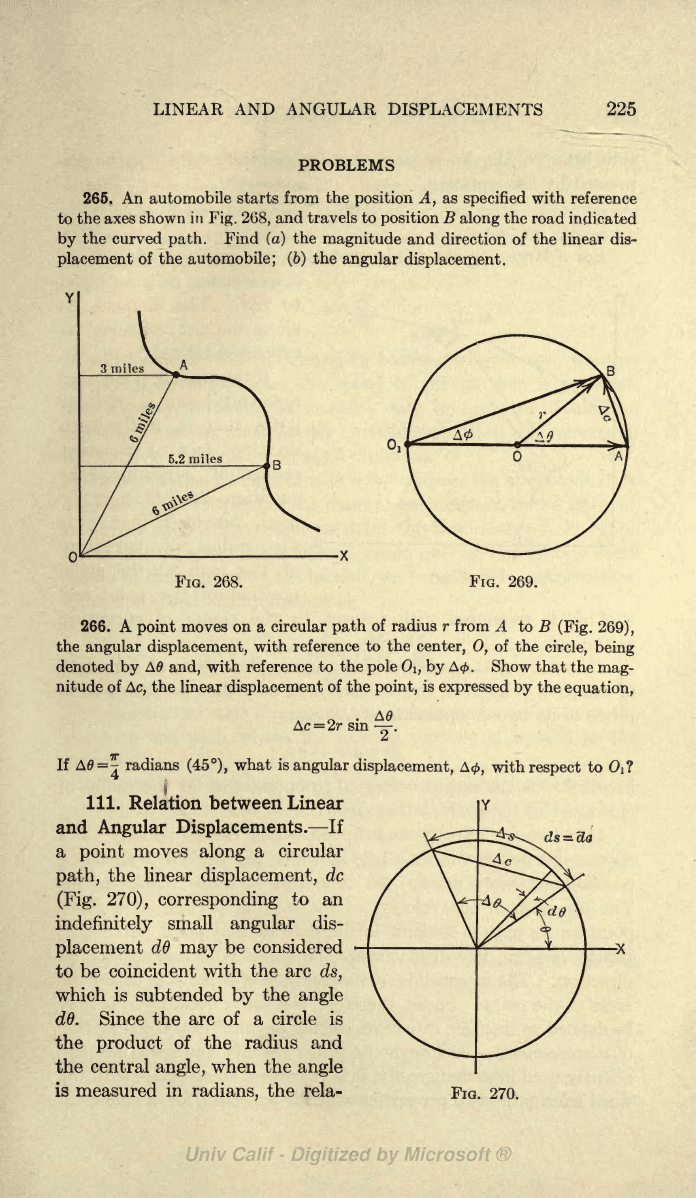
265.
An
automobile
starts
from the
position
A,
as
specified
with
reference
to
the
axes
shown
in
Fig. 268,
and
travels to
position
B
along
the
road
indicated
by
the curved
path.
Find
(a)
the
magnitude
and direction of
the
linear
dis-
placement
of
the
automobile;
(6)
the
angular
displacement.
FIG.
268.
FIG.
269.
ds-Ua
266. A
point
moves on a
circular
path
of radius
r
from
A
to B
(Fig. 269),
the
angular displacement,
with
reference
to the
center,
0,
of
the
circle,
being
denoted
by
A0
and,
with
reference to the
pole 0\, by
A<.
Show
that the
mag-
nitude
of
Ac,
the linear
displacement
of the
point,
is
expressed
by
the
equation,
A0
Ac
=
2r sin
.
If
A0=^
radians
(45),
what
is
angular
displacement,
A<,
with
respect
to
Oi?
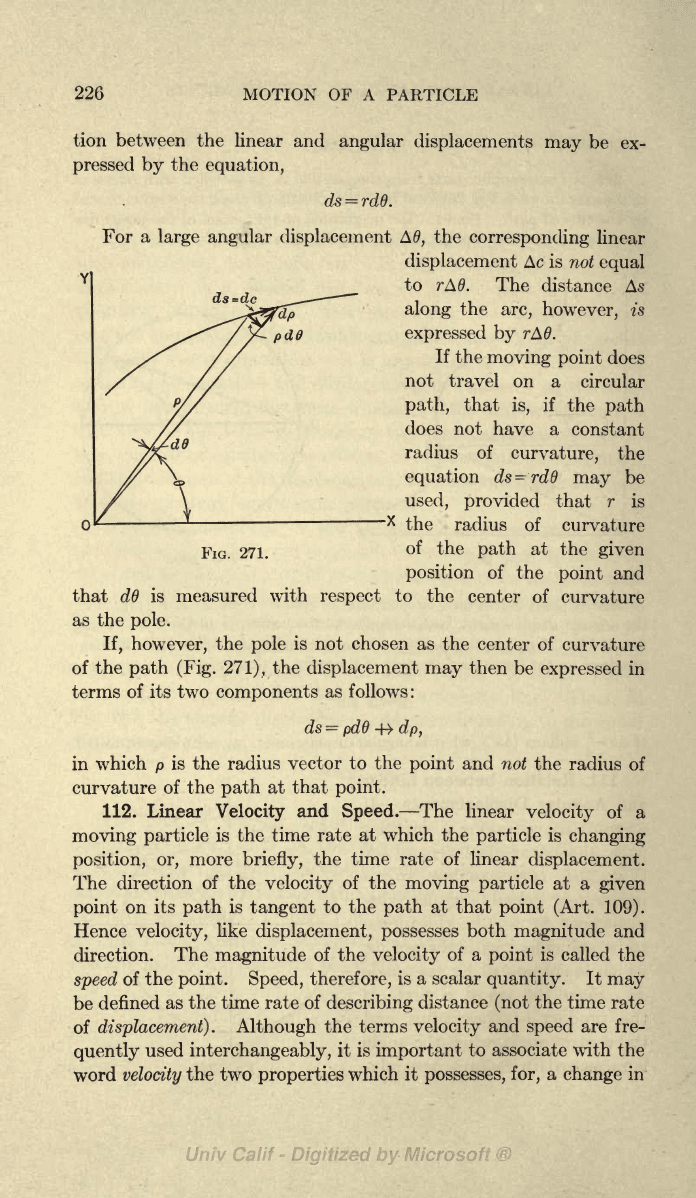
111. Relation between Linear
Y
and
Angular Displacements.
If
a
point
moves
along
a
circular
path,
the
linear
displacement,
dc
(Fig. 270),
corresponding
to an
indefinitely
small
angular
dis-
placement
dd
may
be
considered
to
be coincident with
the arc
ds,
which
is subtended
by
the
angle
dd. Since the arc of
a circle
is
the
product
of the
radius
and
the
central
angle,
when
the
angle
is measured
in
radians,
the
rela-
FIG.
270.
226
MOTION OF
A
PARTICLE
tion between
the
linear
and
angular
displacements
may
be
ex-
pressed
by
the
equation,
ds
=
rdd.
For a
large angular displacement
A0,
the
corresponding
linear
displacement
Ac is
not
equal
to rAd.
The
distance
As
along
the
arc,
however,
is
expressed
by
rAd.
If
the
moving point
does
not
travel
on a
circular
path,
that
is,
if
the
path
does
not
have a
constant
radius of
curvature,
the
equation
ds=rdd
may
be
used, provided
that
r
is
x
the
radius
of
curvature
FIG
.
271.
f
the
path
at the
given
position
of
the
point
and
that d& is
measured
with
respect
to
the
center
of
curvature
as the
pole.
If,
however,
the
pole
is
not chosen
as the
center
of
curvature
of
the
path (Fig.
271),
the
displacement
may
then be
expressed
in
terms
of its
two
components
as
follows:
ds
=
pde
+>
dp,
in which
p
is the
radius vector
to the
point
and
not the
radius of
curvature
of the
path
at that
point.
112. Linear
Velocity
and
Speed.
The
linear
velocity
of
a
moving particle
is
the
time rate at which the
particle
is
changing
position,
or,
more
briefly,
the time rate of linear
displacement.
The direction
of the
velocity
of the
moving particle
at
a
given
point
on
its
path
is
tangent
to the
path
at that
point
(Art.
109).
Hence
velocity,
like
displacement, possesses
both
magnitude
and
direction.
The
magnitude
of the
velocity
of a
point
is called the
speed
of
the
point. Speed,
therefore,
is
a scalar
quantity.
It
may
be
denned
as the
time rate of
describing
distance
(not
the
time rate
of
displacement).
Although
the terms
velocity
and
speed
are fre-
quently
used
interchangeably,
it
is
important
to
associate
with the
word
velocity
the
two
properties
which it
possesses,
for,
a
change
in

LINEAR VELOCITY
AND
SPEED
227
the
direction
of a
velocity
is
fully
as
important
in
the laws of
motion
of
physical
bodies
as
is
a
change
in the
speed.
If a
point
has a
uniform
motion
along
any
path,
the
speed
of
the
point
is
the ratio of
any distance, As,
described
by
the
point,
to the
corresponding
interval of
time,
A2.
Thus,
As
It
will be
noted that
if
a
particle
has uniform
motion,
whether
rectilinear
or
curvilinear,
the
speed
of the
particle
is
constant.
The
velocity,
however,
is
constant
only
in the
case of
uniform
rectilinear
motion,
since in
any
curvilinear motion
the
velocity
of
the
particle
continually
changes
direction.
If
the
motion of the
point
is
non-uniform,
the
above
equation
does not
give
the
speed
of the
point
at each
instant
in
the
interval,
but
gives
only
the
average speed
for the
time
interval,
At.
The
instantaneous
speed
is the
average speed
over an
indefinitely
small
period
of time
including
the
instant,
or,
expressed
in
mathematical
form,
the
speed
at
any
instant
is,
. ..As ds
The direction of
v,
as
already noted,
is
tangent
to
the
path
at the
point
on the
path
where the
moving particle
is
located at
the
instant.
The unit of
velocity may
be
any
convenient
unit
of
length
per
unit
of
time;
such
as,
foot
per
second
(ft./sec.),
mile
per
hour
(mi./hr.),
centimeter
per
second
(cm.
/sec.),
etc.
In order
to
find
the value of v
by
differentiation,
as
indicated in
equation
(1),
s
must be
expressed
algebraically
in
terms of
t.
ILLUSTRATIVE
PROBLEM
267. A
point
moves
along
a
straight
line
path
according
to
the
law,
s
=
6<
2
+4.
What
is
the
velocity
of the
point
at
the end
of
5
sec.?
Solution.
v
=^
=
J
(6*
2
+4)
=12*.
Hence,
when
=
5
sec.,
the
velocity
of the
point
is,
v
=
12X5
=
60
ft./sec.
228
MOTION OF
A
PARTICLE
PROBLEMS
268.
A
point
moves
along
a
path
according
to
the
law s
=
3t*+2t+t-
1
,
s
and
t
being
in feet
and
seconds,
respectively.
What is
the
speed
of the
point
when
<
=
2
sec.?
Ans. v
=
13.75
ft./sec.
269. A
point
moves
along
a
straight
line
according
to
the
law
v
=
<
3
+4<
2
+2.
If s =4
ft.
when
t
=
2
sec.,
what is
the value
of
s
when
t
=
3
sec.?
Ans. 8=
47.
58
ft.
113. Distance-time
Graph.
If
a
point
moves
in
such a
way
that
the
distance
s,
in
equation (1)
of
Art.
112,
cannot
be ex-
pressed
algebraical!}'
in
terms of
t,
or,
if
the
relation
between s
and
t
leads
to a
complex
equation,
the
speed
may
often
be
found
con-
veniently, by
a
graphical process,
from
the
distance-time
(s-t)
curve.
25
3|0
35
4p
t
}
seconds
FIG. 272.
Thus,
instead
of
expressing
the
relation
between
s and
t
algebra-
ically,
it is
shown
graphically by plotting
a
series
of
points,
the
rectangular
coordinates of each
point
being
simultaneously
values
of s
and t.
One
such
graph
is shown in
Fig.
272.
ds
Since the
slope
to the
(s
t)
curve is
represented
by
-^
and since
ds
V
=
-TI
(Art-
112),
then
the
slope
at
any point
of
the
(s-t) graph
represents,
to
some
scale,
the
speed
at
the
corresponding
instant.

ANGULAR VELOCITY
229
ILLUSTRATIVE
PROBLEM
270. If the curve in
Fig.
272
is the
$-t
graph
for
a
point moving
on
a
straight-line
path,
what
is the
velocity
of the
point
at the
end
of
20
sec.?
Solution:
BC
2 units
verticallv
1
Slope
at A
=-r^
=
i, rr
r
.
-r-fr~
=
AB 4 units
horizontally
2
But 1 unit
vertically
represents
50
ft. and
1 unit
horizontally
represents
5 sec.
Hence,
Unit
slope
=
=
=
10
ft.
/sec.
SGC.
Therefore
velocity
at
end
of 20
sec.
=^X10
=
5
ft.
/sec.
114.
Angular
Velocity.
The
angular velocity
of a
moving
particle
is
defined as the time rate of
angular displacement
of the
particle.
If
equal
angular
displacements
occur
in
equal
time
intervals,
however
small,
the
motion is
said
to be
uniform,
and
the
angular
velocity, co,
is
expressed
as the ratio of
any
angular
displacement,
A0,
to the time
interval, A,
during
which the
displacement
occurs.
Thus,
A0
If
unequal angular
displacements
occur in
equal
time
intervals,
the
motion
is
said to be non-uniform or
variable.
For such
motion
the above
equation gives
the
average
angular
velocity during
the
time interval
At.
When the
angular
velocity
varies
during
the
interval,
its value
at
any
instant is
the
average
velocity
over an
indefinitely
small time interval
including
the instant.
Or,
expressed mathematically,
the
instantaneous
angular
velocity
is,
.
A6
c?6
(0=
Limit
-r-=-r:.
The unit
of
angular
velocity
is
any
convenient unit
of
angular
displacement
per
unit of
time;
such
as,
degree
per
second
(deg
/sec.),
revolution
per
minute
(r.p.m.),
radian
per
second
(rad./sec.),
etc.

230
MOTION
OF A
PARTICLE
In
order to determine the
angular
velocity
from
the
above
equation,
6
must be
expressed
algebraically
in
terms
of
t,
a
require-
ment
similar
to that met in
using
the
equation
v
=
-r
in
Art.
112.
The
angular velocity may
also
be
found
from
an
angular
displace-
ment-time
(6-t) graph
by
a
graphical
method
similar
to
that
used
in
determining
the linear
velocity
in
Art. 113.
115.
Relation between
Linear and
Angular
Velocities.
In
many
problems
in
kinematics
it is convenient to
express
the
linear
velocity
of
a
point
in
terms
of its
angular
velocity.
The
relation
between
the
two
velocities
may
be found
as
follows:
Let
a
point
M move
on
a
circular
path
of radius
r
(Fig.
273a);
FIG. 273.
let
v
be the linear
velocity
of
the
point
at
any
instant
and
let
co
be
the
angular
velocity
of the
point
at the same instant.
From
definition,
ds d6
V
=
-T.
and
W
=
-T-.
dt dt
But the
distance
ds
traversed
in the time dt
may
be
expressed
in
terms
of
the
corresponding
angular
displacement
dd, by
the
equation
ds
=
rdd
(Art.
111). Therefore,
rdQ
Hence,
at
any
instant,
the linear
velocity
of
a
point
moving
on
a
