Seely F.B. Analytical Mechanics for Engineers

Подождите немного. Документ загружается.

UNIFORMLY

ACCELERATED

RECTILINEAR MOTION

251

If the

point

starts

from

rest,

in each of

the

above

equations

zero,

and

the

equations

reduce

simpler

forms.

For

freely

falling bodies,

is the acceleration due to

the

earthpull

on the

body

and is

usually

denoted

its value

being

32.2 ft. sec.

(approximately).

Further,

the

above

equations

also

apply

the motion of a

point moving

on a

curved

path

the

speed

changes uniformly

and if the

tangential

acceleration a

of the

point

used

for a.

PROBLEMS

297. Deduce

equations

(6)

and

(7)

calculus

methods,

starting

with

the

equations,

ds ,

-3-

and

-3-.

298.

Draw

speed-time

graph

for

uniformly

accelerated,

rectilinear motion

and

deduce

equations

(7)

and

(9)

299.

The

brakes are set on a train

running

at 30 mi.

per hr.,

when mi.

from a

station.

The

train slows down

uniformly, coming

to rest

the

station.

Find the

acceleration,

and

the

time

stopping.

Ans.

=0.366

ft./sec.

120

sec.

300. If

the maximum allowable

speed

an elevator

800

ft./min.

and

if it

acquires

this

speed

uniformly

distance of

ft.,

what

acceleration

does it have?

301.

train in

starting

uniformly

accelerated and attains a

speed

mi. hr.

min.

After

running

for a

certain

period

of time at this

speed,

the

brakes

are

applied

and

stops

at a

uniform rate

in 4

min.

the total

distance traveled

mi.

find the total

time. Ans.

14.5 min.

FIG.

294.

302. If the cam

(Fig.

294)

moves

the

left, changing

its

velocity uniformly

5 in.

per

sec. each

second,

what

is the acceleration

the

rod

(a)

before the

comes in

contact with the

cam;

(6)

just

comes in

contact

with

the

cam; (c)

while

contact

with

the

cam?

125.

Uniformly

Accelerated

Circular

Motion.

Many prob-

lems

involving

the

motion of

point

on a

circular

path

with

con-

stant

angular

acceleration occur in

engineering

practice.

The

relation

between

the

angular

displacement,

angular

velocity,

252 MOTION

OF A

PARTICLE

angular

acceleration,

and time

may

be deduced

manner similar

to that

used

the

preceding

article.

definition,

_Aco_

cop

. .

A^~

~7~'

.......

(1)

or,

coo+aZ,

........

(2)

which

coo

and

are the

initial and

final

angular velocities,

respectively,

corresponding

to the time

interval

simply

The

angular

displacement

A0,

simply

is the

average

angu-

lar

velocity

times the

time

interval.

Hence,

(3)

(4)

By eliminating

t from

equations

(2)

and

(4)

the

following

equation

obtained,

...

.....

(5)

uniformly

accelerated

circular

motion,

therefore,

the fol-

lowing

equations

apply

........

(6)

........

(7)

........

(8)

will be

noted that

the

above

equations

may

be derived

from

the

corresponding

set of

equations

in Art.

124

making

use

the

equations,

coor,

v=cor,

ra,

and

rd.

PROBLEMS

303. Derive

equations (6)

and

(7)

calculus

methods

starting

with the

equations,

-,.

and oc

-rr.

304. A

wheel

starting

from

rest

turns so

that

point

its

rim

has

its

angular

velocity

increased

uniformly

200

r.p.m.

sec. After

turning

for a

SIMPLE HARMONIC MOTION

253

certain

period

of time at this

speed

a brake

applied

and the

wheel

stops

at a

uniform rate in 5 sec.

If the total

number

revolutions is

3100,

find

the

total

time.

126.

Simple

Harmonic

Motion. If the

velocity

point

does

not

vary uniformly,

the acceleration

not

constant,

and hence

the

equations

of Art.

124

not

apply.

One

special

case

rectilinear motion with variable

acceleration is

simple

harmonic

motion. A

simple

harmonic

motion is

defined as the

motion

of a

point

straight

line such that the acceleration of the

point

proportional

the

distance,

of the

point

from some

fixed

origin 0,

the line and is directed toward

0. Or

expressed

mathematically,

/* \

~di?~

where

k is

constant and the

negative sign

indicates

that the

sense

of the acceleration is

opposite

to that of the

displacement

(Fig.

295),

that

is,

negative

when

x is

positive,

and

positive

when

negative.

One

example

of a

simple

harmonic motion is the

motion

weight

attached to

the

lower

end of

an elastic

spring (the upper

end

being fixed)

which is

allowed to

vibrate

freely.

The motion of the

crosshead of a

steam

engine

closely

approximates

a harmonic

motion,

the

approximation becoming

closer

FIG. 295.

FIG. 296.

as the ratio

the

length

the

connecting

rod to

that of

the

crank

increases.

The motion

oscillating

pendulum

also

approximates

closely

simple

harmonic

motion if the

arc

through

which the

pendulum

swings

small.

Further,

if a

point

moves

with constant

speed

in a

circular

path,

the

motion of

the

projection

the

point

on a

diameter of the

circle

is a

simple

harmonic

motion. This

last statement

may

proved

follows: In

Fig.

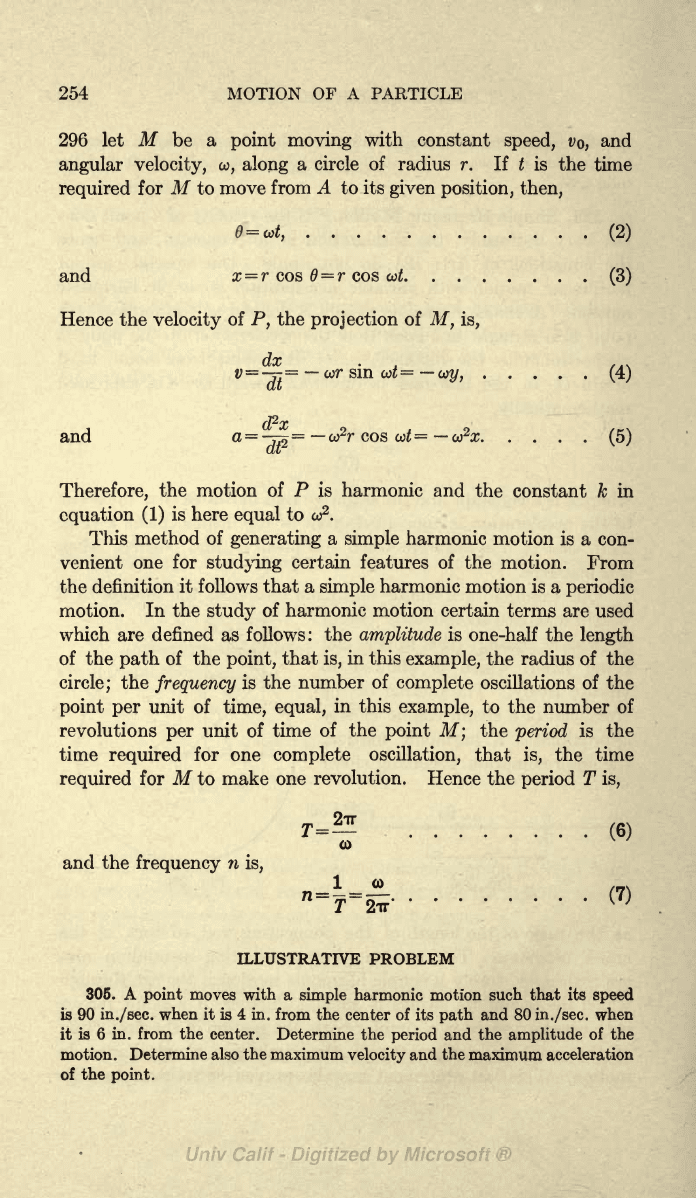
254 MOTION

OF A PARTICLE

296 let

be a

point

moving

with constant

speed, VQ,

and

angular velocity,

co, along

a circle

radius r. If t

the time

required

for

move from

to its

given position,

then,

a>t,

............

(2)

and

cos

........

(3)

Hence the

velocity

the

projection

is,

/JX

-ji=

cor sin ut=

wy,

.....

(4)

d?x

and

-jj2=

u?r cos

ut= u

.....

(5)

Therefore,

the

motion

P is

harmonic and

the

constant k in

equation

(1)

is here

equal

This

method of

generating

simple

harmonic

motion is a

con-

venient

one

for

studying

certain

features of the motion.

From

the definition

it follows that

simple

harmonic motion is

periodic

motion.

the

study

harmonic motion certain

terms are

used

which

are

defined as

follows:

the

amplitude

is one-half

the

length

of the

path

the

point,

that

is,

this

example,

the radius of the

circle;

the

frequency

the

number of

complete

oscillations of the

point

per

unit

time,

equal,

in this

example,

to the number

revolutions

per

unit of

time

the

point

;

the

period

is the

time

required

for one

complete

oscillation,

that

is,

the time

required

for

make one

revolution.

Hence the

period

is,

and the

frequency

is,

ILLUSTRATIVE PROBLEM

306. A

point

moves

with a

simple

harmonic motion

such that its

speed

is 90

in./sec.

when

it is 4

in. from the center

of its

path

and

80 in.

/sec.

when

is 6 in.

from the

center. Determine the

period

and

the

amplitude

the

motion. Determine

also the

maximum

velocity

and

the

maximum acceleration

the

point.

SIMPLE

HARMONIC

MOTION

255

Solution.

From

equation

(4)

Art.

126,

co^

6jV

(1)

Hence,

wVr*-16, (2)

and,

co W

-36

(3)

Dividing (2)

by (3),

Squaring

and

transposing,

81(r

-36)=64(r

-16).

Hence,*

17r

1892,

That

is,

Therefore,

10.56 in.

Substituting

this value

(2),

have,

rad./sec.

From

equation

(6)

of Art.

126,

Hence,

' 68SeC-

The

velocity

any

point may

found

from

equation

(1)

Since

the

velocity

is a

maximum

when

=0,

the

maximum value

is,

9.22X10.56

97.5

in./sec.

The acceleration

maximum when

the

displacement

the

point

greatest.

Hence,

using

Equation

(5)

of Art.

126,

the

maximum value of the

accelera-

tion

found

be,

(9.22)

xl0.56=897

in./sec.

306.

The

drivers

a Mikado

locomotive are 60

in.

diameter

and the

length

the

crank

is 15 in.

the

speed

of the

locomotive is 30

mi.

per

hr.,

determine

the maximum

velocity

and the

maximum

acceleration

the

cross-

head

and

piston

relative

to the

engine

frame,

assuming

that the

connecting

rod is so

long

that

the motion

the crosshead is

harmonic.

Ans. y

ft./sec.;

a=387

ft./sec.

256 MOTION

A PARTICLE

307. A

point

moves with

simple

harmonic motion the

amplitude

which

is 10

in.

If the

period

sec.,

determine

the maximum

velocity

and

maximum

acceleration.

308. The

maximum

velocity

of a

point

which has a

simple

harmonic motion

ft.

per

sec.

and the

period

sec.

Determine the

amplitude

the

motion

and

the maximum acceleration.

127.

Non-uniformly

Accelerated

Motion.

One

special

case

non-uniformly

accelerated

motion is

treated in the

preceding

article.

Each case of this

type

motion

presents

details

peculiar

itself,

but the fundamental

equations

expressing

the relations

between the

displacement, velocity,

acceleration,

and

time

'are the

same

for all

cases. For

rectilinear motion

the

equations

are,

=di<

.......

Eliminating

t from these two

equations,

have

ads

vdv

..........

(3)

By integrating equation

(1),

the

following

equations

are

obtained:

rs2 rt>

ds=

vdt,

Jsi

or,

2 -si

As=

vcf/,

(4)

and,

*dt=

(

^ds,

Jsi

or,

2 -ti

At=:

-ds

(5)

ysi

integrating equation (2),

the

following

equations

are obtained:

dv= I

adt,

Jti

or,

z>2

Av=

( adt

(6)

.Jti

NON-UNIFORMLY

ACCELERATED

MOTION

257

and,

dt=

-efo.

J* J*

or,

(7)

The

above

equations

may

also

used

the case of curvilinear

motion

the

tangential component

the

acceleration is

used,

since

=-r.

The

equations

may

also be used

only

component,

given

direction,

of the motion

considered, provided

that

s, v,

and

a in

the above

equations

replaced

the

components

displace-

ment,

velocity,

and

acceleration, respectively,

in the

given

direc-

tion.

Thus,

Vxdvx

etc.

The

relations between

the

displacement,

velocity,

acceleration,

and

the

time, may,

general,

determined

from

the above

equa-

tions

either

of two

methods;

namely, by solving

the

equations

the

methods

calculus,

graphical

method

through

the

use

distance-tune, velocity-time,

and acceleration-time

graphs.

The use of

distance-time

and

speed-time

graphs

finding

the

speed

and

acceleration,

respectively,

have

been

discussed

Arts.

113 and 119.

The more convenient

the two

methods

for

any given

problem depends

upon

the character of

the

problem.

Calculus

Method.

Equations

(1)

(7)

may

solved

the

methods

calculus

provided

that

certain

relations

between

the

variables

are

known.

Thus,

if s is

expressed

as a

function of

the

velocity

may

be obtained

from

equation

(1).

Likewise,

t; is

expressed

as a function

the time

required

for

given

displacement

may

be obtained from

equation (5),

and so

on.

ILLUSTRATIVE

PROBLEMS

309. A

point

moves

along

straight path

according

to the

law,

v=32

+4,

the

units of distance and

tune

being

the

foot and

second,

respectively.

when

what

the

value of s

when t

sec.?

258 MOTION OF

PARTICLE

Solution.

or s= C*

vd.t.

Hence.

rio r

s=| (3t*+4)dt=\t*-+4t\

=1040

ft.

310. A

point

moves

along

curved

path according

to the

law

tf v

ft./sec.

when

sec.,

what

is the

value

when

7 sec.?

Solution. First Method:

Hence,

Poidt-

(Wt+5)dt

+5<l'=

180

ft./sec

Hence,

the

gain

speed

in the

interval between the end of

the fourth second

and

the end of the

seventh

second

180 ft.

/sec. and,

therefore,

the

speed

the

end

the

seventh second

is,

180

190

ft./sec.

Second Method.

Instead of

using

a definite

integral

above,

the

problem

may

be solved

means of an

indefinite

integral

follows

\atdt

The constant

integration

may

be determined

means

of the initial

condi-

tion that

ft./sec.

when

4 sec.

Hence, using

this

condition,

the

above

equation becomes,

5X4

+5X4+C.

Therefore,

C= 90 and

the

velocity

any

time

may

obtained from

the

equation,

sec.,

the

corresponding

value

is,

5X7H-5X7-90

190

ft./sec.

311.

point

starts from

rest at

the

vertex

of the

parabola

and

moves

along

the

parabola

according

the

law

and

y being

feet

and t in

seconds.

Find the

magnitude

the

velocity

and

of the

acceleration of

the

point

the end of

2 sec.

NON-UNIFORMLY

ACCELERATED

MOTION

259

Solution.

-The

axial

components

the

velocity

and

of the

acceleration

may

be found

from

the

equations

of Art. 122.

Thus,

---

i ft

/sec

- when

(=2 se

Therefore,

and,

312. The

length

of the

crank, OA,

a steam

engine (Fig.

297)

denoted

and

the

length

of the

connecting rod, BA,

is denoted

I. If

the

crank

FIG. 297.

turns

with

constant

angular

velocity, o>,

determine

the

velocity

and the

accel-

eration of

the

crosshead,

terms

r, I,

co*and

the

angle,

which the

crank

makes

with

the

horizontal.

Solution.

The

displacement,

of the

crosshead

from

its

extreme

position

may

be determined

in terms of

and

sincej

ut^s

may

also

expressed

function of

since

w is

known.

Thus,

But,

and,

l-\-r

I cos

<f>

cos

1 sin

<j)=r

sin

260

MOTION OF

PARTICLE

By expanding

the

last

expression

and

using

only

the

first

two

terms of

the

expansion,

since

generally

small,

the

last

equation

may

written,

with

degree

approximation,

cos

Therefore,

sin

Hence,

and,

sin

-r=r

sin

-jT-1 r

sin

COSd

-dt

=rw (sin

6-\

sin

cos 01

==rw

CQS

0_|__

(

Cog2

COS

0+y

COS 20

0-sin

0)1

Graphical

Method. The

solution of

equations (4)

and

(6)

the aid of

speed-time

and

acceleration-time

graphs

will now

shown. The

speed-time graph

has

already

been

defined

(Art.

119).

The

acceleration-time

graph

is a

curve,

the

coordinates

any

point

of which

represent

simultaneous

values of the

accel-

eration

and

the

time.

The

acceleration

used

is either

the total

acceleration

if the

point

has

rectilinear

motion,

the

tangential

acceleration

the

point

moves on

curved

path.

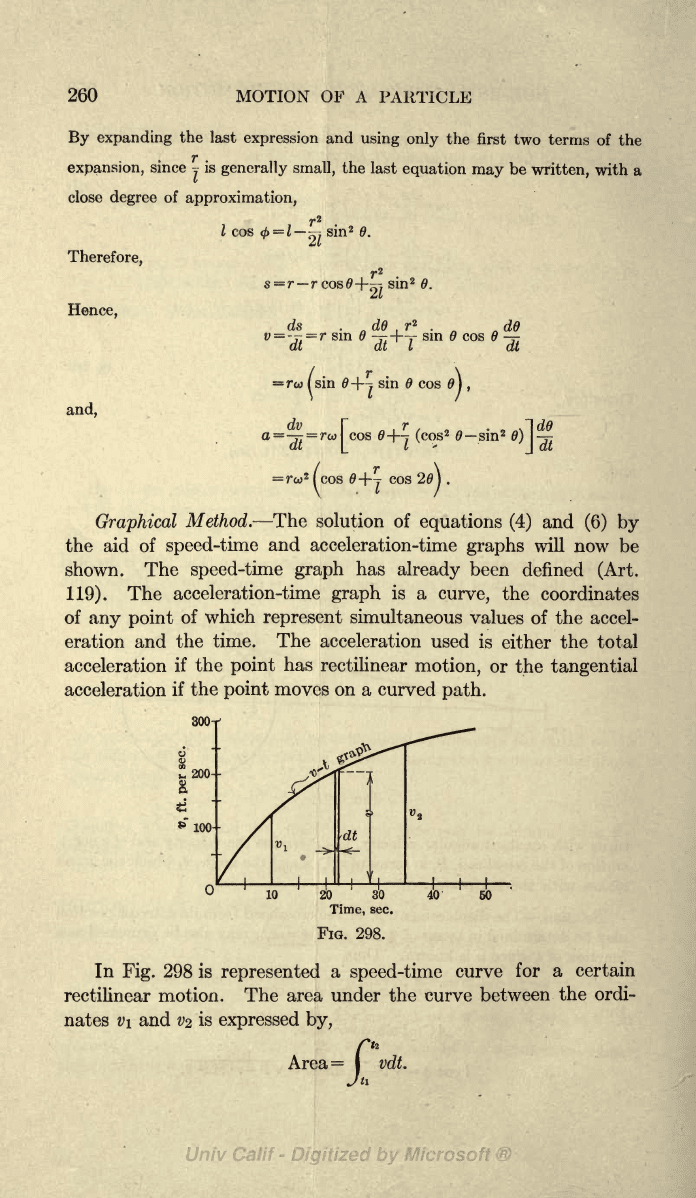
300

Time,

sec.

FlG. 298.

Fig.

298

represented

speed-time

curve

for

certain

rectilinear motion.

The

area

under the curve

between

the ordi-

nates

and

expressed by,

Area

vdt.

Jti