Seely F.B. Analytical Mechanics for Engineers
Подождите немного. Документ загружается.

NON-UNIFORMLY ACCELERATED
MOTION
261
Xd
vdt.
Therefore,
the
area
under
the
speed-time
curve
represents,
to some
scale
(depending
on the
scales used in
plotting
the
graph),
the
dis-
tance traveled
during
the
time
interval
tz
ti,
corresponding
to
a
change
in the
speed
from
v\
to
v%.
ILLUSTRATIVE
PROBLEM
313. The
speed-
time
curve
for the rectilinear motion
of
a certain
point
is
shown
in
Fig.
298.
The
scales are: 1
in.,
vertically,
equals
200
ft./sec.,
and
1
in., horizontally, equals
20
sec.
If
the
area
under
the curve
between
t
=
10
and
t
=
35 is
1.2
sq.
in.,
how far
does the
point
travel
in the interval?
Solution.
I
sq.
in.
represents
200
ft./sec. X20
sec. =4000 ft.
Hence,
the
distance
=1.2X4000
=
4800
ft.
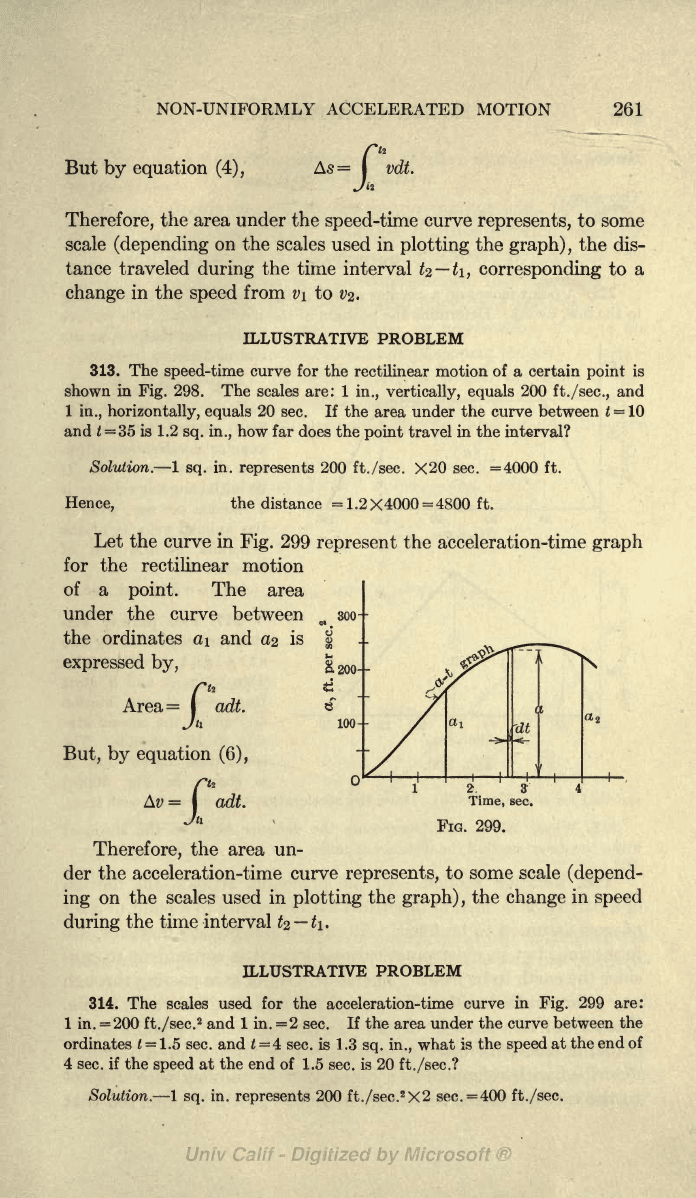
Let the
curve in
Fig.
299
represent
the acceleration-time
graph
for the
rectilinear
motion
of
a
point.
The
area
under the
curve
between 3
the
ordinates
a\
and
expressed
by,
Area= I
adt.
is
i
-.
a
200-
-
100-
-
But,
by equation
(6),
T"*
'dt
2.
3
Time,
sec.
a
2
FIG.
299.
Therefore,
the
area un-
der the acceleration-time
curve
represents,
to some scale
(depend-
ing
on the scales
used
in
plotting
the
graph)
,
the
change
in
speed
during
the time interval
h
ti.
ILLUSTRATIVE
PROBLEM
314. The scales
used
for the
acceleration-time
curve
in
Fig.
299
are:
1
in.
=
200
ft./sec.
2
and
1
in.
=2
sec.
If the area
under
the
curve between
the
ordinates
t
=
1.5
sec. and
t
=
4
sec. is 1.3
sq. in.,
what
is
the
speed
at
the end
of
4
sec.
if
the
speed
at
the end
of
1.5
sec.
is 20
ft./sec.?
Solution.
1
sq.
in.
represents
200
ft./sec.
2
X2
sec.
=400
ft./sec.
262
MOTION
OF A PARTICLE
Hence,
Av
=
1.3X400
=
520ft./sec.
Therefore,
v*
=20+520
=
540
ft./sec.
PROBLEMS
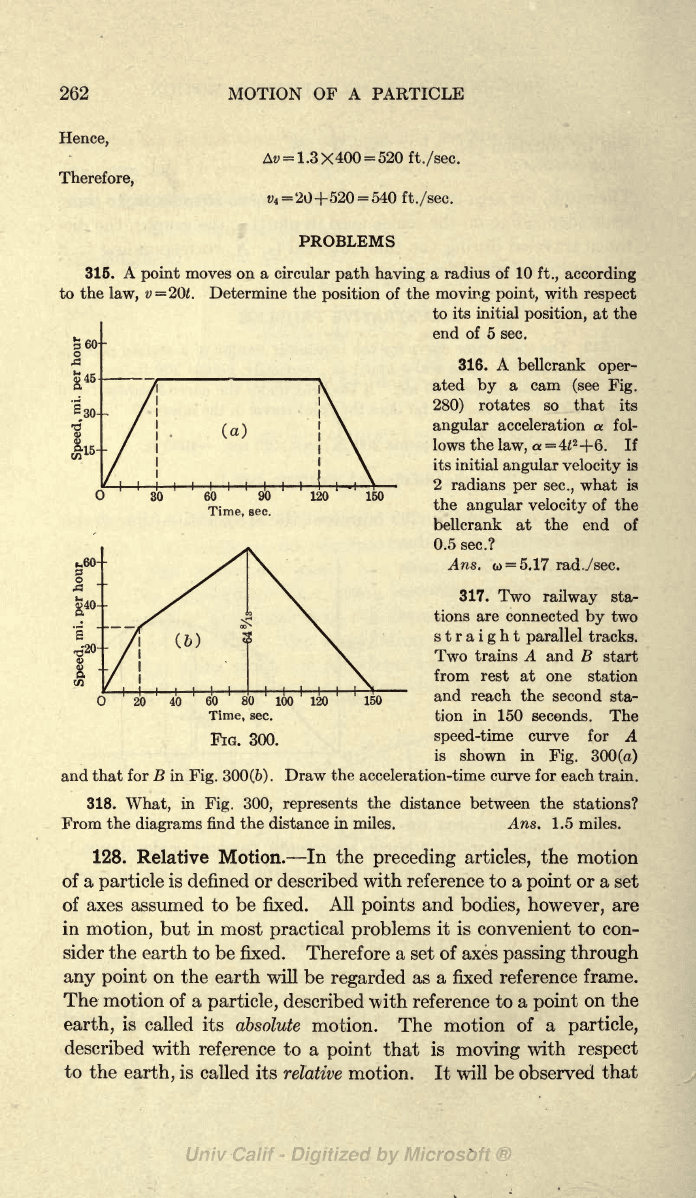
315. A
point
moves
on a circular
path having
a radius of
10
ft.,
according
to
the
law,
v
=
20.
Determine
the
position
of
the
moving
point,
with
respect
to its initial
position,
at
the
360
-
45
B
30-
-
15-
-
(a)
60
90
Time,
sec.
120 150
end
of
5
sec.
316. A
bellcrank
oper-
ated
by
a cam
(see
Fig.
280)
rotates so
that
its
angular
acceleration a
fol-
lows
the
law,
a
=
4t
2
+6
.
If
its
initial
angular velocity
is
2
radians
per
sec.,
what is
the
angular
velocity
of the
bellcrank
at the end
of
0.5
sec.?
Ans, w
=
5.17
80
100 120
Time,
sec.
FIG. 300.
317.
Two
railway
sta-
tions are connected
by
two
straight parallel
tracks.
Two
trains
A
and B
start
from
rest
at one
station
and reach the
second
sta-
tion
in 150
seconds.
The
speed-tune
curve for
A
is
shown
in
Fig.
300(a)
and that
for
B in
Fig.
300(6).
Draw
the
acceleration-time
curve
for
each
train.
318.
What,
in
Fig. 300,
represents
the
distance between the
stations?
From
the
diagrams
find
the
distance
in
miles.
Ans. 1.5
miles.
128.
Relative
Motion. In the
preceding
articles,
the motion
of a
particle
is defined or described with
reference
to
a
point
or
a set
of
axes
assumed to be
fixed. All
points
and
bodies,
however,
are
in
motion,
but in most
practical problems
it
is
convenient
to
con-
sider the earth
to be fixed.
Therefore a set of
axes
passing
through
any
point
on the
earth
will be
regarded
as a
fixed reference
frame.
The
motion of
a
particle,
described
with
reference to
a
point
on the
earth,
is
called
its
absolute
motion. The motion of
a
particle,
described
with
reference
to a
point
that
is
moving
with
respect
to
the
earth,
is
called its
relative motion. It
will
be observed
that
RELATIVE
MOTION
263
the
absolute motion
of a
particle
is its
relative
motion with
respect
to
the
earth.
In
considering
the motion
of
two
moving
particles,
the
motion
of one
particle
relative
to
the other
particle
is
often
required.
The relation
between
the
absolute
and
relative motions
of
two
particles
A and
B
(assumed,
for
convenience,
to be
moving
in a
plane)
may
be
stated
by
the
following
important
theorem.
The
absolute
displacement,
velocity,
or acceleration
of
A
is the
geometric
or vector
sum
of
the
relative
displacement, velocity,
or accel-
eration, respectively,
of
A
with
respect
to
B and
the absolute
dis-
placement, velocity,
or
acceleration,
respectively, of
B.
This theorem
may
be
expressed
in the form of
equations
as
follows
:
a
A
=
a
A
or
V
A
=
V
A
-*V
B
.
B
or
a
A
=
a
A
^CLB
r
FIG.
301.
FIG.
302.
where
S
A
denotes
the
absolute
displacement
of
A,
S
B
denotes
the
absolute
displacement
of
B,
and
S
A
denotes the
relative
displace-
H
ment
of A
with
respect
to B
}
and
similiarly
for
velocities
and
accelerations.
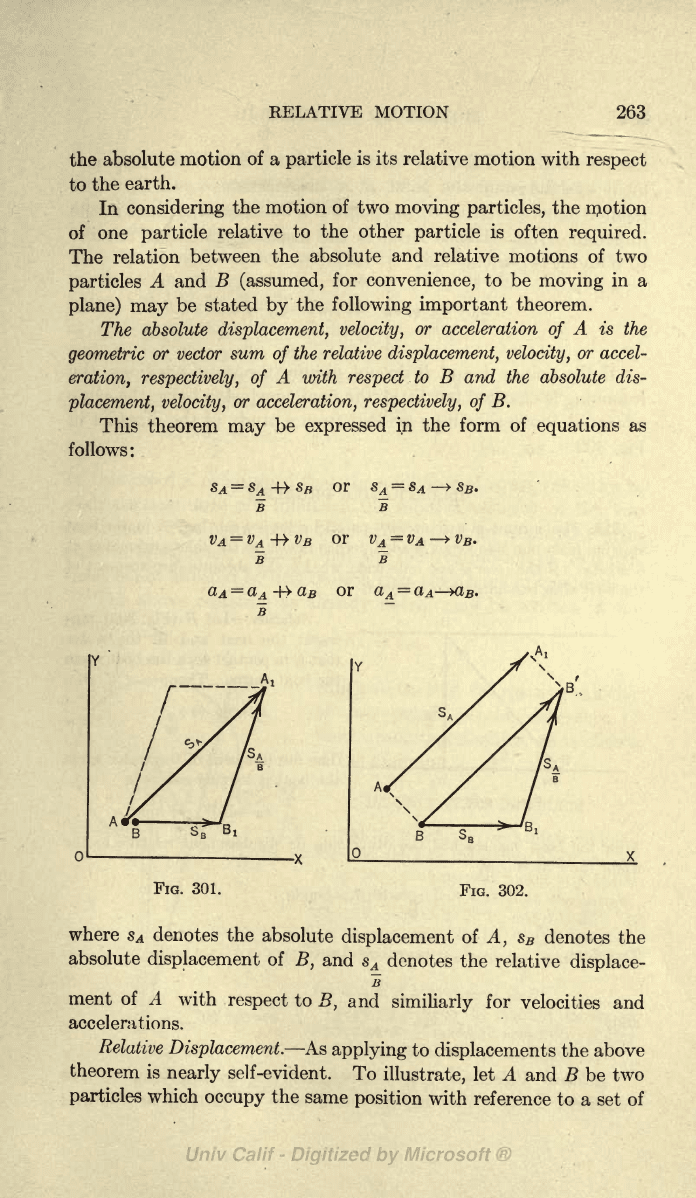
Relative
Displacement.
As
applying
to
displacements
the above
theorem
is
nearly
self-evident.
To
illustrate,
let A
and
B
be
two
particles
which
occupy
the
same
position
with
reference to
a
set
of

264
MOTION OF
A
PARTICLE
axes
as
shown
in
Fig.
301. Let the
point
A
be
given
a
displace-
ment
s
A
=
AAi
and the
point
B,
a
displacement
s
B
=
BBi.
The
point
A
moves
relative
to the
point
B
a distance
B\A\
and
in
the
direction
B\A\.
Hence
B\A\
is the
displacement
of
A
relative
to
B and
it
is evident
that,
or
If the
points
A and
B
do not
occupy
the same
positions,
the
reasoning
is
changed
but
little,
the final
conclusion
being
the same
as
stated
above as will
be evident from
a
study
of the
diagram
in
Fig.
302.
ILLUSTRATIVE PROBLEM
319. The current
in
a
river
with
parallel
sides is 4
mi./hr.
A motor boat
starting
from one
side
keeps
headed
perpendicular
to the sides and moves at
6
mi./hr.
If
the river
is
one
mile
wide,
what
is the
absolute
displacement
of
the
boat
after
reaching
the other
side?
Solution.
Let B
(Fig.
303)
rep-
resent
the
boat and W the water
that is in
contact
with the
boat when
the
boat starts.
Then,
The
displacement
of the
water
while
the boat is
moving
across
is,
After the
boat
has
reached
the other
side its
displacement
relative
to the
water
(now
at
Wi)
is,
=WiBi
=
l
mile.
Therefore,
s
B
=
l-fr
i\/(l)t+(f)*-1.2
miles,
and,
tan 0=
=
f
.'.
0=56 20'.
s
w
Relative
Velocity.
The above
theorem,
as
applying
to the
velocities
of two
moving particles, may
be
proved
as
follows:
RELATIVE MOTION
265
Let
A and
B
(Fig.
304)
be
any
two
moving
particles (assumed
in
a
plane),
let the
absolute
velocity,
V
A}
of
A
be
represented
by
and
let
BB
i
represent
the
abso-
lute
velocity,
V
B)
of
B.
Let
a
velocity
equal
to
V
B
but reversed
in
direction
be
given
to
each
point.
The
point
B will then be
at rest
and,
hence,
the
resulting
velocity
of the
point
A
is the
velocity
of
A relative
to
B.
Hence,
-V
B
^
V
B
it is
evident
from
the
diagram
that,
_ B,
"!
'
FIG.
304.
In
this
proof
it
is assumed
that the
additions
of
equal
velocities
to
each
particle
does
not
influence
the relative
velocity
of
the
two
particles.
This
assumption
is
in
accord with
an
important
prin-
ciple
in
kinematics,
namely,
that
the
relative
motion
of
two
par-
ticles
is
not affected
by any
motion
that
they
have
in
common.
The
above
equation
as
already
noted,
may
be written in the
form
FIG. 306.
which
states
that
the
relative
velocity
of
two
points
is
the
difference of
their
absolute
velocities,
as is
shown
in
the
diagram.
ILLUSTRATIVE
PROBLEM
320. In
the
shaper
mechanism
shown in
Fig. 305,
let A be
the
sliding
block
and
let
B
be the
point
on
the
rocker
arm
OiBM
which
is
coincident
with
A
at the
instant.
The
distance
OOi
is
20
in. and
is
30. If
co
=
20
r.p.m.
and
r
=
\
ft.,
find
VB,
the
abso-
lute
velocity
of
B,
and
VA,
B
the
relative
velocity
of A
with
respect
to
B.
Solution.
Since
the
block
A
moves on
a
circular
arc
at
constant
speed,
its
velocity
is
given
in
magnitude
by
the
equation,
.20X2*
1
~~60~
X
2
ft./sec.

266
MOTION OF
A
PARTICLE
and its
direction is
perpendicular
to
r,
as
shown in
Fig.
305. The
direction of
the
absolute
velocity
of B
is
perpendicular
to
OiBM
and its
magnitude
is
unknown.
Likewise,
the
direction of the
velocity
of
A
relative to
B
is
known
since
it is
along (parallel
to)
the
rocker
arm.
By applying
the
equation,
B
the
magnitudes
of
V
A
and
VB
are determined
by
the
intersection
of the lines
~B
that
represent
their
directions.
By
scaling
off the
magnitudes,
the
following
values are
found,
v
A
=0.70ft./sec.
and
v
B
=
0.79
ft./sec.
PROBLEMS
321.
Two trains A
and
B
travel on
parallel
straight
tracks.
The
speed
of
A is 40
mi./hr.
and that
of B
is 50
mi./hr.
in
the
same
direction. What
is
the
velocity
of A relative
to
?
Of B
relative
to A?
FIG. 307.
322.
A
train
A travels with a
velocity
VA
=40
mi./hr.
and another train
B
travels
with
a
velocity
v.e
=
50
mi./hr.
in the directions
shown
in
Fig.
306.
What
is the
magnitude
and the
direction of
the relative
velocity
of
B
with
respect
to
A1
Ans.
55.4
mi./hr.
323. In
Fig. 307,
let
A be
a
block
which
revolves about
at a
constant
angular
velocity
co
=
30
r.p.m.
and
let B be
the
point
on the
arm
0\BM
coin-
cident
with
A at
the
instant.
If r
=
OA
-9
in.,
OOi
=3
in.,
and
=
45,
find
the
absolute
velocity
of B.
Relative
Acceleration.
In
order
bo
prove
the
above
theorem
as it
relates
to
accelerations,
it will
be assumed that
the
relative accel-

RELATIVE MOTION
267
eration
of
two
particles
is
not
changed
if
equal
additional
accel-
erations
be
given
the two
particles.
This is
analogous
to
the
assumption
made in the
discussion of relative velocities.
Hence,
if
equal
velocities and
accelerations
be
given
to
each of two
particles
the relative
motion
of
one
with
respect
to the other
will
not be
changed.
Consider,
then,
two
particles
A
and
B
which
move
along
paths
as
indicated
in
Fig.
308.
Assume
that a veloci-
ty
equal
and
opposite
to the
velocity
of
B(
v
B
)
is
im-
posed
on each
particle
(not
shown at
A
in
Fig.
308).
Assume
also that acceler-
ations
equal
to the acceler-
ation
of B but of
opposite
sense are
imposed
on
the
two
particles.
This
will
not
change
the relative
motion
of
A
with
respect
to
B.
Imposing
a
velocity
of
VB
and an acceleration
of
a
B
on the
particle
B
will
make its
position fixed,
and
hence
the acceleration
of
A with
respect
to
B will be
the
same
as the
absolute acceleration of
A. The
acceleration
of
A, however,
is
now
the vector sum
of
a
A
and
a
B
and
hence,
a
A
=--
a
A
+
a
B
,
FIG. 308
or,
Hence,
the relative acceleration of one
point
with
respect
to a
second
point
is the
vector difference of the
absolute
accelerations
of the two
points.
ILLUSTRATIVE PROBLEM
324.
Two friction
disks
(Fig.
309)
rotate with constant
angular
velocities.
Let
A
and
B be
points
on the
circumferences of the
large
and small
disks,
respectively.
If
coi
=
40
r.p.m.,
n
=
9
in.,
and
r
2
=
3
in.,
find the
magnitude
and
the
direction of the acceleration of A
relative to
B.
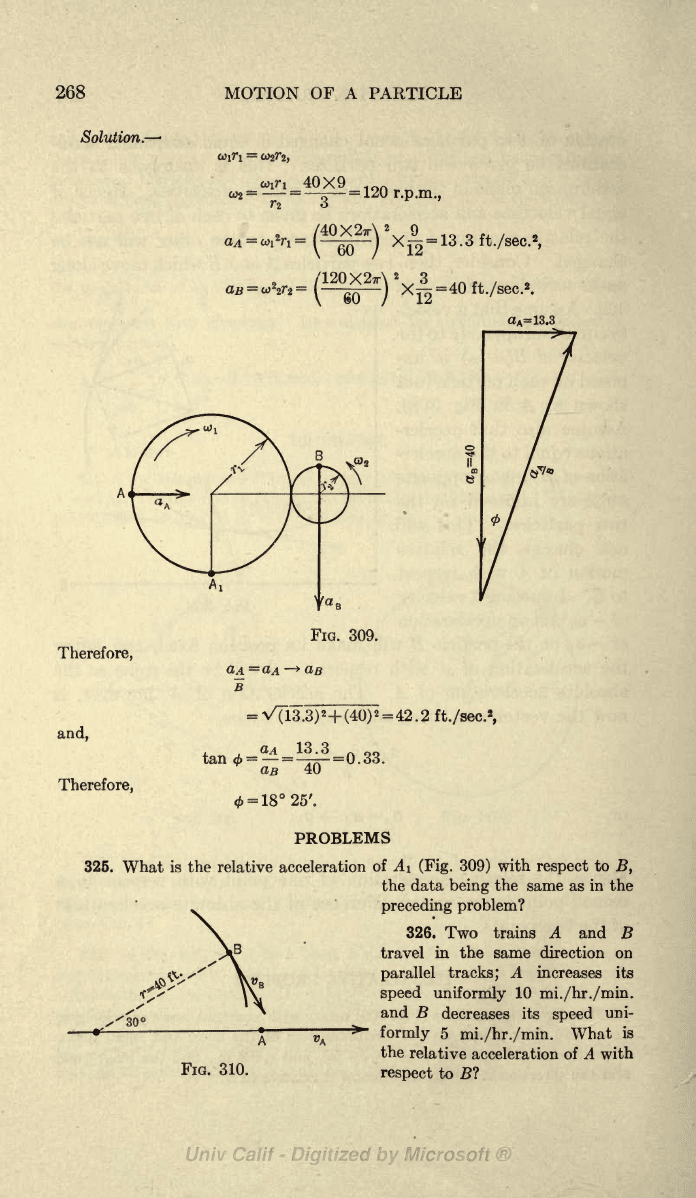
268
Solutions
MOTION
OF A
PARTICLE
Therefore,
and,
Therefore,
coin
40X9
10
_
co
2
=
=
3
=
120
r.p.m.,
a
A
=l3.3
aA=dA-*aB
B
V(i3.3)
2
+(40)
2
=
42.2 ft.
/sec.
2
,
as
41
=
18 25'.
PROBLEMS
325.
What
is the
relative acceleration
of
Ai
(Fig.
309)
with
respect
to
B,
the
data
being
the
same
as in the
preceding
problem?
326. Two trains
A
and B
travel
in the same direction
on
parallel
tracks;
A
increases
its
speed
uniformly
10
mi./hr./min.
and
B
decreases
its
speed
uni-
formly
5
mi./hr./min.
What
is
the
relative
acceleration
of A
with
respect
to ?
FIG. 310.

COMPONENTS
OF
ACCELERATION
269
327.
An
automobile, A,
is
traveling
on a
straight road,
increasing
its
speed
at
the rate
of 300
ft./min./sec.
when
in
the
position
shown
(Fig. 310).
At
the same
time
another
automobile, B,
is
traveling
in
a
circular
path
increasing
its
speed
at
the
rate of
5
ft.
/sec.
2
Its
speed
when
in the
position
shown
is
VB
=
12
mi./hr.
and the radius of
the
circular
path
is 40
ft.
What
is
the
rela-
tive
acceleration of
A
with
respect
to
B
?
Ans.
12.3 ft.
/sec.
2
129. Transverse and
Radial
Components
of
Acceleration. In
addition
to the x-
and
^/-components
and the n-
and
^-components
of the acceleration
of
a
particle
(Art.
122),
the
transverse and
radial
(T
and
R)
components
are sometimes
convenient to use.
The
transverse direction
is
perpendicular
to the
radius vector
(b)
FIG. 311
drawn from
any
point
taken
as the center or
pole,
and
the
radial
direction
is
along,
or
parallel to,
the radius vector
(see
Fig.
311).
The T-
and
/^-components may
be
derived
by
the
application
of
Theorems
I
and
II
(Art. 118).
In
Fig.
311
(a)
let
m
represent
a
particle
moving
on a fixed
path.
Let be
any
center or
pole
(not
the
instantaneous
center of
rotation,
Art.
135).
Then,
the
total
velocity, v,
of
the
particle
may
be
replaced
by
the two com-
ponents
V
T
and V
R
.
Thus,
Fig.
311
(a)
indicates
that in
general
at
any
instant
VT
is
changing
in
magnitude
and also in
direction,
and
that,
VR
is
changing
in
magnitude
and also
in
direction.
Hence
there
will be four
components
of the
acceleration: two
of

270 MOTION
OF A PARTICLE
the
type
-7-' and two
of the
type
vu,
as
follows
(shown
in
Fig.
CLL
3116)
:
<
--
parallel
to
'
being
the rate
of
change
of
the
magnitude
of V
R
.
(2)
V
R
W
perpendicular
to
V
R
,
being
the rate of
change
of V
R
due
to the
change
in
its direction
only.
/o\
dv
T
d(up) dp
. da)
parallel
to
VT
the rate
of
change
of the
magnitude
of
V
T
.
fy
(4)
Vrco
=
co
2
p
=
-^-
perpendicular
to V
T
,
being
the rate of
p
change
of
V
T
due to a
change
in its
direction
only.
The
T- and
/^-components
of the total acceleration
are,
then
(Fig. 26),
r
J
rpr=-
-^(p
2
co),
at at
p
at
dv
R
d
2
p
2
=
'~
=
~~
130. Coriolis' Law.
It is
convenient
to
consider the motion
of a
point
of
a
body
as
being
generated by
a motion of the
point
along
a
path
(line)
as
the
path
moves.
Thus,
in
plane
motion
of
a
rigid body
the
motion of
any point
in
the
body
may
be
con-
sidered
as a
combination of a motion
along
a
path
and a
motion
due to
a translation
of the
path.
If
a
point
moves
along
a
path
as
the
path
is
translated,
the
acceleration
of the
point
is the vector sum of the
acceleration
relative
to the
path
and the acceleration of
the
point
of
the
path
which
is
coincident with the
point
at
the instant
(or
of
any point
of
the
path
since the
path
is
translated).
This
leads to the
same
expression
for the
acceleration of
the
point
as was
obtained
in
Art.
128,
as will be shown later.
If,
however,
a
point
moves
along
a
path
as the
path rotates,
the
acceleration of the
point
is obtained
as the
vector sum
of
three
component
accelerations.
The relation between these
three
component
accelerations
and the total
acceleration is
known
as
Coriolis'
law,
which
may
be
derived
by
use
of
the
theorems of
Art,
118
as follows:
